下载文档原格式
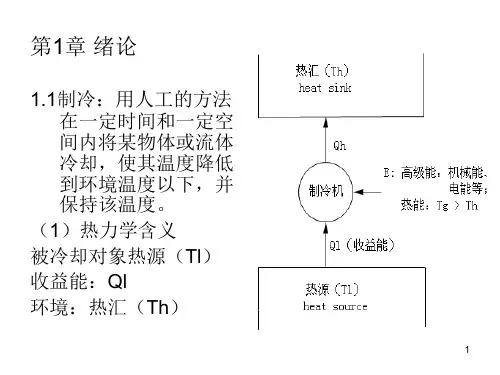
第1章低温热力学基础1.1 实际气体的性质1.1.1 理想气体状态方程气态工质处于平衡状态时，其基本状态压力P、比容υ与温度T之间有一定的关系，这一关系若用数学式表示一般可写成：f（p, υ, T）=0 (1-1) 称为气体的状态方程或特性方程。
克拉贝隆方程是最简单的状态方程，其形式如下：pυ=RT (1-2) 式中，R为气体常数，其值随气体种类而变。
在国际单位制中，当压力及比容的单位分别用kPa及m3/kg时，R的单位为kJ/(kg.K)。
式(1-2)是根据早期的由实验建立的波义尔定律（1662年）及查理定律（1787年）导出的。
它与气体动力论提出的理想气体的物理模型所得的结论完全一致，所以也称为理想气体状态方程。
理想气体状态方程由于没有考虑气体分子间的相互作用力和气体分子本身德体积，因而不能准确地表示实际气体的状态特性，实验证明，当压力较低时（例如在大气压力附近及以下），实际气体的性质同按式（1-2）的计算结果还比较接近，而当压力升高时，却表现出了明显的偏高，这种偏离可用比例pυ/RT来说明。
对于理想气体，由式（1-2）可知，比值pυ/RT=1。
但对于实际气体，比值pυ/RT式一个变量，它随气体的种类及压力和温度而变。
随着温度的降低，实际气体的pυ/RT同理想气体的偏离越来越大，在低温技术领域内，温度比较低，压力又比较高（同常压比），因而所研究的工质一般都不能当作理想气体来进行计算。
因此，必须对实际气体的性质进行分析和讨论。
1.1.2 范德瓦尔方程为了较准确地描述实际气体的特性，自上世纪以来，很多学者根据不同的观点和论据，提出了很多形式的状态方程，其中最有理论价值的是范德瓦尔方程。
范德瓦尔方程是在1873年提出的，它具有如下的形式：（p+a/υ2）(υ-b)=RT （1-3）式中，a及b是范德瓦尔常数，对于一些常见气体，其值列于表1-1中。
表1-1中的数值是对1kmol而言，在检用时应予注意。
11M th d f f i ti1.1 Methods of refrigeration1.1.1 Refrigeration by phase change1.1.2 Refrigeration by gas expansion113Refrigeration by Ranque Hilsch effect 1.1.3 Refrigeration by Ranque-Hilsch effect 1.1.4 Refrigeration by Peltier effect第一节制冷的方法相变制冷一、相变制冷二、气体膨胀制冷五、去磁制冷六、稀释制冷三、气体涡流制冷四、热电制冷七、热声制冷冷八、激光制冷1.1.3 Refrigeration by Ranque-Hilsch effect(1931, French) 兰克管(1931F h)9/16/201121.1.3 Refrigeration by Ranque-Hilsch effect(1931F h)(1931, French)兰克管Flow inletsHot outlet(130℃)Cold outlet (-50℃)OrificeValve9/16/2011311M th d f f i ti1.1 Methods of refrigeration1.1.1 Refrigeration by phase change1.1.2 Refrigeration by gas expansion113Refrigeration by Ranque Hilsch effect 1.1.3 Refrigeration by Ranque-Hilsch effect 1.1.4 Refrigeration by Peltier effect第一节制冷的方法相变制冷一、相变制冷二、气体膨胀制冷五、去磁制冷六、稀释制冷三、气体涡流制冷四、热电制冷七、热声制冷冷八、激光制冷1.1.4 Refrigeration by Peltier effect(1934, French) 热电制冷(1934F h)Seebeck effect(塞贝克1821):发现在两种不同金属组成的闭合线路中，如果两接触点的温度不同，有一个电动势存在。
