结构力学——静定多跨梁资料
- 格式：pdf
- 大小：1.89 MB
- 文档页数：18
下载文档原格式
合集下载
2多跨静定梁
ql
ql
ql
11ql / 4 ql / 2
1 ql 2
ql / 2
ql
5ql / 4
ql / 2
例: 作内力图
ql
q
ql
l l ql
2l q
4l
2l
l
l ql
1 ql 2
内力计算的关键在于: ql ql 正确区分基本部分和附 ql 属部分. 2ql ql / 2 ql 熟练掌握单跨梁的计算.
2 2
多跨 简支梁
练习: 作弯矩图
P
l
l/2
l/2
l
M
M
l
练习: 作弯矩图
q
1 2 ql 2
l
l
M M M
l l
练习: 作弯矩图
P
1 Pl 4 1 Pl 4
P 1 Pl
4
l/2
q
l/2
l/2
1 2 ql 4
l/2
l/2
ql 1 ql 2 4
l/2
l/2
l/2
l/2
l/2
多跨静定梁
(multi-span statically determinate beam)
关键在正确区分基本部分和 附属部分 熟练掌握截面法求控制截面 弯矩 熟练掌握区段叠加法作单跨 梁内力图
二.多跨静定梁
通过整体平衡 条件无法求所 有反力
1.多跨静定梁的组成
附属部分--不能独 立承载的部分。
基本部分--能独立 承载的部分。
面的负弯矩的绝对值相等,确定铰D的位置.
q
A
D
l
B
C
l
x
RD
q
B
结构力学第3章 多跨静定梁课件
（1）选定外力的不连续点（集中力作用点、集中力偶作用点、分布荷载的
始点和终点）为控制截面，首先计算控制截面的弯矩值； （2）分段求作弯矩图。当控制截面间无荷载时，弯矩图为连接控制截面弯
矩值的直线；当控制截面间存在荷载时，弯矩图应在控制截面弯矩值作出的
直线上在叠加该段简支梁作用荷载时产生的弯矩值。 例：利用叠加法求作图示梁结构的内力图。
P=8kN q=4 kN/m
A
P=8kN D 4
MG
r
17 B
7
QG 7 MGr 7
23
G
QG
17 9 A + C D E F G _ B
G
m=16kN.m B
8
7
Q图（kN）
§3-3
多跨静定梁
一、多跨静定梁的几何组成特性
多跨静定梁常用于桥梁结构。从几何组成特点看，它的组成可以区分 为基本部分和附属部分。
如图所示梁，其中 AC 部分不依赖于其它部分，独立地与大地组成一个
几何不变部分，称它为基本部分；而CE部分就需要依靠基本部分AC才能保 证它的几何不变性，相对于AC 部分来说就称它为附属部分。
A
C E A E C
C
E
A
（a）
（b）
（c）
二、分析多跨静定梁的一般步骤
对如图所示的多跨静定梁，应先从附属部分CE开始分析：将支座C 的支反 力求出后，进行附属部分的内力分析、画内力图，然后将支座 C 的反力反向 加在基本部分AC 的C 端作为荷载，再进行基本部分的内力分析和画内力图， 将两部分的弯矩图和剪力图分别相连即得整个梁的弯矩图和剪力图 。
分析下列多跨连续梁结构几何构造关系，并确定内力计算顺序。 q P
A B C D E F G H
始点和终点）为控制截面，首先计算控制截面的弯矩值； （2）分段求作弯矩图。当控制截面间无荷载时，弯矩图为连接控制截面弯
矩值的直线；当控制截面间存在荷载时，弯矩图应在控制截面弯矩值作出的
直线上在叠加该段简支梁作用荷载时产生的弯矩值。 例：利用叠加法求作图示梁结构的内力图。
P=8kN q=4 kN/m
A
P=8kN D 4
MG
r
17 B
7
QG 7 MGr 7
23
G
QG
17 9 A + C D E F G _ B
G
m=16kN.m B
8
7
Q图（kN）
§3-3
多跨静定梁
一、多跨静定梁的几何组成特性
多跨静定梁常用于桥梁结构。从几何组成特点看，它的组成可以区分 为基本部分和附属部分。
如图所示梁，其中 AC 部分不依赖于其它部分，独立地与大地组成一个
几何不变部分，称它为基本部分；而CE部分就需要依靠基本部分AC才能保 证它的几何不变性，相对于AC 部分来说就称它为附属部分。
A
C E A E C
C
E
A
（a）
（b）
（c）
二、分析多跨静定梁的一般步骤
对如图所示的多跨静定梁，应先从附属部分CE开始分析：将支座C 的支反 力求出后，进行附属部分的内力分析、画内力图，然后将支座 C 的反力反向 加在基本部分AC 的C 端作为荷载，再进行基本部分的内力分析和画内力图， 将两部分的弯矩图和剪力图分别相连即得整个梁的弯矩图和剪力图 。
分析下列多跨连续梁结构几何构造关系，并确定内力计算顺序。 q P
A B C D E F G H
§3-2多跨静定梁
§3-2 静定多跨梁
一、定义及常用形式
多跨静定梁：由若干根梁用铰连接而成、用来跨越几个相连跨度的静定梁。
无铰跨和两铰跨交替 出现
除第一跨外，其余各 跨皆有一铰
前两种方式组合
二、几何构造特点及受力特点
主梁或基本部分 1、几何组成 次梁或附属部分 不依赖其它部分的存在，本身就 能独立地承受荷载并能维持平衡 的部分 需要依赖其它部分的支承才可以 承受荷载并保持平衡的部分
F -0.25 -0.25
0.5 0.5 -0.25 -0.25
Step3:绘制内力图。
FPa
D A B C
0.25 Pa F
E F
0.5FP
A B C D E F
0.5FPa
0.25FP
FP
M图
FQ图
【例3.3 】
试求铰D的位置，使负弯矩峰值与正弯矩峰值相等
q
A
q
B C A D B
q
C
l−x
D
x
例：作内力图
1、几何组成分析： 2、分层法：将附 属部分的支座反力 反向指其基本部分， 就是加于基本部分 的荷载； 3、内力使梁正负最大弯矩的绝对值相等，试确定铰B、E的位置。 欲使梁正负最大弯矩的绝对值相等，试确定铰B 的位置。
1、几何组成分析： 2、内力分析：分 层法：将附属部分 的支座反力反向指 其基本部分，就是 加于基本部分的荷 载； 3、内力图：各单跨梁的 内力图连在一起
FRB
FRC
q (l − x) 2 q (l − x) x qx 2 M 跨中 = ，M B = + 8 2 2
得：
M 跨中 = M B
⇒
q (l − x) 2 q (l − x) x qx 2 = + 8 2 2
一、定义及常用形式
多跨静定梁：由若干根梁用铰连接而成、用来跨越几个相连跨度的静定梁。
无铰跨和两铰跨交替 出现
除第一跨外，其余各 跨皆有一铰
前两种方式组合
二、几何构造特点及受力特点
主梁或基本部分 1、几何组成 次梁或附属部分 不依赖其它部分的存在，本身就 能独立地承受荷载并能维持平衡 的部分 需要依赖其它部分的支承才可以 承受荷载并保持平衡的部分
F -0.25 -0.25
0.5 0.5 -0.25 -0.25
Step3:绘制内力图。
FPa
D A B C
0.25 Pa F
E F
0.5FP
A B C D E F
0.5FPa
0.25FP
FP
M图
FQ图
【例3.3 】
试求铰D的位置，使负弯矩峰值与正弯矩峰值相等
q
A
q
B C A D B
q
C
l−x
D
x
例：作内力图
1、几何组成分析： 2、分层法：将附 属部分的支座反力 反向指其基本部分， 就是加于基本部分 的荷载； 3、内力使梁正负最大弯矩的绝对值相等，试确定铰B、E的位置。 欲使梁正负最大弯矩的绝对值相等，试确定铰B 的位置。
1、几何组成分析： 2、内力分析：分 层法：将附属部分 的支座反力反向指 其基本部分，就是 加于基本部分的荷 载； 3、内力图：各单跨梁的 内力图连在一起
FRB
FRC
q (l − x) 2 q (l − x) x qx 2 M 跨中 = ，M B = + 8 2 2
得：
M 跨中 = M B
⇒
q (l − x) 2 q (l − x) x qx 2 = + 8 2 2
多跨静定梁
目录
静定结构的内力\多跨静定梁 【例12.1】 试绘制图a所示多跨静定梁的内力图。 【解】 1）绘层次图。
如图b所示。 2）求支座反力。
FCx=0， FCy=－20kN， FDy=100kN ， FAx=0 ， FAy=48kN， FBy=12kN
3）绘内力图。各段梁 的约束反力求出后，可以 分别绘出各段梁的内力图。 如图（图d、e）所示。
目录
静定结构的内力\多跨静定梁 第二种如图b所示，其特点是第一跨无中间铰，其余各跨各有一
个中间铰。在图b中，AB梁是基本部分，而BC梁、CD梁则是附属部 分。图c为层次图。
目录
静定结构的内力\多跨静定梁
1.3 多跨静定梁的内力计算和内力图绘制
通过层次图可以看出力的传递过程。因为基本部分直接与基础 相连接，所以当荷载作用于基本部分时，仅基本部分受力，附属部 分不受力；当荷载作用于附属部分时，由于附属部分与基本部分相 连接，故基本部分也受力。因此，多跨静定梁的约束力计算顺序应 该是先计算附属部分，再计算基本部分。即从附属程度最高的部分 算起，求出附属部分的约束力后，将其反向加于基本部分即为基本 部分的荷载，再计算基本部分的约束力。当求出每一段梁的约束力 后，其内力计算和内力图的绘制就与单跨静定梁一样，最后将各段 梁的内力图连在一起即为多跨静定梁的内力图。
跨静定梁的承载能力大于系
列简支梁，在同荷载的情况
下可节省材料。
ห้องสมุดไป่ตู้
图2
目录
建筑力学
建筑力学
静定结构的内力\多跨静定梁
多跨静定梁
1.1 工程实例和计算简图
多跨静定梁是由单跨静定梁通过铰加以适当连接而成的结构。 如下面的公路桥梁和檩条梁。
目录
静定结构的内力\多跨静定梁
静定结构的内力\多跨静定梁 【例12.1】 试绘制图a所示多跨静定梁的内力图。 【解】 1）绘层次图。
如图b所示。 2）求支座反力。
FCx=0， FCy=－20kN， FDy=100kN ， FAx=0 ， FAy=48kN， FBy=12kN
3）绘内力图。各段梁 的约束反力求出后，可以 分别绘出各段梁的内力图。 如图（图d、e）所示。
目录
静定结构的内力\多跨静定梁 第二种如图b所示，其特点是第一跨无中间铰，其余各跨各有一
个中间铰。在图b中，AB梁是基本部分，而BC梁、CD梁则是附属部 分。图c为层次图。
目录
静定结构的内力\多跨静定梁
1.3 多跨静定梁的内力计算和内力图绘制
通过层次图可以看出力的传递过程。因为基本部分直接与基础 相连接，所以当荷载作用于基本部分时，仅基本部分受力，附属部 分不受力；当荷载作用于附属部分时，由于附属部分与基本部分相 连接，故基本部分也受力。因此，多跨静定梁的约束力计算顺序应 该是先计算附属部分，再计算基本部分。即从附属程度最高的部分 算起，求出附属部分的约束力后，将其反向加于基本部分即为基本 部分的荷载，再计算基本部分的约束力。当求出每一段梁的约束力 后，其内力计算和内力图的绘制就与单跨静定梁一样，最后将各段 梁的内力图连在一起即为多跨静定梁的内力图。
跨静定梁的承载能力大于系
列简支梁，在同荷载的情况
下可节省材料。
ห้องสมุดไป่ตู้
图2
目录
建筑力学
建筑力学
静定结构的内力\多跨静定梁
多跨静定梁
1.1 工程实例和计算简图
多跨静定梁是由单跨静定梁通过铰加以适当连接而成的结构。 如下面的公路桥梁和檩条梁。
目录
静定结构的内力\多跨静定梁
结构力学静定多跨梁例题
结构力学静定多跨梁例题摘要：1.结构力学静定多跨梁的概念和特点2.静定多跨梁的受力分析方法3.静定多跨梁受力分析的例题解答4.静定多跨梁在实际工程中的应用正文：一、结构力学静定多跨梁的概念和特点结构力学是研究结构在各种外力作用下的受力、变形和破坏规律的学科。
静定多跨梁是结构力学中的一个重要概念，它是指由多个跨度相同的简支梁通过节点连接而成的结构体系。
静定多跨梁具有以下特点：1.结构简单，受力明确2.节点反力可求，便于计算3.可以通过节点法进行受力分析二、静定多跨梁的受力分析方法静定多跨梁的受力分析主要包括以下几个步骤：1.确定受力分析模型：根据题目所给条件，确定多跨梁的跨数、梁材料、截面形状等参数。
2.列方程求解：根据静定多跨梁的受力特点，列出方程组，求解支座反力和杆件内力。
3.检验强度：计算得出的内力是否符合材料强度和结构安全要求。
三、静定多跨梁受力分析的例题解答本文提供的静定多跨梁受力分析例题如下：题目：图示静定多跨梁，d 右侧截面剪力fa,2knb,-2knc,1knd,-1kn。
解答：1.根据题目所给条件，列出方程组：fa + 2knb - 2knc + 1knd - 1kn = 02.求解方程组，得出支座反力和杆件内力。
3.检验强度：计算得出的内力是否符合材料强度和结构安全要求。
四、静定多跨梁在实际工程中的应用静定多跨梁在实际工程中有广泛的应用，如桥梁、桁架等结构。
通过静定多跨梁的受力分析，可以有效地指导工程设计和施工，确保结构的安全和稳定。
总之，结构力学静定多跨梁的受力分析对于理解结构的受力特性和保证结构的安全具有重要意义。
《静定多跨梁》课件
2023-2026
ONE
静定多跨梁
KEEP VIEW
REPORTING
CATALOGUE
目 录
• 静定多跨梁的基本概念 • 静定多跨梁的受力分析 • 静定多跨梁的强度与稳定性 • 静定多跨梁的设计与优化 • 静定多跨梁的施工与维护
PART 01
静定多跨梁的基本概念
定义与特性
定义
静定多跨梁是指在两个或多个支撑点 之间，由一根连续的梁所组成的结构 。
施工准备
在施工前，需要做好现场勘查 、设计图纸审核、材料采购等 工作，确保施工顺利进行。
梁体预制
在预制场或施工现场，按照设 计要求制作梁体，确保尺寸、 强度等符合规范要求。
附属设施安装
根据设计要求，安装栏杆、排 水设施等附属设施，提高桥梁 的安全性和使用功能。
静定多跨梁的维护与保养
日常检查
定期保养
建筑结构
在建筑结构中，静定多跨 梁可以作为楼面、屋面、 平台等的承重结构，提供 稳定和安全的支撑。
机械制造
在机械制造领域，静定多 跨梁可以作为机器部件的 支撑结构，如机床床身、 压力机框架等。
PART 02
静定多跨梁的受力分析
受力分析的基本原理
平衡原理
静定多跨梁在受力时，各 部分受到的力矩和力均达 到平衡状态。
特性
静定多跨梁具有稳定的结构特性，能 够承受多个方向的力和弯矩，且在受 力时不会发生变形或移动。
静定多跨梁的类型
根据支撑点的数量
静定多跨梁可分为双跨梁、三跨梁、 四跨梁等。
根据梁的形状
静定多跨梁可分为直线形梁、弧形梁 、折线形梁等。
静定多跨梁的应用场景
01
02
03
桥梁工程
ONE
静定多跨梁
KEEP VIEW
REPORTING
CATALOGUE
目 录
• 静定多跨梁的基本概念 • 静定多跨梁的受力分析 • 静定多跨梁的强度与稳定性 • 静定多跨梁的设计与优化 • 静定多跨梁的施工与维护
PART 01
静定多跨梁的基本概念
定义与特性
定义
静定多跨梁是指在两个或多个支撑点 之间，由一根连续的梁所组成的结构 。
施工准备
在施工前，需要做好现场勘查 、设计图纸审核、材料采购等 工作，确保施工顺利进行。
梁体预制
在预制场或施工现场，按照设 计要求制作梁体，确保尺寸、 强度等符合规范要求。
附属设施安装
根据设计要求，安装栏杆、排 水设施等附属设施，提高桥梁 的安全性和使用功能。
静定多跨梁的维护与保养
日常检查
定期保养
建筑结构
在建筑结构中，静定多跨 梁可以作为楼面、屋面、 平台等的承重结构，提供 稳定和安全的支撑。
机械制造
在机械制造领域，静定多 跨梁可以作为机器部件的 支撑结构，如机床床身、 压力机框架等。
PART 02
静定多跨梁的受力分析
受力分析的基本原理
平衡原理
静定多跨梁在受力时，各 部分受到的力矩和力均达 到平衡状态。
特性
静定多跨梁具有稳定的结构特性，能 够承受多个方向的力和弯矩，且在受 力时不会发生变形或移动。
静定多跨梁的类型
根据支撑点的数量
静定多跨梁可分为双跨梁、三跨梁、 四跨梁等。
根据梁的形状
静定多跨梁可分为直线形梁、弧形梁 、折线形梁等。
静定多跨梁的应用场景
01
02
03
桥梁工程
结构力学3.2多跨静定梁
G
FYG
2 2 4 5.33kN M F 0 FYG 3 Y 0 FYF 5.33 4 1.33kN
§3-3
CEF部分：
C
3kN -1.33kN F D E
多跨静定梁
3 2 1.33 4 0.23 M C 0 FYE 3
FYC
FYE
E
D
A
C B
F
支撑关系图
§3-3
基 本 部 分
多跨静定梁
附 属 部 分E
D
附 属 部 分
F
A
C B
支撑关系图
我们把ABC称为：基本部分，把CDE、EF称为： 附属部分。显然作用在附属部分上的荷载不仅使附 属部分产生内力，而且还会使基本部分也产生内力。 作用在基本部分上的荷载只会使基本部分产生内力。
F
L-x
D
解：以x表示铰E到B支座、铰F到C支座的距离。 a、层次图
A E B C F D
§3-3
b、求反力 AE、FD部分：
多跨静定梁
c、求弯矩
q( L x) FYA FYE FYF FYD 2
q( L x) qx 2 M B Mc x 2 2
根据要求：M中=MB=qL2/16
1kN/m A
B 4m 1kN
3kN
D E F G
2kN/m
H 1m 1m
C
1m 2m
1m 1m
3m
§3-3
解：a、层次图
1kN/m A 1kN C 1m
多跨静定梁
3kN D 2m E F 3m G 2kN/m H
B
4m
1m 1m
1m 1m
结构力学静定多跨梁例题
结构力学静定多跨梁例题
静定多跨梁是结构力学中的经典问题之一，它涉及到梁的静力
学分析和梁的内力计算。
静定多跨梁例题通常包括确定多跨梁的支
座反力、梁的内力分布以及梁的变形等内容。
首先，我们需要明确多跨梁的几何形状、材料特性和受力情况。
假设我们有一跨数大于等于3的多跨梁，每个支座处有竖向力和弯
矩作用，梁的自重也需要考虑在内。
在解题过程中，我们通常采用
梁的受力平衡方程和变形方程来进行分析。
通过这些方程，我们可
以求解出支座反力、梁的内力分布和梁的变形情况。
其次，针对静定多跨梁的例题，我们可以采用不同的方法进行
求解，比如方法一般有，图解法、力法、位移法等。
在实际应用中，我们可以根据具体情况选择最合适的方法进行分析。
在解题过程中，我们需要考虑梁的受力特点，比如悬臂梁、悬
臂梁等不同类型的受力情况。
同时，还需要考虑梁的材料特性，比
如弹性模量、截面形状和尺寸等因素对梁的受力性能的影响。
此外，静定多跨梁的例题还涉及到梁的内力分布，包括弯矩和
剪力的计算。
这需要我们对梁的受力特点有深入的理解，同时也需要灵活运用力学知识进行分析。
总之，静定多跨梁的例题是结构力学中重要的内容，通过深入分析和综合运用力学知识，我们可以解决这类问题并且加深对结构力学原理的理解。
04-讲义：3.3 多跨静定梁
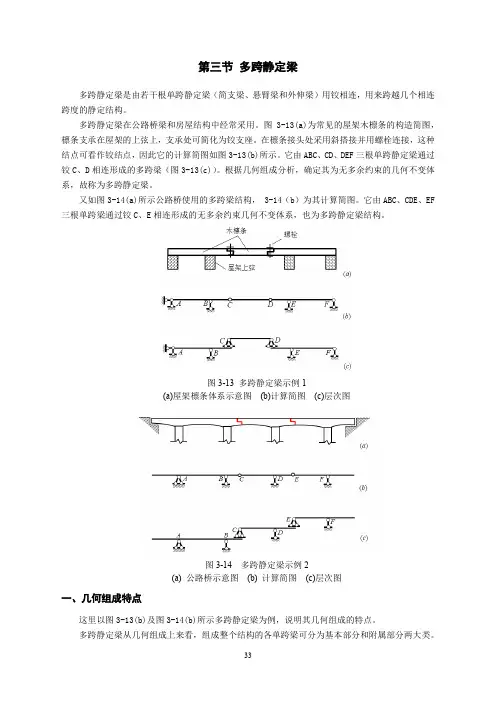
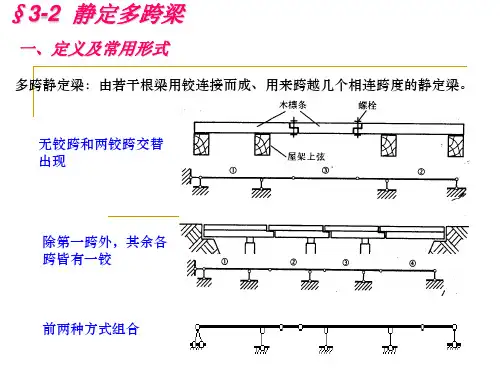
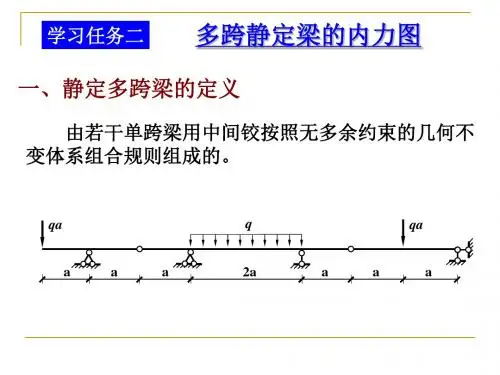
第三节多跨静定梁多跨静定梁是由若干根单跨静定梁（简支梁、悬臂梁和外伸梁）用铰相连，用来跨越几个相连跨度的静定结构。
多跨静定梁在公路桥梁和房屋结构中经常采用。
图3-13(a)为常见的屋架木檩条的构造简图，檩条支承在屋架的上弦上，支承处可简化为铰支座。
在檩条接头处采用斜搭接并用螺栓连接，这种结点可看作铰结点，因此它的计算简图如图3-13(b)所示。
它由ABC、CD、DEF三根单跨静定梁通过铰C、D相连形成的多跨梁（图3-13(c)）。
根据几何组成分析，确定其为无多余约束的几何不变体系，故称为多跨静定梁。
又如图3-14(a)所示公路桥使用的多跨梁结构， 3-14（b）为其计算简图。
它由ABC、CDE、EF 三根单跨梁通过铰C、E相连形成的无多余约束几何不变体系，也为多跨静定梁结构。
图3-13 多跨静定梁示例1(a)屋架檩条体系示意图(b)计算简图(c)层次图图3-14 多跨静定梁示例2(a) 公路桥示意图(b) 计算简图(c)层次图一、几何组成特点这里以图3-13(b)及图3-14(b)所示多跨静定梁为例，说明其几何组成的特点。
多跨静定梁从几何组成上来看，组成整个结构的各单跨梁可分为基本部分和附属部分两大类。
基本部分是指本身能独立维持平衡的部分，而需要依靠其他部分的支承才能保持平衡的部分称为附属部分。
因此，多跨静定梁从几何组成上来看见，是先固定基本部分，再固定附属部分。
如图3-13(b)中多跨静定梁，梁段ABC 由三根不平行也不交于一点的三根链杆固定于基础，它不依赖于其他部分就能独立维持自身的几何不变性；梁段DEF 虽然只有两根链杆与基础相连，但在竖向荷载作用下自身也能维持平衡。
因此，梁段ABC 、梁段DEF 均为基本部分。
而梁段CD 支承于前述两个基本部分上，它必须依赖于梁段ABC 、梁段DEF 才能保持几何不变，所以是附属部分。
为了更清楚地表明多跨静定梁中各梁段之间的支承关系，常把基本部分画在附属部分的下方，附属部分画在基本部分的上方，如图3-13(c)所示，称为层次图。
4第三章 静定梁和多跨静定梁
第三章 静定梁和多跨静定梁
第四节 多跨静定梁
本章教学目标：
3.1掌握利用直梁法进行多跨静定梁的轴
力图、剪力图绘制方法，掌握利用静定平 面刚架弯矩图的绘制方法绘制多跨静定梁 的弯矩图。
本章要解决的问题
1.多跨静定梁分为哪两部分，支座力计算
从哪里入手？ 2.多跨静定梁轴力图、剪力图绘制口诀 是什么？
3.多跨静定梁弯矩图绘制从哪里入手？基
骤是什么？ 4.绘制所布置作业的轴力图、剪力图、弯 矩图。
第四节 多跨静定梁
一、多跨静定梁的组成
基本部分：不依赖于其他部分，能单独存在的部分
附属部分：依赖于其他部分，不能单独存在的部分
结构层次图
二、多跨静定梁的计算
支座反力计算：先计算附属部分，后计算基本部分
计算步骤：
1）找出结构的基本部分及附属部分，计算结构的支座 反力； 2）利用“从左至右，上上下下”的规则绘制多跨梁剪 力图； 3）利用刚架弯矩图作法绘制多跨梁弯矩图。
例题：
P42 例3-3 有力偶作用时的处理
从左至右 顺下逆上
例题：P42 例3-4 EF为最附属部分，应先算
15qa/8
21qa/8
4qa/3
qa/6
题：P42 例3-5 定向支座的处理
例题：P42 例3-6 必要时须计算铰的内力来分析弯矩
总 结
第四节 多跨静定梁
本章教学目标：
3.1掌握利用直梁法进行多跨静定梁的轴
力图、剪力图绘制方法，掌握利用静定平 面刚架弯矩图的绘制方法绘制多跨静定梁 的弯矩图。
本章要解决的问题
1.多跨静定梁分为哪两部分，支座力计算
从哪里入手？ 2.多跨静定梁轴力图、剪力图绘制口诀 是什么？
3.多跨静定梁弯矩图绘制从哪里入手？基
骤是什么？ 4.绘制所布置作业的轴力图、剪力图、弯 矩图。
第四节 多跨静定梁
一、多跨静定梁的组成
基本部分：不依赖于其他部分，能单独存在的部分
附属部分：依赖于其他部分，不能单独存在的部分
结构层次图
二、多跨静定梁的计算
支座反力计算：先计算附属部分，后计算基本部分
计算步骤：
1）找出结构的基本部分及附属部分，计算结构的支座 反力； 2）利用“从左至右，上上下下”的规则绘制多跨梁剪 力图； 3）利用刚架弯矩图作法绘制多跨梁弯矩图。
例题：
P42 例3-3 有力偶作用时的处理
从左至右 顺下逆上
例题：P42 例3-4 EF为最附属部分，应先算
15qa/8
21qa/8
4qa/3
qa/6
题：P42 例3-5 定向支座的处理
例题：P42 例3-6 必要时须计算铰的内力来分析弯矩
总 结