应用统计学时间序列习题及答案

第五章时间序列练习题1、时间序列中，数值大小与时间长短没有关系的是（C）。

A.平均数时间序列B.时期序列C.时点序列D.相对数时间序列2、采用几何平均法计算平均发展速度的依据是（ A ）。

A.各年环比发展速度之积等于总速度B.各年环比发展速度之和等于总速度C.各年环比增长速度之积等于总速度D.各年环比增长速度这和等于总速度3、下列数列中哪一个属于动态数列（D）。

A.学生按学习成绩分组形成的数列B.职工按工资水平分组形成的数列C. 企业按产量多少形成的分组数列D. 企业生产成本按时间顺序形成的数列4．由两个等时期数列相应项对比所形成的相对数动态数列算序时平均数的基本公式是（D）。

A.n aa∑=B.ncc∑=C.∑--++++++=ffaafaafaaannn11232121222D.∑∑=bac5．间隔不等的间断时点数列的序时平均数的计算公式是（ C ）。

A.n aa∑=B.12121121-++++=-naaaaannC.∑--++++++=ffaafaafaaannn11232121222D.∑∑=fafa6．累计增长量与逐期增长量的关系是（ A ）A.逐期增长量之和等于累计增长量B.逐期增长量之积等于累计增长量C.累计增加量之和等于逐期增长量D.两者没有直接关系7．环比发展速度与定基发展速度之间的关系是（ C ）。

A.定基发展速度等于环比发展速度之和B.环比发展速度等于定基发展速度的平方根C.环比发展速度的连乘积等于定基发展速度D.环比发展速度等于定基发展速度减18．某现象前期水平为1500万吨，本期水平为2100万吨，则增长1%的绝对值为( C )。

A.1500万吨B.600万吨C.15万吨D.2100万吨9．已知各期的环比增长速度为9%、8%、10%，则定基增长速度为( C )。

A.9%×8%×10% B.9%×8%×10%-100%C.109%×108%×110%-100%D.109%×108%×110%10．某车间6月、7月、8月、9月末职工人数分别为250人、265人、280人和290人，该公司三季度月职工平均人数为( D )。

计算题：34323*22562584*22582603*22602502*2250254++++++++++=a = (人计算（1）第一季度该店平均每月商品销售额（2）第一季度平均销售员人数（3）第一季度平均每个销售员的销售额 （4）第一季度平均每月每个销售员的销售额 解：（1）商品销售额为时期总量指标时间序列，4月不属一季度，该数据无用3280350300++=a = （万元）（2) 销售员人数是时点总量指标时间序列，间断间隔相等，用首尾折半法，4月初人数相当于3月末人数，这个数据有用32424045240+++=b = （人） （3）32424045240280350300+++++==平均人数一季度销售额c = （万元/人） （4）3324240452403028350300c d =+++++==平均人数一季度月平均销售额 = （万元/人）要求：（1）根据表中资料 ，计算并填制表中空白栏指标（2）计算该地财政收入的这几年的年平均发展水平、年平均增长水平（水平法）和平均增长速度（几何平均法）（3）超过平均增长速度的年份有哪些年？解：注意平均时项数的确定，写计量单位，我以下省略了单位1430%02.193*430116430%02.193*4307%02.193*4304554301)26n 0010-=-=-='-=-=∆+++=+++=a a V V n a a n a a a a n n n （（3）填全表中各年的环比增长速度，和年平均增长速度进行比较即可4. 某地1980~1990年间（以1979年为基期:a0），地区生产总值以平均 每年25%的速度增长(平均增长速度），而1991~2000年间地区生产总值以平均每年30%的速度增长（平均增长速度），2001~2012年间地区生产总值以平均每年18%的速度增长，则1980~2012年间，该地区的生产总值平均每年的增长速度是多少？（重点：正确确定时间段长短）解：注意是以1979年为基期，经过33年发展到2012年，求这段时间的平均增长速度1%118*%130*%125133121011-=-='V V5. 某地1980年的人口是120万人，1981~2000年间人口平均增长率为1.2%，之后下降到1%，按此增长率到2008年人口会达到多少？如果要求到2012年人口控制在170万以内，则2008年以后人口的增长速度应控制在什么范围内？ 解：1)2(%101*%2.101*)140812*******-='==V V V a a a a （（1）分别用最小平方法的普通法和简捷法配合直线方程，并预测2010年该企业产值 （2）比较两种方法得出的结果有无异同。

优质文本一、填空题（24分，每题3分） 1.对任意的T t t n ∈,...1和任意的h 使得n i T h t i ,...,2,1,=∈+有()()()()h t X h t X h t X n +++,...,,21与()()()()n t X t X t X ,...,,21相同的联合分布；2.()()⎪⎩⎪⎨⎧=•<∀-+++=--0,,0...211t s t tp t p t t X E t s WN X X X εσεεφφ; 3. 231,231-+; 4. 拖尾; 5 连续型时间序列分析和离散型时间序列分析;6.频域分析和时域分析;7. 矩估计、极大似然估计和最小二乘估计 8 AIC 和SBC;二、简答题（共20分，每题10分）1．（本题10分）解：（1）时间序列分析方法强调变量值序列顺序的重要性；2分 （2）时间序列各观察值之间存在一定的依存关系； 2分（3）时间序列分析根据自身的变化规律来预测未来； 2分 （4）时间序列是一组随机变量的一次样本实现； 2分 （5）时间序列分析和回归分析的建模思路不同。

2分2.（本题10分）解：（1）模型识别：即确定自回归模型阶数p 和移动平均模型阶数q 。

2 分 （2）参数估计：即给出均值、自回归参数和移动平均参数，以与白噪音方差2σ的估计值。

3分 （3）模型的检验和模型选择：对所选择的不同阶数p 和q 的值，重复估计步骤，直至选出最优模型为止。

3 分（4）应用信息准则法进行模型优化选择。

2 分三．证明题（共12分）证明：()t f 是具有周期T 的函数，因而是有界函数，ε是区间(0,T)上均匀分布的随机变量，因而()()()()011=+•+=•+=⎰⎰t d Tt f d Tt f X E TTεεεε 5分为常数，()()()()()()()()()[]()()[]()()⎩⎨⎧≠-=-=•=-•-=nTs t nTs t t X s X t X E s X E s X t X E t X E s t ,0,var ,γ 5分 因而()t X 的二阶矩都存在，均值函数为常数，协方差函数只与t-s 有关，因而为宽平稳过程。

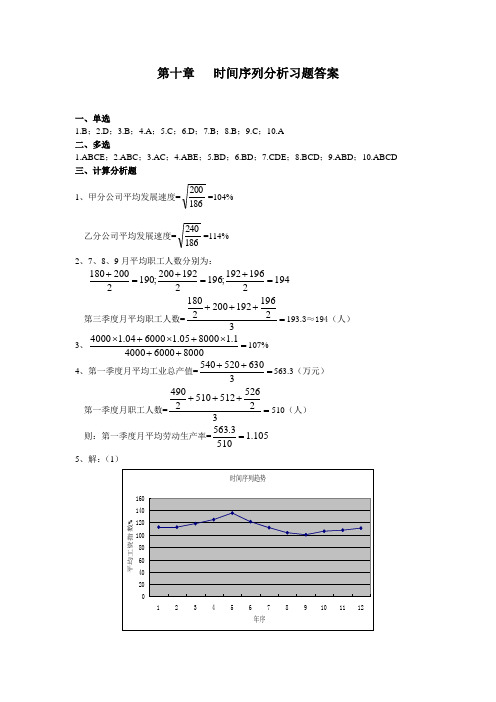
第十章 时间序列分析习题答案一、单选1.B ；2.D ；3.B ；4.A ；5.C ；6.D ；7.B ；8.B ；9.C ；10.A 二、多选1.ABCE ；2.ABC ；3.AC ；4.ABE ；5.BD ；6.BD ；7.CDE ；8.BCD ；9.ABD ；10.ABCD 三、计算分析题1、甲分公司平均发展速度=186200=104% 乙分公司平均发展速度=186240=114% 2、7、8、9月平均职工人数分别为：1942196192;1962192200;1902200180=+=+=+ 第三季度月平均职工人数==+++321961922002180193.3≈194（人） 3、=++⨯+⨯+⨯8000600040001.1800005.1600004.14000107%4、第一季度月平均工业总产值==++3630520540563.3（万元）第一季度月职工人数==+++325265125102490510（人） 则：第一季度月平均劳动生产率=105.15103.563=5、解：（1）（2）年序t 平均工资指数（环比）5期移动平均趋势1 112.70% —2 112.60% —3 118.50% 120.80%4 124.80% 122.60%5 135.40% 122.50%6 121.70% 119.52%7 112.10% 114.60%8 103.60% 108.76%9 100.20% 106.00%10 106.20% 105.78%11 107.90% —12 111.00% —各年份移动平均趋势值和原序列如下：移动平均可以消除原序列中的一些随机扰动和短期波动，期数越长，平滑作用越强；移动平均的作用就是消除序列随机和短期影响，从而能够发现序列的趋势。

（3）年份平均工资指数（环比）指数平滑值α=0.3误差平方指数平滑值α=0.5误差平方1 112.70% ————2 112.60% 112.70% 1E-06 112.70% 1E-063 118.50% 112.67% 0.003399 112.65% 0.0034224 124.80% 114.42% 0.010777 115.58% 0.008515 135.40% 117.53% 0.031922 120.19% 0.0231426 121.70% 122.89% 0.000142 127.79% 0.0037137 112.10% 122.54% 0.01089 124.75% 0.0159948 103.60% 119.40% 0.024979 118.42% 0.0219739 100.20% 114.66% 0.020919 111.01% 0.01168910 106.20% 110.32% 0.001701 105.61% 3.53E-0511 107.90% 109.09% 0.000141 105.90% 0.00039912 111.00% 108.73% 0.000515 106.90% 0.00168—109.41% —108.95% —合计 — — 0.105385 — 0.09056从上表数据看，采用平滑系数α=0.5拟合效果好。

第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1）自相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）白噪声序列2.4，序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。

显著性水平=0.05不能视为纯随机序列。

2.5（1）时序图与样本自相关图如下（2） 非平稳 （3）非纯随机 2.6（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机第三章习题答案3.1 解：1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-）B 7.01(t t t B B B x εε)7.07.01()7.01(221Λ+++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ3.2 解：对于AR （2）模型：⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得：⎩⎨⎧==15/115/721φφ3.3 解：根据该AR(2)模型的形式，易得：0)(=t x E原模型可变为：t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ 3.4 解：原模型可变形为：t t x cB B ε=--)1(2由其平稳域判别条件知：当1||2<φ，112<+φφ且112<-φφ时，模型平稳。

时间序列练习题答案一、选择题1. 时间序列分析中的自回归模型（AR）是指：A. 模型中的误差项B. 模型预测值依赖于自身过去的值C. 模型预测值依赖于其他变量的值D. 模型预测值依赖于未来的值2. 移动平均模型（MA）的主要特征是：A. 预测值依赖于过去的误差项B. 预测值依赖于过去的观测值C. 预测值依赖于未来的误差项D. 预测值依赖于未来的观测值3. 以下哪个不是时间序列分析中的平稳性检验方法？A. 单位根检验B. 协整检验C. KPSS检验D. 方差比检验4. 时间序列的差分操作通常用于：A. 消除季节性效应B. 消除趋势C. 消除周期性变化D. 消除随机波动5. 季节性调整的目的是：A. 消除随机波动B. 消除季节性效应C. 消除长期趋势D. 消除周期性变化二、简答题1. 简述自回归积分滑动平均模型（ARIMA）的基本组成部分。

2. 解释什么是时间序列的平稳性，并说明为什么在时间序列分析中需要考虑平稳性。

3. 描述季节性时间序列的特点，并说明如何识别和处理季节性效应。

三、计算题1. 给定以下时间序列数据：\[ y_t = \{10, 15, 20, 25, 30, 35, 40, 45, 50, 55\} \] 假设这是一个一阶自回归模型AR(1)，其中自回归系数φ=0.8。

请计算下一个时间点的预测值。

2. 假设一个时间序列模型的ACF（自相关函数）在滞后1时显著不为0，而在滞后2及以后时显著为0。

根据这个信息，推测该时间序列可能属于哪种类型的模型？四、案例分析题1. 某公司销售数据呈现明显的季节性变化，如何在时间序列分析中对数据进行季节性调整？2. 一个时间序列模型的ADF（Augmented Dickey-Fuller）检验结果表明存在单位根，这意味着什么？如何对数据进行处理以消除单位根？五、论述题1. 论述时间序列分析在金融领域中的应用，并举例说明。

2. 讨论时间序列分析中的因果关系检验方法，并说明在实际应用中如何选择合适的方法。

第9章 时间序列分析——练习题●1. 某汽车制造厂2003年产量为30万辆。

（1）若规定2004—2006年年递增率不低于6%，其后年递增率不低于5%，2008年该厂汽车产量将达到多少？（2）若规定2013年汽车产量在2003年的基础上翻一番，而2004年的增长速度可望达到7.8%，问以后9年应以怎样的速度增长才能达到预定目标？（3）若规定2013年汽车产量在2003年的基础上翻一番，并要求每年保持7.4%的增长速度，问能提前多少时间达到预定目标？解：设i 年的环比发展水平为x i ，则由已知得：x 2003＝30， （1）又知：320042005200620032004200516%x x x x x x ≥+（），2200720082006200715%x x x x ≥+（），求x 2008由上得32200820072008200320032007(16%)(15%)x x x x x x =≥++ 即为3220081.061.0530x ≥，从而2008年该厂汽车产量将达到 得 x 2008≥30× 31.06×21.05= 30×1.3131 = 39.393（万辆） 从而按假定计算，2008年该厂汽车产量将达到39.393万辆以上。

（2）规定201320032x x ＝，20042003x x ＝1+7.8％由上得＝107.11%==可知，2004年以后9年应以7.11％的速度增长，才能达到2013年汽车产量在2003年的基础上翻一番的目标。

（3）设：按每年7.4%的增长速度n 年可翻一番， 则有 201320031.0742na a == 所以 1.074log 20.30103log 29.70939log1.0740.031004n ====（年）可知，按每年保持7.4%的增长速度，约9.71年汽车产量可达到在2003年基础上翻一番的预定目标。

原规定翻一番的时间从2003年到2013年为10年，故按每年保持7.4%的增长速度，能提前0.29年即3个月另14天达到翻一番的预定目标。

第四章 时间数列习题一、选择：1、作为动态数列水平的指标可以是：(甲〉总量指标；(乙〉相对指标；(丙〉平均指标。

（ ） ①甲 ②乙丙 ③甲乙丙 ④甲丙2、我国"九五"时期每年钢产量是：(甲)时期数列；(乙〉时点数列。

计算这个数列的平均水平要运用的算术平均数是：〈丙〉简单算术平均数；(丁)加权算术平均数。

（ ） ①甲丁 ②乙丙 ③甲丙 ④乙丁3、最近几年每年年末国家外汇储备是：(甲)时期数列；(乙)时点数列。

计算这个数列的平均水平要运用的平均数是：(丙)简单算术平均数；(丁)“首末折半”序时平均数。

（ ） ①甲丙 ②甲丁 ③乙丙 ④乙丁4、某企业工业生产固定资产原值变动资料(单位:千元〉：1998年1月1日8000当年新增2400，当年减少400试确定工业生产固定资产原值平均价值（ ） ① 10000 ②9000 ③5000 ④15005、某车间月初工作人员数资料如下：（ ）一月 二月 三月 四月 五月 六月 七月 280 284 280 300 302 304 320 计算该车间上半年月平均工人数计算式是：①iii f f α∑∑②iiif f α∑∑③inα∑ ④12311122...1n a a a a n -++++-6、2003年上半年某商店各月初棉布商品库存〈千元〉为：（ ） 一月 二月 三月 四月 五月 六月 七月 42 34 36 32 36 33 38 试确定上半年棉布平均商品库存。

①35 ②30 ③35.7 ④407、某银行农业贷款余额(千元)如下： 2002年 1月1日 84 2002年 4月1日 81 2002年 7月1日 104 2002年10月1日 106 1999年 1月1日 94 试确定农业贷款平均余额（ ）①93.8 ②76 ③95 ④117.258、2003年11月某企业在册工作人员发生了如下的变化(人)：2003年11月1日在册 919 2003年11月6日离开 29 2003年11月21日录用 15试确定该企业11月份日平均在册工作人员数（ ） ①900 ②905 ③912 ④9199、某采购点12月1日有牛300头，12月5日卖出230头，12月19日购进130头。

D.平均数数列二、多项选择题1.将不同时期的发展水平加以平均而得到的平均数称为 A. 序时平均数2．定基发展速度和环比发展速度的关系是 ( BD A 相邻两个环比发展速度之商等于相应的定基发展速度B. 环比发展速度的连乘积等于定基发展速度一、单项选择题 第五章 时间序列分析1.构成时间数列的两个基本要素是 ( A.主词和宾词 )(20XX 年 1 月) B. 变量和次数 C.现象所属的时间及其统计指标数值 D.时间和次数2．某地区历年出生人口数是一个 ( A 时期数列 B ） （20XX 年 10月）B.时点数列C.分配数列 3. 某商场销售洗衣机， 共销售 6000 台， 年 10) 年底库存 50 台，这两个指标是 ( C ) 20XXA. 时期指标B. 时点指标C. 前者是时期指标，后者是时点指标 4.累计增长量(A ) (20XX 年 10)A. 等于逐期增长量之和 D. 前者是时点指标，后者是时期指标B. 等于逐期增长量之积C. 等于逐期增长量之差D .与逐期增长量没有关系5. 某企业银行存款余额 4 月初为 80 万元， 160 万元，则该企业第二季度的平均存款余额为( 5 月初为 150 万元， 6 月初为 210 万元， 7 月初为10)A.140 万元B.150 万元6. 下列指标中属于时点指标的是 ( A ) C.160 万元 D.170 万元A. 商品库存量 (10)B .商品销售C. 平均每人销售额D .商品销售额 7. 时间数列中，各项指标数值可以相加的是A. 时期数列10）( A )B.相对数时间数列C.平均数时间数列D.时点数列8. 时期数列中各项指标数值( A A. 可以相加 1月)B. 不可以相C.绝大部分可以相加D. 绝大部分不可以相加10. 某校学生人数 比 增长了 8%，增长了( D )( 10 月)比 增长了 15%， 比 增长了 18%，则 2004- 学生人数共A.8％+15％+18％B. 8 %X 15%X 18%C. （108％+115％+118％） -1D.108 %X 115%X 118% -1( ABD B.动态平均数）（20XX 年 1 月） C.静态平均数 D.平均发展水平 E. 般平均数 ）（20XX 年 10 月）B. 数列中各个指标数值不具有可加性C. 指标数值是通过一次登记取得的D. 指标数值的大小与时期长短没有直接的联系E.指标数值是通过连续不断的登记取得的 ）（20XX 年 1）B. 增加一个百分点所增加的相对量E. 环比增长量除以100再除以环比发展速度7. 增长速度（ ADE ）（ 1 月）A.等于增长量与基期水平之比6. 计算平均发展速度常用的方法有（ A.几何平均法（水平法）C.方程式法（累计法）E.加权算术平均法 AC）（10）B.调和平均法 D.简单算术平均法C.累计增长量与前一期水平之比D. 等于发展速度 -1E.包括环比增长速度和定基增长速度 8. 序时平均数是（ CE ）（ 10 月）A.反映总体各单位标志值的一般水平B. 根据同一时期标志总量和单位总量计算C. 说明某一现象的数值在不同时间上的一般水平D.由变量数列计算E. 由动态数列计算三、判断题 1 .职工人数、产量、产值、商品库存额、工资总额指标都属于时点指标。

第二章习题答案之袁州冬雪创作2.1（1）非平稳（3）典型的具有单调趋势的时间序列样本自相关图（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（2）平稳序列（3）白噪声序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363.显著性水平=0.05，序列不克不及视为纯随机序列.（1）时序图与样本自相关图如下（2）非平稳（3）非纯随机2.6（1）平稳，非纯随机序列（拟合模子参考：ARMA(1,2)） （2）差分序列平稳，非纯随机 第三章习题答案3.13.2 解：对于AR （2）模子：3.3 解：根据该AR(2)3.4 解：原模子可变形为：子平稳.由此可知c即当－1<c<0时，该AR(2)模子平稳. 3.5证明：已知原模子可变形为：不管c 取何值，都会有一特征根等于1，因此模子非平稳.3.6 解：（1 （2（3 （4（5）3.7MA(1)3.8解法1解法2展开等号右边的多项式，整理为 合并同类项，原模子等价表达为3.9解：3.10解法1：（1显然模子的AR 部分的特征根是1，模子非平稳. （2MA(1)模子，平稳.解法2：（1稳序列.（2自相关系数只与时间间隔长度有关，与起始时间无关所以该差分序列为平稳序列.3.11解：（1（2..（3＋（4.（5（6.3.12 解法1解法23.13Green函数3.14 证明：的递推公式得：3.15 （1）成立（2）成立（3）成立（4）不成立3.16 解：（1已知AR(1)模子的Green[9.9892-1.96*，9.9892＋即[3.8275,16.1509]（2[10.045-1.96×，10.045＋即[3.9061,16.1839].3.17 （1）平稳非白噪声序列（2）AR(1)(3) 5年预测成果如下：3.18 （1）平稳非白噪声序列（2）AR(1)(3) 5年预测成果如下：3.19 （1）平稳非白噪声序列（2）MA(1)(3) 下一年95%的置信区间为（80.41,90.96）3.20 （1）平稳非白噪声序列（2）ARMA(1,3)序列（3）拟合及5年期预测图如下：第四章习题答案4.1 解：4.2 解由代入数据得解得4.3解：（1）（2.别（3）在移动平均法下:在指数平滑法中:4.4 解：根据指数平滑的定义有（1）式成立，（1）式等号2）式成立（1）-（2）得limtttxt→∞⎛=⎝4.5 该序列为显著的线性递增序列，操纵本章的知识点，可使用线性方程或者holt两参数指数平滑法停止趋势拟合和预测，答案不唯一，详细成果略.4.6 该序列为显著的非线性递增序列，可以拟合二次型曲线、指数型曲线或其他曲线，也能使用holt两参数指数平滑法停止趋势拟合和预测，答案不唯一，详细成果略.4.7 本例在混合模子布局，季节指数求法，趋势拟合方法等处均有多种可选方案，如下做法仅是可选方法之一，成果仅供参考（1）该序列有显著趋势和周期效应，时序图如下（2）该序列周期振幅几乎不随着趋势递增而变更，所以测（注：如果用乘法模子也可以）首先求季节指数（没有消除趋势，其实不是最切确的季节指数）序列趋势影响（方法不唯一）（注：该趋势模子截距无意义，主要是斜率有意义，反映了长期递增速率）残差序列基本无显著趋势和周期残留.预测1971年奶牛的月度产量序列为得到（3）该序列使用x11方法得到的趋势拟合为趋势拟合图为4.8 这是一个有着曲线趋势,但是有没有固定周期效应的序列,所以可以在疾速预测程序中用曲线拟合（stepar）或曲线指数平滑（expo）停止预测（trend=3）.详细预测值略.第五章习题估计下一5.1 拟合差分平稳序列,天的收盘价为2895.2 拟合模子不唯一，答案仅供参考.拟合ARIMA(1,1,0)模子，五年预测值为：5.4 (1)AR(1)， (2)有异方差性.最终拟合的模子为5.5(1)非平稳（2）取对数消除方差非齐，对数序列一节差分后，拟合疏系数模子AR(1，3)所以拟合模子为（3）预测成果如下：5.6 原序列方差非齐，差分序列方差非齐，对数变换后，差分序列方差齐性.第六章习题6.1 单位根检验原理略.例2.1 原序列不服稳，一阶差分后平稳例2.2 原序列不服稳，一阶与12步差分后平稳例2.3 原序列带漂移项平稳例2.4 原序列不带漂移项平稳例2.5稳.6.2 （1）两序列均为带漂移项平稳（2）谷物产量为带常数均值的纯随机序列，降雨量可以拟合AR（2）疏系数模子.（3）二者之间具有协整关系（46.3 （1）掠食者和被掠食者数量都呈现出显著的周期特征，两个序列均为非平稳序列.但是掠食者和被掠食者延迟2阶.序列具有协整关系.（2径为:未来一周的被掠食者预测序列为：Forecasts for variable xObs Forecast Std Error 95% Confidence Limits掠食者预测值为：Forecasts for variable yObs Forecast Std Error 95% Confidence Limits6.4（1）进出口总额序列均不服稳，但对数变换后的一阶差分后序列平稳.所以对这两个序列取对数后停止单个序列拟合和协整检验.详细口径为：（2）详细口径为：（3（4（5。