复合函数求导法

复合函数求导公式大全大学复合函数求导法则复合函数如何求导？大学符合函数求导公式有哪些？下文小编给大家整理了复合函数的求导公式及法则，供参考！ 复合函数求导公式 复合函数求导法则证法一：先证明个引理 f(x)在点x0可导的充要条件是在x0的某邻域U(x0)内，存在一个在点x0连续的函数H(x),使f(x)-f(x0)=H(x)(x-x0)从而f'(x0)=H(x0) 证明：设f(x)在x0可导，令H(x)=[f(x)-f(x0)]/(x-x0),x∈U'(x0)(x0去心邻域)；H(x)=f'(x0),x=x0 因lim(x->;x0)H(x)=lim(x->;x0)[f(x)-f(x0)]/(x-x0)=f'(x0)=H(x0) 所以H(x)在点x0连续，且f(x)-f(x0)=H(x)(x-x0),x∈U(x0) 反之，设存在H(x),x∈U(x0),它在点x0连续，且f(x)-f(x0)=H(x)(x-x0),x∈U(x0) 因存在极限lim(x->;x0)H(x)=lim(x->;x0)[f(x)-f(x0)]/(x-x0)=lim(x->;x0)f'(x)=H(x0) 所以f(x)在点x0可导，且f'(x0)=H(x0) 引理证毕。

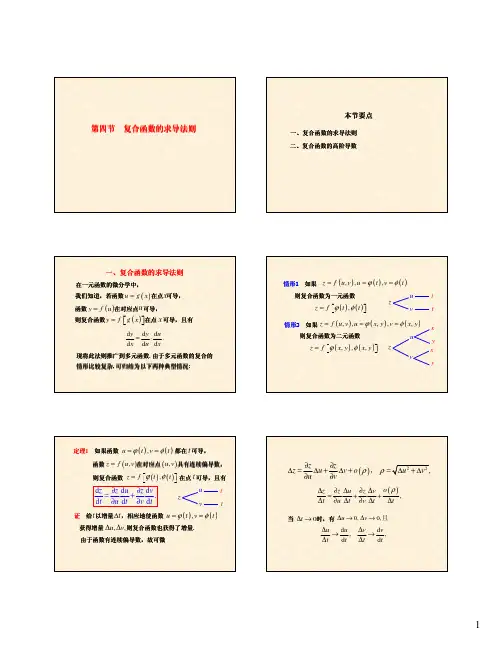
 设u=φ(x)在点u0可导，y=f(u)在点u0=φ(x0)可导，则复合函数F(x)=f(φ(x))在x0可导，且F'(x0)=f'(u0)φ'(x0)=f'(φ(x0))φ'(x0) 证明：由f(u)在u0可导，由引理必要性，存在一个在点u0连续的函数H(u),使f'(u0)=H(u0),且f(u)-f(u0)=H(u)(u-u0)。

et,
则
dz z du z dv z dt u dt v dt t ve t u sin t cos t e t cos t e t sin t cos t
u
z v t
e t (cos t sin t ) cos t . 例3: 设z=f(u, v), u=u(x, y), v=v(x, y), x=x(s, t), z z y=y(s, t)均满足复合函数求偏导数的条件, 计算 , . s t (两重复合问题) 解: 复合函数的变量关系图
例4: 设 w=f( x+y+z, xyz )具有二阶连续偏导数, 求 w 2 w , . x xz 解: 令 u= x+y+z, v= xyz, 记 2 f ( u , v ) f ( u, v ) f1 , f12 , 同理有 f 2, f11 , f 22 . u uv w f u f v 则 f1 y z f 2; u x v x x 2w f1 f 2 ( f1 y z f 2) y f 2 y z ; x z z z z f1 f1 u f1 v 而 f11 x y f12 ; z u z v z f 2 f 2 u f 2 v f 21 x y f 22 ; z u z u, x, y), u=(x, y), 即z=f[(x, y), x, y],
u
y
u y
令 v = x, w = y. 则 v w v w 0, 1. z 1, 0, x x y y
x
y
z z u z z z u z . , y u y w x u x v f z f z , . 则 由于 v=x, w=y. 记 x v y w 两 z f u f z f u f 者 , . 的 x u x x y u y y 区 别

z dz ( u 2 v 2 )
( u 2 v 2 ) 高阶的无穷小，得 z z u z v ( u 2 v 2 )
t 0
lim
u t v t t z du z dv ( u 2 v 2 ) u 2 v 2 lim . 2 2 u dt v dt t 0 t u v z du z dv u dt v dt 所以复合函数 z f [ (t ), (t )] 可导，具有求导公式：
设 u (t ) v (t ) .w (t ) 均 在 点 t 处 可 导 ， z f (u , v, w) 在对应点(u , v, w) 处有连续的偏导数， 写出复合 函数 z f [ (t ), (t ), (t )] 的全导数公式. u t 函数的结构图是 z w t v t 由 z 经u , v, w 到 t 有三条途径，故和式中应有三项，所以全 导数为 dz z du z dv z dw . dt u dt v dt w dt dz 例 1 设 z uv ， u sin t ，v cos t ，求全导数 . dt dz z du z dv 解 dt u dt v dt v cos t u ( sin t ) cos 2 t sin 2 t cos 2t
例 5 设 z arcsin u, u x 2 y 2 ，求
z z , . x y
解 函数的结构如下： x z u y 所以 z z u 1 2x 2x x u x 1 u2 1 ( x 2 y 2 )2 z dz u 1 2y 2y 2 y du y 1 u 1 ( x 2 y 2 )2
t 0
t
lim(

yu (u2 ) 2u , ux (sin x) cos x.
所以
yx yu ux 2u cos x 2sin x cos x.
例 3 设 y = etan x，求 y . 解 y = etan x 可以看成是由 y = eu，u = tan x 复合而成，所以
yx yu ux (eu )u (tan x)x
= elnx ·(ln x) e ln x 1
x
x 1 x 1 .
x
例 12 设 u x2 y2 z2 , 求证：
u x
2
u y
2
u z
2
1
.
证明
u x 2
x2
1 y2
z2
(x2
y2
z 2 )x
x
x
,
x2 y2 z2 u
同理，得
u y ,u z ,代等式左边得解 先用复合函数求导公式，再用加法求导公式，
然后又会遇到复合函数 1 x2 的求导.
[ln(x 1 x2 )]
1
( x 1 x2 )
x 1 x2
1
[1 ( 1 x2 )]
x 1 x2
x
1 1
x2
1
1. 1 x2
x 1
x2
例 11 设 y = sh x， 求 y .
解
y
(shx)
一、复合函数的求导法则
定理 2 设函数 y = f (u)， u = (x) 均可导， 则复合函数 y = f ( (x)) 也可导.
且 或
或
证 设变量 x 有增量 x，相应地变量 u 有 增量 u，从而 y 有增量 y. 由于 u 可导，
所以lim u 0. x0

练习 求下列函数的导数
y = e3x (A)1.
3x 3x 3x 解：y ′ = ( e ) ′ = e ( 3 x ) ′ = 3 e
y = cos( x 3 ) (A)2.
2 3 3 3 3 解：y ′ = (cos x ) ′ = − sin x ( x ) ′ = − 3 x sin x
(B)3. y = e 解： y ′ = e
2x ′ 1 所以 yx = yu ⋅ ux = ⋅ (−2x) = 2 u x −1
′
′
(A) 例3 求函数 y = cos 2 x 的导 数 2 解：设 y = u 则 u = cos x
因为 所以
′ ′ yu = 2u, ux = −sinx
′ ′ ′ yx = yu ⋅ ux = 2u(−sin x) = −2cosx sin x = −sin2x
′ y u = 5u 4 , u ′ = 3, x
′ x y′ = yu ⋅ u′ = 5u4 ×3 = 5(3x + 2)4 ×3 =15(3x + 2)4 所以 x
2 (B) 例2 求函数 y = ln(1 − x ) 的导数
解：设 因为
y = ln u
则
u = 1− x2
′ 1 ′ yu = , u x = −2 x, u
x π (B) 例5 求 y = ln tan( + ) 的导数。 的导数。 2 4
x π 解： 设 y = ln u , u = tan v, v = + 2 4
由
y ′ = f ′ ( u ) ⋅ φ ′( v ) ⋅ ϕ ′( x ) 得
x π ′ = (lnu)′ ⋅ (tanv)′ ⋅ ( + )′ y 2 4

复合函数的导数及导数的运算法则复合函数是指由两个或多个函数组成的函数。

在求复合函数的导数时，需要使用链式法则，即将函数的导数作为求导的一部分。

设有两个函数f(x)和g(x)，假设y=f(g(x))是一个复合函数。

我们的目标是求解复合函数y=f(g(x))的导数dy/dx。

根据链式法则，dy/dx可以表示为：dy/dx = df(g(x))/dx根据上述公式，我们可以按照以下步骤求导：Step 1: 首先对f(g(x))进行求导，即求df(g)/dg。

Step 2: 然后对g(x)进行求导，即求dg(x)/dx。

Step 3: 最后将求导得到的结果相乘，即df(g)/dg * dg(x)/dx =dy/dx。

下面我们讨论一些常见的复合函数和它们的导数运算法则。

1. 复合函数的链式法则（Chain Rule）设有函数f(u)和g(x)，假设y=f(g(x))是一个复合函数。

根据链式法则，复合函数y=f(g(x))的导数可以表示为：dy/dx = f'(g(x)) * g'(x)其中，f'(u)和g'(x)分别表示f(u)和g(x)的导数。

例如，如果y=(2x+1)^3，则可以将它表示为y=u^3，其中u=2x+1、根据链式法则：dy/dx = 3u^2 * du/dx = 3(2x + 1)^2 * 2 = 6(2x + 1)^22.复合函数中的乘法法则如果复合函数中有乘法运算，则可以使用乘法法则来求导。

例如，如果y=x^2*e^x，则可以使用乘法法则来求导：dy/dx = (d/dx)(x^2) * e^x + x^2 * (d/dx)(e^x)对于每一项使用基本求导法则：dy/dx = 2x * e^x + x^2 * e^x3.复合函数中的除法法则如果复合函数中有除法运算，则可以使用除法法则来求导。

例如，如果y=(x^2+1)/(x-1)，则可以使用除法法则来求导：dy/dx = [(d/dx)(x^2 + 1)(x - 1) - (d/dx)(x - 1)(x^2 + 1)]/(x - 1)^2再对每一项使用基本求导法则：dy/dx = [(2x)(x - 1) - (x^2 + 1)]/(x - 1)^24.复合函数中的三角函数法则如果复合函数中包含三角函数，则可以使用三角函数法则来求导。

复合函数求导法则有哪些呢复合函数的求导法则同学们清楚吗，如果不清楚，快来小编这里瞧瞧。

下面是由小编为大家整理的“复合函数求导法则有哪些呢”，仅供参考，欢迎大家阅读。

复合函数求导法则有哪些呢Y=f(u),U=g(x),则y′=f(u)′*g(x)′例1.y=Ln(x^3),Y=Ln(u),U=x^3,y′=f(u)′*g(x)′=[1/Ln(x^3)]*(x^3)′=[1/Ln(x^3)]*(3x^2)=(3x^2)/Ln(x^3)]例2.y=cos(x/3),Y=cosu,u=x/3由复合函数求导法则得y=-sin(x/3)*(1/3 )=-sin(x/3)/3拓展阅读：求导公式运算法则是什么运算法则是：加(减)法则，[f(x)+g(x)]'=f(x)'+g(x)';乘法法则，[f(x)*g(x)]'=f(x)'*g(x)+g(x)'*f(x);除法法则，[f(x)/g(x)]'=[f(x)'*g(x)-g(x)'*f(x)]/g(x)^2。

若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。

导数也叫导函数值，又名微商，是微积分中的重要基础概念。

由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。

求导运算法则是：加(减)法则：[f(x)+g(x)]'=f(x)'+g(x)';乘法法则：[f(x)*g(x)]'=f(x)'*g(x)+g(x)'*f(x);除法法则：[f(x)/g(x)]'=[f(x)'*g(x)-g(x)'*f(x)]/g(x)^2。

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极限的概念对函数进行局部的线性逼近。

幂函数的导数
幂函数是形如$y = x^n$的函数，其 中$n$是实数。
VS
幂函数的导数可以通过幂函数的定义 和极限的定义求得，结果为$y' = nx^{n-1}$。
三角函数的导数
三角函数包括正弦函数、余弦函数和正切函数等。
正弦函数的导数是余弦函数，即$frac{d}{dx}sin x = cos x$；余弦函数的导数是负的正弦函数，即$frac{d}{dx}cos x = -sin x$； 正切函数的导数是正切函数的平方与1的和的倒数，即$frac{d}{dx}tan x = frac{1}{cos^2 x}$。
探讨未来可能的研究方向
复杂复合函数的求导 方法
对于更为复杂的复合函数，如多 层嵌套、多变量复合等，需要进 一步研究更为高效、简洁的求导 方法。这有助于解决实际应用中 更为复杂的数学问题。
复合函数导数的性质 研究
复合函数的导数具有一些独特的 性质，如连续性、可微性等。未 来可以进一步探讨这些性质在复 合函数求导中的应用，以及它们 对导数求解的影响。
对数函数是形如$y = log_a x$的函数，其中$a > 0$且$a neq 1$。
03 复合函数求导举例
简单复合函数求导
举例1
$y = sin(2x)$
分析
这是一个简单的复合函数，其中内层函数是 $2x$，外层函数是$sin u$。
求导过程
根据链式法则，$frac{dy}{dx} = cos(2x) cdot 2 = 2cos(2x)$。
指数函数和对数函数的导数
指数函数的导数是其本身与底数自然对数的乘 积，即$frac{d}{dx}a^x = a^x ln a$。
对数函数的导数是底数的倒数与自变量对数的倒数之 积，即$frac{d}{dx}log_a x = frac{1}{x ln a}$。

= f ′( u0 ) g ′( x0 ).
复合函数的求导法则可以写成: 复合函数的求导法则可以写成
dy dy du = dx du dx
即因变量对自变量求导，等于因变量对中间变量求 即因变量对自变量求导， 导乘以中间变量对自变量求导，我们称它为链式法则 导乘以中间变量对自变量求导，我们称它为链式法则. 复合函数的微分公式为: 复合函数的微分公式为
n n1 (sin x n ) ′(sin x n ) cos x n nx n1
= n 3 x n1 cos x n f n1[ n (sin x n )]
n1 (sin x n ) f ′[ n (sin x n )] ′(sin x n ).
三、一阶微分的形式不变性
设函数 y = f ( x )有导数 f ′( x )
第四节
复合函数求导 法则及其应用
一、复合函数求导法则 二、初等函数的求导问题 三、一阶微分的形式不变性 四、隐函数的导数 五、对数求导法 六、参数形式的函数的求导公式
一、复合函数求导法则
定理4.4.1 (复合函数求导法则 ) 设函数 u = g( x ) 在 x0可导， 可导， 定理 复合函数求导法则 处可导， 而函数 y = f (u) 在 u0 = g( x0 ) 处可导，则复合函数 y = f [ g( x )] 在 x0 可导，且有 可导，且有:
d[ f ( g( x))] = f ′(u) g′( x)dx
推广
设 y = f ( u), u = (v ), v = ψ ( x ),
则复合函数
y = f { [ψ ( x )]}的导数为 :
dy dy du dv = dx du dv dx
例4.4.1 解: 求函数 y = ln sin x 的导数 .

f (u)( x).
证毕
6
推广 设 y f (u), u (v), v ( x), 则复合函数
y f {[ ( x)]}的导数为 dy dy du dv .
dx du dv dx
注意：可推广到有限次复合.
如 y sin2x， 由 y sinu 与 u 2x 复合而成.
(sin2x) (sin u)u (2x) 2cosu 2cos2x
x 复合而成，
2
2
因而
dy dx
dy du dv du dv dx
(ln
u)u
(tanv
)v
(
1 2
x)x
1 sec2 v 1 csc x.
u
2
8
例4
已知 y
x sin x
( x 0)，求 dy .
dx
解 y xsin x esin xln x 由 y eu，u sin x ln x
dy dy du eu e ln x
dx du dx
x
x
x x1. 证毕
x
例6 求y=f(x2)的导数(其中f(x)可导).
解 可分解为 y f (u), u x2 ,
y dy du f (u)(2x) 2 xf ( x 2 ). du dx
10
复合函数的求导法则有三个步骤： （1）分解复合函数，分解到基本初等函数或
lim
t 0
u t
,
函数 x
f (t) 对t可导，xt
dx dt
lim
t 0
x t
,
函数x
f ( y)对y可导，xy
dx dy
lim
y0
x y

= 2 xf u − 2 xf v = 2 xf1′ − 2 xf 2′ ,
其中将偏导数记号记为
y
∂z ∂z +x = y 2 xf1′ − 2 xf 2′ + x −2 yf1′ + 2 yf 2′ ∂x ∂y
= 0.
(
) (
)
∂z ∂z = fu = f1′ , = f v = f 2′ ∂u ∂v
= f 可导，且有 g ( x ) 在点 x 可导，
dy dy du = ⋅ . dx du dx
z= f ϕ ( t ) , φ ( t )
z
u v
t t
情形2 情形2 如果 z = f ( u , v ) , u = ϕ ( x, y ) , v = φ ( x, y ) 则复合函数为二元函数
∂ 2 w ∂f1′ ∂f ′ = + yf 2′ + yz 2 ∂x∂z ∂z ∂z ′′ + xyf12 ′′ + yf 2′ + yz ( f 21 = f11 ′′ + xyf 22 ′′ )
z x = f1′ + yf 2′ ,
z
u
x
y
z xx =
∂f1′ ∂f ′ +y 2 ∂x ∂x
′′ + yf12 ′′ + y ( f 21 ′′ + yf 22 ′′ ) = f11 ′′ + 2 yf12 ′′ + y 2 f 22 ′′ = f11
x
∂z ∂z , . ∂s ∂t s
t
∂y ∂t
可写为
dy dt
s
x
∂z ∂z ∂x = ∂s ∂x ∂s y = et 1 − x2 y2

高等数学,复合函数求导
复合函数求导是高等数学中的一个重要概念，它是求解复合函数的导数的一种方法。

首先，我们来了解复合函数的概念。

复合函数是指一个函数的输入和输出是另一个函数的输入和输出。

比如，函数f （x）=x2+1和函数g（x）=x3+2x，它们的复合函数就是h（x）=g（f（x）），即h（x）=（x2+1）3+2（x2+1）。

其次，复合函数求导的原理是利用链式法则，即如果复合函数h（x）=g（f（x）），那么它的导数就是h'（x）=g'（f （x））*f'（x）。

具体来说，复合函数求导的方法可以分为三步：（1）首先，求出复合函数的具体表达式，即h（x）=g（f（x））；（2）然后，求出函数f（x）和g（x）的导数，即f'（x）和
g'（x）；（3）最后，根据链式法则，求出复合函数h（x）的导数，即h'（x）=g'（f（x））*f'（x）。

从上面的讲解，我们可以看出，复合函数求导的步骤十分简单，只需要按照上述三步来操作即可。

复合函数求导是高等数学中的一个重要概念，它可以帮助我们更加清楚地理解复合函数的特性。

然而，在实际应用中，复合函数求导也有许多技巧和技术可以帮助我们更加有效地求
解复合函数的导数，这些技巧和技术也是高等数学中的重要内容。

总之，复合函数求导是高等数学中的一个重要概念，它可以帮助我们更好地理解复合函数，也可以帮助我们更有效地求解复合函数的导数。

高数复合函数求导公式高数复合函数求导公式：一、概念1. 什么是复合函数？复合函数是指有两个或多个函数构成的函数，它的定义域为第一个函数的定义域，把第一个函数的输出作为第二个函数的输入，这样就定义出了新的函数，即复合函数。

2. 什么是求导公式？求导公式是指用来求一个函数的导数的公式，在数学上是表示求微分的方法。

通常使用微积分的基本公式和一些技巧来计算一个函数的一阶、二阶、三阶及以上导数，得出特定函数的导数。

二、求导公式1. 当复合函数中只有两个函数的时候：复合函数的求导公式使用链式法则，为：f’(x)= f(g(x))’=f’(g(x))*g’(x)，其中f’(g(x))表示第一个函数的导数，g’(x)表示第二个函数的导数。

2. 当复合函数中有三个或者更多函数时：复合函数的求导公式为f’(x)=f(g(h(x))’=f’(g(h(x))*g’(h(x))*h’(x)，其中f’(g(h(x)))表示复合函数第一个函数的导数，g’(h(x))表示复合函数的第二个函数的导数，h’(x)表示复合函数的第三个函数的导数。

三、注意事项1. 求导公式是求复合函数的导数的一种数学方法，它分别通过计算复合函数的各个部分，得出复合函数的导数。

2. 在计算复合函数的求导公式时，必须要清楚不同的函数的定义域，以及函数的各项参数。

3. 要将复合函数分解为不同函数，再分别求每一部分函数的导数，然后将所有的导数求乘积，就能得到复合函数的导数。

4. 如果复合函数的函数部分比较多，那么就要有相应的复杂的求导公式，计算的时候也会很复杂，所以可以使用乘法和傅里叶变换的方法来计算复合函数的导数。

四、总结综上所述，复合函数求导公式一般有两种，对于复合函数中只有两个函数的时候是f’(x)= f(g(x))’=f’(g(x))*g’(x)，而如果有三个或者更多函数，则理论上采用f’(x)=f(g(h(x))’=f’(g(h(x))*g’(h(x))*h’(x)。

复合函数求导公式推导
复合函数的求导公式可以通过链式法则进行推导。

设有函数 y = f(u) 和 u = g(x)，其中 y 是一个关于 x 的函数。

根据链式法则，y 对 x 的导数可以表示为：
dy/dx = dy/du * du/dx
其中，dy/du 表示函数 y 对中间变量 u 的导数，du/dx 表示中间变量 u 对自变量 x 的导数。

首先，求出 dy/du，即函数 y 对中间变量 u 的导数。

这可以通过对函数 y 使用普通的求导方法来得到。

然后，求出 du/dx，即中间变量 u 对自变量 x 的导数。

同样，可以使用普通的求导方法来计算。

最后，将 dy/du 和 du/dx 相乘得到 dy/dx，即函数 y 对自变量 x 的导数。

综上所述，复合函数的求导公式可以表示为：
dy/dx = (dy/du) * (du/dx)
这就是复合函数求导的公式。

y x sin x .
方法:
先在方程两边取对数, 然后利用隐函数的求导 方法求出导数.
--------对数求导法
例5： 设 y ( x 1)3 x 1 , 求y. ( x 4)2 e x
解: 等式两边取对数得
ln y ln( x 1) 1 ln( x 1) 2 ln( x 4) x 3
y
x
y y(cos x ln x sin x 1 ) x
x sin x (cos x ln x sin x ) x
四、由参数方程所确定的函数的导数
若参数方程
x y
(t )确定 (t)
y与x间的函数关系
,
称此为由参数方程所确定的函数.
例如
x 2t,
y
t
2
,
t x 2
消去参数 t
2
1 cos
1.
2
当 t 时, x a( 1), y a.
2
2
所求切线方程为
y a x a( 1) 2
即 y x a(2 )
2
谢谢
上式两边对 x求导得
y 1 1 2 1 y x 1 3( x 1) x 4
y
( x 1)3 x ( x 4)2 e x
1[
x
1
1
1 3( x
1)
x
2
4
1]
例6：设 y xsinx ( x 0), 求y.
解： 等式两边取对数得
上式两边对x求导得
1 y cos x ln x sin x 1
dy
dy dx
dy dt
dt dx
dy dt
1 dx
(t) (t)
即

1 1 1 1 ′′ = = (arcsin x) = (arcsinx ) . = 2 2 (sin y )′ cos y 1 − sin y 1− x
同理可得
(arccos x)′ = −
1 1− x
2
.
1 (arctan x)′ = ; 2 1+ x
1 ( arccot x)′ = − . 2 1+ x
= f ′(u )ϕ ′( x)
推广 设 y = f ( u), u = ϕ ( v ), v = ψ ( x ),
则复合函数 y = f {ϕ [ψ ( x )]}的导数为 dy dy du dv = ⋅ ⋅ . dx du dv dx
例1 求函数 y = ln sin x 的导数 . 解
Q y = ln u, u = sin x .
(7) (sec x)′ = sec x tan x (9)
(a )′ = a ln a
x x
′ = ex (e )
x
1 (11) (log a x)′ = x ln a 1 (13) (arcsin x)′ = 1 − x2 (15) (arctan x)′ = 1 1 + x2
1 (ln x)′ = x
1 特别地 (ln x )′ = . x
dy 例8 设y = arshx( x ∈ R ), 求 . dx 解 y = arshx是双曲正弦x = shy的反函数，
由反函数求导定理得 1 1 1 1 (arshx)′ = = = = 2 2 ( shy )′ chy 1 + sh y 1+ x
所以
f [ g ( x )] =| sin x | 在 x = 0 处不可导，(1) × 处不可导，

高考数学复合函数求导公式总结高考数学中，复合函数求导是一个重要的知识点。

在解题过程中，掌握求导的公式和方法，可以大大减少解题的时间和复杂度。

下面我将总结高考数学中常见的复合函数求导公式。

一、基本复合函数求导法则1.基本求导法则对于单个函数的求导，我们可以用基本求导法则来求解。

例如，对于常数函数 f(x) = c (c为常数)，其导函数为 f'(x) = 0。

而对于多项式函数 f(x) = x^n (n为自然数)，其导函数为 f'(x) = nx^(n-1)。

另外，对于指数函数 f(x) = e^x，其导函数为 f'(x) = e^x。

在求导时，还需要注意链式法则和乘积法则等。

2.复合函数求导法则复合函数是由一个函数的输出作为另一个函数的输入而形成的函数。

在求复合函数的导数时，我们需要先求外函数的导数，然后再乘上内函数的导数。

例如，对于复合函数f(g(x))，其导数可以通过以下公式求解：[f(g(x))]′=f′(g(x))g′(x)这个公式称为复合函数求导的链式法则。

二、特殊复合函数求导公式1.反函数设y=f(x)是x=g(y)的反函数，则有以下公式：[g(f(x))]′=[f'(x)]⁻¹2.自然对数函数的复合设 y = ln(u)，则有以下公式：[ln(u)]′= u' / u3.幂函数的复合设y=u^v，其中u是关于x的函数，v是关于x的函数，则有以下公式：[u^v]′= v' u^(v-1) + v ln(u)u^v u'其中v'是v的导数，u'是u的导数。

4.指数函数的复合设y=a^u，其中a是常数，u是关于x的函数，则有以下公式：[a^u]′= ln(a) a^u u'其中u'是u的导数。

5.对数函数的复合设 y = log_a(u)，其中 a 是常数，u 是关于 x 的函数，则有以下公式：[log_a(u)]′= 1 / (ln(a) u) u'其中u'是u的导数。