用联系的观点看“幂的运算”

幂知识点归纳总结1. 幂的定义幂是指将一个数乘以自身若干次的运算，形式上表示为a^n，其中a为底数，n为指数。

幂运算可以用于表示重复乘法的简便方式。

2. 幂的性质- 幂的乘法：a^m * a^n = a^(m+n)这条性质表示，当底数相同时，指数相加即可得到乘积的幂。

例如，2^3 * 2^4 = 2^(3+4) = 2^7- 幂的除法：a^m / a^n = a^(m-n)这条性质表示，当底数相同时，指数相减即可得到商的幂。

例如，2^5 / 2^2 = 2^(5-2) = 2^3- 幂的乘方：(a^m)^n = a^(m*n)这条性质表示，底数的幂再次取幂，相当于指数相乘。

例如，(2^3)^2 = 2^(3*2) = 2^6- 幂的幂的乘法：a^m * b^m = (a * b)^m这条性质表示，底数分别取幂后再相乘，相当于将底数相乘后再取相同的幂。

例如，2^3 * 3^3 = (2 * 3)^3 = 6^3- 0的幂：任何非零数的0次幂都等于1，即a^0 = 1 (a ≠ 0)这条性质表示，任何非零数的0次幂都是1。

例如，2^0 = 1, 3^0 = 1- 幂的倒数： 1 / a^m = a^(-m)这条性质表示，幂的倒数等于底数的负指数幂。

例如，1 / 2^3 = 2^(-3)- 幂的根：(a^m)^(1/n) = a^(m/n)这条性质表示，幂的根等于指数除以根指数的幂。

例如，(2^4)^(1/2) = 2^(4/2) = 2^2- 幂的负指数：a^(-n) = 1 / a^n (a ≠ 0)这条性质表示，幂的负指数等于倒数的幂。

例如，2^(-3) = 1 / 2^33. 幂的几何意义在几何学中，幂也可以用来表示长度、面积和体积。

- 长度：如果一个线段的长度为a，那么a^n表示这条线段的n次方长。

- 面积：如果一个正方形的边长为a，那么a^n表示这个正方形的n次方面积。

- 体积：如果一个立方体的边长为a，那么a^n表示这个立方体的n次方体积。

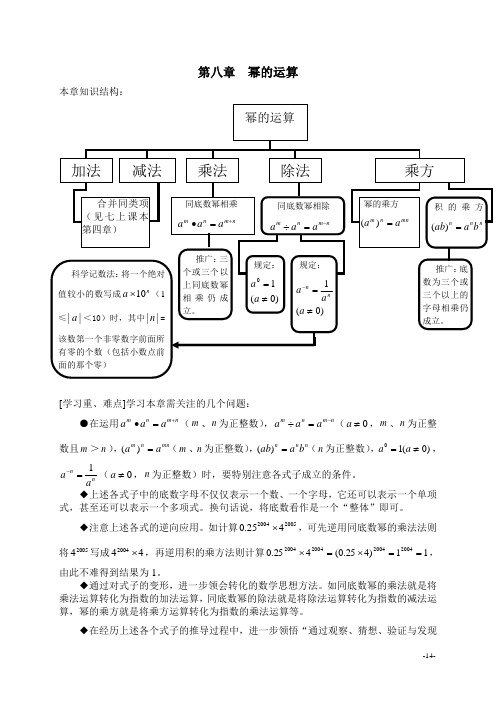
第八章 幂的运算本章知识结构：[学习重、难点]学习本章需关注的几个问题：●在运用n m n m a a a +=∙（m 、n 为正整数），n m n m a a a -=÷（0≠a ，m 、n 为正整数且m ＞n ），mn n m a a =)(（m 、n 为正整数），n n n b a ab =)(（n 为正整数），)0(10≠=a a ，nn a a 1=-（0≠a ，n 为正整数）时，要特别注意各式子成立的条件。

◆上述各式子中的底数字母不仅仅表示一个数、一个字母，它还可以表示一个单项式，甚至还可以表示一个多项式。

换句话说，将底数看作是一个“整体”即可。

◆注意上述各式的逆向应用。

如计算20052004425.0⨯，可先逆用同底数幂的乘法法则将20054写成442004⨯，再逆用积的乘方法则计算11)425.0(425.02004200420042004==⨯=⨯，由此不难得到结果为1。

◆通过对式子的变形，进一步领会转化的数学思想方法。

如同底数幂的乘法就是将乘法运算转化为指数的加法运算，同底数幂的除法就是将除法运算转化为指数的减法运算，幂的乘方就是将乘方运算转化为指数的乘法运算等。

◆在经历上述各个式子的推导过程中，进一步领悟“通过观察、猜想、验证与发现法则、规律”这一重要的数学研究的方法，学习并体会从特殊到一般的归纳推理的数学思想方法。

[例题讲解] 例1 计算：（1）m m m ⨯÷35；（2）)1010(10248÷÷；（3）)()(432x x x x ⋅÷⋅； （4）y y y ⋅÷632)(；（5）1248-÷⨯n n小结：在进行混合运算时，若遇同级运算（加减为同一级，乘除为同一级）时，要严格按照从左到右的顺序进行计算。

如本例中的第（1）小题要避免这样的错误：m m m ⨯÷35=m m m m m =÷=÷+45135。

幂的运算所有法则和逆运算法则幂的运算法则包括乘法法则、除法法则和幂的指数法则。

逆运算法则包括开平方运算和对数运算。

下面将详细介绍这些法则。

一、幂的乘法法则：对于任意实数a和正整数n，有：a^n*a^m=a^(n+m)这条乘法法则表明，当两个幂具有相同的底数时，可以将底数保持不变，指数相加得到新的指数。

二、幂的除法法则：对于任意实数a和正整数n，有：a^n/a^m=a^(n-m)这条除法法则表明，当两个幂具有相同的底数时，可以将底数保持不变，指数相减得到新的指数。

三、幂的指数法则：1.幂的幂法则：对于任意实数a和正整数n、m，有：(a^n)^m=a^(n*m)这条指数法则表明，当一个幂的指数再次被指数化时，可以将指数相乘得到新的指数。

2.幂的乘法法则的推广：对于任意实数a和正整数n_1，n_2，...，n_k，有：a^(n_1)*a^(n_2)*...*a^(n_k)=a^(n_1+n_2+...+n_k)这条指数法则表示，当一个底数出现多次相乘时，可以将所有指数相加得到新的指数。

3.幂的除法法则的推广：对于任意实数a和正整数n_1，n_2，...，n_k，有：a^(n_1)/a^(n_2)/.../a^(n_k)=a^(n_1-n_2-...-n_k)这条指数法则表示，当一个底数出现多次相除时，可以将所有指数相减得到新的指数。

四、逆运算法则：1.幂的开平方运算：对于任意非负实数a和正整数n(a^(1/n))^n=a这条逆运算法则表示，当一个数的n次幂再开n次方时，可以得到该数本身。

2.幂的对数运算：对于任意正实数a、b和正整数n，有：log(base a)(a^n) = n这条逆运算法则表示，当一个数的n次幂再以底数a进行对数运算时，可以得到n。

总结：幂的运算法则包括乘法法则、除法法则和幂的指数法则。

乘法法则指出当两个幂具有相同底数时，可以将指数相加；除法法则指出当两个幂具有相同底数时，可以将指数相减；指数法则包括幂的幂法则和幂的乘法法则的推广，指数可以相乘得到新的指数。

课题指数与指数幂的运算（2）教学目标：1. 理解分数指数幂的概念；掌握有理指数幂的运算性质；会对根式与分数指数幂进行互化；2. 培养学生用“事物相互联系的”观点看问题.通过与初中所学的知识进行类比，理解分数指数幂的概念，进而学习指数幂的性质.3.培养学生观察分析，抽象的能力，渗透“转化”的数学思想；通过运算训练，养成学生严谨治学，一丝不苟的学习习惯；教学重点难点：1．重点：分数指数幂的概念和分数指数幂的运算性质；2．难点：分数指数幂的概念的理解教法与学法：1．教法选择：观察法、归纳推理法、类比分析法2．学法指导：讨论法、发现法、题组练习法教学过程：一、设置情境，激发探索教学环节教学过程设计意图师生活动设置疑问突出主题1.填空（1）；_______32______,6453==-（2）______81______,8144=-=；（3）；______)6(______,)3(5544==(4)；_______a_____,a312510==（5）_____)3(___,27755=-=-）（；（6）.______5____,)4(4466==-分析：对于“填空”中的第四题，既可根据n次方根的概念来解：25101052aa,a)a(=∴=；也可根据n次方根的性质来解：2552510a)a(a==.问题1：观察53102124,a a a a==，结果的指数与被开方数的学习新知前的简单复习，不仅能唤起学生的记忆，而且为学习新课作好了知识上的准备.老师提问，学生回答老师引导学生二、作法总结，变式演练65320)(p p q=⋅2521m m=-三、思维拓展，课堂交流四、归纳小结，课堂延展教学设计说明1．教材地位分析：“指数与指数幂的运算”是高中数学《数学1》第二章《基本初等函数（1）》第一单元《指数函数》的第一节。

“分数指数幂”是“指数与指数幂的运算”第二课时，是在学习了根式的基础上进行的。

分数指数幂是根式的另一种表示，只有学习了根式才能学习指数、指数函数和对数函数。

幂的运算知识要点归纳及答案解析【要点概论】要点一、同底数幂的乘法特点+⋅=m n m n a a a (其中,m n 都是正整数).即同底数幂相乘，底数不变，指数相加.要点诠释：（1）同底数幂是指底数相同的幂，底数可以是任意的实数，也可以是单项式、多项式.（2）三个或三个以上同底数幂相乘时，也具有这一特点，即mnpm n pa a a a++⋅⋅=（,,m n p 都是正整数）.（3）逆用公式：把一个幂分解成两个或多个同底数幂的积，其中它们的底数与原来的底数相同，它们的指数之和等于原来的幂的指数。

即m n m n a a a +=⋅（,m n 都是正整数）.要点二、幂的乘方法则 ()=m nmna a(其中,m n 都是正整数).即幂的乘方，底数不变，指数相乘.要点诠释：（1）公式的推广：(())=m n pmnpa a(0≠a ，,,m n p 均为正整数)（2）逆用公式： ()()nmmnm n aa a ==，根据题目的需要常常逆用幂的乘方运算能将某些幂变形，从而解决问题.要点三、积的乘方法则()=⋅n n n ab a b (其中n 是正整数).即积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘.要点诠释：（1）公式的推广：()=⋅⋅nnnnabc a b c (n 为正整数).（2）逆用公式：()n n na b ab =逆用公式适当的变形可简化运算过程，尤其是遇到底数互为倒数时，算法更简便.如：1010101122 1.22⎛⎫⎛⎫⨯=⨯= ⎪ ⎪⎝⎭⎝⎭重点四、注意事项（1）底数可以是任意实数，也可以是单项式、多项式.（2）同底数幂的乘法时，只有当底数相同时,指数才可以相加.指数为1，算法时不要遗漏.（3）幂的乘方运算时，指数相乘，而同底数幂的乘法中是指数相加.（4）积的乘方运算时须注意，积的乘方要将每一个因式(特别是系数)都要分别乘方. （5）灵活地双向应用运算特点，使运算更加方便、简洁. （6）带有负号的幂的运算，要养成先化简符号的习惯. 【典型例题解析】类型一、同底数幂的乘法特点1、算法：（1）234444⨯⨯；（2）3452622a a a a a a ⋅+⋅-⋅； （3）11211()()()()()nn m n m x y x y x y x y x y +-+-+⋅+⋅+++⋅+．【标准答案与解析】 解：（1）原式234944++==．（2）原式34526177772222aa a a a a a +++=+-=+-=．（3）原式11211222()()()()2()n n m n m n m n m n m x y x y x y x y x y +++-++-+++=+++=+++=+．【总结升华】（2）（3）小题都是混合运算，算法时要注意运算顺序，还要正确地运用相应的运算法则，并要注意区别同底数幂的乘法与整式的加减法的运算法则．在第（2）小题中a 的指数是1．在第（3）小题中把x y +看成一个整体． 举一反三： 【变式】算法：（1）5323(3)(3)⋅-⋅-； （2）221()()ppp x x x +⋅-⋅-（p 为正整数）；（3）232(2)(2)n⨯-⋅-（n 为正整数）．【标准答案】解：（1）原式532532532103(3)333333++=⋅-⋅=-⋅⋅=-=-．（2）原式22122151()ppp p p p p x x x x x +++++=⋅⋅-=-=-． （3）原式525216222(2)22nn n +++=⋅⋅-=-=-．2、已知2220x +=，求2x 的值．【思路点拨】同底数幂乘法的逆用：22222x x +=⋅ 【标准答案与解析】 解：由2220x +=得22220x ⋅=．∴ 25x=．【总结升华】（1）本题逆用了同底数幂的乘法法则，培养了逆向思维能力．（2）同底数幂的乘法法则的逆运用：m nm n aa a +=⋅．类型二、幂的乘方法则3、算法：（1）2()m a ；（2）34[()]m -；（3）32()m a-．【思路点拨】此题是幂的乘方运算，（1）题中的底数是a ，（2）题中的底数是m -，（3）题中的底数a 的指数是3m -，乘方以后的指数应是2(3)62m m -=-． 【标准答案与解析】解：（1）2()m a 2m a =．（2）34[()]m -1212()m m =-=． （3）32()m a-2(3)62m m a a --==．【总结升华】运用幂的乘方法则进行算法时要注意符号的算法及处理，一定不要将幂的乘方与同底数幂的乘法混淆.幂的乘方法则中的底数仍可以为单个数字、字母，也可以是单项式或多项式.4、已知25mx=，求6155m x -的值．【标准答案与解析】 解：∵ 25mx=，∴ 62331115()55520555m m x x -=-=⨯-=．【总结升华】（1）逆用幂的乘方法则：()()mnm n n m a a a ==．（2）本题培养了学生的整体思想和逆向思维能力． 举一反三：【变式1】已知2a x =，3b x =．求32a bx +的值．【标准答案】 解：32323232()()238972a ba b a b xx x x x +===⨯=⨯=g g ．【变式2】已知84=m，85=n，求328+m n的值．【标准答案】 解：因为3338(8)464===mm , 2228(8)525===n n .所以323288864251600+=⨯=⨯=m nm n .类型三、积的乘方法则5、指出下列各题算法是否正确，指出错误并说明原因：（1）22()ab ab =； （2）333(4)64ab a b =； （3）326(3)9x x -=-． 【标准答案与解析】解：（1）错，这是积的乘方，应为：222()ab a b =． （2）对．（3）错，系数应为9，应为：326(3)9x x -=．【总结升华】（1）应用积的乘方时，特别注意观察底数含有几个因式，每个因式都分别乘方． （2）注意系数及系数符号，对系数－1不可忽略．【典型例题】类型一、同底数幂的乘法特点1、算法：(1)35(2)(2)(2)b b b +⋅+⋅+； (2)23(2)(2)x y y x -⋅- ． 【标准答案与解析】解：（1）353519(2)(2)(2)(2)(2)b b b b b +++⋅+⋅+=+=+．（2）23235(2)(2)(2)[(2)](2)x y y x x y x y x y -⋅-=-⋅--=--． 【总结升华】（1）同底数幂相乘时，底数可以是多项式，也可以是单项式．（2）在幂的运算中，经常用到以下变形：()()(),n n n a n a a n ⎧⎪-=⎨-⎪⎩为偶数,为奇数 ()()()()()nnnb a n a b b a n ⎧-⎪-=⎨--⎪⎩为偶数为奇数． 类型二、幂的乘方法则 2、算法：（1）23[()]a b --； （2）32235()()2y y y y +-g ； （3）22412()()m m xx -+⋅； （4）3234()()x x ⋅．【标准答案与解析】解：（1）23[()]a b --236()()a b a b ⨯=--=--．（2）32235()()2y y y y +-⋅666662220y y y y y =+-=-=． （3）22412()()m m xx -+⋅4(22)2(1)8822106m m m m m x x x x x -+-+-=⋅=⋅=．（4）3234()()x x ⋅61218x xx =⋅=．【总结升华】（1）运用幂的乘方法则进行算法时要注意符号的算法及处理，一定不要将幂的乘方与同底数幂的乘法混淆．（2）幂的乘方的法则中的底数仍可以为单个数字、字母，也可以是单项式或多项式．3、已知84=m ，85=n ，求328+m n的值．【思路点拨】由于已知8,8mn的值，所以逆用同底数幂的乘法和幂的乘方把328+m n变成323288(8)(8)m n m n ⨯=⨯，再代入算法.【标准答案与解析】 解：因为3338(8)464===mm , 2228(8)525===n n .所以323288864251600+=⨯=⨯=m nm n .【总结升华】运用整体的观念看待数学问题，是一种重要的数学思维方法.把8,8mn当成一个整体问题就会迎刃而解.同时看到灵活地双向应用运算特点，使运算更加方便、简洁. 举一反三： 【变式】已知322,3mm ab ==，则()()()36322mm m m a b a b b +-⋅＝ ．【标准答案】－5；提示：原式()()()()23223232m m m m ab a b =+-⋅∵∴ 原式＝23222323+-⨯＝－5.类型三、积的乘方法则4、算法：（1）24(2)xy - （2）24333[()]a a b -⋅- 【思路点拨】利用积的乘方的运算特点进行算法. 【标准答案与解析】解：（1）24442448(2)(1)2()16xy x y x y -=-⋅⋅⋅=-． （2）24333[()]a a b -⋅-231293636274227()()()a a b a a ba b =-⋅-=-⋅-⋅=．【总结升华】（1）应用积的乘方时，特别注意观察底数含有几个因式，每个因式都分别乘方．（2）注意系数及系数符号，对系数－1不可忽略． 举一反三：【变式】下列等式正确的个数是( )．①()3236926x yx y -=- ②()326m m a a -= ③()36933a a =④()()57355107103510⨯⨯⨯=⨯ ⑤()()1001001010.520.522-⨯=-⨯⨯A. 1个B. 2个C. 3个D. 4个 【标准答案】A ；提示：只有⑤正确；()3236928x yx y -=-；()326m maa -=-；()3618327aa =；()()57121351071035103.510⨯⨯⨯=⨯=⨯同底数幂的除法【要点梳理】要点一、同底数幂的除法法则同底数幂相除，底数不变，指数相减，即m n m na a a -÷=（a ≠0，m n 、都是正整数，并且m n >）要点诠释：（1）同底数幂乘法与同底数幂的除法是互逆运算.（2）被除式、除式的底数相同，被除式的指数大于除式指数，0不能作除式. （3）当三个或三个以上同底数幂相除时，也具有这一特点. （4）底数可以是一个数，也可以是单项式或多项式. 要点二、零指数幂任何不等于0的数的0次幂都等于1.即01a =（a ≠0）要点诠释：底数a 不能为0，00无意义.任何一个常数都可以看作与字母0次方的积.因此常数项也叫0次单项式.要点三、负整数指数幂任何不等于零的数的n -（n 为正整数）次幂，等于这个数的n 次幂的倒数，即1nna a -=（a ≠0，n 是正整数）.引进了零指数幂和负整数指数幂后，指数的范围已经扩大到了全体整数，以前所学的幂的运算特点仍然成立.m n m n a a a +=（m 、n 为整数，0a ≠）；()mm m ab a b =（m 为整数，0a ≠，0b ≠）()nm mn a a =（m 、n 为整数，0a ≠）.要点诠释：()0na a -≠是n a 的倒数，a 可以是不等于0的数，也可以是不等于0的代数式.例如()1122xy xy -=（0xy ≠），()()551a b a b -+=+（0a b +≠）. 要点四、科学记数法的一般形式（1）把一个绝对值大于10的数表示成10na ⨯的形式，其中n 是正整数，1||10a ≤<（2）利用10的负整数次幂表示一些绝对值较小的数，即10na -⨯的形式，其中n 是正整数，1||10a ≤<.用以上两种形式表示数的方法，叫做科学记数法. 【典型例题】类型一、同底数幂的除法1、算法：（1）83x x ÷；（2）3()a a -÷；（3）52(2)(2)xy xy ÷；（4）531133⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭．【思路点拨】利用同底数幂相除的法则算法．(2)、(4)两小题要注意符号． 【标准答案与解析】解：（1）83835x x xx -÷==．（2）3312()a a aa --÷=-=-．（3）5252333(2)(2)(2)(2)8xy xy xy xy x y -÷===．（4）535321111133339-⎛⎫⎛⎫⎛⎫⎛⎫-÷-=-=-= ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭． 【总结升华】（1）运用法则进行算法的关键是看底数是否相同．（2）运算中单项式的系数包括它前面的符号．2、算法下列各题：（1）5()()x y x y -÷- （2）125(52)(25)a b b a -÷- （3）6462(310)(310)⨯÷⨯ （4）3324[(2)][(2)]x y y x -÷-【思路点拨】（1）若被除式、除式的底数互为相反数时，先将底数变为相同底数再算法，尽可能地去变偶次幂的底数，如1212(52)(25)a b b a -=-．（2）注意指数为1的多项式．如x y -的指数为1，而不是0． 【标准答案与解析】解：（1）5514()()()()x y x y x y x y --÷-=-=-．（2）1251257(52)(25)(25)(25)(25)a b b a b a b a b a -÷-=-÷-=- （3）64626426212(310)(310)(310)(310)910-⨯÷⨯=⨯=⨯=⨯．（4）3324[(2)][(2)]x y y x -÷-9898(2)(2)(2)2x y x y x y x y -=-÷-=-=-．【总结升华】底数都是单项式或多项式，把底数作一个整体利用同底数幂的除法法则进行算法．3、已知32m =，34n =，求129m n+-的值．【标准答案与解析】解： 121222222221222244449(3)33333(3)399(3)33(3)(3)m m m m m m m nn n n n n n ++++-======g g g ． 当32m=，34n=时，原式224239464⨯==． 【总结升华】逆用同底数除法公式，设法把所求式转化成只含3m ，3n的式子，再代入求值．本题是把除式写成了分数的形式，为了便于观察和算法，我们可以把它再写成除式的形式． 举一反三：【变式】已知2552mm⨯=⨯，求m 的值． 【标准答案】解：由2552m m ⨯=⨯得1152m m --=，即11521m m --÷=，1512m -⎛⎫= ⎪⎝⎭，∵ 底数52不等于0和1， ∴ 15522m -⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭，即10m -=，1m =． 类型二、负整数次幂的运算4、算法：（1）223-⎛⎫- ⎪⎝⎭；（2）23131()()a b a b ab ---÷．【标准答案与解析】解：（1）222119434293-⎛⎫-=== ⎪⎝⎭⎛⎫- ⎪⎝⎭； （2）2313123330()()a b a b ab a b a b ab a b b -----÷===g g ．【总结升华】要正确理解负整数指数幂的意义． 举一反三：【变式】算法：4513012222( 3.14)2π----⎛⎫++⨯⨯+- ⎪⎝⎭．【标准答案】解： 4513012222( 3.14)2π----⎛⎫++⨯⨯+- ⎪⎝⎭ 45311111122116212223228=++⨯⨯+=++⨯⨯+ 1151611732832=+++= 5、 已知1327m =，1162n⎛⎫= ⎪⎝⎭，则n m 的值＝________． 【标准答案与解析】解： ∵ 331133273m -===，∴ 3m =-． ∵ 122n n -⎛⎫= ⎪⎝⎭，4162=，∴ 422n -=，4n =-． ∴ 4411(3)(3)81n m -=-==-． 【总结升华】先将127变形为底数为3的幂，122n n -⎛⎫= ⎪⎝⎭，4162=，然后确定m 、n 的值，最后代值求nm ．举一反三： 【变式】算法：（1）1232()a b c --；（2）3232312b c b c ---⎛⎫⨯ ⎪⎝⎭； 【标准答案】 解：（1）原式424626b a b c a c --==． （2）原式8236981212888b b c b cb c c---=⨯==． 类型三、科学记数法6、用科学记数法表示下列各数：（1）0.00001；（2）0.000000203；（3）-0.000135；（4）0.00067【标准答案与解析】解：（1）0.00001＝510-；（2）0.000000203＝72.0310-⨯；（3）-0.000135＝41.3510--⨯；（4）0.00067＝46.710-⨯.【总结升华】注意在10n a -⨯中n 的取值是这个数从左边起第一个不是零的数前面零的个数（包括小数点前边的零）．【巩固练习】一.选择题1. ()()35c c -⋅-的值是( )．A. 8c -B. ()15c -C. 15cD.8c 2．2n n a a +⋅的值是( )．A. 3n a +B. ()2n n a +C. 22n a +D. 8a 3．下列算法正确的是( )．A.224x x x +=B.347x x x x ⋅⋅=C. 4416a a a ⋅=D.23a a a ⋅=4．下列各题中，算法结果写成10的幂的形式，其中正确的是( ).A. 100×210＝310B. 1000×1010＝3010C. 100×310＝510D. 100×1000＝4105．下列算法正确的是( )．A.()33xy xy =B.()222455xy x y -=-C.()22439x x -=-D.()323628xy x y -=-6．若()391528m n a b a b =成立，则( )．A. m ＝6，n ＝12B. m ＝3，n ＝12C. m ＝3，n ＝5D. m ＝6，n ＝5二.填空题7. 若26,25m n ==，则2m n +＝____________．8. 若()319x a a a ⋅=，则x ＝_______．9. 已知35n a =，那么6n a =______．10．若38m a a a ⋅=，则m ＝______；若31381x +=，则x ＝______．11. ()322⎡⎤-=⎣⎦______； ()33n ⎡⎤-=⎣⎦ ______； ()523-＝______．12.若n 是正整数，且210n a =，则3222()8()n n a a --＝__________.三.解答题13. 判断下列算法的正误．（1）336x x x += ( ) （2） 325()y y -=- ( )（3）2224(2)2ab a b -=- （ ） （4） 224()xy xy = ( )14.（1） 3843()()x x x ⋅-⋅-； （2）2333221()()3a b a b -+-；（3）3510(0.310)(0.410)-⨯-⨯⨯⨯； （4）()()3522b a a b --；（5）()()2363353a a a -+-⋅；15.（1）若3335n n x x x +⋅=，求n 的值．（2）若()3915n m a b b a b ⋅⋅=，求m 、n 的值．【标准答案与解析】一.选择练习题1. 【标准答案】D ；【解析】()()()()353588c c c c c +-⋅-=-=-=. 2. 【标准答案】C ；【解析】2222n n n n n a a a a ++++⋅==.3. 【标准答案】D ；【解析】2222x x x +=；348x x x x ⋅⋅=；448a a a ⋅=.4. 【标准答案】C ；【解析】100×210＝410；1000×1010＝1310；100×1000＝510.5. 【标准答案】D ；【解析】()333xy x y =；()2224525xy x y -=；()22439x x -=.6. 【标准答案】C ；【解析】()333915288,39,315m n m n a ba b a b m n ====，解得m ＝3，n ＝5. 二.填空题7. 【标准答案】30；【解析】2226530m n m n +==⨯=g .8. 【标准答案】6；【解析】3119,3119,6x a a x x +=+==.9. 【标准答案】25；【解析】()2632525n n a a ===. 10.【标准答案】5；1；【解析】338,38,5m m a a a a m m +⋅==+==；3143813,314,1x x x +==+==.11.【标准答案】64；9n -；103-；12.【标准答案】200；【解析】()()32322222()8()81000800200n n n n a a a a --=-=-=. 三.解答题13.【解析】解：（1）×；（2）×；（3）×；（4）×14.【解析】解：（1）3843241237()()x x x x x xx ⋅-⋅-=-⋅⋅=-； （2）233322696411()()327a b a b a b a b -+-=-+； （3）3535810(0.310)(0.410)0.30.4101010 1.210-⨯-⨯⨯⨯=⨯⨯⨯⨯=⨯；（4）()()()()()3535822222b a a b a b a b a b --=---=--； （5）()()236331293125325272aa a a a a a -+-⋅=-⋅=-. 15.【解析】解：（1）∵3335n n x xx +⋅= ∴ 4335n x x +=∴4n ＋3＝35∴n ＝8（2）m ＝4，n ＝3解：∵()3915n m a b ba b ⋅⋅= ∴ 333333915n m n m a b b a b a b +⋅⋅=⋅=∴3n ＝9且3m ＋3＝15∴n ＝3且m ＝4就这么多了，祝大家思修不挂科！！！页眉设计。

幂和对数的联系和区别知识点幂和对数是数学中经常被用到的概念，它们在数学和各个领域中都有广泛的应用。

幂和对数之间存在着密切的联系和明显的区别，下面将详细介绍它们的知识点。

一、幂的概念及特性幂是数学中的一个基本运算符号，用来表示某个数自乘若干次的结果。

其中，底数表示要进行幂运算的数，指数表示幂运算的次数。

幂的基本形式为aⁿ，读作“a的n次幂”或“a的n次方”。

幂的特性有以下几点：1. 相同底数的幂相乘，指数相加：aⁿ × aᵐ= aⁿᵐ2. 幂的幂，指数相乘：(aⁿ)ᵐ= aⁿᵐ3. 幂的倒数，指数取负：a⁻ⁿ = 1/aⁿ4. 幂的零次方等于1：a⁰ = 1 （其中a ≠ 0）5. 幂的一次方等于自身：a¹ = a二、对数的概念及特性对数是幂运算的逆运算，用来描述一个数是以另一个数为底的幂的指数。

对数的基本形式为logₐb，读作“以 a 为底 b 的对数”。

对数的特性有以下几点：1. 对数的底数必须大于0且不等于1。

2. 对数中的真数必须是正数。

3. 对数函数的定义域是正实数集，值域是实数集。

4. 对数函数是一个递增函数，即当 b₁ > b₂时，logₐb₁> logₐb₂。

5. 对数函数满足以下等式：logₐ(m×n) = logₐm + logₐn，logₐ(m/n) =logₐm - logₐn，logₐ(m^p) = p × logₐm。

三、幂与对数的联系幂与对数是数学中的基本运算，它们之间存在以下联系：1. 幂和对数是互为逆运算的，即aⁿ = b 等价于n = logₐb。

2. 指数函数和对数函数是互为反函数的，即aⁿ = b 等价于logₐb = n。

3. 幂函数和对数函数的图像关于直线 y = x 对称。

四、幂与对数的区别幂和对数在数学中有明显的区别，主要体现在以下几个方面：1. 幂的运算结果是一个数，而对数是一个指数。

2. 幂的运算是底数自乘若干次，对数的运算是找到一个数是以特定底数的幂的指数。

幂的四种运算法则摘要：一、幂的定义与性质1.幂的定义2.幂的性质二、幂的运算法则1.幂的乘方2.幂的除法3.幂的加法4.幂的减法三、实际应用与例子1.幂在实际生活中的应用2.幂的运算例子四、总结与展望1.总结幂的四种运算法则2.展望幂的进一步研究正文：幂的四种运算法则广泛应用于数学、物理、化学等领域，掌握这些运算法则对于解决实际问题具有重要的意义。

一、幂的定义与性质幂是指将一个数连乘若干次，其中乘方的指数表示连乘的次数。

例如，2的3 次方（2）表示将2 连乘3 次，即2×2×2=8。

幂的性质包括：幂的乘方、幂的除法、幂的加法和幂的减法等。

二、幂的运算法则1.幂的乘方：幂的乘方是指将一个幂与另一个幂相乘，例如，a 的m 次方与a 的n 次方相乘，结果为a 的m+n 次方。

如：2 × 2 = 2。

2.幂的除法：幂的除法是指将一个幂除以另一个幂，例如，a 的m 次方除以a 的n 次方，结果为a 的m-n 次方。

如：2 ÷ 2 = 2。

3.幂的加法：幂的加法是指将两个同底数的幂相加，例如，a 的m 次方与a 的n 次方相加，结果为a 的m+n 次方。

如：2 + 2 = 2。

4.幂的减法：幂的减法是指将两个同底数的幂相减，例如，a 的m 次方与a 的n 次方相减，结果为a 的m-n 次方。

如：2 - 2 = 2。

三、实际应用与例子幂在实际生活中有广泛的应用，如计算机科学中的二进制运算、物理学中的量子力学、化学中的化学反应等。

例如，在计算机科学中，二进制数的幂运算可以用于实现加密和解密算法。

在物理学中，量子力学中的波函数和薛定谔方程都涉及幂运算。

以下是一些幂运算的例子：1.计算2 的5 次方：2 = 2×2×2×2×2 = 32。

2.计算2 的3 次方除以2 的2 次方：2 ÷ 2 = 2×2×2 ÷ 2×2 = 2。

幂的运算以及指数律幂是数学中常见的运算方式之一，它可以用来表示一个数被自身乘以若干次的结果。

指数律是描述幂运算中一些重要规律的数学原理。

本文将深入探讨幂的运算以及指数律的应用。

一、幂的定义及运算法则幂运算的定义如下：对于任意实数a和自然数n，a的n次幂，记作a^n，表示将a连乘n次的结果。

其中，a称为底数，n称为指数。

例如，2的3次幂即为2^3，结果为8。

在幂的运算中，我们需要了解以下几个法则：1. 相同底数幂的乘法法则：a^m * a^n = a^(m+n)这个法则表明，当底数相同时，幂的乘法等价于指数的相加。

例如，2的2次幂乘以2的3次幂等于2的5次幂，即2^2 * 2^3 = 2^(2+3) = 2^5。

2. 相同底数幂的除法法则：a^m / a^n = a^(m-n)这个法则表明，当底数相同时，幂的除法等价于指数的相减。

例如，2的5次幂除以2的2次幂等于2的3次幂，即2^5 / 2^2 = 2^(5-2) = 2^3。

3. 幂的乘法法则：(a^m)^n = a^(m*n)这个法则表明，一个数的指数的指数等于原数的底数和指数相乘。

例如，(2的3次幂)的2次幂等于2的6次幂，即(2^3)^2 = 2^(3*2) =2^6。

4. 幂的除法法则：(a/b)^n = (a^n) / (b^n)这个法则表明，一个数的商的指数等于被除数和除数的指数同时作用于商的分子和分母。

例如，(3/2)的4次幂等于3的4次幂除以2的4次幂，即(3/2)^4 = (3^4) / (2^4)。

二、幂运算的应用幂运算在数学中有着广泛的应用。

以下是几个常见的应用场景：1. 科学计数法科学计数法是一种用于表示非常大或非常小数的方法，它使用幂运算来简化表示。

例如，光速的近似值为3 × 10^8米/秒，其中的10^8表示10的8次幂。

2. 指数函数指数函数是一种常见的数学函数，其定义为y = a^x，其中a是常数，x是自变量。

幂的运算性质
在代数中，幂是一种常见的数学运算符号，表示一个数的某个整数次方。

幂的运算性质在数学中起着重要的作用，掌握这些性质可以帮助我们更好地理解数学中的运算规律和关系。

本文将介绍幂的运算性质，包括乘法法则、除法法则、幂的零次和一次幂、幂的乘方法则以及幂的幂等法则等内容。

乘法法则
•相同底数幂相乘：两个幂的底数相同，指数相加。

–$a^m \\times a^n = a^{m+n}$。

•幂的指数次幂：一个幂的指数乘以另一个幂的指数。

–(a m)n=a mn。

除法法则
•相同底数幂相除：两个幂的底数相同，指数相减。

–$\\frac{a^m}{a^n} = a^{m-n}$。

幂的零次和一次幂
•零次幂：任何非零数的零次幂均等于1。

–a0=1。

•一次幂：任何数的一次幂等于该数本身。

–a1=a。

幂的乘方法则
•幂的乘方：幂的乘方即为底数相同且指数相乘。

–(a m)n=a mn。

幂的幂等法则
•幂的幂：在幂的乘方中，指数的幂即为幂的乘方结果。

–a m n=a mn。

通过学习和理解幂的运算性质，我们不仅可以更加灵活地运用幂运算，还可以在解决数学问题时更加便捷地进行推导和计算。

希望本文对读者有所帮助。

幂的运算知识归纳总结,(知识点,关系,典型考题)A4思维导图问题：幂的运算知识归纳总结，1、自然数幂的定义。

①从1开始到 n（不包括0）这个范围内都是有限个相同因子组成的自然数叫做自然数；②正整数和零既不能被看作是自然数也不能被看作非自然数.只有正数才可以称为自然数。

③在所有自然数中，正整数有无穷多个，负整数有无穷多个。

这些无穷多个正整数和无穷多个负整数统称为整数。

2、整数指数幂：整数 a 的指数是1时，我们就说 a 是一个正整数的指数幂。

例如：2^3，2^2…2^ n，其中， a 是整数， n 是自然数或者正整数．3、有理数指数幂：整数 a 的指数是1时，我们还可以把它写成小数形式，即 a= a×(n/ m)，其中 m 是整数， n 是大于等于1的正整数。

当 a 的指数是正整数时，我们通常用字母 x 表示，而且小数部分的数值保留到整数部分后面。

例如：2^ x，2^ x…2^(x-1)，其中， x 是整数， x-1是小数点。

3、有理数指数幂：整数 a 的指数是1时，我们还可以把它写成小数形式，即 a= a×(n/ m)，其中 m 是整数， n 是大于等于1的正整数。

当 a 的指数是正整数时，我们通常用字母 x 表示，而且小数部分的数值保留到整数部分后面。

例如：2^ x，2^ x…2^(x-1)，其中， x 是整数， x-1是小数点。

4、对于实际问题，应该先计算出各种可能的结果，再利用公式进行推导。

5、要求，每条推论的前提必须是正确的，但在解决具体问题时，我们往往会忽略掉某些条件，使得最终的结果与预期的存在偏差。

因此，遇到需要运用公式进行推导的问题时，一定要先判断好已知条件的真假性，否则会影响到最终结果的准确性。