Ch05_风险资产组合

证券资产组合的风险公式（实用版）目录一、证券资产组合的定义与特点二、证券资产组合的风险与收益公式三、证券资产组合的风险类型及其衡量四、证券资产组合的预期收益率五、结论正文一、证券资产组合的定义与特点证券资产组合是指由两个或两个以上资产构成的集合，这些资产通常是有价证券，如股票、债券等。

证券资产组合的特点是可以通过分散投资降低风险，提高投资回报。

证券资产组合可以包括不同类型的资产，如股票、债券、基金等，这些资产之间的组合可以实现风险与收益的平衡。

二、证券资产组合的风险与收益公式证券资产组合的风险与收益可以通过以下公式来计算：风险 = ∑(wi * ri)其中，wi 表示第 i 项资产在整个组合中的价值比例，ri 表示第 i 项资产的收益率。

通过这个公式，我们可以看到证券资产组合的风险分散效果，即通过合理配置不同资产的价值比例，可以降低整体风险。

收益 = e(rp) * wi其中，e(rp) 表示证券资产组合的预期收益率，wi 表示第 i 项资产在整个组合中的价值比例。

这个公式告诉我们，证券资产组合的收益是通过各资产的预期收益率与它们在组合中的价值比例相乘得到的。

三、证券资产组合的风险类型及其衡量证券资产组合的风险主要分为两类：非系统风险和系统风险。

1.非系统风险：也称为公司风险或可分散风险，它是由于某种特定原因对某一资产收益率产生的影响。

非系统风险可以通过证券资产组合进行分散，降低投资风险。

2.系统风险：也称为市场风险或不可分散风险，它是影响所有资产的、不能通过风险分散而消除的风险。

系统风险通常与政治、经济和其他影响所有资产的市场因素有关。

四、证券资产组合的预期收益率证券资产组合的预期收益率是组成证券资产组合的各种资产收益率的加权平均数，其权数为各种资产在组合中的价值比例。

即：e(rp) = ∑(wi * e(ri))通过这个公式，我们可以计算出证券资产组合的预期收益率，从而为投资者提供投资决策的依据。

71 资产组合选择第四章的购买力风险包括通货膨胀风险（inflation risk ）与通货紧缩风险（deflation risk ）。

商品与服务项目价格的持续上升称为通货膨胀；但其价格的持续下降称为通货紧缩（deflation ）。

通货膨胀与紧缩都会造成证券价格下跌，使投资者蒙受损失。

这是因为在通货膨胀期间，投资者与一般大众的投资财富与收入（房地产投资除外）的购买力因物价上升而下降。

通货紧缩造成商品与财富价值下降，也就是大众购买力降低。

自从第二次世界大战以后，大部分的工业国家很少面临通货紧缩，绝大部分时期面临通货膨胀。

因此，一般人将购买力风险称为通货膨胀风险。

持续宽松的货币政策终会导致通货膨胀的来临。

此外，原料成本的普遍上涨与商品及服务需求的急速增加都是造成通货膨胀的因素。

4．商业风险与财务风险前已述及，属于公司本身的商业风险与财务风险是构成非系统风险的内容。

但公司的某些商业风险与经济变动有周期性的关系。

例如，当经济情况良好时，公司盈利（EBIT ）增加且稳定；但当经济情况恶化时，公司盈利降低，且呈现不稳定。

此种商业风险称为周期性营运风险（cyclical operating risk ），它也属于系统风险。

同理，公司财务风险也会随经济情况的变动（或周期）而变化（升降）。

因此，与经济情况周期变动有关系的财务风险也属于系统风险。

第三节 风险资产与无风险资产之间的资本配置一、风险资产与无风险资产组合资本配置决策主要解决的问题是在整个资产组合中确定各项资产的比例。

简单地说，就是在资产组合中风险资产占多大比重，无风险资产占多大的比重。

如果假定股票和债券为风险资产的代表，国库券为无风险资产的代表，那么，投资者制定资本配置决策就是要解决将投资的多大比例购买股票和债券，多大比例购买国库券。

这也是投资者面临的最基本的决策。

上文中的国库券是指美国的短期国库券，常用来代表无风险资产，但无风险资产有时也指全部货币市场工具，有时则将货币市场中的国库券、商业票据和大额存单作为无风险资产的代表，因为货币市场基金真正大量投资的主要是货币市场中的这三种工具。

资产组合的风险公式
资产组合的风险可以通过计算组合的标准差（或方差）来衡量。

标准差是衡量资产组合收益率波动性的一种指标，它反映了资产收益率相对于其平均值的偏离程度。

假设有n个资产，它们的收益率分别为r1, r2, ..., rn，权重分别为w1, w2, ..., wn，且满足∑wi = 1（即所有权重之和等于1）。

资产组合的预期收益率（即平均收益率）为：
E(rp) = ∑(wi * ri)
其中，E(rp)表示资产组合的预期收益率。

资产组合的方差（或标准差）可以用以下公式计算：
Var(rp) = ∑∑(wi * wj * Cov(ri, rj))
其中，Var(rp)表示资产组合的方差，Cov(ri, rj)表示资产i和资产j之间的协方差。

资产组合的标准差可以通过将方差取平方根得到：
σ(rp) = √Var(rp)
其中，σ(rp)表示资产组合的标准差。

需要注意的是，资产组合的风险并不只由个别资产的风险决定，还受到资产之间的相关性（即协方差）影响。

如果资产之间存在正相关性，那么组合的风险可能较高，而如果资产之间存在负相关性或者没有相关性，那么组合的风险可能较低。

资产组合理论的基本概念由美国经济学家哈里·马科维茨（Harry Markowitz）于1952年提出，他因此获得了1990年的诺贝尔经济学奖。

通过合理的资产配置和风险分散，投资者可以最大程度地实现在给定风险水平下的预期收益。

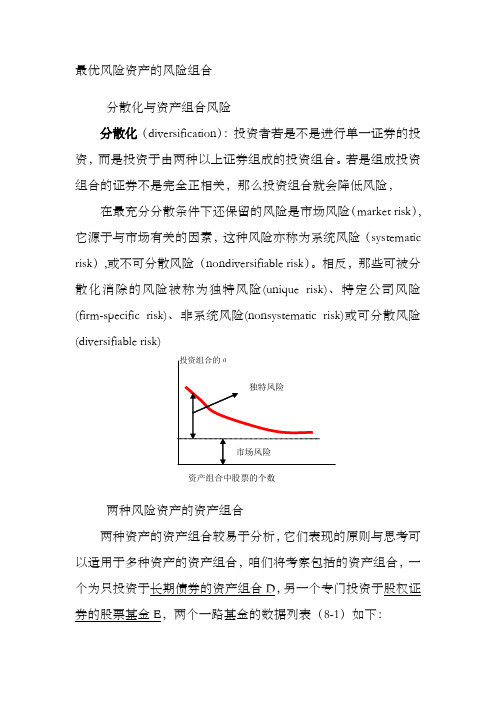
最优风险资产的风险组合分散化与资产组合风险分散化（diversification）：投资者若是不是进行单一证券的投资，而是投资于由两种以上证券组成的投资组合。

若是组成投资组合的证券不是完全正相关，那么投资组合就会降低风险，在最充分分散条件下还保留的风险是市场风险（market risk）,它源于与市场有关的因素，这种风险亦称为系统风险（systematic risk）,或不可分散风险（nondiversifiable risk）。

相反，那些可被分散化消除的风险被称为独特风险(unique risk)、特定公司风险(firm-specific risk)、非系统风险(nonsystematic risk)或可分散风险(diversifiable risk)资产组合中股票的个数两种风险资产的资产组合两种资产的资产组合较易于分析，它们表现的原则与思考可以适用于多种资产的资产组合，咱们将考察包括的资产组合，一个为只投资于长期债券的资产组合D，另一个专门投资于股权证券的股票基金E，两个一路基金的数据列表（8-1）如下：债券 股权 期望收益率E(r)（%） 8 13 标准差为σ（%） 12 20 协方差Cov(r D, r E ) 72 相关系数ρDE 投资于债券基金的份额为w D ,剩下的部份为w E =1- w D 投资于股票基金，这一资产组合的投资收益r p 为： r p =w D r D,+ w E r Er D 为债券基金收益率 r E 为股权基金的收益率。

资产组合的期望收益：E(r p )=w D E(r D )+ w E E(r E )两资产的资产组合的方差： σ2P =W D 2σ2D + WE 2σE 2+2W D W E Cov(r D ,r E )按照第六章式[6-5]得：ρDE =[Cov(r r D, r E )]/[ σD *σE ] Cov(r r D, r E )= ρDE *σD *σE所以：σ2P =W D 2σ2D + WE 2σE 2+2W D W E ρDE *σD *σE当完全正相关时：ρDE =1σ2P =W D 2σ2D + WE 2σE 2+2W D W E *σD *σE =（W D σD + W E σE ）2资产组合的标准差 σP =W D σD + W E σE 当完全负相关时：ρDE =-1σ2P =W D 2σ2D - WE 2σE 2+2W D W E *σD *σE =（W D σD - W E σE ）2资产组合的标准差σP =︱W D σD - W E σE ︱当完全负相关时：ρDE=-1 则W DσD- W EσE=0 因为w E=1- w D 两式成立联立方程得运用表（8-1）中的债券与股票数据得：E(r p)=w D E(r D)+ w E E(r E)= 8w D+ 13w Eσ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE=122 W D2+ 202W E2+2*12*20**W D W E=144 W D2+400 W E2+144 W D W E表8-3 不同相关系数下的期望收益与标准差给定相关性下的资产组合的标准差W D We E(rp) ρ=-1ρ=0ρ=ρ=1011320202020121141610910812121212图8-3中，当债券的投资比例从0-1（股权投资从1-0）时，资产组合的期望收益率从13%（股票的收益率）下降到8%（债券的收益率）1.0 0 -1.0 债券如果w D〉1，w E〈0时，此时的资产组合策略是做一股权基金空头，并把所取得的资金投入到债券基金。

第20讲：投资组合理论（二）风险资产和无风险资产的组合先发放上一讲的答案。

第1题：C。

如果向左弯曲的程度较大，最小方差组合下方的点无效，所以A错误；此时，最小方差组合以下的点的收益率都低于最小方差组合，所以B也错误。

弯曲程度和相关系数有关，和证券各自的标准差无关，所以D错误。

第2题：ABC。

相关系数为1时，组合的标准差刚好是证券标准差的加权平均，D错误；相关系数小于1时，组合的标准差小于证券标准差的加权平均，ABC 正确。

上一讲我们讨论的是风险资产的组合，即单项资产的标准差都大于零。

后来人们想，能不能引入无风险资产，和风险资产组合再组合呢？当然可以。

假设：风险资产组合的平均收益率和标准差分别为r风险组合和σ风险组合无风险资产的平均收益率和标准差分别为R f和σf这两者组合的平均收益率和标准差分别为r p和σp投资于风险资产组合的比重为Q，则投资于无风险资产的比重为1-Q那么：r p = Qr风险组合+ (1-Q) R fσ2p = Q2σ2风险组合+ (1-Q)2σ2f + 2Qσ风险组合(1-Q)σf r风险组合,f这两个式子看不懂的回去看上一讲！接下来开始变魔术。

首先，人家都叫无风险资产了，风险为零，所以σf=0；其次，无风险资产都是我行我素的，和任何人没有关系，所以r风险组合,f=0。

因此，σ2p = Q2σ2风险组合，即σp = Qσ风险组合，再加上r p = Qr风险组合+ (1-Q) R f，不难发现，r p和σp呈线性关系（不明白的回去看上一讲的虚线框，思路是一样的，这里还简单很多）。

既然如此，两点确定一直线，说明无风险资产（假设R f =8%，而σf = 0，所以是纵轴上的点）和机会集中的任何一点都可以连起来。

这就有无数条直线了，到底选哪条呢？看下图：随便画垂直线（黄色虚线），和三条直线的交点风险相同，但收益1最高、2其次，3最低，所以3排除，而1又达不到（和机会集没有交集），那只能是2了。