典型题型的一题多解,培养学生发散性思维能力

例谈如何利用一题多解培养学生的发散思维能力
利用一题多解的教学模式可以帮助学生培养发散思维能力，并激发他们的创造力和想象力。

以下是一些可以采取的教学方法：
1. 提供多种解答方式：在呈现问题或任务时，故意设计多种可能的解答方式，并鼓励学生思考不同的角度和方法。

教师可以引导学生发现和探索问题的多个解决方案，并促进他们进行多样化的思考。

2. 引导学生提出问题：鼓励学生对问题提出疑问，并帮助他们分析问题的本质。

通过不同的提问方式和各种角度的思考，学生可以培养批判性思维和创新思维。

3. 提供资源和工具：教师可以提供学生所需的资源和工具，如图书、网络资源、实验设备等，鼓励学生利用这些资源进行独立的探索和创新。

这样，学生可以根据自己的兴趣和需求选择适合自己的解决方案。

4. 开展小组合作：组织学生进行小组合作，让他们共同讨论问题，并尝试提出不同的解决方案。

小组合作可以激发学生的合作精神和创造思维，帮助他们借鉴和汲取其他同学的想法。

5. 鼓励学生试错和修改：学生在探索过程中可能会遇到困难和错误，教师应鼓励他们从失败中学习，并帮助他们调整和改进解决方案。

这种反思和修改的过程可以促进学生的反馈能力和创造性思维。

通过以上教学方法，学生可以从不同的角度和思路来解决问题，培养他们的发散思维能力。

此外，学生在解决问题的过程中还可以培养一些其他的能力，如分析能力、判断能力、合作能力等。

“一题多解与一题多变”在培养学生发散思维能力中的应用引言：在数学教学中，常用一题多解、一题多变的方法开拓学生的思路，克服思维定势，培养发散性思维的创造性能力。

所谓“一题多解”，就是尽可能用多种不同方法去解决同一道题，更重要的是可以培养学生的思考能力和创造能力。

所谓“一题多变”就是指一个题目反复变换，有利于扩大学生的视野，从而提高解题能力，更能激发学生学习的兴趣，增强求知欲。

一、利用一题多解训练学生的思维能力发散思维是从同一来源材料中探求不同答案的思维过程，培养这种思维能力，有利于提高学生学习的主动性和创新性等。

通过一题多解，引导学生就不同的角度、不同的观点审视分析同一题中的数量关系，用不同解法求得相同结果，可以激发学生去发现和去创造的强烈欲望，训练学生对数学思想和数学方法的娴熟运用，从而培养学生的思维品质，发展学生的创造性思维。

二、利用一题多变培养学生的广阔思维提高学生综合分析能力是帮助学生解答应用题的重要教学手段。

通过“一题多变”的练习可以达到这一目的。

在习题课教学过程中，通过一题多解的表现形式对于培养学生数学兴趣和培养发散性思维的创造能力等起着不可估量的作用。

即通过对习题的题设或结论进行变换，而对同一个问题从多个角度来研究。

这种训练可以增强学生解题的应变能力，培养思维的广阔性和深刻性，从而培养创新思维的品质。

三、在例题讲解中运用一题多解和一题多变（一）在例题讲解中运用一题多解一题多解，一道数学题，因思考的角度不同可得到多种不同的思路，广阔寻求多种解法，提高学生分析问题的能力。

一题多变，对一道数学题或联想，可以得到一系列新的题目，积极开展多种变式题的求解，有助于增强学生面对新问题敢于联想分析予以解决的意识。

下面仅举一例进行一题多解和一题多变来说明：例：已知x、y≥0且x+y=1，求x2+y2的取值范围。

解答此题的方法比较多，下面给出几种常见的思想方法，以作示例。

解法一：（函数思想）由x+y=1得y=1-x，则由于x∈[0，1]，根据二次函数的图象与性质知当x= 时，x2+y2取最小值；当x=0或1时，x2+y2取最大值1。

《一题多解、一题多变，培养学生发散性和创造性思维》江德小学田彩霞在数学教学中，用一题多解、一题多变的方法可以开拓学生的思路，克服思维定势，培养发散性思维的创造性能力。

当解一道题时，由于解题途径、解题方法和计量单位不同，得到多种解法，达到殊途同归的目的。

在多种解法中，根据具体情况进行比较，选择其中最合理，最简捷的一种解法，可以有效地培养学生分析问题和解决问题的能力，并逐步形成解题的灵活性和解题技巧。

一、利用一题多解，训练学生创造性思维。

怎样才能高效率地利用习题课，更好地让学生掌握知识、培养学生创新思维能力？这个问题一直困扰着教师。

我们在上习题课时，不求多讲，而求精讲。

通过一题多解，引导学生就不同的角度、不同的方位、不同的观点分析思考同一问题，从而扩充思维的机遇，使学生不满足固有的方法，而求新法。

例如，讲解例题，如图：搭１个正方形需要４根火柴棒。

（１）按图中方式，搭２个正方形需要几根火柴棒，搭３个正方形需要几根火柴棒。

（２）搭１０个这样的正方形需要多少根火柴棒？与同伴进行交流。

在解决第（2）问时，教师设计了４种思路，为学生提供充分的“体验”和“感知”的广阔平台。

即第一个思路：第一个正方形用４根，每增加一个正方形增加３根，那么搭ｘ个正方形就需要火柴棒［４＋３（ｘ－１）］根；第二个思路：上面的一排和下面的一排各用了ｘ根火柴棒，竖直方向用了（ｘ＋１）根火柴棒，共用了［ｘ＋ｘ＋（ｘ＋１）］根火柴棒；第三个思路的解法是以课后习题的数学理解呈现的：搭ｘ个这样的正方形需要［４ｘ－（ｘ－１）］根火柴棒；第四个思路的解法是第一个正方形可以看成是３根火柴棒加１根火柴棒搭成的。

此后每增加一个正方形就增加３根，搭ｘ个正方形共需（３ｘ＋１）根。

这样，让学生开展变题方法研究并在教学中不断反复运用，可以培养学生解题兴趣，养成独立思考、敢于“标新立异”的好习惯，在练习中学会探索，学会创造，达到获得新知识和培养能力的目的。

运用一题多解的呈现形式，为关注每一个学生的差异和进一步发展他们的思维提供了可能。

略论小学数学教学中的一题多解与学生发散思维的培养摘要：小学数学教育是基础教育性学科，对于培养学生智力和思维能力都具有重要作用。

长期以来，我国小学数学教学对学生发散性思维能力的培养力度不够，在此结合一题多解教学方式对小学数学发散思维的培养进行探索。

关键词：小学数学教学；一题多解；发散思维一、一题多解对培养小学生发散思维的重要作用1.一题多解的数学教学方法能够激发小学生对数学知识的好奇心，让小学生有学习数学的动力。

小学数学知识凝结了人类长期以来摸索的数学知识最基本也是最基础的精华。

传统的数学教学模式中，往往通过数学习题和数学例题的练习帮助小学生掌握数学知识，这是一种比较枯燥和无趣的教学方式，会导致小学生对数学丧失学习兴趣。

针对小学生的年龄特征和心理发展状况，小学数学教师在教学过程中最好能够设置有趣的、生动的教学情境来激发学生的求知欲，让他们产生自觉、自发的去学习数学知识的愿望，而一题多解刚好可以起到这种作用。

一题多解并不是说把一道数学题的多种解法教给学生就万事大吉了，而是要通过一题多解的教学方式培养小学生去探索、去研究、去发现。

在教学中，教师可以常常使用以下用语来诱导学生：想想看这道题还有没有其他的解决方法？你们还有其他的解题思路吗？勇敢智慧的孩子会探索等等，小学生在教师的引导下可以形成善于思考、乐于思考的好习惯。

2.一题多解的数学解题方法可以锻炼小学生的发散性思维和创新性思维。

小学数学不同于小学语文的根本之处在于小学数学着重对学生的思维进行锻炼和提高。

为了增强小学生的发散思维和创新思维，教师可以运用一题多解的教学方式来增强小学生思维的灵活性和变通性。

在探寻一道习题多种解法的过程中，小学生的创新思维也能够得到发展，小学生独立思考的能力在一题多解教学的过程中得到加强。

教师在教学过程中要改变以前自己一个人滔滔不绝的习惯，要把小学生放在学习主体地位上，让学生在课堂上勇于提出自己的见解和疑问，鼓励学生之间进行融洽的沟通和探讨，实现陶行知先生描述的教学相长的教学境界。

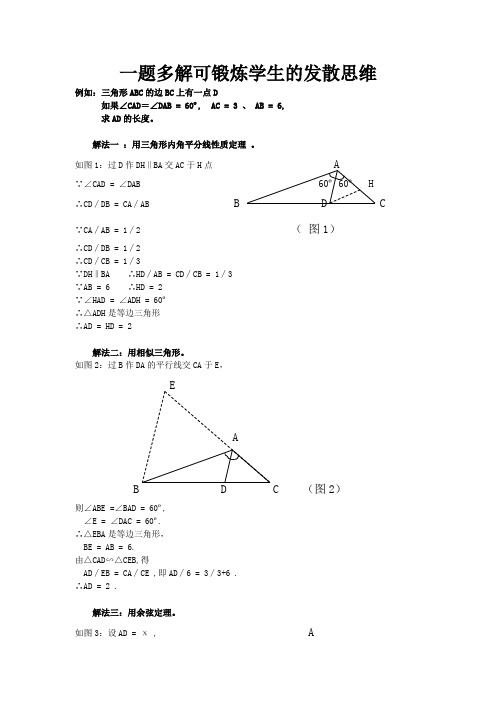
一题多解可锻炼学生的发散思维例如：三角形ABC的边BC上有一点D如果∠CAD＝∠DAB = 60º, AC = 3 、 AB = 6,求AD的长度。

解法一：用三角形内角平分线性质定理。

如图1：过D作DH‖BA交AC于H点 A∵∠CAD = ∠DAB 60º 60º H∴CD∕DB = CA∕AB B D C∵CA∕AB = 1∕2 （图1）∴CD∕DB = 1∕2∴CD∕CB = 1∕3∵DH‖BA ∴HD∕AB = CD∕CB = 1∕3∵AB = 6 ∴HD = 2∵∠HAD = ∠ADH = 60º∴△ADH是等边三角形∴AD = HD = 2解法二：用相似三角形。

如图2：过B作DA的平行线交CA于E，EA（图2）则∠ABE =∠BAD = 60º,∠E = ∠DAC = 60º.∴△EBA是等边三角形，BE = AB = 6.由△CAD∽△CEB,得AD∕EB = CA∕CE ,即AD∕6 = 3∕3+6 .∴AD = 2 .解法三：用余弦定理。

如图3：设AD = х , A则 BD =х²-6χ+36 , 6 60º60º 3DC ²=χ²-3х+9 .（图3） ∴BD ∕DC=AB ∕AC=2 ,∴χ²-6χ+36 = 4(χ²-3χ+9).解得 χ1= O(舍)，χ2 ＝ 2 。

∴AD = 2 .解法四：用坐标法。

如图4：建立直角坐标系，则△ABC 的各顶点的坐标为（图4）A(0,0)、B(6,0)、C(-3/2,33/2) .∵AD 是∠BAC 的平分线，∴BD/DC = 2 = λ ,代入分点坐标公式，得D 点的坐标为χ＝1，у＝3。

用两点间距离公式，得|AD │==+22)3(1 2 .解法五：用面积公式。

由图5，延长CA 到E ，则∠EAB=60º EA6 3B DC （图 5）∵S △ABD+ S △ACD = S △ABC ,∴1/2(6ADsin60º)＋1/2（3ADsin60º）=1/2(3×6sin60º).解得AD ＝2。

2013-09课堂内外教学不只是继承和吸收前人的知识成果，还必须应用和创新，教师应该把传授知识和培养能力、掌握方法放在同等重要的位置。

通过例题示范和习题的一题多解，可以开拓思路，培养学生的发散性思维能力，还可以通过纵横发散，使知识串联、综合沟通，达到举一反三的目的。

一、发散性思维的定义发散性思维，又称扩散性思维、辐射性思维、求异思维，是一种从不同的方向、途径和角度去设想，探求多种答案，最终使问题获得圆满解决的思维方法。

发散性思维的特点是：充分发挥人的想象力，突破原有的知识圈，从一点向四面八方辐射开，并通过知识、观念的重新组合，寻找更新更多的设想、答案或方法。

例如，一题多解、一词多组、一字多意或通过不同方法去探究答案的思维活动。

例如，风筝的用途是什么？有人回答：放在空中玩儿、测量风向、当射击靶子。

还有人回答：传递军事情报、作联络暗号等等。

他们根据不同的想法说出他们各自的答案，这样从不同的角度考虑问题将会促使学生拓展思维，把所学的知识灵活地运用，提高解题能力。

二、培养学生一题多解一题多解训练，就是启发和引导学生从不同的角度、不同的思路，用不同的方法和不同的运算过程去分析、解答同一道数学题的练习活动。

教师在教学活动中做好学生课堂教学的引导者和组织者，在课堂教学中，引导学生从多方面考虑问题，培养学生的一题多解能力，培养学生的发散思维能力，使其养成一个良好的解题方法和思路。

1.启发联想，诱发一题多解联想是由一事物想到另一个事物的思维过程，它是创造性思维的起点。

课堂上启发学生展开联想，进行发散性思维，可以帮助学生突破感官时空限制，扩大感知领域，唤起学生对已有知识和经验的回忆，沟通新旧知识之间的联系，达到一题多解，发展学生的思维。

例.某厂有工人126人，男女工人之比是5∶4，男工有多少人？读题后，引导学生根据“男女工人数之比是5∶4”展开联想：①男工人数是女工人数的；②女工人数是男工人数的；③男工人数占全厂工人的；④女工人数占全厂工人的；⑤男工人数比女工人数多；⑥女工人数比男工人数少；⑦男工人数占5份，女工人数占4份。

在初中数学一题多解中培养学生数学思维的探讨在初中数学教学中，我们经常会遇到一题多解的情况，即一个问题有多种解法。

这种情况对于学生来说可能会有些困惑，但同时也是一个很好的培养学生数学思维的机会。

在本文中，我们将探讨在初中数学教学中如何利用一题多解的情况来培养学生的数学思维能力。

让我们来看一下一题多解的情况在数学教学中的具体体现。

在初中数学课上，老师可能会给学生出一些题目，需要他们利用不同的解法来解答。

一个简单的算术问题，学生可以利用长除法、短除法、列竖式等不同的方法来解决。

或者对于一道几何问题，学生可以利用勾股定理、相似三角形、角平分线定理等不同的定理来求解。

这种情况下，学生需要思考不同的方法，选择适合自己的解法来解决问题，这样就能够激发学生的数学思维。

让我们探讨一题多解如何培养学生的数学思维。

一题多解能够帮助学生建立数学的多元思维。

通过不同的解题方法，学生可以发现数学问题的多样性和灵活性，理解到数学并不是死板的，而是可以有多种不同的解法。

一题多解能够帮助学生提高问题解决能力。

通过不同的解题方法，学生可以学会分析问题、归纳总结问题的特点，培养问题解决的能力。

一题多解可以培养学生的创新思维。

当学生熟练掌握了几种不同的解题方法后，他们可以尝试将这些方法进行综合运用，发现新的规律和方法，从而培养学生的创新意识和能力。

而在实际的教学中，我们可以采用一些方法来引导学生利用一题多解来培养他们的数学思维。

我们可以在教学中特意布置一些一题多解的问题，引导学生思考不同的解法。

我们可以鼓励学生在解题过程中主动探索不同的解法，并鼓励他们分享自己的解题思路，交流讨论不同的解题方法。

我们可以设计一些有关一题多解的探究性问题，让学生通过实际的探索，体会到一题多解对数学思维的重要性。

一题多解是数学教学中的一种特殊情况，它不仅能够激发学生的学习兴趣，而且能够培养学生的数学思维。

在教学中，我们应该充分利用一题多解的机会，培养学生的多元思维、问题解决能力和创新思维。

发展学生思维的求异性——一题多解在平时的教学中，不但要训练学生的集中思维，同时也要给学生创设较多的训练发散性思维的机会，教师要鼓励学生从不同的角度去思考，用自己喜欢的方法去解答，从自身的生活背景中发现数学，创造数学，使用数学，使学生不但擅长单向思维，而且习惯于多向思维，发展学生求异思维。

案例1：在复习相遇问题时，向学生出示了这样一道应用题。

客车和火车同时从相距360千米的甲乙两地相对而行，经过3小时相遇，已知货车每小时行68千米，客车每小时行多少千米？师：大家认真分析题中的数量关系，看有哪些不同的解法。

解法1：（360-68×3）÷3＝（360-204）÷3＝156÷3=52(千米) 答：客车每小时行52千米。

解法2:360÷3-68=120-68=5 2（千米）答：客车每小时行52千米。

师：还能够用什么方法解答?解法3：解：设客车每小时行X千米68×3＋3X=3603X=360-204X=52（千米）答：客车每小时行52千米。

解法4：解：设客车每小时行X千米3（68+X）=36068+X=120X=52（千米）答：客车每小时行52千米。

案例2：学习了比的应用后，向学生出示了这样一道题。

福和希望小学五六年级学生参加植树活动，六年级植树的棵树比五年级多1／4，五六年级共植树180棵，五六年级各植树多少棵？师：同学们对于这道题，大家有哪些不同的解法？学生纷纷展示解法1:由题意可知五六年级植树的棵树比为4：5180×4／9＝80(棵)180×5/9=100（棵）答：五年级植树80棵，六年级植树100棵。

解法2:由题意可知六年级植树的棵树是五年级的5／4 180÷（1+5／4）=80（棵）80×5／4＝100（棵）答：五年级植树80棵，六年级植树100棵。

解法3：解：设五年级植树X棵X+5／4X=180或（1+5／4）X=180X=85／4X=100 答：五年级植树80棵，六年级植树100棵。

亠题多解，培养学生的发散性思维教学不只是继承和吸收前人的知识成果，还必须应用和创新，教师应该把传授知识和培养能力、掌握方法放在同等重要的位置。

通过例题示范和习题的一题多解，可以幵拓思路，培养学生的发散性思维能力，还可以通过纵横发散，使知识串联、综合沟通，达到举一反三的目的。

一、发散性思维的定义发散性思维，又称扩散性思维、辐射性思维、求异思维，是一种从不同的方向、途径和角度去设想，探求多种答案，最终使问题获得圆满解决的思维方法。

发散性思维的特点是：充分发挥人的想象力，突破原有的知识圈，从一点向四面八方辐射幵，并通过知识、观念的重新组合，寻找更新更多的设想、答案或方法。

例如，一题多解、一词多组、一字多意或通过不同方法去探究答案的思维活动。

例如，风筝的用途是什么？有人回答：放在空中玩儿、测量风向、当射击靶子。

还有人回答：传递军事情报、作联络暗号等等。

他们根据不同的想法说出他们各自的答案，这样从不同的角度考虑问题将会促使学生拓展思维，把所学的知识灵活地运用，提高解题能力。

二、培养学生一题多解一题多解训练，就是启发和引导学生从不同的角度、不同的思路，用不同的方法和不同的运算过程去分析、解答同一道数学题的练习活动。

教师在教学活动中做好学生课堂教学的引导者和组织者，在课堂教学中，引导学生从多方面考虑问题，培养学生的一题多解能力，培养学生的发散思维能力，使其养成一个良好的解题方法和思路。

1. 启发联想，诱发一题多解联想是由一事物想到另一个事物的思维过程，它是创造性思维的起点。

课堂上启发学生展开联想，进行发散性思维，可以帮助学生突破感官时空限制，扩大感知领域，唤起学生对已有知识和经验的回忆，沟通新旧知识之间的联系，达到一题多解，发展学生的思维。

例•某厂有工人126人，男女工人之比是5 ：4,男工有多少人？读题后，引导学生根据“男女工人数之比是5 : 4”展幵联想：①男工人数是女工人数的；②女工人数是男工人数的；③男工人数占全厂工人的：④女工人数占全厂工人的；⑤男工人数比女工人数多；⑥女工人数比男工人数少；⑦男工人数占5份，女工人数占4份。