复合场大题压轴

带电粒子在复合场中的运动压轴难题知识归纳总结附答案解析一、带电粒子在复合场中的运动压轴题1．如图所示，以两虚线为边界，中间存在平行纸面且与边界垂直的水平电场，宽度为d，两侧为相同的匀强磁场，方向垂直纸面向里．一质量为m、带电量q+、重力不计的带电粒子，以初速度1v垂直边界射入磁场做匀速圆周运动，后进入电场做匀加速运动，然后第二次进入磁场中运动，此后粒子在电场和磁场中交替运动．已知粒子第二次在磁场中运动的半径是第一次的二倍，第三次是第一次的三倍，以此类推．求：（1）粒子第一次经过电场的过程中电场力所做的功1W（2）粒子第n次经过电场时电场强度的大小n E（3）粒子第n次经过电场所用的时间n t（4）假设粒子在磁场中运动时，电场区域场强为零．请画出从粒子第一次射入磁场至第三次离开电场的过程中，电场强度随时间变化的关系图线（不要求写出推导过程，不要求标明坐标刻度值）．【来源】河北省衡水中学滁州分校2018届高三上学期全真模拟物理试题【答案】（1）21132mvW =（2）21(21)2nn mvEqd+=（3）12(21)ndtn v=+（4）如图；【解析】（1）根据mvrqB=，因为212r r=，所以212v v=，所以221211122W mv mv=-,（2）=，，所以．（3），，所以．(4)2．如图所示，在坐标系xoy中，过原点的直线OC与x轴正向的夹角φ=120°，在OC右侧有一匀强电场；在第二、三象限内有一匀强磁场，其上边界与电场边界重叠、右边界为y 轴、左边界为图中平行于y轴的虚线，磁场的磁感应强度大小为B，方向垂直抵面向里。

一带正电荷q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域，并从O 点射出，粒子射出磁场的速度方向与x轴的夹角θ＝30°，大小为v，粒子在磁场中的运动轨迹为纸面内的一段圆弧，且弧的半径为磁场左右边界间距的两倍。

粒子进入电场后，在电场力的作用下又由O点返回磁场区域，经过一段时间后再次离开磁场。

带电粒子在复合场中的运动压轴难题综合题及答案解析一、带电粒子在复合场中的运动压轴题1．如图所示，直径分别为D 和2D 的同心圆处于同一竖直面内，O 为圆心，GH 为大圆的水平直径。

两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场．间距为d 的两平行金属极板间有一匀强电场，上极板开有一小孔．一质量为m 、电量为＋q的粒子由小孔下方2d 处静止释放，加速后粒子以竖直向上的速度v 射出电场，由H 点紧靠大圆内侧射入磁场。

不计粒子的重力。

(1)求极板间电场强度的大小；(2)若粒子运动轨迹与小圆相切，求Ⅰ区磁感应强度的大小；(3)若Ⅰ区、Ⅱ区磁感应强度的大小分别为2mv qD 、4mv qD,粒子运动一段时间后再次经过H 点，求这段时间粒子运动的路程．【来源】2015年全国普通高等学校招生统一考试物理（山东卷带解析) 【答案】（1）2mv qd（2）4mv qD 或43mv qD （3）5.5πD 【解析】【分析】【详解】(1)粒子在电场中，根据动能定理2122d Eq mv ⋅=，解得2mv E qd= (2)若粒子的运动轨迹与小圆相切，则当内切时，半径为/2E R 由211v qvB m r =，解得4mv B qD = 则当外切时，半径为e R由212v qvB m r =，解得43mv B qD = (2)若Ⅰ区域的磁感应强度为220932qB L m U =，则粒子运动的半径为0010016819U U U ≤≤；Ⅱ区域的磁感应强度为2012qU mv =，则粒子运动的半径为2v qvB m r=； 设粒子在Ⅰ区和Ⅱ区做圆周运动的周期分别为T 1、T 2，由运动公式可得：1112R T v π=；034r L =据题意分析，粒子两次与大圆相切的时间间隔内，运动轨迹如图所示，根据对称性可知，Ⅰ区两段圆弧所对的圆心角相同，设为1θ，Ⅱ区内圆弧所对圆心角为2θ，圆弧和大圆的两个切点与圆心O 连线间的夹角设为α，由几何关系可得：1120θ=；2180θ=；60α=粒子重复上述交替运动回到H 点，轨迹如图所示，设粒子在Ⅰ区和Ⅱ区做圆周运动的时间分别为t 1、t 2，可得：r U ∝；1056U L U L =设粒子运动的路程为s ，由运动公式可知：s=v(t 1+t 2)联立上述各式可得：s=5.5πD2．小明受回旋加速器的启发，设计了如图1所示的“回旋变速装置”．两相距为d 的平行金属栅极板M 、N ，板M 位于x 轴上，板N 在它的正下方．两板间加上如图2所示的幅值为U 0的交变电压，周期02m T qBπ=．板M 上方和板N 下方有磁感应强度大小均为B 、方向相反的匀强磁场．粒子探测器位于y 轴处，仅能探测到垂直射入的带电粒子．有一沿x 轴可移动、粒子出射初动能可调节的粒子发射源，沿y 轴正方向射出质量为m 、电荷量为q （q ＞0）的粒子．t =0时刻，发射源在（x ，0）位置发射一带电粒子．忽略粒子的重力和其它阻力，粒子在电场中运动的时间不计．（1）若粒子只经磁场偏转并在y =y 0处被探测到，求发射源的位置和粒子的初动能； （2）若粒子两次进出电场区域后被探测到，求粒子发射源的位置x 与被探测到的位置y 之间的关系【来源】【省级联考】浙江省2019届高三上学期11月选考科目考试物理试题【答案】（1）00x y = ，()202qBy m（2）见解析 【解析】【详解】（1）发射源的位置00x y =，粒子的初动能：()2002k qBy E m=；（2）分下面三种情况讨论： （i ）如图1，002k E qU >由02101mv mv mv y R R Bq Bq Bq ===、、， 和221001122mv mv qU =-，222101122mv mv qU =-， 及()012x y R R =++，得()()22002224x y yqB mqU yqB mqU qB qB =++（ii ）如图2，0002k qU E qU <<由020mv mv y d R Bq Bq --==、， 和220201122mv mv qU =+， 及()032x y d R =--+，得()222023)2x y d y d q B mqU qB =-++++（；（iii ）如图3，00k E qU <由020mv mv y d R Bq Bq --==、， 和220201122mv mv qU =-， 及()04x y d R =--+，得()222042x y d y d q B mqU qB =--++-；3．如图所示，以两虚线为边界，中间存在平行纸面且与边界垂直的水平电场，宽度为d ，两侧为相同的匀强磁场，方向垂直纸面向里．一质量为m 、带电量q +、重力不计的带电粒子，以初速度1v 垂直边界射入磁场做匀速圆周运动，后进入电场做匀加速运动，然后第二次进入磁场中运动，此后粒子在电场和磁场中交替运动．已知粒子第二次在磁场中运动的半径是第一次的二倍，第三次是第一次的三倍，以此类推．求：（1）粒子第一次经过电场的过程中电场力所做的功1W（2）粒子第n 次经过电场时电场强度的大小n E（3）粒子第n 次经过电场所用的时间n t（4）假设粒子在磁场中运动时，电场区域场强为零．请画出从粒子第一次射入磁场至第三次离开电场的过程中，电场强度随时间变化的关系图线（不要求写出推导过程，不要求标明坐标刻度值）．【来源】河北省衡水中学滁州分校2018届高三上学期全真模拟物理试题【答案】（1）21132mv W = （2）21(21)2n n mv E qd +=（3）12(21)n d t n v =+ （4）如图；【解析】（1）根据mv r qB =，因为212r r =，所以212v v =，所以221211122W mv mv =-, （2）=，，所以． （3），，所以．(4)4．如图所示，在无限长的竖直边界NS 和MT 间充满匀强电场，同时该区域上、下部分分别充满方向垂直于NSTM 平面向外和向内的匀强磁场，磁感应强度大小分别为B 和2B ，KL 为上下磁场的水平分界线，在NS 和MT 边界上，距KL 高h 处分别有P 、Q 两点，NS 和MT 间距为1.8h，质量为m，带电荷量为＋q的粒子从P点垂直于NS边界射入该区域，在两边界之间做圆周运动，重力加速度为g．(1)求电场强度的大小和方向；(2)要使粒子不从NS边界飞出，求粒子入射速度的最小值；(3)若粒子能经过Q点从MT边界飞出，求粒子入射速度的所有可能值．【来源】【全国百强校】2017届浙江省温州中学高三3月高考模拟物理试卷（带解析)【答案】（1）mgqE=，方向竖直向上（2）min(962)qBhvm-=（3）0.68qBhvm=；0.545qBhvm=；0.52qBhvm=【解析】【分析】（1）粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，电场力与重力合力为零；（2）作出粒子的运动轨迹，由牛顿第二定律与数学知识求出粒子的速度；（3）作出粒子运动轨迹，应用几何知识求出粒子的速度．【详解】（1）粒子在磁场中做匀速圆周运动，电场力与重力合力为零，即mg=qE，解得：mgqE=，电场力方向竖直向上，电场方向竖直向上；（2）粒子运动轨迹如图所示：设粒子不从NS 边飞出的入射速度最小值为v min ，对应的粒子在上、下区域的轨道半径分别为r 1、r 2，圆心的连线与NS 的夹角为φ，粒子在磁场中做匀速圆周运动，由牛顿第二定律得：2v qvB m r =， 解得，粒子轨道半径：v r qBπ=， min1v r qB π=，2112r r =， 由几何知识得：（r 1+r 2）sin φ=r 2，r 1+r 1cos φ=h ， 解得：min 962)qBh v m=（﹣； （3）粒子运动轨迹如图所示，设粒子入射速度为v ，粒子在上、下区域的轨道半径分别为r 1、r 2，粒子第一次通过KL 时距离K 点为x ，由题意可知：3nx =1.8h （n =1、2、3…）3(962)2h x -≥()2211x r h r =--， 解得：120.361)2h r n =+（，n ＜3.5， 即：n =1时， 0.68qBh v m=，n =2时，0.545qBh v m =， n =3时，0.52qBh v m=； 答：（1）电场强度的大小为mgq E =，电场方向竖直向上； （2）要使粒子不从NS 边界飞出，粒子入射速度的最小值为min 962)qBh v m=（﹣． （3）若粒子经过Q 点从MT 边界飞出，粒子入射速度的所有可能值为：0.68qBh v m =、或0.545qBh v m =、或0.52qBh v m=． 【点睛】本题考查了粒子在磁场中的运动，分析清楚粒子运动过程、作出粒子运动轨迹是正确解题的前提与关键，应用平衡条件、牛顿第二定律即可正确解题，解题时注意数学知识的应用．5．质谱分析技术已广泛应用于各前沿科学领域．汤姆孙发现电子的质谱装置示意如图，M 、N 为两块水平放置的平行金属极板，板长为L ，板右端到屏的距离为D ，且D 远大于L ，O O '为垂直于屏的中心轴线，不计离子重力和离子在板间偏离O O '的距离．以屏中心O 为原点建立xOy 直角坐标系，其中x 轴沿水平方向，y 轴沿竖直方向．（1）设一个质量为0m 、电荷量为0q 的正离子以速度0v 沿O O '的方向从O '点射入，板间不加电场和磁场时，离子打在屏上O 点．若在两极板间加一沿y +方向场强为E 的匀强电场，求离子射到屏上时偏离O 点的距离0y ；（2）假设你利用该装置探究未知离子，试依照以下实验结果计算未知离子的质量数． 上述装置中，保留原电场，再在板间加沿y -方向的匀强磁场．现有电荷量相同的两种正离子组成的离子流，仍从O ＇点沿O O '方向射入，屏上出现两条亮线．在两线上取y 坐标相同的两个光点，对应的x 坐标分别为3.24mm 和3.00mm ，其中x 坐标大的光点是碳12离子击中屏产生的，另一光点是未知离子产生的．尽管入射离子速度不完全相等，但入射速度都很大，且在板间运动时O O '方向的分速度总是远大于x 方向和y 方向的分速度．【来源】2018年9月29日 《每日一题》一轮复习-周末培优【答案】（1）00200q ELD y m v =（2）214u m ≈故该未知离子的质量数为14【解析】：（1）离子在电场中受到的电场力 0y F q E =①离子获得的加速度0yy F a m =②离子在板间运动的时间00L t v =③ 到达极板右边缘时，离子在y +方向的分速度0y y v a t =④离子从板右端到达屏上所需时间00'D t v =⑤ 离子射到屏上时偏离O 点的距离00'y y v t =由上述各式，得00200q ELD y m v =⑥ （2）设离子电荷量为q ，质量为m ，入射时速度为v ，磁场的磁感应强度为B ，磁场对离子的洛伦兹力x F qvB =⑦已知离子的入射速度都很大，因而离子在磁场中运动时间甚短，所经过的圆弧与圆周相比甚小，且在板间运动时，'O O 方向的分速度总是远大于在x 方向和y 方向的分速度，洛伦兹力变化甚微，故可作恒力处理，洛伦兹力产生的加速度x qvB a m=⑧ x a 是离子在x 方向的加速度，离子在x 方向的运动可视为初速度为零的匀加速直线运动，到达极板右端时，离子在x 方向的分速度()x x qvB L qBL v a t m v m===⑨ 离子飞出极板到达屏时，在x 方向上偏离O 点的距离'()x qBL D qBLD x v t m v mv==⑩ 当离子的初速度为任意值时，离子到达屏上时的位置在y 方向上偏离O 点的距离为y ，考虑到⑥式，得2qELD y mv =⑾ 由⑩、⑾两式得 2k x y m =⑿ 其中2qB LD k E= 上式表明，k 是与离子进入板间初速度无关的定值，对两种离子均相同，由题设条件知，x 坐标3.24mm 的光点对应的是碳12离子，其质量为112m u =，x 坐标3.00mm 的光点对应的是未知离子，设其质量为2m ，由⑿式代入数据可得214m u ≈⒀故该未知离子的质量数为14．6．如图所示，两条竖直长虚线所夹的区域被线段MN 分为上、下两部分，上部分的电场方向竖直向上，下部分的电场方向竖直向下，两电场均为匀强电场且电场强度大小相同。

高考物理带电粒子在复合场中的运动压轴题综合题及答案解析一、带电粒子在复合场中的运动压轴题1．如图甲所示，空间存在一范围足够大的垂直于xOy 平面向外的匀强磁场，磁感应强度大小为B ．让质量为m ，电荷量为q （q ＞0）的粒子从坐标原点O 沿xOy 平面以不同的初速度大小和方向入射到磁场中．不计重力和粒子间的影响．（1）若粒子以初速度v 1沿y 轴正向入射，恰好能经过x 轴上的A （a ，0）点，求v 1的大小；（2）已知一粒子的初速度大小为v （v ＞v 1），为使该粒子能经过A （a ，0）点，其入射角θ（粒子初速度与x 轴正向的夹角）有几个？并求出对应的sin θ值；（3）如图乙，若在此空间再加入沿y 轴正向、大小为E 的匀强电场，一粒子从O 点以初速度v 0沿y 轴正向发射．研究表明：粒子在xOy 平面内做周期性运动，且在任一时刻，粒子速度的x 分量v x 与其所在位置的y 坐标成正比，比例系数与场强大小E 无关．求该粒子运动过程中的最大速度值v m ．【来源】2013年全国普通高等学校招生统一考试理科综合能力测试物理（福建卷带解析) 【答案】⑴；⑵两个 sin θ=；⑶＋．【解析】试题分析：(1)当粒子沿y 轴正向入射，转过半个圆周至A 点，半径R 1＝a/2由运动定律有2111v Bqv m R =解得12Bqav m=(2)如右图所示，O 、A 两点处于同一圆周上，且圆心在x ＝2a的直线上，半径为R ，当给定一个初速率v 时， 有2个入射角，分别在第1、2象限．即 sinθ′＝sinθ＝2a R另有2v Bqv m R=解得 sinθ′＝sinθ＝2aqBmv(3)粒子在运动过程中仅电场力做功，因而在轨道的最高点处速率最大，用y m 表示其y 坐标，由动能定理有 qEy m＝12mv2m－12mv2由题知 v m＝ky m若E＝0时，粒子以初速度v0沿y轴正向入射，有 qv0B＝m2vR在最高处有 v0＝kR0联立解得22()mE Ev vB B=++考点：带电粒子在符合场中的运动；动能定理．2．如图甲所示，间距为d、垂直于纸面的两平行板P、Q间存在匀强磁场．取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示。

复合场大题1．(12分）在平面直角坐标系xOy 中，第Ⅰ象限存在沿y 轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B 。

一质量为m 、电荷量为q 的带正电的粒子从y 轴正半轴上的M 点以速度v 0垂直于y 轴射入电场,经x 轴上的N 点与x 轴正方向成θ＝60°角射入磁场,最后从y 轴负半轴上的P 点垂直于y 轴射出磁场,如图所示．不计粒子重力， 求(1)M 、N 两点间的电势差U MN ；(2）粒子在磁场中运动的轨道半径r ； （3)粒子从M 点运动到P 点的总时间t 。

【答案】（1）2032mv q (2)02mv qB （3）3323mqBπ+【解析】试题分析： （1）设粒子过N 点时的速度为v ，有0v v＝cos θ ①故v ＝2v 0② 粒子从M 点运动到N 点的过程，有 qU MN ＝12mv 2－12m 20v ③U MN ＝2032mv q④（2）粒子在磁场中以O ′为圆心做匀速圆周运动，半径为O ′N,有qvB ＝2mv r ⑤ r ＝02mv qB⑥（3)由几何关系得ON ＝rsin θ ⑦设粒子在电场中运动的时间为t 1，有ON ＝v 0t 1⑧t 1＝3mqB粒子在磁场中做匀速圆周运动的周期T ＝2m qB π⑩设粒子在磁场中运动的时间为t 2，有t 2＝2πθπ-T ⑪t 2＝23M qB π ⑫ t ＝t 1＋t 2 t ＝3323mqBπ+ 考点:该题考察了电子在电场中的偏转和在磁场中的匀速圆周运动,点评:此题要求首先要分析电子在各个区域内的运动情况，必要时画出电子的运动轨迹图，了解图中的几何关系．利用电子在电场中偏转时的速度的合成与分解，解决电子 在电场中运动的相关问题;利用电子在匀速圆周运动的半径和周期公式，结合洛伦兹力提供向心力可解答电子在磁场中运动的相关问题．电子从磁场边界以一定的角度射入只有一个边界的匀强磁场,当再次射出磁场时，速度与边界的夹角与原来的相等．解题时充分利用这个结论,对解题有非常大的帮助．2．（14分）如图所示，真空中有以()0,r 为圆心，半径为r 的圆形匀强磁场区域，磁场的磁感应强度大小为B ，方向垂直于纸面向里，在r y =的虚线上方足够大的范围内,有方向水平向左的匀强电场，电场强度的大小为E ,从O 点向不同方向发射速率相同的质子，质子的运动轨迹均在纸面内，且质子在磁场中的偏转半径也为r ,已知质子的电荷量为q ，质量为m ,不计重力、粒子间的相互作用力及阻力的作用。

高考物理带电粒子在复合场中的运动压轴难题综合题附答案解析一、带电粒子在复合场中的运动压轴题1．如图甲所示，间距为d 、垂直于纸面的两平行板P 、Q 间存在匀强磁场．取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示。

t =0时刻，一质量为m 、带电荷量为+q 的粒子（不计重力），以初速度0v 由Q 板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区．当0B 和B T 取某些特定值时，可使0t =时刻入射的粒子经t ∆时间恰能垂直打在P 板上（不考虑粒子反弹）。

上述0m q d v 、、、为已知量。

（1）若B 12t T ∆= ，求0B ； （2）若B 32t T ∆=，求粒子在磁场中运动时加速度的大小； （3）若004mv B qd=，为使粒子仍能垂直打在P 板上，求B T 。

【来源】2014年全国普通高等学校招生统一考试理科综合能力测试物理（山东卷带解析)【答案】（1）0mv qd （2）203v d（3）03d v π 或01arcsin 242d v π⎛⎫+ ⎪⎝⎭【解析】 【分析】 【详解】（1）设粒子做匀速圆周运动的半径1R ，由牛顿第二定律得2001mv qv B R = ……①据题意由几何关系得1R d = ……②联立①②式得0mv B qd=……③ （2）设粒子做圆周运动的半径为2R ，加速度大小为a ，由圆周运动公式得202v a R= ……④据题意由几何关系得23R d = ……⑤联立④⑤式得203v a d= ……⑥ （3）设粒子做圆周运动的半径为R ，周期为T ，由圆周运动公式得2RT v π=……⑦ 由牛顿第二定律得2000mv qv B R= ……⑧ 由题意知004mv B qd=，代入⑧式得 4d R = ……⑨粒子运动轨迹如图所示，1O 、2O 为圆心，1O 、2O 连线与水平方向夹角为θ，在每个B T 内，只有A 、B 两个位置才有可能垂直击中P 板，且均要求02πθ<<，由题意可知B 222T T πθθ+= ……⑩ 设经历完整B T 的个数为n （0n =，1，2，3．．．．．．） 若在B 点击中P 板，据题意由几何关系得2(sin )R R R n d θ++= ……⑪当n =0时，无解； 当n =1时联立⑨⑪式得6πθ=或（1sin 2θ=）……⑫ 联立⑦⑨⑩⑫式得B 03dT v π=……⑬当2n ≥时，不满足090θ︒<<的要求；若在B 点击中P 板，据题意由几何关系得2sin 2(sin )R R R R n d θθ+++=……⑭当0n =时无解当1n =时，联立⑨⑭式得1arcsin 4θ= 或（1sin 4θ=）……⑰联立⑦⑧⑨⑩⑰式得B 01arcsin 242d T v π⎛⎫=+ ⎪⎝⎭ ……⑱当2n ≥时，不满足090θ︒<<的要求。

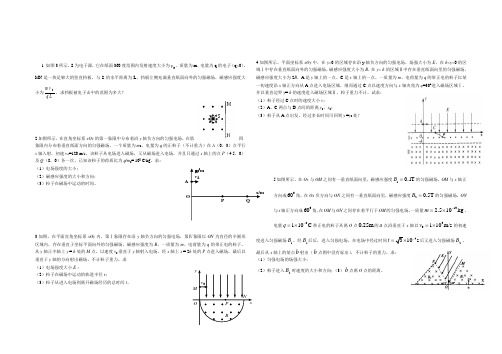
1如图3所示，S为电子源，它在纸面360度范围内发射速度大小为v0，质量为m，电量为q的电子（q<0），MN是一块足够大的竖直挡板，与S的水平距离为L，挡板左侧充满垂直纸面向外的匀强磁场，磁感应强度大小为m vq L0，求挡板被电子击中的范围为多大？2如图所示，在直角坐标系xOy的第一象限中分布着沿y轴负方向的匀强电场，在第四象限内分布着垂直纸面方向的匀强磁场。

一个质量为m0，电量为q的正粒子（不计重力）在A（0，3）点平行x轴入射，初速v A=120 m/s，该粒子从电场进入磁场，又从磁场进入电场，并且只通过x轴上的点P（4.5，0）及Q（8，0）各一次，已知该粒子的荷质比为q/m0= 108 C/kg。

求：（1）电场强度的大小；（2）磁感应强度的大小和方向；（3）粒子在磁场中运动的时间。

3如图，在平面直角坐标系xOy内，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限以ON为直径的半圆形区域内，存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。

一质量为m、电荷量为q的带正电的粒子，从y轴正半轴上y = h处的M点，以速度v0垂直于y轴射入电场，经x轴上x = 2h处的P点进入磁场，最后以垂直于y轴的方向射出磁场。

不计粒子重力。

求（1）电场强度大小E；（2）粒子在磁场中运动的轨道半径r；（3）粒子从进入电场到离开磁场经历的总时间t。

4如图所示，平面坐标系xOy中，在y>0的区域存在沿y轴负方向的匀强电场，场强大小为E，在-h<y<0的区域Ⅰ中存在垂直纸面向外的匀强磁场，磁感应强度大小为B，在y<-h的区域Ⅱ中存在垂直纸面向里的匀强磁场，磁感应强度大小为2B，A是y轴上的一点，C是x轴上的一点。

一质量为m、电荷量为q的带正电的粒子以某一初速度沿x轴正方向从A点进入电场区域，继而通过C点以速度方向与x轴夹角为φ=30°进入磁场区域Ⅰ，并以垂直边界y=-h的速度进入磁场区域Ⅱ，粒子重力不计。

高考物理带电粒子在复合场中的运动压轴难题知识归纳总结及答案解析一、带电粒子在复合场中的运动压轴题1．两块足够大的平行金属极板水平放置，极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律分别如图1、图2所示（规定垂直纸面向里为磁感应强度的正方向）。

在t =0时刻由负极板释放一个初速度为零的带负电的粒子（不计重力），若电场强度E 0、磁感应强度B 0、粒子的比荷qm均已知，且002m t qB π=，两板间距202010mE h qB π=。

（1）求粒子在0～t 0时间内的位移大小与极板间距h 的比值。

（2）求粒子在板板间做圆周运动的最大半径（用h 表示）。

（3）若板间电场强度E 随时间的变化仍如图1所示，磁场的变化改为如图3所示，试画出粒子在板间运动的轨迹图（不必写计算过程）。

【来源】带电粒子的偏转【答案】（1）粒子在0～t 0时间内的位移大小与极板间距h 的比值115s h = （2）粒子在极板间做圆周运动的最大半径225h R π= （3）粒子在板间运动的轨迹如图：【解析】 【分析】 【详解】（1）设粒子在0～t 0时间内运动的位移大小为s 121012s at =① 0qE a m=② 又已知200200102,mE m t h qB qB ππ== 联立解得：115s h = （2）解法一粒子在t 0~2t 0时间内只受洛伦兹力作用，且速度与磁场方向垂直，所以粒子做匀速圆周运动。

设运动速度大小为v 1，轨道半径为R 1，周期为T ，则10v at =21101mv qv B R =联立解得：15h R π= 又002mT t qB π== 即粒子在t 0~2t 0时间内恰好完成一个周期的圆周运动。

在2t 0~3t 0时间内，粒子做初速度为v 1的匀加速直线运动，设位移大小为s 22210012s v t at =+解得：235s h =由于s 1+s 2＜h ，所以粒子在3t 0~4t 0时间内继续做匀速圆周运动，设速度大小为v 2，半径为R 2，有：210v v at =+22202mv qv B R =解得225h R π=由于s 1+s 2+R 2＜h ，粒子恰好又完成一个周期的圆周运动。

高考物理带电粒子在复合场中的运动压轴难题专项复习一、带电粒子在复合场中的运动压轴题1．如图所示，在无限长的竖直边界NS和MT间充满匀强电场，同时该区域上、下部分分别充满方向垂直于NSTM平面向外和向内的匀强磁场，磁感应强度大小分别为B和2B，KL为上下磁场的水平分界线，在NS和MT边界上，距KL高h处分别有P、Q两点，NS和MT间距为1.8h ，质量为m，带电荷量为＋q的粒子从P点垂直于NS边界射入该区域，在两边界之间做圆周运动，重力加速度为g．(1)求电场强度的大小和方向；(2)要使粒子不从NS边界飞出，求粒子入射速度的最小值；(3)若粒子能经过Q点从MT边界飞出，求粒子入射速度的所有可能值．【来源】【全国百强校】2017届浙江省温州中学高三3月高考模拟物理试卷（带解析)【答案】（1）mgqE=，方向竖直向上（2）min(962)qBhv-=（3）0.68qBhvm=；0.545qBhvm=；0.52qBhvm=【解析】【分析】（1）粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，电场力与重力合力为零；（2）作出粒子的运动轨迹，由牛顿第二定律与数学知识求出粒子的速度；（3）作出粒子运动轨迹，应用几何知识求出粒子的速度．【详解】（1）粒子在磁场中做匀速圆周运动，电场力与重力合力为零，即mg=qE，解得：mgqE=，电场力方向竖直向上，电场方向竖直向上；（2）粒子运动轨迹如图所示：设粒子不从NS边飞出的入射速度最小值为v min，对应的粒子在上、下区域的轨道半径分别为r1、r2，圆心的连线与NS的夹角为φ，粒子在磁场中做匀速圆周运动，由牛顿第二定律得：2vqvB mr=，解得，粒子轨道半径：vrqBπ=，min1vrqBπ=，2112r r=，由几何知识得：（r1+r2）sinφ=r2，r1+r1cosφ=h，解得：min 962)qBhvm=（﹣；（3）粒子运动轨迹如图所示，设粒子入射速度为v ，粒子在上、下区域的轨道半径分别为r 1、r 2， 粒子第一次通过KL 时距离K 点为x ， 由题意可知：3nx =1.8h （n =1、2、3…）32x ≥x =， 解得：120.361)2hr n =+（，n ＜3.5， 即：n =1时， 0.68qBhv m=， n =2时，0.545qBhv m =， n =3时，0.52qBhv m=； 答：（1）电场强度的大小为mg qE =，电场方向竖直向上；（2）要使粒子不从NS 边界飞出，粒子入射速度的最小值为min 9qBhv m=． （3）若粒子经过Q 点从MT 边界飞出，粒子入射速度的所有可能值为：0.68qBhv m=、或0.545qBh v m =、或0.52qBhv m=． 【点睛】本题考查了粒子在磁场中的运动，分析清楚粒子运动过程、作出粒子运动轨迹是正确解题的前提与关键，应用平衡条件、牛顿第二定律即可正确解题，解题时注意数学知识的应用．2．如图，空间存在匀强电场和匀强磁场，电场方向为y 轴正方向，磁场方向垂直于xy 平面（纸面）向外，电场和磁场都可以随意加上或撤除，重新加上的电场或磁场与撤除前的一样．一带正电荷的粒子从P (x ＝0，y ＝h )点以一定的速度平行于x 轴正向入射．这时若只有磁场，粒子将做半径为R 0的圆周运动；若同时存在电场和磁场，粒子恰好做直线运动．现在，只加电场，当粒子从P 点运动到x ＝R 0平面（图中虚线所示）时，立即撤除电场同时加上磁场，粒子继续运动，其轨迹与x 轴交于M 点．不计重力．求： （1）粒子到达x ＝R 0平面时速度方向与x 轴的夹角以及粒子到x 轴的距离； （2）M 点的横坐标x M ．【来源】磁场 【答案】（1）20122R H h at h =+=+；（2）22000724M x R R R h h =+- 【解析】 【详解】（1）做直线运动有，根据平衡条件有：0qE qB =v ①做圆周运动有：200qB m R =v v ②只有电场时，粒子做类平抛，有：qE ma =③ 00R t =v ④ y v at =⑤解得：0y v v =⑥ 粒子速度大小为：22002y v v v v =+=⑦速度方向与x 轴夹角为：π4θ=⑧ 粒子与x 轴的距离为：20122R H h at h =+=+⑨（2）撤电场加上磁场后，有：2v qBv m R=⑩解得：02R R =⑾. 粒子运动轨迹如图所示圆心C 位于与速度v 方向垂直的直线上，该直线与x 轴和y 轴的夹角均为4π，有几何关系得C 点坐标为：02C x R =⑿02C R y H R h =-=-⒀ 过C 作x 轴的垂线，在ΔCDM 中：02CM R R ==⒁2C R CD y h ==-⒂） 解得：22220074DM CM CD R R h h =-=+- M 点横坐标为：22000724M x R R R h h =+-3．如图所示，在坐标系xoy 中，过原点的直线OC 与x 轴正向的夹角φ=120°，在OC 右侧有一匀强电场；在第二、三象限内有一匀强磁场，其上边界与电场边界重叠、右边界为y 轴、左边界为图中平行于y 轴的虚线，磁场的磁感应强度大小为B ，方向垂直抵面向里。

高考物理带电粒子在复合场中的运动压轴难题知识点及练习题及答案一、带电粒子在复合场中的运动压轴题1．两块足够大的平行金属极板水平放置，极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律分别如图1、图2所示（规定垂直纸面向里为磁感应强度的正方向）。

在t=0时刻由负极板释放一个初速度为零的带负电的粒子（不计重力），若电场强度E0、磁感应强度B0、粒子的比荷qm均已知，且02mtqBπ=，两板间距2210mEhqBπ=。

（1）求粒子在0～t0时间内的位移大小与极板间距h的比值。

（2）求粒子在板板间做圆周运动的最大半径（用h表示）。

（3）若板间电场强度E随时间的变化仍如图1所示，磁场的变化改为如图3所示，试画出粒子在板间运动的轨迹图（不必写计算过程）。

【来源】带电粒子的偏转【答案】（1）粒子在0～t0时间内的位移大小与极板间距h的比值115sh=（2）粒子在极板间做圆周运动的最大半径225hRπ=（3）粒子在板间运动的轨迹如图：【解析】【分析】【详解】（1）设粒子在0～t0时间内运动的位移大小为s121012s at =① 0qE a m=② 又已知200200102,mE m t h qB qB ππ== 联立解得：115s h = （2）解法一粒子在t 0~2t 0时间内只受洛伦兹力作用，且速度与磁场方向垂直，所以粒子做匀速圆周运动。

设运动速度大小为v 1，轨道半径为R 1，周期为T ，则10v at =21101mv qv B R =联立解得：15h R π= 又002mT t qB π== 即粒子在t 0~2t 0时间内恰好完成一个周期的圆周运动。

在2t 0~3t 0时间内，粒子做初速度为v 1的匀加速直线运动，设位移大小为s 22210012s v t at =+解得：235s h =由于s 1+s 2＜h ，所以粒子在3t 0~4t 0时间内继续做匀速圆周运动，设速度大小为v 2，半径为R 2，有：210v v at =+22202mv qv B R =解得225h R π=由于s 1+s 2+R 2＜h ，粒子恰好又完成一个周期的圆周运动。