N-S(纳维斯托克斯)方程推导过程
- 格式:docx
- 大小:201.07 KB
- 文档页数:7




黏性流体动量平衡方程−纳维-斯托克斯方程(Navier-Stokes equations ) 1.动量平衡的定义流体在流动过程中遵守能量守恒定律,称为能量平衡根据牛顿第二定律:⎩⎨⎧≠∑=∑,运动,动力平衡,静止,静力平衡0F 0F 作用力的合力 = 单位时间内动量的变化量作用力形式 动量形式[动量传入量] - [动量传出量] +[系统作用力的总和] = [动量蓄积量][动量传入量] - [动量传出量] + [系统作用力的总和] = 0稳定流动系统:不稳定流动系统:动量收支差量动量收支差量⒉ 动量传递方式1 黏性动量传输dydv x yx μτ-= 2 对流动量传输对流动量传输vvρ⒊ 作用力的形式体积力表面力压力重力作用力⒋ 动量平衡方程的推导元体分析法牛顿第二定律分析法建立方法建立依据在直角坐标系中由于有三个方向的分速度,所以共有九个动量通量。
⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅⋅⋅⋅⋅zz yz xz z y y y x y z x y x xx v v v v v v v v v v v v v v v v v ρρρρρρρρρv 以v x动量通量收支差量⑴ 对流动量收支差量x 方向的速度、x 方向的动量通量对流动量收支差量为同理,以v x 为准,y 方向、z 方向的对流动量收支差量:以v x 为准,元体对流动量收支差量为同理,以v y 、v z 为准,元体对流动量收支差量为 v x → v y 、v z⑵黏性动量收支差量黏性动量通量同样由九个分量组成以v x为准,C、D黏性动量通量收支差量黏性动量收支差量同理,v x在y、x以v x为准,元体黏性动量收支差量为同理,以⑶作用力的总和zxgxddydρzxgyddydρzxgzddydρx方向:P Ax方向合压力为x方向的总压力为同理,y、z方向的总压力为x →y、z重力⑷ 动量蓄积量z 方向x 方向y 方向 单位时间内元体动量的变化量[动量传入量] - [动量传出量] +[系统作用力的总和] = [动量蓄积量]⒌ 动量平衡方程式将以上式子代入下式,整理得:N-S 方程简化:const=ρ,连续性方程⑵const=μ,牛顿黏性定律⑴动量收支差xx x x x x x x g x p zv y v x v z v v y v v x v v v ρμτρ+∂∂-∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂)()(222222z y x yy y y y y y y g xp zv yv xv zv v yv v xv v v ρμτρ+∂∂-∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂)()(222222zyxzz z z z z z z g xp zv yv xv zv v yv v xv v v ρμτρ+∂∂-∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂)()(222222zyx黏性力引起压力 体积力积累动量收支差量⒍ 动量平衡方程的讨论x2x 22x 22x 2x z x y x x x g x P z v y v x v z v y v v x v v ρμτρ+∂∂-⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂=⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂+∂∂v v 对流动量动量蓄积量黏性动量压重(1)方程的物理意义:运动的流体能量守恒的表现⎩⎨⎧作用力形式动量形式z zv y y v x x v v v d d d d d ⋅∂∂+⋅∂∂+⋅∂∂+⋅∂∂=ττz y x v zv v y v v x v v ⋅∂∂+⋅∂∂+⋅∂∂+∂∂=v d d ττz y x v zvv y v v x v v a ⋅∂∂+⋅∂∂+⋅∂∂+∂∂=τz x y x x x x x v zvv y v v x v v a ⋅∂∂+⋅∂∂+⋅∂∂+∂∂=τ全微分)z ,y ,x ,(v v τ=x2x 22x 22x 2g x Pz v y v xv ρμρ+∂∂-⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂=xa y 2y 22y 22y2g Pz v y v xv ρμρ+∂∂-⎥⎥⎦⎤⎢⎢⎣⎡∂∂+∂∂+∂∂=ya y z 2z 22z 22z 2g Pz v y v xv ρμρ+∂∂-⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂=z az惯性力黏性力压力重力流体在运动中以作用力及动量形式表现能量平衡 关系是统一的⑵ 适用条件黏性流体、不稳定流动、不可压缩流体(元体范围内)、层流流动理想流体:=μ没有黏性的流体简化: 0v =∂∂τ② 稳定流动, ③ 单位质量流体 0=μ①时,N-S 方程简化为欧拉方程理想流体、稳定流动、不可压缩流体(元体范围内)流动微分方程的应用求解步骤(1)根据问题特点对一般形式的运动方程进行简化,获得针对具体问题的微分方程或方程组。

很多人一听到N-S 方程就有点头皮发麻,因为涉及到流体力学的知识比较多,如果没有一个完整有逻辑的思路,理解N-S 方程是有点困难。
其中涉及到欧拉法,场论,随体导数,流体力学连续性方程(即质量守恒方程),流体力学N-S 方程(即动量方程),动量方程在流体力学中有两种,一种是理想流体动量方程,一种是粘性流体动量方程,粘性流体的动量方程也叫纳维-斯托克斯方程,也简称N-S 方程。
我试图想把N-S 方程弄清楚点,所以写了一点东西,分享一下。
首先要讲一下流体力学的欧拉法,在课本中还讲了拉格朗斯法,因为连续性方程和N-S 方程是用欧拉法得出的,和拉格朗日法没什么关系。
我就不讲拉格朗日法,以免产生混乱。
欧拉方法的着眼点不是流体质点而是空间点。
设法在空间中的每一点上描述出流体运动随时间的变化状况。
如果每一点的流体运动都已知道,则整个流体的运动状况也就清楚了。
欧拉方法中流体质点的运动规律数学上可表示为下列矢量形式:假设空间一点的坐标(x,y,z,t),其中x,y,z 是该空间的坐标,t 是此刻时间。
u,v,w 是这一空间点的三个方向速度。
p,ρ,T 是这一空间点的压力,密度和温度。
这样就有了每一个点的速度,压力,密度,温度,就可以描述运动流体的状态。
这里需要强调一点的是下面这六个式子,可以换一个角度把他们看成方程,对后面理解连续性方程和N-S 方程有帮助,比如u=x+2y+3z),,,();,,,();,,,();,,,();,,,();,,,(t z y x T T t z y x t z y x p p t z y x w w t z y x v v t z y x u u ======ρρ因为后面需要随体导数的概念,还需要把速度函数表示成矢量的形式。
前面u,v,w 是标量,是ν在(x,y,z,t)直角坐标系三个方向的速度。
),(t rνν=M 点(x,y,z,t ),速度为),(t M ν ,过了t ∆之后,在M '点,速度为),(t t M ∆+'ν。

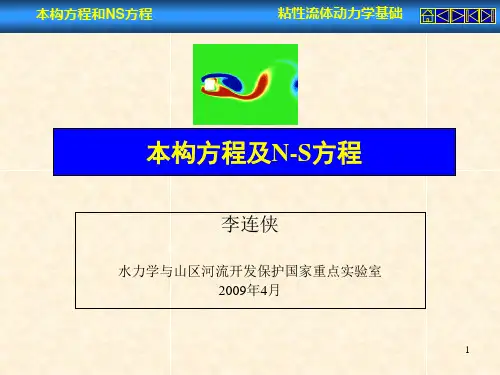

Navier-Stocks 方程组1、直角坐标系下的Navier-Stocks 方程组①.连续方程 非守恒形式0D V Dtρρ+∇⋅= 守恒形式()0V tρρ∂+∇⋅=∂ ②.动量方程 非守恒形式 x 方向yx xx zx x Du p f Dt x x y zτττρρ∂∂∂∂=-++++∂∂∂∂ y 方向xy yy zy y Dv p f Dt y x y zτττρρ∂∂∂∂=-++++∂∂∂∂ z 方向yz xz zz z Dw p f Dt z x y zτττρρ∂∂∂∂=-++++∂∂∂∂ 守恒形式x 方向()()yx xx zx x u p uV f t x x y zτρττρρ∂∂∂∂∂+∇⋅=-++++∂∂∂∂∂ y 方向()()xy yy zy y v p vV f t y x y zτττρρρ∂∂∂∂∂+∇⋅=-++++∂∂∂∂∂ z 方向()()yz xz zz z w p wV f t z x y zτρττρρ∂∂∂∂∂+∇⋅=-++++∂∂∂∂∂③.能量方程 非守恒形式()()()()()()()()()()()22yx xx zx xy yy zy yz xz up D V T TT e q k k k Dt x x y y z zx u vp wp u u y z x y z v v u w w xyz x yρρττττττττ∂⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫⎛⎫+=+++-- ⎪ ⎪ ⎪ ⎪∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭∂∂∂∂∂ -++++∂∂∂∂∂∂∂∂∂∂ ++++∂∂∂∂∂()zz w f V zτρ+∂+⋅∂守恒形式()()()()()()2222yx xx zx up V V TT T e e V q k k k t x x y yz zx u vp wp u u y z x y z ρρρτττ⎡⎤⎡⎤∂⎛⎫⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫⎛⎫++∇⋅+=+++--⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦∂∂∂∂∂ -++++∂∂∂∂∂ ()()()()()()xy yy zy yz xz zz v v u w w xyzx yw f V zττττττρ∂∂∂∂∂ +++++∂∂∂∂∂∂+⋅∂2、直角坐标系下直角坐标参数表示的矩阵守恒形式N-S 方程上述方程写成矩阵形式()()()v v v F F G G H H Q S t x y z∂-∂-∂-∂+++=∂∂∂∂ 其具体表达式为:(),,,,TQ u v w E ρρρρρ=()()()()()()222,,,,,,,,,,,,TTTF u u p uv uw pE p uG v uv v p vw E p vH w uw vw w p E p w ρρρρρρρρρρρρρρ=++=++=++()()()0,,,,0,,,,0,,,,Tv xx xy xz x Tv yx yy yz y Tv zx zy zz z F b G b H b τττττττττ=== ()()0,,,,Tx y z x y z S f f f f vf wf q ρρρρμρ=+++⋅其中,若忽略质量力,并可以将研究的气体视为绝热流动,则0S =。


很多人一听到N-S 方程就有点头皮发麻,因为涉及到流体力学的知识比较多,如果没有一个完整有逻辑的思路,理解N-S 方程是有点困难。
其中涉及到欧拉法,场论,随体导数,流体力学连续性方程(即质量守恒方程),流体力学N-S 方程(即动量方程),动量方程在流体力学中有两种,一种是理想流体动量方程,一种是粘性流体动量方程,粘性流体的动量方程也叫纳维-斯托克斯方程,也简称N-S 方程。
我试图想把N-S 方程弄清楚点,所以写了一点东西,分享一下。
首先要讲一下流体力学的欧拉法,在课本中还讲了拉格朗斯法,因为连续性方程和N-S 方程是用欧拉法得出的,和拉格朗日法没什么关系。
我就不讲拉格朗日法,以免产生混乱。
欧拉方法的着眼点不是流体质点而是空间点。
设法在空间中的每一点上描述出流体运动随时间的变化状况。
如果每一点的流体运动都已知道,则整个流体的运动状况也就清楚了。
欧拉方法中流体质点的运动规律数学上可表示为下列矢量形式:假设空间一点的坐标(x,y,z,t),其中x,y,z 是该空间的坐标,t 是此刻时间。
u,v,w 是这一空间点的三个方向速度。
p,ρ,T 是这一空间点的压力,密度和温度。
这样就有了每一个点的速度,压力,密度,温度,就可以描述运动流体的状态。
这里需要强调一点的是下面这六个式子,可以换一个角度把他们看成方程,对后面理解连续性方程和N-S 方程有帮助,比如u=x+2y+3z),,,();,,,();,,,();,,,();,,,();,,,(t z y x T T t z y x t z y x p p t z y x w w t z y x v v t z y x u u ======ρρ因为后面需要随体导数的概念,还需要把速度函数表示成矢量的形式。
前面u,v,w 是标量,是ν在(x,y,z,t)直角坐标系三个方向的速度。
),(t rνν=M 点(x,y,z,t ),速度为),(t M ν ,过了t ∆之后,在M '点,速度为),(t t M ∆+'ν。
根据位置的变化,分解成这两部分,正是基于这两个原因。
写成直角坐标系,用u,v,w 三个方向速度表示成如下:);,,,();,,,();,,,(t z y x w w t z y x v v t z y x u u === 代入上面加速度公式,得到至此已经用欧拉法推到出了流体速度和加速度(即随体导数)的公式。
随体导数也可以用复合函数求导的方法得到。
用复合函数链导法则会更容易理解一些。
后面接下来要推导的是流体力学连续方程。
连续性方程是质量守恒定律在流体力学中的具体表述形式。
它的前提是对流体采用连续介质模型,速度和密度都是空间坐标及时间的连续、可微函数。
x2dx x u ∂∂假设有一个微体积正六面体,正六面体的中心三个方向的速度是u,v,w 。
左表面的流速2dxx u u u M ∂∂-= 右表面的流速2N dxx u u u ∂∂+=单位时间内x 方向流出和流进的质量流量差:dxdydz x u dydz dx x u u dydz dx x u u M M ∂∂=⎥⎦⎤⎢⎣⎡∂∂--⎥⎦⎤⎢⎣⎡∂∂+=-)()(21)(21ρρρρρ进出同理y 方向和z 方向的质量流量差:dxdydz yv ∂∂)(ρ dxdydz z)w (∂∂ρ 在dt 时间内因为密度变化而减少的质量为:dxdydz tdxdydz t dxdydz ∂∂-=∂∂+-ρρρρ)( 由质量守恒,单位时间内流出与流入六面体的流体质量差综合应等于六面体因密度变化而减少的质量。
0)()()(=∂∂+∂∂+∂∂+∂∂⇒∂∂-=⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂zw y v x u t dxdydz t dxdydz z w y v x u ρρρρρρρρ以上就已经得到了连续性方程。
对不可压缩流体,连续性方程可以简化,可以得到以下简化的连续性方程:0=∂∂+∂∂+∂∂zw y v x u 这个不可压缩流体的连续性方程很重要,下面推导N-S 方程的时候要用到。
接下来要推导出流体力学的N-S 方程。
在推导N-S 方程之前,有很多人都在这里有困惑。
这里有两个概念要搞清楚,那就是什么是理想流体和粘性流体。
我们很多课本在讲流体力学的时候是先讲了理想流体的动量方程,之后又没有接着讲粘性流体的动量方程,所以有些人到后面再讲N-S 方程就混淆了。
另外就是很多人一听到N-S 方程就心里有点害怕,畏惧了,还没来得及去仔细研究就放弃了,如果仔细研究一下,其实也不难,很多流体力学的书是用场论的知识去推导出N-S 方程的,我们工科学校对场论没有接触,最好还是用正六面体的方法来推导N-S 方程。
哈工大陈卓如和王洪杰老师的工程流体力学对N-S 方程的推导用的是正六面体法,很容易看懂。
清华大学的书就比较难,可以参考。
在这里得先推到一下理想流体的动量方程,后面再推导粘性流体的动量方程。
这里必须先分清理想流体和粘性流体的概念。
理想流体是一种不可压缩、不计粘性(粘度为零)的流体。
欧拉在忽略粘性的假定下,建立了描述理想流体运动的基本方程。
实际上,理想流体在自然界中是不存在的,它只是真实流体的一种近似模型。
但实际上由于流体中存在着粘性,流体的一部分机械能将不可逆地转化为热能,并使流体流动出现许多复杂现象,例如边界层效应、摩阻效应、非牛顿流动效应等。
自然界中各种真实流体都是粘性流体。
下面推导理想流体动量方程。
理想流体和粘性流体的区别在于是否有粘性力,即切应力。
在理想流体内部取一微体积正六面体。
中心点压力p(x,y,z),受力分析沿x 轴方向: 1.表面力,因为是理想流体,没有切应力,0=τ。
左表面dydz dxx p p A p P M M )2(∂∂-== 右表面dydz dxx p p A p P N N )2(∂∂+==2.质量力,单位质量力在三个坐标轴上分量是z y x f f f ,,。
x 轴方向质量力dxdydz f x ρ。
在x 轴方向由牛顿第二定律:zu wy u v x u u t u x p f dt du x p f dtdudxdydz dxdydz f dydz dx x p p dydz dx x p p ma F x x x ∂∂+∂∂+∂∂+∂∂=∂∂-−−−−−→−=∂∂-⇒=+∂∂+-∂∂-⇒=∑ρρρρ11)2()2(由前面速度随体导数同样y 轴z 轴列方程,可以得到理想流体动量方程组。
x2dx x p p ∂∂+z w wy w v x w u t w z p f z v w y v v x v u t v y p f z uw y u v x u u t u x p f z y x ∂∂+∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂+∂∂=∂∂-ρρρ111;;下面要推导粘性流体动量方程,也就是纳维斯托克斯方程,也叫做N-S 方程。
同样取一个微六面体,但粘性流体有切应力,分别对六个面做受力分析如图所示:x 方向的受力,质量力,左右方向压力,前后面切力,上下面切力。
由牛顿第二定律列方程:dtdudxdydzdydx dz z dydx dxdz dy y dxdz dydz dx x dydz dxdydz f zx zx zx yx yx yx xx xx xx x ρττττττσσσρ=⎥⎦⎤⎢⎣⎡∂∂+--⎥⎦⎤⎢⎣⎡∂∂+--⎥⎦⎤⎢⎣⎡∂∂+-+)()()(对粘性流体,切应力由广义牛顿内摩擦定律确定:x yzoxzzx zy yz yx xy zux w y zz v x vy u τμττμττμτ=∂∂+∂∂==∂∂+∂∂==∂∂+∂∂=)(;)(;)(粘性流体中某一点三个方向的压力是不相等的,任意点的压力与三个方向的正应力有以下关系式:z wp y vp x up p zz yy xx zz yy xx ∂∂-=∂∂-=∂∂-=++=μσμσμσσσσ2;2;2);(31以上广义牛顿内摩擦定律以及压力与正应力的关系可以找陈卓如老师的工程流体力学,有相关的解释。
代入化简上面由牛顿第二定律得到的方程:)(1)()()( dtdu z y x f dtdudxdydz dydx dz z dydx dxdz dy y dxdz dydz dx x dydz dxdydz f zx yx xx x zx zx zx yx yx yx xx xx xx x ρττσρρττττττσσσρ=∂∂+∂∂+∂∂-⇒=⎥⎦⎤⎢⎣⎡∂∂+--⎥⎦⎤⎢⎣⎡∂∂+--⎥⎦⎤⎢⎣⎡∂∂+-+ 把)();(;2zux w x v y u x u p zx yx xx ∂∂+∂∂=∂∂+∂∂=∂∂-=μτμτμσ代入上式(1)中:zu wy u v x u u t u z u y u x u x p f dtdu z w y v x u x z u y u x u x p f dt du z x w y x v x u z u y u x u x p f dt duz u z x w y x v y u x u x p f dt du z z u x w y x v y u x x u p f dtduz y x f x x x x x zx yx xx x ∂∂+∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂-⇒=∂∂+∂∂+∂∂∂∂+∂∂+∂∂+∂∂+∂∂-⇒=∂∂∂+∂∂∂+∂∂+∂∂+∂∂+∂∂+∂∂-⇒=∂∂+∂∂∂+∂∂∂+∂∂+∂∂+∂∂-⇒=∂∂∂+∂∂∂+∂∂∂+∂∂∂+∂∂∂-∂-⇒=∂∂+∂∂+∂∂-22222202222222222222222222222221)(2)()()2(νννρρμμμμρρμμμμμμρρμμμμμρρμμμρρττσρ随体导数代入前面可以得到这部分为由不可压缩流体连续性z w wy w v x w u t w z w y w x w p f z v wy v v x v u t v z v y v x v y p f zuw y u v x u u t u z u y u x u x p f z y x ∂∂+∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂-∂∂+∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂-∂∂+∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂-222222222222222222z 111νννρνννρνννρ这样对得到了粘性流体的动量方程,也叫运动微分方程,也叫纳维斯托克斯方程,也叫N-S 方程。
至此,从一个点开始,用欧拉法定义了速度,压力,密度,温度。
再后来得到随体导数的概念,从随体导数到能量守恒方程,也即连续性方程。
然后先推导了理想流体运动微分方程,后面加入了广义牛顿内摩擦定律得到了粘性流体运动微分方程,也就是N-S 方程。