一类混沌系统动力学行为的突变分析
- 格式:pdf
- 大小:272.81 KB
- 文档页数:4

《两个混沌系统的动力学分析及其系统控制与同步研究》篇一一、引言混沌系统是一种复杂的非线性动态系统,其运动状态表现出对初始条件的敏感依赖性,即“蝴蝶效应”。
近年来,随着非线性科学的发展,混沌系统的研究逐渐成为了一个重要的研究方向。
本文将针对两个典型的混沌系统进行动力学分析,并探讨其系统控制与同步问题。
二、两个混沌系统的动力学分析(一)第一个混沌系统:Lorenz系统Lorenz系统是一种经典的混沌系统,由三个非线性微分方程组成。
通过对Lorenz系统的动力学分析,我们可以了解其运动轨迹、稳定性和分岔行为等特性。
该系统的运动轨迹表现出极度的复杂性,即使在微小的初始条件变化下,也会产生显著的差异。
此外,Lorenz系统还具有多种不同的稳定状态和分岔行为,这为我们的研究提供了丰富的素材。
(二)第二个混沌系统:Chua-Cichon系统Chua-Cichon系统是一种新型的混沌系统,其数学模型具有更加复杂的非线性特性。
与Lorenz系统相比,Chua-Cichon系统的运动轨迹更为复杂,分岔和稳定性分析更为丰富。
在分析Chua-Cichon系统的过程中,我们可以深入探讨其与Lorenz系统之间的异同,以及在不同条件下的运动特性。
三、系统控制与同步研究(一)控制策略与方法针对混沌系统的控制与同步问题,本文将介绍多种控制策略与方法。
包括反馈控制法、优化控制法、自适应控制法等。
这些方法可以有效地抑制混沌系统的运动复杂性和随机性,使其趋于稳定或达到某种特定的运动状态。
同时,针对不同的混沌系统,我们可以根据其特性和需求选择合适的控制策略和方法。
(二)同步技术研究在混沌同步方面,本文将探讨各种同步技术及其应用。
包括主从同步法、变结构同步法等。
这些方法可以实现不同混沌系统之间的同步,从而在通信、信号处理等领域具有广泛的应用前景。
通过实验验证和仿真分析,我们可以评估不同同步技术的性能和效果,为实际应用提供指导。
四、实验验证与仿真分析为了验证本文的理论分析结果,我们将进行实验验证和仿真分析。

《两个混沌系统的动力学分析及其系统控制与同步研究》篇一一、引言混沌系统是物理学、数学、工程学和许多其他领域研究的热点问题。
混沌现象表现为系统对初始条件的敏感依赖性,以及在非线性系统中出现的复杂、不可预测的行为。
本文将针对两个典型的混沌系统进行动力学分析,并探讨其系统控制与同步的有关问题。
二、两个混沌系统的动力学分析(一)第一个混沌系统:Lorenz系统Lorenz系统是一个经典的混沌系统,其动力学行为表现为对初始条件的极度敏感性。
该系统由三个非线性微分方程组成,描述了大气中温度的复杂变化过程。
我们将通过数值模拟和相图分析等方法,深入探讨Lorenz系统的动力学特性。
(二)第二个混沌系统:Chua's电路Chua's电路是一个电子电路混沌系统的典型代表,其电路中的非线性元件导致了复杂的混沌行为。
我们将对Chua's电路的电路方程进行推导,并通过时域分析和频域分析等方法,揭示其混沌特性和动力学行为。
三、系统控制与同步研究(一)Lorenz系统的控制与同步针对Lorenz系统的混沌特性,我们将探讨如何通过外部控制信号或系统参数调整等方法,实现对该系统的有效控制。
同时,我们将研究Lorenz系统的同步问题,探讨不同Lorenz系统之间的同步方法及其在通信、计算等领域的应用。
(二)Chua's电路的控制与同步对于Chua's电路的混沌行为,我们将尝试利用反馈控制、自适应控制等手段,实现对系统的稳定控制和参数调整。
此外,我们还将研究Chua's电路的同步问题,包括电路间的同步方法和其在信号处理、电子设备同步等方面的应用。
四、实验与结果分析(一)实验设计我们将设计一系列实验来验证上述理论分析的正确性。
对于Lorenz系统和Chua's电路,我们将分别进行数值模拟实验和实际电路实验,以观察系统的混沌行为和验证控制与同步方法的可行性。
(二)结果分析通过实验数据的分析和处理,我们将验证所提出的控制与同步方法的可行性和有效性。

《两个混沌系统的动力学分析及其系统控制与同步研究》篇一一、引言混沌系统是一种复杂的非线性动态系统,其状态变化具有不可预测性、敏感依赖初始条件和长期行为的不规则性等特点。
近年来,随着非线性科学的发展,混沌系统的研究逐渐成为了一个重要的研究方向。
本文将针对两个典型的混沌系统进行动力学分析,并探讨其系统控制与同步的方法。
二、两个混沌系统的动力学分析(一)Lorenz混沌系统Lorenz混沌系统是一种典型的流体动力学系统,具有三维非线性微分方程描述。
通过对该系统的动力学分析,我们可以发现其状态变化具有对初始条件的敏感性、具有分岔和混沌等现象。
具体地,我们可以通过分析该系统的相图、功率谱等特征,进一步了解其动力学特性。
(二)Chua's电路混沌系统Chua's电路混沌系统是一种电子电路系统,其电路元件包括电阻、电感和非线性电容等。
该系统的动力学行为表现为复杂的混沌振荡,具有一定的应用价值。
通过对该系统的动力学分析,我们可以了解到混沌系统在不同参数条件下的动态变化情况。
三、系统控制与同步研究(一)系统控制对于混沌系统的控制,主要是通过调整系统参数或者引入外部控制信号等方式,使得系统的状态达到预期的稳定状态。
针对Lorenz混沌系统和Chua's电路混沌系统,我们可以采用不同的控制策略,如参数微调法、反馈控制法等,以实现对系统状态的稳定控制。
(二)系统同步混沌系统的同步是指两个或多个混沌系统在一定的条件下,其状态变化达到某种程度的协调和一致性。
针对两个混沌系统的同步问题,我们可以采用不同的同步方法,如完全同步法、延迟同步法等。
这些方法可以通过调整系统参数或者引入适当的控制器来实现两个混沌系统的同步。
四、实验结果与分析(一)实验设计为了验证上述理论分析的正确性,我们设计了相应的实验方案。
具体地,我们采用了数值模拟和实际电路实验两种方式来验证Lorenz混沌系统和Chua's电路混沌系统的动力学特性和控制与同步效果。

动力系统中的混沌现象研究动力系统是涉及物体或系统运动的力学领域,而混沌现象则是指在一些简单的动力系统中出现的看似随机、无序的行为。
混沌现象的研究对于我们理解自然界的复杂性以及应用于科学、工程等领域具有重要意义。
本文将对动力系统中的混沌现象进行研究和讨论。
一、混沌现象的背景和定义混沌现象最早在20世纪60年代由Edward Lorenz研究气象学时发现。
他的研究发现,即使是在一个简单的天气系统中,微小差异的初始条件也可能导致系统的完全不同行为,这就是“蝴蝶效应”的提出。
混沌现象被定义为一个动力系统在某种程度上高度敏感于初始条件的现象,即使微小变化也能产生巨大的影响,导致不可预测的结果。
这一现象使得长期的天气预测变得困难,并且在其他领域也具有深远的影响。
二、混沌现象的数学模型为了研究混沌现象,数学家引入了一系列的混沌模型,其中最著名和最广泛研究的是洛伦兹系统。
洛伦兹系统由一组非线性微分方程组成,描述了流体力学中的对流现象。
这个系统的特点是对于初始条件高度敏感,产生了混沌行为。
混沌现象的数学模型可以通过图像、时间序列和相图等方式进行分析。
图像是通过绘制系统动力学随时间的变化而得到的,可以展示系统的特殊性质和周期性行为。
时间序列则是将系统状态的演化按时间顺序排列而得到的,可以通过频域分析等方法获取系统的频谱特征。
相图则是将系统的状态用相空间中的点表示,展示了系统的相空间流动性质。
三、混沌现象在科学和工程中的应用混沌现象的研究不仅仅是理论学科和数学领域中的一项重要研究,还具有广泛的应用价值。
在科学研究中,混沌现象的理解有助于我们对自然界中复杂系统的认识。
例如,在气象学中,混沌现象的研究可以提高天气预测的准确性,有助于人们更好地了解气候变化。
在工程领域,混沌现象的应用也十分广泛。
例如,混沌现象可以用于增强通信系统的安全性和可靠性。
混沌加密技术利用了系统非线性和高度敏感的特性,使得加密通信更具保密性。
此外,混沌现象在信号处理、图像识别、电力系统和控制系统等领域也得到了广泛的应用。
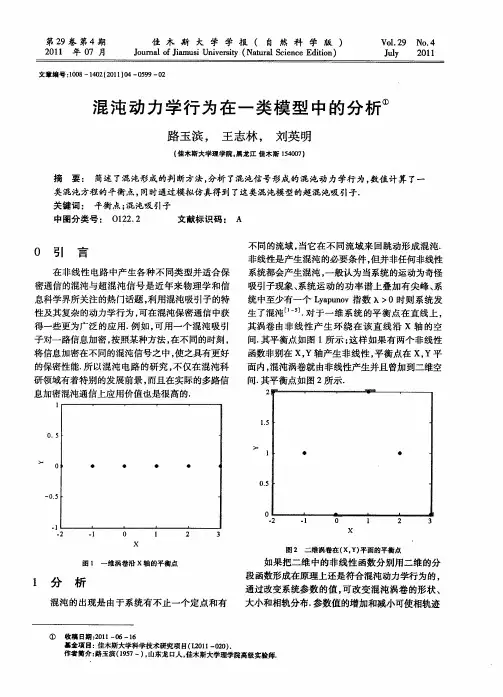
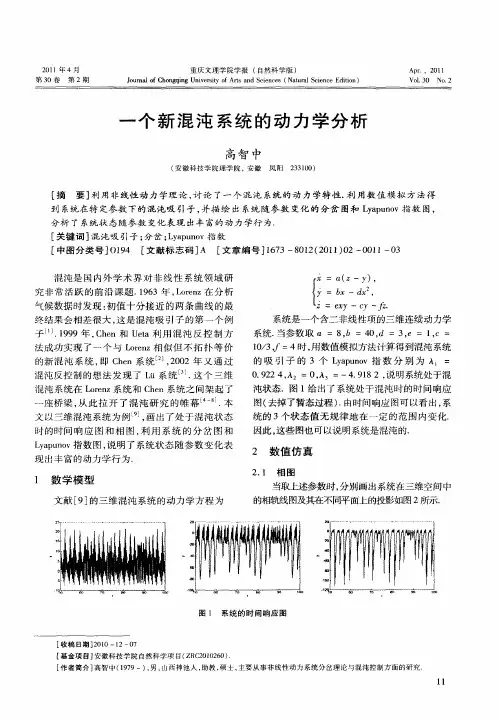

机械系统动力学模型的混沌分析方法研究在当今的工程领域,机械系统的动力学行为研究至关重要。
随着技术的不断进步和系统的日益复杂,对机械系统动力学模型的深入理解和准确分析成为了关键。
其中,混沌分析方法为我们揭示机械系统的复杂动态特性提供了有力的手段。
机械系统动力学模型描述了系统中各个部件的运动以及它们之间的相互作用。
这些模型可以基于牛顿定律、拉格朗日方程或哈密顿原理等建立。
然而,在实际情况中,由于非线性因素的存在,机械系统的行为可能变得极其复杂,甚至表现出混沌现象。
混沌是一种看似随机但实际上具有内在规律的复杂动态行为。
在机械系统中,例如发动机的运转、机器人的运动控制等,混沌现象都可能出现。
对于这类系统,如果仅仅采用传统的线性分析方法,往往无法准确捕捉其真实的动态特性,从而导致设计和控制上的失误。
为了有效地分析机械系统动力学模型中的混沌现象,研究人员提出了多种方法。
其中,相空间重构是一种常用的手段。
通过选取合适的观测变量和延迟时间,将一维的时间序列数据重构到高维的相空间中,从而能够更清晰地揭示系统的动态结构。
另外,Lyapunov 指数也是混沌分析中的重要指标。
它可以用来定量地描述系统在相空间中相邻轨道的发散或收敛程度。
如果系统至少存在一个正的 Lyapunov 指数,那么就可以判定系统处于混沌状态。
通过计算多个Lyapunov 指数,还能够进一步了解系统的混沌程度和复杂性。
功率谱分析也是研究机械系统混沌行为的一种有效方法。
混沌系统的功率谱通常呈现出连续、宽带的特征,与周期系统的离散谱线有明显区别。
通过对功率谱的观察和分析,可以初步判断系统是否处于混沌状态。
在实际应用中,机械系统的混沌分析方法面临着诸多挑战。
例如,系统中的噪声会干扰对混沌特征的准确提取;复杂的系统结构和多个非线性因素的相互作用使得分析变得困难。
此外,不同的分析方法可能会给出不同的结果,需要综合多种方法进行判断和验证。
为了应对这些挑战,一方面需要不断改进和完善现有的分析方法,提高其抗噪能力和准确性;另一方面,结合先进的实验技术和数值模拟手段,获取更精确的系统数据,为混沌分析提供可靠的基础。

《两个混沌系统的动力学分析及其系统控制与同步研究》篇一一、引言混沌系统是一种复杂的非线性动态系统,其状态变化具有不可预测性、敏感依赖初始条件和长期行为的不规则性等特点。
近年来,随着非线性动力学理论的发展,混沌系统的研究受到了广泛的关注。
本文以两个典型的混沌系统为例,对其动力学行为进行深入分析,并探讨其系统控制与同步技术。
二、两个混沌系统的动力学分析(一)Lorenz混沌系统Lorenz混沌系统是一种经典的混沌系统,其动力学行为表现为对初值的敏感依赖性以及长期行为的不可预测性。
该系统的动力学方程包括三个一阶微分方程,通过对这些方程的求解和分析,可以揭示Lorenz系统的混沌特性。
(二)Chua's电路混沌系统Chua's电路混沌系统是一种电路形式的混沌系统,其动力学行为同样具有复杂性和不可预测性。
该系统的动力学方程包括非线性电阻和电容等元件的电压和电流关系,通过对这些关系的分析和求解,可以揭示Chua's电路的混沌特性。
三、系统控制与同步技术(一)控制技术针对混沌系统的控制技术,主要包括参数控制和外部扰动控制。
参数控制是通过调整系统的参数来改变其动力学行为,使其从混沌状态转变为周期状态或稳定状态。
外部扰动控制则是通过引入外部扰动信号来影响系统的状态,从而实现对混沌系统的控制。
(二)同步技术混沌系统的同步技术是实现多个混沌系统之间状态同步的一种方法。
常见的同步技术包括主从同步、自适应同步和基于观测器的同步等。
这些技术可以通过对系统状态的观测和调整,实现多个混沌系统之间的状态同步,从而实现对复杂系统的控制和优化。
四、实验研究为了验证上述理论分析的正确性,本文进行了实验研究。
首先,通过仿真实验对Lorenz系统和Chua's电路系统的动力学行为进行了分析和比较,得到了它们在不同参数下的行为变化规律。
然后,采用了参数控制和外部扰动控制的方法对这两个系统进行了控制实验,实现了对系统状态的调整和优化。

动力系统中的混沌现象与控制研究混沌理论,作为非线性动力学中的重要研究领域,不仅在数学领域有重要应用,也在物理、生物、经济等多个领域得到广泛应用。
混沌现象的产生和控制成为动力系统研究中的一个热点。
本文将从混沌现象的定义、产生机制、数学模型以及相关控制研究等方面进行探讨。
一、混沌现象的定义和特征混沌现象,最早由美国数学家E. N. Lorenz在1963年提出,用来描述某些非线性动力系统中出现的随机且不可预测的行为。
相对于简单周期性行为的规律性,混沌现象表现出无规则、无周期性和高度敏感依赖于初始条件的特点。
混沌现象的特征在于系统的轨迹表现出看似随机的变化,但却受到确定性规律的支配。
在混沌系统中,微小的扰动可能引发系统的巨大变化,这被称为“蝴蝶效应”。
此外,混沌系统的轨迹通常具有分形结构,即存在着自相似的特征。
二、混沌现象的产生机制混沌现象的产生机制是非线性动力学中的重要问题。
在简单系统中,存在着一类称为“映射”的特殊动力学函数,通过不断迭代这些映射函数,系统可能进入混沌状态。
混沌的产生也可以通过连续非线性系统实现。
例如,当一个非线性振荡系统的驱动频率接近系统的固有频率时,系统可能由有序运动突然转变为混沌运动。
此时,系统会出现频率锁定现象,这使得微小的扰动也能引发系统的混沌行为。
三、混沌系统的数学模型为了更好地理解混沌现象,并对其进行研究和控制,研究者们借助数学模型对混沌系统进行描述。
常见的混沌系统包括Logistic映射、Henon映射、Lorenz方程等。
Logistic映射是最著名的一类混沌映射之一,由R. May在1975年引入,其形式为:\[x_{n+1}=rx_n(1-x_n)\]其中,\(x_n\)表示第n次迭代时的变量值,r为非线性参数。
Henon映射是另一个常用的二维混沌系统,其形式为:\[x_{n+1} = 1- ax_n^2 + y_n, y_{n+1} = bx_n\]其中,\(a\)和\(b\)为非线性参数。

《两个混沌系统的动力学分析及其系统控制与同步研究》篇一一、引言混沌系统是一种复杂的非线性动态系统,其状态在时间上表现出不可预测的、敏感依赖于初始条件的特性。
近年来,随着科技的不断进步和理论研究的深入,两个混沌系统的动力学分析、系统控制以及同步问题引起了众多研究者的广泛关注。
本文将对两个典型的混沌系统进行动力学分析,并探讨其系统控制与同步的研究方法。
二、两个混沌系统的动力学分析(一)第一个混沌系统本部分选取经典Lorenz混沌系统为例进行详细的动力学分析。
该系统通过一系列的数学公式,揭示了系统在一定的参数范围内如何展现出混沌行为。
通过对该系统的状态变量、控制参数及其变化的分析,了解其在相空间中的行为,进而预测和推断出系统在不同状态下的行为模式。
(二)第二个混沌系统第二个混沌系统则以Chua-Comellas混沌电路为例进行分析。
该电路通过非线性元件和电容、电感等元件构成,其动态行为呈现出混沌特性。
本文将通过电路的数学模型,分析其动力学特性,如分岔、周期轨道等,以及其与系统行为之间的关系。
三、系统控制研究针对两个混沌系统的控制问题,本文将探讨不同的控制策略和方法。
首先,将介绍基于反馈控制的策略,如线性反馈控制和非线性反馈控制等。
其次,将探讨基于智能算法的控制方法,如神经网络控制、模糊控制等。
这些方法旨在使混沌系统的行为变得可预测和可控,以便于实际工程应用中的使用。
四、同步问题的研究针对两个不同混沌系统的同步问题,本文将提出基于线性控制和基于非线性控制的同步方法。
首先,将介绍基于主从同步的思想,通过设计合适的控制器使两个混沌系统达到同步状态。
其次,将探讨基于自适应同步的方法,使两个不同特性的混沌系统在动态过程中实现同步。
此外,还将对同步的稳定性和性能进行评估,确保同步方法的可靠性和有效性。
五、实验验证与结果分析为了验证上述理论分析的正确性,本文将进行一系列的实验验证和结果分析。
首先,通过搭建Lorenz混沌系统和Chua-Comellas混沌电路的实验平台,观察和分析系统的动态行为。

动力学中的混沌理论研究“混沌”这个词在日常生活中经常被用来形容一种无序、混乱的状态,但在物理学中,混沌理论却有着严谨的定义和数学模型。
动力学中的混沌现象指的是一种看似无规律的、高度敏感的系统行为,引发了研究人员的极大兴趣。
1. 系统的敏感性和确定性混沌混沌现象的出现通常和系统内部的敏感性有关。
我们知道,在一个确定性系统中,初始状态的微小变化可以引起系统产生激烈的反应,比如万有引力场中行星的运动轨迹。
但在普通的确定性系统中,这种敏感性通常会逐渐衰减,最终转化为可预测的运动轨迹。
然而,在某些特殊的情况下,系统内部的微小变化会被逐渐放大,进而导致系统行为的不确定性和复杂性。
这种现象也被称为“确定性混沌”。
“确定性混沌”在动力学中是一种特殊现象,它表现出了系统的极高敏感度和不可预测性。
2. 混沌系统模型和常见应用混沌现象的研究是非常复杂和严峻的,通常需要构建出适当的混沌系统模型以及运用高度复杂的数学方法进行分析。
早期的混沌系统研究主要集中于天体力学以及其他物理学领域的基础研究领域,比如流体力学、量子力学等。
随着混沌研究的深入,这一理论开始在更多的领域得到应用,比如经济学、社会科学等。
在经济学中,混沌理论有着广泛的应用,尤其是在预测股票价格和研究经济波动等方面。
社会科学方面则主要应用于人类行为和集体行为的建模。
3. 混沌理论的意义和展望混沌理论的出现和发展对于人类认识自然的深度和广度有着重要的影响。
混沌现象的探索,让我们重新认识到了自然界的复杂性和多样性。
许多此前认为是随机、无序现象的自然现象,比如气象、生物进化等,现在都可以用系统动力学的方法进行建模和研究。
同时,混沌理论也对人类社会的发展产生了深远影响。
混沌系统模型和相关的数学方法具有广泛的应用潜力,可以用于分析和优化复杂系统,比如城市交通、食物供应、能源消耗等。
这些应用不仅能够提高系统的效率和可持续性,还有助于人们对社会和环境问题的更深入认识。
在未来,混沌理论的研究还将继续深入,同时也将不断涌现出越来越多的应用场景。
《微型机与应用》2014年第33卷第4期欢迎网上投稿人们对混沌现象的认识可以追溯到19世纪,法国数学家Poincare 在研究太阳系三体运动时不经意间发现了它,1990年,美国海军实验室的学者Pecora 和他的同伴Carroll 在电子学线路的设计实验中观察到混沌同步的现象[1]。
在最近几十年中,混沌更是受到了广大学者和专家的关注和青睐。
从发现混沌现象到现在,混沌被应用在人们生活的各个方面,如机械系统、电子系统、生态系统、信息系统、应用数学和物理学中[2-6]。
随着混沌系统维数的增加,人们发现了超混沌现象,其中人们熟知的超混沌系统有超混沌Chen 系统、超混沌L ü系统等[7-8]。
超混沌的动力学行为比混沌动力学行为更加复杂,相轨迹在更多的方向上分离,超混沌现象利用信息加密使得对信息密码的破解更加困难,因此,超混沌系统在科技领域有着巨大的研究价值。
本文在前人所做工作的基础上,先构造了一个新的超混沌系统,并采用经典的动力学分析方法(包括相轨迹、平衡点、耗散性、Lyapunov 指数和poincare 截面等方面)对新系统从定性和定量两方面做了详细的分析,加深了对该超混沌系统的认识。
并借助Multisim 对新超混沌系统搭建了仿真电路,实验结果与理论分析相一致,验证了该超混沌系统的实际物理意义。
1新超混沌系统数学模型构造的新超混沌系统数学模型如下:x 觶=a (y -x )y觶=-xz -w z觶=-b+xy+x 2w觶=my (1)当系统初值取为[x 0,y 0,z 0,w 0]=[0.5,0.8,0.2,0.4],a =5,b =90,m =5时,计算机仿真的系统相轨迹如图1所示,初步判断该系统具有超混沌吸引子。
2新超混沌系统的动力学分析2.1平衡点分析通过求解下面的方程可以得到系统的平衡点:鄢基金项目:西北农林科技大学国家级“大学生创新创业训练计划”资助课题(1210712090)一个新超混沌系统的动力学分析及其电路实现鄢徐家宝,吴凤娇,黄心笛,赵嘉,王坤,宋芮(西北农林科技大学水利与建筑工程学院电气系,陕西杨凌712100)摘要:构造了一个新的超混沌系统,通过Matlab 绘制其相轨迹图,初步判断该系统具有混沌吸引子。
基于混沌电路的动力学分析及控制
混沌电路是一种具有非线性和复杂动力学行为的电路,近年来在科学研究和工程应用中引起了广泛关注。
本文将对基于混沌电路的动力学进行分析,并探讨其在控制系统中的应用。
首先,我们将对混沌电路的动力学特性进行分析。
混沌电路是一种非线性系统,其输出信号呈现出无规则且高度复杂的动态行为。
这种动力学行为可以通过Lyapunov指数和分岔图等方法进行分析和描述。
通过分析混沌电路的动力学特性,我们可以更好地理解其复杂性和不确定性。
其次,我们将探讨混沌电路在控制系统中的应用。
混沌电路具有灵活性和可变性的特点,可以用于实现各种控制目标。
例如,通过引入外部反馈控制,混沌电路可以用作混沌同步和混沌控制器。
混沌同步是指将两个或多个混沌电路的输出信号同步到相同的状态,这种同步可以实现信息传输和加密通信等应用。
而混沌控制器则可以利用混沌电路的复杂动力学行为来实现非线性控制,提高控制系统的性能和稳定性。
最后,我们将讨论混沌电路控制的挑战和前景。
混沌电路的动力学行为非常敏感,对初始条件和参数的微小变化都会导致系统的巨大差异。
这给混沌电路的控制带来了一定的困难。
然而,
随着混沌电路理论的深入研究和控制方法的不断发展,我们相信混沌电路在控制系统中的应用前景将会越来越广阔。
综上所述,基于混沌电路的动力学分析及控制是一个具有挑战性和前景广阔的研究领域。
通过深入理解混沌电路的动力学特性,并结合合适的控制方法,我们可以更好地利用混沌电路的复杂性和不确定性,实现各种控制目标。
相信在不久的将来,混沌电路在控制系统中的应用将会取得更大的突破和进展。
第5卷第4期2007年12月1672-6553/2007/05 /324-6动力学与控制学报J OURNA L O F DYNAM ICS AND CONTROLV o.l 5N o .4D ec .20072007-03-23收到第1稿,2007-05-13收到修改稿.*甘肃省自然科学基金资助项目(3ZS042-B25-049);兰州交通大学科研基金(DXS -2006-74,DXS -2006-75)一个新类Lorenz 混沌系统的动力学分析及电路仿真*李险峰1张建刚2褚衍东1常迎香2(1.兰州交通大学非线性研究中心,兰州 730070)(2.兰州交通大学数理与软件工程学院,兰州 730070)摘要 提出了一个新的三维自治类L orenz 系统.理论分析了该系统的动力学特性,并通过数值计算分析了系统在平衡点处的稳定性,以及产生H opf 分岔的条件.通过计算系统的时间序列的Lyapunov 指数谱、L ya -punov 维数、分岔图、Po i ncar 截面图等研究了系统的动力学特性.最后对该系统的一个混沌吸引子进行了实际电路的设计与仿真模拟.关键词 新类Lo renz 系统, L yapunov 指数, 分数维数, P o i nca r 截面图, 电路仿真引言混沌振动是存在于自然界中的一种普遍运动形式,是在确定系统中产生的不规则运动,其基本特征是具有对初始条件的敏感性[1].人们在认识和研究混沌理论和应用的过程中,逐步认识到混沌的研究价值和应用价值.随着对混沌的深入研究和实际工程需要,各种非线性混沌系统也被相继提出,并得到了广泛的研究.特别是自从上世纪60年代提出Lorenz 系统[2]以来,许多新的自治混沌系统也相继提出并得到了广泛的研究[3-8].其中最为著名的是Rossler 系统[3],在Lorenz 混沌系统反控制中被发现的Chen 系统[4,5]、L 系统[6]、统一混沌系统[7]、L i u 系统[8]以及Q i 系统[9-11]等,特别是L系统在Lorenz 系统和Chen 系统之间架起了一道桥梁,实现了从一个系统到另一个系统的过渡[6,7].本文提出了一个新的类Lorenz 系统,该系统含有2个非线性项,文中利用理论推导、数值仿真、Lyapunov 指数谱、Lyapunov 维数、分岔图、Po incar 截面图等分析了该系统的基本动力学特性,从数值和理论上分析了系统的混沌特性.结果表明该系统和Lorenz 系统族中[12-14]每一个系统有着类似的性质,并且奇怪吸引子都具有较低分数维数.最后设计了模拟该混沌系统的实际电路,同时基于E W B 软件平台及电子仪器进行了实际电路仿真验证.1 新的类Lorenz 系统的模型及基本动力学特性该系统是根据Lorenz 吸引子和Chen 吸引子线性部分系数的特征,构造了一个三维非线性动力学系统.系统的模型如下:x =a (y -x ) y =abx -axz z =xy -cz(1)其中x =(x,y,z )TR 3为系统的状态变量,a,b ,c 为参数,且a 0.系统(1)中共含有2个非线性项,分别是xz ,xy .可以通过严格的数学证明系统(1)与上述Lorenz 系统族中每一个系统都不具有拓扑等价性,是一个完全新的类Lorenz 系统.由于严格证明拓扑等价性是十分困难和繁琐的,故在此略去.1.1 几条最基本的性质(1)对称性和不变性首先,注意到系统(1)在变换S:(x,y ,z ) (-x ,-y,z)下对于所有的参数a,b ,c 具有不变性,则此变换表明系统关于z 轴是对称的,即若 是系统的解,则在此意义下,S 也是系统的解.显然,z 轴本身也是系统的一条解轨线,也就是说,若t =0时有x =0,y =0,则对于所有的t >0,仍然有x =0,y =0.更进一步说,对于t 0,z 轴上所有的解轨线都趋向于原点.第4期李险峰等:一个新类L orenz混沌系统的动力学分析及电路仿真(2)耗散性和吸引子的存在性可以验证,系统(1)在a>0,b<0,c>0时是关于原点是全局,一致渐近稳定的.可以构造如下的正定的Lyapunov函数V(x,y,z)=-bx2+y2+az2(2)容易验证V (x,y,z)=-2b xx+2yy+2azz=-2bx(a(y-x))+2y(ax(b-z))+2az(xy-cz)=2a(bx2-cz2)<0(3)同时,考虑系统(1)的向量场散度(4),也就是系统的Jacob i n矩阵(5)的迹(6)V=1V d Vd t=div V=xx+yy+zz(4)J=-a a0a(b-z)0-axy x-c(5)Tr(J)=-(a+c)(6)又由于所有Lyapunov特征指数之和反映相空间体积元随时间演化的变化率,根据L i o uv ille定理,变化率反映为系统的Jacobin矩阵的迹,则有V=1V d Vd t=div V=xx+yy+zz=Tr(J)=-(a+c)= 3i=1i= LE s(7) V(t)=V(0)e-(a+c)t(8)其中, i(i=1,2,3)为矩阵(5)的特征根,LES为系统的3个Lyapunov特征指数.所以只要a+c>0,则系统(1)始终是耗散的,并以指数形式收敛.即d Vd t=e-(a+c)(9)也就是说,一个初始体积为V(0)的体积元在时间t 时收缩为体积元V(0)e-(a+c)t.这就意味着,当t 时,包含系统轨线的每一个体积元都以指数的速率-(a+c)收缩到0.因此,系统的所有轨线最终都会被限制在一个体积为0的点集合上,并且他的渐近动力学行为会被固定在一个吸引子上,这就说明了吸引子的存在性.并且当且仅当a+c=0,系统(1)是保守的,由L i o uv ill e定理可知,保守系统在运动过程中其相体积保持不变[15].当参数a=5,=4,c=2时,系统是耗散的,-(a+c)=-7<有一个混沌吸引子,如图1和图2所示,该混沌吸引子的三个Lyapunov指数分别为LE s=(0.6263,0,-7.6263),和 LE s=-7=-(a+c),由K aplan-Yorke猜想公式可求得Lyapunov维数D KY=2.0821.图1 3维相空间中的一个典型混沌吸引子F i g.1 Ph ase traj ectory of a typ ical chaotic attractor i n3-D space图2 图1中的混沌吸引子在不同平面上的投影F i g.2 Vari ous p rojecti ons of the chaotic attractor s ho w n i n F i g.11.2 平衡点稳定性分析如果bc>0系统的三个平衡点为O(0,0,0), P+(bc,bc,b),P-(-bc,bc,b),如果bc< 0,系统只有一个平衡点O(0,0,0).对于bc=0,有唯一的平衡点,形式为(0,0,b),b R.这里只考虑bc>0的条件下的三个平衡点为O,P+,P-的稳定性的情况,其中不动点P+和P-对称的落在z轴的两侧.命题1 如果a 0,b>0,则平衡点O都是不稳定的.证明:根据系统(1)的Jacobin矩阵(5),可得系统(1)在平衡点O处的线性化后的Jacob i n矩阵(10)和特征多项式(11)分别为325动 力 学 与 控 制 学 报2007年第5卷3+(a+c) 2+(ac-a2b) -a2bc=0( +c)( 2+a -ba2)=0(11)三个特征值分别为1=-c, 2,3=-a2 ba2+a24所以对于a>0有 2=a2(-1+4b+1)>0,a<0有 3=a2(-1-4b+1)>0,得证.下面来讨论平衡点P+和P-的稳定性.由于系统(1)在变换S:(x,y,z) (-x,-y,z)下对于所有的参数a,b,c具有不变性,系统关于z轴对称,而且平衡点P+和P-也关于z轴对称,所以二者的性质完全相同,只需分析其中之一即可.考虑线性变换T:(x,y,z) (X,Y,Z)T:x=X+bcy=Y+bcz=Z+b(12)于是系统(1)就化为x=a(Y-X)y=-a(X+bc)Zz=(X+bc)(Y+bc)-c(Z+b)(13)经过坐标平移变化以后,原系统(1)的不动点P+在线性变换T的作用下新的系统(13)的坐标原点O (0,0,0).下面讨论新的平衡点O (0,0,0)的稳定性.系统(13)在平衡点O 处的线性化后的Jacob i n 矩阵(14)和特征多项式(15)分别为J o =-a a0-az0-a bc Y+bcX+bc-c(0,0,0)=-a a000-a bcbc bc-c(14)3+(a+c) 2+(ac+abc) +2a2bc>0(15)由Rout h-H ur w itz判据,当且仅当满足下列条件时a+c>0(a+c)(ac+abc)-2a2bc>0(16)特征方程(15)的根都有负实部.所以当且仅当条件(16)满足时,系统(1)的平衡点P+和P-才是渐近稳定的.并且还可以推证特征根方程(15)有一对纯虚根,另一个根具有负实部当且仅当以下条件成立a+c>0ac(b+1)>0a+c+bc=ab(17)并且其中的一个实特征根 1=-(a+c),一对纯虚根 2,3= i ac(b+1).于是可以得到下面的结论命题2 如果条件(17)满足时,系统(1)有一个负实根 1=-(a+c)和一对共轭的纯虚根 2,3= i2a2ca-c,并且R e(c(c)) 0,所以此时平衡点P+失稳,发生H op f分岔.证明:令 =(X,Y,Z)T,则有=xyz=a(Y-X)-a(X+bc)Z(X+bc)(Y+bc)-c(Z+b)=f( ,a,b,c)(18)容易验证对于 a,b,c R,有f(0,a,b,c)=0恒成立.并且由条件(17)可知,b 1,且参数a,b与c之间的相互关系为a=c(b+1)b-1,c=a(b-1)b+1,b=a+ca-c(19)于是从特征方程(15),可以得到c=-2+a(b+1) +2a2b3 2+2(a+c) +ac(b+1)(20)c=-2+a(b+1) +2a2b3 2+2(a+c) +ac(b+1)c=a(b-1)b+1=-(b+1)2+a(b+1)2 +2a2b(b+1)3(b+1) 2+4ab +a2(b2-1)(21)将 2,3= i ac(b+1)代入(21)中有R e( c(c))=-b3+b2-b-12b3+10b2-2b-2=-(b2-1)(b+1)2b3+10b2-2b-2I m( c(c))=b-1(b4-2b2+1)2b+8b-12b+2=b-1(b+1)2(b-1)22b+8b-12b+2于是可以得出,系统(13)在平衡点O (0,0,0)处发生了H op f分岔,所以系统(1)在平衡点P+b)处发生了H opf分岔,并且经过一系326第4期李险峰等:一个新类L orenz 混沌系统的动力学分析及电路仿真列复杂的推导之后,可得H opf 分岔是亚临界的.2 数值仿真与电路实现2.1 分岔图、Lyapunov 指数谱、Lyapunov 维数、Po incar 截面图下面考虑系统(1)在特定参数下的动力学行为仿真情形1 考虑固定参数b =4,c =2,改变控制参数a 在区间[0,60]内连续变化.图3为系统(1)关于z 轴的分岔图以及所对应的Lyapunov 指数谱.图3 控制参数a 变化时的关于z 轴的分岔图及Lyapunov 指数谱F i g .3 B if u rcati on d i agra m and Lyapunov-exponent spectrum f or specifi c val ues set(b =4,c =2)versus t h e con trol para m eter a情形2 固定参数b =4,a =5,c 作为分岔参数,c [0.1,0.6]系统关于轴的分岔图以及所对应的Lyapunov 指数谱如图4所示.沿着控制参数增大的方向,系统由倍周期分岔通向混沌,混沌区域内含有数个较窄的周期窗口,并且每一个周期窗口又都是经由倍周期分岔走向混沌.并且通过K a -plan-Yorke 猜想计算系统的吸引子的Lyapunov 维数可知,系统(1)在这组参数下,随着控制参数的变化,分数维数数值都很小,D KY <2.1,如图4(c)所示.图4(d )为c =0.3时,在x -y (z =0)平面上的Po incar 映像,其中吸引子的叶片清晰可见,并且吸引子的叶片被折叠,这就导致了系统复杂的动力学行为.图4 系统(1)在控制参数c 变化时的动力学仿真F i g .4 Dyna m ics s i m u lati on s f orspeci fi c val ues s et(a=5,b=4)versus the con trol para m eter a情形3 考虑固定参数a =5,c =2,改变参数b ,b [1,20],系统关于z 轴的分岔图以及所对应的Lyapunov 指数谱如图5所示.随着分岔控制参图5 控制参数b 变化的关于z 轴的分岔图及Lyapunov 指数谱F i g .5 B if u rcati on d i agra m and Lyapunov-exponen t spectrum for s p ecific values set(a=5,b =2)vers u s the control para m et er a数b 的逐渐增大,系统由不动点突然直接进入一个较长的含有数个周期窗口的混沌区域,在每一个区域长短不等的周期窗口内都内嵌着倍周期分岔序327动 力 学 与 控 制 学 报2007年第5卷列,并且都是从周期到混沌的阵发过渡.最后,系统历经了一段较长的逆倍周期分岔,并且由Kap lan-Y or ke 猜想公式确定的系统吸引子的分数维数也很低,以上这两个特征与Lorenz 系统特别类似.2.2 电路实现下面设计一个电路来实现这个新的混沌系统的吸引子.这里设计的电路由三个部分组成,可实现系统(1)在确定参数下的吸引子,如图6所示.这三部分将三个状态标量连接成一个整体.运动放大器,模拟乘法器,线性电阻和电容器等来执行加、减、乘运算,为了明晰起见,各个电子元件参数标示在图上.图7为采用E W B 软件平台对电路进行仿真实验的结果.比较图2,图7,不难发现数值仿真与电路试验观测得到的不同平面上的相图是基本一致的.图6 基于EW B 软件平台的电路图F i g .6 C ircu it d i agra m f or realizi ngthe c h aotic attractor of syste m bas ed on E W B s oft ware图7 实际电路仿真实验图F i g .7 Experm i ental obs ervati ons of the c haoti c at tract or i n different p l anes3 结论本文构造并研究了一类新的类Lorenz 系统.较为细致地研究了该系统的一些非线性动力学行为,其中包括一些基本的动力学特征、分岔、周期窗口和通向混沌道路等,并对该系统的一个混沌吸引子设计了实际电路来仿真验证.但是需要指出的是该混沌系统仍然有许多复杂的动力学行为没有被揭示出来,因此该系统值得更进一步的研究.参 考 文 献1 刘延柱,陈立群.非线性振动.北京:高等教育出版社,2001(L i u Y anzhu ,Chen L i qun .N on linear v i bration .Be-i ji ng :H i gher Educati on P ress ,2001(i n Chi nese))2L orenz E N.D ete r m inistic nonper i od i c flow .J.A t m os .Sci .,1963,20:130~1413 R ossler ,O E .A n equation fo r con tinuous chaos .P hys ics Let -ter A,1976,57:397~3984 Chen G R,U e ta T.Y et anothe r chao ti c a ttractor .Interna -tional Journal of B i furcation and Chao s ,1999,9:1465~14665 C eli kovsk y S ,Chen G R.On a genera li zed Lo renz canon ica lf o r m of chao ti c sy stem s v i a a nonli near obse rved approach .Interna tional Journal of B i furcation and Chaos,2002,8:1789~18126 L J H,Chen G R.A new chaotic a ttractor co ined .Interna -tional Journal of B ifurcati on and Chaos ,2002,3:659~6617 L JH,Chen G R,Cheng D Z et a.l Br i dge t he gap be -t w een the Lo renz sy stem and t he Chen system .Interna tional Journal of B i furcation and Chaos,2002,12:2917~29268 L i u C X,L i u T,L i u L.A new chaotic a ttractor .Chaos ,Solitons and F ractals ,2004,5:1031~10389 Q iG Y,Chen G R,Du S Z,Chen Z Q,Yuan Z Z .A na l y si sof a new chaotic syste m.P hy sica A,2005,352(2-4):295~30810 Q i G Y,Chen G R.Ana l ys i s and c ircu it i m ple m entati onof a ne w 4D chaotic syste m.Phys ics L etters A,2006,352:386~39711 王琳,倪樵,黄玉盈.Q i 四维系统的暂态混沌现象.动力学与控制学报,2007,5(1):18~22(W ang L i n ,N iQ i ao ,H uang Y uy i ng .Chao ti c transients i n Q i s 4D syste m.Journal of D yna m ics and C ontro l ,2007,5(1):18~22(i n Ch i nese))12 陈关荣,吕金虎.Lo renz 系统族的动力学分析、控制与同步.北京:科学出版社,2003(Chen G R,L J H.Dy -nam ics o f the L orenz sy stem fa m ily :ana lysis ,control and synchron izati on .Be iji ng :Sc ience P ress ,2003(i n Chinese))13 王琳,倪樵,刘攀,黄玉盈.一种新的类Lo renz 系统的混沌行为与形成机制.动力学与控制学报,2005,3(4):1~6(W ang L i n ,N i Q i ao ,L i u pan ,H uang Y uy i ng .Chaos and its for m i ng m echan i s m of a ne w Lo renz-like syste m.328第4期李险峰等:一个新类L orenz 混沌系统的动力学分析及电路仿真Journal of Dy na m ics and Contro l ,2005,3(4):1~6(i n Ch i nese))14 严艳,张隆阁.L orenz 系统的分数阶控制算法.动力学与控制学报,2006,4(2):132~135(Y an Y an ,Zhang L ongge .F racti onal contro l a l gor ith m o fL orenz system.Jour -nal of D yna m ics and Control ,2006,4(2):132~135(i n Ch i nese))15 刘秉正,彭解华.非线性动力学.北京:高等教育出版社,2004(L i u B i ngzheng ,Peng Ji ehua .N on li nea r D ynam -i cs .Beiji ng :H i gher Educati on P ress ,2001(i n Chi nese))Received 23M arch 2007,revis ed 13M ay 2007.*Th is research i s s upported by t he Nature S cience Founderati on of Gansu Provi nce (3ZS -042-B25-049)and S ci en tifi c Research Foundati ons of L anz hou Jiaotong Un i versity (DXS -2006-74and DXS-2006-75)DYNA M ICS ANALYSIS AND CIRCU IT EXPER IM ENT SIMULAT I ONFOR A NE W LORENZ-LIKE CHAOTIC S YSTE M*LiX ianfeng 1Zhang Jiangang 2Chu Yandong 1Chang Y i n gx iang2(1.N onlinear S cience R esearc h C enter,Lanzhou J iao tong Universit y,Lanzhou 730070,China)(2.Schoo l of M athe m atics ,Phy sics and Soft ware Eng ineering,Lanzhou J iao t ong University,Lanzhou 730070,Ch i na)Abst ract A ne w Lorenz -like chaotic syste m w as presented.The non li n ear characteristic and basic dyna m ic pr op -erties o f th is t h ree -d i m ensional autono m ous syste m w ere stud i e d by m eans o f nonli n ear dyna m ics theory ,nu m er-i ca l si m u lation ,Lyapunov -exponent spectr um,Lyapunov d i m ensi o n ,b ifurcati o n diagra m and Poincar secti o n m ap .The osc illator circuit of the ne w chaoti c syste m w as designed by usi n g E W B so ft w are ,and a typical chaotic attrac-t or w as de m onstrated by circu it experi m en.tK ey w ords ne w Lorenz -like syste m , Lyapunov exponen,t fracta l d i m ensi o n, Po incar secti o n m ap ,circuit si m u lation329。
第3期屈双惠等:一类混沌系统动力学行为的突变分析225
2突变行为分析
2.1发生突变行为的条件
系统(1)之所以会在口∈[3.5,3.86J出现2个吸引子,是因为在此区域系统出现2个稳定不动点,围绕这2个稳定不动点形成了2个混沌吸引子.为了分析系统产生稳定不动点的情况,图3给出了当Co=17.0时,随口变化,F(x。
)与分角线相交的情况.
——一凡h);——一y2z
图3C。
=17.0时,系统(1)的_F(z。
)曲线
口较小时,系统与分角线只有一个交点C,为稳定不动点,此时系统只有围绕该稳定不动点C的吸引子;当肛增大到3.5时,系统与分角线相切,另一稳定不动点D(与切点B重合)开始出现,此时Xtr-。
=z。
,系统斜率F7(z。
)一1;随着肚的继续增大,系统与分角线出现3个交点,交点E为不稳定不动点,D点和C点为稳定不动点,在此区域可出现围绕稳定不动点C,D的2混沌吸引子;当口增大到3.86时,系统再次与分角线相切,交点C减小到与切点A重合;当∥超越此值时,在C点处系统与分角线分离,交点C消失,系统与分角线只有一个交点D,此时系统只有围绕稳定不动点D的吸引子[4].2.2突变行为走向分析
在系统发生突变过程的区域。
交点E为不稳定不动点,其系统值zE与系统状态参数C。
及系统参数/.t有关,即
zE一号COSq--[-psing+号,
式中:p2√一3(一÷+吉),923.5时,由稳定不动点C决定的吸引子处于混沌状态;当系统参数口增大超过临界值3.5时,系统与分角线交点由1个增至3个,出现另一稳定不动点D及不稳定不动点E,由于吸引子不能跨越不稳定不动点(虚线)同时占据2吸引子空间,因此卢=3.5时,系统从由原稳定不动点C决定的吸引子(混沌状态)突变到另一稳定不动点D决定的吸引子上;随着岸的继续增大,不动点D决定的吸引子进入混沌状态,其吸引域不断逼近不稳定不动点,在口=3.78时将超越不稳定不动点,由于同一吸引子不能跨越不稳定不动点同时占据2吸引子空间,此时其吸引子将突变回由不动点C决定的吸引子上;当“增大到另一临界值3.86时,不稳定不动点C消失,吸引子突变到D决定的吸引子上.麒减小时的情况与此类似,系统也发生3次突变.
系统状态参数C。
略有变动时,系统的动力学行为会略有不同,但仍会在特定区域出现突变.图4,5分别给出了C。
=16.0,系统参数肛∈E3.4。
3.953时,混沌系统(1)随系统参数增大或减小时的分岔情况.可以看出:随着口的增大,原稳定不动点C决定的吸引子始终未超越不稳定不动点(虚线),直到口越过临界值3.73时,交点C消失,系统值才突变到另一稳定不动点D决定的吸引子上;随着肛的减小,当其越过另一临界值3.47时。
原不动点D消失,系统突变到稳定不动点C决定的吸引子上.
图4Co一16.0,卢增大时系统(1)的分f岔ltt
÷arc。
s:::!j2;i!:::i:{;
一.
226宁夏大学学报(自然科学版)第31卷
给出了Co=17.0时。
随肛的增大,系统在突变区域的吸引子.可以看出:Co=17.0时,随着系统参数的增大,突变区域出现2吸引子,吸引子以不稳定不动点(虚线)为界线,除个别误差点外不会逾越不稳定不动点而同时占据2吸引子空间.
图6Co=17.0时的吸引子
-£n
图7Co=16.0时的吸引子
图7给出了C。
一16.0时,随且的增大,系统在突变区域的吸引子.可以看出:随着口的增大,突变区域只出现一围绕稳定不动点C的吸引子,即在此区域,该吸引子不会突变到另一吸引子上,只在临界点才发生突变.
对于高阶次突变系统,由于系统与分角线的交点可更多,在突变区域可出现多个由稳定不动点决定的吸引子,当某一吸引子的吸引域逾越不稳定不动点界限或临界点时,也会发生突变【5卅].zE=0.743,迭代将围绕不动点D进行,系统为混沌状态;若选定的初始值大于不稳定不动点,迭代将围绕不动点C进行,系统为二周期轨道.如图9所示,口一3.73时,取迭代次数玎=300,当初始值选定为0.4时,系统处于混沌状态;当初始值选定为0.8时,系统处于二周期轨道[8].
Ⅳ
图8Co一17.0时。
由初值决定的2吸引子图9砧-----3.73。
迭代次数挖300时系统的状态
3初始值对系统动力学行为的影响
月继适
‘士;口p口
对于系统(1),由于在突变区域,以不稳定不动点(虚线)为界线,不动点把迭代数值分为了2个混沌区域,如图8所示.
当口一定时,以不稳定不动点为界限,如果初始值大于不稳定不动点,迭代将围绕稳定不动点C进行,如果初始值小于不稳定不动点,迭代将围绕稳定不动点D进行.因此,通过对初始值的调节,可以实现对系统动力学行为迭代范围的控制.在图8中,当卢=3.73时,若选定的初始值小于不稳定不动点
通过对突变系统突变行为的分析发现,在系统突变区域可出现2个由稳定不动点决定的混沌吸引子,随着系统参数的变化,当某个吸引子的吸引域逾越不稳定不动点界限或临界状态时。
系统将突变到另一吸引子上.并且在此区域,随着系统参数变化趋势的不同,系统的动力学行为要发生变化.据此,在突变区域,通过适当调节系统的初始值,可对系统的动力学行为走向加以控制,这对分析和调节复杂混沌系统的非线性动力学行为具有重要的理论意义.。