高考数学一轮复习试题 x42 理

高考数学总复习考点知识讲解与提升练习专题42 数列中的构造问题数列中的构造问题是历年高考的一个热点内容，主、客观题均可出现，一般通过构造新的数列求数列的通项公式．题型一形如a n＋1＝pa n＋f(n)型命题点1a n＋1＝pa n＋q(p≠0,1，q≠0)例1(1)数列{a n}满足a n＝4a n－1＋3(n≥2)且a1＝0，则a2024等于()A．22023－1 B．42023－1 C．22023＋1 D．42023＋1答案B解析∵a n＝4a n－1＋3(n≥2)，∴a n＋1＝4(a n－1＋1)(n≥2)，∴{a n＋1}是以1为首项，4为公比的等比数列，则a n＋1＝4n－1.∴a n＝4n－1－1，∴a2024＝42023－1.(2)已知数列{a n}的首项a1＝1，且1an＋1＝3an＋2，则数列{a n}的通项公式为__________．答案a n＝1 2·3n－1－1解析∵1a n＋1＝3an＋2，等式两边同时加1整理得1an＋1＋1＝3⎝⎛⎭⎪⎫1an＋1，又∵a 1＝1，∴1a 1＋1＝2，∴⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n ＋1是首项为2，公比为3的等比数列．∴1a n＋1＝2·3n －1，∴a n ＝12·3n －1－1.命题点2a n ＋1＝pa n ＋qn ＋c (p ≠0,1，q ≠0)例2已知数列{a n }满足a n ＋1＝2a n －n ＋1(n ∈N *)，a 1＝3，求数列{a n }的通项公式． 解∵a n ＋1＝2a n －n ＋1， ∴a n ＋1－(n ＋1)＝2(a n －n )， ∴a n ＋1－(n ＋1)a n －n＝2，∴数列{a n －n }是以a 1－1＝2为首项，2为公比的等比数列， ∴a n －n ＝2·2n －1＝2n ， ∴a n ＝2n ＋n .命题点3a n ＋1＝pa n ＋q n (p ≠0,1，q ≠0,1)例3(1)已知数列{a n }中，a 1＝3，a n ＋1＝3a n ＋2·3n ＋1，n ∈N *.则数列{a n }的通项公式为() A ．a n ＝(2n ＋1)·3n B ．a n ＝(n －1)·2n C ．a n ＝(2n －1)·3n D ．a n ＝(n ＋1)·2n 答案C解析由a n ＋1＝3a n ＋2·3n ＋1得a n ＋13n ＋1＝a n 3n ＋2·3n ＋13n ＋1， ∴a n ＋13n ＋1－a n3n ＝2，即数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n 3n 是首项为1，公差为2的等差数列，∴a n3n ＝2n －1，故a n ＝(2n －1)·3n .(2)在数列{a n }中，a 1＝1，且满足a n ＋1＝6a n ＋3n ，则a n ＝________. 答案6n3－3n －1解析将已知a n ＋1＝6a n ＋3n 的两边同乘13n ＋1，得a n ＋13n ＋1＝2·a n 3n ＋13，令b n ＝a n3n ，则b n ＋1＝2b n ＋13，利用命题点1的方法知b n ＝2n 3－13，则a n ＝6n3－3n －1.思维升华跟踪训练1(1)在数列{a n }中，a 1＝1，a n ＋1＝2a n ＋2n .则数列{a n }的通项公式a n 等于() A ．n ·2n －1 B ．n ·2n C ．(n －1)·2n D ．(n ＋1)·2n 答案A解析由a n ＋1＝2a n ＋2n 得a n ＋12n＝a n 2n －1＋1，设b n ＝a n 2n －1，则b n ＋1＝b n ＋1，又b 1＝1，∴{b n }是首项为1，公差为1的等差数列． ∴b n ＝n ， ∴a n ＝n ·2n －1.(2)(2023·黄山模拟)已知数列{a n }满足a 1＝1，(2＋a n )·(1－a n ＋1)＝2，设⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 的前n 项和为S n，则a2023(S2023＋2023)的值为()A．22023－2 B．22023－1 C．2 D．1 答案C解析(2＋a n)(1－a n＋1)＝2，则a n＋1＝a na n ＋2，即1an＋1＝2an＋1，得1an＋1＋1＝2⎝⎛⎭⎪⎫1an＋1，故⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1an＋1是以2为首项，2为公比的等比数列，1an＋1＝2n，1an＝2n－1，a n＝12n－1，S2023＋2023＝2＋22＋…＋22023＝22024－2，∴a2023(S2023＋2023)＝2.(3)已知数列{a n}满足a n＋1＝2a n＋n，a1＝2，则a n＝________.答案2n＋1－n－1解析令a n＋1＋x(n＋1)＋y＝2(a n＋xn＋y)，即a n＋1＝2a n＋xn＋y－x，与原等式比较得，x＝y＝1，所以an＋1＋(n＋1)＋1an＋n＋1＝2，所以数列{a n＋n＋1}是以a1＋1＋1＝4为首项，2为公比的等比数列，所以a n＋n＋1＝4×2n－1，即a n＝2n＋1－n－1. 题型二相邻项的差为特殊数列(形如a n＋1＝pa n＋qa n－1)例4(1)已知数列{a n}满足：a1＝a2＝2，a n＝3a n－1＋4a n－2(n≥3)，则a9＋a10等于() A．47 B．48 C．49 D．410答案C解析由题意得a1＋a2＝4，由a n＝3a n－1＋4a n－2(n≥3)，得a n ＋a n －1＝4(a n －1＋a n －2)， 即a n ＋a n －1a n －1＋a n －2＝4(n ≥3)，所以数列{a n ＋a n ＋1}是首项为4，公比为4的等比数列，所以a 9＋a 10＝49.(2)已知数列{a n }满足a 1＝1，a 2＝2，且a n ＋1＝2a n ＋3a n －1(n ≥2，n ∈N *)．则数列{a n }的通项公式为a n ＝________. 答案3n －(－1)n4解析方法一因为a n ＋1＝2a n ＋3a n －1(n ≥2，n ∈N *)， 设b n ＝a n ＋1＋a n ，所以b n b n －1＝a n ＋1＋a n a n ＋a n －1＝3(a n ＋a n －1)a n ＋a n －1＝3，又因为b 1＝a 2＋a 1＝3，所以{b n }是以首项为3，公比为3的等比数列． 所以b n ＝a n ＋1＋a n ＝3×3n －1＝3n ， 从而a n ＋13n ＋1＋13·a n 3n ＝13， 不妨令c n ＝a n 3n ，即c n ＋1＋13c n ＝13，故c n ＋1－14＝－13⎝ ⎛⎭⎪⎫c n －14，即c n ＋1－14c n －14＝－13，又因为c 1－14＝a 13－14＝112，所以数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫c n －14是首项为112，公比为－13的等比数列，故c n －14＝112×⎝ ⎛⎭⎪⎫－13n －1＝a n 3n －14，从而a n ＝3n －(－1)n4.方法二因为方程x 2＝2x ＋3的两根为－1,3， 可设a n ＝c 1·(－1)n －1＋c 2·3n －1， 由a 1＝1，a 2＝2， 解得c 1＝14，c 2＝34，所以a n ＝3n －(－1)n4.思维升华可以化为a n ＋1－x 1a n ＝x 2(a n －x 1a n －1)，其中x 1，x 2是方程x 2－px －q ＝0的两个根，若1是方程的根，则直接构造数列{a n －a n －1}，若1不是方程的根，则需要构造两个数列，采取消元的方法求数列{a n }．跟踪训练2若x ＝1是函数f (x )＝a n ＋1x 4－a n x 3－a n ＋2x ＋1(n ∈N *)的极值点，数列{a n }满足a 1＝1，a 2＝3，则数列{a n }的通项公式a n ＝________. 答案3n －1解析f ′(x )＝4a n ＋1x 3－3a n x 2－a n ＋2，∴f ′(1)＝4a n ＋1－3a n －a n ＋2＝0，即a n ＋2－a n ＋1＝3(a n ＋1－a n )，∴数列{a n ＋1－a n }是首项为2，公比为3的等比数列， ∴a n ＋1－a n ＝2×3n －1，则a n ＝a n －a n －1＋a n －1－a n －2＋…＋a 2－a 1＋a 1＝2×3n －2＋…＋2×30＋1＝3n －1.题型三倒数为特殊数列⎝ ⎛⎭⎪⎫形如a n ＋1＝pa n ra n ＋s 型 例5(1)已知数列{a n }满足a 1＝1，a n ＋1＝a n 4a n ＋1(n ∈N *)，则满足a n >137的n 的最大取值为()A ．7B ．8C ．9D ．10 答案C 解析因为a n ＋1＝a n 4a n ＋1，所以1a n ＋1＝4＋1a n ，所以1a n ＋1－1a n ＝4，又1a 1＝1，所以数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 是以1为首项，4为公差的等差数列．所以1a n ＝1＋4(n －1)＝4n －3，所以a n ＝14n －3，由a n >137，即14n －3>137，即0<4n －3<37，解得34<n <10，因为n 为正整数，所以n 的最大取值为9.(2)(多选)数列{a n }满足a n ＋1＝a n 1＋2a n(n ∈N *)，a 1＝1，则下列结论正确的是()A.2a 10＝1a 3＋1a 17B.1{2}na 是等比数列C ．(2n －1)a n ＝1D ．3a 5a 17＝a 49 答案ABC解析由a n ＋1＝a n1＋2a n ，可得1a n ＋1＝1＋2a na n ＝1a n ＋2，所以1a n ＋1－1a n ＝2，且1a 1＝1，所以数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 是等差数列，且该数列的首项为1，公差为2，所以1a n＝1＋2(n －1)＝2n －1，则(2n －1)a n ＝1，其中n ∈N *，故C 对；1111112=22n n nna a a a ++-＝22＝4，所以数列1{2}na 是等比数列，故B 对；由等差中项的性质可得2a 10＝1a 3＋1a 17，故A 对；由上可知a n ＝12n －1，则3a 5a 17＝3×12×5－1×12×17－1＝199，a 49＝12×49－1＝197，所以3a 5a 17≠a 49，故D 错． 思维升华两边同时取倒数转化为1a n ＋1＝s p ·1a n ＋r p的形式，化归为b n ＋1＝pb n ＋q 型，求出1a n的表达式，再求a n .跟踪训练3已知函数f (x )＝x 3x ＋1，数列{a n }满足a 1＝1，a n ＋1＝f (a n )(n ∈N *)，则数列{a n }的通项公式为____________． 答案a n ＝13n －2(n ∈N *) 解析由已知得，a n ＋1＝a n 3a n ＋1，∴1a n ＋1＝1a n＋3，即1a n ＋1－1a n＝3，∴数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 是首项为1a 1＝1，公差为d ＝3的等差数列，∴1a n＝1＋(n －1)×3＝3n －2.故a n ＝13n －2(n ∈N *)．课时精练1．已知数列{a n }满足a 1＝2，a n ＋1＝2a n ＋1，则a 4的值为() A ．15 B ．23 C ．32 D ．42 答案B解析因为a n ＋1＝2a n ＋1，所以a n＋1＋1＝2(a n＋1)，所以{a n＋1}是以3为首项，2为公比的等比数列，所以a n＋1＝3·2n－1，所以a n＝3·2n－1－1，a4＝23.2．在数列{a n}中，a1＝5，且满足an＋12n－5－2＝an2n－7，则数列{a n}的通项公式为()A．2n－3B．2n－7C．(2n－3)(2n－7) D．2n－5 答案C解析因为a n＋12n－5－2＝an2n－7，所以an＋12n－5－an2n－7＝2，又a12－7＝－1，所以数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫an2n－7是以－1为首项，公差为2的等差数列，所以an2n－7＝－1＋2(n－1)＝2n－3，所以a n＝(2n－3)(2n－7)．3．已知数列{a n}满足：a1＝1，且a n＋1－2a n＝n－1，其中n∈N*，则数列{a n}的通项公式为()A．a n＝2n－n B．a n＝2n＋nC．a n＝3n－1D．a n＝3n＋1答案A解析由题设，a n＋1＋(n＋1)＝2(a n＋n)，而a1＋1＝2，∴{a n＋n}是首项、公比均为2的等比数列，故a n＋n＝2n，即a n ＝2n －n .4．已知数列{a n }满足a 2＝14，a n －a n ＋1＝3a n a n ＋1，则数列的通项公式a n 等于()A.13n －2B.13n ＋2C ．3n －2D ．3n ＋2 答案A解析∵a n －a n ＋1＝3a n a n ＋1，a 2＝14，∴a 1－a 2＝3a 1a 2， 即a 1－14＝34a 1，解得a 1＝1. 由题意知a n ≠0， 由a n －a n ＋1＝3a n a n ＋1得1a n ＋1－1a n＝3，又1a 1＝1，∴数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 是以1为首项，3为公差的等差数列，∴1a n＝1＋3(n －1)＝3n －2，则a n ＝13n －2.5．在数列{a n }中，若a 1＝3，a n ＋1＝a 2n ，则a n 等于() A ．2n －1 B.3n －1 C ．132n － D ．123n －答案D解析由a 1＝3，a n ＋1＝a 2n 知a n >0，对a n ＋1＝a 2n 两边取以3为底的对数得，log 3a n ＋1＝2log 3a n ，则数列{log 3a n }是以log 3a 1＝1为首项，2为公比的等比数列， 则log 3a n ＝1·2n －1＝2n －1，即a n ＝123n －.6．设数列{a n }满足a 1＝1，a n ＝－a n －1＋2n (n ≥2)，则数列的通项公式a n 等于() A.13·2n ＋13 B.13·2n＋13·(－1)n C.2n ＋13＋13 D.2n ＋13＋13·(－1)n 答案D解析∵a n －1＋a n ＝2n ，两边同时除以2n得，a n 2n ＋12·a n －12n －1＝1.令c n ＝a n2n ，则c n ＝－12c n －1＋1.两边同时加上－23得c n －23＝－12·⎝⎛⎭⎪⎫c n －1－23.∴数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫c n－23是以c 1－23为首项，－12为公比的等比数列，∴c n －23＝⎝ ⎛⎭⎪⎫c 1－23·⎝ ⎛⎭⎪⎫－12n －1＝13·⎝ ⎛⎭⎪⎫－12n ，∴c n ＝23＋13·⎝ ⎛⎭⎪⎫－12n，∴a n ＝2n·c n ＝2n ＋13＋13·(－1)n .7．(多选)已知数列{a n }满足a 1＝1，a n ＋1＝a n 2＋3a n(n ∈N *)，则下列结论正确的是()A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n ＋3为等差数列 B ．{a n }的通项公式为a n ＝12n －1－3C ．{a n }为递减数列 D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 的前n 项和T n ＝2n ＋2－3n －4答案CD 解析因为a n ＋1＝a n 2＋3a n，所以1a n ＋1＝2＋3a na n＝2a n＋3，所以1a n ＋1＋3＝2⎝ ⎛⎭⎪⎫1a n ＋3， 且1a 1＋3＝4≠0，所以⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n ＋3是以4为首项，2为公比的等比数列，即1a n＋3＝4×2n －1，所以1a n＝2n ＋1－3，可得a n ＝12n ＋1－3， 故选项A ，B 错误； 因为1a n＝2n ＋1－3单调递增，所以a n ＝12n ＋1－3单调递减， 即{a n }为递减数列，故选项C 正确；⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 的前n 项和T n ＝(22－3)＋(23－3)＋…＋(2n ＋1－3)＝(22＋23＋…＋2n ＋1)－3n＝22×1－2n1－2－3n ＝2n ＋2－3n －4，故选项D 正确．8．将一些数排成如图所示的倒三角形，其中第一行各数依次为1,2,3，…，2023，从第二行起，每一个数都等于它“肩上”的两个数之和，最后一行只有一个数M ，则M 等于()A ．2023×22020B ．2024×22021C ．2023×22021D ．2024×22022 答案B解析记第n 行的第一个数为a n ，则a 1＝1，a 2＝3＝2a 1＋1，a 3＝8＝2a 2＋2，a 4＝20＝2a 3＋4，…，a n ＝2a n －1＋2n －2，∴a n 2n －2＝a n －12n －3＋1，即⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n 2n －2是以a 12－1＝2为首项，1为公差的等差数列．∴a n 2n －2＝2＋(n －1)×1＝n ＋1，∴a n ＝(n ＋1)×2n －2.又每行比上一行的数字少1个， ∴最后一行为第2023行， ∴M ＝a 2023＝2024×22021.9．已知数列{a n }满足a 1＝32，a n ＋1＝3a n a n ＋3，若c n ＝3n a n ，则c n ＝____________.答案(n ＋1)3n －1解析因为a 1＝32，a n ＋1＝3a na n ＋3，所以1a n ＋1＝a n ＋33a n ＝13＋1a n， 即1a n ＋1－1a n ＝13， 所以数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 是首项为1a 1＝23，公差为13的等差数列，所以1a n ＝23＋13(n －1)＝n ＋13，则c n ＝3na n＝(n ＋1)3n －1.10．已知数列{a n }满足a n ＋1＝3a n －2a n －1(n ≥2，n ∈N *)，且a 1＝0，a 6＝124，则a 2＝________. 答案4解析由a n ＋1＝3a n －2a n －1(n ≥2，n ∈N *)可得a n ＋1－a n ＝2(a n －a n －1)， 若a n －a n －1＝0，则a 6＝a 5＝…＝a 1，与题中条件矛盾，故a n －a n －1≠0， 所以a n ＋1－a na n －a n －1＝2，即数列{a n ＋1－a n }是以a 2－a 1为首项，2为公比的等比数列，所以a n ＋1－a n ＝a 2·2n －1，所以a 6－a 1＝a 2－a 1＋a 3－a 2＋a 4－a 3＋a 5－a 4＋a 6－a 5＝a 2·20＋a 2·21＋a 2·22＋a 2·23＋a 2·24＝31a 2＝124，所以a 2＝4.11．在数列{a n }中，a 1＝1，且满足a n ＋1＝3a n ＋2n ，则a n ＝________. 答案52·3n －1－n －12解析∵a n ＋1＝3a n ＋2n ①，∴a n ＝3a n －1＋2(n －1)(n ≥2)，两式相减得，a n ＋1－a n ＝3(a n －a n －1)＋2，令b n ＝a n ＋1－a n ，则b n ＝3b n －1＋2(n ≥2)，利用求a n ＋1＝pa n ＋q 的方法知，b n ＝5·3n －1－1，即a n ＋1－a n ＝5·3n －1－1②，再利用累加法知，a n ＝52·3n－1－n－12⎝⎛⎭⎪⎫或联立①②解出a n＝52·3n－1－n－12.12．英国著名物理学家牛顿用“作切线”的方法求函数零点时，给出的“牛顿数列”在航空航天中应用广泛，若数列{x n}满足x n＋1＝x n－f(xn)f′(xn)，则称数列{x n}为牛顿数列．如果函数f(x)＝2x2－8，数列{x n}为牛顿数列，设a n＝ln xn＋2xn－2，且a1＝1，x n>2.数列{a n}的前n项和为S n，则S n＝________. 答案2n－1解析∵f(x)＝2x2－8，∴f′(x)＝4x，又∵x n＋1＝x n－f(xn)f′(xn)＝x n－2x2n－84x n＝x2n＋42x n，∴x n＋1＋2＝(x n＋2)22x n，x n＋1－2＝(x n－2)22x n，∴xn＋1＋2xn＋1－2＝⎝⎛⎭⎪⎫x n＋2xn－22，又x n>2，∴ln xn＋1＋2xn＋1－2＝ln⎝⎛⎭⎪⎫x n＋2xn－22＝2lnxn＋2xn－2，又a n＝ln xn＋2xn－2，且a1＝1，∴a n＋1＝2a n，∴数列{a n}是首项为1，公比为2的等比数列，∴{a n}的前n项和S n＝1×(1－2n)1－2＝2n－1.。

2021年高三理科数学一轮复习题组层级快练42含答案1．下列不等式中解集为R 的是( ) A ．－x 2＋2x ＋1≥0 B ．x 2－25x ＋5>0 C ．x 2＋6x ＋10>0 D ．2x 2－3x ＋4<0答案 C解析 在C 项中，Δ＝36－40＝－4<0，所以不等式解集为R .2．若0＜m ＜1，则不等式(x －m )(x －1m )＜0的解集为( )A ．{x |1m ＜x ＜m }B ．{x |x ＞1m 或x ＜m }C ．{x |x ＞m 或x ＜1m }D ．{x |m ＜x ＜1m}答案 D解析 当0<m <1时，m <1m .3．函数y ＝ln (x ＋1)－x 2－3x ＋4的定义域为( )A ．(－4，－1)B ．(－4,1)C ．(－1,1)D ．(－1,1]答案 C解析 由⎩⎪⎨⎪⎧x ＋1>0，－x 2－3x ＋4>0，解得－1<x <1.4．不等式x 2－x －6x －1>0的解集为( )A.{}x |x <－2或x >3B.{}x |x <－2或1<x <3C.{}x |－2<x <1或x >3D.{}x |－2<x <1或1<x <3 答案 C解析 x 2－x －6x －1>0，(x －3)(x ＋2)x －1>0，所以－2<x <1或x >3.5．(xx·重庆文)关于x 的不等式x 2－2ax －8a 2<0(a >0)的解集为(x 1，x 2)，且x 2－x 1＝15，则a ＝( )A.52B.72C.154D.152答案 A解析 由条件知x 1，x 2为方程x 2－2ax －8a 2＝0的两根，则x 1＋x 2＝2a ，x 1x 2＝－8a 2.故(x 2－x 1)2＝(x 1＋x 2)2－4x 1x 2＝(2a )2－4×(－8a 2)＝36a 2＝152，得a ＝52，故选A.6．已知不等式ax 2＋bx ＋2>0的解集为{x |－1<x <2}，则不等式2x 2＋bx ＋a <0的解集为( ) A ．{x |－1<x <12}B ．{x |x <－1或x >12}C ．{x |－2<x <1}D ．{x |x <－2或x >1} 答案 A解析 由题意知x ＝－1，x ＝2是方程ax 2＋bx ＋2＝0的根．由韦达定理⎩⎨⎧－1＋2＝－b a，(－1)×2＝2a⇒⎩⎪⎨⎪⎧a ＝－1，b ＝1. ∴不等式2x 2＋bx ＋a <0，即2x 2＋x －1<0. 可知x ＝－1，x ＝12是对应方程的根，∴选A.7．不等式(a －2)x 2＋2(a －2)x －4<0，对一切x ∈R 恒成立，则实数a 的取值范围是( ) A ．(－∞，2] B ．(－2,2] C ．(－2,2) D ．(－∞，2)答案 B解析 ∵⎩⎪⎨⎪⎧a －2<0，Δ<0，∴－2<a <2，另a ＝2时，原式化为－4<0，恒成立，∴－2<a ≤2.故选B.8．已知偶函数f (x )在区间[0，＋∞)上单调递增，则满足f (2x －1)<f (|x |)的x 的取值范围是( )A ．(13，23)B ．(13，1)C ．(12，23)D ．(12，1)答案 B解析由于f(x)是偶函数，故f(x)＝f(|x|)，故f(|2x－1|)<f(|x|)．再根据f(x)的单调性得|2x－1|<|x|⇒(2x－1)2<x2⇔3x2－4x＋1<0⇔(3x－1)(x－1)<0⇔13<x<1.9．(xx·郑州质检)不等式f(x)＝ax2－x－c>0的解集为{x|－2<x<1}，则函数y＝f(－x)的图像为()答案 C解析由题意得⎩⎨⎧a<0，－2＋1＝1a，－2×1＝－ca，解得a＝－1，c＝－2.则函数y＝f(－x)＝－x2＋x＋2.10．已知a1>a2>a3>0，则使得(1－a i x)2<1(i＝1,2,3)都成立的x的取值范围是()A．(0，1a1) B．(0，2a1)C．(0，1a3) D．(0，2a3)答案 B11．(xx·安徽理)已知一元二次不等式f(x)<0的解集为{x|x<－1或x>12}，则f(10x)>0的解集为()A．{x|x<－1或x>lg2} B．{x|－1<x<lg2}C．{x|x>－lg2} D．{x|x<－lg2}答案 D解析方法一：由题意可知f(x)>0的解集为{x|－1<x<12}，故f(10x)>0等价于－1<10x<12.由指数函数的值域为(0，＋∞)，知一定有10x>－1.而10x<12可化为10x<10lg12，即10x<10－lg2.而指数函数的单调性可知x <－lg2，故选D.方法二：当x ＝1时，f (10)<0，排除A ，C 选项．当x ＝－1时，f (110)>0，排除选项B ，选D.12．不等式2x 2－3|x |－35>0的解集为________． 答案 {x |x <－5或x >5}解析 2x 2－3|x |－35>0⇔2|x |2－3|x |－35>0⇔(|x |－5)(2|x |＋7)>0⇔|x |>5或|x |<－72(舍)⇔x >5或x <－5.13．已知－12<1x <2，则实数x 的取值范围是________．答案 x <－2或x >12解析 当x >0时，x >12；当x <0时，x <－2.所以x 的取值范围是x <－2或x >12.14．二次函数y ＝ax 2＋bx ＋c (x ∈R )的部分对应值如表：则不等式答案 (－∞，－2)∪(3，＋∞)解析 方程的根是对应不等式解集的端点，画草图即可．15．(xx·四川理)已知f (x )是定义域为R 的偶函数，当x ≥0时，f (x )＝x 2－4x .那么，不等式f (x ＋2)<5的解集是________．答案 (－7,3)解析 当x ≥0时，f (x )＝x 2－4x <5的解集为[0,5)，又f (x )为偶函数，所以f (x )<5的解集为(－5,5)．所以f (x ＋2)<5的解集为(－7,3)．16．若不等式a ·4x －2x ＋1>0对一切x ∈R 恒成立，则实数a 的取值范围是________． 答案 a >14解析 不等式可变形为a >2x －14x ＝(12)x －(14)x ，令(12)x ＝t ，则t >0.∴y ＝(12)x －(14)x ＝t －t 2＝－(t －12)2＋14，因此当t ＝12时，y 取最大值14，故实数a 的取值范围是a >14.17．解关于x 的不等式log 2a x －log a x 2－3>0.答案 a >1时，不等式解集为(0，1a )∪(a 3，＋∞)；0<a <1时，不等式解集为(0，a 3)∪(1a ，＋∞)解析 原不等式化为log 2a x －2log a x －3>0(a ≠1)， 令log a x ＝t ，则原不等式变为t 2－2t －3>0， 得t <－1或t >3. ∴log a x <－1或log a x >3. 当a >1时，0<x <1a 或x >a 3；当0<a <1时，0<x <a 3或x >1a.∴a >1时，不等式解集为(0，1a )∪(a 3，＋∞)；0<a <1时，不等式解集为(0，a 3)∪(1a ，＋∞)．18．解关于x 的不等式：a (x －1)x －2>1(a <1)．答案 0<a <1时，{x |2<x <a －2a －1}；a ＝0时，∅；a <0时，{x |a －2a －1<x <2}解析 (x －2)[(a －1)x ＋2－a ]>0， 当a <1时有(x －2)(x －a －2a －1)<0，若a －2a －1>2，即0<a <1时，解集为{x |2<x <a －2a －1}． 若a －2a －1＝2，即a ＝0时，解集为∅. 若a －2a －1<2，即a <0时，解集为{x |a －2a －1<x <2}．1．(xx·江苏)已知f (x )是定义在R 上的奇函数．当x >0时，f (x )＝x 2－4x ，则不等式f (x )>x 的解集用区间表示为________．答案 (－5,0)∪(5，＋∞)解析 由于f (x )为R 上的奇函数，所以当x ＝0时，f (0)＝0；当x <0时，－x >0，所以f (－x )＝x 2＋4x ＝－f (x )，即f (x )＝－x 2－4x ，所以f (x )＝⎩⎪⎨⎪⎧x 2－4x ，x >0，0，x ＝0，－x 2－4x ，x <0.由f (x )>x ，可得⎩⎨⎧x 2－4x >x ，x >0或⎩⎪⎨⎪⎧－x 2－4x >x ，x <0，解得x >5或－5<x <0，所以原不等式的解集为(－5,0)∪(5，＋∞)．2．不等式log 2(x ＋1x ＋6)≤3的解集为________．答案 (－3－22，－3＋22)∪{1}解析 原不等式⇔0<x ＋1x＋6≤8⇔①⎩⎪⎨⎪⎧x >0，x 2＋6x ＋1>0，x 2－2x ＋1≤0或②⎩⎪⎨⎪⎧x <0，x 2＋6x ＋1<0，x 2－2x ＋1≥0.解①得x ＝1，解②得－3－22<x <－3＋2 2. ∴原不等式的解集为(－3－22，－3＋22)∪{1}．3．定义在(－1,1)上的函数f (x )＝－5x ＋sin x ，如果f (1－a )＋f (1－a 2)>0，求实数a 的取值范围．答案 1<a < 2解析 ∵f (－x )＝－f (x )，x ∈(－1,1)， ∴f (x )为奇函数．又∵f ′(x )＝－5＋cos x <0， ∴f (x )在x ∈(－1,1)上单调递减． ∴f (1－a )＋f (1－a 2)>0⇔f (1－a )>f (a 2－1)⇔⎩⎪⎨⎪⎧－1<1－a <1，－1<a 2－1<1，1－a <a 2－1.解之得1<a < 2.4．已知二次函数f (x )＝ax 2－(a ＋2)x ＋1(a ∈Z )，且函数f (x )在(－2，－1)上恰有一个零点，求不等式f (x )>1的解集．答案 (－1,0)解析 ∵f (x )＝ax 2－(a ＋2)x ＋1，Δ＝(a ＋2)2－4a ＝a 2＋4>0， ∴函数f (x )＝ax 2－(a ＋2)x ＋1必有两个不同的零点． 因此f (－2)f (－1)<0，∴(6a ＋5)(2a ＋3)<0.∴－32<a <－56.又a ∈Z ，∴a ＝－1.不等式f (x )>1即为－x 2－x >0，解得－1<x <0.#}30951 78E7 磧Ar27101 69DD 槝36309 8DD5 跕w[31397 7AA5 窥 %30589 777D 睽e0。

一、填空题1．已知f (x )＝⎩⎨⎧－cos (πx )，x >0，f (x ＋1)＋1，x ≤0，则f (43)＋f (－43)的值等于________． 解析：f (43)＝12；f (－43)＝f (－13)＋1＝f (23)＋2 ＝52，f (43)＋f (－43)＝3. 答案：32．已知f (1－x 1＋x )＝1－x 21＋x 2，则f (x )的解析式可取为________．解析：(换元法)令t ＝1－x 1＋x ，由此得x ＝1－t1＋t，所以f (t )＝1－(1－t 1＋t )21＋(1－t 1＋t)2＝2t1＋t2，从而f (x )的解析式可取为2x1＋x 2. 答案：2x1＋x 23．设f (x )＝⎩⎪⎨⎪⎧|x －1|－2，|x |≤1，11＋x 2，|x |>1，则f [f (12)]＝________. 解析：f [f (12)]＝f (－32)＝413. 答案：4134．定义在R 上的函数f (x )满足f (x ＋y )＝f (x )＋f (y )＋2xy (x ，y ∈R)，f (1)＝2，则f (－3)等于________． 解析：令x ＝－3，y ＝1，则f(－2)＝f(1)＋f(－3)－6.又∵f(1)＝2，∴f(－3)＝f(－2)＋4.令x＝－2，y＝1，则f(－1)＝f(1)＋f(－2)－4，∴f(－2)＝f(－1)＋2.令x＝－1，y＝1，f(0)＝f(－1)＋f(1)－2.又x＝y＝0时，f(0)＝0，∴f(－1)＝0，∴f(－3)＝f(－2)＋4＝f(－1)＋6＝6.答案：65．已知函数f(x)＝ax＋bx－4(a，b为常数)，f(lg 2)＝0，则f(lg12)＝________.解析：由题意得f(lg 2)＝a lg 2＋blg 2－4＝0，有a lg 2＋blg 2＝4，则f(lg 12)＝a lg12＋blg12－4＝－a lg 2－blg 2－4＝－8.答案：－86．定义在R上的函数f(x)满足f(m＋n2)＝f(m)＋2[f(n)]2，m，n∈R，且f(1)≠0，则f(2 014)＝________.解析：令m＝n＝0，得f(0＋02)＝f(0)＋2[f(0)]2，所以f(0)＝0；令m＝0，n＝1，得f(0＋12)＝f(0)＋2[f(1)]2，由于f(1)≠0，所以f(1)＝12；令m＝x，n＝1，得f(x＋12)＝f(x)＋2[f(1)]2，所以f(x＋1)＝f(x)＋2×(12)2，即f(x＋1)＝f(x)＋12，这说明数列{f(x)}(x∈Z)是首项为12，公差为12的等差数列，所以f(2 014)＝12＋(2 014－1)×12＝1007.答案：1 0077．已知f (2x ＋1)＝lg x ，则f (x )＝________. 解析：令2x ＋1＝t (t >1)，则x ＝2t －1，∴f (t )＝lg2t －1(t >1)，f (x )＝lg 2x －1(x >1)． 答案：lg2x －1(x >1)8．函数f (x )在闭区间[－1,2]上的图象如图所示，则函数的解析式为________．答案：f (x )＝⎩⎪⎨⎪⎧x ＋1，－1≤x <0，－12x ，0≤x ≤29．已知a 、b 为实数，集合M ＝⎩⎨⎧⎭⎬⎫b a ，1，N ＝{a, 0}，f ：x → x 表示把集合M 中的元素x 映射到集合N 中仍为x ，则a ＋b ＝________.解析：由题意可知ba ＝0，a ＝1，解得a ＝1，b ＝0，所以a ＋b ＝1. 答案：1 二、解答题10．已知f (x )＝x 2－1，g (x )＝⎩⎨⎧x －1，x >0，2－x ，x <0，(1)求f [g (2)]和g [f (2)]的值； (2)求f [g (x )]和g [f (x )]的表达式． 解析：(1)由已知，g (2)＝1，f (2)＝3， ∴f [g (2)]＝f (1)＝0，g [f (2)]＝g (3)＝2. (2)当x >0时，g (x )＝x －1， 故f [g (x )]＝(x －1)2－1＝x 2－2x ；当x <0时，g (x )＝2－x ，故f [g (x )]＝(2－x )2－1＝x 2－4x ＋3，∴f [g (x )]＝⎩⎪⎨⎪⎧x 2－2x ，x >0，x 2－4x ＋3，x <0.当x >1或x <－1时，f (x )>0， 故g [f (x )]＝f (x )－1＝x 2－2； 当－1<x <1时， f (x )<0， 故g [f (x )]＝2－f (x )＝3－x 2.∴g [f (x )]＝⎩⎪⎨⎪⎧x 2－2，x >1或x <－1，3－x 2，－1<x <1.11．如图，在△AOB 中，点A (2,1)，B (3,0)，点E 在射线OB 上自O开始移动．设OE ＝x ，过E 作OB 的垂线l ，记△AOB 在直线l 左边部分的面积为S ，试写出S 与x 的函数关系式，并画出大致的图象．解析：当0≤x ≤2时，△OEF 的高EF ＝12x ， ∴S ＝12x ·12x ＝14x 2；当2<x ≤3时，△BEF 的高EF ＝3－x ， ∴S ＝12×3×1－12(3－x )·(3－x ) ＝－12x 2＋3x －3； 当x >3时，S ＝32.∴S ＝f (x )＝⎩⎪⎨⎪⎧x 24(0≤x ≤2)－12x 2＋3x －3(2<x ≤3)32(x >3).函数图象如图所示．12．已知定义域为R 的函数f (x )满足f (f (x )－x 2＋x )＝f (x )－x 2＋x . (1)若f (2)＝3，求f (1)；又若f (0)＝a ，求f (a )；(2)若有且仅有一个实数x 0，使得f (x 0)＝x 0，求函数f (x )的解析式． 解析： (1)因为对任意x ∈R 有 f (f (x )－x 2＋x )＝f (x )－x 2＋x ， 所以f (f (2)－22＋2)＝f (2)－22＋2， 又f (2)＝3，从而f (1)＝1.又f (0)＝a ，则f (a －02＋0)＝a －02＋0，即f (a )＝a . (2)因为对任意x ∈R ， 有f (f (x )－x 2＋x )＝f (x )－x 2＋x ，又有且仅有一个实数x 0，使得f (x 0)＝x 0， 故对任意x ∈R ，有f (x )－x 2＋x ＝x 0. 在上式中令x ＝x 0，有f (x 0)－x 20＋x 0＝x 0. 又因为f (x 0)＝x 0， 所以x 0－x 20＝0， 故x 0＝0或x 0＝1.若x0＝0，则f(x)＝x2－x，但方程x2－x＝x有两个不相同实根，与题设条件矛盾，故x0≠0. 若x0＝1，则有f(x)＝x2－x＋1，易验证该函数满足题设条件．综上，函数f(x)的解析式为f(x)＝x2－x＋1.。

高考数学一轮复习 42课时作业一、选择题1．(2010·重庆卷，文)在等差数列{a n }中，a 1＋a 9＝10，则a 5的值为( ) A ．5 B ．6 C ．8 D ．10答案 A解析 依题意得a 1＋a 9＝2a 5＝10，a 5＝5，选A.2．在等差数列{a n }中，a 2＋a 6＝3π2，则sin(2a 4－π3)＝( )A.32 B.12 C ．－32D ．－12答案 D解析 ∵a 2＋a 6＝3π2，∴2a 4＝3π2，∴sin(2a 4－π3)＝sin(3π2－π3)＝－cos π3＝－12，选D.3．(2011·合肥质检)设S n 是等差数列{a n }的前n 项和，若a 4＝9，S 3＝15，则数列{a n }的通项a n ＝( )A ．2n －3B ．2n －1C ．2n ＋1D ．2n ＋3答案 C解析 由⎩⎪⎨⎪⎧a 4＝9S 3＝15⇒⎩⎪⎨⎪⎧a 1＋3d ＝93a 1＋3d ＝15⇒⎩⎪⎨⎪⎧a 1＝3d ＝2，所以通项a n ＝2n ＋1.4．等差数列{a n }的前n 项和为S n ，已知a m －1＋a m ＋1－2a 2m ＝0，S 2m －1＝39，则m ＝( ) A ．38 B ．39 C ．20 D ．19答案 C解析 ∵a m －1＋a m ＋1＝2a 2m 又∵a m －1＋a m ＋1＝2a m ∴a m ＝1或0(舍去) ∵S 2m －1＝2m －1a 1＋a 2m －12＝(2m －1)a m∴(2m －1)a m ＝39，∴2m －1＝39 ∴m ＝20.5．设{a n }是公差为正数的等差数列，若a 1＋a 2＋a 3＝15，a 1a 2a 3＝80，则a 11＋a 12＋a 13＝( ) A ．120 B ．105 C ．90 D ．75答案 B解析 设公差为d 且d >0.由已知⎩⎪⎨⎪⎧a 1＋a 2＋a 3＝15a 1a 2a 3＝80，得⎩⎪⎨⎪⎧a 1＋d ＝5a 1a 1＋d a 1＋2d ＝80.解得a 1＝2，d ＝3(∵d >0)．∴a 11＋a 12＋a 13＝3a 12＝3(a 1＋11d )＝1056．若两个等差数列{a n }和{b n }的前n 项和分别是S n ，T n ，已知S n T n ＝7n n ＋3，则a 5b 5等于( )A ．7 B.23 C.278D.214答案 D解析 a 5b 5＝2a 52b 5＝a 1＋a 9b 1＋b 9＝92a 1＋a 992b 1＋b 9＝S 9T 9＝214. 7．等差数列{a n }的前n 项和为S n ，且S 3＝6，a 3＝4，则公差d 等于( ) A ．1 B.53 C ．2 D ．3答案 C解析 由⎩⎪⎨⎪⎧3a 1＋42＝6a 1＋2d ＝4，解得d ＝2.二、填空题8．已知S n 是等差数列{a n }的前n 项和，且a 4＝15，S 5＝55，则过点P (3，a 3)、Q (4，a 4)的直线的斜率是________．解析 设数列{a n }的公差为d ，则依题意，得⎩⎪⎨⎪⎧a 4＝a 1＋3d ＝15S 5＝5a 1＋10d ＝55⇒⎩⎪⎨⎪⎧a 1＝3d ＝4，故直线PQ 的斜率为a 4－a 34－3＝d1＝4.9．已知数列{a n }中，a 3＝2，a 5＝1，若{11＋a n}是等差数列，则a 11＝________. 答案 0解析 记b n ＝11＋a n ，则b 3＝13，b 5＝12，数列{b n }的公差为12×(12－13)＝112，b 1＝16，∴b n ＝n ＋112，即11＋a n ＝n ＋112，∴a n ＝11－nn ＋1，故a 11＝0. 10．等差数列{a n }中，S n 是其前n 项和，a 1＝－2010，S 20092009－S 20072007＝2，则S 2010的值为________．答案 －2010解析 在等差数列{a n }中，设公差为d ，则S n n＝na 1＋n2n －1dn＝a 1＋d 2(n －1)，∴S 20092009－S 20072007＝a 1＋d 2×2008－a 1－d2×2006＝d ＝2，∴S 2010＝－2010×2010＋2010×20092×2＝－2010×2010＋2010×2009＝－2010.11．方程(x 2－x ＋m )(x 2－x ＋n )＝0有四个不等实根，且组成一个公差为12的等差数列，则mn 的值为________．答案 －15256解析 设四个根组成的等差数列为x 1，x 2，x 3，x 4，根据等差数列的性质，则有x 1＋x 4＝x 2＋x 3＝1∴2x 1＋3d ＝1，又d ＝12，∴x 1＝－14∴x 2＝14，x 3＝34，x 4＝54∴mn ＝(x 1x 4)(x 2x 3)＝－1525612．(2010·浙江卷，文)在如下数表中，已知每行、每列中的数都成等差数列，那么位于表中的第n 行第n ＋1列的数是________． 答案 n 2＋n解析 第n 行的第一个数是n ，第n 行的数构成以n 为公差的等差数列，则其第n ＋1项为n ＋n ·n ＝n 2＋n .13．(2010·苏北四市调研)已知数列{a n }共有m 项，记{a n }的所有项和为S (1)，第二项及以后所有项和为S (2)，第三项及以后所有项和为S (3)，…，第n 项及以后所有项和为S (n )，若S (n )是首项为1，公差为2的等差数列的前n 项和，则当n <m 时，a n ＝________.答案 －2n －1解析 由题意得S (n )＝a n ＋…＋a m ＝n ×1＋n n －12×2＝n 2，当n <m 时，S (n ＋1)＝a n ＋1＋…＋a m ＝(n ＋1)2.故a n ＝S (n )－S (n ＋1)＝n 2－(n ＋1)2＝－2n －1.三、解答题14．在编号为1～9的九个盒子中，共放有351粒米，已知每个盒子都比前一号盒子多放同样粒数的米．(1)如果1号盒子内放了11粒米，那么后面的盒子比它前一号的盒子多放几粒米？ (2)如果3号盒子内放了23粒米，那么后面的盒子比它前一号的盒子多放几米粒？ 答案 (1)7 (2)8解析 1～9号的九个盒子中米的粒数依次组成等差数列{a n } (1)a 1＝11，S 9＝351，求得：d ＝7 (2)a 3＝23，S 9＝351，求得：d ＝815．(2010·浙江卷，文)设a 1，d 为实数，首项为a 1，公差为d 的等差数列{a n }的前n 项和为S n ，满足S 5S 6＋15＝0.(1)若S 5＝5，求S 6及a 1； (2)求d 的取值范围．解析 (1)由题意知S 6＝－15S 5＝－3，a 6＝S 6－S 5＝－8，所以⎩⎪⎨⎪⎧5a 1＋10d ＝5，a 1＋5d ＝－8.解得a 1＝7，所以S 6＝－3，a 1＝7.(2)因为S 5S 6＋15＝0，所以(5a 1＋10d )(6a 1＋15d )＋15＝0， 即2a 21＋9da 1＋10d 2＋1＝0， 故(4a 1＋9d )2＝d 2－8，所以d 2≥8. 故d 的取值范围为d ≤－22或d ≥2 2.16．设等差数列{a n }的首项a 1及公差d 都为整数，前n 项和为S n . (1)若a 11＝0，S 14＝98，求数列{a n }的通项公式；(2)若a 1≥6，a 11>0，S 14≤77，求所有可能的数列{a n }的通项公式．答案 (1)a n ＝22－2n (2)a n ＝12－n 和a n ＝13－n解 (1)由S 14＝98得2a 1＋13d ＝14， 又a 11＝a 1＋10d ＝0，故解得d ＝－2，a 1＝20. 因此{a n }的通项公式是a n ＝22－2n ，n ＝1,2,3，….(2)由⎩⎪⎨⎪⎧S 14≤77a 11>0a 1≥6，得⎩⎪⎨⎪⎧2a 1＋13d ≤11a 1＋10d >0a 1≥6，即⎩⎪⎨⎪⎧2a 1＋13d ≤11 ①－2a 1－20d <0， ②－2a 1≤－12 ③由①＋②得－7d <11，即d >－117.由①＋③得13d ≤－1， 即d ≤－113.于是－117<d ≤－113.又d ∈Z ，故d ＝－1.④ 将④代入①②得10<a 1≤12. 又a 1∈Z ，故a 1＝11或a 1＝12. 所以所有可能的数列{a n }的通项公式是a n ＝12－n 和a n ＝13－n ，n ＝1,2,3，….。

一、选择题（每题5分，共50分）1. 若函数f(x) = ax^2 + bx + c在x=1时取得最小值，则下列选项中正确的是（）A. a > 0, b = 0, c < 0B. a < 0, b = 0, c > 0C. a > 0, b ≠ 0, c > 0D. a < 0, b ≠ 0, c < 02. 下列各数中，无理数是（）A. √3B. -√2C. 3/4D. 1.4143. 若复数z满足|z - 2i| = 3，则复数z在复平面内对应的点的轨迹是（）A. 圆B. 线段C. 直线D. 双曲线4. 已知函数f(x) = log2(x - 1)，则f(x)的定义域是（）A. (1, +∞)B. (0, 1)C. (1, 2]D. (2, +∞)5. 若等差数列{an}的前n项和为Sn，且S3 = 9，S5 = 21，则该数列的公差d是（）A. 2B. 3C. 4D. 56. 下列命题中，正确的是（）A. 若两个函数的图像关于y轴对称，则这两个函数互为反函数B. 若两个函数的图像关于x轴对称，则这两个函数互为反函数C. 若两个函数的图像关于原点对称，则这两个函数互为反函数D. 若两个函数的图像关于直线y = x对称，则这两个函数互为反函数7. 已知函数f(x) = x^3 - 3x，若存在实数a和b，使得f(a) + f(b) = 0，则a + b的值为（）A. 0B. 1C. -1D. 28. 下列方程中，无解的是（）A. x^2 + 2x + 1 = 0B. x^2 + 2x - 1 = 0C. x^2 - 2x + 1 = 0D. x^2 - 2x - 1 = 09. 若不等式x^2 - 4x + 3 < 0的解集是（）A. (1, 3)B. (-∞, 1) ∪ (3, +∞)C. (-∞, 1) ∩ (3, +∞)D. (1, +∞) ∪ (-∞, 3)10. 已知函数f(x) = (x - 1)/(x + 1)，则f(-1)的值为（）A. 0B. 1C. -1D. 不存在二、填空题（每题5分，共50分）11. 已知等差数列{an}的前n项和为Sn，若a1 = 2，d = 3，则S10 = ________.12. 若复数z = a + bi（a, b ∈ R），则|z|^2 = ________.13. 函数f(x) = log2(3 - 2x)的定义域为 ________.14. 若等比数列{an}的公比q = -2，且a1 = 3，则第5项a5 = ________.15. 已知函数f(x) = x^2 - 2x + 3，则f(-1) = ________.16. 若不等式x^2 - 4x + 3 ≤ 0的解集为A，则不等式x^2 - 4x + 3 > 0的解集为 ________.17. 已知函数f(x) = 2x - 1，则f(-3) + f(2) = ________.18. 若复数z满足|z - 2i| = 3，则复数z在复平面内对应的点的坐标是________.19. 已知函数f(x) = (x - 1)/(x + 1)，则f(1)的值为 ________.20. 若等差数列{an}的前n项和为Sn，且S3 = 9，S5 = 21，则该数列的第4项a4 = ________.三、解答题（每题20分，共60分）21. （本题满分20分）已知函数f(x) = ax^2 + bx + c（a ≠ 0），若f(1) = 2，f(2) = 5，求a，b，c的值。

随堂巩固训练(42)1. 已知集合M ＝{(x ，y)|x ＋y ＝2}，N ＝{(x ，y)|x －y ＝4}，则集合M ∩N ＝__{(3，－1)}__．解析：联立方程组⎩⎪⎨⎪⎧x ＋y ＝2，x －y ＝4，解得⎩⎪⎨⎪⎧x ＝3，y ＝－1，则M ∩N ＝{(3，－1)}．2. 已知直线l 经过两直线l 1：x －2y ＋4＝0和l 2：x ＋y －2＝0的交点P ，且与直线l 3：3x －4y ＋5＝0垂直，则直线l 的方程为__4x ＋3y －6＝0__．解析：方法一：解方程组⎩⎪⎨⎪⎧x －2y ＋4＝0，x ＋y －2＝0，得⎩⎪⎨⎪⎧x ＝0，y ＝2，故点P(0，2)．因为l 3的斜率为34，且l ⊥l 3，所以直线l 的斜率为－43，由斜截式可知直线l 的方程为y ＝－43x ＋2，即4x ＋3y －6＝0.方法二：设直线l 的方程为x －2y ＋4＋λ(x ＋y －2)＝0，即(1＋λ)x ＋(λ－2)y ＋4－2λ＝0.又l ⊥l 3，所以3×(1＋λ)＋(－4)×(λ－2)＝0，解得λ＝11，所以直线l 的方程为4x ＋3y －6＝0.点评：本题方法一采用常规方法，先通过方程组求出两直线交点，再根据垂直关系求出斜率，由于交点在y 轴上，故采用斜截式求解；方法二则采用了过两直线A 1x ＋B 1y ＋C 1＝0与A 2x ＋B 2y ＋C 2＝0的交点的直线系方程：A 1x ＋B 1y ＋C 1＋λ(A 2x ＋B 2y ＋C 2)＝0，直接设出过两直线交点的直线方程，再根据垂直条件用待定系数法求解．3. 若三条直线2x ＋3y ＋8＝0，x －y －1＝0，x ＋ky ＝0相交于一点，则实数k 的值为__－12__．解析：联立方程⎩⎪⎨⎪⎧2x ＋3y ＋8＝0，x －y －1＝0，解得⎩⎪⎨⎪⎧x ＝－1，y ＝－2，所以交点为(－1，－2)．又三条直线交于一点，所以－1－2k ＝0，解得k ＝－12.4. 点P(4，3)关于直线x －y ＋1＝0的对称点Q 的坐标是__(2，5)__．解析：设点Q(x ，y)，由题意得⎩⎪⎨⎪⎧y －3x －4＝－1，x ＋42－y ＋32＋1＝0，解得⎩⎪⎨⎪⎧x ＝2，y ＝5.故点Q 的坐标是(2，5)．5. 若三条直线ax －y ＋1＝0，x －ay －1＝0，x ＋y ＋a ＝0能构成三角形，则实数a 满足的条件是__a ≠2且a ≠±1__．解析：由题意知任意两条直线都相交，则a 1≠－1－a 且a 1≠－11，故a ≠±1.因为三条直线不共点，所以直线x －ay －1＝0与x ＋y ＋a ＝0的交点(1－a ，－1)不在直线ax －y ＋1＝0上，即a(1－a)＋1＋1≠0，解得a ≠2且a ≠－1.综上，a ≠2且a ≠±1.6. 若一条直线被直线4x ＋y ＋6＝0和3x －5y －6＝0截得的线段的中点恰好是坐标原点，则这条直线的方程为__x ＋6y ＝0__．解析：设A ，B 为截得的线段的两个端点，若点A(m ，n)在直线4x ＋y ＋6＝0上，则点B(－m ，－n)在直线3x －5y －6＝0上，所以⎩⎪⎨⎪⎧4m ＋n ＋6＝0，－3m －（－5n ）－6＝0，解得⎩⎨⎧m ＝－3623，n ＝623.因为所求直线过原点，所以斜率k ＝n m ＝623×⎝⎛⎭⎫－2336＝－16，故所求方程为y ＝－16x ，即x ＋6y ＝0.7. 已知定点A(0，1)，点B 在直线x ＋y ＝0上运动，当线段AB 最短时，点B 的坐标为__⎝⎛⎭⎫－12，12__． 解析：当线段AB 最短时，就是直线AB 与直线x ＋y ＝0垂直时，则直线AB 的方程为y －1＝x ，联立x ＋y ＝0，解得x ＝－12，y ＝12，所以点B 的坐标为⎝⎛⎭⎫－12，12.8. 设直线l 1的方程为x ＋2y －2＝0，将直线l 1绕原点按逆时针方向旋转90°得到直线l 2，则直线l 2的方程是__y ＝2x ＋2__．解析：直线l 1绕原点按逆时针方向旋转90°得到直线l 2，则原点到直线l 1和直线l 2的距离相等，且直线l 1和直线l 2相互垂直，所以设直线l 2的方程为y ＝2x ＋b ，所以|b|5＝25，解得b ＝±2.又直线是按逆时针方向旋转90°，所以b＝2，所以直线l 2的方程是y ＝2x ＋2.9. 直线2x ＋3y ＋1＝0关于直线x －y －1＝0的对称直线方程为__3x ＋2y ＝0__．解析：在对称直线上任取一点A(x ，y)，点A 关于直线x －y －1＝0的对称点A′(x′，y′)，所以⎩⎪⎨⎪⎧y －y′x －x′＝－1，x ＋x′2－y ＋y′2－1＝0，解得⎩⎪⎨⎪⎧x′＝1＋y ，y′＝x －1，即点A′(1＋y ，x －1)在直线2x ＋3y ＋1＝0上，代入得3x ＋2y ＝0.故所求对称直线的方程为3x ＋2y＝0.10. 已知正方形ABCD 的相对顶点A(0，－1)和C(2，5)，则顶点B 和D 的坐标分别为__(4，1)，(－2，3)__．解析：由已知得AC 的中点坐标为(1，2)且k AC ＝3，则k BD ＝－13.设点B 的坐标为(a ，b)，则⎩⎪⎨⎪⎧b ＋1a ·b －5a －2＝－1，b －2a －1＝－13，解得⎩⎪⎨⎪⎧a ＝4，b ＝1或⎩⎪⎨⎪⎧a ＝－2，b ＝3，所以点B 的坐标为(4，1)，点D 的坐标为(－2，3)．11. 已知△ABC 的顶点A(5，1)，AB 边上的中线CM 所在的直线方程为2x －y －5＝0，AC 边上的高BH 所在的直线方程为x －2y －5＝0，求顶点C 的坐标．解析：由题意知BH 与AC 垂直，所以k BH ·k AC ＝12k AC ＝－1，即k AC ＝－2，所以直线AC 的方程为2x ＋y －11＝0.联立⎩⎪⎨⎪⎧2x －y －5＝0，2x ＋y －11＝0，解得⎩⎪⎨⎪⎧x ＝4，y ＝3，所以点C 的坐标为(4，3)．12. 已知点A(1，3)，B(3，1)，C 是直线l 1：3x －2y ＋3＝0和直线l 2：2x －y ＋2＝0的交点． (1) 求交点C 的坐标； (2) 求△ABC 的面积．解析：(1) 联立⎩⎪⎨⎪⎧3x －2y ＋3＝0，2x －y ＋2＝0，解得⎩⎪⎨⎪⎧x ＝－1，y ＝0，所以直线l 1与l 2的交点C 的坐标为(－1，0)．(2) 由题意知AB ＝（3－1）2＋（1－3）2＝22，AB 边所在直线方程为y －31－3＝x －13－1，即x ＋y －4＝0，所以点C 到直线x ＋y －4＝0的距离为h ＝|－1＋0－4|12＋12＝52，所以S △ABC ＝12×22×52＝5.13. 已知过点A(1，1)且斜率为－m(m>0)的直线l 与x 轴、y 轴分别交于P ，Q 两点，过点P ，Q 作直线2x ＋y ＝0的垂线，垂足分别为R ，S.求四边形PRSQ 面积的最小值．解析：如图，由题意知直线l 的方程为y －1＝－m(x －1)，则点P ⎝⎛⎭⎫1＋1m ，0，Q(0，1＋m)， 从而可得直线PR ，QS 的方程分别为：x －2y －m ＋1m＝0，x －2y ＋2(m ＋1)＝0.又PR ∥QS ，所以RS ＝⎪⎪⎪⎪2m ＋2＋1＋1m 5＝3＋2m ＋1m 5.又PR ＝2＋2m 5，QS ＝m ＋15，四边形PRSQ 为梯形，所以S梯形PRSQ ＝ ＝15⎝⎛⎭⎫m ＋1m ＋942－180 ≥15×⎝⎛⎭⎫2＋942－180＝3.6， 当且仅当m ＝1m，即m ＝1时取等号，所以当m ＝1时，四边形PRSQ 面积的最小值为3.6.。

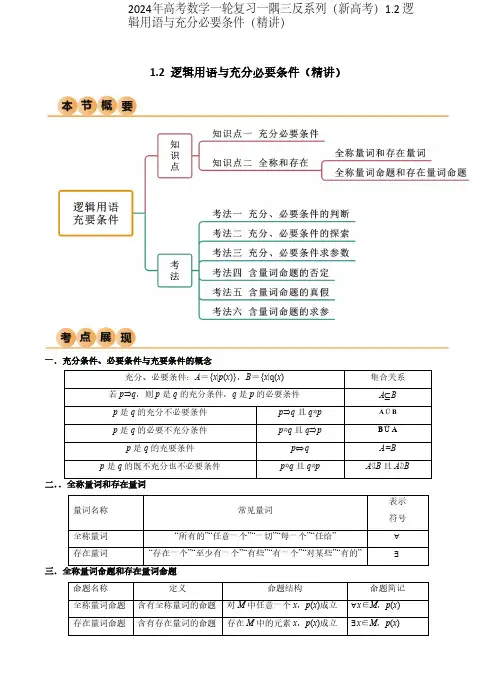
1.2 逻辑用语P充V必要条þÿ精讲Ā一．充V条þ、必要条þP充要条þ的概念2024年高考数学一轮复习一隅三反系列（新高考）1.2 逻辑用语与充分必要条件（精讲）1.判断充V、必要条þ的3种方法(1)定义法:根据p⇒q,q⇒p进行判断,适用于定义、定理判断性问题.(2)集合法:根据p,q成立的对象的集合之间的包含关系进行判断,多适用于命题中涉及_母范围的推断问题.(3)数形结合法:充要条þ的判定问题中,若给出的条þP结论之间有明显的几何意义,`ÿ以`出满足条þ的几何Ā形,则ÿ`出其几何Ā形^利用数形结合思想求解.2.根据充V、必要条þ求解参数范围的方法(1)把充V条þ、必要条þ或充要条þ转W为集合之间的关系,然^根据集合之间的关系列出关于参数的O等式(或O等式Ā)求解.(2)要注意区间端点值的检验.尤其是利用两个集合之间的关系求解参数的取值范围时,O等式是否能够取等号决定端点值的取舍,处理O当容易出现漏解或增解的现象.3.充V、必要条þ的探求方法(1)若P范围有关，ÿ先求使结论成立的充要条þ，然^根据<以小推大=的方法确定符合题意的条þ．(2)若P范围无关，则利用定义法从充V性和必要性两个方面推理探求．(3)探求充要条þ的关键在于转W的等ÿ性，解题时要考虑条þ包含的各种情况，保证条þ的充V性和必要性．4.全称量词P`在量词命题真假的判断(1)要确定一个全称量词命题是真命题,需保证该命题对所有的元素都成立;若能举出一个反例说明命题O成立,则该全称量词命题是假命题;(2)要确定一个`在量词命题是真命题,举出一个例子说明该命题成立即ÿ;若经过逻辑推理得到命题对所有的元素都O成立,则该`在量词命题是假命题.考法一充V、必要条þ的判断0例1-11ÿ2023·y津河X·统考一模Ā设xþR，则<2x==是<24x==的ÿĀA．充VO必要条þB．必要O充V条þC．充要条þD．既O充V_O必要条þ0例1-21ÿ2023春·y津和平·高O耀华中学校考阶段ÿ`Ā在ABC 中，<π6A þ=是<1sin 2A þ=的ÿ Ā A ．充VO必要条þB ．必要O充V条þC ．充要条þD ．既O充V_O必要条þ0例1-31ÿ2023·广东_山·统考二模Ā记数列{}n a 的前n 项和为n S ，则<323S a ==是<{}n a 为等差数列=的ÿ Ā A ．充VO必要条þ B ．必要O充V条þ C ．充要条þ D ．既O充V_O必要条þ0一隅O反11．ÿ2023·重庆·统考二模Ā<20x x −ü=是<e 0x þ=的ÿ Ā A ．充VO必要条þ B ．必要O充V条þ C ．充要条þ D ．既O充V_O必要条þ2．ÿ2023·y津·y津市宁河区芦Ā第一中学校联考模拟预测Ā设x þR ，则<1x ü=是<ln 0x ü=的ÿ Ā A ．充VO必要条þ B ．必要O充V条þ C ．充要条þ D ．既O充V_O必要条þ3．ÿ2023·山西z原·z原五中校考一模Ā"2sin 2sin cos 0ααα−="是<tan 2α="的ÿ Ā A ．充要条þ B ．充VO必要条þ C ．必要O充V条þ D ．既O充V_O必要条þ4．ÿ2023·X京延庆·统考一模Ā若R m þ，则<1m ==是<复数2(1i)(i 1)z m m =++−是纯虚数=的ÿ Ā A ．充V而O必要条þ B ．必要而O充V条þ C ．充V必要条þD ．既O充V_O必要条þ考法二 充V、必要条þ的探索0例2-11ÿ2023·全ÿ·高O_题ÿ`Ā<O等式20x x m −+þ在R P恒成立=的必要O充V条þ是ÿ Ā A ．m >0 B ．m <14C ．m <1D ．m >140例2-21．ÿ2023·全ÿ·高O_题ÿ`Āÿ多选Ā函数()23f x x mx =−+在区间[]1,2−O单调的充VO必要条þ是ÿ ĀA ．24m −üüB ．1m =C ．22m −üüD ．44m −üü0一隅O反11．ÿ2023·云南Ā函数()()2lg 23f x x x =−−在[),+∞a P单调递增的一个充VO必要条þ是ÿ ĀA ．0a þB ．1a þC ．3a þD ．4a þ2．ÿ2023·全ÿ·高O_题ÿ`Ā圆221x y +=P直线3y kx =−有}共点的充要条þ是ÿ Ā A ．k ≤−k ≥B ．k ≤−C ．2k ≥ D ．k ≤−2k þ3．ÿ2023·全ÿ·高O_题ÿ`Āÿ多选Ā命题<23R,208x kx kx ∀þ+−ü=为真命题的一个充VO必要条þ是ÿ ĀA ．()30−，B ．(]30−，C ．()31−−，D ．()3∞−+，考法O 充V、必要条þ的求参0例3-11ÿ2023·湖南邵阳·统考二模Ā已知集合[]2,5A =−，[]1,21B m m =+−．若<x B þ=是<x A þ=的充V O必要条þ，则m 的取值范围是ÿ Ā A ．(],3−∞ B ．(]2,3C ．∅D ．[]2,30例3-21ÿ2023·全ÿ·高O_题ÿ`Ā设命题():0ln 2ln 3p x ü−≤，命题()():2230q x m x m −−−≤．若q 是p 的必要O充V条þ，则实数m 的取值范围是______．0一隅O反11．ÿ2023·福建福Þ·高O福ÞO中校考阶段ÿ`Ā设431p x −üÿĀ210q x a −+üÿÿĀ，若p 是q 的充VO必要条þ，则ÿ Ā A ．0a þB ．1a þC ．0a ≥D ．1a ≥2．ÿ2023·安徽Ā若<12x üü=是<O等式2()1x a −ü成立=的充VO必要条þ，则实数a 的取值范围是ÿ Ā A ．[)1,2 B ．(]1,2C ．[]1,2D ．()1,23．ÿ2023·全ÿ·高O对口高考Ā已知集合{}2|320,|0,02x a A x x x B x a x −üü=−+≤=þþýý+þþ，若<x A þ=是<x B þ=的充V非必要条þ，则a 的取值范围是ÿ Ā A ．01a üüB ．2a ≥C ．12a üüD ．1a ≥考法四 含量词命题的否定0例4-11ÿ2023·四Ý达Þ·统考二模Ā命题p ÿx ∀þR ，2210x x x +−+þ，则p ⌝为ÿ Ā A ．x ∀þR ，2210x x x +−+≤B ．x ∀þR ，2210x x x +−+üC ．0x ∃þR ，0200210x x x +−+üD ．0x ∃þR ，0200210x x x +−+≤0例4-21ÿ2023·重庆·统考模拟预测Ā命题R x ∃þ，0x x +ü的否定是ÿ Ā A ．R x ∃þ，0x x +≥ B ．R x ∀þ，0x x +ü C ．R x ∀þ，0x x +≥ D ．R x ∀þ，0x x +þ0一隅O反11．ÿ2023·y津河东·一模Ā命题<有一个偶数是素数=的否定是ÿ Ā A ．任意一个奇数是素数 B ．`在一个偶数O是素数 C ．`在一个奇数O是素数 D ．任意一个偶数都O是素数2．ÿ2023·河南郑Þ·统考二模Ā命题ÿR x ∀þ，ln 0x x +þ的否定是ÿ Ā A ．R x ∀ÿ，ln 0x x +þ B ．R x ∀ÿ，ln 0x x +≤ C ．R x ∃þ，ln 0x x +þ D ．R x ∃þ，ln 0x x +≤3ÿ2023·河南·校联考模拟预测Ā已知命题p ÿ1x ∀þ，()10x x −≥，则p ⌝为ÿ Ā A ．1x ∀þ，()10x x −ü B ．1x ∃þ，()10x x −ü C ．1x ∀ü，()10x x −≥D ．1x ∃þ，()10x x −≥考法五 含量词命题的真假0例5-11ÿ2023·全ÿ·高O_题ÿ`Ā已知集合{}0A x x =≥，集合{}1B x x =þ，则以Q命题为真命题的是ÿ ĀA ．x A ∃þ，xB þ B ．x B ∃þ，x A ÿC ．x A ∀þ，x B þD ．x B ∀þ，x A ÿ0例5-21ÿ2023·全ÿ·高O_题ÿ`ĀQ列命题中，真命题是ÿ Ā A ．<1,1a b þþ=是<1ab þ=的必要条þ B ．R x ∀þ，e 0x þ C ．2R,2x x x ∀þþ D ．0a b +=的充要条þ是1ab=−0一隅O反11．ÿ2023·全ÿ·高O_题ÿ`ĀQ列命题中，真命题的是ÿ Ā A ．函数sin ||y x =的周期是2π B ．2,2x x R x ∀þþ C ．函数2()ln 2x f x x+=−是奇函数. D ．0a b +=的充要条þ是1ab=−2．ÿ2023·全ÿ·高O_题ÿ`ĀQ列命题为真命题的是ÿ Ā A ．10þ`34þ B ．12þ或45þ C ．x R ∃þ，cos 1x þ D ．x ∀þR ，20x ≥3．ÿ2023春·河X ·高O统考阶段ÿ`Ā已知命题:N e 0，x p x ∃þüÿe 为自然对数的底数Ā2;:R 0q x x x ∀þ+≥，，则Q列为真命题的是ÿ Ā A ．p 真，q 假 B ．p 真，q 真 C ．p 假，q 真D ．p 假，q 假4．ÿ2023春·黑龙江哈尔滨·高O哈九中校考开学考试ĀQ列命题中，真命题是ÿ ĀA ．0R x ∃þ，4300x üB ．0x ∀þ，lg 0x þC ．<31x þ=是<1x þ=的必要O充V条þD ．命题<0x ∀≥，tan sin x x ≥=的否定为<00x ∃ü，00tan sin x x ≥=考法~ 含量词命题的求参0例6-11ÿ2023·河南郑Þ·统考一模Ā若<2,630x x ax a ∃þ−+üR =为假命题，则实数a 的取值范围为_____.0例6-21ÿ2023春·河X衡水·高O河X衡水中学校考阶段ÿ`Ā条þ[]:1,3p x ∃þ，230x ax −+þ，则p 的一个必要O充V条þ是ÿ ĀA ．5a üB ．5a þC ．4a üD ．4a þ0一隅O反11.ÿ2023·全ÿ·高O_题ÿ`Ā若命题:p x ∃þR ，220x ax a ++≤是假命题，则实数a 的一个值为_____________． 2．ÿ2023·全ÿ·高O_题ÿ`Āp ÿ[]4,2x ∀þ−，20x a −≥为真命题的一个充VO必要条þ是ÿ ĀA ．2a ≤−B ．0a ≤C ．4a ≤D ．16a ≤3．ÿ2023·全ÿ·高O_题ÿ`Ā若命题<[]()21,3,2130a ax a x a ∃þ−−−+−ü=为假命题，则实数x 的取值范围为ÿ ĀA ．[]1,4−B ．50,3ùùúúûûC ．[]51,0,43ùùúúû−ûD ．[)51,0,43öù−÷úøû4．ÿ2023·全ÿ·高O_题ÿ`Ā命题<,e 1e x x x R a −∃þ+ü−=为假命题，则实数a 的取值范围为___________.1.2 逻辑用语P充V必要条þÿ精讲Ā一．充V条þ、必要条þP充要条þ的概念1.判断充V、必要条þ的3种方法(1)定义法:根据p ⇒q,q ⇒p 进行判断,适用于定义、定理判断性问题.(2)集合法:根据p,q 成立的对象的集合之间的包含关系进行判断,多适用于命题中涉及_母范围的推断问题. (3)数形结合法:充要条þ的判定问题中,若给出的条þP结论之间有明显的几何意义,`ÿ以`出满足条þ的几何Ā形,则ÿ`出其几何Ā形^利用数形结合思想求解. 2.根据充V、必要条þ求解参数范围的方法(1)把充V条þ、必要条þ或充要条þ转W为集合之间的关系,然^根据集合之间的关系列出关于参数的O等式(或O等式Ā)求解.(2)要注意区间端点值的检验.尤其是利用两个集合之间的关系求解参数的取值范围时,O等式是否能够取等号决定端点值的取舍,处理O当容易出现漏解或增解的现象. 3.充V、必要条þ的探求方法(1)若P范围有关，ÿ先求使结论成立的充要条þ，然^根据<以小推大=的方法确定符合题意的条þ． (2)若P范围无关，则利用定义法从充V性和必要性两个方面推理探求．(3)探求充要条þ的关键在于转W的等ÿ性，解题时要考虑条þ包含的各种情况，保证条þ的充V性和必要性．4.全称量词P`在量词命题真假的判断(1)要确定一个全称量词命题是真命题,需保证该命题对所有的元素都成立;若能举出一个反例说明命题O成立,则该全称量词命题是假命题;(2)要确定一个`在量词命题是真命题,举出一个例子说明该命题成立即ÿ;若经过逻辑推理得到命题对所有的元素都O成立,则该`在量词命题是假命题.考法一 充V、必要条þ的判断0例1-11ÿ2023·y津河X ·统考一模Ā设x þR ，则<2x ==是<24x ==的ÿ Ā A ．充VO必要条þ B ．必要O充V条þ C ．充要条þ D ．既O充V_O必要条þ0答案1A0解析1当2x =时24x =，故充V性成立，由24x =ÿ得2x =或2x =−，故必要性O成立，所以<2x ==是<24x ==的充VO必要条þ.故选ÿA0例1-21ÿ2023春·y津和平·高O耀华中学校考阶段ÿ`Ā在ABC 中，<π6A þ=是<1sin 2A þ=的ÿ Ā A ．充VO必要条þB ．必要O充V条þC ．充要条þD ．既O充V_O必要条þ0答案1B0解析1在ABC 中，()0,πA þ，由1sin 2A þ，ÿ得π5π66A üü，所以<π6A þ=是<1sin 2A þ=的必要O充V条þ.故选ÿB.0例1-31ÿ2023·广东_山·统考二模Ā记数列{}n a 的前n 项和为n S ，则<323S a ==是<{}n a 为等差数列=的ÿ Ā A ．充VO必要条þ B ．必要O充V条þ C ．充要条þ D ．既O充V_O必要条þ0答案1B0解析1等差数列{}n a 的前n 项和为n S ，则312323S a a a a =++=， 数列{}n a 的前n 项和为n S ，取12341,2,3,5a a a a ====，显然有323S a =， 而43322a a a a −=≠−，即数列{}n a O是等差数列， 所以<323S a ==是<{}n a 为等差数列=的必要O充V条þ. 故选ÿB 0一隅O反11．ÿ2023·重庆·统考二模Ā<20x x −ü=是<e 0x þ=的ÿ Ā A ．充VO必要条þ B ．必要O充V条þ C ．充要条þ D ．既O充V_O必要条þ 0答案1A0解析1由20x x −üÿ得其解集为ÿ}{01x x x þüü，由e 0x þÿ得其解集为ÿx þR .而}{01x x üüÜR ，即由<20x x −ü=ÿ以推出<e 0x þ=，反过来<e 0x þ=O能推出<20x x −ü=，故<20x x −ü=是<e 0x þ=的充VO必要条þ.故选ÿA2．ÿ2023·y津·y津市宁河区芦Ā第一中学校联考模拟预测Ā设x þR ，则<1x ü=是<ln 0x ü=的ÿ Ā A ．充VO必要条þ B ．必要O充V条þ C ．充要条þD ．既O充V_O必要条þ0答案1B0解析1当1x ü时，若0x ≤，则ln x 无意义，充V性O成立Ā 当ln 0x ü时，01x üü，1x üü成立，必要性成立Ā 综P所述ÿx þR ，则<1x ü=是<ln 0x ü=的必要O充V条þ. 故选ÿB.3．ÿ2023·山西z原·z原五中校考一模Ā"2sin 2sin cos 0ααα−="是<tan 2α="的ÿ Ā A ．充要条þ B ．充VO必要条þ C ．必要O充V条þ D ．既O充V_O必要条þ0答案1C0解析1因为2sin 2sin cos 0ααα−=，所以()sin sin 2cos 0ααα−=，sin 2cos 0αα−=或sin 0α=， 所以tan 2α=或tan 0α=，故<2sin 2sin cos 0ααα−=是<tan 2α==的必要O充V条þ.故选ÿC. 4．ÿ2023·X京延庆·统考一模Ā若R m þ，则<1m ==是<复数2(1i)(i 1)z m m =++−是纯虚数=的ÿ Ā A ．充V而O必要条þ B ．必要而O充V条þ C ．充V必要条þ D ．既O充V_O必要条þ0答案1C0解析1()()222(1i)(i 1)i z m m m m m m =++−=−++，当1m =时，复数2i z =，是纯虚数Ā复数2(1i)(i 1)z m m =++−是纯虚数时，有220m m m m ü−=ý+≠þ，解得1m =. 则<1m ==是<复数2(1i)(i 1)z m m =++−是纯虚数=的充V必要条þ.故选ÿC考法二 充V、必要条þ的探索0例2-11ÿ2023·全ÿ·高O_题ÿ`Ā<O等式20x x m −+þ在R P恒成立=的必要O充V条þ是ÿ Ā A ．m >0 B ．m <14C ．m <1D ．m >140答案1A0解析1因为<O等式20x x m −+þ在R P恒成立=，所以等ÿ于二次方程的20x x m −+=判别式140m ∆=−ü，即14m þ.易知D 选项是充要条þ，O成立Ā A 选项中，14m þÿ推导0m þ，`0m þOÿ推导14m þ，故0m þ是14m þ的必要O充V条þ，正确ĀB 选项中，14m þOÿ推导出14m ü，B O成立ĀC 选项中，14m þOÿ推导1m ü，C O成立.故选ÿA.0例2-21．ÿ2023·全ÿ·高O_题ÿ`Āÿ多选Ā函数()23f x x mx =−+在区间ûý1,2−O单调的充VO必要条þ是ÿ Ā A ．24m −üü B ．1m = C ．22m −üü D ．44m −üü0答案1BC 0解析1()23f x x mx =−+在区间ûý1,2−PO单调，又()f x 的Ā象是开口向P，对称轴为12x m =的抛物线，ü原命题的充要条þ为1122m −üü，即24m −üü，ü原命题的一个充VO必要条þ只有B 、C 选项满足，故选ÿBC ． 0一隅O反11．ÿ2023·云南Ā函数()()2lg 23f x x x =−−在û),+∞a P单调递增的一个充VO必要条þ是ÿ ĀA ．0a þB ．1a þC ．3a þD ．4a þ0答案1D0解析1设()223g x x x =−−，ÿ得函数()g x 在(),1−∞单调递减，在()1,+∞单调递增，又由函数()2lg 23y x x =−−，满足2230x x −−þ，解得1x ü−或3x þ，根据复合函数的单调性，ÿ得函数()f x 的单调递增区间为()3,+∞.()()2lg 23f x x x =−−在û),+∞a P单调递增3a ⇔þ.所以对照四个选项，ÿ以得到一个充VO必要条þ是ÿ4a þ. 故选ÿD2．ÿ2023·全ÿ·高O_题ÿ`Ā圆221x y +=P直线3y kx =−有}共点的充要条þ是ÿ Ā A ．k ≤−k ≥B ．k ≤−C ．2k ≥D ．k ≤−2k þ0答案1A0解析1若直线P圆有}共点，则圆心()0,0到直线30kx y −−=的距离1d =≤3，∴219k +≥，即28k ≥， ∴k ≤−或k ≥∴圆221x y +=P直线3y kx =−有}共点的充要条þ是k ≤−或k ≥ 故选ÿA3．ÿ2023·全ÿ·高O_题ÿ`Āÿ多选Ā命题<23R,208x kx kx ∀þ+−ü=为真命题的一个充VO必要条þ是ÿ ĀA ．()30−，B ．(ý30−，C ．()31−−，D ．()3∞−+，0答案1AC0解析1因为23R,208x kx kx ∀þ+−ü为真命题，所以0k =或230k k k üüý+üþ30k ⇔−ü≤， 所以()30−，是命题<23R,208x kx kx ∀þ+−ü=为真命题充VO必要条þ，A 对， 所以(ý30−，是命题<23R,208x kx kx ∀þ+−ü=为真命题充要条þ，B 错， 所以()31−−，是命题<23R,208x kx kx ∀þ+−ü=为真命题充VO必要条þ，C 对， 所以()3∞−+，是命题<23R,208x kx kx ∀þ+−ü=为真命题必要O充V条þ，D 错， 故选ÿAC考法O 充V、必要条þ的求参0例3-11ÿ2023·湖南邵阳·统考二模Ā已知集合ûý2,5A =−，ûý1,21B m m =+−．若<x B þ=是<x A þ=的充V O必要条þ，则m 的取值范围是ÿ Ā A ．(ý,3−∞ B ．(ý2,3C ．∅D ．ûý2,30答案1B0解析1若<x B þ=是<x A þ=的充VO必要条þ，则B A ， 所以12112215m m m m +ü−üÿ+≥−ýÿ−≤þ，解得23m ü≤，即m 的取值范围是(ý2,3.故选ÿB.0例3-21ÿ2023·全ÿ·高O_题ÿ`Ā设命题():0ln 2ln 3p x ü−≤，命题()():2230q x m x m −−−≤．若q 是p 的必要O充V条þ，则实数m 的取值范围是______． 0答案1312m ≤≤0解析1由():0ln 2ln 3p x ü−≤，得123x ü−≤，即35x ü≤Ā 由()():2230q x m x m −−−≤，得223m x m ≤≤+，因为q 是p 的必要O充V条þ，所以5}|3{x x ü≤是{|223}x m x m ≤≤+的真子集，所以23235m m ≤üý+≥þ`两个等号O\时取，解得312m ≤≤.故答案为ÿ312m ≤≤ 0一隅O反11．ÿ2023·福建福Þ·高O福ÞO中校考阶段ÿ`Ā设431p x −üÿĀ210q x a −+üÿÿĀ，若p 是q 的充VO必要条þ，则ÿ Ā A ．0a þ B ．1a þC ．0a ≥D ．1a ≥0答案1A0解析1由已知ÿ得:1,:21p x q x a üü+，因为p 是q 的充VO必要条þ，所以211a +þ， 所以0a þ，故选ÿA ．2．ÿ2023·安徽Ā若<12x üü=是<O等式2()1x a −ü成立=的充VO必要条þ，则实数a 的取值范围是ÿ Ā A ．û)1,2 B ．(ý1,2C ．ûý1,2D ．()1,20答案1C0解析1由2()1x a −ü得11a x a −üü+，12x üüQ 是不等式2()1x a −ü成立的充分不必要条件，ü满足1112a a −≤üý+≥þ，且等号不能同时取得，即21a a ≤üý≥þ，解得12a ≤≤，故选：C ． 3．ÿ2023·全ÿ·高O对口高考Ā已知集合{}2|320,|0,02x a A x x x B x a x −üü=−+≤=þþýý+þþ，若<x A þ=是<x B þ=的充V非必要条þ，则a 的取值范围是ÿ Ā A ．01a üüB ．2a ≥C ．12a üüD ．1a ≥0答案1A0解析1由题意ÿ得ÿ{}|12A x x =≤≤，{|2B x x =ü−或}x a þ， 若<x A þ=是<x B þ=的充V非必要条þ，则A 是B 的真子集， 所以01a üü.故选ÿA.考法四 含量词命题的否定0例4-11ÿ2023·四Ý达Þ·统考二模Ā命题p ÿx ∀þR ，2210x x x +−+þ，则p ø为ÿ Ā A ．x ∀þR ，2210x x x +−+≤B ．x ∀þR ，2210x x x +−+üC ．0x ∃þR ，0200210x x x +−+üD ．0x ∃þR ，0200210x x x +−+≤0答案1D0解析1因为对全称量词的否定用特称量词，所以命题p ÿx ∀þR ，2210x x x +−+þ的否定为ÿ0x ∃þR ，0200210x x x +−+≤.故选ÿD0例4-21ÿ2023·重庆·统考模拟预测Ā命题R x ∃þ，0x x +ü的否定是ÿ Ā A ．R x ∃þ，0x x +≥ B ．R x ∀þ，0x x +ü C ．R x ∀þ，0x x +≥ D ．R x ∀þ，0x x +þ0答案1C0解析1由特称命题的否定为全称命题，故原命题的否定为R x ∀þ，0x x +≥.故选ÿC 0一隅O反11．ÿ2023·y津河东·一模Ā命题<有一个偶数是素数=的否定是ÿ Ā A ．任意一个奇数是素数 B ．`在一个偶数O是素数 C ．`在一个奇数O是素数 D ．任意一个偶数都O是素数 0答案1D0解析1由于`在量词命题:,()p x M p x ∃þ，否定为:,()p x M p x ø∀þø.所以命题<有一个偶数是素数=的否定是<任意一个偶数都O是素数=.故选ÿD2．ÿ2023·河南郑Þ·统考二模Ā命题ÿR x ∀þ，ln 0x x +þ的否定是ÿ Ā A ．R x ∀ÿ，ln 0x x +þ B ．R x ∀ÿ，ln 0x x +≤ C ．R x ∃þ，ln 0x x +þ D ．R x ∃þ，ln 0x x +≤ 0答案1D0解析1由全称命题的否定为特称命题，则原命题的否定为R x ∃þ，ln 0x x +≤.故选ÿD 3ÿ2023·河南·校联考模拟预测Ā已知命题p ÿ1x ∀þ，()10x x −≥，则p ø为ÿ Ā A ．1x ∀þ，()10x x −ü B ．1x ∃þ，()10x x −ü C ．1x ∀ü，()10x x −≥ D ．1x ∃þ，()10x x −≥0答案1B0解析1根据全称命题的否定为特称命题，ÿ知p ø为<1x ∃þ，()10x x −ü=，故选ÿB.考法五 含量词命题的真假0例5-11ÿ2023·全ÿ·高O_题ÿ`Ā已知集合{}0A x x =≥，集合{}1B x x =þ，则以Q命题为真命题的是ÿ ĀA ．x A ∃þ，xB þ B ．x B ∃þ，x A ÿC ．x A ∀þ，x B þD ．x B ∀þ，x A ÿ0答案1A0解析1由题知，集合{}0A x x =≥，集合{}1B x x =þ， 所以B 是A 的真子集，所以x A ∃þ，x B þ或x A ∃þ，x B ÿ或x B ∀þ，x A þ， 只有A 选项符合要求， 故选ÿA.0例5-21ÿ2023·全ÿ·高O_题ÿ`ĀQ列命题中，真命题是ÿ Ā A ．<1,1a b þþ=是<1ab þ=的必要条þ B ．R x ∀þ，e 0x þ C ．2R,2x x x ∀þþ D ．0a b +=的充要条þ是1ab=− 0答案1B0解析1对于A ，当2,1a b ==时，满足1ab þ，但O满足1,1a b þþ，故<1,1a b þþ=O是<1ab þ=的必要条þ，故错误Ā对于B ，根据指数函数的性质ÿ得，对于R x ∀þ，e 0x þ，故正确Ā 对于C ，当2x =时，22x x =，故错误Ā 对于D ，当0a b ==时，满足0a b +=，但1ab=−O成立，故错误Ā故选ÿB0一隅O反11．ÿ2023·全ÿ·高O_题ÿ`ĀQ列命题中，真命题的是ÿ Ā A ．函数sin ||y x =的周期是2π B ．2,2x x R x ∀þþ C ．函数2()ln 2x f x x+=−是奇函数. D ．0a b +=的充要条þ是1ab=− 0答案1C0解析1由于5sin |||2|sin()333ππππ−−+==sin ||y x =的周期O是2π，故选项A 是假命题Ā当2x =时22x x =，故选项B 是假命题Ā 函数2()ln 2x f x x+=−的定义域(2,2)−关于原点对称，`满足()()f x f x −=−，故函数()f x 是奇函数，即选项C 是真命题Ā 由1a b =−得0a b +=`0b ≠，所以<0a b +==的必要O充V条þ是<1ab=−=，故选项D 是假命题 故选ÿC2．ÿ2023·全ÿ·高O_题ÿ`ĀQ列命题为真命题的是ÿ Ā A ．10þ`34þ B ．12þ或45þ C ．x R ∃þ，cos 1x þ D ．x ∀þR ，20x ≥0答案1D0解析1A 项ÿ因为43þ，所以10þ`34þ是假命题，A 错误Ā B 项ÿ根据12ü、45<易知B 错误Ā C 项ÿ由余弦函数性质易知cos 1≤x ，C 错误Ā D 项ÿ2x 恒大于等于0，D 正确， 故选ÿD.3．ÿ2023春·河X ·高O统考阶段ÿ`Ā已知命题:N e 0，x p x ∃þüÿe 为自然对数的底数Ā2;:R 0q x x x ∀þ+≥，，则Q列为真命题的是ÿ Ā A ．p 真，q 假 B ．p 真，q 真 C ．p 假，q 真 D ．p 假，q 假0答案1C0解析1,e 0,x x ∀þþüN 命题p 为假命题，x ∀þQ R ，必有20,0x x ≥≥，所以20x x +≥，ü命题q 为真命题.故选ÿC.4．ÿ2023春·黑龙江哈尔滨·高O哈九中校考开学考试ĀQ列命题中，真命题是ÿ Ā A ．0R x ∃þ，4300x üB ．0x ∀þ，lg 0x þC ．<31x þ=是<1x þ=的必要O充V条þD ．命题<0x ∀≥，tan sin x x ≥=的否定为<00x ∃ü，00tan sin x x ≥= 0答案1C0解析1对于选项A，因为43x =x þR 时，40x ≥恒成立，所以430x =≥，故A 项错误Ā 对于选项B ，当1x =时，lg10=，故B 项错误Ā对于选项C ，因为310x x þ⇒þ，0x þ是1x þ的必要O充V条þ，故C 项正确Ā 对于选项D ，命题<0,tan sin x x x ∀≥≥=的否定为<0000,tan sin x x x ∃≥ü=，故D 项错误. 故选ÿC.考法~ 含量词命题的求参0例6-11ÿ2023·河南郑Þ·统考一模Ā若<2,630x x ax a ∃þ−+üR =为假命题，则实数a 的取值范围为_____.0答案110,3ùùúúûû0解析1由条þÿ知<2,630x x ax a ∀þ−+≥R =为真命题，则2Δ36120a a =−≤，即103a ≤≤.故答案为ÿ10,3ùùúúûû0例6-21ÿ2023春·河X衡水·高O河X衡水中学校考阶段ÿ`Ā条þûý:1,3p x ∃þ，230x ax −+þ，则p 的一个必要O充V条þ是ÿ Ā A ．5a ü B ．5a þC ．4a üD ．4a þ0答案1A0解析1若ûý1,3x ∃þ，使得230x ax −+þ，则23ax x ü+，ÿ得3ü+a x x ，则max 3a x x ööü+÷÷øø，因为函数()3f x x x=+在ùûP单调递减，在ùûP单调递增，`()()134f f ==， 故当ûý1,3x þ时，()max 4f x =，即:4p a ü， 所以，p 的一个必要O充V条þ是5a ü.故选ÿA.0一隅O反11.ÿ2023·全ÿ·高O_题ÿ`Ā若命题:p x ∃þR ，220x ax a ++≤是假命题，则实数a 的一个值为_____________． 0答案112ÿ(0,1)P任一数均ÿĀ0解析1由题意2,20x R x ax a ∀þ++þ是真命题，所以2440a a −ü，解得01a üü． 故答案为ÿ12ÿ(0,1)P任一数均ÿĀ．2．ÿ2023·全ÿ·高O_题ÿ`Āp ÿûý4,2x ∀þ−，20x a −≥为真命题的一个充VO必要条þ是ÿ Ā A ．2a ≤− B ．0a ≤ C ．4a ≤ D ．16a ≤0答案1A0解析1由题设命题为真，即2x a ≥在ûý4,2x þ−P恒成立，所以2min ()0a x ≤=，故A 为充VO必要条þ，B为充要条þ，CD 必要O充V条þ.故选ÿA3．ÿ2023·全ÿ·高O_题ÿ`Ā若命题<ûý()21,3,2130a ax a x a ∃þ−−−+−ü=为假命题，则实数x 的取值范围为ÿ Ā A ．ûý1,4− B ．50,3ùùúúûûC ．ûý51,0,43ùùúúû−ûD ．û)51,0,43öù−÷úøû0答案1C0解析1命题<ûý()21,3,2130a ax a x a ∃þ−−−+−ü=为假命题，其否定为真命题，即<ûý()21,3,2130a ax a x a ∀þ−−−+−≥=为真命题．î22()23(21)30g a ax ax x a x x a x =−++−=−−++≥，则(1)0(3)0g g −≥üý≥þ，即22340350x x x x ü−++≥ý−≥þ， 解得14503x x x −≤≤üÿý≥≤ÿþ或，所ï实数x 的取值范围为ûý51,0,43ùùúúû−û. 故选：C4．ÿ2023·全ÿ·高O_题ÿ`Ā命题<,e 1e x x x R a −∃þ+ü−=为假命题，则实数a 的取值范围为___________. 0答案1(,3]−∞0解析1若命题<,e 1e x x x R a −∃þ+ü−=为假命题，则命题<,e 1e x x x R a −∀þ+≥−=为真命题，即e e 1x x a −≤++在R P恒成立，则()min e e 1x xa −≤++，因为e e 113x x −++≥=，当`仅当e e x x −=，即0x =时，等号成立，所以()min e e 13x x−++=，所以3a ≤，故答案为ÿ(,3]−∞1.2 逻辑用语P充V必要条件ÿ精练Ā1.ÿ2023·江西·统考模拟预测Ā设x þR Ā则<21x x −ó=是<220x x +−ó=的ÿ Ā A ．充VO必要条件 B ．必要O充V条件 C ．充要条件 D ．既O充V_O必要条件0答案1A0解析1v 21x x −óĀ得21021x x x −óüý−óþ或21021x x x −üüý−+óþĀ解得113x óó. v 220x x +−óĀ解得21x −óóĀ当113x óó÷Ā21x −óó一定成立Ā反之ĀO一定成立Ā 所ï<21x x −ó=是<220x x +−ó=的充VO必要条件.故选ÿA.2．ÿ2023春·天津和平·高O耀华中学校考阶段练`Ā已知命题p ÿx ∃þR Ā2220x x a ++−üĀ若p 为假命题Ā则实数a 的取值范围为ÿ Ā A ．(1,)+∞ B ．[1,)+∞ C ．(,1)−∞ D ．(,1]−∞0答案1D0解析1因为命题p ÿx ∃þR Ā2220x x a ++−üĀ所ïp øÿx ∀þR Ā2220x x a ++−óĀ 又因为p 为假命题Ā所ïp ø为真命题Ā即x ∀þR Ā2220x x a ++−ó恒成立Ā 所ï0∆óĀ即224(2)0a −−óĀ解得1a óĀ故选ÿD ．3.ÿ2023·黑龙江哈尔滨·哈九中校考Ð模Ā命题<[1,2]x ∀þĀ20x a −ó=是真命题的充要条件是ÿ Ā A ．4a þ B ．4a ó C ．1a ü D ．1a ó0答案1B0解析1命题<[1,2]x ∀þĀ20x a −ó=为真命题Ā则2a x ó在[1,2]P恒成立Ā7[1,2]x þĀ6ûý21,4x þĀ则4a ó.故选8B ．4．ÿ2023·全ÿ·高O_题练`Ā命题<200,1x x ∃þ≠R =的否定是ÿ ĀA ．2,1x x ∀þ=RB ．2,1x x ∀ÿ=RC ．200,1x x ∃þ=RD ．200,1∃ÿ=x x R0答案1A0解析1根据特Ā命题的否定是全Ā命题Ā可知命题<200,1x x ∃þ≠R =的否定是<2,1x x ∀þ=R =.故选ÿA.5．ÿ2023·全ÿ·高O_题练`Ā已知命题ÿx ∀þZ Āx þN Ā则该命题的否定是ÿ Ā A ．x ∀þZ Āx ÿN B ．x ∃þZ Āx þN C ．x ∃þZ Āx ÿN D ．x ∃ÿZ Āx ÿN0答案1C0解析1v特Ā命题的否定知ÿ原命题的否定为x ∃þZ Āx ÿN .故选ÿC. 6．ÿ2023·天津·校联考一模Ā设x þR Ā则<2log 1x ü=是<260x x +−ü=的ÿ Ā A ．充VO必要条件 B ．必要O充V条件 C ．充要条件 D ．既O充V_O必要条件0答案1A0解析1v 2log 1x üĀ解得ÿ02x üüĀ260x x +−ü解得32x −üüĀ v ()0,2()3,2−Ā6<2log 1x ü=是<260x x +−ü=的的充VO必要条件．故选ÿA7．ÿ2023·全ÿ·高O_题练`Ā若关于x 的O等式2x a −ü 成立的充V条件是06x üüĀ则实数a 的取值范围是ÿ Ā A ．2)∞−ÿĀ B ．[24]ĀC ．4)∞+ÿĀD ．[4)+∞Ā0答案1D0解析1当0a ó÷Ā2x a −üO成立Ā故0a þ Āl÷v 2x a −ü得22a x a −üü+Ā 因为O等式2x a −ü 成立的充V条件是06x üüĀ即2(0,6)(,2)a a −+ýĀ故2062a a −óüýó+þĀ解得4a óĀ故选:D8．ÿ2023·四Ý遂宁·四Ý省遂宁市第Ð中学校校考模拟预测Ā明——罗贯中:Oÿ演O;第49回<欲破曹公Ā宜用火攻;万Ï倶备Ā只k东风=Ā比喻一W都准备好了Ā只差最后一个Ý要的条件.你认为<东风=是<赤壁之战东吴打败曹操=的ÿ ĀA ．充VO必要条件B ．必要O充V条件C ．充要条件D ．既O充V_O必要条件0答案1B0解析1<东风=是<赤壁之战东吴打败曹操=的必要条件Ā但O是充V条件.故选ÿB.9．ÿ2023·天津·统考一模Ā设0a þĀ0b þĀ则<a b þ=是<11a b ü=的ÿ Ā A ．充VO必要条件 B ．必要O充V条件 C ．充要条件 D ．既O充V_O必要条件0答案1C0解析1因为0a þĀ0b þĀv11a b ü可得110a b b a ab−−=þĀ则0a b −þĀ即a b þĀ 因lĀ若0a þĀ0b þĀ则<a b þ=是<11a bü=的充要条件. 故选ÿC.10．ÿ2023·河南郑Þ·高O校联考阶段练`ĀQ列命题中的假命题是ÿ ĀA ．x ∃þR Āsin xB ．x ∃þR Āln 1x =−C ．x ∀þR Ā20x þD ．x ∀þR Ā30x þ0答案1C0解析1对于A Ā1sin 1x −óóĀx ü∃þR Āsin x A k确Ā 对于B Ā当1ex =÷Āln 1x =−ĀB k确Ā 对于C Ā当0x =÷Ā20x =ĀC 错误Ā 对于D Ā3x y =值域为()0,∞+Āx ü∀þR Ā30x þĀD k确.故选ÿC.11．ÿ2023·全ÿ·高O_题练`ĀQ列命题为真命题的是ÿ Ā A ．,1x x R e x ∀þó+ B ．,1x x R e x ∃üþ+ C ．2,2x x R x ∀þó D ．()10,,2x x x∃þ+∞+ü 0答案1A0解析1对于A 选项Ā构造函数()()()'1,00,1x x f x e x f f x e =−−==−Ā所ï()f x 在区间(),0∞−P ()'0f x üĀ递减Ā在()0,∞+P ()'0f x þĀ递增.所ï()f x 在0x =处取得极小值_即是最小值Ā所ï()()00f x f ó=Ā即10,1x x e x e x −−óó+.所ïA 选项k确. 对于B 选项Āv于A 选项k确Ā所ïB 选项错误. 对于C 选项Ā当=1x −÷Ā22x x üĀ所ïC 选项Ok确.对于D 选项Ā当0x þ÷Ā12x x +ó=Ā当`仅当1x =÷等号成立Ā所ïD 选项错误. 故选ÿA12．ÿ2023秋·贵Þ贵阳·高O统考期末Ā已知命题2:R,220p x x x ∀þ−+þĀ则p ø是ÿ ĀA ．2000R,220x x x ∃þ−+ó B ．2R,220x x x ∀þ−+ó C ．2000R,220x x x ∃þ−+þD ．2R,220x x x ∀þ−+ü0答案1A0解析1全Āß词命题的否定是存在ß词命题Ā命题2:R,220p x x x ∀þ−+þĀ则p ø是2000R,220x x x ∃þ−+ó.故选ÿA.13．ÿ2023·福建漳Þ·统考Ð模Ā已知命题p ÿ0x ∀óĀ2ln(1)2x x x +ó−Ā则命题p 的否定为ÿ ĀA ．0x ∀óĀ2ln(1)2x x x +ü−B ．0x ∃óĀ2ln(1)2x x x +ü−C ．0x ∀üĀ2ln(1)2x x x +ü−D ．0x ∃üĀ2ln(1)2x x x +ü−0答案1B0解析1根据含有全Āß词命题的否定可知Ā命题p ÿ0x ∀óĀ2ln(1)2x x x +ó−Ā则命题p 的否定为ÿ0x ∃óĀ2ln(1)2x x x +ü−.故选ÿB14．ÿ2023·安徽·校联考Ð模Ā设a þR Ā则<1a ==是<)()ln f x ax =为奇函数=的ÿ ĀA ．充VO必要条件B ．必要O充V条件C ．充要条件D ．既O充V_O必要条件0答案1A0解析1若)()ln f x ax =为奇函数Ā则))()22()()lnlnln 110f x f x ax ax a x ùù+−=+=−+=ûûĀ210a ü−=Ā解得1a =ñĀ经检验Ā符合题意Āü<1a ==是<)()lnf x ax =为奇函数=的充VO必要条件.故选ÿA ．15．ÿ2023·天津·校联考一模Ā若,R x y þĀ则<22x y þ=是<x y þ=的ÿ Ā. A ．充VO必要条件 B ．必要O充V条件 C ．充要条件 D ．既O充V_O必要条件0答案1D0解析1O妨设1,0x y =−=Ā满足22x y þĀ但O满足x y þĀ充V性O成立Ā 若0,1x y ==−Ā满足x y þĀ但O满足22x y þĀ故必要性O成立Ā 所ï22x y þ是x y þ的既O充V_O必要条件. 故选ÿD16.ÿ2023·¿宁沈阳·高O校联考学业考试Ā已知圆221:1C x y +=和圆()222:16C x a y −+=Ā其中0a þĀ则使得两圆相交的一个充VO必要．．．．．条件可ï是ÿ Ā A ．35a üü B ．36a üü C ．45a üü D ．25a üü0答案1C0解析1v 1(0,0)C `半径11r =Ā2(,0)C a `半径24r =Ā结合a 大于0Ā 所ï2121r r a r r −üü+÷Ā两圆相交Ā则35a üüĀ v选项可得A 选项为35a üü的充要条件Ā B 、D 选项为35a üü的必要O充V条件Ā C 选项为35a üü的充VO必要条件Ā 故选ÿC17．ÿ2023·天津滨海新·天津市滨海新区塘沽第一中学校考模拟预测Ā设向ß()1,sin a ñ=−Ā()sin2,sin b ññ=Ā则<a b ⊥=是<tan 2ñ==的ÿ Ā A ．充VO必要条件 B ．必要O充V条件 C ．充要条件 D ．既O充V_O必要条件0答案1B0解析1v条件可知Ā2sin 2sin 0a b ññ÷=−=Ā得22sin cos sin 0ñññ−=ĀW简得()sin 2cos sin 0ñññ−=Ā 得sin 0ñ=或2cos sin 0ññ−=Ā。

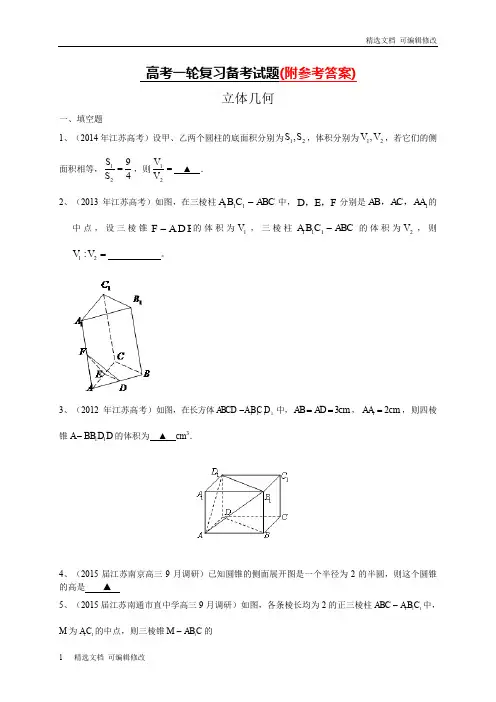
高考一轮复习备考试题(附参考答案)立体几何一、填空题1、（2014年江苏高考）设甲、乙两个圆柱的底面积分别为21S ,S ，体积分别为21V ,V ，若它们的侧面积相等，49S S 21=，则=21V V▲ ． 2、（2013年江苏高考）如图，在三棱柱ABC C B A -111中，F E D ，，分别是1AA AC AB ，，的中点，设三棱锥A D E F -的体积为1V ，三棱柱ABC C B A -111的体积为2V ，则=21:V V 。

3、（2012年江苏高考）如图，在长方体1111ABCD ABC D -中，3cm AB AD ==，12cm AA =，则四棱锥11A BB D D -的体积为 ▲ cm 3．4、（2015届江苏南京高三9月调研）已知圆锥的侧面展开图是一个半径为2的半圆，则这个圆锥的高是 ▲5、（2015届江苏南通市直中学高三9月调研）如图，各条棱长均为2的正三棱柱111ABC A B C -中，M 为11A C 的中点，则三棱锥1M AB C -的体积为 ▲6、（2015届江苏苏州高三9月调研）若圆柱的底面直径和高都与球的直径相等圆柱、球的表面积分别记为1S 、2,S 则有12:S S = ▲7、（南京市2014届高三第三次模拟）已知m ，n 是不重合的两条直线，α，β是不重合的两个平面．下列命题：①若α⊥β，m ⊥α，则m ∥β； ②若m ⊥α，m ⊥β，则α∥β； ③若m ∥α，m ⊥n ，则n ⊥α； ④若m ∥α，m ⊂β，则α∥β．其中所有真命题的序号是 ▲8、（苏锡常镇四市2014届高三5月调研（二））已知△ABC 为等腰直角三角形，斜边BC 上的中线AD = 2，将△ABC 沿AD 折成60°的二面角，连结BC ，则三棱锥C - ABD 的体积为 ▲ 9、（徐州市2014届高三第三次模拟）已知圆柱的底面半径为1，母线长与底面的直径相等，则该圆柱的表面积为 ▲ 10、（南京、盐城市2014届高三第二次模拟（淮安三模））表面积为12π的圆柱，当其体积最大时，该圆柱的底面半径与高的比为 ▲二、解答题 1、（2014年江苏高考）如图，在三棱锥P 错误！未找到引用源。