下载文档原格式
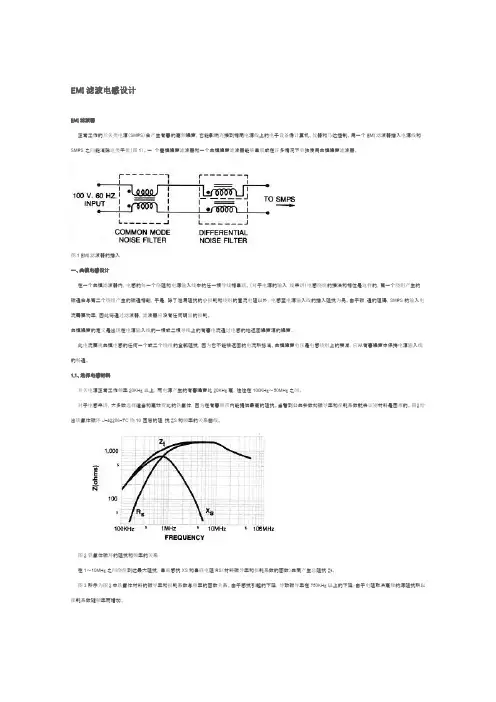
EMI滤波电感设计EMI滤波器正常工作的开关类电源（SMPS）会产生有害的高频噪声，它能影响连接到相同电源线上的电子设备像计算机、仪器和马达控制。
用一个EMI滤波器插入电源线和SMPS之间能消除这类干扰（图1）。
一个差模噪声滤波器和一个共模噪声滤波器能够串联或在许多情况下单独使用共模噪声滤波器。
图1 EMI滤波器的插入一、共模电感设计在一个共模滤波器内，电感的每一个绕阻和电源输入线中的仸一根导线相串联。
（对于电源的输入线来讲）电感绕组的接法和相位是这样的，第一个绕组产生的磁通会与第二个绕组产生的磁通相削. 于是，除了泄漏阻抗的小损耗和绕组的直流电阻以外，电感至电源输入线的插入阻抗为另。
由于磁通的阻碍，SMPS的输入电流需要功率，因此将通过滤波器，滤波器应没有仸何明显的损耗。
共模噪声的定义是出现在电源输入线的一根或二根导线上的有害电流通过电感的地返回噪声源的噪声。
此电流要视共模电感的仸何一个或二个绕组的全部阻抗，因为它不能被返回的电流所抵消。
共模噪声电压是电感绕组上的衰减，应从有害噪声中保持电源输入线的畅通。
1.1、选择电感材料开关电源正常工作频率20KHz以上，而电源产生的有害噪声比20KHz高，往往在100KHz～50MHz之间。
对于电感来讲，大多数选择适当和高效费比的铁氧体，因为在有害频带内能提供最高的阻抗。
当看到公共参数如磁导率和损耗系数就去识别材料是困难的。
图2给出铁氧体磁环J-42206-TC绕10匝后的阻抗ZS和频率的关系曲线。
图2铁氧体磁环的阻抗和频率的关系在1～10MHz之间绕组到达最大阻抗，串联感抗XS和串联电阻RS（材料磁导率和损耗系数的函数）共同产生总阻抗Zt。
图3所示为图2中铁氧体材料的磁导率和损耗系数与频率的函数关系。
由于感抗引起的下降，导致磁导率在750KHz以上的下降；由于电阻取决高频的源阻抗所以损耗系数随频率而增加。
图3铁氧体磁环的磁导率、损耗系数和频率的关系图4给出三种不同材料的总阻抗和频率的关系。
周洁敏调制方式有2种：单极性调制和双极性调制单极性调制（桥）双极性调制（推挽）正弦脉宽调制技术SPWMU 某点正弦波幅值N I f U U D I f U U D I f u U L k L πsin π22o 1o dc max o o d k ,ko,dc βαα⋅⋅⋅⋅-=⋅⋅⋅-=⋅∆⋅-=+最大电感量而且随着正弦波的调制，磁芯的直流工作点按正弦规律（50Hz ）在磁滞回线的1和3象限移动。
可以获得比较稳定的电感材料是气隙磁芯δA cR c R δΦu (t)i （t ）Nl cμ20c A L N μδ=电感不同于变压器，需要储存能量，开气隙后可以储存磁场能量，并使电感量稳定。
即电感为逆变器交流滤波电感中的磁密波形双极性调制单极性调制B L 曲线是曲线Ⅰ减去曲线Ⅱ积分所得，但是很难用精确的数学表达式表示。
输出正弦波输入为AB 端电压波形()t t U u NA B d sin 21π20o AB e L ⎰-=∆ω交流滤波电感不但有基波分量，而且叠加较大的高频分量，磁芯选择不仅要考虑基波损耗，而且要考虑磁芯涡流损耗。
同时线圈中除了流过基波电流，还要流过高次谐波电流，线圈应当考虑高频电流损耗。
纵坐标放大的结果线圈窗口利用率自然冷却经验值K1线圈损耗等于磁芯损耗K2210.707K K各种系数与电感类型的关系决定热阻R T 和允许损耗磁芯损耗线圈损耗损耗热阻最大允许温升决定损耗极限lim /thP T R =∆允许温升由设计需求确定th 20/R K W=。
周洁敏调制方式有2种：单极性调制和双极性调制单极性调制（桥）双极性调制（推挽）正弦脉宽调制技术SPWMU 某点正弦波幅值N I f U U D I f U U D I f u U L k L πsin π22o 1o dc max o o d k ,ko,dc βαα⋅⋅⋅⋅-=⋅⋅⋅-=⋅∆⋅-=+最大电感量而且随着正弦波的调制，磁芯的直流工作点按正弦规律（50Hz ）在磁滞回线的1和3象限移动。
可以获得比较稳定的电感材料是气隙磁芯δA cR c R δΦu (t)i （t ）Nl cμ20c A L N μδ=电感不同于变压器，需要储存能量，开气隙后可以储存磁场能量，并使电感量稳定。
即电感为逆变器交流滤波电感中的磁密波形双极性调制单极性调制B L 曲线是曲线Ⅰ减去曲线Ⅱ积分所得，但是很难用精确的数学表达式表示。
输出正弦波输入为AB 端电压波形()t t U u NA B d sin 21π20o AB e L ⎰-=∆ω交流滤波电感不但有基波分量，而且叠加较大的高频分量，磁芯选择不仅要考虑基波损耗，而且要考虑磁芯涡流损耗。
同时线圈中除了流过基波电流，还要流过高次谐波电流，线圈应当考虑高频电流损耗。
纵坐标放大的结果线圈窗口利用率自然冷却经验值K1线圈损耗等于磁芯损耗K2210.707K K各种系数与电感类型的关系决定热阻R T 和允许损耗磁芯损耗线圈损耗损耗热阻最大允许温升决定损耗极限lim /thP T R =∆允许温升由设计需求确定th 20/R K W=。
直流滤波电感设计
一、直流滤波电感的基本原理
具体来说，当直流信号通过电感时，电感的自感性会导致电流的变化速度减慢，从而滤除高频成分；同时，电感的互感性也会使得电感对高频成分产生阻抗，进一步增强了滤波效果。
因此，电感在电子电路中被广泛应用于直流滤波。
二、直流滤波电感的设计方法
1.选择合适的电感值：电感的大小决定了其对高频信号的滤波效果。
一般来说，电感的值越大，对高频信号的滤波效果越好。
但是同时也要考虑到电感的大小对电路的稳定性和成本的影响。
因此，在设计中需要综合考虑这些因素，选择合适的电感值。
2.考虑电感的直流电阻：电感的直流电阻是电感中电流通过时产生的电阻。
由于直流信号是通过电感的主要信号，因此电感的直流电阻必须尽量小，以减小对直流信号的影响。
3.选择合适的电感材料和制造工艺：电感的材料和制造工艺也会对滤波效果产生影响。
一般来说，选择高导磁材料和适当的制造工艺，可以提高电感的工作效率和滤波性能。
4.保证电感的负载能力：电感在设计中也需要考虑其负载能力。
由于直流滤波电感通常工作在大电流环境下，因此电感的负载能力必须要能够满足电路的需求。
上述是直流滤波电感设计的一些基本原理和方法，通过综合考虑电感的电阻、直流电阻、材料和制造工艺等因素，可以设计出性能稳定、效果
良好的直流滤波电感。
在实际设计中，还需要根据具体的应用需求进行优化和调整。
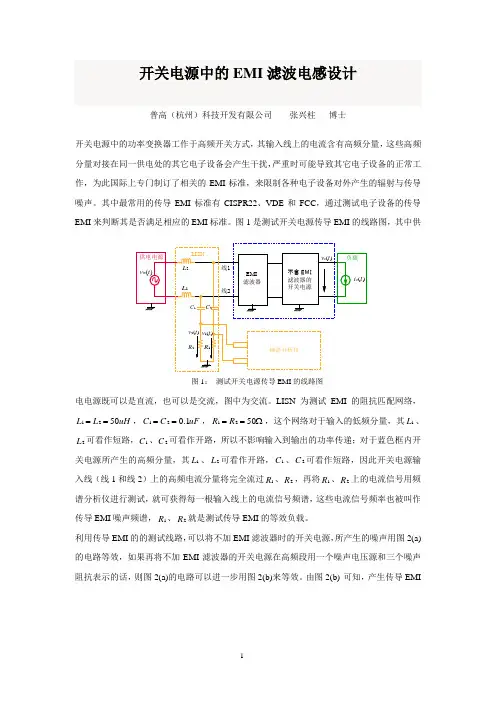
开关电源中的EMI 滤波电感设计普高（杭州）科技开发有限公司 张兴柱 博士开关电源中的功率变换器工作于高频开关方式，其输入线上的电流含有高频分量，这些高频分量对接在同一供电处的其它电子设备会产生干扰，严重时可能导致其它电子设备的正常工作，为此国际上专门制订了相关的EMI 标准，来限制各种电子设备对外产生的辐射与传导噪声。
其中最常用的传导EMI 标准有CISPR22、VDE 和FCC ，通过测试电子设备的传导EMI 来判断其是否满足相应的EMI 标准。
图1是测试开关电源传导EMI 的线路图，其中供电电源既可以是直流，也可以是交流，图中为交流。
LISN 为测试EMI 的阻抗匹配网络，uH L L 5021==，uF C C 1.021==，Ω==5021R R ，这个网络对于输入的低频分量，其1L 、2L 可看作短路，1C 、2C 可看作开路，所以不影响输入到输出的功率传递；对于蓝色框内开关电源所产生的高频分量，其1L 、2L 可看作开路，1C 、2C 可看作短路，因此开关电源输入线（线1和线2）上的高频电流分量将完全流过1R 、2R ，再将1R 、2R 上的电流信号用频谱分析仪进行测试，就可获得每一根输入线上的电流信号频谱，这些电流信号频率也被叫作传导EMI 噪声频谱，1R 、2R 就是测试传导EMI 的等效负载。
利用传导EMI 的的测试线路，可以将不加EMI 滤波器时的开关电源，所产生的噪声用图2(a)的电路等效，如果再将不加EMI 滤波器的开关电源在高频段用一个噪声电压源和三个噪声阻抗表示的话，则图2(a)的电路可以进一步用图2(b)来等效。
由图2(b)可知，产生传导EMIii (a) (b) 图2： 不加EMI 滤波器的开关电源之EMI 等效电路的根源有三个，一个是EMI 源N v ，一个是EMI 途径1Z 、2Z 和c Z ，再一个就是EMI 的负载1R 和2R 。
等效电路中的EMI 负载是固定的50欧电阻，而变化的是EMI 源及EMI 途径。
多路输出正激式变换器耦合滤波电感的设计多路输出正激式变换器耦合滤波电感的设计1引言近年来高频开关电源在电子产品中得到广泛应用。
正激式DC/DC变换器以其输出纹波小、对开关管的要求较低等优点而适合于低压、大电流、功率较大的场合。
但正激变换器对输出电感的设计有较高要求，特别在多路输出的情况。
本文分析对比正激变换器多路输出滤波电感采用独立方式和耦合方式的不同特点，讨论了耦合电感的设计方法，给出了一个设计实例，并给出仿真及试验结果。
2正激变换器普通多路输出的分析图1所示为180W正激变换器的变压器及输出部分。
两路输出分别采用无耦合的滤波电感。
其一路输出UO1为：UO1=(Uin1－UV1a)D－UV1b(1－D)=Uin1D－UV1b(1)式（1）中，D为初级开关脉冲的占空比，UV1a、UV1b分别为整流二极管和续流二极管的压降，并假设它们相等。
该电路L的最小值一般由所需维持最小负载电流的要求决定，而电感L中的电流又分连续和不连续两种工作情况。
如果负载电流IO逐步降低，L中的波动电流最小值刚好为0时，即定义为临界情况。
在控制环中，连续状况的传递函数有两个极点，不连续状况只有一个极点。
因而在临界点上下，传递函数是突变的。
图1电路的Uin1,Uin2绕组通常都为紧耦合状态，而每一路LC滤波器的串联谐振频率不相同，这一情况将使控制环在连续状况时传递函数增加新的极点。
在多路输出时，如果辅助输出电压要保持在一定的稳定范围内，则主输出的电感必须一直超过临界值，即一直处于连续状态。
从性能上讲，L过大限制了输出电流的最大变化率，而且带直流电流运行的大电感造价昂贵。
在图1所示的电路中，当UO1保持5V不变时，随着UO2负载上的突然变化，其15.8V的电压有可能突变4V～5V，且在经过数十至数百毫秒后才能恢复。
图1独立滤波电感两路输出正激变换器图2耦合滤波电感的两路输出正激变换器图3图4 图3电路的归一化电路图5 图4电路的重新排列为了简化设计，通常都使电感电流工作于连续状态。
电感的滤波原理电感滤波是一种常用的电子电路滤波技术，它利用电感元件的特性来实现对电路中的高频信号进行滤除或衰减，从而达到滤波的目的。
本文将从电感的工作原理、电感滤波的基本原理和分类、电感滤波器的设计以及电感滤波器的应用等方面进行阐述。
一、电感的工作原理电感是一种储存磁能的元件，它由导体线圈组成。
当通过电感的电流发生变化时，会在电感的周围产生磁场。
根据电磁感应的原理，当电流变化时，电感中会产生电动势，并阻碍电流的变化。
因此，电感对交流信号具有阻抗，可以实现对不同频率信号的阻隔或衰减。
二、电感滤波的基本原理和分类电感滤波是利用电感元件对不同频率的电信号产生不同的阻抗，从而实现对特定频率信号的滤除或衰减。
根据电感滤波的基本原理，可以将电感滤波器分为低通滤波器和高通滤波器两种基本类型。
1. 低通滤波器：低通滤波器允许低频信号通过，而对高频信号进行滤除或衰减。
它的基本原理是通过串联电感元件，在电感的高阻抗作用下，将高频信号滤除或衰减，从而使低频信号可以顺利通过。
2. 高通滤波器：高通滤波器则相反，它允许高频信号通过，而对低频信号进行滤除或衰减。
高通滤波器的基本原理是通过并联电感元件，在电感的低阻抗作用下，将低频信号滤除或衰减，从而使高频信号可以顺利通过。
三、电感滤波器的设计电感滤波器的设计需要考虑滤波器的截止频率、阻带范围、阻抗匹配等因素。
根据滤波器的需求，选择合适的电感元件，并根据电感元件的参数计算滤波器的电路参数。
1. 低通滤波器的设计：低通滤波器的设计关键是确定截止频率。
根据所需的截止频率，选择合适的电感元件，并根据电感元件的电感值和电容元件的容值计算滤波器的截止频率。
2. 高通滤波器的设计：高通滤波器的设计同样需要确定截止频率。
选择合适的电感元件，并根据电感元件的电感值和电容元件的容值计算滤波器的截止频率。
四、电感滤波器的应用电感滤波器广泛应用于各种电子电路中，常见的应用领域包括音频处理、通信系统、电源滤波等。
1. 滤波电感的设计
在全桥逆变器中，输出滤波电感是一个关键性的元件，并网系要要求在逆变器的输出侧实现功率因数为1，波形为正弦波，输出电流与网压同频相同。
因而，电感值选取的合适与否直接影响电路的工作性能。
对电感值的选取，可以从以下两个方面来考虑： ① 电流的波纹系数
输出滤波电感的值直接影响着输出纹波的大小，由电感的基本伏安关
系dt Ldi V /=可得：dt t i Ton
f
i
L
v ⎰=∆0
)( （5-14）
其中)(t v l 电感两端电压，考虑到当输出电压处于峰值附近，即
V
v N o
t max
)(=时，输出电流波纹最大，设此时开关周期为T ，占空比为
D,则有下式：
L
V f
N i max =∆ （5-15）
另外，根据电感的伏秒平衡原理，我们可以得到，
T D DT V V V
N dc N )1)((max max
--= （5-16）
于是求得，
V
V V dc
N dc
D max
-= （5-17）
从（5-15）、（5-16）式可得，
V V V V
L
dc
N dc N f
i T ∆-=)(max max
（5-18）
在本系统中，,400,5.9,3112202max V A V V I V dc N N ===⨯=开关管的工作频率,125,8us T kHz f ==取电流波纹系数,15.0=r i 则由式（5-18）计算可：
mH L
f
1.6400
15.05.910125)311400(3116
≈⨯⨯⨯⨯-⨯=-
因此，要保证实际电流纹,425.115.05.9A i I r N i =⨯=≤∆则滤波器电感满足mH L f 1.6≥。
②从逆变器的矢量三角形关系可知，
V
I L V
N
N
f
o
j +=ϖ
（5-19）
于是，它们的基波幅值满足下式
V I L
V N N f
o 2
2
2
)(+=ϖ
（5-20）
由正弦脉宽调制理论可知，
V V
dc o
m = （5-21）
其中，m 为调制比，且,1≤m 从而：
V V I L
dc N N f
2
22
)(≤+ϖ
（5-22）
于是，我们可以得到下式：
mH L
f
4.375
.95022204002
2=⨯⨯-≤π 综上，滤波电感的取值范围为mH mH L f 4.361.6≤≤。
在实际设计过程中，由于电感的体积、成本等因素的影响，一般只需考虑电感的下限值，即取稍大于下下至即可。
另外需要特别指出的是，以上的计算是建立在额定输出电压，即V V N 220=的基础上，考虑到实际情况
下网压的波动范围，在设计电感时最终选取电感值mH L f 7=，电感的额定电流为A 11。
1.输入电容的设计
假设电网电压和电网的电流只含有基波分量并且相同，则注入到电网的瞬时功率为：
)(2sin 2
t grld grld grld
P P
⋅⋅=ϖ （5-24）
其中P grld 是注入电网的平均功率，ϖgrld 是角频率，t 是时间。
因此，中间直流侧电压有小的脉动，同时由前述的Boost 的光伏阵列的输出电流是在直流之上叠加了一个高频分量。
同时雷击等尖峰电压和一些额外的因素引起的波动会对逆变器造成影响。
因此有必要设置输入电容，使其与光伏阵列与逆变器之间的导线上的分布电感组成一个低通滤波，使各部分产生的干扰尽量不影响另一部分。
由经验值可得:输入电容的值一般取F μ500。
考虑到耐压，我们选取2个V F 400/1000μ的电解电容进行串联。
由于电容的串联涉及到均压的问题，采用并联均压电阻的措施。
采用每组并联的电容上并联一个K 100电阻，由三个W K 1/33电阻串联组成。
5.3.3功率因数（PF ）
当逆变器的输出大于其额定输出的20%，平均功率因数应不小于0.85（超前或滞后），当逆变器的输出大于其额定输出的50%，平均功率因数不应小于0.95（超前或滞后）。
一段时期内的平均功率因数（PF ）公式：
P P
P REACTIVE
REAL
REAL
PF 2
2+=
(5)
式中：
E REAL
——有功功率； E
REACTIVE
———无功功率。
注1：在供电机构许可下，特殊设计以提供无功功率补偿的逆变器可超出此限制工作； 注2：用于并网运行而设计的大多数逆变器功率因数接近1。
5.3.5工作频率
逆变器并网时应与电网同步运行。
逆变器交流输出端频率的允许偏差为,5.0Hz ±电网额定频率为Hz 50。
5.3.6直流分量
并网运行时，逆变器向电网馈送的直流电流分量应不超过其输出电流额定值的0.5%或5mA,应取二者中较大值。
5.4.2发射要求
)a 在居住、商业和轻工业环境中正常工作的逆变器的电磁发射
应不超过GB 17799.3规定的发射限制；
)b 连接到工业电网和在工业环境中正常工作的逆变器的电磁发
射不应超过GB 17799.3规定的发射限制。
2.3太阳电池阵列输出功率数学模型
本文采用TRW 太阳电池阵列输出功率数学模型[3,4]。
任意太阳辐射强度)(2-⋅cm mW R 和环境温度)(C o a T 条件下，太阳电池温度)(C o c T
为
R T T T c a c ⋅+= (21) 设在参考条件下，I sc 为短路电流；V oc 为开路电压；I m 、V m 为最大功率点电流和电压，则当光伏阵列电压为V ，其对应点电流I 为：
⎥
⎥⎦⎤
⎢⎢⎣
⎡⎥⎥⎦⎤⎢⎢⎣⎡--=⋅1121V c e oc V sc C I I
（22）
V c V e
oc
m
I
I C sc
m
⋅-=2)/1(1
（23） {})/1ln(/)1/(2
I I V V C sc
m
oc
m
--= （24）
考虑太阳辐射变化和温度的影响时，
DI V c e oc DV V sc C I I
+⎥
⎥⎦⎤
⎢⎢⎣
⎡⎥⎥⎦⎤⎢⎢⎣⎡--=--1121
（25）
I R R R R DI sc ref ref DT )1/()/(-+=α （26）
DI R DT DV
s ⋅-⋅-=β （27）
T
T DT ref
c
-= （28）
其中，R ref 、T ref 分别为太阳辐射和光电池温度参考值，一般分别取为2/1m KW 和C o 25;α为在参考日照下的电流变化温度系数（C Amps o /）;β为在参考日照下的电压变化温度系数（C V o /）；R s 为光伏阵列的串联电阻。
2.4逆变器输出功率数学模型 逆变器输出功率为
B P P P
out NL in out
/)(-= （29）
其中，P out 为输出功率；P in 为输入功率；P NL 为无载功率；P RO
为额定输出功率；P out 为常数，表明输入与输出间的关系，由下式决定
P P P B
RO NL R
RO out
/)/(-=η （30）
其中，ηR 为逆变器的效率。
