手拉手模型——全等三角形常见模型介绍一 ppt课件

全等三角形之手拉手模型
本文将介绍手拉手模型，这是指有公共顶点的两个等腰三角形，顶角相等。

因为顶点相连的四条边，形象的可以看作两双手，所以通常称为手拉手模型。

一个基本的手拉手模型例题是：已知，△ABB'和△ACC'都是等腰三角形，AB=AB'，AC=AC'，且∠BAB'=∠CAC'。

可以得出三个结论：第一，△ABC≌△AB'C'（SAS），因为BC=B'C'；第二，∠BOB'=∠BAB'；第三，AO平分∠BOC'。

在共顶点的等腰直角三角形中，也可以使用手拉手模型。

例如，如果△ABC和△ADE是等腰直角三角形，且
∠BAC=∠DAE=90°，则可以证明BD=CE和BD⊥CE。

另外一个例子是在共顶点的等边三角形中。

如果点A为线段BD上一点，△ABC和△ADE均是等边三角形，则可以求出CD=BE，以及∠DAE＋∠BFD=180°和
∠BFA=∠DFA=60°。

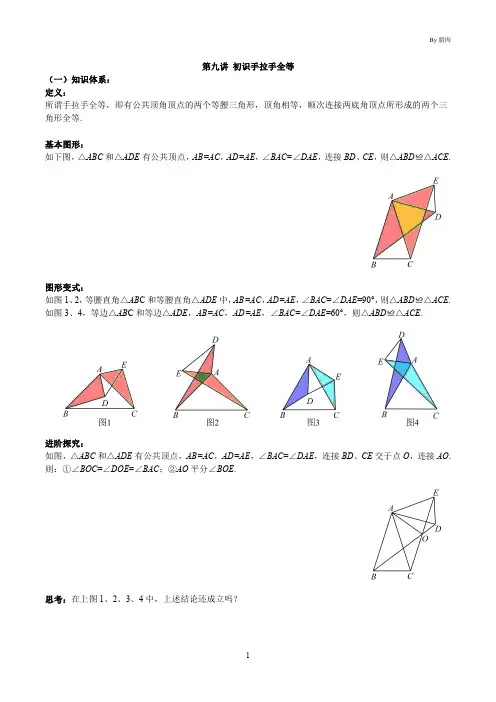
第九讲初识手拉手全等（一）知识体系：定义：所谓手拉手全等，即有公共顶角顶点的两个等腰三角形，顶角相等，顺次连接两底角顶点所形成的两个三角形全等.基本图形：如下图，△ABC和△ADE有公共顶点，AB=AC，AD=AE，∠BAC=∠DAE，连接BD、CE，则△ABD≌△ACE.图形变式：如图1、2，等腰直角△AB C和等腰直角△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°，则△ABD≌△ACE.如图3、4，等边△AB C和等边△ADE，AB=AC，AD=AE，∠BAC=∠DAE=60°，则△ABD≌△ACE.进阶探究：如图，△ABC和△ADE有公共顶点，AB=AC，AD=AE，∠BAC=∠DAE，连接BD、CE交于点O，连接AO.则：①∠BOC=∠DOE=∠BAC；②AO平分∠BOE.思考：在上图1、2、3、4中，上述结论还成立吗？（二）典例精讲例1.在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=30°，CD、BE交于点O，连接OA （1）如图1，求证：△ABE≌△ACD；（2）如图1，求∠AOE的大小；（3）当绕点A旋转至如图2所示位置时，若∠BAC=∠DAE=α，∠AOE=_________.练：如图，A在DE上，F在AB上，且AC=CE，∠1=∠2=∠3=α求∠BAC.（用α表示）例2：如图，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，连接BD、CE交于点P.（1）求证：△ABD≌△ACE；（2）判断BD、CE的关系并证明；（3）连接PA，求∠APB的度数.练：在例2的条件下，将△ADE旋转至如图所示的位置时，BD与CE的关系还成立吗？请说明理由.例3：如图，分别以△ABC的边AB、AC向外作等边△ABD和等边△ACE，连接BE、CD交于点P，连接AP.（1）求证：BE=CD；（2）求∠BPD的度数；（3）求证：PA平分∠DPE.变式：在例3的条件下，若点F为CD上一点，且∠DBF=∠ADC，试判断△BFP的形状并证明.练：已知，Rt△ABC中，∠ACB＝90°，∠CAB＝30°．分别以AB、AC为边，向三角形外作等边△ABD和等边△ACE.（1）如图1，连接线段BE、CD，求证：BE＝CD；（2）如图2，连接DE交AB于点F，求证：F为DE中点.例4：如图，△ADC和△CBE均为等边三角形，连接AE、AB、BD，∠ABD=80°，求∠EAB的度数.练1.如图，△ABC 和△CDE 都是等边三角形，∠EBD =78°，则∠AEB =_________度.练2.已知AC=BC ，DC=EC ，∠ACB =∠ECD =90°，且∠EBD =42°，则∠AEB =.例5.如图，ΔAOB 是等边三角形，以直线OA 为x 轴建立平面直角坐标系，B （a ，b ）且a ，b 满足2(0b -=，D 为y 轴上一动点，以AD 为边作等边ΔADC ，直线CB 交y 轴于点E .（1）如图1，求A 点坐标；（2）如图2，D 在y 轴正半轴上，C 在第二象限，CE 的延长线交x 轴于点M ，当D 点在y 轴正半轴上运动时，M 点的坐标是否发生变化，若不变，求M 点的坐标，若变化，说明理由.练1.如图，已知直线AB 交x 轴于点A （a ，0），交y 轴于点B （0，b ），且a ，b 满足2(4)0a b a +++=，若点C 在第一象限，且BE ⊥AC 于点E ，延长BE 至点D ，使BD=AC ，连接OC 、OD 、CD ，试判断ΔCOD 的形状，并说明理由.练2.如图，ΔAOB和ΔACD是等边三角形，其中AB⊥x轴于E点.（1）如图，若OC=5，求BD的长；（2）设BD交x轴于点F，求证：∠OFA=∠DFA.例6.如图，已知△ABC是等边三角形，点E在线段AB上，点D在射线CB上，且DE=CE，以CE为边作等边三角形CEF，连接EF.（1）求证：BE=AF；（2）试猜想线段AB、DB、AF之间的数量关系，并证明你的猜想.练1.如图，ΔBAC为等腰直角三角形，其中AB=AC，∠BAC=90°，点A、D在BC的异侧且∠BDC=90°，连接AD，过点A作AE⊥AD交DB的延长线于点E，求∠E的度数.。

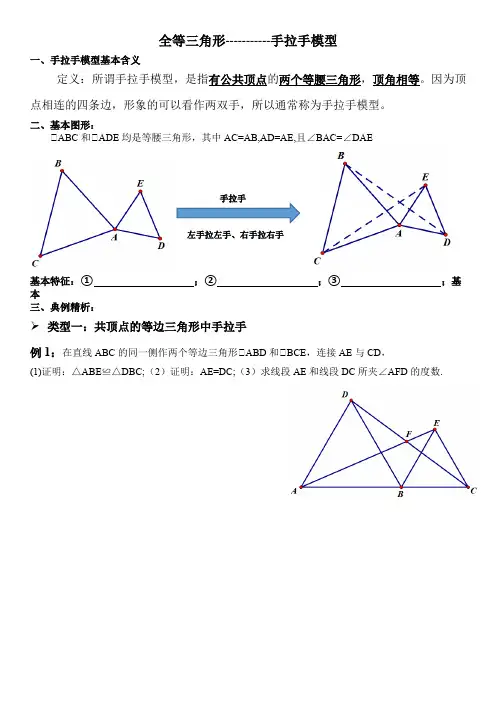
全等三角形-----------手拉手模型一、手拉手模型基本含义定义：所谓手拉手模型，是指有公共顶点的两个等腰三角形，顶角相等。

因为顶点相连的四条边，形象的可以看作两双手，所以通常称为手拉手模型。

二、基本图形：△ABC和△ADE均是等腰三角形，其中AC=AB,AD=AE,且∠BAC=∠DAE手拉手左手拉左手、右手拉右手基本特征：① ；② ；③ ；基本三、典例精析：➢类型一：共顶点的等边三角形中手拉手例1：在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，(1)证明：△ABE≌△DBC;（2）证明：AE=DC;（3）求线段AE和线段DC所夹∠AFD的度数.变式练习1：在例1的基础上，将△BEC绕点B逆时针旋转一定角度，连接AE，CD，如图.(1)证明：AE=DC;（2）求线段AE所在直线和线段DC所在直线之间的夹角.➢共顶点的等腰直角三角形的手拉手例2：如图，ACB∆均为等腰直角三角形，且90∆和DCEACB DCE∠=∠=︒，连接AD,BE.判断线段AD与线段BE之间的关系，请说明理由变式练习2：如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE、GC.(1)试猜想AE与GC有怎样的数量位置关系，并证明你的结论；(2)将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和GC. 你认为(1)中的结论是否还成立?若成立，给出证明；若不成立，请说明理由.总结归纳：如下图△ABC和△ADE均是等腰三角形，其中AC=AB,AD=AE,且∠BAC=∠DAE=α，则∠BEC 的大小是多少？GEFDABCOE DA BCA B CD E 321AB DE全等三角形-----------手拉手模型课后练习1.如图，AB=AC ，AD=AE ，∠BAC=∠DAE ，∠1=25°，∠2=30°，则∠3=__________．2.如图，△ABD ，△AEC 都是等边三角形，BE 交CD 于点O ，求△DOE 的度数.3．如图，四边形ABCD ，BEFG 均为正方形，连接AG ，CE.（1）求证：AG=CE ；（2）求证：AG△CE.4.如图，AC=BC ，DC=EC ，∠ACB=∠ECD=90°，且∠EBD=42°，求∠AEB 的度数.。

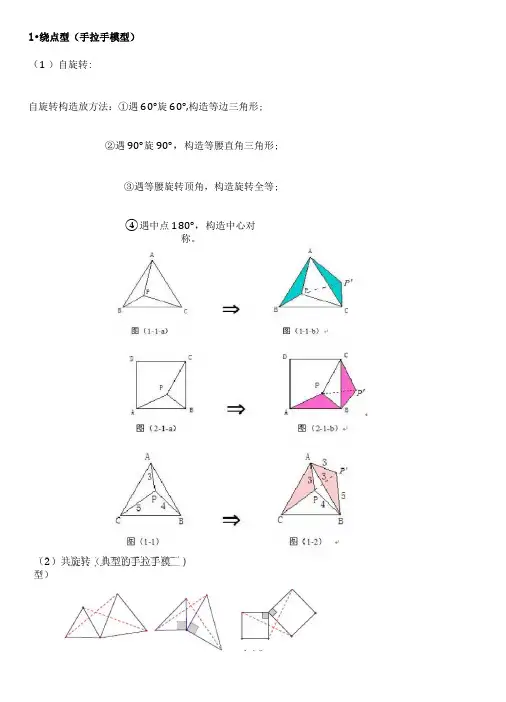
1•绕点型（手拉手模型）（1 ）自旋转:自旋转构造放方法：①遇60°旋60°,构造等边三角形;②遇90°旋90°，构造等腰直角三角形;③遇等腰旋转顶角，构造旋转全等;④遇中点180°，构造中心对称。

（2）共旋转（典型的手拉手模型）例1、在直线ABC的同一侧作两个等边三角形4ABD和aBCE,连接AE与CD,证明：(1)A ABE^A DBC(2)) AE=DC(3)AE与DC的夹角为60。

(4)A AGB^A DFB(5)A EGB^A CFB(6)BH 平分N AHC(7)GFllAC变式练习1、如果两个等边三角形4ABD和aBCE,连接AE与CD,证明：(1) A ABE^A DBC(2 ) AE=DC(3)AE与DC的夹角为60。

(4)AE与DC的交点设为H,BH平分N AHC变式练习2、如果两个等边三角形MBD和aBCE,连接AE与CD,证明：⑴MBE空4DBC(2)AE=DC(3)AE与DC的夹角为60。

(4)AE与DC的交点设为H,BH平分N AHC(1)如图1,点C是线段AB上一点，分别以AC, BC为边在AB的同侧作等边MCM和4BN，连接AN,BM .分别取BM , AN的中点E,F,连接CE,CF,EF .观察并猜想^CEF的形状，并说明理由.（2）若将（1）中的“以AC, BC为边作等边MCM和482 改为“以AC, BC为腰在AB的同侧作等腰4ACM和4BN，〃如图2，其他条件不变，那么（1）中的结论还成立吗？若成立，加以证明；若不成立，请说明理由.例4、例题讲解：1.已知^ABC为等边三角形，点D为直线BC上的一动点（点D不与B,C重合），以AD为边作菱形ADEF（按A,D,E,F逆时针排列），使NDAF=60°,连接CF.⑴如图1,当点D在边BC上时，求证：①BD=CF ,②AC=CF+CD.（2）如图2,当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；（3）如图3,当点D在边BC的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD之间存在的数量关系。