习题作业-第四章 并行算法的设计基础
- 格式:pdf
- 大小:121.53 KB
- 文档页数:2



第5章算法与复杂性习题一、选择题1. B2. D3. C4. A5. B6. B7. D8.B9.C 10.A11.A 12.C 13.A 14.A二、简答题1.什么是算法,算法的特性有哪些?答:“算法(Algorithm)是一组明确的、可以执行的步骤的有序集合,它在有限的时间内终止并产生结果”。
算法的特性有:(1) 有穷性(可终止性):一个算法必须在有限个操作步骤内以及合理的有限时间内执行完成。
(2) 确定性:算法中的每一个操作步骤都必须有明确的含义,不允许存在二义性。
(3) 有效性(可执行性):算法中描述的操作步骤都是可执行的,并能最终得到确定的结果。
(4) 输入及输出:一个算法应该有零个或多个输入数据、有1个或多个输出数据。
2.什么是算法的时间复杂度和空间复杂度,如何表示?答:时间复杂度是与求解问题规模、算法输入相关的函数,该函数表示算法运行所花费的时间。
记为,T(n),其中,n代表求解问题的规模。
算法的空间复杂度(Space complexity)度量算法的空间复杂性、即执行算法的程序在计算机中运行所占用空间的大小。
简单讲,空间复杂度也是与求解问题规模、算法输入相关的函数。
记为,S(n),其中,n代表求解问题的规模。
时间复杂度和空间复杂度同样,引入符号“O”来表示T(n)、S(n)与求解问题规模n之间的数量级关系。
3.用图示法表示语言处理的过程。
答:语言处理的过程如图所示:4.简述算法设计的策略。
答:作为实现计算机程序实现时解决问题的方法,算法研究的内容是解决问题的方法,而不是计算机程序的本身。
一个优秀的算法可以运行在比较慢的计算机上,但一个劣质的算法在一台性能很强的计算机上也不一定能满足应用的需要,因此,在计算机程序设计中,算法设计往往处于核心地位。
要想充分理解算法并有效地应用于实际问题,关键是对算法的分析。
通常可以利用实验对比分析、数学方法来分析算法。
实验对比分析很简单,两个算法相互比较,它们都能解决同一问题,在相同环境下,一般就会认为哪个算法的速度快这个算法性能更好。

1.并行算法:一些可同时执行的诸进程的集合,这些进程相互作用和相互协调。
2.并行与并发的关系:并行<并发并发是指两个或者多个事件在同一时间间隔内发生。
在单处理机系统中,每一时刻仅能有一道程序执行,宏观上多道程序在同时运行,微观上这些程序是分时交替执行。
3.并行与分布式的关系:网络;并行更注重性能,而分布式更注重透明共享。
4.并行与网格计算(普适计算)的关系:网格通过网络连接地理上分布的各类计算资源、存储资源、通信资源、软件资源、信息资源、知识资源等,形成对用户相对透明的虚拟的高性能计算环境,让人们透明地使用这些资源和功能。
它们与并行计算存在规模上的差异。
5.并行与云计算的关系:云计算以开放的标准和服务为基础,以互联网为中心,提供安全、快速、便捷的数据存储和网络计算服务,让互联网这片“云”上的各种计算机共同组成数个庞大的数据中心及计算中心。
云计算把计算及存储以服务的形式提供给互联网用户,用户所使用的数据、服务器、应用软件、开发平台等资源都来自互联网上的虚拟化计算中心,该数据中心负责对分布在互联网上的各种资源进行分配、负载的均衡、软件的部署、安全的控制等。
6.为什么要研究并行算法?(1)CPU的发展速度:Moore Law。
(2)“深蓝”计算机以3.5:2.5战胜卡斯帕罗夫。
(3)需求:快速(天气预报),提高计算精度,与理论、实验并重的科学方法(代替核武器实验)7.并行计算机分类1. SISD,Single Instruction Stream & Single Data Stream:特征:串行的和确定的。
指令系统: CISC, RISC2. SIMD,Single Instruction Stream & Multiple Data Stream:特征:同步的;确定的;适合于指令/操作级并行。
1)阵列处理机(资源重复);2)流水线处理机(时间重叠).3. MISD,Multiple Instruction Stream & Single Data Stream :4. MIMD,Multiple Instruction Stream & Multiple Data Stream共享存储MIMD,也称对称多处理机(SMP,Symmetry MultiProcessors),属于紧密耦合的多处理机系统适合于小粒度并行分布式共享存储MIMD,也称为非一致内存访问(NUMA, Non-Uniform Memory Access),属于松耦合的多处理机系统(共享虚拟存储技术),适合于中小粒度并行分布式存储MIMD1).大规模并行系统MPP (Massively Parallel Processing)CM-5、曙光1000、神州-Ⅱ巨型机可以最大限度地增加处理机的数量,但结点间需要依赖消息传递进行通信,适合于中小粒度并行2).群集系统Cluster特点:适合于粗粒度并行8.网络直径(network diameter):网络中最远的两台处理机间的距离,即处理机间通信所需要跨越的网络边的条数的最大值。

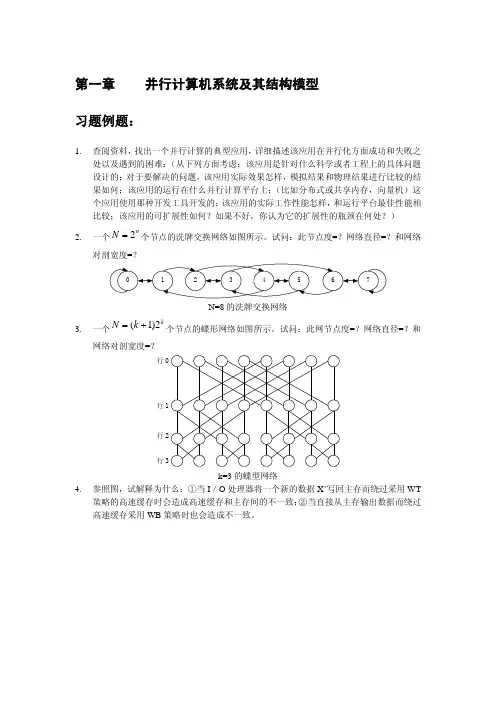



1 •并行算法:一些可同时执行的诸进程的集合,这些进程相互作用和相互协调。
2•并行与并发的关系:并行v并发并发是指两个或者多个事件在同一时间间隔内发生。
在单处理机系统中,每一时刻仅能有一道程序执行,宏观上多道程序在同时运行,微观上这些程序是分时交替执行。
3•并行与分布式的关系:网络;并行更注重性能,而分布式更注重透明共享。
4•并行与网格计算(普适计算)的关系:网格通过网络连接地理上分布的各类计算资源、存储资源、通信资源、软件资源、信息资源、知识资源等,形成对用户相对透明的虚拟的高性能计算环境,让人们透明地使用这些资源和功能。
它们•并行计算存在规模上的差显。
5•并行与云计算的关系:云计算以开放的标准和服务为基础,以互联网为中心,提供安全、快速、便捷的数据存储和网络计算服务,让互联网这片“云”上的各种计算机共同组成数个庞大的数据中心及计算屮心。
云计算把计算及存储以服务的形式提供给互联网用户,用户所使用的数据、服务器、应用软件、开发平台等资源都來自互联网上的虚拟化计算中心,该数据中心负责対分布在互联网上的各种资源进行分配、负载的均衡、软件的部署、安全的控制等。
6•为什么要研究并行算法?(1)CPU 的发展速度:Moore Law0(2)“深蓝”计算机以3.5:2.5战胜卡斯帕罗夫。
(3)需求:快速(天气预报),提高计算精度,与理论、实验并重的科学方法(代替核武器实验)7•并行计算机分类1.SISD,Single Instruction Stream & Single Data Stream:特征:串行的和确定的。
指令系统:CISC, RISC2.SIMD,Single Instruction Stream & Multiple Data Stream:特征:同步的;确定的;适合于指令/操作级并行。
1)阵列处理机(资源重复);2)流水线处理机(时间重叠).3・ MISD,Multiple Instruction Stream & Single Data Stream :4.MIMD,Multiple Instruction Stream & Multiple Data Stream共享存储MIMD,也称对称多处理机(SMP, Symmetry MultiProcessors),属于紧密耦合的多处理机系统适合于小粒度并行分布式共享存储MIMD,也称为非一致内存访问(NUMA, Non-Uniform Memory Access),属于松耦合的多处理机系统(共享虚拟存储技术),适合于屮小粒度并行分布式存储MIMD1).大规模并行系统MPP (Massively Parallel Processing)CM・5、曙光1000、神州・II巨型机可以最大限度地增加处理机的数量,但结点间需要依赖消息传递进行通信,适合于中小粒度并行2)・群集系统Cluster特点:适合于粗粒度并行8•网络直径(network diameter):网络中最远的两台处理机间的距离,即处理机间通信所需要跨越的网络边的条数的最人值。


并行程序设计导论第四章:并行算法的设计与分析并行算法是并行程序设计的核心,它直接影响着程序的性能和效率。
本章将介绍并行算法的设计方法,分析并行算法的性能,并探讨如何评估并行算法的效率。
一、并行算法的设计方法1.分治法分治法是一种常见的并行算法设计方法,它将问题分解成若干个子问题,分别解决后再合并结果。
分治法的关键在于子问题的划分和结果的合并。
在并行计算中,分治法可以充分利用多核处理器的并行性,提高程序的执行效率。
2.流水线法流水线法是一种将计算过程分解成多个阶段,每个阶段由不同的处理器并行执行的算法设计方法。
在流水线法中,数据在各个阶段之间流动,每个阶段只处理部分数据。
这种方法可以充分利用处理器的计算能力,提高程序的执行效率。
3.数据并行法数据并行法是一种将数据分解成多个部分,每个部分由不同的处理器并行处理的算法设计方法。
在数据并行法中,每个处理器处理相同的数据结构,执行相同的操作。
这种方法可以充分利用处理器的计算能力,提高程序的执行效率。
二、并行算法的性能分析1.时间复杂度时间复杂度是衡量算法性能的一个重要指标,它表示算法执行时间与输入规模之间的关系。
在并行算法中,时间复杂度通常表示为多个处理器执行时间的总和。
对于一个并行算法,我们希望其时间复杂度尽可能低,以提高程序的执行效率。
2.加速比加速比是衡量并行算法性能的另一个重要指标,它表示并行算法执行时间与最优串行算法执行时间的比值。
加速比越高,说明并行算法的性能越好。
在实际应用中,我们希望并行算法的加速比尽可能接近处理器的核心数量。
3.可扩展性可扩展性是衡量并行算法性能的另一个重要指标,它表示算法在增加处理器数量时的性能变化。
对于一个好的并行算法,我们希望其在增加处理器数量时,性能能够得到有效提升。
三、并行算法的效率评估1.性能模型性能模型是一种用于评估并行算法效率的工具,它将算法的性能与处理器数量、数据规模等因素联系起来。
通过性能模型,我们可以预测并行算法在不同条件下的性能表现,为算法设计和优化提供依据。
计算机学院研究生《并行计算》课程考试试题(2010级研究生,2011.1)1.(12分)定义图中节点u 和v 之间的距离为从u 到v 最短路径的长度。
已知一个d 维的超立方体,1)指定其中的一个源节点s ,问有多少个节点与s 的距离为i ,其中0≤i ≤d 。
证明你的结论。
2)证明如果在一个超立方体中节点u 与节点v 的距离为i ,则存在i !条从u 到v 的长度为i 的路径。
1)有id C 个节点与s 的距离为i 。
证明:由超立方体的性质知:一个d 维的超立方体的每个节点都可由d 位二进制来表示,则与某个节点的距离为i 的节点必定在这d 位二进制中有i 位与之不同,那么随机从d 位中选择i 位就有id C 种选择方式,即与s 的距离为i 得节点就有id C 个。
2)证明:由1)所述可知:节点u 与节点v 的距离为i 则分别表示u 、v 节点的二进制位数中有i 位是不同的。
设节点u 表示为:121D .........j j i j i d D D D D D +-+,节点v 表示为:''121D .........j j i j i dD D D D D +-+,则现在就是要求得从121D .........j j i j i d D D D D D +-+变换到''121D .........j j i j i d D D D D D +-+ 的途径有多少种。
那么利用组合理论知识可知共有*(1)*(2)*...*2*1i i i --即!i 中途径。
所以存在i !条从u 到v 的长度为i 的路径。
2.(18分)6个并行程序的执行时间,用I-VI 表示,在1-8个处理器上执行了测试。
下表表示了各程序达到的加速比。
对其中的每个程序,选出最适合描述其在16个处理器上性能的陈述。
a ) 在16个处理器上的加速比至少比8个处理器上的加速比高出40%。
b ) 由于程序中的串行程序比例很大,在16个处理器上的加速比不会比8个处理器上的加速比高出40%。
第5章算法与复杂性习题一、选择题1. B2. D3. C4. A5. B6. B7. D8.B9.C 10.A11.A 12.C 13.A 14.A二、简答题1.什么是算法,算法的特性有哪些?答:“算法(Algorithm)是一组明确的、可以执行的步骤的有序集合,它在有限的时间内终止并产生结果”。
算法的特性有:(1) 有穷性(可终止性):一个算法必须在有限个操作步骤内以及合理的有限时间内执行完成。
(2) 确定性:算法中的每一个操作步骤都必须有明确的含义,不允许存在二义性。
(3) 有效性(可执行性):算法中描述的操作步骤都是可执行的,并能最终得到确定的结果。
(4) 输入及输出:一个算法应该有零个或多个输入数据、有1个或多个输出数据。
2.什么是算法的时间复杂度和空间复杂度,如何表示?答:时间复杂度是与求解问题规模、算法输入相关的函数,该函数表示算法运行所花费的时间。
记为,T(n),其中,n代表求解问题的规模。
算法的空间复杂度(Space complexity)度量算法的空间复杂性、即执行算法的程序在计算机中运行所占用空间的大小。
简单讲,空间复杂度也是与求解问题规模、算法输入相关的函数。
记为,S(n),其中,n代表求解问题的规模。
时间复杂度和空间复杂度同样,引入符号“O”来表示T(n)、S(n)与求解问题规模n之间的数量级关系。
3.用图示法表示语言处理的过程。
答:语言处理的过程如图所示:4.简述算法设计的策略。
答:作为实现计算机程序实现时解决问题的方法,算法研究的内容是解决问题的方法,而不是计算机程序的本身。
一个优秀的算法可以运行在比较慢的计算机上,但一个劣质的算法在一台性能很强的计算机上也不一定能满足应用的需要,因此,在计算机程序设计中,算法设计往往处于核心地位。
要想充分理解算法并有效地应用于实际问题,关键是对算法的分析。
通常可以利用实验对比分析、数学方法来分析算法。
实验对比分析很简单,两个算法相互比较,它们都能解决同一问题,在相同环境下,一般就会认为哪个算法的速度快这个算法性能更好。
从简到繁,由浅入深地来探讨ustc并行程序设计作业这一主题。
ustc 是我国科学技术大学的简称,而并行程序设计则是计算机科学与技术领域的重要概念,结合起来,就意味着在我国科学技术大学开设的并行程序设计课程的学习和作业内容。
1. 概述ustc并行程序设计课程在学习并行程序设计课程时,学生将接触到并行计算的基本概念、原理和应用。
通过学习并行计算的理论知识,并且学习如何使用不同的技术和工具来实现高效的并行程序设计。
在完成作业时,学生将需要掌握并行算法的设计与分析,掌握多线程编程、并行程序调试和性能优化等技能。
2. ustc并行程序设计作业要求ustc并行程序设计作业旨在让学生深入理解并行程序设计的核心概念,并通过实际操作来加深对知识的掌握。
作业通常包括以下内容:- 设计并实现一个基于多线程或消息传递的并行算法。
- 分析并行算法的性能,包括加速比、效率和可伸缩性等指标。
- 通过实验对并行程序进行调优,提高程序的并行性能。
- 撰写并提交作业报告,总结并共享设计过程和实验结果。
3. 撰写ustc并行程序设计作业报告的步骤在完成ustc并行程序设计作业时,学生通常需要按照以下步骤进行:- 确定并行算法的设计目标和实验方案。
- 实现并行程序,并进行调试和测试。
- 对比并分析实验结果,评估并行算法的性能。
- 撰写作业报告,包括引言、并行算法设计、实验设置、实验结果和分析、总结和展望等内容。
4. 个人观点和理解在我看来,ustc并行程序设计作业是一个很好的锻炼学生实际能力的机会。
通过设计并实现并行算法,学生不仅可以加深对并行计算原理的理解,还可以掌握并行程序设计的实际技能。
通过对并行程序进行性能分析和优化,学生能够提升问题解决能力和创新思维。
撰写作业报告可以帮助学生总结实践经验,提升写作和表达能力。
总结回顾经过对ustc并行程序设计作业的探讨,我们深入了解了该课程的内容和作业要求,并对撰写作业报告的步骤有了清晰的认识。
第四章 并行算法的设计基础 习题例题:1. 试证明Brent 定理:令W (n)是某并行算法A 在运行时间T(n)内所执行的运算数量,则A 使用p 台处理器可在t(n)=O(W(n)/p+T(n))时间内执行完毕。
2. 假定P i (1≤i ≤n )开始时存有数据d i , 所谓累加求和指用1ijj d=∑来代替P i 中的原始值d i 。
算法 PRAM-EREW 上累加求和算法 输入: P i 中保存有d i , l ≤ i ≤ n 输出: P i 中的内容为ijj ld=∑beginfor j = 0 to logn – 1 do for i = 2j + 1 to n par-do(i) P i = d i-(2^i) (ii) d i = d i + d i-(2^j) endfor endfor end(1)试用n=8为例,按照上述算法逐步计算出累加和。
(2)分析算法时间复杂度。
3. 在APRAM 模型上设计算法时,应尽量使各处理器内的局部计算时间和读写时间大致与同步时间B 相当。
当在APRAM 上计算M 个数的和时,可以借用B 叉树求和的办法。
假定有j 个处理器计算n 个数的和,此时每个处理器上分配n/p 个数,各处理器先求出自身的局和;然后从共享存储器中读取它的B 个孩子的局和,累加后置入指定的共享存储单元SM 中;最后根处理器所计算的和即为全和。
算法如下:算法 APRAM 上求和算法 输入: n 个待求和的数输出: 总和在共享存储单元SM 中 Begin(1) 各处理器求n/p 个数的局和,并将其写入SM 中 (2) Barrier(3) for k = [ log B ( p(B – 1) + 1) ] – 2 downto 0 do3.1 for all P i , 0 ≤ i ≤ p – 1,doif P i 在第k 级 thenP i 计算其B 各孩子的局和并与其自身局和相加,然后将结果写入SM 中 endifend for3.2barrierend forEnd(1)试用APRAM模型之参数,写出算法的时间复杂度函数表达式。
并行计算的参考题目1、讨论某一种算法的可扩放性时,一般指什么?88答:讨论某一种算法的可扩放性时,实际上是指该算法针对某一特定机器结构的可扩放性2、使用“Do in Parallel”语句时,表示的是什么含义105答:表示算法的若干步要并行执行3、并行计算机的存储访问类型有哪几种?26答:存储访问类型有:UMA(均匀存储访问)、NUMA(非均匀存储访问)、COMA(全高速缓存存储访问)、CC-NUMA(高速缓存一致性非均匀存储访问)、NORMAl(非远程存储访问)4、什么是同步?它有什么作用?如何实现?107答:同步是在时间上强使各执行进程在某一点必须相互等待。
作用:确保个处理器的正确工作顺序以及对共享可写数据的正确访问(互斥访问)。
实现方法:用软件、硬件和固件的方法实现。
5 在并行加速比的计算中,常用的三种加速比定律分别是哪三种?(P83)答:常用的三种加速比定律分别是:适用于固定计算负载的Amdahl定律,适用于可扩放问题的Gustafson定律和受限于存储器的Sun和Ni定律。
6、试比较Amdahl定律、Gustafson定律、Sun和Ni定律三种加速定律的应用场合。
83 答:Amdahl定律适用于固定计算负载的问题Gustafson定律适用于可扩放性问题Sun和Ni定律适用于受限于存储器的问题。
7.并行算法的基本设计技术有哪些?它们的基本思想是什么?139答:(1)基本技术有:划分设计技术(又分为均匀划分技术、方根划分技术、对数划分技术和功能划分技术)、分治设计技术、平衡树设计技术、倍增设计技术、流水线设计技术等。
(2)基本思想分别如下:a.划分设计技术:(P139) 将一原始问题分成若干部分,然后各部分由相应的处理器同时执行。
b.分治设计技术:(P144)将一个大二复杂的问题分解成若干特性相同的子问题分而治之。
若所得的子问题规模仍嫌过大,可反复使用分治策略,直至很容易求解诸子问题为止。
第一章绪论什么是并行计算机答:简单地讲,并行计算机就是由多个处理单元组成的计算机系统,这些处理单元相互通信和协作,能快速高效求解大型的复杂的问题。
简述Flynn分类法:答:根据指令流和数据流的多重性将计算机分为:1)单指令单数据流SISD2)单指令多数据流SIMD3)多指令单数据流MISD4)多指令多数据流MIMD简述当代的并行机系统答:当代并行机系统主要有:1)并行向量机(PVP)2)对称多处理机(SMP)3)大规模并行处理机(MPP)4)分布式共享存储(DSM)处理机5)工作站机群(COW)为什么需要并行计算机答:1)加快计算速度2)提高计算精度3)满足快速时效要求4)进行无法替代的模拟计算简述处理器并行度的发展趋势答:1)位级并行2)指令级并行3)线程级并行简述SIMD阵列机的特点答:1)它是使用资源重复的方法来开拓计算问题空间的并行性。
2)所有的处理单元(PE)必须是同步的。
21m 3)阵列机的研究必须与并行算法紧密结合,这样才能提高效率。
4)阵列机是一种专用的计算机,用于处理一些专门的问题。
简述多计算机系统的演变答:分为三个阶段:1)1983-1987年为第一代,代表机器有:Ipsc/1、Ameteks/14等。
2)1988-1992年为第二代,代表机器有:Paragon 、Intel delta 等。
3)1993-1997年为第三代,代表机器有:MIT 的J-machine 。
简述并行计算机的访存模型答:1)均匀存储访问模型(UMA )2)非均匀存储访问模型(NUMA )3)全高速缓存存储访问模型(COMA )4)高速缓存一致性非均匀访问模型(CC-NUMA )简述均匀存储访问模型的特点答:1)物理存储器被所有处理器均匀共享。
2)所有处理器访问任何存储字的时间相同。
3)每台处理器可带私有高速缓存。
4)外围设备也可以一定的形式共享。
简述非均匀存储访问模型的特点答:1)被共享的存储器在物理上分布在所有的处理器中,其所有的本地存储器的集合构成了全局的地址空间。
第4章 并行算法的设计基础
习题例题:
1.试证明Brent 定理:令W (n)是某并行算法A 在运行时间T(n)内所执行的运算数量,则A 使用p 台处理器可在t(n)=O(W(n)/p+T(n))时间内执行完毕。
2.假定P i (1≤i ≤n )开始时存有数据d i , 所谓累加求和指用 MERGEFORMAT 1i j j d =¥来代替P i 中的原始值d i 。
算法 PRAM-EREW 上累加求和算法
输入: P i 中保存有d i , l ≤ i ≤ n
输出: P i 中的内容为i j
j l d
=¥begin for j = 0 to logn – 1 do for i = 2j + 1 to n par-do (i) P i = d i-(2^i)(ii) d i = d i + d i-(2^j)endfor endfor end (1)试用n=8为例,按照上述算法逐步计算出累加和。
(2)分析算法时间复杂度。
3.在APRAM 模型上设计算法时,应尽量使各处理器内的局部计算时间和读写时间大致与同步时间B 相当。
当在APRAM 上计算M 个数的和时,可以借用B 叉树求和的办法。
假定有j 个处理器计算n 个数的和,此时每个处理器上分配n/p 个数,各处理器先求出自身的局和;然后从共享存储器中读取它的B 个孩子的局和,累加后置入指定的共享存储单元SM 中;最后根处理器所计算的和即为全和。
算法如下:算法 APRAM 上求和算法
输入: n 个待求和的数
输出: 总和在共享存储单元SM 中
Begin
(1)各处理器求n/p 个数的局和,并将其写入SM 中
(2)Barrier
(3)for k = [ log B ( p(B – 1) + 1) ] – 2 downto 0 do
3.1for all P i , 0 ≤ i ≤ p – 1,do
if P i 在第k 级 then。