大物2期末复习

大物2知识点总结大气物理学是研究地球大气现象及其规律的一门科学。

这门学科涉及到大气的结构、运动、热量传递、湿气平衡以及各种气象现象的生成原理和发展规律。

在大气物理学的学习中，我们需要掌握许多基础知识和理论，接下来将对大气物理学的一些重要知识点进行总结。

1. 大气结构大气结构是大气科学的基础。

大气分为对流层、平流层、中间层、热层和外大气层。

对流层是最接近地球表面的一层大气，海拔范围为0-15公里;平流层的海拔范围为15-50公里;中间层为50-80公里;热层为80-500公里;外大气层则超过500公里。

对流层与平流层的隔离位置在对流层顶上的对流层顶温的转折上升压力高度，称为对流层顶，又称对流层隔离位置。

平流层对流层细微隔离位置在平流层上的直接上升压力高度，称为平流层顶。

2. 气压和气压分布气压是大气分布状态的一项基本参数。

气压是指大气对于单位面积的压力。

气压是一个变量参数，一般情况下以帕斯卡（Pa）为单位。

在大气静力学中，我们还需要了解气压的垂直分布规律，即随着海拔的升高，气压是如何变化的。

气压的垂直分布规律不仅与地球的地理位置有关，还与气温、密度、重力加速度等因素有关。

3. 温度和温度分布温度是大气中分子活动强烈程度的一种度量，是表示气体热量的物理量。

在大气物理学中，我们需要了解大气温度的测量单位和方法，以及大气的温度分布规律。

温度分布与地表的纬度、季节、海拔高度等因素密切相关，不同的地区和时间，大气的温度分布规律是不同的。

4. 湿度和湿度分布湿度是大气中水分子含量的一个量度，也是一个重要的气象要素。

了解大气湿度的测量方法，以及大气湿度的分布规律对于预测气象变化、计算气象条件等方面具有重要意义。

湿度在大气中的分布是随着时间和地域的变化而变化的，需要认真研究。

5. 大气稳定性大气稳定性是指大气在受到扰动后能够恢复到平衡状态的能力。

了解大气稳定性对于气象灾害预警、飞行气象等有重要意义。

在大气物理学的学习中，我们需要掌握大气稳定性的测定方法，以及大气稳定性与地表气温、湿度等因素之间的关系。

大物期末考试题及答案一、选择题（每题2分，共20分）1. 根据牛顿第二定律，物体的加速度与作用力成正比，与物体的质量成反比。

以下哪个选项正确描述了这一定律？A. F = maB. F = ma^2C. F = m/aD. F = 1/(ma)答案：A2. 一个物体从静止开始自由下落，其下落距离与时间的关系为：A. s = gtB. s = 1/2 gtC. s = 1/2 g(t^2)D. s = gt^2答案：C3. 根据能量守恒定律，以下哪个选项正确描述了能量守恒？A. 能量可以被创造或消灭B. 能量守恒定律只适用于封闭系统C. 能量可以在不同形式之间转换，但总量保持不变D. 能量守恒定律不适用于微观粒子答案：C4. 以下哪个选项正确描述了动量守恒定律？A. 动量守恒定律只适用于碰撞过程B. 动量守恒定律适用于所有物理过程C. 动量守恒定律只适用于没有外力作用的系统D. 动量守恒定律只适用于宏观物体答案：C5. 以下哪个选项正确描述了波的干涉条件？A. 波源必须相同B. 波源必须不同C. 波的频率必须相同D. 波的振幅必须相同答案：C6. 以下哪个选项正确描述了光的折射现象？A. 光线在不同介质中传播速度会改变B. 光线在不同介质中传播方向不变C. 光线在不同介质中传播速度不变D. 光线在不同介质中传播方向总是改变答案：A7. 根据热力学第一定律，以下哪个选项正确描述了能量的转换？A. ΔE = Q + WB. ΔE = Q - WC. ΔE = Q / WD. ΔE = W / Q答案：B8. 以下哪个选项正确描述了理想气体的状态方程？A. PV = nRTB. PV = nT/RC. PV = RTD. PV = nR答案：A9. 以下哪个选项正确描述了电磁感应现象？A. 变化的磁场可以产生电流B. 电流可以产生磁场C. 磁场可以产生电流D. 电流可以产生变化的磁场答案：A10. 以下哪个选项正确描述了相对论中时间膨胀现象？A. 运动的物体在运动方向上的长度会变长B. 运动的物体在运动方向上的时间会变慢C. 运动的物体在垂直于运动方向上的长度会变短D. 运动的物体在垂直于运动方向上的时间会变慢答案：B二、填空题（每空1分，共10分）11. 牛顿第一定律又称为________定律。

中国⽯油⼤学华东2012年期末⼤物2-1试卷2011—2012学年第⼆学期《⼤学物理（2-1）》期末试卷⼀、选择题1、（本题3分）两辆⼩车A 、B ，可在光滑平直轨道上运动．第⼀次实验，B 静⽌，A 以0.5 m/s 的速率向右与B 碰撞，其结果A 以 0.1 m/s 的速率弹回，B 以0.3 m/s 的速率向右运动；第⼆次实验，B 仍静⽌，A 装上1 kg 的物体后仍以 0.5 m/s 的速率与B 碰撞，结果A 静⽌，B 以0.5 m/s 的速率向右运动，如图．则A 和B 的质量分别为(A) m A = 2 kg m B = 1 kg ． (B) m A = 1 kg m B = 2 kg ．(C) m A = 3 kg m B = 4 kg ． (D) m A = 4 kg m B = 3 kg ．［］2、(本题3分）有⼀劲度系数为k 的轻弹簧，原长为l 0，将它吊在天花板上．当它下端挂⼀托盘平衡时，其长度变为l 1．然后在托盘中放⼀重物，弹簧长度变为l 2，则由l 1伸长⾄l 2的过程中，弹性⼒所作的功为(A)-21d l l x kx ． (B)21d l l x kx ．(C)---0201d l l l l x kx ． (D)--0201d l l l l x kx ．［］3、（本题3分）⼀圆盘绕过盘⼼且与盘⾯垂直的光滑固定轴O 以⾓速度ω按图⽰⽅向转动.若如图所⽰的情况那样，将两个⼤⼩相等⽅向相反但不在同⼀条直线的⼒F 沿盘⾯同时作⽤到圆盘上，则圆盘的⾓速度ω(A) 必然增⼤． (B) 必然减少． (C) 不会改变． (D) 如何变化，不能确定．［］4、（本题3分）在狭义相对论中，下列说法中哪些是正确的？(1) ⼀切运动物体相对于观察者的速度都不能⼤于真空中的光速．(2) 质量、长度、时间的测量结果都是随物体与观察者的相对运动状态⽽改变的．(3) 在⼀惯性系中发⽣于同⼀时刻，不同地点的两个事件在其他⼀切惯性系中也是同时发⽣的．(4)惯性系中的观察者观察⼀个与他作匀速相对运动的时钟时，会看到这时钟⽐与他相对静⽌的相同的时钟⾛得慢些．(A) (1)，(3)，(4)．(B) (1)，(2)，(4)．(C) (1)，(2)，(3)．(D) (2)，(3)，(4)．［］5、（本题3分）某核电站年发电量为100亿度，它等于36×1015 J的能量，如果这是由核材料的全部静⽌能转化产⽣的，则需要消耗的核材料的质量为(A) 0.4 kg．(B) 0.8 kg．(C) (1/12)×107 kg．(D) 12×107 kg．［］6、（本题3分）已知⼀定量的某种理想⽓体，在温度为T1与T2时的分⼦最概然速率分别为v p1和v p2，分⼦速率分布函数的最⼤值分别为f(v p1)和f(v p2)．若T1>T2，则(A) v p1 > v p2， f (v p1)> f (v p2)．(B) v p1 > v p2， f (v p1)< f (v p2)．(C) v p1 < v p2， f (v p1)> f (v p2)．(D) v p1 < v p2， f (v p1)< f (v p2)．［］7、（本题3分）关于热功转换和热量传递过程，有下⾯⼀些叙述：(1) 功可以完全变为热量，⽽热量不能完全变为功；(2) ⼀切热机的效率都只能够⼩于1；(3) 热量不能从低温物体向⾼温物体传递；(4) 热量从⾼温物体向低温物体传递是不可逆的．以上这些叙述（A）只有(2)、(4)正确．（B）只有(2)、(3) 、(4)正确．（C）只有(1)、(3) 、(4)正确．（D）全部正确．［］8、（本题3分）频率为 100 Hz ，传播速度为300 m/s 的平⾯简谐波，波线上距离⼩于波长的两点振动的相位差为π31，则此两点相距（A ） 2.86 m ．（B) 2.19 m ．（C ） 0.5 m ．（D) 0.25 m ．［］ 9、（本题3分）如图，S 1、S 2是两个相⼲光源，它们到P 点的距离分别为r 1和r 2．路径S 1P 垂直穿过⼀块厚度为t 1，折射率为n 1的介质板，路径S 2P 垂直穿过厚度为t 2，折射率为n 2的另⼀介质板，其余部分可看作真空，这两条路径的光程差等于 (A) )() (111222t n r t n r +-+．(B) ])1([])1([211222t n r t n r -+--+． (C) )()(111222t n r t n r ---． (D) 1122t n t n -．［］10、（本题3分）⼀束平⾏单⾊光垂直⼊射在光栅上，当光栅常数（a+b ）为下列哪种情况时（a 代表每条缝的宽度），k ＝3、6、9等级次的主极⼤均不出现？（A ） a+b ＝2a ．（B ） a+b ＝3a ．（C ） a+b ＝4a ．（D ） a+b ＝6a ．［］⼆、简单计算与问答题（共6⼩题，每⼩题5分，共30分） 1、（本题5分）⼀质点作直线运动，其x- t 曲线如图所⽰，质点的运动可分为OA 、AB 、BC 和CD 四个区间，AB 为平⾏于t 轴的直线，CD 为直线，试问每⼀区间速度、加速度分别是正值、负值，还是零？PS 1S 2 r 1n 1n 2t 2r 2t 1x2、（本题5分）⼀车轮可绕通过轮⼼O 且与轮⾯垂直的⽔平光滑固定轴，在竖直⾯内转动，轮的质量为M ，可以认为均匀分布在半径为R 的圆周上，绕O 轴的转动惯量J ＝MR 2．车轮原来静⽌，⼀质量为m 的⼦弹，以速度v 0沿与⽔平⽅向成α⾓度射中轮⼼O 正上⽅的轮缘A 处，并留在A 处，如图所⽰．设⼦弹与轮撞击时间极短．问：(1) 以车轮、⼦弹为研究系统，撞击前后系统的动量是否守恒？为什么？动能是否守恒？为什么？⾓动量是否守恒？为什么？ (2) ⼦弹和轮开始⼀起运动时，轮的⾓速度是多少？3、（本题5分）经典⼒学的相对性原理与狭义相对论的相对性原理有何不同？4、（本题5分）试从分⼦动理论的观点解释：为什么当⽓体的温度升⾼时，只要适当地增⼤容器的容积就可以使⽓体的压强保持不变？5、（本题5分）⼀质点作简谐振动，其振动⽅程为x = 0.24)3121cos(π+πt (m)，试⽤旋转⽮量法求出质点由初始状态（t = 0的状态）运动到x = -0.12 m ，v < 0的状态所需最短时间?t ．6、（本题5分）让⼊射的平⾯偏振光依次通过偏振⽚P 1和P 2．P 1和P 2的偏振化⽅向与原⼊射光光⽮量振动⽅向的夹⾓分别是α和β．欲使最后透射光振动⽅向与原⼊射光振动⽅向互相垂直，并且透射光有最⼤的光强，问α和β各应满⾜什么条件？三．计算题（共4⼩题，每⼩题10分，共40分） 1、（本题10分）两个质量分别为m 1和m 2的⽊块A 和B ，⽤⼀个质量忽略不计、劲度系数为k 的弹簧联接起来，放置在光滑⽔平⾯上，使A 紧靠墙壁，如图所⽰．⽤⼒推⽊块B 使弹簧压缩x 0，然后释放．已知m 1 = m ，m 2 = 3m ，求： (1) 释放后，A 、B 两⽊块速度相等时的瞬时速度的⼤⼩；(2) 释放后，弹簧的最⼤伸长量．2、（本题10分）1 mol 双原⼦分⼦理想⽓体从状态A (p 1,V 1)沿p -V 图所⽰直线变化到状态B (p 2,V 2)，试求：（1）⽓体的内能增量．（2）⽓体对外界所作的功．（3）⽓体吸收的热量．（4）此过程的摩尔热容．3、（本题10分）已知⼀平⾯简谐波的表达式为 )24(cos x t A y +π= (SI)． (1) 求该波的波长λ，频率ν和波速u 的值；(2) 写出t = 4.2 s 时刻各波峰位置的坐标表达式，并求出此时离坐标原点最近的那个波峰的位置；(3) 求t = 4.2 s 时离坐标原点最近的那个波峰通过坐标原点的时刻t ．4、（本题10分）（1）单缝夫琅⽲费衍射实验中，垂直⼊射的光含有两种波长，λ 1 = 400 nm ，λ2 = 760 nm (1 nm =10 -9 m)．已知单缝宽度a = 1.0×10 -2 cm ，透镜焦距f = 50 cm ．求两种光第⼀级衍射明纹中⼼之间的距离．（2）⽤光栅常数-3101.0?=d cm 的光栅替换单缝，其他条件和上⼀问相同，求两种光第⼀级主极⼤之间的距离．p 1p p 12答案⼀、1、B 2、C 3、A 4、B 5、A 6、B 7、A 8、C 9、B 10、B ⼆、1、1、答： OA 区间：v > 0 , a < 0 2分AB 区间：v = 0 , a = 0 1分 BC 区间：v > 0 , a > 0 1分 CD 区间：v > 0 , a = 0 1分2、答：(1) 系统动量不守恒．因为在轴O 处受到外⼒作⽤，合外⼒不为零． 1分动能不守恒．因为是完全⾮弹性碰撞(能量损失转化为形变势能和热运动能)．1分⾓动量守恒．因为合外⼒矩为零． 1分 (2) 由⾓动量守恒 m v 0R cos α = (M + m )R 2ω∴()Rm M m +=αωcos 0v 2分3、答：经典的⼒学相对性原理是指对不同的惯性系，⽜顿定律和其它⼒学定律的形式都是相同的． 2分狭义相对论的相对性原理指出：在⼀切惯性系中，所有物理定律的形式都是相同的，即指出相对性原理不仅适⽤于⼒学现象，⽽且适⽤于⼀切物理现象。

4.2.5 MV 232X 10 3X 1002:.AT =iR质量为100g 的水蒸汽，温度从积不变的情况下加热，需热量= ？ o二 7.7K5x831120 C 升高到150 C,若视水蒸汽为理想气体，体Qv = ?在压强不变的情况下加热，需热量 Qp解：1（）（加4的斥尔数 m 100 50 v=—=——=—mol Jtf IS 9喝。

是多原子分子：：二6Q*3*8.31*30 = 4155/4皆 v93.50Q p = vC p M = y * 4* 8.31*30 = 5540J•定量的单原子理想气体在等压膨胀过程中对外作的功A/Q = 2/5，若为双原子理想气体，则比值解：A 与吸收的热量 Q 之比A/Q = 27 oAE =皿任—八；—2单原子分子：i = 3；CP ，+ 2双原子分子：1=5由刚性双原子分子组成的理想气体，温度为 T 时，贝U 1mol 该理想气体的内能为？？？5/2RTiff解：一1.储有氧气的容器以速度 V = 100m • s-1运动，假设该容器突然停止，全部定向运动 的动能都变为气体分子热运动的动能，问容器中的氧气的温度将会上升多少？ 解，氧气:Z = 5M2 25. 原在标准状况下的 2mol 的氢气，经历一过程吸热 500J,问：(1)若该过程是等容过程，气体对外作功多少？末态压强 P =? (2)若该过程是等压过强，末态温度 T =?, 气体对外作功多少？解：初态：标准状况^=1.013*105?«7；=2731氢气：i=5A _QAT =^-=1000=12K(1)等容过程人末态温度 T r = T 0+AT=285K末态压强 P 二 F 0 T=1.01 3* 105*285= 1.057* 105PaT 。

273等压过程A=.RT Q p J 2R Tp p2T p二 T 0：T =281.6K6. 2mol 多原子理想气体，从状态(P0 ,V0 ,T0)o 开始作准静态绝热 膨胀，体积增大到原体积的3倍，则膨胀后气体压强P= 解：多原子分子：i=6i +24比热比： 二」i 3绝热过程：PV 二P0V0V0 7所以：P =P0(一)V2 2A Q *500 =142.9Ji 2 72Q♦ (i 2)R2* 7*8.31(2)7. 在高温热源为127C，低温热源为27C之间工作的卡诺热机，对外做净功8000JL维持低温热源温度不变，提高高温热源温度, 使其对外做净功100004若这两次循环该热机都工作在相同的两条绝热线之间，试求：(1) 后一个卡诺循环的效率；(2) 后一个卡诺循环的高温热源的温度解：(1)T!=127o C=400K;T2=27°C=300K=1-& =25%T iQ, -32000JQ2= Q, - A = 24000JT2二T2= 300K Q2 = Q2= 2 4 0 J 0A =10000J Q, = A2Q2二24000J=A /Q2=10000/34000 二29.4%(2)又十半丁1=严=器=425K=152O C8. 一卡诺热机在每次循环过程中都要从温度为400K的高温热源吸热418J,向低温热源放热334・4J,低温热源温度为？320K解：由得a人L二鈿=320所以(3)气体吸收的热量 。

练习一 静电场中的导体三、计算题1. 已知某静电场在xy 平面内的电势函数为U =Cx/(x 2+y 2)3/2,其中C 为常数.求(1)x 轴上任意一点,(2)y 轴上任意一点电场强度的大小和方向.解：. E x =-∂U/∂x=-C [1/(x 2+y 2)3/2+x (-3/2)2x /(x 2+y 2)5/2]= (2x 2-y 2)C /(x 2+y 2)5/2E y =-∂U/∂y=-Cx (-3/2)2y /(x 2+y 2)5/2=3Cxy /(x 2+y 2)5/2x 轴上点(y =0) E x =2Cx 2/x 5=2C /x 3 E y =0E =2C i /x 3 y 轴上点(x =0) E x =-Cy 2/y 5=-C /y 3 E y =0E =-C i /y 32．如图,一导体球壳A (内外半径分别为R 2,R 3),同心地罩在一接地导体球B (半径为R 1)上,今给A 球带负电-Q , 求B 球所带电荷Q B 及的A 球的电势U A .静电场中的导体答案解： 2. B 球接地,有 U B =U ∞=0, U A =U BAU A =(-Q+Q B )/(4πε0R 3)U BA =[Q B /(4πε0)](1/R 2-1/R 1)得 Q B =QR 1R 2/( R 1R 2+ R 2R 3- R 1R 3)U A =[Q/(4πε0R 3)][-1+R 1R 2/(R 1R 2+R 2R 3-R 1R 3)]=-Q (R 2-R 1)/[4πε0(R 1R 2+R 2R 3-R 1R 3)]练习二 静电场中的电介质三、计算题1. 如图6.6所示,面积均为S 2的两金属平板A ,B 平行对称放置,间距为d =1mm,今给A , B 两板分别带电 Q 1×10－9C, Q 2×10－9C.忽略边缘效应,求：(1) 两板共四个外表的面电荷密度 σ1, σ2, σ3, σ4;(2) 两板间的电势差V =U A －U B .解：1. 在A 板体内取一点A , B 板体内取一点B ,它们的电场强度是四-Q图5.6Q2σ 2 σ 4个外表的电荷产生的,应为零,有E A =σ1/(2ε0)-σ2/(2ε0)-σ3/(2ε0)-σ4/(2ε0)=0E A =σ1/(2ε0)+σ2/(2ε0)+σ3/(2ε0)-σ4/(2ε0)=0而 S (σ1+σ2)=Q 1 S (σ3+σ4)=Q 2 有 σ1-σ2-σ3-σ4=0σ1+σ2+σ3-σ4=0 σ1+σ2=Q 1/S σ3+σ4=Q 2/S解得 σ1=σ4=(Q 1+Q 2)/(2S ⨯10-8C/m 2σ2=-σ3=(Q 1-Q 2)/(2S ⨯10-8C/m 2两板间的场强 E=σ2/ε0=(Q 1-Q 2)/(2ε0S )V=U A －U B ⎰⋅=BAl E d=Ed=(Q 1-Q 2)d /(2ε0S )=1000V四、证明题1. 如图所示，置于静电场中的一个导体，在静电平衡后，导体外表出现正、负感应电荷.试用静电场的环路定理证明，图中从导体上的正感应电荷出发，终止于同一导体上的负感应电荷的电场线不能存在.解：1.ACB 作环路ACBA ,导体内直线BA 的场强为零,ACB 的电场与环路同向于是有=⋅⎰l E d l+⋅⎰ACBl E d ⎰⋅AB l E d 2=⎰⋅ACBl E d ≠0与静电场的环路定理=⋅⎰l E d l0相违背,故在同一导体上不存在从正感应电荷出发，终止于负感应电荷的电场线.练习三 电容 静电场的能量三、计算题1. 半径为R 1的导体球带电Q ,球外一层半径为R 2相对电容率为εr 的同心均匀介质球壳,其余全部空间为空气.如图所示.求:(1)离球心距离为r 1(r 1<R 1), r 2(R 1<r 1<R 2), r 3(r 1>R 2)处的D 和E ；(2)离球心r 1, r 2, r 3,处的U ；(3)介质球壳内外外表的极化电荷. 解：1. (1)因此电荷与介质均为球对称,电场也球对称,过场点作与金属球同心的球形高斯面,有iSq0d ∑=⋅⎰S D4πr 2D=∑q 0i当r=5cm <R 1, ∑q 0i =0得 D 1=0, E 1=0 当r=15cm(R 1<r <R 1+d ) ∑q 0i =Q=1.0×10-8C 得 D 2=Q /(4πr 2)×10-8C/m 2E 2=Q /(4πε0εr r 2)=7.99×103N/C 当r=25cm(r >R 1+d ) ∑q 0i =Q=1.0×10-8C 得 D 3=Q /(4πr 2)=1.27×10-8C/m 2 E 3=Q /(4πε0r 2)=1.44×104N/C D 和E 的方向沿径向. (2) 当r=5cm <R 1时 U 1=⎰∞⋅rl E d⎰=R rr E d 1⎰++dR Rr E d 2⎰∞++dR r E d 3=Q/(4πε0εr R )-Q/[4πε0εr (R+d )]+Q/[4πε0(R+d )]=540V当r=15cm <R 1时U 2=⎰∞⋅rl E d ⎰+=dR rr E d 2⎰∞++dR r E d 3=Q/(4πε0εr r )-Q/[4πε0εr (R+d )]+Q/[4πε0(R+d )]=480V当r=25cm <R 1时U 3=⎰∞⋅rl E d ⎰∞=rr E d 3=Q/(4πε0r )=360V(3)在介质的内外外表存在极化电荷,P e =ε0χE=ε0(εr -1)E σ'= P e ·nr=R 处, 介质外表法线指向球心σ'=P e ·n =P e cos π=-ε0(εr -1)Eq '=σ'S =-ε0(εr -1) [Q /(4πε0εr R 2)]4πR 2=-(εr -1)Q /εr =-0.8×10-8Cr=R+d 处, 介质外表法线向外σ'=P e ·n =P e cos0=ε0(εr -1)Eq '=σ'S =ε0(εr -1)[Q /(4πε0εr (R+d )2]4π(R +d )2=(εr -1)Q /εr =0.8×10-8C2.两个相距很远可看作孤立的导体球，半径均为10cm ，分别充电至200V 和400V ，然后用一根细导线连接两球，使之到达等电势. 计算变为等势体的过程中，静电力所作的功. 解;2.球形电容器 C =4πε0RQ 1=C 1V 1= 4πε0RV 1 Q 2=C 2V 2= 4πε0RV 2W 0=C 1V 12/2+C 2V 22/2=2πε0R (V 12+V 22)两导体相连后 C =C 1+C 2=8πε0RQ=Q 1+Q 2= C 1V 1+C 2V 2=4πε0R (V 1+V 2)W=Q 2/(2C )= [4πε0R (V 1+V 2)]2/(16πε0R )=πε0R (V 1+V 2)2静电力作功 A=W 0-W=2πε0R (V 12+V 22)-πε0R (V 1+V 2)2=πε0R (V 1-V 2)2=1.11×10-7J练习六 磁感应强度 毕奥—萨伐尔定律三、计算题1. 如图所示, 一宽为2a 的无限长导体薄片, 沿长度方向的电流I 在导体薄片上均匀分布. 求中心轴线OO '上方距导体薄片为a 的磁感强度.解：1.取宽为d x 的无限长电流元d I=I d x/(2a ) d B=μ0d I/(2πr )=μ0I d x/(4πar )d B x =d B cos α=[μ0I d x/(4πar )](a/r ) =μ0I d x/(4πr 2)= μ0I d x/[4π(x 2+a 2)] d B y =d B sin α= μ0Ix d x/[4πa (x 2+a 2)]()⎰⎰-+==aax x a x xI B B 2204d d πμ=[μ0I/(4π)](1/a )arctan(x/a )a a-=μ0I/(8a )()⎰⎰-+==aay y ax a xIx B B 2204d d πμ=[μ0I/(8πa )]ln(x 2+a 2)aa-=02. 如图所示，半径为R 的木球上绕有密集的细导线，线圈平面彼此平行，且以单层线圈覆盖住半个球面. 设线圈的总匝数为N ，通过线圈的电流为I . 求球心O 的磁感强度.解：2. 取宽为d L 细圆环电流, d I=I d N=I [N/(πR/2)]R d θ =(2IN/π)d θd B=μ0d Ir 2/[2(r 2+x 2)3/2]r=R sin θ x=R cos θd B=μ0NI sin 2θ d θ /(πR )⎰⎰==πππθθμ220d sin d RNI B B=μ0NI/(4R )xr练习七 毕奥—萨伐尔定律(续) 磁场的高斯定理三、计算题S 1和S 2的两个矩形回路, 回路旋转方向如图所示, 两个回路与长直载流导线在同一平面内, 且矩形回路的一边与长直载流导线平行. 求通过两矩形回路的磁通量及通过S 1回路的磁通量与通过S 2回路的磁通量之比.解： 1.取窄条面元d S =b d r , 面元上磁场的大小为 B =μ0I /(2πr ),Φ1=⎰-=aabIbdr r I 2002ln 2cos 2πμππμ Φ2=⎰-=aabI bdr r I 42002ln 2cos 2πμππμ Φ1/Φ2=12. 半径为R 的薄圆盘均匀带电，总电量为Q . 令此盘绕通过盘心且垂直盘面的轴线作匀速转动，角速度为ω，求轴线上距盘心x 处的磁感强度的大小和旋转圆盘的磁矩.解;2. 在圆盘上取细圆环电荷元d Q =σ2πr d r , [σ=Q /(πR 2) ],等效电流元为d I =d Q /T =σ2πr d r/(2π/ω)=σωr d r(1)求磁场, 电流元在中心轴线上激发磁场的方向沿轴线,且与ω同向,大小为 d B=μ0d Ir 2/[2(x 2+r 2)3/2]=μ0σωr 3d r /[2(x 2+r 2)3/2]()()()⎰⎰++=+=RRx rx r r x r rr B 02322222002/32230d 42d σωμσωμ=()()()⎰+++Rx rx r x r23222222d 4σωμ-()()⎰++Rx rx r x 023222220d 4σωμ=⎪⎪⎭⎫⎝⎛+++RRx r x x r 022202202σωμ =⎪⎪⎭⎫ ⎝⎛-++x x R x R R Q 222222220πωμ (2)求磁距. 电流元的磁矩d P m =d IS=σωr d r πr 2=πσωr 2d r⎰=Rm dr r P 03πσω=πσωR 4/4=ωQR 2/4练习八 安培环路定律三、计算题1. 如图所示，一根半径为R 的无限长载流直导体，其中电流I 沿轴向流过，并均匀分布在横截面上. 现在导体上有一半径为R '的圆柱形空腔，其轴与直导体的轴平行，两轴相距为 d . 试求空腔中任意一点的磁感强度.解：1. 此电流可认为是由半径为R 的无限长圆柱电流I 1和一个同电流密度的反方向的半径为R '的无限长圆柱电流I 2组成. I 1=J πR 2 I 2=-J πR '2 J =I/[π (R 2-R '2)] 它们在空腔内产生的磁感强度分别为 B 1=μ0r 1J/2 B 2=μ0r 2J/2B x =B 2sin θ2-B 1sin θ1=(μ0J/2)(r 2sin θ2-r 1sin θ1)=0 B y =B 2cos θ2＋B 1cos θ1=(μ0J/2)(r 2cos θ2＋r 1cos θ1)=(μ0J/2)d 所以 B = B y = μ0dI/[2π(R 2－R '2)] 方向沿y 轴正向2. 设有两无限大平行载流平面,它们的电流密度均为j ,电流流向相反. 求： (1) 载流平面之间的磁感强度； (2) 两面之外空间的磁感强度.解;2. 两无限大平行载流平面的截面如图.平面电流在空间产生的磁场为 B 1=μ0J /2在平面①的上方向右,在平面①的下方向左;电流②在空间产生的磁场为 B 2=μ0J /2 在平面②的上方向左,在平面②的下方向右.(1) 两无限大电流流在平面之间产生的磁感强度方向都向左,故有 B=B 1+B 2=μ0J (2) 两无限大电流流在平面之外产生的磁感强度方向相反,故有 B=B 1-B 2=0练习九 安培力图I 1 I 2①②1. 一边长a =10cm 的正方形铜导线线圈(铜导线横截面积S mm 2, 铜的密度ρg/cm 3), 放在均匀外磁场中. B 竖直向上, 且B = ⨯10-3T, 线圈中电流为I =10A . 线圈在重力场中 求:(1) 今使线圈平面保持竖直, 则线圈所受的磁力矩为多少. (2) 假假设线圈能以某一条水平边为轴自由摆动,当线圈平衡时,线圈平面与竖直面夹角为多少.解：1. (1) P m =IS=Ia 2 方向垂直线圈平面.线圈平面保持竖直,即P m 与B M m =P m ×BM m =P m B sin(π/2)=Ia 2B=×10－4m ⋅N(2) 平衡即磁力矩与重力矩等值反向 M m =P m B sin(π/2－θ)=Ia 2B cos θ M G = M G 1 + M G 2 + M G 3= mg (a/2)sin θ+ mga sin θ+ mg (a/2)sin θ =2(ρSa )ga sin θ=2ρSa 2g sin θ Ia 2B cos θ=2ρSa 2g sin θ tan θ=IB/(2ρSg )= θ=15︒2. 如图13.5所示，半径为R 的半圆线圈ACD 通有电流I 2, 置于电流为I 1的无限长直线电流的磁场中, 直线电流I 1 恰过半圆的直径, 两导线相互绝缘. 求半圆线圈受到长直线电流I 1的磁力. 解：2.在圆环上取微元 I 2d l = I 2R d θ 该处磁场为B =μ0I 1/(2πR cos θ)I 2d l 与B 垂直,有d F= I 2d lB sin(π/2) d F=μ0I 1I 2d θ/(2πcos θ) d F x =d F cos θ=μ0I 1I 2d θ /(2π) d F y =d F sin θ=μ0I 1I 2sin θd θ /(2πcos θ)⎰-=22102πππθμd I I F x =μ0I 1I 2/2因对称F y =0.故 F =μ0I 1I 2/2 方向向右.练习十 洛仑兹力I图13.5I1. 如图所示，有一无限大平面导体薄板，自下而上均匀通有电流，已知其面电流密度为i(即单位宽度上通有的电流强度)(1) 试求板外空间任一点磁感强度的大小和方向.(2) 有一质量为m，带正电量为q的粒子，以速度v沿平板法线方向向外运动. 假设不计粒子重力.求：(A) 带电粒子最初至少在距板什么位置处才不与大平板碰撞.(B) 需经多长时间，才能回到初始位置..解：1. (1)求磁场.用安培环路定律得B=μ0i/2在面电流右边B的方向指向纸面向里,在面电流左边B的方向沿纸面向外.(2) F=q v×B=m a qvB=ma n=mv2/R带电粒子不与平板相撞的条件是粒子运行的圆形轨迹不与平板相交,即带电粒子最初位置与平板的距离应大于轨道半径.R=mv/qB= 2mv/(μ0iq)t=T=2πR/v= 4πm/(μ0iq)2. 一带电为Q质量为m的粒子在均匀磁场中由静止开始下落,磁场的方向(z轴方向)与重力方向(y轴方向)垂直,求粒子下落距离为y时的速率.并讲清求解方法的理论依据.解：2. 洛伦兹力Q v×B垂直于v,不作功,不改变v的大小；重力作功.依能量守恒有mv2/2=mgy，得v=(2gy)1/2.练习十一磁场中的介质三、计算题1. 一厚度为b的无限大平板中通有一个方向的电流,平板内各点的电导率为γ,电场强度为E,方向如图15.6所示,平板的相对磁导率为μr1,平板两侧充满相对磁导率为μr2的各向同性的均匀磁介质,试求板内外任意点的磁感应强度.解：1. 设场点距中心面为x,因磁场面对称以中心面为对称面过场点取矩形安培环路，有⎰⋅l lH d=ΣI02∆LH=ΣI0(1)介质内,0<x<b/2. ΣI0=2x∆lJ=2x∆lγE,有H=xγE B=μ0μr1H=μ0μr1xγE(2)介质外,|x|>b/2. ΣI0=b∆lJ=b∆lγE,有H=bγE/2B=μ0μr2H=μ0μr2bγE/2i v•图2. 一根同轴电缆线由半径为R 1的长导线和套在它外面的半径为R 2的同轴薄导体圆筒组成，中间充满磁化率为χm 的各向同性均匀非铁磁绝缘介质，如图所示. 传导电流沿导线向上流去, 由圆筒向下流回，电流在截面上均匀分布. 求介质内外外表的磁化电流的大小及方向.解：2. 因磁场柱对称 取同轴的圆形安培环路，有 ⎰⋅ll H d =ΣI 0在介质中(R 1<r <R 2)，ΣI 0=I ，有 2πrH = I H = I /(2πr ) 介质内的磁化强度 M =χm H =χm I /(2πr )介质内外表的磁化电流 J SR 1=| M R 1×n R 1|=| M R 1|=χm I /(2πR 1) I SR 1=J SR 1⋅2πR 1=χm I (与I 同向) 介质外外表的磁化电流J SR 2=| M R 2×n R 2|=| M R 2|=χm I /(2πR 2) I SR 2=J SR 2⋅2πR 2=χm I (与I 反向)练习十二 电磁感应定律 动生电动势三、计算题1. 如图所示，长直导线AC 中的电流I 沿导线向上，并以d I /d t = 2 A/s 的变化率均匀增长. 导线附近放一个与之同面的直角三角形线框，其一边与导线平行，位置及线框尺寸如下图. 求此线框中产生的感应电动势的大小和方向.解： 1.d S =y d x =[(a+b -x )l/b ]d xΦm =⎰⋅S d S B=()⎰+-+⋅ba abldxx b a x I πμ20 =()⎥⎦⎤⎢⎣⎡-++b a b a b a b Il ln 20πμ图图图εi =-d Φm /d t=()dtdIa b a ba b b l ⎥⎦⎤⎢⎣⎡++-ln 20πμ =-×10－8V负号表示逆时针2. 一很长的长方形的U 形导轨，与水平面成θ 角，裸导线可在导轨上无摩擦地下滑，导轨位于磁感强度B 垂直向上的均匀磁场中，如图所示. 设导线ab 的质量为m ，电阻为R ，长度为l ，导轨的电阻略去不计, abcd 形成电路. t=0时，v=0. 求：(1) 导线ab 下滑的速度v 与时间t 的函数关系; (2) 导线ab 的最大速度v m .解：2. (1) 导线ab 的动生电动势为εi = ⎰l v×B ·d l=vBl sin(π/2+θ)=vBl cos θI i =εi /R = vBl cos θ/R方向由b 到a . 受安培力方向向右,大小为F =| ⎰l (I i d l×B )|= vB 2l 2cos θ/RF 在导轨上投影沿导轨向上,大小为F '= F cos θ =vB 2l 2cos 2θ/R重力在导轨上投影沿导轨向下,大小为mg sin θmg sin θ -vB 2l 2cos 2θ/R=ma=m d v /d t dt=d v /[g sin θ -vB 2l 2cos 2θ/(mR )]()[]{}⎰-=vmR l vB g dv t 0222cos sin θθ()()()mR t l B e l B mgR v θθθ222cos 2221cos sin --=(2) 导线ab 的最大速度v m =θθ222cos sin l B mgR .练习十三 感生电动势 自感三、计算题1. 在半径为R 的圆柱形空间中存在着均匀磁场B ,B R 的金属棒MN 放在磁场外且与圆柱形均匀磁场相切,切点为金属棒的中点,金属棒与磁场BB 随时间的变化率d B /d t 为大于零的常量.求:棒上感应电动势的大小,并指出哪一个端点的电势高. (分别用对感生电场的积分εi =⎰l E i ·d l 和法拉第电磁感应定律εi =－d Φ/d t 两种方法解). .解：(1) 用对感生电场的积分εi =⎰l E i ·d l 解:在棒MN 上取微元d x (-R<x<R ), 该处感生电场大小为E i =[R 2/(2r )](d B/d t )与棒夹角θ满足tan θ=x/R εi =⎰⋅NMl E i d =⎰NMi x E θcos d=()⎰-⋅RRr R r x t B R 22d d d =⎰-+⋅RR R x x t B R 2232d d d =[R 3(d B/d t )/2](1/R )arctan(x/R )R R-=πR 2(d B/d t )/4因εi =>0,故N 点的电势高. (2) 用法拉第电磁感应定律εi =－d Φ/d t 解: 沿半径作辅助线OM ,ON 组成三角形回路MONM=⎰⋅NMl E i d =⎰⋅-MNl E i dεi=-⎢⎣⎡⋅⎰MNl E i d +⎰⋅OM l E i d +⎥⎦⎤⋅⎰NO l E i d =－(－d ΦmMONM /d t ) =d ΦmMONM /d t而 ΦmMONM =⎰⋅Sd S B =πR 2B/4故 εi =πR 2(d B/d t )/4 N 点的电势高.2. 电量Q 均匀分布在半径为a ,长为L (L >>a )的绝缘薄壁长圆筒外表上,圆筒以角速度ωa ,电阻为R 总匝数为N ω=ω0(1-t/t 0)的规律(ω0,t 0为已知常数)随时间线性地减小,求圆线圈中感应电流的大小和流向.解：2. .等效于螺线管B 内=μ0 nI=μ0 [Q ω /(2π)]/L=μ0 Q ω /(2πL )B 外=0Φ=⎰S B ⋅d S=B πa 2=μ0Q ω a 2 /(2 L ) εi =－d Φ/d t=－[μ0Q a 2 /(2 L )]d ω /d t=μ0ω 0Q a 2 /(2 L t 0)I i =εi /R=μ0ω 0Q a 2 /(2 LR t 0)方向与旋转方向一致.练习十四 自感〔续〕互感 磁场的能量三、计算题1. 两半径为a 的长直导线平行放置,相距为d ,组成同一回路,求其单位长度导线的自感系数L 0.解：1. 取如下图的坐标,设回路有电流为I ,则两导线间磁场方向向里,大小为 0≤r ≤a B 1=μ0Ir/(2πa 2)+ μ0I/[2π(d -r )] a ≤r ≤d -a B 2=μ0I/(2πr )+μ0I/[2π(d -r )] d -a ≤r ≤d B 3=μ0I/(2πr )+ μ0I (d -r )/(2πa 2) 取窄条微元d S=l d r ,由Φm =⎰⋅SS B d 得Φml =⎰aa r Irl 0202d πμ+()⎰-a r d r Il 002d πμ +⎰-ad ar r Il πμ2d 0+()⎰--a d ar d r Il πμ2d 0+⎰-ad ar r Il πμ2d 0+()⎰-a d aa rl r -d I 202d πμ =μ0Il/(4π)+[μ0Il/(2π)]ln[d/(d -a )]+[μ0Il/(2π)]ln[(d -a )/a ] +[μ0Il/(2π)]ln[(d -a )/a ]+[μ0Il/(2π)]ln[d/(d -a )]+μ0Il/(4π)=μ0Il/(2π)+(μ0Il/π)ln(d/a )由L l =Φl /I ,L 0= L l /l=Φl /(Il ).得单位长度导线自感 L 0==μ0l/(2π)+(μ0l/π)ln(d/a )2 内外半径为R 、r 的环形螺旋管截面为长方形,共有N 匝线圈.另有一矩形导线线圈与其套合,如图19.4(1)所示. 其尺寸标在图19.4(2) 所示的截面图中,求其互感系数.解：2. 设环形螺旋管电流为I , 则管内磁场大小为B =μ0NI/(2πρ) r ≤ρ≤RS=h d ρ,由Φm =⎰⋅SS B d 得Φm =⎰RrNIh πρρμ2d 0=μ0NIh ln(R/r )/(2π) M =Φm /I ==μ0Nh ln(R/r )/(2π)(1)。

总加速度:1 .牛顿第一定律：当豆外=0时, V =怛矢量O2 .牛顿第二定律：F = ma =m— dtdPdt期末考试说明第1章质点运动学9分，重点：求导法和积分法，圆周运动切向加速度和法向加速度；第2章质点动力学3分，重点：动量定理、动能定理、变力做功；第3章刚体6分，重点：转动定律、角动量守恒定律、机械能守恒定律；第5章振动17分，重点：旋转矢量法、振动方程、速度方程、加速度方程、振动能量、振动合成。

第6章波动14分，重点：波动方程以及波动方程的三层物理意义、相位差与波程差的关系；大学物理1期末复习提纲第一•章质点运动学主要公式：1.质点运动方程(位矢方程)：r(t) = x(t)i + y(t)j + z(t)k(x = x(t)参数方程：y = y(f) T消去f得轨迹方程。

Z — Z(02.速度：v =K,加速度：a = ^dt dt3.平均速度—Ar:V =——，平均加速度：5 =—4.角速度:口 =岑，5.线速度与角速度关系：v 角加速度：/3(a)=—dt =0)r6.切向加速度：a T = — = r(3 ,dt ra =』a；第二章质点动力学主要公式：3.牛顿第三定律(作用力和反作用力定律)：F = -F^4.动量定理：I = \ 2 F dt = mAv = m(v2~v{) = AP5.动量守恒定律：当合外力理外力=O,AP = Ocx口16 动能定理：W= -dx = \E k =-m（v22-vf）J*】口 27.机械能守恒定律：当只有保守内力做功时，AE =08.力矩：M = rxF大小：M = Fr sin 0方向：右手螺旋，沿了x产的方向。

9.角动量：L = rxP大小：L = mvr sin 3方向：右手螺旋，沿rxP的方向。

淤质点间发生碰撞：完全弹性碰撞：动量守恒，机械能守恒。

完全非弹性碰撞：动量守恒，机械能不守恒，且具有共同末速度。

一般的非弹性碰撞：动量守恒，机械能不守恒。

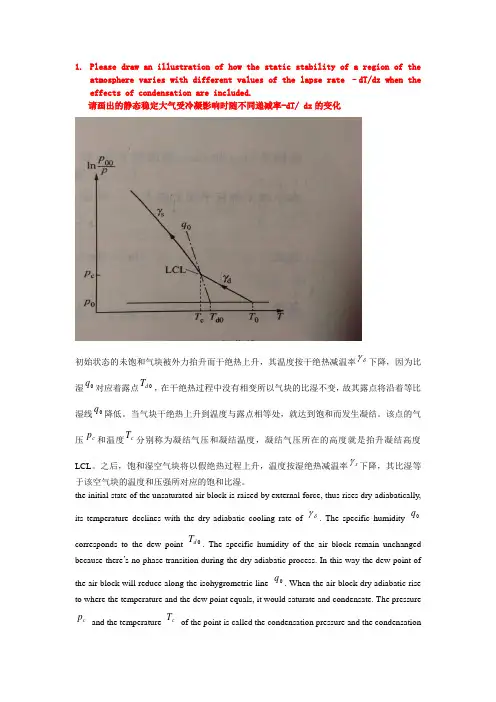
1. Please draw an illustration of how the static stability of a region of theatmosphere varies with different values of the lapse rate –dT/dz when the effects of condensation are included.请画出的静态稳定大气受冷凝影响时随不同递减率-dT/ dz 的变化初始状态的未饱和气块被外力抬升而干绝热上升，其温度按干绝热减温率δγ下降，因为比湿0q 对应着露点0d T ，在干绝热过程中没有相变所以气块的比湿不变，故其露点将沿着等比湿线0q 降低。

当气块干绝热上升到温度与露点相等处，就达到饱和而发生凝结。

该点的气压c p 和温度c T 分别称为凝结气压和凝结温度，凝结气压所在的高度就是抬升凝结高度LCL 。

之后，饱和湿空气块将以假绝热过程上升，温度按湿绝热减温率s γ下降，其比湿等于该空气块的温度和压强所对应的饱和比湿。

the initial state of the unsaturated air block is raised by external force, thus rises dry adiabatically, its temperature declines with the dry adiabatic cooling rate ofδγ. The specific humidity 0q corresponds to the dew point 0d T . The specific humidity of the air block remain unchangedbecause there ’s no phase transition during the dry adiabatic process. In this way the dew point of the air block will reduce along the isohygrometric line0q . When the air block dry adiabatic rise to where the temperature and the dew point equals, it would saturate and condensate. The pressure c p and the temperature c T of the point is called the condensation pressure and the condensationtemperature. The height of the condensation pressure is the lifting condensation level(LCL). After that, the saturated moist air block would rise in fake adiabatic process and the temperature would decrease with moist adiabatic lapse rate s . Its specific humidity equals the saturated specific humidity of the temperature and the pressure of the air block.2. How to comprehend that the atmosphere is a physical system?如何理解大气是一个物理系统？The atmosphere is a physical system 。