电力系统三相短路的分析与计算

算算3【例1】在图1所示网络中，设8.1;;100===M av B BK U U MVA S，求K 点发生三相短路时的冲击电流、短路电流的最大有效值、短路功率？解：采用标幺值的近似计算法 ①各元件电抗的标幺值1008.03.610008.05.0222.13.03.631001004100435.0301001005.10121.01151004.0402*2**2*1=⨯⨯==⨯⨯⨯=⨯==⨯==⨯⨯=L N B R T L X I I X X X②从短路点看进去的总电抗的标幺值： 7937.1*2***1*=+++=∑L R T L X X X X X③短路点短路电流的标幺值，近似认为短路点的开路电压fU 为该段的平均额定电压avU5575.01****===∑∑XX U I f f4④短路点短路电流的有名值kA I I I Bf f113.53.631005575.0*=⨯⨯=⨯=⑤冲击电流kAI i f M 01.13113.555.255.2=⨯== ⑥最大有效值电流kAI I f M 766.7113.552.152.1=⨯==⑦短路功率MVAI I S S S B f B f f 75.551005575.0**=⨯=⨯=⨯=[例2] 电力系统接线如图2（a ）所示，A 系统的容量不详，只知断路器B 1的切断容量为3500MV A ，C 系统的容量为100MV A ，电抗X C ＝0.3，各条线路单位长度电抗均为0.4Ω/km ，其他参数标于图中，试计算当f 1点发生三相短路时短路点的起始次暂态电流''1f I 及冲击电流i M ，(功率基准值和电压基准值取avBBU U MVA S ==,100)。

50km40kmf 1(3)A40km40km B 135kV(a)f 2(3)5X AX CX 1 X 2X 3X 4 X 5 f 1S AS C(b)S CX 9 X 7 X 8 X 10f 1X CS A(c)X 1X 11 (d)图2 简单系统等值电路(a) 系统图 (b)、(c)、(d)等值电路简化解：采用电源电势|0|''1E ≈和忽略负荷的近似条件，系统的等值电路图如图7-7(b)所示。

三相短路分析及短路电流计算三相短路分析及短路电流计算是电力系统中一个重要的问题，在电力系统运行和设计中起着至关重要的作用。

理解和计算三相短路电流对于保护设备和系统的可靠性至关重要。

下面我将详细介绍三相短路分析及短路电流计算的内容。

1.三相短路分析三相短路是指三相电源之间或电源与负载之间发生短路故障，造成电流突然增加。

三相短路会导致电流剧增，电网负载增大，电网发电机负荷骤降。

因此，对于电力系统而言，短路是一种严重的故障。

短路的原因主要有以下几种：-外部因素，如雷击、设备故障等；-人为因素，如误操作、设备维护不当等。

短路的位置主要有以下几种：-发电机绕组内部；-输电线路中；-终端设备终端内部。

短路的类型主要有以下几种：-对地短路（单相接地短路、双相接地短路）；-相间短路；-相对地短路；-三相短路。

短路电流是指在短路发生时，电路中的电流值。

短路电流的计算是电力系统设计、保护设备选择、线路容量选择的重要依据。

正确计算短路电流能够保证系统的安全运行。

短路电流的计算包括以下步骤：-确定故障位置和类型；-确定电路参数，包括发电机额定电流、负载电流、接地电阻等；-选择合适的计算方法，如对称分量法、复杂网络法、解耦法等；-根据选定的计算方法进行计算，并考虑系统运行时的各种条件，如电源电压波动、电源短路容量等；-对计算结果进行验证和分析，确保结果的准确性。

在进行短路电流计算时，还需要考虑以下几个因素：-各种设备的短路容量，包括母线、断路器、继电器等；-系统的整体阻抗和电流限制；-瞬时电流和持续电流的功率损耗；-预测设备短路容量的变化趋势。

总之，三相短路分析及短路电流计算对于电力系统的正常运行和设备的保护至关重要。

准确计算短路电流能够帮助电力系统工程师定位和解决故障，从而确保系统的安全运行。

电力系统三相短路分析电力系统短路是指电力系统中正常工作状态下的导体相互接触或与大地接触，导致电流过大而瞬间形成一个低阻值的回路，称为短路。

短路可能导致电力系统设备受损、事故发生甚至引发火灾等严重后果，因此对电力系统进行短路分析显得尤为重要。

电力系统短路分析的主要目的是确定短路电流大小及其分布情况，以便确定保护装置的设置参数和电气设备的选型设计。

在进行短路分析时需要考虑各种电力设备的参数、电力系统的拓扑结构以及电力系统的操作方式等因素。

电力系统短路分析可以分为对发电机、变压器、线路和负荷等不同组件进行短路分析。

首先对发电机进行短路分析，需要考虑其内部参数以及与系统的连接方式。

通常将发电机模型化为两个序列，即正序和负序。

正序各个参数均与实际相同，而负序则将相序改为逆序。

通过正序和负序的计算，可以得出发电机的短路电流。

接下来进行变压器的短路分析，变压器的短路分析主要是通过计算其短路阻抗，从而得出短路电流。

变压器的短路阻抗一般分为正序、负序和零序三种模式。

根据变压器的接法和绕组的配置，可以计算出不同模式下的短路电流。

线路的短路分析主要是通过计算线路的电阻、电抗和电容等参数，以及线路的长度和材料来得出短路电流。

线路的短路电流可以通过正序和零序计算得出。

负荷的短路分析一般较为简单，只需根据负荷的类型和连接方式计算出其短路电流。

在进行电力系统短路分析时，有两个重要的指标需要考虑，即故障电流和短路持续时间。

故障电流是指发生短路时电流的最大值，它对于各种保护设备的选择和设置均有重要的影响。

短路持续时间是指短路时电流的持续时间，它对于保护设备的热稳定性和热分散性有一定要求。

对于电力系统短路分析，目前常用的方法有解析法和数值计算法两种。

解析法主要是通过解析电路方程组，利用复数计算方法来求解短路电流。

数值计算法则通过建立系统的数值模型，利用计算机软件进行电流计算。

目前较为常用的软件有DigSILENT、PSS/E等。

总结起来，电力系统短路分析是对电力系统中各个组件进行短路计算，通过计算短路电流大小和分布情况，确定保护装置的设置参数和电力设备的选型设计。

第七章电力系统三相短路的分析与计算电力系统三相短路是指在电力系统中发生的电路短路故障，其中涉及到三个相位之间的短路。

在电力系统中，电路短路是一种严重的故障，可能会导致系统故障、设备损坏和人员伤亡。

因此，对电力系统三相短路进行分析和计算十分重要。

首先，为了进行电力系统三相短路的分析与计算，需要了解电力系统的拓扑结构和电气参数。

电力系统的拓扑结构包括发电厂、变电站、输电线路和配电系统等组成部分。

电力系统的电气参数包括电压、频率、电流和阻抗等。

在进行电力系统三相短路分析与计算时，首先需要确定电路的故障类型。

电力系统的三相短路可以分为对地短路和相间短路。

对地短路是指电路的任意一相与地之间发生短路，相间短路是指电路的任意两个相之间发生短路。

对地短路通常是系统中最简单的短路类型，而相间短路通常是更严重的故障。

然后，需要根据电力系统的电气参数和拓扑结构，进行电力系统三相短路计算。

电力系统三相短路计算包括短路电流的计算和短路电流的传递。

短路电流的计算需要根据电力系统的阻抗和电流进行计算，可以使用相序基准法、对称分量法和潮流法等方法进行计算。

短路电流的传递是指确定电路中各个节点的短路电流，根据电力系统的拓扑结构和电气参数进行计算。

最后，需要根据电力系统三相短路的分析结果，采取相应的保护措施。

电力系统的保护装置能够及时检测和隔离电路的短路故障，以保护电力系统的设备和人员的安全。

保护措施包括过电流保护、地跳保护和差动保护等。

过电流保护用于检测电流异常，地跳保护用于检测对地短路，差动保护用于检测相间短路。

总而言之，电力系统三相短路的分析与计算是电力系统运行和保护的重要组成部分。

通过对电力系统的拓扑结构和电气参数进行分析与计算，可以有效地预防和处理电力系统中的短路故障，以保护电力系统设备和人员的安全。

第一节电力系统故障概述在电力系统的运行过程中,时常会发生故障,如短路故障、断线故障等。

其中大多数是短路故障（简称短路)。

所谓短路,是指电力系统正常运行情况以外的相与相之间或相与地（或中性线)之间的连接。

在正常运行时，除中性点外,相与相或相与地之间是绝缘的。

表7—1示出三相系统中短路的基本类型。

电力系统的运行经验表明，单相短路接地占大多数。

三相短路时三相回路依旧是对称的，故称为对称短路;其它几种短路均使三相回路不对称，故称为不对称短路。

上述各种短路均是指在同一地点短路,实际上也可能是在不同地点同时发生短路，例如两相在不同地点短路.产生短路的主要原因是电气设备载流部分的相间绝缘或相对地绝缘被损坏。

例如架空输电线的绝缘子可能由于受到过电压(例如由雷击引起）而发生闪络或由于空气的污染使绝缘子表面在正常工作电压下放电。

再如其它电气设备，发电机、变压器、电缆等的载流部分的绝缘材料在运行中损坏.鸟兽跨接在裸露的导线载流部分以及大风或导线覆冰引起架空线路杆塔倒塌所造成的短路也是屡见不鲜的.此外，运行人员在线路检修后未拆除地线就加电压等误操作也会引起短路故障。

电力系统的短路故障大多数发生在架空线路部分。

总之,产生短路的原因有客观的，也有主观的,只要运行人员加强责任心，严格按规章制度办事，就可以把短路故障的发生控制在一个很低的限度内。

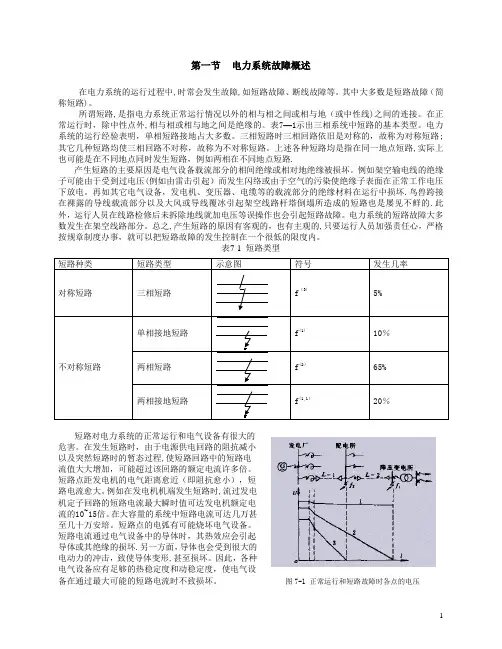
表7-1 短路类型短路对电力系统的正常运行和电气设备有很大的Array危害。

在发生短路时，由于电源供电回路的阻抗减小以及突然短路时的暂态过程,使短路回路中的短路电流值大大增加，可能超过该回路的额定电流许多倍。

短路点距发电机的电气距离愈近（即阻抗愈小），短路电流愈大。

例如在发电机机端发生短路时,流过发电机定子回路的短路电流最大瞬时值可达发电机额定电流的10~15倍。

在大容量的系统中短路电流可达几万甚至几十万安培。

短路点的电弧有可能烧坏电气设备。

短路电流通过电气设备中的导体时，其热效应会引起导体或其绝缘的损坏.另一方面，导体也会受到很大的电动力的冲击，致使导体变形,甚至损坏。

电⼒系统【第七章：电⼒系统三相短路的分析与计算】⼀.电⼒系统故障概述 1.短路 短路是指电⼒系统正常运⾏情况下以外的相与相或相与地【或中性线】之间的故障连接。

2.对称短路与不对称短路 三相短路时三相回路依旧是对称的，故称为对称短路。

其它⼏种短路均使三相回路不对称，故称为不对称短路，如下： 3.产⽣短路的主要原因是电⽓设备载流部分的相间绝缘或相对地绝缘被损坏。

4.系统中发⽣短路相当于改变了电⽹的结构，必然引起系统中功率分布的变化，⽽且发电机输出功率也相应发⽣变化。

5.为了减少短路对电⼒系统的危害，可以采⽤限制短路电流的措施，在线路上装设电抗器。

但是最主要的措施是迅速将发⽣短路的部分与系统其它部分进⾏隔离，这样发电机就可以照常向直接供电的负荷和配电所的负荷供电。

6.电⼒系统的短路故障有时也称为横向故障，因为它是相对相【或相对地】的故障。

还有⼀种故障称为纵向故障，即断线故障，指的是⼀相或多相断线使系统运⾏在⾮全相运⾏的情况。

在电⼒系统中的不同地点【两处以上】同时发⽣不对称故障的情况，称为复杂故障。

⼆.⽆限⼤功率电源供电的系统三相短路电流分析 1.电源功率⽆限⼤时外电路发⽣短路（⼀种扰动）引起的功率改变对电源来说微不⾜道，因⽽电源的电压和频率对应于同步发电机的转速保持恒定。

2.⽆限⼤电源可以看做由多个有限功率电源并联⽽成的，因其内阻抗为零，电源电压保持恒定。

实际上，真正的⽆限⼤电源是不存在的，只能是⼀种相对概念往往是以供电电源的内阻抗与短路回路总阻抗的相对⼤⼩来判断电源是否作为⽆限⼤功率电源。

若供电电源的内阻抗⼩于短路回路总阻抗的10%时，则可认为供电电源为⽆限⼤功率电源。

在这种情况下，外电路发⽣短路对电源影响较⼩，可近似认为电源电压幅值和频率保持恒定。

3.当短路点突然发⽣三相短路时，这个电路即被分成两个独⽴的回路。

及有电源连接的回路和⽆电源连接的回路。

在有电源连接的回路中，其每相阻抗减⼩，对应的稳态电流必将增⼤。

三相短路故障分析与计算及其程序设计首先，我们来介绍三相短路故障的定义和特点。

三相短路故障是指三相电源之间或三相电源与大地之间发生的短路现象。

它的特点是发生瞬间，短路电流非常大，会导致电压降低、设备损坏、线路过载和停电等问题。

针对三相短路故障，我们需要进行以下分析与计算：1.短路电流计算：短路电流是指在短路点的瞬时电流值。

它的大小直接影响到电力设备的安全性能。

短路电流的计算方法一般有阻抗法、复合法和解析法等。

其中，阻抗法是最常用的方法。

通过测量电源电压、设备电压和短路电流等参数，可以计算出短路电流的大小。

2.短路电流传播计算：短路电流传播是指短路电流在电力系统中的传输过程。

短路电流传播计算主要包括节点电位法和分布参数法等。

节点电位法是计算电力设备节点电位的方法。

通过遍历电力系统的所有节点，计算每个节点的电位差，从而得出短路电流传播的路径。

3.短路电流定位计算：短路电流定位是指确定短路故障点的位置。

短路故障点的位置对于维修和恢复电力系统的供电很关键。

常用的短路电流定位方法有追溯法、相对法和电压法等。

追溯法是通过追溯电力设备的运行状态和瞬时测量数据，推测短路故障点的位置。

在三相短路故障分析与计算的过程中，可以设计相应的程序来辅助实施。

程序设计的关键是根据电力系统的拓扑结构、元件参数和测量数据，实现短路电流的计算、传播和定位。

程序的具体设计需要根据实际情况进行，但一般包括以下几个步骤：1.数据输入：程序需要用户输入电力系统的拓扑结构、元件参数和测量数据等。

这些数据可以通过数据库或者手动输入的方式获取。

2.短路电流计算：根据输入的电力系统数据，程序通过相关的计算方法，计算出短路电流的大小。

3.短路电流传播计算：程序根据短路电流的大小和拓扑结构，实现短路电流传播的计算。

这可以通过节点电位法或分布参数法来实现。

4.短路电流定位计算：程序根据短路电流的传播路径，结合测量数据，实现短路电流的定位计算。

这可以通过追溯法或电压法来实现。

电力系统三相对称短路电流计算_实用计算方法和程序电力系统三相对称短路电流计算是电力系统中常见的一项计算工作。

计算三相对称短路电流有助于评估系统的短路能力，确保系统的正常运行和设备的安全性。

本篇文章将介绍电力系统三相对称短路电流的实用计算方法和程序。

首先，我们需要先了解一些基本的电路参数和公式。

在三相对称系统中，短路电流是由以下公式计算得出：I=U/Z其中，I表示短路电流，U表示电压，Z表示短路阻抗。

根据短路故障类型的不同，Z可以分为三种情况：对称短路阻抗Zs、负序短路阻抗Z2和零序短路阻抗Z0。

接下来，我们将介绍两种常用的计算方法和程序。

方法一：直接计算法直接计算法是一种较为简单直接的计算方法，适用于系统较简单、负载较少的情况。

步骤一：确定短路故障点的位置和类型。

常见的短路故障类型有对称短路、单相接地短路和两相接地短路。

步骤二：根据短路故障类型确定所需的短路参数，如短路阻抗Zs、负序短路阻抗Z2和零序短路阻抗Z0。

步骤三：根据系统的电压等级和拓扑结构选取合适的计算方法和程序。

对于一般的配电系统，可以使用常见的短路电流计算软件，如ETAP、CYME等。

步骤四：输入所需的系统参数和短路参数，进行计算。

计算的结果一般包括三个方向的对称短路电流、负序短路电流和零序短路电流。

方法二：梯级计算法梯级计算法是一种逐步递推计算的方法，适用于系统结构复杂、负载多变的情况。

步骤一：将电力系统划分为若干个较小的区域，每个区域由一个发电机和若干个负载组成。

步骤二：根据每个区域的电源和负载参数确定区域内的电压和短路阻抗，并计算出各区域内的对称短路电流、负序短路电流和零序短路电流。

步骤三：根据区域之间的连接关系和相应的变压器参数，逐步计算各区域之间的短路电流。

步骤四：将各区域之间的短路电流相加，得到整个系统的短路电流。

需要注意的是，梯级计算法需要依赖于电力系统的拓扑结构和参数，对于大型复杂系统，计算过程较为繁琐，因此需要借助计算软件进行计算。

电力系统三相短路的分析计算
三相短路是指电力系统中三相导体之间发生短路故障，通常是由于设
备故障或外部原因引起的。

三相短路可能引起电流突然增大，电流过大很
容易导致设备的损坏或损坏。

因此，对三相短路进行及时的分析和计算非
常重要。

三相短路的分析计算主要包括以下几个方面：
1.短路电流计算：根据电力系统的拓扑结构和设备参数，通过计算和
仿真得到短路电流。

这是确定系统中短路故障的重要步骤，可以帮助工程
师了解系统中电流的大小和方向。

2.短路电流传播计算：根据系统中设备的参数，计算短路电流在系统
中的传播路径和传播过程。

这可以帮助工程师确定短路故障的类型和位置，以及各个设备受到的短路电流大小。

3.设备保护装置设定计算：根据短路电流的计算结果，确定设备保护
装置的动作时间和动作电流。

这可以帮助工程师对电力系统的保护装置进
行设置和校验，确保系统中的设备在短路故障发生时能够及时动作，保护
设备的安全运行。

4.短路电流对设备的影响计算：根据短路电流的计算结果，分析短路
故障对系统中设备的影响。

这可以帮助工程师评估设备的稳定性和可靠性，确保设备能够在短路故障发生时正常运行。

总之，电力系统三相短路的分析计算是电力系统工程中的重要任务之一、通过对短路电流的计算和分析，可以帮助工程师了解系统中的故障状态，确定短路故障的类型和位置，并对设备的保护装置进行设置和校验，
以确保系统的安全运行。

电力系统三相短路的分析与计算电力系统三相短路是指电力系统中发生的由于过大的电流流过电气设备、电缆、电缆接头、电线路等导体元件而引起的电气故障。

三相短路是一种严重的故障，可能导致设备损坏、事故发生甚至火灾爆炸。

因此，对电力系统三相短路进行准确分析和计算是非常重要的。

首先，我们来看一下三相短路的类型。

三相短路可以分为对称短路和不对称短路两种情况。

对称短路是指三相短路电流大小相等，相位相同的短路；不对称短路是指三相短路电流大小不等，相位差大于120度的短路。

接下来，我们介绍一下三相短路的分析方法。

三相短路的分析可以采用阻抗法、复数法和对称分量法等方法进行。

其中，阻抗法是最常用的一种方法。

阻抗法的基本原理是利用设备和导线的等效阻抗来分析三相短路。

首先，需要测量或查表得到电源电压、设备电流和电源电阻的值。

然后，根据欧姆定律和基尔霍夫定律，利用等效电路模型计算电路中电流和电压的数值。

最后，通过计算得到的电压和电流值，可以得出电力系统中设备的功率损耗、电流大小等信息。

接下来，我们来看一下三相短路计算的具体步骤。

首先，需要收集电力系统的相关信息，包括电源电压、设备电流、电源电阻等。

然后，根据短路的类型选择相应的计算方法。

对于对称短路，可以使用复数法进行计算；对于不对称短路，可以使用对称分量法进行计算。

在计算中，可以采用手动计算或使用专业软件进行模拟计算。

最后，根据计算结果对电力系统的安全性进行评估，并采取相应的措施进行处理。

三相短路的分析和计算是一项复杂的工作，需要对电力系统和相关理论有较深入的了解。

在实际工作中，应该高度重视电力系统的安全问题，采取相应的预防措施和应急措施，保障电力系统的正常运行和人员的安全。

同时，还需要不断学习和更新电力系统的相关知识，提高自身的技术水平。

总结起来，电力系统三相短路的分析与计算是一项重要的工作，需要掌握相应的理论和方法。

只有进行准确的分析和计算，才能及时发现电力系统中的故障，保障电力系统的安全和可靠运行。

某电力系统三相短路故障计算与分析电力系统的三相短路故障是指电力系统中三相线路之间、线路与地之间发生低阻抗短路故障。

这种故障会带来严重的电气安全隐患，甚至导致设备的损坏甚至发生火灾等事故。

因此，对电力系统的三相短路故障进行计算与分析具有重要意义。

为了进行三相短路故障计算与分析，我们首先需要了解电力系统的基本参数，包括电压、电流、阻抗等信息。

通过对电力系统的拓扑结构进行建模，可以建立系统节点之间的电位方程以及支路之间的电流方程。

以节点电压为未知数，利用基尔霍夫电流定律和基尔霍夫电压定律，可以得到节点电流和支路电流之间的关系。

接下来，我们可以根据三相短路故障的特性，在短路点附近建立等效电路模型。

对于三相短路故障，通常可以采用对称分量法进行分析。

通过将三相短路故障转化为正序、负序和零序三个独立的故障计算问题，可以更加简化和明确问题的处理过程。

正序短路是指故障时三相电压和电流的幅值相等，相位角相差120度的情况。

负序短路则是指三相电流和电压的相位相同，但幅值不相等的情况。

零序短路是指三相电流和电压的幅值都为零的情况。

对于电力系统的三相短路故障的计算，通常可以采用负序等效法和正序等效法来进行分析。

负序等效法是指将负序短路等效为对称短路，从而将三相短路问题转化为正序短路问题的方法。

正序等效法则是指将正序短路等效为对称短路，从而简化三相短路故障计算的方法。

对于短路故障计算过程中所得到的电流和电压值，我们还可以通过对故障电流和故障电压进行比较，来判断是否存在故障点的位置。

比如，如果故障电流较大，而故障点附近的电压较低，那么可以判断故障点位置在电流流动方向上的接地侧。

通过对电力系统的三相短路故障进行计算和分析，可以确定故障点的位置和故障类型，为故障排除和设备维修提供准确的依据。

同时，还可以对系统的保护装置进行校验和调整，提高电力系统的安全性和可靠性。

总之，电力系统的三相短路故障计算与分析是电力系统运行和维护中至关重要的一环。

电力系统三相短路的分析与计算及三相短路的分类电力系统中，三相短路是指电力系统中三相导线之间发生短路现象，导致电力系统中产生大电流甚至爆炸的一种故障。

三相短路的分析与计算是电力系统运行和维护中非常重要的一项工作，可以帮助电力系统工程师及时发现并解决问题，确保电力系统的安全可靠运行。

三相短路的分析与计算主要包括以下几个方面：1.短路电流计算：短路电流是指在电力系统中出现短路时的电流大小。

短路电流的计算是分析短路故障的重要步骤，可以通过进行电力系统拓扑分析和电源参数测量等方法来得到准确的短路电流数值。

2.短路电压计算：电力系统中的短路电压是指在短路故障发生时，短路点之间的电压差。

短路电压的计算可以通过短路电流和系统的阻抗参数来得到，可以帮助判断短路故障的严重程度。

3.短路过程分析：短路过程分析是指对电力系统中短路故障的发展过程进行详细的分析，包括短路产生的原因、短路发展的路径等。

通过对短路过程的分析，可以帮助电力系统工程师找到故障点并及时解决。

4.短路保护设备设计：为了保护电力系统免受短路故障的影响，需要设计合理的短路保护设备。

短路保护设备设计包括选择合适的短路保护器件和设置合理的保护动作参数等。

三相短路可以分为以下几类：1.对地短路：对地短路是指系统其中一相或多相导线与大地之间发生短路。

对地短路会导致系统中出现过电压和过电流现象，严重时会引发设备损坏甚至火灾。

2.对相短路：对相短路是指发电系统的两个相之间产生短路。

对相短路会导致系统中产生高热现象，增加设备负荷，严重时会引发系统的瘫痪。

3.三相短路：三相短路是指系统的三个相之间全部发生短路。

三相短路会导致系统中产生非常高的短路电流，严重时会导致设备损坏和系统宕机。

总之，三相短路的分析与计算是电力系统安全运行的重要环节，通过详细的分析和计算，可以及时发现短路故障并采取相应的措施，确保电力系统的安全可靠运行。

三相短路过程分析和短路电流的计算方法电力系统三相短路时，出现的短路冲击电流值为该短路点的极限值。

三相短路电流通常是选择和校验一二次设备的重要依据。

本文对三相短路过程进行了理论分析，采用多种方法计算三相短路电流，仿真结果验证了电路三要素法不能直接应用于交流激励源作用下的过渡过程分析。

标签：三相短路，短路电流计算0.引言电力系统发生三相短路的概率很小，但是当系统发生三相短路时，电流值是发生短路故障的地点可能出现的最大值。

该短路电流值的大小与短路地点的位置有关系，与短路回路中的导体阻抗大小有关系，还与电力系统中电源的短路阻抗有关系。

三相短路电流主要用于校验该电力网络中的电气设备和导线的热稳定度和动稳定度。

因此，在某一电压等级的电力网络中计算三相短路电流时，通常假定该网络中发生最不理想的状况，即在可能出现最大三相短路电流的地点发生短路。

1.三相短路的过程发生三相短路前，电力系统是处于正常运行的状态，即已达到负荷稳定的正弦稳态，此稳态为电力系统的初始状态。

当由于某种原因电力系统中某一点发生三相短路，其短路的过程等效为电力系统中的阻抗突变，使得电力系统由原来的负荷稳态向三相短路稳态过渡，即三相短路过程为大阻抗稳态向小阻抗稳态切换。

在这个过程中，阻抗发生突变，但由于回路中存在储能元件，电流不能突变。

因此，三相短路的过渡过程是其短路电流在短时间内剧增的过程。

2.短路电流的计算电力系统中进行三相短路电流的计算时s，作如下假定：（1）电力系统为无限大容量或電力系统的电源阻抗非常小，即使在三相短路时其母线上的电压也能基本维持不变。

（2）电力系统短路切换前后其阻抗都为简单的阻感性。

由于电源、电力线路、变压器和用电设备大都是阻感性，因此这个假定是合理的。

（3）假设短路前电力系统中的阻抗为短路后电力系统的阻抗为A.电路三要素法由以上假定可知，三相短路电流的计算为一阶线性电路的求解，可以尝试应用电路三要素法分析。

电路三要素即初始值、稳态值和时间常数。