窄带随机过程ppt课件

第五章 窄带随机过程5.1 窄带随机过程的概念1． 通信工程中的信号频率在通信工程中，如雷达、广播、电视等信号，在传输中信号有相对固定的信号频率。

对于有相对固定频率的信号，其数学表达方法的研究是非常重要的。

2． 窄带随机过程（1） 带通随机过程的定义若随机过程)(t X 的谱密度满足：⎩⎨⎧∆<-=其它0)()(0ωωωωωS S X 则称)(t X 为带通过程。

带通过程的谱密度的图解如下图。

（2） 窄通随机过程的定义若)(t X 为带通过程，且0ωω<<∆，即中心频率过大于谱宽，则称)(t X 为窄通随机过程。

3． 窄带随机过程的解析表达方法之一：莱斯表示法（1）窄带随机过程的莱斯表示定理：任何一个实窄带随机过程)(t X 都可表示为下式：)sin()()cos()()(00t t b t t a t X ωω-=证明：略。

注：证明过程要用到一种重要的数学变换――希尔伯特变换，此变换需掌握。

（2） )(t a 、)(t b 的性质 ①)(t a 、)(t b 都是实随机过程。

②0))(())((==t b E t a E . 。

③)(t a 与)(t b 各自广义平稳，联合平稳，且：)()(ττb a R R =。

④))(())(())((222t X E t b E t a E ==，由此可得方差22b a σσ=。

⑤0)0(=ab R ，这说明)(t a 与)(t b 在同一时刻正交。

⑥)()(ωωb a S S =。

4． 窄带随机过程的解析表达方法之二：准正弦振荡表示法定理：实窄带随机过程)(t X 都可表示为下式：))(cos()()(0t t t A t X Φ+=ω证明：由莱斯表示法有：)()()(22t b t a t A +=， )()()(t a t b arctgt =Φ )(t A 与)(t Φ都是慢变化的随机过程。

慢变化是指)(t A 与)(t Φ随时间变化比)cos(0t ω随时间的变化要缓慢得多。

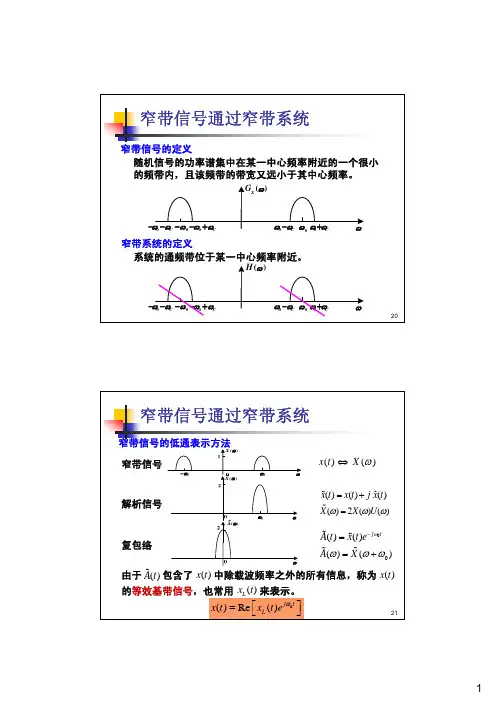
窄带信号通过窄带系统窄带信号通过窄带系统窄带信号的低通表示方法Xω(A中除载波频率之外的所有信息，称为)窄带信号通过窄带系统窄带系统的表示方法H(H窄带信号通过窄带系统窄带信号通过窄带系统的计算方法例已知，，且，。

窄带信号通过窄带系统()0()cos x t m t t =ωr t ()0cos ,00,t t Th t <<⎧=⎨⎩ω其他02T >>πω()h t 求()解法1：T=∗()()()r t x t h t +∞−∞=−∫()()x t h d τττ=−−∫000()cos ()cos Tm t t d τωτωττ=−+−−∫∫000011()cos ()cos (2)22T Tm t td m t t d τωττωττ1t d =−u t τt =−2u t τ=∫cos ()t m u du ω++∫1()cos u tm udu ω窄带信号通过窄带系统解法2：先求等效基带信号T先求等效带信号()=0()cos x t m t tω()()()=+=000()cos sin j t xt m t t jm t t m t e ωωω ()()0()j t L x t xt e m t ω−== 再求系统的等效低通表示=−−0()[()()]cos h t U t U t T tω=−−=−−0j t h ω +⎡⎤⎣⎦00()[()()]cos sin [()()]t U t U t T t j t U t U t T e ωω窄带随机过程的统计特性窄带随机过程的统计特性窄带随机过程的统计特性窄带随机过程的统计特性窄带随机过程的统计特性表示形式1()()cos ()C A t A t t =Φ()()sin ()S A t A t t =Φ00ˆ()()cos ()sin C A t X t t X t t ωω=+00ˆ()()sin ()cos S A t X t t X t t ωω=−+A t A t 表示形式1：表示形式2：30和都是实随机过程()C ()S 如果，则，由此有[()][()]0C S E A t E A t ==[()]0E X t =ˆ[()]0E Xt =窄带随机过程的统计特性()A t ,+τ窄带随机过程的统计特性A t()+τ,t窄带随机过程的统计特性A t()窄带随机过程的统计特性GG2ωG窄带随机过程的统计特性A t()窄带随机过程的统计特性对零值的窄带平稳随机过程对于零均值的窄带平稳随机过程同相分量和正交分量均为零均值的平稳随机过程同相分量和正交分量的自相关函数相同，且方差均等于窄带随机过程的方差同相分量和正交分量联合平稳，且互相关函数为奇函数联合平稳关函数为奇函数36窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布由于窄带正态随机过程包络和相位的分布ˆ由窄带正态随机过程包络和相位的分布()()cos ()=A t A t t ϕ窄带正态随机过程包络和相位的分布222⎪⎜⎟d 包络的一维概率密度为()()0,0,0==⎨⎝⎠⎪<⎩∫A A f A f A A ϕϕϕσσ分布41窄带正态随机过程包络和相位的分布相位的一维概率密度为窄带正态随机过程包络和相位的分布()cos ()A t a N t θ=+窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布作业。

窄带实平稳随机过程¾ 1概述6 确定性窄带信号窄带信号的数学表达式 同相分量、正交分量 包络和相位分量6 窄带实平稳信号的Hilbert 变换Hilbert 变换（冲击响应、频率响应）和等效的线性系统窄带实平稳信号和它的 Hilbert 变换，它们的自相关函数和功率谱 窄带实平稳信号和它的 Hilbert 变换，它们的互相关函数和互功率谱¾ 2线性调制过程（1）6 由两个均值为零实宽平稳过程()a t 、()b t ，常数0ω，构造线性调制过程6线性调制过程的广义平稳的条件 6 构造线性调制过程的对偶过程 6 线性调制过程的复数表示6 线性调制过程相关函数和功率谱 6 单边带调制过程 ¾ 3线性调制过程（2）6 由线性调制过程)(t ξ构造对偶过程，解析信号6等效低通信号定义、频谱、功率谱，数学表达式时域表示，等效低通信号，它的同相分量、正交分量窄带实平稳信号和它的 Hilbert 变换，它们的同相分量、正交分量¾ 4计算调制过程分量的相关函数和功率谱 6 自相关函数和功率谱)(t x c 、)(t x s 的自相关函数和自功率谱6互相关函数和功率谱)(),(t x t x s c ；)(),(t x t x c s 的互相关函数和互功率谱6相关函数和相关矩阵进一步讨论 定理：窄带实平稳的随机过程的功率谱、时域的同相分量和正交分量表示、同相分量和正交分量的自功率谱、同相分量和正交分量的互功率谱、 6 相关函数和功率谱密度的小结¾ 5窄带实平稳随机过程的相关函数和相关矩阵： 6 相关函数 6 相关矩阵1概述1.1 确定性窄带信号窄带信号，信号的频谱分量仅仅集中在载波频率附近。

窄带信号的数学表达式是：()()()cos 2()()cos ()cos2()sin ()sin 2()cos2()sin 2c c c c c s c x t V t f t t V t t f t V t t f t x t f t x t f tπφφπφπππ=−=+=+ 同相分量、正交分量分别是：)(sin )()()(cos )()(t t V t x t t V t x s c φφ⋅=⋅=包洛和相位分量分别是：1()()()tan ()s c V t x t t x t φ−=⎡⎤=⎢⎥⎣⎦1.2 窄带实平稳信号的Hilbert 变换Hilbert 变换和等效的线性系统如果把变换看作一个线性系统，Hilbert 变换的频率响应和冲击响应分别是f j jf H sgn )(⋅−= tt h π1)(=随机过程)(t ξ的Hilbert 变换记作)(ˆt ξ11ˆ()()()()t t u du u du u t u ξξξππ=−=−∫∫ 窄带实平稳信号和它的 Hilbert 变换的自相关函数、互相关函数、功率谱和互功率谱：它们的相关函数和功率谱是)()()()(2ˆf P f P f H f P ξξξ== )()(ˆττξξR R =它们的互相关函数和互功率谱是)()()()sgn()()()()()sgn()()()(ˆˆ*ˆˆττξξξξξξξξξξξξR R f P f j f P f H f P f P f j f P f H f P −=⋅==⋅⋅−== 2线性调制过程（1）2.1构造线性调制过程线性调制过程：给定两个均值为零实宽平稳过程()a t 、()b t ，常数0ω，构造过程()x t ，[]000()()cos ()sin ()cos ()x t a t t b t tr t t t ωωωϕ=−=+其中振幅过程()r t 、相位过程()t ϕ()()()/()r t tg t b t a t ϕ==该过程是具有振幅调制()r t 和相位调制的调制过程。