随机过程总复习87页PPT

求X(t)的均值、均方值和方差。
.
2.3 平稳随机过程
三、相关系数及相关时间
也称为归一化协方差函 数或标准协方差函数。
相关系数： rX()KXX 2 ()RX()X 2mX 2
相关时间：
0
0 rX()d
rX ( )
1
rX(0) 0.05
0
0
相关时间示意图
.
2.3 平稳随机过程
三、相关系数及相关时间
为随机过程X(t)的二维概率分布。定义
fX(x1,x2,t1,t2)2FX(xx11,xx22,t1,t2)
为随机过程X(t)的二维概率密度。 注意：X(t1)及X(t2)为同一随机过程上的随机变量。
.
2.2 随机过程的统计描述
2、二维概率分布
例2、设随机相位信号
X (n )co s( n/1 0 )
.
2.2 随机过程的统计描述
二、随机过程的数字特征（连续）
• 协方差函数
K X ( t 1 , t 2 ) E { [ X ( t 1 ) m X ( t 1 ) ] [ X ( t 2 ) m X ( t 2 ) ] } （1）如果 KX(t1,t2)0，则称 X (t1 )和 X (t2 )是不相关的。
.
2.3 平稳随机过程
一、定义
(1)严格平稳随机过程
f X ( x 1 , ,x n ,t 1 , ,t n ) f X ( x 1 , ,x n ,t 1 , ,t n )
一维概率密度： fX(x,t)fX(x)
二维概率密度： fX (x 1 ,x 2 ,t1 ,t2 ) fX (x 1 ,x 2 ,) t1 t2
接收机噪声
5
x1(t) 0

可见，（1）其均值与t无关，为常数a；
（2）自相关函数只与时间间隔有关。
14
第3章 随机过程
数字特征：
E (t) x1 f1 (x1 )dx1 a R(t1,t2 ) E[ (t1) (t1 )]
x1x2 f2 (x1, x2 ; )dx1dx2 R( )
可见，（1）其均值与t 无关，为常数a ；
随机过程 (t)的二维概率密度函数：
f2 (x1,
x2 ; t1, t2
)
2F2 (x1, x2;t1,t2 x1 x2
)
若上式中的偏导存在的话。
随机过程 (t) 的n维分布函数：
Fn (x1, x2 , , xn ;t1, t2 , tn )
P (t1 ) x1, (t2 ) x2 , , (tn ) xn
f1 (x1,t1 ) f1 (x1 )
而二维分布函数只与时间间隔 = t2 – t1有关：
f2 (x1, x2 ;t1,t2 ) f2 (x1, x2 ; )
数字特征：
E (t) x1 f1 (x1 )dx1 a R(t1,t2 ) E[ (t1) (t1 )]
x1x2 f2 (x1, x2 ; )dx1dx2 R( )
换句话说，随机过程在任意时刻的值是一个随机变量。 因此，我们又可以把随机过程看作是在时间进程中处于不同
时刻的随机变量的集合。 这个角度更适合对随机过程理论进行精确的数学描述。
5
第3章 随机过程
3.1.1随机过程的分布函数
设 (t)表示一个随机过程，则它在任意时刻t1的值 (t1)
是一个随机变量，其统计特性可以用分布函数或概率密 度函数来描述。
【解】(1)先求(t)的统计平均值：

3
一维、二维或一般的多维随机变量的研究是概率论的研究内容，而 随机序列、随机过程则是随机过程学科的研究内容。从前面的描述中看 到，它的每一样本点所对应的，是一个数列或是一个关于t的函数。
定义：设T是一无限实数集，X (e,t), e S,t T是对应于e和t的实数，
即为定义在S 和T 上的二元函数。
DX
(t)
E
[ X (t) X (t)]2
---方差函数
X (t)
2 X
(t
)
---标准差函数
又设任意t1,t2 T RXX (t1,t2 ) E[ X (t1) X (t2 )] (自)相关函数
CXX (t1,t2 ) Cov[ X (t1), X (t2 )]
E [ X (t1) X (t1)][ X (t2 ) X (t2 )] (自)协方差函数
定义： X (t),t T是一随机过程，若它的每一个有限维分布
都是正态分布，即对任意整数n 1及任意t1,t2,
X (t1), X (t2 ), X (tn )服从n维正态分布， 则称X (t),t T是正态过程
tn T ,
正态过程的全部统计特性完全由它的均值函数和自协方差函数所确定。
16
例3：设A, B是两个随机变量，试求随机过程:
当A
N 1,4, B
U 0, 2时，E(A) 1, E( A2 ) 5, E(B) 1, E(B2)
4 3
又因为A, B独立， 故E(AB) E(A)E(B) 1
X (t) t 3, RX (t1, t2 ) 5t1t2 3(t1 t2 ) 12 t1, t2 T
17
例4：求随机相位正弦波X (t) acos(t ) t ,

称这个特性为马尔可夫性，简称马氏性 称这个特性为马尔可夫性，简称马氏性。
马氏性实质上是无后效性， 所以也称马氏过程 马氏性实质上是无后效性 ， 无后效过程。 为无后效过程。
（4）平稳随机过程 ）
平稳过程的统计特性与马氏过程不同， 平稳过程的统计特性与马氏过程不同，它不 随时间的推移而变化，过程的“过去” 随时间的推移而变化，过程的“过去”可以对 未来”有不可忽视的影响。 “未来”有不可忽视的影响。
是相互独立的， 是相互独立的，
则 X(t) 为 有 立 量 随 过 。 称 具 独 增 的 机 程
（3）马尔可夫过程 ）
设 { X (t ) ， t ∈ T } 对任意 n 个不同的 t1 ， t 2 ，…， t n ∈ T
且 t1 < t 2 < L < t n −1 < t n
P( X (t n ) ≤ x n | X (t n −1 ) = x n −1 ，…， X (t1 ) = x1 )
E ( Z ) = E ( X ) + iE (Y )
为随机变量， 设X为随机变量，称复随机变量 为随机变量 的数学期望
e
itX
ϕX (t) = E[e itX ]
的特征函数， 是实数。 为X的特征函数，其中 是实数。 的特征函数 其中t是实数 还可写成
ϕ X (t ) = E[costX ] + iE[sintX ]
一维 概率 密度
若 存 在 二 元 非 负 函 数 f ( t 1； x 1 ) ， 使
F ( t1； x1 ) =
∫
x1
−∞
f ( t1； y 1 ) dy 1
则 称 f ( t 1； x 1 ) 为 随 机 过 程 X (t ) 的 一 维 概 率 密 度

所以X与Y不相关。 故 (X,Y )=0 X与Y不相关
几何直观意义
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间，若 V，存在一个实数|| ||与
之对应，且具有下列性质：
(1) || ||0 , 且|| ||=0 =0 ； (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||； c R (3) || + || || ||+ || ||； V 则称|| || 为V中元素 的范数(norm)(模、长度)，此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合，K是一个数域，又设
(a)在V中定义加法： , V : + V ; (b)在V中定义数乘： V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .

2020/6/10
140－29
2、样本函数与状态空间
❖ 随机过程X(t,)是定义在TΩ上的二元函数：一 方面，当tT固定时，X(t,)是定义在Ω上的随 机变量；另一方面，当Ω固定时，X(t,)是 定义在T上的函数，称为随机过程的样本函数。
❖ 随机过程在时刻t所取的值X(t)=x称为时刻t时随 机 过 程 {X(t),tT} 处 于 状 态 x ， 随 机 过 程 {X(t),tT}所有状态构成的集合称为状态空间， 记为E，即：
140－17
边缘分布律、条件分布律
称 pi P{X xi } pij，i 1,2, j1
为r.v.X的边缘分布律。称
pj P{Y y j} pij，j 1,2, i1
为r.v.Y的边缘分布律。称
pi|j pij pj ，i, j 1,2,
为在已知Y=yj的条件下，r.v.X的条件分布律。称 为在已知X=pxj|ii的 条pij件pi下，，i, jr.v1.Y,2的,条件分布律。
随机过程与排队论
教学内容
1) 概率论的基本知识 2) 随机过程的基本概念
随机过程的定义及分类 随机过程的分布及数字特征 3) 独立过程与独立增量过程 4) 泊松过程 5) 更新过程
2020/6/10
140－2
教学内容
1) 马尔可夫过程 马尔可夫过程的概念 离散参数马氏链 齐次马氏链状态的分类 连续参数马氏链 生灭过程
2020/6/10
140－25
4）协方差
若E{[X-E(X)][Y-E(Y)]}，称 cov(X,Y)＝E{[X-E(X)][Y-E(Y)]} ＝E(XY)-E(X)E(Y)
为随机变量X和Y的协方差，称
XY
cov(X, Y) D(X) D(Y)

练习: 设二维随机向量（X，Y）的联合概率密度为
e x 0 y x 1
f (x, y) 0
其它
求1) f X ( x), fY ( y); 2) fY X ( y x);
3)E[Y X ];
4)讨论X ,Y的独立性.
解： fX (x)
f ( x, y)dy
x exdy
0
xex , 0 x 1
注意：分母不等于0
2、条件期望的定义
离散型 连续型
E( X |Y y j ) xi P( X xi | Y y j ) i1
其中
P(X
xi
|Y
yj
)
P(X xi ,Y P(Y yj )
yj
)
E(X |Y y)
x f ( x | y)dx
其中 f ( x | y) 条件概率密度
t 3
x1
et
x1 et
随机过程的数字特征
1．均值函数 X (t ) E[ X (t )]
2．方差函数
D[ X (t)] E[( X (t) X (t))2 ]
3．协方差函数
E[ X 2 (t )] X 2 (t )
(t1, t2 ) E[( X (t1 ) X (t1 ))( X (t2 ) X (t2 ))]
当X为连续型随机变量，
则
E(Y ) E[g(X)]
g(x) f (x)dx
2.方差
称随机变量 [X E(X )]2 的期望 为X的方差，即
var(X ) D( X ) E[( X E( X ))2]
计算方差时通常用下列关系式：
var(X ) D(X ) E[X 2][E(X )]2
随机过程的分类

t 0
X ( t)W (s )ds , t 0 ，求 { X ( t), t 0 } 的均值 函数与相关函数 .
第三章 随机分析
2. 均方随机微分方程的求解
X () t at () Xt () Yt () ,t t 0 (0) X 0 Xt
t 0 X ( t ) X e 0
2)
对 0st,N ( t)N (s ) 服从参数为
( t s ) 的 poisson 分布
定理 (到达时间间隔分布) 设{N(t),t≥0} 是参数为λ 的Poisson过程， 是其到达时间间隔序列，则 Tn , 1 ,2 , n 是相互独立同服从参数为λ 的指数分布．
第三章 随机分析
1. 均方连续、均方可导、均分积分的判别准 则以及三者之间的关系
均方连续准则
{X(t), t∈T}在t0处均方连续的充要条件是其相关函数 RX(s, t)在(t0, t0)处连续.
均方可导准则
{X(t),t∈T}均方可导的充要条件是 对任意的t∈T, RX(s, t)在（t, t)处一阶偏导数存在，二阶偏导数存在且 连续． m t m () t () X X
x
2 x x 3 2
（ 2 ） F ( 0 ,; x , x ) P (( X 0 ) x , X () x )
3
12
3 A P (A x 2) x 1 2
1
2
P ( A x1 ) x 1 2 x 2 P ( A 2 x2 ) x 1 2 x 2
称 {X(t),t≥0}为复合Poisson过程.
2 2 E Y , 则 m ( t ) t E Y , D ( t ) t E Y n X n X n

无穷大的分类
0, 1 ,2 ,3,……(自然数集合的无限多 为0， 0集合的所有子集构成的集合的 “无限多（势）”为1 ， 1集合的所有 子集构成的集合的势为2 ， ……)，在数 学上已经严格证明： 0, 1 ,2 ,3,等之 间不能建立双射的关系。
对于无穷大，“整体大于部分”的直觉不再成立
对于自然数集 N 1,2,3,4,5,L ，偶数集合
原像集
像集 单射（不同的原
f
像具有不同的像）
f a1 f a2
满射（每一个像都有原像）
原像集
像集
f
b, a, s.t.
b f a
双射（既是单射，又是满射）
原像集
像集
f
从直觉上承认能建立双射关系的两 个集合，其所含元素的“个数”一样多。
可数和不可数的定义
凡是能和自然数集合或者自然数集合的 一个子集建立双射关系的集合称为可数 集合；否则称为不可数集合。 可数和不可数是人类认识“无穷”所产 生的概念，是对无穷的分类。 已经证明连续的区间，和实数集等都是 不可数集合：[1,2],(0.1,0.01),R,等等
事件和Borel集
事件：样本空间中满足一定条件的全体 元素构成子集，“一定条件”有事件的 意义，因此称样本空间的子集为事件。
（举例说明）
不可能事件 必然事件 基本事件：可数和不可数 Borel集：规定了事件的全体及其相容性
概率空间的定义
阅读讲解p.16定义2.1 理解概率空间
概率空间是对随机现象的基本建模方法 概率空间有三个要素：样本空间、Borel事
《随机过程》教程
第三讲 随机对象（一）
本章要义（阅读引言部分）
本章介绍如何对随机现象建立数学模型。

5 理解并掌握条件概率的定义，掌握乘法公式，
全概率公式与贝叶斯公式
7 理解并会运用事件独立性的概念
5
重点：
概率的概念，古典概率，加法公式，乘
法公式，全概率公式，Bayes 公式
6
第二章 随机变量及其分布
• 随机变量
• 随机变量的分布函数
• 离散性随机变量及其概率分布
• 两点分布，二项分布，泊松分布
复 习 提 纲
1
期末不考内容
第四章 第三节 中 Z=max(X,Y),或min(X,Y) 其中(X,Y)连续型随机变量，求Z的分布， X,Y不独立时，不要求。独立时要求 掌握 . 第五章 第五节 第七章

2
分布，F分布，t 分布密度不要求
第八章 第五节，(二元正态均值差，方差比的 区间估计)
第九章 第三、四节，(二元正态均值差，
y (c, d ) 其它
二维随机变量函数z=g(x,y)的密度
计算 f Z (z) 的方法: 先构造一个新的二维随机变量(Z ,U ), 它们是 ( X , Y ) 的函数，而Z = g(X,Y) 比如 Z=aX +bY + c 等 求( Z , U ) 的联合密度函数 f ( z, u ) 求边缘密度 f Z (z)
34
重
点
• 随机过程的概念； • 随机过程的均值、方差、均方值、自相关 函数、自协方差函数。
35
第十二章
• • • • 严平稳过程； 广义平稳过程； 正态平稳过程； 遍历过程；
平稳过程
36
基本要求
• 了解严平稳过程的概念及其数字特征的特 点； • 掌握广义平稳过程的定义，并会判别； • 了解正态平稳过程； • 有所了解两个平稳过程平稳相关的概念； • 了解随机过程的时间均值、时间相关函数 的概念； • 了解遍历过程及其数字特征。

=
=
，
故随机过程{X(t)，t>0}的一、二维概率密度分别为
即可.
ft(x)=
exp{-
}，t>0，
fs,t(x1,x2)=
.exp{
[
]},s,t>0,
其中 4、设{X(t)，t≧0}是实正交增量过程，X(0)=0，V 是标准正态随机变量，若对任意的 t≧0， X(t)与 V 相互独立,令 Y(t)=X(t)+V，求随机过程{Y(t)，t≧0}的协方差函数. 解：依题意知EX(t)=0，EV=0,DV=1,所以 EY(t)=E[X(t)+V]=EX(t)+EV=0， BY(t1，t2)=E(X(t1)+V)(X(t2)+V) =E[X(t1)X(t2))]+EV2=σ 2X(min(t1,t2))+1.
C p q pX k
(2)令 X~b(n,p),则
k k nk
n
, q 1 p, k 1,2..n.
e C p q
gt
itk
k
k nk
n
k0
C e p q
k it
n
k nk
k0
有特征函数定义，可知 eit pq n
k
e p( X k) ,0, k 0,1...n
(3)令 X~p(λ),则
解：X 的分布列为P(X=k)=
C
k n
p k q n 1 ,q=1-p,k=0,1,2,...n,
g
n t
e
i
t
k
C
k n
k 0
pkqnk
n
C nk
k 0
peit

PPT文档演模板
第三章通信原理《随机过程》
•结论：平稳随机过程的均值（和方差是与时间t无关 的常数，自相关函数只是时间间隔τ的函数，而与所 选取的时间起点无关。
• 在工程中，我们常用这两个条件来直接判断随机 过程的平稳性，并把同时满足均值为常数、自相关 函数只与时间间隔 有关的随机过程定义为广义平稳 随机过程。
• 显然，严平稳必定是广义平稳，反之不一定成立。
• 在通信系统中所遇到的信号及噪声，大多可视为 平稳的随机过程。以后的讨论除特殊说明，均假定 是广义平稳的，简称平稳。
PPT文档演模板
第三章通信原理《随机过程》
• 下面我们来看一道例题，来判断一个随机过程 是否是平稳随机过程？
•例题：某随机过程是一个幅度、角频给定的正弦波， •其相位值是随机的，即 •式中： 与 为常数， 在 内均匀分布随 •机变量，试证明其为广义平稳过程。
•是二维概率密度函数。
• 协方差函数、 相关函数体现了随机过程
的二维统计特性。
PPT文档演模板
第三章通信原理《随机过程》
(3) 协方差函数与 相关函数的关系：
若随机过程的数学期望为零，则协方差函数与相 关函数是相同的。即使数学期望不为零，协方差函数 与相关函数尽管形式不同，但它们所描述的随机过程 内部联系的效果是相同的。本书将采用相关函数。
一维分布函数：
一维概率密度函数：
PPT文档演模板
第三章通信原理《随机过程》
•一般情况下： 一维分布函数： 一维概率密度函数：
和
即是 的函数，又是时间 的函数。很显然，
一维分布函数及一维概率密度函数仅仅表示了随机过程
在任一瞬间的统计特性，它对随机过程的描述很不充分，
通常需要在足够多的时间上考察随机过程的多维分布。

则称 X (t)为宽平稳过程， 简称平稳过程
注:(3)可等价描述为: 自相关函数R(t1, t2 )仅与 t1 t2有关.
R(t1, t2 ) E[ X (t1) X (t2 )] R( )
因为 均值函数 X (t )
( ) R( ) 2
注1 严平稳过程不一定是宽平稳过程。
因为严平稳过程不一定是二阶矩过程。 若严平稳过程存在二阶矩，则它一定是宽平稳过程。
X (0,1)
x y 1dy x 0x 2
2
4) f XY ( x, y) f X ( x) fY ( y) 所以X ,Y 不独立.
练习:对于随机变量X和Y，满足条件 E( X ) 2, E(Y ) 10,
2 则有 E[E(X Y )]
结论 : (1)若X是随机变量,则E( X ) X , a.s.
当X为连续型随机变量，
则
E(Y ) E[g(X)]
g(x) f (x)dx
2.方差
称随机变量 [X E(X )]2 的期望 为X的方差，即
var(X ) D( X ) E[( X E( X ))2]
计算方差时通常用下列关系式：
var(X ) D(X ) E[X 2][E(X )]2
（n) (0) E[ X n ]
3．和的矩母函数
定理1 设相互独立的随机变量 X1，X2， ，Xr 的
矩母函数分别为 1(t ) ，2 (t ) ，…，r (t ) ，
则其和 Y X1 X2 Xr 的矩母函数为
Y (t) 1(t) 2(t) …r (t)
两个相互独立的随机变量之和的矩母函数等于它 们的矩母函数之积.
(2)协方差函数的性质
性质1 (0) var[X (t)]

设{X (t),t T}是一随机过程,对于参数集 T中的任意
n 个元素: t1,t2 , ,tn , 过程的 n 个状态:
X (t1) X (e,t1), X (t2 ) X (e,t2 ), , X (tn ) X (e,tn )
( n 个随机变量)的联合分布
F (x1, , xn ;t1, ,tn ) P{X (t1 ) x1, , X (tn ) xn}
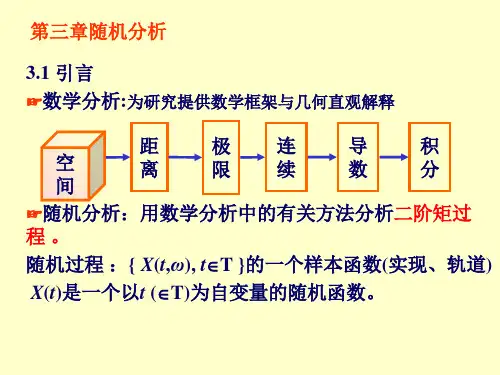
一. 随机过程的概念 概率论复习： 随机试验 E , 样本空间 S {e}. 随机变量 X X (e) ,分布函数F(x) ； 二维随机变量 (X ,Y ) ，联合分布函数F(x, y)
n 维随机变量 (X1, X 2,, X n )，联合分布
函数 F (x1, x2 , , xn )
为了研究随机现象,引入了上述这些概念工具.但 这些还不够用,还有一些随机现象,上述工具无法描述.
数学期望(均值)
EX
xf X (x)dx
xf (x, y)dxdy
E[g( X ,Y )] g(x, y) f (x, y)dxdy
二阶原点矩
EX 2
x2
f
X
(x)dx
x 2 f (x, y)dxdy
方差
DX
E( X EX )2
(x
EX
)2
f
X
(x)dx
EX 2 (EX )2
,
t
' n
)
FX
(x1, ,
xm ; t1, , tm )
FY
(
y1 ,
,
yn
; t1' ,
,
t
' n
)
都成立,则称两个随机过程相互独立.