下载文档原格式
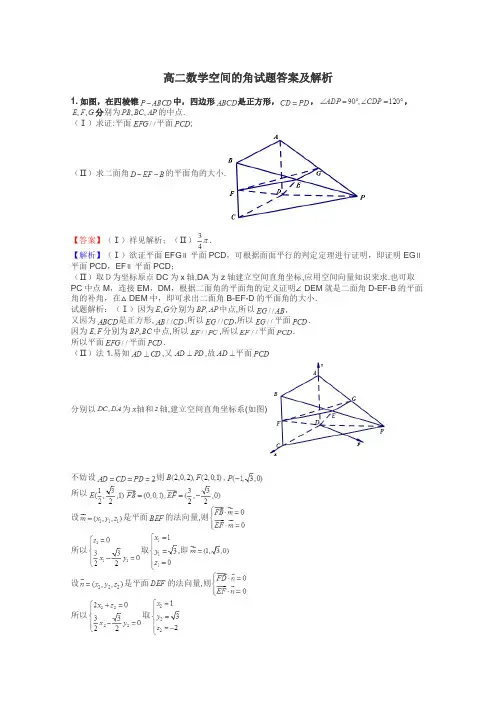
高二数学空间的角试题答案及解析1.如图，在四棱锥中，四边形是正方形，，，分别为的中点.（Ⅰ）求证:平面平面;（Ⅱ）求二面角的平面角的大小.【答案】（Ⅰ）祥见解析；（Ⅱ）．【解析】（Ⅰ）欲证平面EFG∥平面PCD，可根据面面平行的判定定理进行证明，即证明EG∥平面PCD，EF∥平面PCD；（Ⅱ）取Ｄ为坐标原点DC为x轴,DA为z轴建立空间直角坐标,应用空间向量知识来求.也可取PC中点M，连接EM，DM，根据二面角的平面角的定义证明∠DEM就是二面角D-EF-B的平面角的补角，在△DEM中，即可求出二面角B-EF-D的平面角的大小．试题解析：（Ⅰ）因为分别为中点,所以,又因为是正方形,,所以,所以平面.因为分别为中点,所以,所以平面.所以平面平面.（Ⅱ）法1.易知,又,故平面分别以为轴和轴,建立空间直角坐标系(如图)不妨设则,所以设是平面的法向量,则所以取,即设是平面的法向量,则所以取设二面角的平面角的大小为所以,二面角的平面角的大小为.法2.取中点,联结则,又平面,,所以平面,所以平面,所以,.因为,则,所以平面.又因为,所以所以就是二面角的平面角的补角.不妨设,则,,.所以二面角的平面角的大小为.【考点】１．平面与平面平行的判定；２．与二面角有关的立体几何综合题．2.如图，在直三棱柱中-A BC中，AB AC，AB=AC=2，=4，点D是BC的中点．（1）求异面直线与所成角的余弦值；（2）求平面与所成二面角的正弦值.【解析】（1）以为单位正交基底建立空间直角坐标系,利用向量法能求出异面直线与所成角的余弦值；（2）分别求出平面的法向量与的法向量，利用法向量能求出平面与所成二面角的余弦值，再由三角函数知识能求出平面与所成二面角的正弦值.试题解析：（1）以为单位正交基底建立空间直角坐标系,则,,,,,.,异面直线与所成角的余弦值为.（2）是平面的的一个法向量，设平面的法向量为,，，由，得，取,得，,所以平面的法向量为.设平面与所成二面角为 ., 得.所以平面与所成二面角的正弦值为.【考点】与二面角有关的立体几何综合题；异面直线及其所成的角．3.已知三棱柱的侧棱与底面边长都相等，在底面上的射影为的中点，则异面直线与所成的角的余弦值为A．B．C．D．【答案】D【解析】设BC的中点为D，连接A1D、AD、A1B，易知即为异面直线AB与CC1所成的角；并设三棱柱的侧棱与底面边长为1，则【考点】两条异面直线所成的角，余弦定理．4.在正四棱锥P-ABCD中，PA=2，直线PA与平面ABCD所成角为60°，E为PC的中点，则异面直线PA与BE所成角为（）A．B．C．D．【答案】C【解析】连接交于点，连接,。
空间角专题练习步骤：一、 两条异面直线所成的角 1、定义： 2、范围：3、⎪⎩⎪⎨⎧况）法三：证垂直（特殊情法二：向量法法一：平移法方法4、典例分析：例1、 90=∠∆BCA ABC Rt 中，，现将ABC ∆沿着平面ABC 的法向量平移到111C B A ∆位置，已知111111111,,,,AF BD F D C A B A CC CA BC 与求的中点取==所成角的余弦值例2、已知三棱柱111C B A ABC -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ） A 、43 B 、45 C 、47 D 、43例3、在正三棱柱111C B A ABC -中，若12BB AB =, 则B C AB 11与与所成的角的大小为（ ）A 、 60B 、 90C 、 105D 、 75二、 直线与平面所成的角 1、定义： 2、范围：3、⎪⎩⎪⎨⎧法三：向量法法二：等体积法法一：定义法方法4、典例分析：例1、正三棱柱111C B A ABC -的底面边长为a ，侧棱长为a 2，求111A ABB AC 与侧面所成的角例2、正四棱锥ABCD S -，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO=OD ，则直线BC 与平面PAC 所成的角是（ ） A 、 30 B 、 45 C 、 60 D 、 75三、平面与平面所成的角 1、定义 2、范围：3、⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧法六：射影面积法法五：找交线法法四：找垂面法法向量法方向向量法法三：向量法法二：三垂线法法一：定义法方法4、典例分析：例1、过正方形ABCD 的顶点A 作线段ABCD PA 面⊥，设PA=AB=a ， （1） 求二面角B-PC-D 的大小（2） 求平面PAB 和平面PCD 所成二面角的大小例2、已知ABC ∆和DBC ∆所在的平面互相垂直，且AB=BC=BD ，120=∠=∠DBC CBA ,求（1） 直线AD 与平面BCD 所成角的大小（2） 直线AD 与直线BC 所成角的大小 （3） 二面角A-BD-C 的余弦值例3、把矩形ABCD 沿对角线BD 折成锐二面角A-BD-C ，若AB=1，AD=273=AC 且,则二面角A-BD-C 的余弦值为（ ） A 、21B 、22C 、23D 、0例4、几何体ABC-ADE 是由正三棱柱111C B A ABC -被面ADE 截得的，若CE=BC=2BD ，求截面AED 与底面ABC 所成的角练习：已知：直角梯形OABC 中，，面OABC OS AOC BC OA ⊥=∠,90,// 且OS=OC=BC=1，OA=2，求（1） 异面直线SA 和OB 所成的角的余弦值 （2） OS 与面SAB 所成角的余弦值 （3） 二面角B-AS-O 的余弦值如何建系：例1、 在棱锥P-ABCD 中，侧面PDC 是边长为2的正三角形，且与底面垂直，底面ABCD 是菱形，且 60=∠ADC M 为PB 的中点 （1） 求证：CD PA ⊥（2） 求二面角P-AB-D 的大小例2、(2009山东理) 如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB//CD ，AB=4, BC=CD=2, AA 1=2, E 、E 1、F 分别是棱AD 、AA 1、AB 的中点。
2023年高考数学----空间角问题规律方法与典型例题讲解【规律方法】1、用综合法求空间角的基本数学思想主要是转化与化归，即把空间角转化为平面角，进而转化为三角形的内角，然后通过解三角形求得．求解的一般步骤为：（1）作图：作出空间角的平面角．（2）证明：证明所给图形是符合题设要求的． （3）计算：在证明的基础上计算得出结果． 简称：一作、二证、三算．2、用定义作异面直线所成角的方法是“平移转化法”，可固定一条，平移另一条；或两条同时平移到某个特殊的位置，顶点选在特殊的位置上．3、求直线与平面所成角的常见方法（1）作角法：作出斜线、垂线、斜线在平面上的射影组成的直角三角形，根据条件求出斜线与射影所成的角即为所求．（2）等积法：公式θ=sin hl，其中θ是斜线与平面所成的角，h 是垂线段的长，是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可构造三棱锥，利用等体积法来求垂线段的长．（3）证垂法：通过证明线面垂直得到线面角为90°． 4、作二面角的平面角常有三种方法（1）棱上一点双垂线法：在棱上任取一点，过这点分别在两个面内作垂直于棱的射线，这两条射线所成的角，就是二面角的平面角．（2）面上一点三垂线法：自二面角的一个面上一点向另一面引垂线，再由垂足向棱作垂线得到棱上的点（即垂足），斜足与面上一点连线和斜足与垂足连线所夹的角，即为二面角的平面角．（3）空间一点垂面法：自空间一点作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角．【典型例题】例19．（2022·浙江金华·高三期末）已知正方体1111ABCD A B C D −中，P 为1ACD △内一点，且1113PB D ACD S S =△△，设直线PD 与11AC 所成的角为θ，则cos θ的取值范围为（ ）A ．⎡⎢⎣⎦B ．⎤⎥⎣⎦C ．10,2⎡⎤⎢⎥⎣⎦D ．1,12⎡⎤⎢⎥⎣⎦【答案】C【解析】如图1，设1B D 与平面1ACD 相交于点E ，连接BD 交AC 于点O ，连接11B D ， ∵1BB ⊥平面ABCD ，AC ⊂平面ABCD ，则1BB AC ⊥，AC BD ⊥，1BD BB B ⋂=，1,BD BB ⊂平面11BDD B∴AC ⊥平面11BDD B ，由1B D ⊂平面11BDD B ，则1AC B D ⊥， 同理可证：11AD B D ⊥， 1AD AC A =，1,AD AC ⊂平面1ACD ，∴1B D ⊥平面1ACD ，∵111111AC AD CD AB B D B C =====，由正三棱锥的性质可得：E 为1ACD △的中心， 连接1OD ，∵O 为AC 的中点，∴1OD 交1B D 于点E ，连接PE ，由1B D ⊥平面1ACD ，PE ⊂平面1ACD ，则1B D PE ⊥，即PE 是1PB D 的高，设AB a =，PE d =，则1,B D AC =，且1ACD △的内切圆半径r OE ==，则1112PB D S B D PE =⋅=△，))1212ACD S =⨯=△，∵1113PB DACD S S =△△213=，则13d a r =<， ∴点P 的轨迹是以E 为圆心，13a 为半径的圆.∵1B D ⊥平面1ACD ，1OD ⊂平面1ACD ，则11B D OD ⊥，∴DE ， 故PD 为底面半径为13a，高为=DE 的圆锥的母线，如图2所示，设圆锥的母线与底面所成的角α，则3tan 13a α== 所以π3α=，即直线PD 与平面1ACD 所成的角为π3. 直线AC 在平面1ACD 内，所以直线PD 与直线AC 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦，因为11AC AC ∥，所以直线PD 与直线11AC 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦，即ππ,32θ⎡⎤∈⎢⎥⎣⎦， 所以10cos 2θ≤≤. 故选：C.例20．（2022·浙江·效实中学模拟预测）在等腰梯形ABCD 中，AD BC ∥，12AB AD CD BC ===，AC 交BD 于O 点，ABD △沿着直线BD 翻折成1A BD ，所成二面角1A BD C −−的大小为θ，则下列选项中错误的是（ ）A ．1A BC θ∠≤B ．1AOC θ∠≥ C ．1A DC θ∠≤ D ．11A BC A DC θ∠+∠≥【答案】C【解析】等腰梯形ABCD 中，AD BC ∥，12AB AD CD BC ===,可知：30,ACB ACD BD DC ∠=∠=⊥取BD 中点N ,BC 中点M 连接1,A N NM ,则1A N BD ⊥，NM BC ⊥,所以1A NM ∠为 二面角1A BD C −−的平面角，即1A NM θ∠=设122AB AD CD BC ====，则1111,1,2,2A N MN A B A D ==== 2222211111111cos 1222A N NM A M A M A M A N NM θ+−+−∴===−⋅,2222222111111221cos 122228A B BM A M A M A BC A M A B BM +−+−∴∠===−⋅⨯⨯,因为在[]0,π上余弦函数单调递减，又2211111111cos cos 82A M A M A BC A BC θθ−≥−⇒∠≥⇒∠≤，故A 对. 2222222111111221cos 122228A D DC AC AC A DC AC A D CD +−+−∴∠===−⋅⨯⨯222122221111153cos 2416AC AO OC AC AOC AC AO OC +−+−∴∠===−⋅ 当0θ=时,1A 与M 重合,此时160A DC ∠=,故C 不对. 1A DC ∠在翻折的过程中，角度从120减少到60 1AOC ∠在翻折的过程中，角度从180减少到30BD 选项根据图形特征及空间关系，可知正确.. 故选:C例21．（2022·浙江·湖州中学高三阶段练习）如图，ABC 中，90C ∠=︒，1AC =，BC D 为AB 边上的中点，点M 在线段BD （不含端点）上，将BCM 沿CM 向上折起至'B CM △，设平面'B CM 与平面ACM 所成锐二面角为α，直线'MB 与平面AMC 所成角为β，直线MC 与平面'B CA 所成角为γ，则在翻折过程中，下列三个命题中正确的是（ ）①tan βα，②γβ≤，③γα>. A ．① B ．①② C ．②③ D ．①③【答案】B 【解析】如图，设直线BN 与直线CM 垂直相交于点N ，在折叠图里，线段B T '与平面ACM 垂直相交于点T ，,(0,30)BCM θθ∠=∈，由图像知：;B NT B MT αβ''∠=∠=，B N BN θ=='， ()sin ;/sin 30B T B M θαθθ=*='︒+'，cos NT θα*，()tan 60MN θθ=*︒−，()()2sin 30CM θ=︒+，①tan β==，tan β=≤≤，所以tan βα；② ()Δ1sin 902ACM S CM CA θ=*︒−= 设ACB δ∠'=，则()()()2cos cos cos 90sin sin 90cos cos 0.5sin2δθθθθααθ=*︒−+*︒−=*，Δsin ACB S δ'== 由ΔΔ1133ACM M ACB ACB B T S d S −''**=**'，得M ACB d −'=()sin sin 30sin M ACB d B TMC B M γβθα'−====︒+*''，则()()sin sin 2tan 21sin 2sin 30cos 22sin 30γθθβθθθ=≤=≤︒+︒+， 由sin sin γβ≤得γβ≤； ③sin sin sin γγα=⇒，则sin sin 2tan 2sin 2cos 22γθθαθ≤=<sin γα<，所以sin sin γα<，则γα<.故选：B例22．（2022·浙江·高三专题练习）已知等边ABC ，点,E F 分别是边,AB AC 上的动点，且满足EF BC ∥，将AEF △沿着EF 翻折至P 点处，如图所示，记二面角P EF B −−的平面角为α，二面角P FC B −−的平面角为β，直线PF 与平面EFCB 所成角为γ，则（ ）A ．αβγ≥≥B ．αγβ≥≥C ．βαγ≥≥D ．βγα≥≥【答案】A【解析】在等边ABC 中，取BC 边中点D ，连接AD ，交EF 于O ，连接PO ， 则,EF PO EF DO ⊥⊥，=PO DO O ⋂，PO ⊂平面POD ，DO ⊂平面POD 故EF ⊥平面POD ，又EF ⊂平面EFCB ，则平面POD ⊥平面EFCB 在POD 中，过P 做PM 垂直于OD 于M ，则PM ⊥平面EFCB ，连接MF ， 在等边ABC 中，过M 做MN 垂直于AC 于N ，连接PN.由,EF PO EF DO ⊥⊥，则POM ∠为二面角P EF B −−的平面角即POM α∠=， 由PM ⊥平面EFCB ，MN AC ⊥，则PNM ∠为二面角P FC B −−的平面角即PNM β?由PM ⊥平面EFCB ，则PFM ∠直线PF 与平面EFCB 所成角，即PFM γ?，设AO ，则PO ，=FO a ，sin PM α，cos MO αFM ，)1=cos (1cos )2MN αα+=+， 则有FM OM >，FM NM >由cos MO MN α-(1cos )(cos 1)0αα-+=-<可得MO MN <，则有FM MN OM >>，则111FM MN OM<< 又tan tan ,tan PM PM PMOM NM FMαβγ，=== 故tan tan tan αβγ>>，又0,2παβγ⎛⎫∈ ⎪⎝⎭、、故αβγ>> 故选：A例23．（2022·全国·高三专题练习）设三棱锥V ABC −的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P AC B −−的平面角是γ则三个角α，β，γ中最小的角是（ ） A ．α B ．β C ．γD ．不能确定【答案】B【解析】如图，取BC 的中点 D ，作VO ⊥平面ABC 于点O ， 由题意知点O 在AD 上，且AO =2OD .作PE //AC ，PE 交VC 于点E ，作PF ⊥AD 于点F ，连接BF ，则PF ⊥平面ABC 取AC 的中点M ，连接BM ，VM ，VM 交 PE 于点H ， 连接BH ，易知BH ⊥PE ， 作于点G ，连接FG ，由PG ⊥AC ，PF ⊥AC ，PG PF =P ，由线面垂直判定定理可得AC ⊥平面PGF ，又FG ⊂平面PGF ∴ FG ⊥AC , 作FN ⊥BM 于点N . ∵ PG ∥VM ，PF ∥VN∴ 平面PGF ∥平面VMB ， 又 PH ∥FN , 四边形PFNH 为平行四边形， 所以PH =FN因此，直线PB 与直线AC 所成的角=BPE α∠， 直线PB 与平面ABC 所成的角PBF β=∠， 二面角P -AC -B 的平面角PGF γ=∠， 又cos cos PH FN BFPB PB PBαβ==<=又,[0,]2παβ∈，∴ αβ> 因为 tan =tan PF PFGF BF γβ>= ,(0,)2πβγ∈∴ γβ>综上所述，,,αβγ中最小角为β，故选 B.。
高一数学空间的角试题答案及解析1.正方体中,异面直线与所成角度为 .【答案】【解析】如图，连结，由正方体的性质可知，所以或其补角为异面直线与所成的角，而为正三角形，所以，故异面直线与所成的角为.【考点】异面直线及其所成的角.2.如图，长方体中，，点分别是的中点，则异面直线与所成的角是（）A．30°B．45°C．60°D．90°【答案】D【解析】连接。
因为分别是的中点，所以∥且,所以四边形为平行四边形，所以∥，所以或其补角为异面直线与所成的角。
由已知可得，,，所以,所以为直角三角形且。
故D正确。
【考点】异面直线所成角。
3.如图平面SAC⊥平面ACB，ΔSAC是边长为4的等边三角形，ΔACB为直角三角形，∠ACB=90°，BC=，求二面角S-AB-C的余弦值。
【答案】【解析】先作出二面角的平面角。
由面面垂直可得线面垂直，作SD⊥平面ACB，然后利用三垂线定理作出二面角的平面角解：过S点作SD⊥AC于D，过D作DM⊥AB于M，连SM∵平面SAC⊥平面ACB∴SD⊥平面ACB∴SM⊥AB又∵DM⊥AB∴∠DMS为二面角S-AB-C的平面角在ΔSAC中SD=4×在ΔACB中过C作CH⊥AB于H∵AC=4，BC=∴AB=∵S=1/2AB·CH=1/2AC·BC∴CH=∵DM∥CH且AD=DC∴DM=1/2CH=∵SD⊥平面ACB DMÌ平面ACB∴SD⊥DM在RTΔSDM中SM===∴cos∠DMS===【考点】二面角的平面角点评：主要是考查了二面角的平面角的求解的运用，属于基础题。
4.如图，在棱长为的正方体中，分别是的中点，则异面直线与所成角等于【答案】【解析】注意到EF//BD,BD//,连，三角形是正三角形，所以，三角形内角为60°。
由异面直线所成角的定义，异面直线与所成角等于60°。
【考点】本题主要考查正方体的几何特征，异面直线所成的角，平行关系。
空间角计算专题典型题1、三棱锥P-ABC 中，PA=5，AB=3，BC=4，∠ABC=900，PA ⊥面ABC ，求：（1）PC 与平面ABC 所成角的大小的余弦值；（2）二面角P-BC-A 的大小的正切值。
2、三棱锥P-ABC 中，PA=6，AB=BC=AC=4，PA ⊥面ABC ，求：（1）PC 与平面ABC 所成角的大小余弦值；（2）二面角P-BC-A 的大小的正切值。
3、正三棱锥P-ABC 中，侧棱PA=6，底面AB=4，求：（1）PC 与平面ABC 所成角的大小余弦值；（2）侧面与底面所成二面角的大小的正切值。
4、四棱锥P-ABCD 中，PA=6，底面ABCD 是矩形，且AB=3，BC=4，PA ⊥面ABCD ，求：（1）PB 与CD 所成角的正切值；（2）PC 与平面ABC 所成角的大小的余弦值；（3）二面角P-BC-A 的大小的正切值。
5、正四棱锥P-ABCD 中，PA=6，底面BC=4，求：（1）PB 与CD 所成角的余弦值；（2）PC 与平面ABC所成角的大小的余弦值；（3）二面角P-BC-A 的大小的正切值。
AAA6、正四棱锥P-ABCD 中，每条棱长均为6，取棱PC 的中点E ，求：（1）AE 与BC 所成角的余弦值；（2）PB 与平面BDE 所成角的大小的余弦值；（3）二面角E-BD-C 的大小的正切值。
7、直三棱柱ABC-A 1B 1C 1中，底面AB=3，BC=4，∠ABC=900，侧棱长为5，求：（1）A 1B 与B 1C 1所成角大小的余弦值；（2）A 1C 与面ABB 1A 1所成角大小的余弦值；（3）二面角A-BC-A1的大小的正切值。
8、直三棱柱ABC-A 1B 1C 1中，底面AB=3，BC=4，∠ABC=900，侧棱长为5，取A 1C 1中点D 1，求：二面角A-BC-D 1的大小的正切值。
9、正三棱柱ABC-A 1B 1C 1中，底面AB=3，侧棱长为5，求：（1）A 1B与B 1C 1所成角大小的余弦值；（2）A 1C 与面ABB 1A 1所成角大小的余弦值；（3）二面角A-BC-A 1的大小的正切值。
高三数学空间的角试题答案及解析1.已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为( ) A．B．C．D．【答案】B【解析】设AD的中点为F，连接EF，CE则EF∥BD，所以异面直线CE与EF所成的夹角就是CE与BD所成的夹角，设正四面体ABCD的棱长为2a，则EF=a，CE=CF=a，由余弦定理可得cos∠CEF=,故选B.【考点】正多面体的性质和异面直线的夹角以及余弦定理.2.如图,在四棱锥P ABCD中,底面是边长为2的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2,M、N分别为PB、PD的中点.(1)证明:MN∥平面ABCD;(2)过点A作AQ⊥PC,垂足为点Q,求二面角A MN Q的平面角的余弦值.【答案】（1）见解析（2）【解析】(1)证明:连接BD,因为M、N分别是PB、PD的中点,所以MN是△PBD的中位线,所以MN∥BD.又因为MN⊄平面ABCD,BD⊂平面ABCD,所以MN∥平面ABCD.(2)解: 如图所示,在菱形ABCD中,∠BAD=120°,得AC=AB=BC=CD=DA,BD=AB.又因为PA⊥平面ABCD,所以PA⊥AB,PA⊥AC,PA⊥AD.所以PB=PC=PD.所以△PBC≌△PDC.而M、N分别是PB、PD的中点,所以MQ=NQ,且AM=PB=PD=AN.取线段MN的中点E,连接AE,EQ,则AE⊥MN,QE⊥MN,所以∠AEQ为二面角A MN Q的平面角.由AB=2,PA=2,故在△AMN中,AM=AN=3,MN=BD=3,得AE=.在直角△PAC中,AQ⊥PC,得AQ=2,QC=2,PQ=4,在△PBC中,cos∠BPC==,得MQ==.在等腰△MQN中,MQ=NQ=,MN=3,得QE==.在△AEQ中,AE=,QE=,AQ=2,得cos∠AEQ==.所以二面角A MN Q的平面角的余弦值为.3.在正四棱锥V ABCD中,底面正方形ABCD的边长为1,侧棱长为2,则异面直线VA与BD所成角的大小为()A．B．C．D．【答案】D【解析】如图所示,连接AC、BD,设AC∩BD=O,∵BD⊥AC,BD⊥VO,AC∩VO=O,∴BD⊥平面VAC,VA⊂平面VAC,∴BD⊥VA,即异面直线BD与VA所成的角是.4.正四棱锥S-ABCD的侧棱长为，底面边长为，E为SA的中点，则异面直线BE和SC所成的角为()．A．30°B．45°C．60°D．90°【答案】C【解析】设AC中点为O，则OE∥SC，连结BO，则∠BEO(或其补角)即为异面直线BE和SC 所成的角，EO＝SC＝，BO＝BD＝，在△SAB中，cos A＝＝＝＝，∴BE＝.△BEO中，cos∠BEO＝，∴∠BEO＝60°.5.如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB＝3，BC＝5．（1）求直线B1C1与平面A1BC1所成角的正弦值；（2）在线段BC1上确定一点D，使得AD⊥A1B，并求的值．【答案】（1）（2）【解析】（1）解决这类问题的思路是，根据几何体的结构特征找出或作出所求的线面角，再设法利用三角形知识求其正弦；或是建立适当的空间直角坐标系，借助法向量和直线的方向向量求直线与平面所成角的正弦；由于该问题中的几何体中棱的垂直关系较为明显，可采用后者. （2）在（1）中已建立空间直角坐标系的基础上，用向量法解决垂直问题很是方便.设D(x，y，z)是线段BC1上一点，且＝λ（λ∈[0，1]）,求出向量的坐标，利用互相垂直的向量的数量积为零建立方程，求出的值.试题解析：（1）∵AA1C1C为正方形，∴AA1⊥AC．∵平面ABC⊥平面AA1C1 C，∴AA1⊥平面ABC，∴AA1⊥AC，AA1⊥AB．由已知AB＝3，BC＝5，AC＝4，∴AB⊥AC．如图，以A为原点建立空间直角坐标系A-xyz，则B(0，3，0)，A1(0，0，4)，B1(0，3，4)，C1(4，0，4)，∴＝(0，3，－4)，＝(4，0，0)，＝(4，－3，0)．设平面A1BC1的法向量为n＝(x，y，z)，则即令z＝3，则x＝0，y＝4，∴n＝(0，4，3)．设直线B1C1与平面A1BC1所成的角为θ，则sinθ＝|cos＜，n＞|＝＝＝．故直线B1C1与平面A1BC1所成角的正弦值为． 6分（2）设D(x，y，z)是线段BC1上一点，且＝λ（λ∈[0，1]），∴(x，y－3，z)＝λ(4，－3，4)，∴x＝4λ，y＝3－3λ，z＝4λ，∴＝(4λ，3－3λ，4λ)．又＝(0，3，－4)，由·＝0，得3(3－3λ)－4×4λ＝0，即9－25λ＝0，解得λ＝∈[0，1]．故在线段BC1上存在点D，使得AD⊥A1B．此时＝λ＝． 12分【考点】1、直线与平面所成角的概念；2、空间直角坐标系；3、空间向量的夹角公式的应用. 6.如图，平面平面，是等腰直角三角形，，四边形是直角梯形，∥ＡＥ，，,分别为的中点．（1）求异面直线与所成角的大小；（2）求直线和平面所成角的正弦值．【答案】（1），（2）【解析】（1）求空间角，一般利用空间向量解决.首先要建立恰当的空间直角坐标系，由平面平面及，运用面面垂直性质定理，可得，这样确定竖坐标.横坐标与纵坐标可根据右手系建立.因为异面直线与所成角等于向量与夹角或其补角，而异面直线与所成角范围为，所以，（2）直线和平面所成角与向量与平面法向量夹角互余或相差，而直线和平面所成角范围为，所以.试题解析：∵，又∵面面，面面，，∴，∵BD∥AE，∴， 2分如图所示，以C为原点，分别以CA，CB为x，y轴，以过点C且与平面ABC垂直的直线为z 轴，建立空间直角坐标系，∵，∴设各点坐标为，，，，，则，，，，，.（1），则与所成角为. 5分（2）设平面ODM的法向量，则由，且可得令，则，，∴，设直线CD和平面ODM所成角为，则，∴直线CD和平面ODM所成角的正弦值为． 10分【考点】利用空间向量求异面直线所成角及直线与平面所成角.7.将正方形沿对角线折成一个直二面角，点到达点，则异面直线与所成角是( )A．B．C．D．【答案】B【解析】试题分析:方法一:如图,则所以与所成的角即为异面直线与所成角,设正方形边长为2,则,所以为等边三角形,故异面直线与所成角是.方法二:建立如图所示的空间坐标系,则所以 ,所以,故异面直线与所成角是.【考点】异面直线夹角的求法.8.如图，E,F分别是三棱锥的棱的中点，,则异面直线AB 与PC所成的角为( )A．B．C．D．【答案】C【解析】如图，取中点，连接，则,且或其补角为异面直线AB与PC所成的角，因为，所以，故其补角为异面直线AB与PC所成的角且等于，选C.【考点】余弦定理、异面直线所成的角.9.如图，正四棱柱中，，则异面直线与所成角的余弦值为( )A．B．C．D．【答案】D【解析】如图，连接，则，∴异面直线与所成的角等于.令，∴中，∴，即异面直线与所成角的余弦值为.故选D．【考点】几何体的结构特征，异面直线所成的角，余弦定理的应用.10.在三棱锥中，，底面是正三角形，、分别是侧棱、的中点. 若平面平面，则侧棱与平面所成角的正切值是( )A．B．C．D．【答案】A【解析】设的中点为，的中点为，连接，，．∵,∴在平面内的射影是等边的中心.∴是侧棱与平面所成的角.由已知得，设的中点为，则.∵平面平面，∴平面.∵，分别是侧棱，的中点，∴是的中点.∵，∴.设等边的边长为，侧棱长为，则.∵,∴.∴故选A.【考点】线面角11.如图,在长方体中,点在棱上.(1)求异面直线与所成的角；(2)若二面角的大小为,求点到面的距离.【答案】（1）对于异面直线的所成的角，一般采用平移法，平移到一个三角形中，借助于余弦定理求解。
考纲要求:1．能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题．了解向量方法在研究立体几何问题中的应用．基础知识回顾:1．两条异面直线所成角的求法设两条异面直线a，b的方向向量为a，b，其夹角为θ，则cos φ＝|cos θ|＝|a·b||a||b|(其中φ为异面直线a，b所成的角)．2．直线和平面所成的角的求法如图甲所示，设直线l的方向向量为e，平面α的法向量为n，直线l与平面α所成的角为φ，两向量e与n的夹角为θ，则有sin φ＝|cos θ|＝|n·e||n||e|.3．二面角的求法(1)如图乙中①，AB，CD是二面角α -l -β的两个面内与棱l垂直的直线，则二面角的大小θ＝〈AB，CD〉．(2)如图乙中②③，n1，n2分别是二面角α -l -β的两个半平面α，β的法向量，则二面角的大小θ＝〈n1，n2〉或π－〈n1，n2〉．应用举例:类型一、线线角问题1、利用共顶点互相垂直的三条棱建立空间直角坐标系例1．直三棱柱ABC -A 1B 1C 1中，∠BCA ＝90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC ＝CA ＝CC 1，则BM 与AN 所成角的余弦值为A ．110B ．25C ．3010D ．222、利用面面垂直建立空间直角坐标系例2．在正三棱柱ABC -A 1B 1C 1中，已知AB ＝2，CC 1＝2，则异面直线AB 1和BC 1所成角的正弦值为 ( )A ．1B ．77 C ．12 D ．32小结：注意向量的夹角与异面直线所成角的区别，当异面直线的方向向量的夹角为锐角或直角时，就是此异面直线所成的角；当异面直线的方向向量的夹角为钝角时，其补角才是异面直线所成的角． 类型二、线面角问题1、利用线面垂直建立空间直角坐标系例1、在三棱柱ABC -A 1B 1C 1中，侧面ABB 1A 1为矩形，AB ＝1，AA 1＝2，D 为AA 1的中点，BD 与AB 1交于点O ，CO ⊥侧面ABB 1A 1.(1)证明：BC ⊥AB 1；(2)若OC ＝OA ，求直线C 1D 与平面ABC 所成角的正弦值．解：(1)证明：由题意tan ∠ABD ＝AD AB ＝22，tan ∠AB 1B ＝AB BB 1＝22，注意到0<∠ABD ，∠AB 1B <π2，所以∠ABD ＝∠AB 1B ，所以∠ABD ＋∠BAB 1＝∠AB 1B ＋∠BAB 1＝π2，所以AB 1⊥BD ，又CO ⊥侧面ABB 1A 1，所以AB 1⊥CO .又BD 与CO 交于点O ， 所以AB 1⊥平面CBD ，又BC ⊂平面CBD ，所以BC ⊥AB 1.2、利用共顶点互相垂直的三条棱建立空间直角坐标系例2、四面体ABCD 及其三视图如图5所示，过棱AB 的中点E 作平行于AD ，BC 的平面分别交四面体的棱BD ，DC ，CA 于点F ，G ，H .(1)证明：四边形EFGH是矩形；(2)求直线AB与平面EFGH夹角θ的正弦值．解：(1)证明：由该四面体的三视图可知，BD⊥DC，BD⊥AD，AD⊥DC，BD＝DC＝2，AD＝1.由题设，BC∥平面EFGH，平面EFGH∩平面BDC＝FG，平面EFGH∩平面ABC＝EH，∴BC∥FG，BC∥EH，∴FG∥EH.同理EF∥AD，HG∥AD，∴EF∥HG，∴四边形EFGH是平行四边形．又∵AD⊥DC，AD⊥BD，∴AD⊥平面BDC，∴AD⊥BC，∴EF⊥FG，∴四边形EFGH是矩形．小结：利用平面的法向量求线面角时注意事项(1)求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)，取其余角即为所求．(2)若求线面角的余弦值，要注意利用平方关系sin2θ＋cos2θ＝1求出其值．不要误为直线的方向向量与平面的法向量所夹角的余弦值为所求．类型三、面面角问题1、利用线面垂直建立空间直角坐标系例1．如图7所示，在多面体ABCD-A1B1C1D1中，上、下两个底面A1B1C1D1和ABCD互相平行，且都是正方形，DD1⊥底面ABCD，AB＝2A1B1＝2DD1＝2a.(1)已知F 是AD 的中点，求证：FB 1⊥平面BCC 1B 1； (2)在(1)的条件下，求二面角F -CC 1-B 的余弦值．(2)由(1)知，1FB 为平面BCC 1B 1的一个法向量． 设n ＝(x 1，y 1，z 1)为平面FCC 1的法向量，∵1CC ＝(0，－a ，a )，FC ＝(－a,2a,0)，∴⎩⎨⎧n ·1CC ＝0，n ·FC ＝0，得⎩⎪⎨⎪⎧－ay 1＋az 1＝0，－ax 1＋2ay 1＝0.令y 1＝1，则n ＝(2,1,1)，∴cos 〈1FB ，n 〉＝1FB ·n |1FB |·|n |＝33，∵二面角F -CC 1-B 为锐角，∴二面角F -CC 1-B 的余弦值为33. 2、利用正方体建立空间直角坐标系例2、如图9，在棱长为2的正方体ABCD -A 1B 1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ ；(2)是否存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角？ 若存在，求出λ的值；若不存在，说明理由．(2)设平面EFPQ 的一个法向量为n ＝(x ，y ，z )，则由⎩⎨⎧FE ·n ＝0，FP ·n ＝0，可得⎩⎪⎨⎪⎧x ＋y ＝0，－x ＋λz ＝0.于是可取n ＝(λ，－λ，1)．同理可得平面MNPQ 的一个法向量为m ＝(λ－2,2－λ，1)． 若存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角， 则m ·n ＝(λ－2,2－λ，1)·(λ，－λ，1)＝0，即λ(λ－2)－λ(2－λ)＋1＝0，解得λ＝1±22.故存在λ＝1±22，使面EFPQ 与面PQMN 所成的二面角为直二面角．小结：求二面角时要注意判断其平面角是锐角还是钝角时，若不能判断二面角的平面角是锐角还是钝角时，要利用法向量的方向来判断法向量的夹角与二面角之间的关系是相等还是互补．方法、规律归纳:求空间角的基本方法：(1)建立适当的空间直角坐标系，便于坐标的求解．(2)利用向量法求异面直线1l 与2l 所成的角θ，主要求出两直线的方向向量1v 与2v ， 则cos θ＝12cos()v v .(3)利用向量法求斜线与平面所成的角的方法：①分别求出斜线和它在平面内的射影所在直线的方向向量，转化为求两个方向向量的夹角(或其补角)． ②通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角(若是钝角，取其补角)，取其余角就是斜线和平面所成的角． (4)利用向量法求二面角的方法：①分别求出二面角的两个面所在平面的法向量，然后通过两个面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．②分别在二面角的两个面内找到与棱垂直且以垂足出发的两个向量，则这两个向量的夹角的大小就是二面角的大小．实战演练:1．已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为( )A ．30°B ．60°C ．120°D ．150°解析 A ∵cos 〈m ，n 〉＝－12，∴〈m ，n 〉＝120°，∴直线l 与α所成的角为30°，故选A.2．如图11所示，在正方体ABCD -A 1B 1C 1D 1中，M ，N 分别为棱AA 1和BB 1的中点，则sin 〈CM →，D 1N →〉=()A.19B.459C.259D.23解析 B 设正方体的棱长为2，以D 为坐标原点，DA 为x 轴，DC 为y 轴， DD 1为z 轴建立空间直角坐标系(如图所示)，可知CM →＝(2，－2,1)， D 1N →＝(2,2，－1)． ∴cos 〈CM →，D 1N →〉＝－19，∴sin 〈CM →，D 1N →〉＝459.故选B.3．如图13，在正方体AC 1中，M 是棱DD 1的中点，O 是平面ABCD 的中心，P 是A 1B 1上的任意一点，则直线AM 与OP 所成角是( )A.π6B.π4C.π3D.π24.如图15所示，ABCD -A 1B 1C 1D 1是棱长为6的正方体，E 、F 分别是棱AB ， BC 上的动点，且AE ＝BF .当A 1，E ，F ，C 1共面时，平面A 1DE 与平 面C 1DF 所成锐二面角的余弦值为( )A.3 2B.12 C.15 D.265解析：以D为原点，DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，易知当E(6，3,0)、F(3,6,0)时，A1、E、F、C1共面，设平面A1DE的法向量为n1＝(a，b，c)，依题意得⎩⎪⎨⎪⎧n1·DE→＝6a＋3b＝0，n1·DA1→＝6a＋6c＝0，可取n1＝(－1,2,1)，同理可得平面C1DF的一个法向量为n2＝(2，－1,1)，故平面A1DE与平面C1DF所成锐二面角的余弦值为|n1·n2||n1|·|n2|＝12. 选B.5．在正三棱柱ABC -A1B1C1中，已知AB＝1，D在棱BB1上，且BD＝1，则AD与平面AA1C1C所成的角的正弦值为()A.64B．－64 C.104D．－1046. 如图17，棱长为a的正方体ABCD-A1B1C1D1，E、F分别为BC与A1D1的中点，则直线AD与平面B1EDF 所成角的余弦值为()图16A.32B.33C.12D ．－337．如图18，直三棱柱ABC -A 1B 1C 1中，AB ＝AC ＝1，AA 1＝2，∠B 1A 1C 1＝90°， D 为BB 1的中点，则异面直线C 1D 与A 1C 所成角的余弦值为________．解析：以A 为原点建立空间直角坐标系，如图19，A 1(0,0,2)，C (0,1,0)， D (1,0,1)，C 1(0,1,2)，则C 1D →＝(1，－1，－1)，A 1C →＝(0,1，－2)，|C 1D →|＝3， |A 1C →|＝5，C 1D →·A 1C →＝1，cosC 1D →，A 1C→C 1D →·A 1C →|C 1D →||A 1C →|＝1515， 故异面直线C 1D 与A 1C 所成角的余弦值为1515.8．正四棱锥S -ABCD中，O为顶点在底面上的射影，P为侧棱SD的中点，且SO＝OD，则直线BC与平面P AC所成的角是________．9．如图21，在四棱锥P-ABCD中，侧面P AD⊥底面ABCD，侧棱P A＝PD＝2，P A⊥PD，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AB＝BC＝1，O为AD的中点．(1)求直线PB与平面POC所成角的余弦值；(2)求B点到平面PCD的距离；(3)线段PD上是否存在一点Q，使得二面角Q-AC-D的余弦值为6 3？若存在，求出PQQD的值；若不存在，请说明理由．解：(1)在△P AD中，P A＝PD，O为AD的中点，所以PO⊥AD，又侧面P AD⊥底面ABCD，平面P AD∩平面ABCD＝AD，PO⊂平面P AD，所以PO⊥平面ABCD.又在直角梯形ABCD中，连结OC，易得OC⊥AD，所以以O 为坐标原点，直线OC 为x 轴，直线OD 为y 轴，直线OP 为z 轴建立空间直角坐标系，则P (0,0,1)，A (0，－1,0)，B (1，－1,0)，C (1,0,0)，D (0,1,0)， ∴PB ＝(1，－1，－1)，易证OA ⊥平面POC ，∴OA ＝(0，－1,0)是平面POC 的法向量，则cos 〈PB ，OA 〉＝PB ·OA |PB ||OA |＝33. ∴直线PB 与平面POC 所成角的余弦值为63.10．如图23，在四棱柱ABCD -A 1B 1C 1D 1中，底面ABCD 是等腰梯形，∠DAB ＝60°，AB ＝2CD ＝2，M 是线段AB 的中点．(1)求证：C 1M ∥平面A 1ADD 1；(2)若CD 1垂直于平面ABCD 且CD 1＝3，求平面C1D1M和平面ABCD所成的角(锐角)的余弦值．.解：(1)证明：因为四边形ABCD是等腰梯形，且AB＝2CD，所以AB∥DC，又由M是AB的中点，因此CD∥MA且CD＝MA. 连接AD1，在四棱柱ABCD-A1B1C1D1中，因为CD∥C1D1，CD＝C1D1，可得C1D1∥MA，C1D1＝MA，所以四边形AMC1D1为平行四边形，因此C1M∥D1A.又C1M⊄平面A1ADD1，D1A⊂平面A1ADD1，所以C1M∥平面A1ADD1.：。
高二数学空间的角试题答案及解析1.在正方体中，直线与平面所成角的大小为____________．【答案】.【解析】连接，，连接.由正方体的性质可得，且，所以平面，所以可得为直线与平面所成的角.设正方体的棱长为，则，.在中，，从而得到答案为.【考点】直线与平面所成的角；棱柱的结构特征．2.如图是一个正方体的表面展开图，A、B、C均为棱的中点，D是顶点，则在正方体中，异面直线AB和CD的夹角的余弦值为。
【答案】【解析】试题分析:把正方体的表面展开图还原成正方体，设的中点为，连接，又，则为异面直线AB和CD所成的角，由余弦定理可得。
【考点】（1）异面直线所成角的定义；（2）平行公里；（3）余弦定理的应用。
3.空间四边形ABCD中，M，N分别是AB和CD的中点，AD=BC=6，MN=则AD和BC所成的角是（）A．B．C．D．【答案】B【解析】取线段AC的中点P.由于M,N都是中点.所以QN=3，QM=3.又因为.所以三角形MNP是直角三角形.即MP⊥PN,又因为MP∥BC, PN∥AD.所以AD⊥BC.本题主要是应用三角形的中位线的知识.含中点的题一般都的转化为中位线的知识.【考点】1.异面直线所成的角.2.中位线定理.3.空间问题向平面问题转化.4.在正方体中，是的中点，则异面直线与所成角的大小是（）A．B．C．D．【答案】D【解析】在正方体中，容易得到平面，又因为平面,故得到.【考点】异面直线所成角.5.在三棱锥中,是边长为2的正三角形,平面平面,,分别为的中点.(1)证明:;(2)求锐二面角的余弦值;【答案】（1）见试题解析；（2）．【解析】（1）要证线线垂直，一般可先证线面垂直，而本题中有，是等边三角形，故可以取中点为，则有，，这是等腰三角形的常用辅助线的作法；（2）关键是作出所求二面角的平面角，由已知及（1）中辅助线，可知平面，由于是中点，故只要取中点，则有，也即平面，有了平面的垂线，二面角的平面角就容易找到了。
空间三大角一、线线角1．（2021年全国高考乙卷数学（文）试题）在正方体1111ABCD A B C D -中，P 为11B D 的中点，则直线PB 与1AD 所成的角为（ ）A ．π2B ．π3C ．π4D ．π62.（2018年全国普通高等学校招生统一考试理数（全国卷II ））在长方体1111ABCD A B C D -中，1AB BC ==，13AA =，则异面直线1AD 与1DB 所成角的余弦值为（ ）A ．15B ．56C ．55D ．223.（2015年全国普通高等学校招生统一考试理科数学（新课标Ⅰ））如图，四边形ABCD 为菱形，ⅠABC =120°，E ，F 是平面ABCD 同一侧的两点，BE Ⅰ平面ABCD ，DF Ⅰ平面ABCD ，BE =2DF ，AE ⅠEC ． （1）证明：平面AEC Ⅰ平面AFC ；（2）求直线AE 与直线CF 所成角的余弦值．二、线面角1.（2018年全国普通高等学校招生统一考试理科数学（新课标I 卷））如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥. （1）证明：平面PEF ⊥平面ABFD ；（2）求DP 与平面ABFD 所成角的正弦值.2. （2018年全国普通高等学校招生统一考试理数（全国卷II ））如图，在三棱锥P ABC -中，22AB BC ==，4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30，求PC 与平面PAM 所成角的正弦值．3.（2016年全国普通高等学校招生统一考试理科数学（新课标3卷））如图，四棱锥P−ABCD 中，PAⅠ底面ABCD ，ADⅠBC ，AB=AD=AC=3，PA=BC=4，M 为线段AD 上一点，AM=2MD ，N 为PC 的中点. （Ⅰ）证明MNⅠ平面PAB;（Ⅰ）求直线AN 与平面PMN 所成角的正弦值.三、二面角1（2021年全国高考乙卷数学（理）试题）如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，1PD DC ==，M 为BC 的中点，且PB AM ⊥．（1）求BC ；（2）求二面角A PM B --的正弦值．2.（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））如图，在长方体1111ABCD A B C D -中，点,E F 分别在棱11,DD BB 上，且12DE ED =，12BF FB =．（1）证明：点1C 在平面AEF 内；（2）若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．3.（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，ⅠBAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MNⅠ平面C1DE；（2）求二面角A-MA1-N的正弦值．4.（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BEⅠEC1.（1）证明：BEⅠ平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值.5. （2018年全国卷Ⅰ理数高考试题）如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点．（1）证明：平面AMD ⊥平面BMC ；（2）当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．6.（2017年全国普通高等学校招生统一考试理科数学（新课标1卷））如图，在四棱锥P−ABCD 中，AB//CD ，且90BAP CDP ∠=∠=.（1）证明：平面P AB Ⅰ平面P AD ；（2）若P A =PD =AB =DC ，90APD ∠=，求二面角A −PB −C 的余弦值.7.（2017年全国普通高等学校招生统一考试理科数学（新课标3））（2017新课标全国Ⅰ理科）如图，四面体ABCD 中，ⅠABC 是正三角形，ⅠACD 是直角三角形，ⅠABD =ⅠCBD ，AB =BD ．（1）证明：平面ACD Ⅰ平面ABC ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D –AE –C 的余弦值.8.（2016年全国普通高等学校招生统一考试）试题）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，四边形ABEF 为正方形，2AF FD =，90AFD ∠=︒，且二面角D AF E --与二面角C BE F --都是60︒.（1）证明：平面ABEF ⊥平面EFDC ；（2）求二面角E BC A --的余弦值.9.（2016年全国普通高等学校招生统一考试数学）如图，菱形ABCD 的对角线AC 与BD 交于点,5,6O AB AC ==，点,E F 分别在,AD CD 上，5,4AE CF EF ==交BD 于点H ，将DEF ∆沿EF 折到D EF '∆位置，10OD '=.（1）证明：D H '⊥平面ABCD ；（2）求二面角B D A C '--的正弦值.答 案一、线线角1【答案】D如图，连接11,,BC PC PB ，因为1AD Ⅰ1BC ，所以1PBC ∠或其补角为直线PB 与1AD 所成的角， 因为1BB ⊥平面1111D C B A ，所以11BB PC ⊥，又111PC B D ⊥，1111BB B D B ⋂=，所以1PC ⊥平面1PBB ，所以1PC PB ⊥，设正方体棱长为2，则1111122,22BC PC D B === 1111sin 2PC PBC BC ∠==，所以16PBC π∠=. 2.【答案】C 【详解】：以D 为坐标原点，DA,DC,DD 1为x,y,z 轴建立空间直角坐标系，则11(0,0,0),(1,0,0),(1,13),3)D A B D ,所以11(1,0,3),(1,13)AD DB =-=, 因为11111115cos ,25AD DB AD DB AD DB ⋅-===⨯，所以异面直线1AD 与1DB 5 3.【解析】：（Ⅰ）连接BD ，设BD∩AC=G ，连接EG ，FG ，EF ，在菱形ABCD 中，不妨设GB=1易证EGⅠAC ，通过计算可证EGⅠFG ，根据线面垂直判定定理可知EGⅠ平面AFC ，由面面垂直判定定理知平面AFCⅠ平面AEC ；（Ⅰ）以G 为坐标原点，分别以,GB GC 的方向为x 轴，y 轴正方向，||GB 为单位长度，建立空间直角坐标系G -xyz ，利用向量法可求出异面直线AE 与CF 所成角的余弦值.试题解析：（Ⅰ）连接BD ，设BD∩AC=G ，连接EG ，FG ，EF ，在菱形ABCD 中，不妨设GB=1，由ⅠABC=120°，可得3由BEⅠ平面ABCD ，AB=BC 可知，AE=EC ，又ⅠAEⅠEC ，3，EGⅠAC ，在RtⅠEBG 中，可得2，故DF=22.在RtⅠFDG 中，可得6 在直角梯形BDFE 中，由BD=2，2，2可得32，Ⅰ222EG FG EF +=，ⅠEGⅠFG ， ⅠAC∩FG=G ，ⅠEGⅠ平面AFC ，ⅠEG ⊂面AEC ，Ⅰ平面AFCⅠ平面AEC.（Ⅰ）如图，以G 为坐标原点，分别以,GB GC 的方向为x 轴，y 轴正方向，||GB 为单位长度，建立空间直角坐标系G -xyz ，由（Ⅰ）可得A （030），E （1,0, 2，F （－1,02，C （030），ⅠAE =（1，3，2），CF =（-1，-3，22）.…10分 故3cos ,3AE CFAE CF AE CF ⋅==-. 所以直线AE 与CF 所成的角的余弦值为33. 二、线面角1.【分析】（1）由已知可得，BF PF ⊥，BF EF ⊥，又PFEF F =，所以BF ⊥平面PEF . 又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD ；（2）作PH EF ⊥，垂足为H .由（1）得，PH ⊥平面ABFD .以H 为坐标原点，HF 的方向为y 轴正方向，BF 为单位长，建立如图所示的空间直角坐标系H xyz -. 由（1）可得，DE PE ⊥.又2DP =，1DE =，所以3PE =.又1PF =，2EF =，故PE PF ⊥.可得33,22PH EH ==.则()33330,0,0,0,0,,1,,0,1,,,2222H P D DP ⎛⎫⎛⎫⎛⎫--= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭30,0,2HP ⎛⎫= ⎪ ⎪⎝⎭为平面ABFD 的法向量. 设DP 与平面ABFD 所成角为θ，则334sin 43HP DP HP DPθ⋅===⋅. 所以DP 与平面ABFD 所成角的正弦值为34. 2.【分析】（1）因为4AP CP AC ===，O 为AC 的中点，所以OP AC ⊥，且23OP =． 连结OB ．因为22AB BC AC ==，所以ABC 为等腰直角三角形，且1,22OB AC OB AC ⊥== 由222OP OB PB +=知PO OB ⊥．由,OP OB OP AC ⊥⊥知PO ⊥平面ABC ．（2）如图，以O 为坐标原点，OB 的方向为x 轴正方向，建立空间直角坐标系O xyz -由已知得(0,0,0),(2,0,0),(0,2,0),(0,2,0),(0,0,23),(0,2,23)O B A C P AP -= 取平面PAC 的法向量(2,0,0)OB =．设(,2,0)(02)M a a a -<≤，则(,4,0)AM a a =-． 设平面PAM 的法向量为(,,)n x y z =．由0,0AP n AM n ⋅=⋅=得2230(4)0y z ax a y ⎧+=⎪⎨+-=⎪⎩， 可取2(3(4),3,)n a a a =--所以22223(4)cos 23(4)3a OB n a a a -〈⋅〉=-++ ．由已知得3cos 2OB n 〈⋅〉= ． 所以22223|4|3223(4)3a a a a -=-++ ．解得4a =-(舍去)，43a = ．所以83434,,333n ⎛⎫=-- ⎪ ⎪⎝⎭ ． 又(0,2,23)PC =- ，所以3cos ,4PC n 〈〉=． 所以PC 与平面PAM 所成角的正弦值为34． 3.【详解】（Ⅰ）由已知得. 取的中点T ，连接，由为中点知，. 又，故=TN AM ∥，四边形AMNT 为平行四边形，于是MN AT ∥. 因为平面，平面，所以平面. （Ⅰ）取的中点，连结.由得，从而，且 . 以A 为坐标原点， AE 的方向为轴正方向，建立如图所示的空间直角坐标系.由题意知， ，，，， (0,2,4)PM =-， 5(,1,2)2PN =-，5(,1,2)2AN =.设(,,)x y z =n 为平面 PMN 的一个法向量，则0,{0,n PM n PN ⋅=⋅=即 240,520,2y z x y z -=+-= 可取(0,2,1)n =.于是85cos ,25n AN n AN n AN⋅〈〉==. 三、二面角1【分析】（1）PD ⊥平面ABCD ，四边形ABCD 为矩形，不妨以点D 为坐标原点，DA 、DC 、DP所在直线分别为x 、y 、z 轴建立如上图所示的空间直角坐标系D xyz -， 设2BC a =，则()0,0,0D 、()0,0,1P 、()2,1,0B a 、(),1,0M a 、()2,0,0A a ， 则()2,1,1PB a =-，(),1,0AM a =-，PB AM ⊥，则2210PB AM a ⋅=-+=，解得22a =，故22BC a ==； （2）设平面PAM 的法向量为()111,,m x y z =，则22AM ⎛⎫=-⎪ ⎪⎝⎭，()2,0,1AP =-， 由111120220m AM x y m AP x z ⎧⋅=-+=⎪⎨⎪⋅=-+=⎩，取12x =，可得()2,1,2m =，设平面PBM 的法向量为()222,,n x y z =，2,0,02BM ⎛⎫=- ⎪ ⎪⎝⎭，()2,1,1BP =--，由222220220n BM x n BP x y z ⎧⋅=-=⎪⎨⎪⋅=--+=⎩，取21y =，可得()0,1,1n =，3314cos ,1472m n m n m n⋅<>===⨯⋅，所以，270sin ,1cos ,14m n m n <>=-<>=，因此，二面角A PM B --的正弦值为7014. 2.【分析】（1）在棱1CC 上取点G ，使得112C G CG =，连接DG 、FG 、1C E 、1C F ， 在长方体1111ABCD A B C D -中，//AD BC 且AD BC =，11//BB CC 且11BB CC =，112C G CG =，12BF FB =，112233CG CC BB BF ∴===且CG BF =，所以，四边形BCGF 为平行四边形，则//AF DG 且AF DG =， 同理可证四边形1DEC G 为平行四边形，1//C E DG ∴且1C E DG =，1//C E AF ∴且1C E AF =，则四边形1AEC F 为平行四边形，因此，点1C 在平面AEF 内；（2）以点1C 为坐标原点，11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系1C xyz -，则()2,1,3A 、()12,1,0A 、()2,0,2E 、()0,1,1F ， ()0,1,1AE =--，()2,0,2AF =--，()10,1,2A E =-，()12,0,1A F =-，设平面AEF 的法向量为()111,,m x y z =，由0m AE m AF ⎧⋅=⎪⎨⋅=⎪⎩，得11110220y z x z --=⎧⎨--=⎩取11z =-，得111x y ==，则()1,1,1m =-，设平面1A EF 的法向量为()222,,n x y z =，由1100n A E n A F ⎧⋅=⎪⎨⋅=⎪⎩，得22222020y z x z -+=⎧⎨-+=⎩，取22z =，得21x =，24y =，则()1,4,2n =，37cos ,7321m n m n m n⋅<>===⨯⋅， 设二面角1A EF A --的平面角为θ，则7cos 7θ=，242sin 1cos 7θθ∴=-=. 因此，二面角1A EF A --的正弦值为427. 3【分析】（1）连接ME ，1B CM ，E 分别为1BB ，BC 中点 ME ∴为1B BC ∆的中位线 1//ME B C ∴且112ME B C =又N 为1A D 中点，且11//A D B C 1//ND B C ∴且112ND B C =//ME ND ∴ ∴四边形MNDE 为平行四边形//MN DE ∴，又MN ⊄平面1C DE ，DE ⊂平面1C DE //MN ∴平面1C DE（2）设AC BD O ⋂=，11111A C B D O ⋂= 由直四棱柱性质可知：1OO ⊥平面ABCD 四边形ABCD 为菱形 AC BD ∴⊥则以O 为原点，可建立如下图所示的空间直角坐标系： 则：()3,0,0A，()0,1,2M ，()13,0,4A ，D （0，-1,0）31,,222N ⎛⎫- ⎪ ⎪⎝⎭取AB 中点F ，连接DF ，则31,,022F ⎛⎫⎪⎪⎝⎭四边形ABCD 为菱形且60BAD ∠= BAD ∴∆为等边三角形 DF AB ∴⊥ 又1AA ⊥平面ABCD ，DF ⊂平面ABCD 1DF AA ∴⊥DF ∴⊥平面11ABB A ，即DF ⊥平面1AMADF ∴为平面1AMA 的一个法向量，且33,,022DF ⎛⎫= ⎪ ⎪⎝⎭设平面1MA N 的法向量(),,n x y z =，又()13,1,2MA =-，33,,022MN ⎛⎫=- ⎪ ⎪⎝⎭132033022n MA x y z n MN x y ⎧⋅=-+=⎪∴⎨⋅=-=⎪⎩，令3x =，则1y =，1z =- ()3,1,1n ∴=-315cos ,515DF n DF n DF n⋅∴===⋅ 10sin ,5DF n ∴=∴二面角1A MA N --的正弦值为：1054.【分析】证明（1）因为1111ABCD A B C D -是长方体，所以11B C ⊥侧面11A B BA ，而BE ⊂平面11A B BA ，所以11BE B C ⊥又1BE EC ⊥，1111B C EC C ⋂=，111,B C EC ⊂平面11EB C ，因此BE ⊥平面11EB C ； （2）以点B 坐标原点，以1,,BC BA BB 分别为,,x y z 轴，建立如下图所示的空间直角坐标系，1(0,0,0),(,0,0),(,0,),(0,,)2b B C a C a b E a ，因为1BE EC ⊥，所以2210(0,,)(,,)002224b b b BE EC a a a a b a ⋅=⇒⋅-=⇒-+=⇒=，所以(0,,)E a a ，1(,,),(0,0,2),(0,,)EC a a a CC a BE a a =--==， 设111(,,)m x y z =是平面BEC 的法向量，所以111110,0,(0,1,1)0.0.ay az m BE m ax ay az m EC +=⎧⎧⋅=⇒⇒=-⎨⎨--=⋅=⎩⎩， 设222(,,)n x y z =是平面1ECC 的法向量，所以2122220,0,(1,1,0)0.0.az n CC n ax ay az n EC =⎧⎧⋅=⇒⇒=⎨⎨--=⋅=⎩⎩， 二面角1B EC C --的余弦值的绝对值为11222m n m n ⋅==⨯⋅，所以二面角1B EC C --的正弦值为2131()22-=. 5.【分析】解：（1）由题设知,平面CMD Ⅰ平面ABCD ,交线为CD .因为BC ⅠCD ,BC ⊂平面ABCD ,所以BC Ⅰ平面CMD ,故BC ⅠDM .因为M 为CD 上异于C ，D 的点,且DC 为直径，所以 DM ⅠCM . 又 BC CM =C ,所以DM Ⅰ平面BMC . 而DM ⊂平面AMD ,故平面AMD Ⅰ平面BMC .（2）以D 为坐标原点,DA 的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz . 当三棱锥M −ABC 体积最大时，M 为CD 的中点.由题设得()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,1,1D A B C M ，()()()2,1,1,0,2,0,2,0,0AM AB DA =-==设(),,n x y z =是平面MAB 的法向量,则0,0.n AM n AB ⎧⋅=⎨⋅=⎩即20,20.x y z y -++=⎧⎨=⎩ 可取()1,0,2n =.DA 是平面MCD 的法向量, 因此5cos ,5n DA n DA n DA⋅==，25sin ,5n DA =，所以面MAB 与面MCD 所成二面角的正弦值是255. 6.【详解】（1）由已知90BAP CDP ∠=∠=︒，得AB ⅠAP ，CD ⅠPD ．由于AB//CD ，故AB ⅠPD ，从而AB Ⅰ平面P AD ．又AB ⊂平面P AB ，所以平面P AB Ⅰ平面P AD ． （2）在平面PAD 内作PF AD ⊥，垂足为F ，由（1）可知，AB ⊥平面PAD ，故AB PF ⊥，可得PF ⊥平面ABCD .以F 为坐标原点，FA 的方向为x 轴正方向，AB 为单位长，建立如图所示的空间直角坐标系F xyz -. 由（1）及已知可得2,0,02A ⎛⎫ ⎪⎪⎝⎭，20,0,2P ⎛⎫ ⎪ ⎪⎝⎭，2,1,02B ⎛⎫ ⎪ ⎪⎝⎭，2,1,02C ⎛⎫- ⎪ ⎪⎝⎭. 所以22,1,22PC ⎛⎫=-- ⎪ ⎪⎝⎭，()2,0,0CB =，22,0,22PA ⎛⎫=- ⎪ ⎪⎝⎭，()0,1,0AB =.设(),,n x y z =是平面PCB 的法向量，则0,0,n PC n CB ⎧⋅=⎨⋅=⎩即220,2220,x y z x ⎧-+-=⎪⎨⎪=⎩可取()0,1,2n =--. 设(),,m x y z =是平面PAB 的法向量，则0,0,m PA m AB ⎧⋅=⎨⋅=⎩即220,220.x z y ⎧-=⎪⎨⎪=⎩可取()1,0,1m =. 则3cos ,3n m n m n m ⋅==-， 所以二面角A PB C --的余弦值为33-. 7.【解析】：（1）由题设可得，ABD CBD ≌△△，从而AD DC =. 又ACD △是直角三角形，所以=90ADC ∠︒. 取AC 的中点O ，连接DO ,BO ,则DO ⅠAC ,DO =AO . 又由于ABC 是正三角形，故BO AC ⊥. 所以DOB ∠为二面角D AC B --的平面角. 在Rt AOB 中，222BO AO AB +=.又AB BD =，所以222222BO DO BO AO AB BD +=+==，故90DOB ∠=. 所以平面ACD Ⅰ平面ABC .（2）由题设及（1）知，,,OA OB OD 两两垂直，以O 为坐标原点，OA 的方向为x 轴正方向，OA 为单位长，建立如图所示的空间直角坐标系O xyz -.则()()()()1,0,0,0,3,0,1,0,0,0,0,1A B C D -.由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得310,,22E ⎛⎫ ⎪ ⎪⎝⎭. 故()()311,0,1,2,0,0,1,,22AD AC AE ⎛⎫=-=-=- ⎪ ⎪⎝⎭.设(),,n x y z =是平面DAE 的法向量，则00n AD n AE ⎧⋅=⎨⋅=⎩，，即0,310.22x z x y z -+=⎧⎪⎨-++=⎪⎩可取31,,13⎛⎫= ⎪ ⎪⎝⎭n . 设m 是平面AEC 的法向量，则00m AC m AE ⎧⋅=⎨⋅=⎩，，同理可取()0,1,3=-m .则7cos ,7⋅==n m n m n m . 所以二面角D -AE -C 的余弦值为77.8.【分析】（Ⅰ）因为四边形ABEF 为正方形，所以AF FE ⊥， 又AF DF ⊥，DF FE F ⋂=，所以AF ⊥平面EFDC ． 又AF ⊂平面ABEF ，故平面ABEF ⊥平面EFDC ． （Ⅰ）过D 作DG EF ⊥，垂足为G ， 因为平面ABEF ⊥平面EFDC ，平面ABEF平面EFDCEF ，DG ⊂平面EFDC ，故DG ⊥平面ABEF ．以G 为坐标原点，GF 的方向为x 轴正方向，GD 的方向为z 轴正向， 建立如图所示的空间直角坐标系G xyz -．由（Ⅰ）知DFE ∠为二面角D AF E --的平面角，故60DFE ∠=︒， 设()20DF a a =>，则3DG a =，FG a =，所以(),4,0A a a ，()3,4,0B a a -，()3,0,0E a -，()0,0,3D a ． 由已知，//AB EF ，而AB ⊄平面EFDC ，EF ⊂平面EFDC ， 所以//AB 平面EFDC ，又平面ABCD 平面EFDC DC =，AB ⊂平面ABCD ，故//AB CD ，所以//CD EF ．由//BE AF ，可得BE ⊥平面EFDC ，同理CEF ∠为二面角C BE F --的平面角， 所以60CEF ∠=︒，从而可得()2,0,3C a a -．所以(),0,3EC a a =，()0,4,0EB a =，()3,4,3AC a a a =--，()4,0,0AB a =-． 设(),,n x y z =是平面BCE 的法向量，则00n EC n EB ⎧⋅=⎨⋅=⎩，即3040ax az ay ⎧+=⎪⎨=⎪⎩，取3x =，则0,3y z ==-，可取()3,0,3n =-．设m 是平面ABCD 的法向量，则00m AC m AB ⎧⋅=⎨⋅=⎩，同理可取()0,3,4m =，则43219cos ,192319n m n m n m⋅〈〉==-=-⨯．因为二面角E BC A --的平面角为钝角，故二面角E BC A --的余弦值为21919-．9.【详解】：(1)由已知得AC BD ⊥，AD CD =,又由AE CF =得AE CFAD CD=，故AC ⅠEF ，因此 EF HD ⊥，从而EF ⅠD H '.由56AB AC ==，得224DO BO AB AO ==-=.由AC ⅠEF 得14OH AE DO AD ==.所以1OH =,3D H DH '==. 于是222223110D H OH D O +=+='=',故D H OH '⊥.又D H EF '⊥,而OH EF H =,所以D H'⊥平面ABCD .如图，以H 为坐标原点，HF 的方向为x 轴的正方向，建立空间直角坐标系H xyz -，则()0,0,0H ，()3,1,0A --，()0,6,0B -，()3,1,0C -，()0,0,3D '，()3,4,0AB =-，()6,0,0AC =，()3,1,3AD '=.设()111,,m x y z =是平面ABD '的法向量， 则0{m AB m AD '⋅=⋅=，即11111340{330x y x y z -=++=，可取()4,3,5m =-.设()222,,n x y z =是平面ACD '的法向量， 则0{n AC n AD '⋅=⋅=，即222260{330x x y z =++=，可取()0,3,1n =-于是1475cos ,255010m n m n m n ⋅-===-⨯， 设二面角的大小为θ，295sin 25θ=.因此二面角B D A C '--的正弦值是29525.。
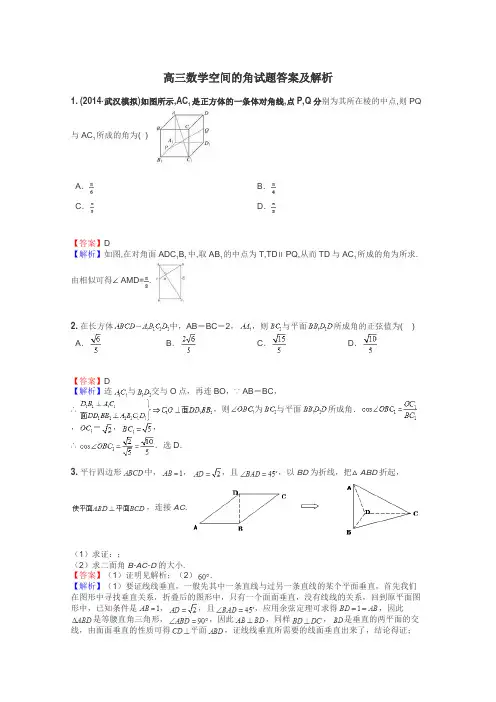
高三数学空间的角试题答案及解析1.(2014·武汉模拟)如图所示,AC1是正方体的一条体对角线,点P,Q分别为其所在棱的中点,则PQ与AC1所成的角为( )A．B．C．D．【答案】D【解析】如图,在对角面ADC1B1中,取AB1的中点为T,TD∥PQ,从而TD与AC1所成的角为所求.由相似可得∠AMD=.2.在长方体中，AB＝BC＝2，，则与平面所成角的正弦值为( ) A．B．C．D．【答案】D【解析】连与交与O点，再连BO，∵AB＝BC，∴，则为与平面所成角．，＝，，∴．选D．3.平行四边形中，，，且，以BD为折线，把△ABD折起，，连接AC.（1）求证：；（2）求二面角B-AC-D的大小.【答案】（1）证明见解析；（2）．【解析】（1）要证线线垂直，一般先其中一条直线与过另一条直线的某个平面垂直，首先我们在图形中寻找垂直关系，折叠后的图形中，只有一个面面垂直，没有线线的关系，回到原平面图形中，已知条件是，，且，应用余弦定理可求得，因此是等腰直角三角形，，因此，同样，是垂直的两平面的交线，由面面垂直的性质可得平面，证线线垂直所需要的线面垂直出来了，结论得证；（2）求二面角，可以根据二面角的定义作二面角的平面角，首先寻找两个面中其中一个平面的垂线，由题意，取中点，则，从而可证平面，那么只要作，垂足为，则就是所要的平面角，当然本题也可用空间向量法求．试题解析：（1）在中，,易得．面面面4分（2）法一：在四面体ABCD中，以D为原点，DB为x轴，DC为y轴，过D垂直于平面BDC 的直线为z轴，建立如图空间直角坐标系.则D（0，0，0），B（1，0，0），C（0，1，0），A （1，0，1）. 6分设平面ABC的法向量为，而，由得：，取 8分再设平面DAC的法向量为，而，由得：，取 10分所以，所以二面角B-AC-D的大小是60°. 12分法二：取BC的中点E,连DE,过D作DF AC于F,连EF,则是二面角B-AC-D的平面角 8分,∴ 12分法三：补成正方体．【考点】（1）证线线垂直；（2）求二面角．4.已知圆锥母线长为6，底面圆半径长为4，点是母线的中点，是底面圆的直径，底面半径与母线所成的角的大小等于．（1）当时，求异面直线与所成的角；（2）当三棱锥的体积最大时，求的值．【答案】（1）或，（2）.【解析】（1）求异面直线所成角，关键在平移，即将空间角转化为平面角.利用中位线实现线线之间平移. 连，过作，则等于异面直线与所成的角或其补角.又，所以为异面直线OC与PB所成的角或其补角.明确角之后，只需在相应三角形中求解即可.（2）因为三棱锥的高确定，所以要使得三棱锥的体积最大只要底面积的面积最大．而的两边确定为半径，因此要使得的面积最大，只需两半径夹角的正弦值最大，也即为直角.试题解析：解：（1）连，过作交于点，连．又，．又．，等于异面直线与所成的角或其补角．，或． 5分当时，．，当时，．，综上异面直线与所成的角等于或． 8分（2）三棱锥的高为且长为，要使得三棱锥的体积最大只要底面积的面积最大．而当时，的面积最大． 10分又，此时，， 12分【考点】异面直线所成角5.四棱锥P-ABCD的底面ABCD是边长为2的正方形，PA⊥底面ABCD且PA =4，则PC与底面ABCD所成角的正切值为．【答案】【解析】因为PA⊥底面ABCD，所以PC与底面ABCD所成角的为，因此【考点】直线与平面所成角6.如图所示，在正三角形ABC中，D，E，F分别为各边的中点，G，H分别为DE，AF的中点，将△ABC沿DE，EF，DF折成正四面体P－DEF，则四面体中异面直线PG与DH所成的角的余弦值为________．【答案】【解析】折成的四面体是正四面体，画出立体图形，根据中点找平行线，把所求的异面直线所成角转化为一个三角形的内角．如图所示，联结HE，取HE的中点K，联结GK，PK，则GK∥DH，故∠PGK即为所求的异面直线所成角或其补角．设这个正四面体的棱长为2，在△PGK中，PG＝，GK＝，PK＝＝，故cos∠PGK＝＝，即异面直线PG与DH所成的角的余弦值是.7.如图，平面平面，是等腰直角三角形，，四边形是直角梯形，∥ＡＥ，，,分别为的中点．（1）求异面直线与所成角的大小；（2）求直线和平面所成角的正弦值．【答案】（1），（2）【解析】（1）求空间角，一般利用空间向量解决.首先要建立恰当的空间直角坐标系，由平面平面及，运用面面垂直性质定理，可得，这样确定竖坐标.横坐标与纵坐标可根据右手系建立.因为异面直线与所成角等于向量与夹角或其补角，而异面直线与所成角范围为，所以，（2）直线和平面所成角与向量与平面法向量夹角互余或相差，而直线和平面所成角范围为，所以.试题解析：∵，又∵面面，面面，，∴，∵BD∥AE，∴， 2分如图所示，以C为原点，分别以CA，CB为x，y轴，以过点C且与平面ABC垂直的直线为z 轴，建立空间直角坐标系，∵，∴设各点坐标为，，，，，则，，，，，.（1），则与所成角为. 5分（2）设平面ODM的法向量，则由，且可得令，则，，∴，设直线CD和平面ODM所成角为，则，∴直线CD和平面ODM所成角的正弦值为． 10分【考点】利用空间向量求异面直线所成角及直线与平面所成角.8.已知三棱柱的侧棱与底面垂直，体积为，底面是边长为的正三角形.若为底面的中心，则与平面所成角的大小为( )A．.B．C．D．【答案】B【解析】如图所示，∵底面，∴为与平面所成角，∵平面∥平面，∴为与平面所成角，∵，∴，解得，又为底面正三角形的中心，∴在中，，∴，故选B．【考点】直线与平面所成的角．9.在三棱柱中，各侧面均为正方形，侧面的对角线相交于点，则与平面所成角的大小是（）A．30°B．45°C．60°D．90【答案】C【解析】由题意可知此三棱柱为正三棱柱，点为侧面的中心，取中点，连接为与平面所成角，设侧棱长为2，【考点】直线与平面所成角点评：求线面角时要先通过斜线上一点做平面的垂线，进而得到斜线的射影，只需在三角形中求解斜线与射影的夹角10.已知正方体中，、分别为、的中点，则异面直线与所成角的余弦值为（）A．B．C．D．0【答案】C【解析】如图，，是异面直线与所成的角，，选C。
