数学中等职业学校《基础模块》第一册期末考试--数学试卷

中职数学（基础模块）期末试题一 选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个 选项中只有一项是符合题目要求，把正确选项写在表格中。

1.给出 四个结论：①｛1，2，3，1｝是由4个元素组成的集合② 集合｛1｝表示仅由一个“1”组成的集合③｛2，4，6｝与｛6，4，2｝是两个不同的集合④ 集合｛大于3的无理数｝是一个有限集其中正确的是 ( );A.只有③④B.只有②③④C.只有①②D.只有②2.,M =｛0,1,2,3｝ ,N =｛0,3,4｝,N M =( );A.｛0｝B.｛0,3｝C.｛0,1,3｝D.｛0,1,2,3｝3.I =｛a,b,c,d,e ｝ ,N=｛b,f ｝,则N I =( );A.｛a,b,c,d,e ｝B.｛a,b,c,d ｝C.｛a,b,c,e ｝D.｛a,b,c,d,e,f ｝4.A =｛0,3｝ ,B=｛0,3,4｝,C=｛1,2,3｝则=A C B )(( );A.｛0,1,2,3,4｝B.φC.｛0,3｝D.｛0｝5．设集合M =｛-2,0,2｝,N =｛0｝,则( );A.φ=NB.M N ∈C.M N ⊂D.N M ⊂6.设、、均为实数，且＜，下列结论正确的是( )。

A.＜B.＜C.－＜－D.＜7.设、、均为实数，且＜，下列结论正确的是( )。

A.＜B.＜C.－＜－D.＜8.下列不等式中，解集是空集的是( )。

A.x 2 - 3 x –4 ＞0B. x 2- 3 x + 4≥ 0C. x 2 - 3 x + 4＜0D. x 2 - 4x + 4≥09.一元二次方程x 2– mx + 4 = 0 有实数解的条件是m ∈（ ）A.（－４,４）B. ［－４,４］C.（－∞，－４）∪（４, ＋∞）D. （－∞，－４］∪［４, ＋∞） 10．设a ＞＞0且＞＞0，则下列结论不正确的是( )A.＋＞＋B.－＞－C.－＞－D. ＞11.函数1y x=的定义域为( ) Ａ．[]1,+∞ Ｂ．()1,−+∞ Ｃ．[1,)−+∞ Ｄ．[1,0)(0,)−+∞12.下列各函数中，既是偶函数，又是区间（0, ＋∞）内的增函数的是( )Ａ．y x = Ｂ．3y x = Ｃ．22y x x =+ Ｄ．2y x =− 二 填空题：本大题共6小题，每空5分，共30分. 把答案填在题中横线上.1.｛m,n ｝的真子集共3个，它们是 ;2.集合{}2x x ≥−用区间表示为 ．3. 如果一个集合恰由5个元素组成，它的真子集中有两个分别是B =｛a,b,c ｝,C =｛a,d,e ｝ 那么集合A =4.042=−x 是x +2=0的 条件.5．设2x -3 ＜7,则 x ＜6.已知函数()22f x x x =+，则1(2)()2f f ⋅= 三 解答题：(60分）1.已知集合A={}4,3,2，B={}5,4,3,2,1,求A ∩B ，A ∪B2.已知集合A={}{}B A B A x x B x x ,,71,40求<<=<<.3.设全集I={}{}{},2,3,1,3,4,322+−=−=−a a M C M a I 求a 值.4.()1427+≤−x x5.比较大小：2x 2 －7x ＋ 2与x 2－5x6.解不等式组 2 x - 1 ≥3x - 4≤ 77.设函数()227,f x x =−求()()()()1,5,,f f f a f x h −+的值8.求函数2()43f x x x =−+的最大或最小值8.设集合{}{},52,41<≤=≤<=x x N x x M 则=B A ( ); A.{}51<<x x B.{}42≤≤x x C.{}42<<x x D.{}4,3,29.设集合{}{},6,4<=−≥=x x N x x M 则=N M ( );A.RB.{}64<≤−x xC.φD.{}64<<−x x10．设集合{}{}==−−=≥=B A x x x B x x A 则,02,22( );。

中职数学基础模块上册期末试题中职数学（基础模块）期末试题一、选择题：1.给出四个结论：①｛1，2，3，1｝是由4个元素组成的集合②集合｛1｝表示仅由一个“1”组成的集合③｛2，4，6｝与｛6，4，2｝是两个不同的集合④集合｛大于3的无理数｝是一个有限集其中正确的是（B）：只有②③④。

2.M=｛0,1,2,3｝,N=｛0,3,4｝,M∩N=（B）：｛0,3｝。

3.I=｛a,b,c,d,e｝,N=｛b,f｝,则I∪N=（D）：｛a,b,c,d,e,f｝。

4.A=｛0,3｝,B=｛0,3,4｝,C=｛1,2,3｝则(B∪C)∩A=（C）：｛0,3｝。

5.设集合M=｛-2,0,2｝,N=｛｝，则（A）：N=∅。

6.设a、b、c均为实数，且a<b<c，则下列结论正确的是（A）：a<c。

7.设a、b、c均为实数，且a<b<c，则下列结论正确的是（D）：a<b。

8.下列不等式中，解集是空集的是（A）：x-3x–4＞。

9.一元二次方程x–mx+4=0有实数解的条件是m∈（C）：（－∞，－４）∪（４,＋∞）。

10.设a＞0，b＞0且ab。

11.函数y=x+1-1/x的定义域为（B）：（-1,+∞)。

12.下列各函数中，既是偶函数，又是区间（0,＋∞）内的增函数的是（C）：y=x+2x2.二、填空题：1.｛m,n｝的真子集共3个，它们是：｛m｝，｛n｝，｛｝。

2.集合{ x | x≥-2 }用区间表示为[-2,+∞)。

1.已知集合A={1,2,3,4,5}，B={(x,y)|3x+y=1}，求A∩B和A∪B。

A∩B=空集，因为A中只有整数，而B中只有满足3x+y=1的有序数对。

A∪B=A∪{1}，因为B中的所有有序数对都不属于A，所以A∪B=A∪{1}={1,2,3,4,5,1}={1,2,3,4,5}。

2.已知集合A={2,3,4}，B={x|2<x<7}，求A∩B和A∪B。

一年级第一学期数学期末试题（共三大题22小题，满分100分，考试时间90分钟）班级___________ 姓名___________ 学号__________ 成绩____________一、选择题（只有一项答案符合题意，共10题，每题4分，共40分）1、N 是自然数集，Z 是整数集，则下列表述正确的是（ ）。

A. N=ZB. N ZC. N ZD. N Z2、如果a>b ，下列不等式不一定成立的是（ ）。

A. b <aB. a +c >b +cC. ac 2>bcD. ac 2 bc 23、下列一元一次不等式组的解集用区间表示为（ ）。

A. (-∞, 25) B. ( -23, +∞) C. (-∞, -23 ) ∪( 25 , +∞) D. ( -23 , 25) 4、| x −2 |>0的解集为（ ）。

A. (-2,2)B. (-∞,-2)∪ (2,+∞)C. (-∞,-2)D. (2,+∞) 5、| x |−3<0的解集为（ ）。

A. (-3,3)B. (-∞,-3) ∪(3,+∞)C. (-∞, -3)D. (3, +∞)6、函数y =3x +5 的定义域用区间表示为（ ）。

A. (-35 ,35) B. (-∞, -35 ) ∪( 35 ,+∞) C. (-∞, -35 ) D. (-35, +∞) ⎩⎨⎧>+<-023025x x7、下列函数是偶函数的是（）。

A. y=x+2B. y=x2C. y= 2x D. y=2x8、已知二次函数f(x)=x2+2x-3，则f(2)=（）。

A. 5B. -3C. -5D. 39、二次函数y=3x2的对称轴方程为（）。

A. x=3B. x=2C. x=0D. x=-310、一元二次不等式x2-5>0的解集为（）。

A. (- 5 , 5 )B. (-∞, - 5 ) ∪( 5 ,+∞)C. (-∞, - 5 )D. ( 5 , +∞)二、填空题（每空3分，共30分）11、已知集合A={1,3,5,7,9}、B={7,9,11}，则A∩B=______________，A∪B______________。

精选全文完整版（可编辑修改）2020-2021学年（下）中职数学基础模块上册数学试卷一、选择题（10小题，每小题5分，计50分） 1.下列命题错误的是（ ）A.{}Φ=0B.{}2,00∈ C. {}{}2,00⊆ D. {}Φ⊇0 2.不等式12≤x 的解集是（ ）A. {}0|≥x xB. {}0|≤x xC. {}0|>x xD. {}0|<x x 3. 下列各等式中正确的是（ ）A ．mn n m a a a =B ．mn n m lg lg lg =•C ．nmnma a= D ．n m n m lg lg )lg(+=+4.对数函数x x f a log )(=，且1)2(=f ，则a 的值是（ ） A.4 B.3 C. 1 D. 25.式子1000lg 的值是（ ）A.3B.-3C.2D.-2 6.o 60sin 的值为（ ） A.21B.3C. 23D. 17.若0sin <θ，且0cos >θ，则θ所在的象限是（ ） A.一 B.二 C.三 D.四 8.下列图象表示的函数中，奇函数是（ ）9. 下列命题中正确的是（ ）A ．ααπsin )sin(-=- B ．ααπcos )2cos(-=+ C ．ααsin )sin(-=- D ．ααπtan )tan(-=+ 10. 已知παα20且,3tan ≤≤=，则α值为（ ）A. 3πB. 3π或32πC. 3π或35πD. 3π或34π二、选择题（4小题，每小题5分，计20分）11. 函数)2(log )(2-=x x f 的定义域为： 。

12. =+αα22cos sin 。

13. “2<x ”是“5<x ”成立的 条件。

14. 已知α的终边过）1，1（-P ，则角αcos ＝ 。

AB2020-2021学年（下）20级第二次月考数学试卷答题卡成绩： .一、选择题（每题5分）二、填空题（每题5分）11. 12. 13. 14. 三、解答题（3小题，每小题10分，计30分）15.已知全集求R U =，集合求{}{},2|,31|>=≤<=x x B x x A 求B A ⋂、B A ⋃、)(B A C u ⋂．16.若θ为第三象限角，且53sin -=θ，试求θcos 、θtan 的值。

高一年级第一学期数学期末考试试卷班级姓名考号一、选择题〔每题3分共30分〕1以下对象能组成集合的是( );A.最大的正数B.最小的整数0的数2，假设A={m，n}，那么以下结论正确的选项是A, . {m}∈A B . n∉A .C{m}⊂A D.{n}⊄A3.I =｛0,1,2,3,4｝,M=｛0,1,2,3｝,N=｛0,3,4｝,)(NCMI=( );A.｛2,4｝B.｛1,2｝C.｛0,1｝D.｛0,1,2,3｝4，设、、均为实数，且＜，以下结论正确的选项是( )。

(A)＜(B)＜(C)－＜－(D)＜,5，假设a<0,那么不等式〔x-2a〕〔x+2a〕<0的解集是〔〕A.{x∣-a<x<2a} B, {x∣x<-a 或x>2a}C,{x∣2a<x<-a} D,{x∣x<2a或x>-a}6以下不等式中，解集是空集的是( )。

(A)x 2 - 3 x–4 ＞0 (B) x 2 - 3 x + 4≥0 (C) x 2 - 3 x + 4＜0 (D) x 2 - 4x + 4≥07，设函数()logaf x x=〔0a>且1a≠〕，(4)2f=，那么(8)f=------ 〔〕A. 2B. 12C. 3D. 138，函数f(x)=3x+x 是〔〕A，偶函数B, 奇函数C,非奇非偶函数D,既是奇函数也是偶函数9，函数y=-2x+2的单调递增区间是〔〕A, [0,+∞) B(-∞,0] C,(- ∞,-1) D [-1,+ ∞)10, 假设函数22log(3)y ax x a=++的定义域为R，那么a的取值范围是-------------------------------〔〕A. 1(,)2-∞- B. 3(,)2+∞ C. 1(,)2-+∞ D.3(,)2-∞二、填空题〔每题4分，共32分〕2.042=-x是x+2=0的条件3. |x3|＞1解集的区间表示为________________;4. ㏒2 7+㏒2 4-㏒2 14=；5.f(x)=√1-2x ,那么f(-2)= .6. 函数f(x)=3-4x, x∈[-1,1]的值域是。

精选全文完整版（可编辑修改）中职数学基础模块上册期末试卷2姓名： 座号： 成绩：（考试时间90分钟，满分100分）一、选择题（本大题共15小题，每小题3分，共45分。

在每小题列出的四个备选项中只有一个是符合题目要求的，请选出并把答案写在答题卡的相应位置上）1、设全集I=｛0,1,2,3,4｝，集合A=｛0,1,2,3｝，集合B=｛2,3,4｝，则（C I A ）∪（C I B ）=（ ）。

A ．｛0｝B ．｛0,1｝C ．｛0,1,4｝D ．｛0,1,2,3,4｝ 2、|X|=1是 X=1的（ ）。

A ．充分条件但非必要条件B ．必要条件但非充分条件C ．充分必要条件D ．既非必要条件也非充分条件 3、不等式x 2-x-6＞0的解集是（ ）。

A ．｛x │x ＞3｝B ．｛x │x ＜-2｝C ．｛x │x ＜-2或x ＞3｝D ．φ4、已知函数1()1x f x x +=-，则(2)f -=（ ）A. 13-B. 13C. 1D. 35、下列各式正确的是（ ）。

A.4774a a = B.5353a a = C.2332a a = D.52521a a-=6、计算3332963⨯⨯的值是（ ）。

A. 612B.613C.312D.3127、下列各函数，指数函数的是（ ）。

A.x y )3.1(-=B.31x y = C. 22x y = D.x y )32(=8、lg4+lg25-lg10+lg1=（ ）。

A.3B.1C.2D. 254lg9、若33log log a b <，则a 、b 之间的关系为（ ）。

A ．a<b<0 B ．a>b>0 C ．b<a<0 D ．b>a>0 10、下列函数是增函数的是（ ）。

A. xy 9.0= B.xy -=)2(πC.23xy = D.x y -=311、下列函数的定义域为R 的是（ ）。

A.x y -=12 B. 931-=x y C. 813-=x y D. xy 31-= 12、下列函数是幂函数的是（ ）。

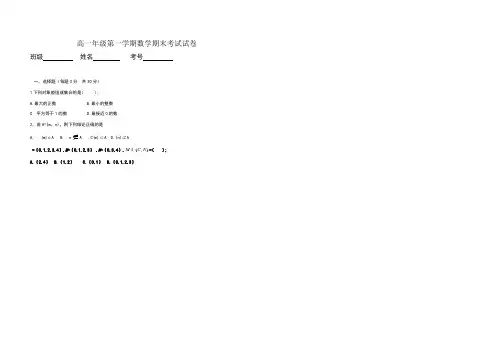
高一年级第一学期数学期末考试试卷班级 姓名 考号一、选择题（每题3分 共30分） 1下列对象能组成集合的是( );A.最大的正数B.最小的整数C. 平方等于1的数D.最接近0的数 2，若A={m ，n}，则下列结论正确的是 A, . {m}∈A B . n∉A .C{m}⊂A D.{n}⊄A=｛0,1,2,3,4｝,M =｛0,1,2,3｝ ,N =｛0,3,4｝,)(N C M I I =( );A.｛2,4｝B.｛1,2｝C.｛0,1｝D.｛0,1,2,3｝4，设、、，下列结论正确的是( )。

均为实数，且＜(A)＜(B)＜(C)－＜－(D)＜,5，若a<0,则不等式（x-2a）（x+2a）<0的解集是（）A.{x∣-a<x<2a} B, {x∣x<-a 或x>2a}C,{x∣2a<x<-a} D,{x∣x<2a或x>-a}6下列不等式中，解集是空集的是( )。

(A)x 2 - 3 x–4 ＞0 (B) x 2 - 3 x + 4≥ 0 (C) x 2 - 3 x + 4＜0 (D) x 2 - 4x + 4≥07，设函数()logaf x x=（0a>且1a≠），(4)2f=，则(8)f=------ （）A. 2B.12C. 3D.138，函数 f(x)=3x+x是（）A，偶函数 B, 奇函数 C,非奇非偶函数 D,既是奇函数也是偶函数9，函数 y=-2x +2的单调递增区间是（）A, [0,+∞) B(-∞,0] C,(- ∞,-1) D [-1,+ ∞)10, 若函数22log(3)y ax x a=++的定义域为R，则a的取值范围是-------------------------------（）A. 1(,)2-∞-B. 3(,)2+∞C. 1(,)2-+∞ D.3(,)2-∞二、填空题（每题4分， 共32分）1.用列举法表示集合{}=<<-∈42x Z x ;2.042=-x 是x +2=0的 条件 3. | x3 |＞1解集的区间表示为________________;4. ㏒2 7+㏒2 4-㏒2 14= ；5.已知f(x)=√1-2x ,则f(-2)= .6. 函数f(x)=3-4x, x ∈[-1,1]的值域是 。

.第 1 页 共 2 页中职数学基础模块上册期末考试试题（附答案）一、选择题（每小题3分，共30分）1.设集合A={x ｜x ＜4} ，B={x ｜x ≥1}，则A ∪B = ( ). A.R B.{x ｜1＜x ＜4} C.∅ D.{x ｜1≤x ＜4}2.下列结论正确的是（ ）A.若am 2＞cm 2，则a ＞c B.若a ＞b ，则1a＜1bC.若a ＞b 且c ＜d ，则a+c ＞b+dD.若a 2＞a ，则a ＞1 3.一元二次不等式-x 2-3x+4＜0的解集是（ ）A.（-∞，-4）∪（1，+∞）B.（-∞，-4）C.（-∞，-4）D.（-4,1） 4.不等式｜x-2｜＞-2 的解集是（ ） A.（-∞，0）∪（3，+∞） B.（0，+∞） C.（-∞，+∞） D.∅ 5.函数f （x ）=√x+2A.（-∞，-2）B.（-2，+∞）C.（-∞，-2）∪（-2，+∞）D.（-∞，0）∪（0，+∞）6.下列函数是奇函数的是（ ）A.y=-2x 2B.y=x+4C.y=3xD.y=x 3+x 27.若sinx=35,且cosx=-45,则角x 是（ ）A ．第一象限角B.第二象限角C ．第三象限角 D.第四象限角 8.sin30°+sin150°-tan45°的值为（ ） A.0 B.√3-1 C.2-√22 D.√3-√229. 如果α+β=π，那么下列等式正确的是（ ）A.sin α=sin βB.sin α=-cos βC.cos α=cos β D .tan α=tan β 10.函数y=3+2sinx 的最小值是（ ） A.3 B.2 C.5D.1 二、填空题（每空2分，共20分）1.f （x ）=x 3+1 ，则f （-1）= 。

2. 函数f （x ）=-x+1在（-∞，+∞）上是 函数。

（填“增”或“减”）3.把下列各角由角度转换为弧度。

（1）-120°= 。

职高数学（基础模块上）期末（ 考试内容: 三、四、五章）（考试时间120分钟, 满分150分）学校 姓名 考号一、选择题: 每题4分, 共60分（答案填入后面表格中, 否则不得分） 1.设集合{}{},52,41<≤=≤<=x x N x x M 则=B A ( );A.{}51<<x xB.{}42≤≤x xC.{}42<<x xD.{}4,3,2 2.函数 ...);A.(][)∞+∞-，，51B.()），（，∞+∞-51 C.(]），（，∞+∞-51 D.[)∞+∞-，），（51 3.下列函数中既是奇函数又是增函数的是.. );A.x y 3=B.xy 1= C.22x y = D.x y 31-=4.已知x ＞0,y ＞0,下列式子正确的是（ ）；A..B..C..D.5.有下列运算结果（1） ；（2） ；（3） ；（4） ；（5） ，则其中正确的个数是.. ）。

A.0B.1C.2D.36.若角 第三象限角, 则化简 的结果为( );A.αsin -B.αsinC.αcosD.αcos - 7.已知 , 则 .. ）;A.2B.4C.8D.168.如果定义在区间[3+a,5]上的函数f(x)是偶函数, 则a=..) A.-8, B.8 C.2 D.-29.二次函数y=ax2-4x+1的最小值是-1, 则其顶点坐标是（ ） A.(2，-1. B.(1，-1. C.(-1，-1. D.(-2，-1.10. 设函数f(x)=ax3+bx+10, f(1)=5,则f （-1）=( ) A...B.-..C.1. D.1511.y=(]8,0,log 2∈x x 的值域是（ ） A.. B...C.(0, 3. D.12. 下列函数中, 定义域为R 的是( ) A.y=. B.y= .C.y=. D.y= 13. sin(-15600)= （ ）A.21-B.21C.23-D.2314若 , 那么下列式子正确的是( ).A.sin α=-sin βB.cos α=cos βC.tan α=tan βD.sin α=sin β15已知 , 则sin cos =（ ） A.43-B.83-C.163- D.以上答案都不正确二、填空题（每题4分, 共20分） 16. ; 17.若 , 则 ;18.y=3cosx+1的最大值...，最小值... ；19.tan （655π-）= .20.设函数 ,则...... .三、解答题(每题10分, 共70分）21.如图，二次函数 的图象经过.、B.C 三点.（1）观察图象, 写出A 、B 、C 三点的坐标, 并求出抛物线解析式; （2）求此抛物线的顶点坐标和对称轴;（3）观察图象, 当x 取何值时, y ＜0？ y ＝0？ y ＞22. 如图, 一边靠墙（墙有足够长）, 其他三边用12米长的篱笆围成一个矩形（ABCD ）花园, 求当长和宽分别是多少米时, 这个花园的面积最大？ 最大面积是多少？23.计算求值: （1）352021381320023.025.043--⨯++⨯ （2）27log 01.0lg 2125lg 213+-+g24.已知函数f(x)= ,（1）求函数的定义域；（2）判断函数的奇偶性, 并证明。

中等职业学校《基础模块》第一册期末考试——数学试题卷(试卷总分100分；考试时间120分钟)注意事项:１.必须将所有答案作在答案卷上,超出答题区域、在其它题的答题区域内以及在密封线内书写的答案无效。

2.考试结束后,只交答案卷.姓名： 班级： 考场：一、选择题:本题共12小题,每小题3分,共36（在每小题给出的四个选项中,1。

下列函数是奇函数的是（ )A. f （x)=sinxB.f （x ）=cosx C 。

f 2。

下列函数中，在区间(0,+A.y=x1 B.y=x2 C 。

y=—x —3.根式32）（b a 改写成分数指数幂的形式是A.3232b -a B 。

23b -a ）（ C.32b -a ）（4。

下列式子正确的是（ ）A 。

2.26.1〉4.26.1 B.1.0-3.0〉2.0-3.0C.22.0<32.0 D 。

5.0-2.3〈3.0-2.3 5。

下列式子正确的是（ ）A 。

5.0log 3.0 〈6.0log 3.0B 。

lg6〉8lgC 。

4.1log 5.1〈6.1log 5.1D 。

4.1log 5.0〈6.1log 5.06. 与—120o 终边相同的角的集合是（ ）A 。

{x|x=120o +k •360o ，k ∈Z ｝B 。

{x|x=—120o +k •360o ,k ∈Z} C.{x|x=120o -k •360o ，k ∈Z} D 。

｛x ｜x=220o +k •360o ,k ∈Z ｝ 7. 如果cos α<0,tan α〉0，则角α的终边所在的象限是（ ） A. 第一象限 B.第二象限C 。

第三象限D 。

第四象限 ）。

cos （π-α）=cos α π+α)=-sin α ）．若a+c ＞b+c,则a ＞b ．若a ＞b ，则a-c ＞b —c）o >cos 155o o >sin 250o4｝，B={x|0≤x<6}。

则下列表述不正确的是（ )∪B={x|—3<x 〈6}U A= ｛x|。