信息安全数学基础试卷A2014

信息安全数学基础期末考试试卷及答案(A卷)装订线装订线三、解同余方程（本大题共2小题，每小题10分，共20分）1.求解一次同余方程1714(mod21)x 。

2.解同余方程组2(mod3)3(mod5)2(mod7) xxx≡≡≡⎧⎪⎨⎪⎩四、证明题（本大题共3小题，每小题7分，共21分）2.f是群G到G'的一个同态，{}=∈=，其f a a G f a e'ker|,()中e'是G'的单位元。

证明：ker f是G的正规子群。

3. 证明：如果p 和q 是不同的素数，则111(mod )q p p q pq --+=。

五、应用题（共11分）RSA 公钥加密算法的密钥生成步骤如下：选择 两个大的素数p 和q ，计算n =pq 。

选择两个正整数e 和d ，满足：ed =1(mod ()n )。

Bob 的公钥是（n ，e ），对外公布。

Bob 的私钥是d ，自己私藏。

如果攻击者分解n 得到p =47，q =23，并且已知e =257，试求出Bob 的私钥d 。

答案 一、填空题（每空2分，共24分） 1. 两个整数a ，b ，其最大公因数和最小公倍数的关系为[,](,)ab a b a b =。

2. 给定一个正整数m ，两个整数a ,b 叫做模m 同余，如果|m a b -，记作(mod )a b m ≡；否则，叫做模m 不同余，记作a ≡(mod )b m 。

3. 设m ，n 是互素的两个正整数，则()mn ϕ=()()m n ϕϕ。

4. 设1m >是整数，a 是与m 互素的正整数。

则使得1(mod )e a m ≡成立的最小正整数e 叫做a 对模m 的指数，记做()m ord a 。

如果a 对模m 的指数是()m ϕ，则a 叫做模m 的 原根 。

5. 设n 是一个奇合数，设整数b 与n 互素，如果整数n 和b 满足条件11(mod )n b n -≡，则n 叫做对于基b 的拟素数。

信息安全数学基础习题答案第一章整数的可除性1．证明：因为2|n 所以n=2k , k∈Z5|n 所以5|2k ，又（5，2）=1，所以5|k 即k=5 k1，k1∈Z7|n 所以7|2*5 k1 ,又（7，10）=1，所以7| k1即k1=7 k2，k2∈Z 所以n=2*5*7 k2即n=70 k2, k2∈Z因此70|n2．证明：因为a3-a=(a-1)a(a+1)当a=3k，k∈Z 3|a 则3|a3-a当a=3k-1，k∈Z 3|a+1 则3|a3-a当a=3k+1，k∈Z 3|a-1 则3|a3-a所以a3-a能被3整除。

3．证明：任意奇整数可表示为2 k0+1，k0∈Z（2 k0+1）2＝4 k02+4 k0+1=4 k0 (k0+1)+1由于k0与k0+1为两连续整数，必有一个为偶数，所以k0 (k0+1)=2k所以（2 k0+1）2=8k+1 得证。

4．证明：设三个连续整数为a-1,a,a+1 则(a-1)a(a+1)= a3-a由第二题结论3|（a3-a）即3|(a-1)a(a+1)又三个连续整数中必有至少一个为偶数，则2|(a-1)a(a+1)又（3，2）=1 所以6|(a-1)a(a+1) 得证。

5．证明：构造下列k个连续正整数列：(k+1)！+2, (k+1)！+3, (k+1)！+4,……, (k+1)！+(k+1), k∈Z对数列中任一数 (k+1)！+i=i[(k+1)k…(i+1)(i-1)…2*1+1], i=2,3,4,…(k+1)所以i|(k+1)！+i 即(k+1)！+i为合数所以此k个连续正整数都是合数。

6．证明：因为1911/2＜14 ,小于14的素数有2，3，5，7，11，13经验算都不能整除191 所以191为素数。

因为5471/2＜24 ,小于24的素数有2，3，5，7，11，13，17，19，23经验算都不能整除547 所以547为素数。

由737=11*67 ,747=3*249 知737与747都为合数。

《信息安全数学基础》参考试卷一．选择题(在每小题的备选答案中只有一个正确答案，将正确答案序号填入下列叙述中的括号内，多选不给分)：（每题2分，共20分）1．576的欧拉函数值ϕ(576) ＝()。

(1) 96，(2) 192，(3) 64，(4) 288。

2．整数kn和k(n+2)的最大公因数(kn , k(n+2))=()。

(1) 1或2，(2) | kn|，(3) | n|或| kn|，(4) | k|或2| k|。

3．模10的一个简化剩余系是( )。

(1) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10，(2) 11, 17, 19 , 27(3) 11, 13, 17, 19，(4) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9。

4．29模23的逆元是( )。

(1) 2，(2) 4，(3) 6，(4) 11。

5．设m1，m2是两个正整数，x1遍历模m1的完全剩余系，x2遍历模m2的完全剩余系，若( )遍历m1m2的完全剩余系。

(1) (m1，m2)=1，则m1x1＋m2x2(2) m1和m2是素数，则m1x1＋m2x2(3) (m1，m2)=1，则m2x1＋m1x2(4)m1和m2是素数，则m2x1＋m1x26．下面的集合和运算构成群的是( ) 。

(1) <N，＋> （N是自然数集，“＋”是加法运算）(2) <R，×> （R是实数集，“×”是乘法运算）(3) <Z，＋> （Z是整数集，“＋”是加法运算）(4) <P（A），∩> （P(A)＝{U | U是A的子集}是集合A的幂集，“∩”是集合的交运算）7．下列各组数对任意整数n均互素的是( ) 。

(1) 3n+2与2n，(2) n－1与n2＋n＋1，(3) 6n+2与7n，(4) 2n+1与4n+1。

8．一次同余式234x ≡ 30（mod 198）的解数是( )。

信息安全数学基础习题答案[1]信息安全数学基础习题答案第一章整数的可除性1．证明：因为2|n 所以n=2k , k∈Z5|n 所以5|2k ，又（5，2）=1，所以5|k 即k=5 k1，k1∈Z7|n 所以7|2*5 k1 ,又（7，10）=1，所以7| k1即k1=7 k2，k2∈Z 所以n=2*5*7 k2即n=70 k2, k2∈Z因此70|n2．证明：因为a3-a=(a-1)a(a+1)当a=3k，k∈Z 3|a 则3|a3-a当a=3k-1，k∈Z 3|a+1 则3|a3-a当a=3k+1，k∈Z 3|a-1 则3|a3-a所以a3-a能被3整除。

3．证明：任意奇整数可表示为2 k0+1，k0∈Z（2 k0+1）2＝4 k02+4 k0+1=4 k0 (k0+1)+1由于k0与k0+1为两连续整数，必有一个为偶数，所以k0 (k0+1)=2k所以（2 k0+1）2=8k+1 得证。

4．证明：设三个连续整数为a-1,a,a+1 则(a-1)a(a+1)= a3-a由第二题结论3|（a3-a）即3|(a-1)a(a+1)又三个连续整数中必有至少一个为偶数，则2|(a-1)a(a+1)又（3，2）=1 所以6|(a-1)a(a+1) 得证。

5．证明：构造下列k个连续正整数列：(k+1)！+2, (k+1)！+3, (k+1)！+4,……, (k+1)！+(k+1), k∈Z对数列中任一数(k+1)！+i=i[(k+1)k…(i+1)(i-1)…2*1+1], i=2,3,4,…(k+1)所以i|(k+1)！+i 即(k+1)！+i为合数所以此k个连续正整数都是合数。

6．证明：因为1911/2＜14 ,小于14的素数有2，3，5，7，11，13经验算都不能整除191 所以191为素数。

因为5471/2＜24 ,小于24的素数有2，3，5，7，11，13，17，19，23经验算都不能整除547 所以547为素数。

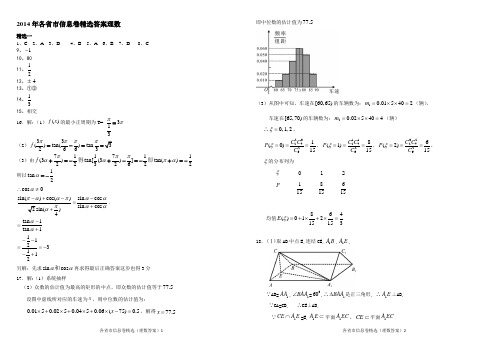
2014年各省市信息卷精选答案理数精选一1、C2、A3、D4、B5、A6、B7、D8、C9、1- 10、8011、1212、±413、①③14、3115、相交16．解：（1）()f x 的最小正周期为T= 313ππ=（2）33()tan()tan 2663f ππππ=-==（3）由711711(3)tan[(3)]tan()2232622f πππααπα+=-+-=-+=-得即所以1tan 2α=-cos 0α∴≠sin cos sin cos αααα-=+．tan 1tan 1αα-=+ 1123112--==--+另解：先求sin cos αα和再求得最后正确答案这步也得3分 17．解:（1）系统抽样（2）众数的估计值为最高的矩形的中点，即众数的估计值等于77.5 设图中虚线所对应的车速为x ，则中位数的估计值为：0.0150.0250.0450.06(75)0.5x ⨯+⨯+⨯+⨯-=，解得77.5x =即中位数的估计值为77.5（3）从图中可知，车速在[60,65)的车辆数为：10.015402m =⨯⨯=（辆），车速在[65,70)的车辆数为：20.025404m =⨯⨯=（辆） ∴0,1,2ξ=，2024261(0)15C C P C ξ===，1124268(1)15C C P C ξ===，0224266(2)15C C P C ξ===， ξ的分布列为ξ 012P115815615均值864()01215153E ξ=+⨯+⨯=.18．(Ⅰ)取AB 中点E,连结CE,1A B ,1A E ,∵AB=1AA ,1BAA ∠=060,∴1BAA ∆是正三角形, ∴1A E ⊥AB, ∵CA=CB, ∴CE⊥AB,∵1CE A E ⋂=E,1A E ⊂平面1A EC ，CE ⊂平面1A EC∴AB⊥面1CEA , ∴AB⊥1AC ; (Ⅱ)由(Ⅰ)知EC⊥AB,1EA ⊥AB,又∵面ABC⊥面11ABB A ,面ABC∩面11ABB A =AB,∴EC⊥面11ABB A ,∴EC⊥1EA ,∴EA,EC,1EA 两两相互垂直,以E 为坐标原点,EA 的方向为x 轴正方向,|EA|为单位长度,建立如图所示空间直角坐标系O xyz -, ………9分有题设知A(1,0,0),1A则BC1BB =1AA),1A C),设n =(,,)x y z 是平面11CBB C 的法向量,则100BC BB ⎧∙=⎪⎨∙=⎪⎩n n ,即0x x ⎧=⎪⎨=⎪⎩,可取n∴1cos ,A C n =11|A C A C ∙n |n||,∴直线A 1C 与平面BB 1C 1C19．解:(Ⅰ)由已知得到:22221311(22)54(1)50(2)(11)25(5)a a a a d a d d d +=⇒++=+⇒+=+224112122125253404611n n d d d d d d d a n a n==-⎧⎧⇒++=+⇒--=⇒⎨⎨=+=-⎩⎩或;(Ⅱ)由(1)知,当0d<时,11n a n =-,①当111n ≤≤时,123123(1011)(21)0||||||||22n n n n n n n a a a a a a a a a +--≥∴++++=++++==②当12n ≤时,1231231112132123111230||||||||()11(2111)(21)212202()()2222n n n n a a a a a a a a a a a a n n n n a a a a a a a a ≤∴++++=++++-+++---+=++++-++++=⨯-=所以,综上所述:1232(21),(111)2||||||||21220,(12)2n n n n a a a a n n n -⎧≤≤⎪⎪++++=⎨-+⎪≥⎪⎩ ;20．解：（1）两圆的圆心坐标分别为1(1,0),C 和2(1,0)C -∵1212||||||2PC PC C C +=>=∴根据椭圆的定义可知，动点P 的轨迹为以原点为中心，1(1,0),C 和2(1,0)C -为焦点，长轴长为2a =的椭圆，1,1a c b =====∴椭圆的方程为2212x y +=，即动点P 的轨迹M 的方程为2212x y += （2）(i)当直线l 的斜率不存在时，易知点(2,0)A 在椭圆M 的外部，直线l 与椭圆M 无交点，所以直线l 不存在。

信息安全数学基础期末考试试卷及答案（A 卷）一、 填空题（本大题共8小题，每空2分，共24分）1. 两个整数a ，b ，其最大公因数和最小公倍数的关系为 ________________。

2. 给定一个正整数m ，两个整数a ,b 叫做模m 同余，如果______________，记作(mod )a b m ≡；否则，叫做模m 不同余，记作_____________。

3. 设m ，n 是互素的两个正整数，则()mn ϕ=________________。

4. 设1m >是整数，a 是与m 互素的正整数。

则使得1(mod )ea m ≡成立的最小正整数e 叫做a 对模m 的指数，记做__________。

如果a 对模m 的指数是()m ϕ，则a 叫做模m 的____________。

5. 设n 是一个奇合数，设整数b 与n 互素，如果整数n 和b 满足条件________________，则n 叫做对于基b 的拟素数。

6. 设,G G '是两个群，f 是G 到G '的一个映射。

如果对任意的,a b G ∈，都有_______________，那么f 叫做G 到G '的一个同态。

7. 加群Z 的每个子群H 都是________群，并且有0H =<>或H =______________。

8. 我们称交换环R 为一个域，如果R 对于加法构成一个______群，*\{0}R R =对于乘法构成一个_______群。

二、计算题（本大题共 3小题，每小题8分，共24分）1. 令1613,a = 3589b =。

用广义欧几里德算法求整数,s t ，使得(,)sa tb a b +=。

2. 求同余方程22(mod 67)x ≡-的解数。

3. 计算3模19的指数19ord (3)。

三、解同余方程（本大题共2小题，每小题10分，共20分）1. 求解一次同余方程1714(mod 21)x ≡。

信息安全数学基础----习题集一一、填空题1、设a=18、b=12,c=27,求a、b、c的最小公倍数a,b,c= .2、求欧拉函数φ(3000)= .3、设m=9,则模m的最小非负简化剩余系={ }.4、设m=11,则模m的所有平方剩余= .5、设m=22,则模m的所有原根个数= .6. 设m,n是互素的两个正整数,则φmn=________________;7. 设m是正整数,a是满足 m?a的整数,则一次同余式：ax≡b mod m有解的充分必要条件是_________________ ;8. 设m 是一个正整数,a是满足____________的整数,则存在整数a’,1≤a’＜m ,使得aa’≡1 mod m;9. 设a∈Z,(a,m)=1, 如果同余方程x2≡a(mod m)__________, 则a叫做模m的平方剩余.10. 设a,m∈Z,m>1,(a,m)=1, 则使得a e≡1(mod m)成立的最小正整数e叫做a对模m的__________.二、判断题在题目后面的括号中,对的画“√”,错的画“×”1、若k是任意正整数, 则(ak,bk)=(a,b).2、设a1,a2,…,a n是n个不全为零的整数,则a1,a2,…,a n与a1, |a2|, |a3|,…, |a n|的公因数相同3、设m是正整数, 若m│ab, 则m│a或m│b.4、设m为正整数, a,b为整数, a≡b(mod m), d│b且d>0, 则ad≡b d (mod md).5、{1,-3,8,4,-10}是模5的一个完全剩余系.6、设m是素数, 模m的最小非负完全剩余系和最小非负简化剩余系中元素个数相等.7、设p=17为奇素数, 模p的平方剩余和平方非剩余的数量各为8.8、一次同余方程9x≡1(mod 24)有解.9、设p是素数, g是模p的原根, 若g x≡1(mod p), 则x是p−1的整数倍.10、设m>1,(a,m)=1, 则1=a0,a,a2, …, a ord m(a)−1构成模m的简化剩余系.11. b≠0, 则(0,b)＝|b|.12. 设a,b是两个互素正整数, 那么a│m,b│m, 则ab│m.13. 设m是一个正整数, a,b,d都不为0,若ad≡bdmodm;则a≡bmod m;14. 设m为正整数, a是满足(a,m)=1的整数,b为整数. 若r1,r2,…,rφ(m)为模m的一个简化剩余系, 则ar1+b,ar2+b,…,arφ(m)+b也为模m的一个简化剩余系.15. p为素数,n为整数且与p互素,则n2为模p的平方剩余.16. 设p为正整数, 设a∈Z,(a,p)=1, 则a是模p的平方剩余的充要条件是: a p+12≡1(mod p).17. 3是模7的原根;18. 设a,m∈Z,m>1,(a,m)=1,d为正整数, 若a d≡1(mod m),则ord m(a)|d.19. 整数集关于整数的乘法构成群;20. 适当定义加法和乘法,集合{0,1}可以构成一个有限域;三、单项选择题把答案写在题目后面的括号中1. 设a与b是两个整数, 则存在整数s,t, 使得(a,b)=sa+tb,下面关于a与b 线性组合描述错误的是：A. 整数s,t的取值仅有一组唯一的值；B. 整数a,b的线性和所能表示的最小的正整数是a,b最大公因数,即sa+ tb=(a,b)；C. (a,b)的倍数也可以用a,b的线性和表示；D. 整数s,t,可以使用辗转相除法欧几里得算法反推得到;2、下面关于整除的描述错误的是：A. ±1是任何整数的因子；B.设a,b∈Z整数集合,c≠0c|b, c|a, 则c|a±b；C. 0是任何整数的倍数；D. 设a,b∈Z, 若 b|a, b≠0,则b|−a, −b|−a。

“信息安全数学基础”习题答案第一章1、证明： (1)|()|()()|a b b ma m Z c d d nc n Z bd acmn mn Z ac bd ⇒=∈⇒=∈∴=∈∵，，，即。

(2)12111112|,|,,|11(3)|(),,k k k k a b a b a b a b c b c b c c c c ∴−+++∵ ，根据整除的性质及递归法，可证得：，其中为任意整数。

2、证明：1-2(2)(3,5)13|5|15|,(15,7)17|105|a a a a a =∴=∴∵∵∵根据例题的证明结论知：，又且,又，且,。

3、证明：1n p n p n >>因为，且是的最小素因数，若假设n/p 不是素数，则有121223131312,2,,,,2,,k k n p p p p k p p p p k n p p p p n p p n n p n n p =×××≥≥==×≥∴≥≤>> （其中为素数且均）若，则即,与题设矛盾，所以假设不成立，即为素数得证。

7、证明：首先证明形如6k -1的正整数n 必含有6k -1形式的素因子，这显然是成立的。

因为如果其所有素因数均为6k +1形式，则12,(61,1,2,,)j i i n p p p p k i j =×××=+= ,从而得到n 是形如6k +1形式的正整数，这与题设矛盾。

其次，假设形如6k -1的素数为有限个，依次为1212,,6s s q q q n q q q = ，考虑整数-1， 则n 是形如6k -1的正整数，所以n 必有相同形式的素因数q ，使得使得q = q j (1≤j ≤s )。

由整数的基本性质(3)有：12|(6)1s q q q q n −= ，这是不可能的。

故假设错误，即存在无穷多个形如4k -1的素数得证。

2n3n最小非负余数最小正余数绝对值最小余数最小非负余数最小正余数绝对值最小余数3 0、1 1、3 0、1 0、1、2 1、2、3 -1、0、14 0、1 1、4 0、1 0、1、3 1、3、4 -1、0、1 8 0、1、4 1、4、8 1，0 0、1、3、5、7 1、3、5、7、8 3、1、-3、-1、0 10 0、1、4、5、6、9 1、4、5、6、9、10 -4、-1、0、1、4、5 0,1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,10-5,-4,-3,-2,-1,0,1,2,3,413、解： (1)259222137222376(222,259)37372592221,1,1s t =×+=×⇒==−×∴==−(2)139571316827136821316823122(1395,713)31317136821713(13957131)2713(1)1395,1,2s t =×+=×+=×⇒==−×=−−×=×+−×∴=−=16、解： (1)(112,56)5611256[112,56]112(112,56)=×== (2)(67,335)6767335[67,335]335(67,335)=×== (3)(1124,1368)411241368[1124,1368]384408(1124,1368)=×==(7,4)1,0,7(1)4211,24410,1,2,771||1000142||100040,1,1427c s t k x k k k y k x k y x kk y k ==∴×−+×=∴=−=⎧=−=−⎪⎪=±±⎨⎪==⎪⎩≤⎧∴≤⎨≤⎩=−⎧∴=±±⎨=⎩∵ 而不定方程的一切解为：　其中，又方程的全部解为　，其中 ，第二章1、解：(1) 错误。

某某市2014届高三信息卷数学（理工类）注意事项：本试卷共4页，满分150分．考试用时120分钟． 考试结束后，只交答题卷．一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．并把答案填在答题卡中对应题号内．1．已知2a ib i i +=-（a ，b ∈R ），其中i 为虚数单位，则a+b=A ．1-B ．1C ．2D ．32．一个总体分为A ，B 两层，其个体数之比为5：3，用分层抽样方法从总体中抽取一个容量为120的样本．则A 层中应该抽取的个数为 A ．30 B ．45 C ．50 D ．753．在△ABC 中，角,,A B C 所对应的边分别为,,a b c ，若a=9，b=6， A=060，则sin B =A ． 13-B ．13C．3 D．3-4．若某空间几何体的三视图如图1所示，则该几何体的表面 积是A ．60B ．54C ．48D ．245．设f(x)为定义在R 上的奇函数，当x≥0时，f(x)=2x+2x+m (m 为常数)，则(1)f -= A ．3 B ．1 C ．1- D ．3- 6．已知ABC 和点M 满足0MA MB MC ++=．若存在实数k 使得CA CB kCM +=成立，则k =A ．2B ．3C ．4D ．57．已知实数x ，y 满足条件22(3)(2)110x y x y ⎧-+-≤⎨--≥⎩，则2y z x =-的最小值为 A．3+ B．2．34 D ．438．定义在R 上的函数()f x 满足：()()f x f x '>恒成立，若12x x <，则12()x e f x 与21()x e f x侧视图正视图图1图2的大小关系为 A ．12()x e f x >21()x e f x B ．12()x e f x <21()x e f xC ．12()x e f x =21()x e f x D ．12()x e f x 与21()x e f x 的大小关系不确定二、填空题：本大题共7个小题，每小题5分，共35分，把答案填在答题卡中对应题号后的横线上．9． 20cos xπ⎰dx =________．10．不等式|1|1x x +>+的解集是________．11．命题“∀x ∈R 3>”的否定是________． 12．执行如图2所示的程序框图，若0.9P =，则输出的n ＝____．13．若各项均为正数的等比数列{na }满足123a a a =5，789a a a =10，则192021a a a =________．14．若以F 为焦点的抛物线24y x =上的两点A 、B 满足 2AF FB =，则弦AB 的中点到准线的距离为____________．15．已知数列{}n a 满足：当(1)(1)(,22k k k k n -+∈（,n *k N ∈）时，1(1)k n a k +=-⋅，n S 是数列{}n a 的前n 项和，定义集合{|m n T n S =是n a 的整数倍，*,n m N ∈，且1n m ≤≤}，()Card A 表示集合A 中元素的个数，则15()Card T = ，2014()Card T = ．三、解答题：本大题共6小题，共75分．解答应写文字说明，证明过程或演算步骤．16．（本小题12分）已知向量(23,2)2x m =，2(cos ,cos 22x xn =，()f x m n =⋅（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，且满足(2)cos cos 0a c B b C ++=，若()1f A =，求角C 的值．17．（本小题12分）学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分．现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎，个位数字为叶)：（Ⅰ）指出这组数据的众数和中位数；（Ⅱ）若满意度不低于98分，则评价该教师为“优秀”．求从这10人中随机选取3人，至多有1人评价该教师是“优秀”的概率；（Ⅲ）以这10人的样本数据来估计整个班级的总体数据，若从该班任选3人，记ξ表示抽到评价该教师为“优秀”的人数，求ξ的分布列及数学期望．18．（本小题12分）在如图４所示的几何体中，四边形ABCD 为正方形，ABE ∆为等腰直角三角形，90BAE ∠=︒，且AD AE ⊥． （Ⅰ）证明：平面AEC ⊥平面BED ．（Ⅱ）求直线EC 与平面BED 所成角的正弦值． 19．（本小题13分）中国人口已经出现老龄化与少子化并存的结构特征，测算显示中国是世界上人口老龄化速度最快的国家之一，再不实施“放开二胎”新政策，整个社会将会出现一系列的问题．若某地区2012年人口总数为45万，实施 “放开二胎” 新政策后专家估计人口总数将发生如下变化：从2013年开始到2022年每年人口比上年增加0.5万人，从2023年开始到2032年每年人口为上一年的99%． （Ⅰ）某某施新政策后第n 年的人口总数n a 的表达式（注：2013年为第一年）；（Ⅱ）若新政策实施后的2013年到2032年人口平均值超过49万，则需调整政策，否则继续实施．问到2032年后是否需要调整政策？20．（本小题13分）已知椭圆22221(0)x y a b a b +=>>的离心率为12，且经过点3(1,)2P ． 过A BC D E 图４ 7 8 8 7 7 7 8 9 9 6 8 9 9图3它的两个焦点1F ，2F 分别作直线1l 与2l ，1l 交椭圆于A 、B 两点，2l交椭圆于C 、D 两点，且12l l ⊥．（Ⅰ）求椭圆的标准方程；（Ⅱ）求四边形ACBD 的面积S 的取值X 围．21．（本小题13分）已知函数2()xx f x e =． （Ⅰ）求函数()f x 的单调区间；（Ⅱ）若方程()mf x x =有解，某某数m 的取值X 围；（Ⅲ）若存在实数12x x ≠，使1122()()x f x x f x ⋅=⋅成立，求证：126x x +>．某某市2014届高三信息卷 数学（理工类）参考答案一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的．1.D2.D3．C 4.A5.D 6.B 7.C 8.A二、填空题：本大题共7个小题，每小题5分，共35分，把答案填在题中的横线上. 9.110. (,1)-∞-11.03x R ∃∈≤12.513. 40 14.94 15. 9, 1022 （答对一空记3分, 答对二空记5分）三、解答题：本大题共6小题，共75分.解答应写文字说明，证明过程或演算步骤.16.解：由2()23sin cos 2cos cos 1222x x xf x m n x x =⋅=⋅+=++ 2sin()16x π=++………………4分(Ⅰ)∵T=221ππ=()f x π∴的最小正周期是2………………6分 图５(Ⅱ)由()1f A =即sin()6A π+=62A ππ=或………………8分 又(2)cos cos 0a c B b C ++=，在ABC ∆中由正弦定理知2sin cos sin cos sin cos 0A B C B B C ⋅+⋅+⋅=即2sin cos sin()A B B C ⋅=-+1cos 2B ∴=-23B π∴=………………10分A B ∆由、均为ABC 的内角且B 为钝角∴6A π=………………11分故()6C A B ππ=-+=………………12分17.解：（Ⅰ）众数：87；中位数：88.5 ……………2分（Ⅱ）设i A 表示所取3人中有i 个人评价该教师为“优秀”，至多有1人评价该教师为“优秀”记为事件A ，则604912098)()()(31027133103710==+=+=C C C C C A P A P A P ……………6分 （Ⅲ）ξ的可能取值为0、1、2、3 ……………7分1000342)107()0(3===ξP ； 1000441)107(103)1(213===C P ξ 1000189107)103()2(223===C P ξ；100027)103()3(3===ξP 分布列为……………11分1000273100018921000441110003420⨯+⨯+⨯+⨯=ξE 9.0=. ……………12分注：用二项分布直接求解也可以．18. .解法一：（Ⅰ）由已知有AE ⊥AB ，又AE ⊥AD ，所以AE ⊥平面ABCD ，所以AE ⊥DB ，………………………………………………3分 又ABCD 为正方形，所以DB ⊥AC ，……………………………………………4分 所以DB ⊥平面AEC ，而BD ⊂平面BED故有平面AEC ⊥平面BED. ………………………………………………6分（Ⅱ）设AC 与BD 交点为O ，所以OE 为两平面AEC 和BED 的交线.过C 作平面BED 的垂线，其垂足必在直线EO 上，即∠OEC 为EC 与平面BED 所成的角.……………7分 设正方形边长为2a ，则，AE=2a ， 所以，EC=，…………………9分 所以在三角形OEC 中，由余弦定理得 cos ∠OEC=3，故所求为sin ∠OEC=13………………………12分解法二：以A 为原点，AE 、AB 、AD 分别为x,y,z 轴建立空间直角坐标系．……1分（Ⅰ）设正方形边长为2，则E(2,0,0)，B(0,2,0)，C(0,2,2)，D(0,0,2)………………2分AC =(0,2,2)，BD =(0,-2,2)，AE =(2,0,0)，ED =(-2,0,2)，从而有0BD AC ⋅=，0BD AE ⋅=，即BD ⊥AC ，BD ⊥AE ， 所以BD ⊥平面AEC ，故平面BED ⊥平面AEC.………………………6分 （Ⅱ）设平面BED 的法向量为(,,)n x y z =，由00n ED n BD ⎧⋅=⎪⎨⋅=⎪⎩，得z x y z =⎧⎨=⎩，故取(1,1,1)n =…………8分 而EC =(-2,2,2)，设直线EC 与平面BED 所成的角为θ，则有||1sin |cos ,|3||||n EC n EC n EC θ⋅=<>==…………………………12分19.解：（Ⅰ）当10≤n 时，数列{}n a 是首项为5.45，公差为5.0的等差数列，nn a n 5.045)1(5.05.45+=-⨯+=∴………………2分当11≥n 时，数列{}n a 是以公比为99.0的等比数列，又5010=a1099.050-⨯=∴n n a………………4分因此，新政策实施后第n 年的人口总数n a （单位：万元）的表达式为y图４-2ABCD E 图４-1O10450.5,110500.99,1120n n n n a n -+≤≤⎧=⎨⨯≤≤⎩………………6分(Ⅱ)设n S 为数列{}n a 的前n 项和，则从2013年到2032年共20年，由等差数列及等比数列的求和公式得：2010111220()S S a a a =++++10477.54950(10.99)972.5=+⨯-≈万……10分(说明：10100.99(10.01)0.9=-≈) ∴新政策实施到2032年年人口均值为2048.6220S ≈万………………12分由204920S <，故到2032年不需要调整政策．………………13分20解：（Ⅰ）由122c a c a =⇒=，所以22224,3a c b c ==，………………2分将点P 的坐标代入椭圆方程得21c =，………………4分故所求椭圆方程为22143x y +=………………5分（Ⅱ）当1l 与2l中有一条直线的斜率不存在，则另一条直线的斜率为0，此时四边形的面积为6S =，………………7分若1l 与2l 的斜率都存在，设1l 的斜率为k ，则2l 的斜率为1k -．∴直线1l 的方程为(+1y k x =），设11(,)A x y ，22(,)B x y ，联立22(1)143y k x x y =+⎧⎪⎨+=⎪⎩，消去y 整理得，2222(43)84120k x k x k +++-=（1） ∴2122843k x x k +=-+，212241243k x x k -⋅=+，………………8分∴122||43x x k -=+，∴212212(1)|||43k AB x x k +=-=+（2）………………9分注意到方程（1）的结构特征，或图形的对称性，可以用1k -代替（2）中的k ，得2212(1)||34k CD k +=+，………………10分 ∴2222172(1)||||2(43)(34)k S AB CD k k +=⋅=+⋅+，令2(0,)k t =∈+∞， ∴22272(1)6(122512)6662886612(43)(34)12251249491225t t t t S t t t t t t +++-===-≥-=+⋅+++++，∴288[,6)49S ∈，综上可知，四边形ACBD 面积的288[,6]49S ∈. (13)分21.解：（Ⅰ）'2()(2)x f x x x e -=-，令'()002f x x >⇒<<，'()00f x x <⇒<或2x >………………3分所以()f x 递增区间为(0,2)，递减区间为(,0),(2,)-∞+∞………………4分（Ⅱ）()m f x x =3(0)x x m x e ⇔=≠，令3()(0)x x g x x e =≠，则'23()(3)xg x x x e -=-令'()03g x x >⇒<，'()03g x x <⇒>，所以()g x 在(,0),(0,3)-∞递增，在(3,)+∞递减，………………6分max 327(3)g g e ==，故327(,0)(0,]m e ∈-∞………………8分(Ⅲ)令3()()()x x h x xf x x R e ==∈，则由（2）知，()h x 在(,3)-∞递增，在(3,)+∞递减.由条件有12()()h x h x =，不妨设12x x <，则必有123,3x x <>，于是263x -<…9分假设126x x +≤，则121263()(6)x x h x h x ≤-<⇒≤-，即223322226(6)()(6)x x x x h x h x e e --≤-⇔≤2263232(6)x x x e e x --⇔≤，令23(0)x t t -=<，则有3233333(0)33tt t e t t e t e t t +-++⎛⎫≤⇔≤< ⎪--⎝⎭，即23(3)30t t e t ---≤（*），令23()(3)3xu x x ex =---(0)x <.232()(1)13xx u x e '=--，………………11分因为234()0(0)9xu x xe x ''=-><恒成立，所以()u x '在(,0)-∞上是增函数，所以()(0)0u x u ''<=，所以()u x 在(,0)-∞上是减函数，故()(0)0u x u >=,0t ∴<时，()0u t >，这与（*）矛盾！所以原不等式得证，即126x x +>．…………13分。

信息安全数学基础期末考试试卷及答案（A 卷）一、 填空题（本大题共8小题，每空2分，共24分）1. 两个整数a ，b ，其最大公因数和最小公倍数的关系为 ________________。

2. 给定一个正整数m ，两个整数a ,b 叫做模m 同余，如果______________，记作(mod )a b m ≡；否则，叫做模m 不同余，记作_____________。

3. 设m ，n 是互素的两个正整数，则()mn ϕ=________________。

4. 设1m >是整数，a 是与m 互素的正整数。

则使得1(mod )ea m ≡成立的最小正整数e 叫做a 对模m 的指数，记做__________。

如果a 对模m 的指数是()m ϕ，则a 叫做模m 的____________。

5. 设n 是一个奇合数，设整数b 与n 互素，如果整数n 和b 满足条件________________，则n 叫做对于基b 的拟素数。

6. 设,G G '是两个群，f 是G 到G '的一个映射。

如果对任意的,a b G ∈，都有_______________，那么f 叫做G 到G '的一个同态。

7. 加群Z 的每个子群H 都是________群，并且有0H =<>或H =______________。

8. 我们称交换环R 为一个域，如果R 对于加法构成一个______群，*\{0}R R =对于乘法构成一个_______群。

二、计算题（本大题共 3小题，每小题8分，共24分）1. 令1613,a = 3589b =。

用广义欧几里德算法求整数,s t ，使得(,)sa tb a b +=。

2. 求同余方程22(mod 67)x ≡-的解数。

3. 计算3模19的指数19ord (3)。

三、解同余方程（本大题共2小题，每小题10分，共20分）1. 求解一次同余方程1714(mod 21)x ≡。