1建立反比例函数模型
- 格式:ppt
- 大小:189.00 KB
- 文档页数:17

建立反比例函数模型教学目标:理解反比例函数概念,能根据实际问题中的条件确定反比例函数的关系式。
重点:理解反比例函数的概念及求表达式。
难点:根据实际问题列出反比例函数关系式的分析过程。
教学过程:知识回顾:什么是函数?一次函数?正比例函数?一、创设情景探究问题情境1:当路程一定时,速度与时间成什么关系?( vt=s)当一个长方形面积一定时,长与宽成什么关系?情境2:汽车从南京出发开往上海(全程约300km),全程所用时间t(h)随速度v(km/h)的变化而变化.问题:(1)你能用含有v的代数式表示t吗?(2)利用(1)的关系式完成下表:随着速度的变化,全程所用时间发生怎样的变化?(3)速度v是时间t的函数吗?为什么?问题:(1)这些函数关系式与我们以前学习的一次函数、正比例函数关系式有什么不同?(2)它们有一些什么特征?一般地,如果两个变量y与x的关系可以表示成y=kx(k为常数,k≠0)的v(km/h) 60 80 90 100 120 t(h)形式,那么称y是x的反比例函数,其中x是自变量,y是因变量,y是x的函数,k是比例系数. (有的书上写成y=kx-1的形式.)二、例题教学例1:下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?(1)y=x15;(2)y=2x-1;(3)y=-3x;(4)y=1x-3;(5)y=2+1x;(6)y=x3+2;(7)y=-12x.例2:在函数y=2x-1,y=2x+1,y=x-1,y=12x中,y是x的反比例函数的有个.例3:若y与x成反比例,且x=-3时,y=7,则y与x的函数关系式为.三、拓展练习1、写出下列问题中两个变量之间的函数关系式,并判断其是否为反比例函数. 如果是,指出比例系数k的值.(1)底边为5cm的三角形的面积y(cm2)随底边上的高x(cm)的变化而变化;(2)某村有耕地面积200ha,人均占有耕地面积y(ha)随人口数量x (人)的变化而变化;2、下列哪些关系式中的y是x的反比例函数?如果是,比例系数是多少?(1)y=23x;(2)y=23x;(3)xy+2=0;(4)xy=0;(5)x=23y .3、已知函数y=(m+1)x22m是反比例函数,则m的值为.四、课堂小结这节课你学到了什么?还有那些困惑?1、牢记反比例函数的概念;2、能正确区别正、反比例函数五、布置作业:书P4 A组[教学后记]。

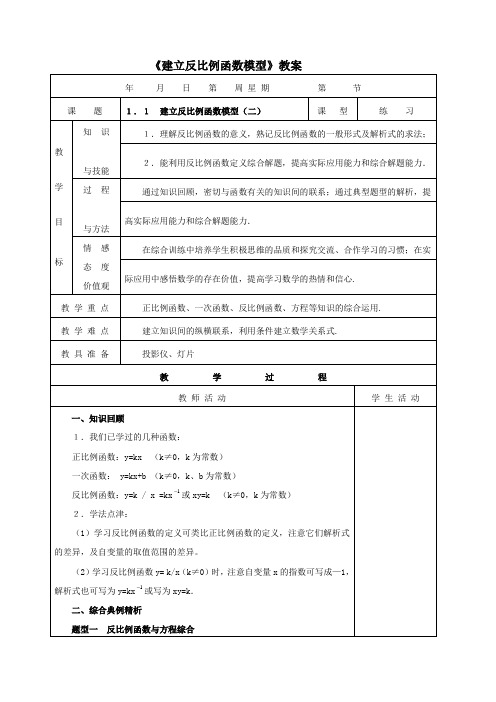
课题建立反比例函数模型(一)课型新授知识与技能1.理解反比例函数的意义;2.熟记反比例函数的一般形式:y=k/x(k≠0,k为常数);3.能在实际问题中建立反比例函数模型.过程与方法通过实际问题情境建立反比例函数模型,抽象其一般形式及自变量的取值范围,并能在实际问题中建立反比例函数模型.情感与态度培养学生独立思考、积极探索的思维品质,善于用数学知识解决身边的数学问题,提高学习数学的热情和积极性.教学重点反比例函数的意义及一般形式:y=k/x(k≠0,k为常数).教学难点建立反比例函数模型及生活中的反比例函数.教具准备透影仪、灯片.教学过程教师活动学生活动一、创设情境,引出问题1.知识回顾:我们已学过哪几种函数?它们的图象是什么?2.【问题情境一】新安与常德相距82km,李老师乘座快巴昨天去常德和今天乘座快巴回新安分别用时75分钟和80分钟,问李老师乘座的两辆快巴谁的平均速度快?这是什么道理?与高速公路上行驶的汽车的正常速度(一般在110km/h左右,最高限速140km/h)相比,你觉得快巴“快”吗?3.【问题情境二】谁先到达终点?小明、小亮、小华和小强他们跑400m的平均速度分别为5.3m/s,5m/s,4.8m/s,那么他们谁先到达终点?这是什么道理?分析:当路程s=400m时,所花的时间t与速度v的关系是t=400/v.利用这个公式,可计算出小明、小亮、小华、和小强所花的时间分别为75.5s,80s, 83.3s,和 88.9s.二、利用情境,解决问题抽象归纳在上面的问题情境一中,当路程s=32km时,平均速度v(km/h)与时间t(h)的关系为 v=32/t在上面的问题情境二中,当路程s=400m时,所花的时间t(s)与速度v(m/s)的关系为t=400/v.上述式子表明:当路程一定时,平均速度v是时间t的函数;所花时间t是速度v的函数.由于当路程一定时,平均速度v与时间t成反比例关系,因此我们把这样的函数叫作反比例函数.定义:一般地,如果两个变量y与x的关系可以表示成y=k/x=kx-1(k为常数,k≠0)的形式,那么称y是x的反比例函数。



湘教版数学九年级上册1.1《建立反比例函数模型》教学设计一. 教材分析湘教版数学九年级上册 1.1《建立反比例函数模型》是本册教材的第一节内容,主要介绍了反比例函数的概念和性质。
通过本节课的学习,学生能够理解反比例函数的定义,掌握反比例函数的性质,并能运用反比例函数解决实际问题。
二. 学情分析九年级的学生已经掌握了函数的基本概念和性质,具备了一定的函数知识基础。
但反比例函数的概念和性质相对较为抽象,学生可能难以理解和掌握。
因此,在教学过程中,需要注重引导学生通过实例来理解和掌握反比例函数的概念和性质。
三. 教学目标1.知识与技能:学生能够理解反比例函数的概念,掌握反比例函数的性质。
2.过程与方法:学生能够通过实例探究反比例函数的性质,培养学生的观察、分析和解决问题的能力。
3.情感态度与价值观:学生能够体验到数学与生活的紧密联系,增强学习数学的兴趣和信心。
四. 教学重难点1.反比例函数的概念和性质。
2.运用反比例函数解决实际问题。
五. 教学方法1.情境教学法:通过生活实例引入反比例函数的概念,让学生感受到数学与生活的紧密联系。
2.引导发现法:引导学生通过观察、分析和归纳反比例函数的性质。
3.实践操作法:让学生通过实际操作,加深对反比例函数的理解。
六. 教学准备1.教学课件:制作反比例函数的概念和性质的课件。
2.实例素材:准备一些与反比例函数相关的实际问题作为教学素材。
3.学具:准备一些反比例函数的模型或图片。
七. 教学过程导入(5分钟)教师通过展示一些实际问题,如商场打折、比例尺等,引导学生回顾函数的概念和性质。
然后提出问题:“如果我们把函数看作是自变量和因变量之间的关系,那么有没有一种函数,它的值总是保持不变呢?”呈现(10分钟)教师通过课件介绍反比例函数的概念,引导学生观察和分析反比例函数的性质。
同时,教师可以通过展示一些实例,让学生感受到反比例函数在实际生活中的应用。
操练(15分钟)教师提出一些有关反比例函数的问题,让学生进行解答。