Quark Mass Dependence of Nucleon Properties and Extrapolation from Lattice QCD

Charge separation relative to the reaction plane in Pb-Pb collisions at ffiffiffiffiffiffiffiffiffis NN p ¼2:76TeVB.Abelev et al.*(ALICE Collaboration)(Received 5July 2012;published 2January 2013)Measurements of charge-dependent azimuthal correlations with the ALICE detector at the LHC arereported for Pb-Pb collisions at ffiffiffiffiffiffiffiffis NN p ¼2:76TeV .Two-and three-particle charge-dependent azimuthal correlations in the pseudorapidity range j j <0:8are presented as a function of the collision centrality,particle separation in pseudorapidity,and transverse momentum.A clear signal compatible with a charge-dependent separation relative to the reaction plane is observed,which shows little or no collision energy dependence when compared to measurements at RHIC energies.This provides a new insight for under-standing the nature of the charge-dependent azimuthal correlations observed at RHIC and LHC energies.DOI:10.1103/PhysRevLett.110.012301PACS numbers:25.75.Ld,11.30.Er,11.30.Qc,12.38.AwThe possibility to observe parity violation in the strong interaction using relativistic heavy-ion collisions has been discussed for many years [1–3].In quantum chromody-namics (QCD),this symmetry violation originates in the interaction between quarks and topologically nontrivial gluonic fields,instantons,and sphalerons [4].This interac-tion,which is characterized by the topological charge [5],breaks the balance between the number of quarks with different chirality,resulting in a violation of the P and CP symmetry.In [6,7],it was suggested that in the vicinity of the deconfinement phase transition,and under the influ-ence of the strong magnetic field generated by the colliding nuclei,the quark spin alignment along the direction of the angular momentum (i.e.the direction of the magnetic field)and the imbalance of the left-and right-handed quarks,generates an electromagnetic current.The experimental search of these effects has intensified recently,following the realization that the consequent quark fragmentation into charged hadrons results in a charge separation along the direction of the magnetic field,and perpendicular to the reaction plane (the plane of symmetry of a collision defined by the impact parameter vector and the beam direction).This phenomenon is called the chiral magnetic effect (CME).Because of fluctuations in the sign of the topologi-cal charge,the resulting charge separation averaged over many collisions is zero.This makes the observation of the CME possible only via P -even observables,expressed in terms of two-particle and multiparticle correlations.The previous measurement of charge separation by the STAR Collaboration [8]is consistent with the qualitative expec-tations for the CME and has triggered an intense discussion [9–13].A significant source of uncertainty in the theoretical consideration of the CME is related to the expected center-of-mass energy dependence.In [7],the authors argued that the uncertainty in making any quantitative prediction relies on the time integration over which the magnetic field develops and decays.As long as a decon-fined state of matter is formed in a heavy-ion collision,the magnitude of the effect should either not change or should decrease with increasing energy [7].In addition,in [12]it is also suggested that there should be no energy depen-dence between the top RHIC and the LHC energies,based on arguments related to the universality of the underlying physical process,without however explicitly quantifying what the contribution of the different values and time evolution of the magnetic field for different energies will be.On the other hand,in [13]it is argued that the CME should strongly decrease at higher energies,because the magnetic field decays more rapidly.Such spread in the theoretical expectations makes it important to measure the charge-dependent azimuthal correlations at the LHC,where the collision energy is an order of magnitude higher compared to the RHIC.In this Letter we report the measurement of charge-dependent azimuthal correlations at midrapidity in Pb-Pb collisions at the center-of-mass energy per nucleon pair ffiffiffiffiffiffiffiffis NN p ¼2:76TeV by the ALICE Collaboration at the LHC.Azimuthal correlations among particles produced in a heavy-ion collision provide a powerful tool for the experi-mental study of particle production with respect to the reaction plane.They are usually quantified by the aniso-tropic flow coefficients,v n ,in a Fourier decomposition [14].Local violation of parity symmetry may result in the additional P -odd sinus terms [3,8,15]:dNd’ $1þ2X n ½v n; cos ðn Á’ Þþa n; sin ðn Á’ Þ ;(1)where Á’ ¼’ ÀÉRP is the azimuthal angle ’ of the charged particle of type relative to the reaction plane*Full author list given at the end of the article.Published by the American Physical Society under the terms of the Creative Commons Attribution 3.0License .Further distri-bution of this work must maintain attribution to the author(s)and the published article’s title,journal citation,and DOI.angle,ÉRP.The leading order coefficient a1; reflects the magnitude while the higher orders(a n; for n>1)describe the specific shape in azimuth of the effects from local parity violation.We thus employ a multiparticle correlator [15]that probes the magnitude of the a1coefficient,and at the same time suppresses the background correlations unrelated to the reaction plane:h cosð’ þ’ À2ÉRPÞi¼h cosÁ’ cosÁ’ iÀh sinÁ’ sinÁ’ i:(2) The indices and refer to the charge of the particles.The brackets denote an average over the particle pairs within the event as well as an average over the analyzed events.In practice,the reaction plane angle is not known and is esti-mated by constructing the event plane using azimuthal par-ticle distributions.In Eq.(2),the terms h cosÁ’ cosÁ’ i and h sinÁ’ sinÁ’ i quantify the correlations in-and out-of plane,respectively.The latter is sensitive to the charge correlations resulting from the CME:h sinÁ’ sinÁ’ i$ h a1; a1; i.The construction of the correlator in Eq.(2)as the difference between these two contributions suppresses correlations not related to the reaction plane orientation (nonflow).The contribution from the CME to the correla-tions of pairs of particles with same and opposite charge is expected to be similar in magnitude and opposite in sign. This expectation could be further modified by the medium created in a heavy-ion collision,that may result in the dilution of the correlations between particles with opposite sign[6,7].In order to evaluate each of the two terms in Eq.(2),we also measure the two-particle correlator:h cosð’ À’ Þi¼h cosÁ’ cosÁ’ iþh sinÁ’ sinÁ’ i;(3) which in contrast to the correlator in Eq.(2)is independent of the reaction plane angle and susceptible to the large P-even background contributions.The combination of these correlators provides access to both components, h cosÁ’ cosÁ’ i and h sinÁ’ cosÁ’ i,which is impor-tant for detailed comparisons with model calculations.It should be pointed out that both correlators of Eq.(2) and Eq.(3)could be affected by background sources.In [10],it is argued that the effect of momentum conservation influences in a similar way the pairs of particles with opposite and same charge,and could result in a potentially significant correction to both h cosð’ þ’ À2ÉRPÞi and h cosð’ À’ Þi.Also in[10],it was suggested that local charge conservation effects may be responsible for a sig-nificant part of the observed charge dependence of the correlator h cosð’ þ’ À2ÉRPÞi.Recent calculations [16]suggest that the correlator in Eq.(2)may have a negative(i.e.out-of-plane),charge-independent,dipole flow contribution originating fromfluctuations in the initial energy density of a heavy-ion collision.A description of the ALICE detector and its perform-ance can be found in[17,18].For this analysis,the follow-ing detector subsystems were used:the time projection chamber(TPC)[19],the silicon pixel detector(SPD), two forward scintillator arrays(VZERO),and two zero degree calorimeters(ZDC)[17].We analyzed a sample of about13Â106minimum-bias trigger events of Pb-Pb collisions atffiffiffiffiffiffiffiffis NNp¼2:76TeV collected with the ALICE detector.The standard ALICE offline event selection criteria[20]were applied,including a collision vertex cut ofÆ7cm along the beam axis.The collision centrality is estimated from the amplitude mea-sured by the VZERO detectors[17].The data sample is divided into centrality classes which span0%-70%of the hadronic interaction cross section,with the0%-5%class corresponding to the most central(i.e.smaller impact pa-rameter)collisions.Charged particles reconstructed by the TPC are accepted for analysis within j j<0:8and0:2< p T<5:0GeV=c.A set of requirements described in[20] were applied in order to ensure the quality of the tracks but also to reduce the contamination from secondary particles. To evaluate the systematic uncertainties in the analysis, events recorded with two different magneticfield polarities were analyzed leading to an uncertainty that is less than7% for all centrality classes.The cut on the collision vertex was varied fromÆ7cm toÆ10cm from the nominal collision point,with steps of1cm,contributing a maximum of5%to the total uncertainty.A bias due to the centrality determina-tion was studied by using multiplicities measured by the TPC or the SPD,rather than the VZERO,and was found to be less than10%.Contamination due to secondary tracks that do not originate from the collision vertex was reduced by requiring that the distance of closest approach between tracks and the primary vertex is less than2cm.The effect of secondary tracks on the measurement was estimated by varying the cut from2to4cm in steps of0.5cm and was calculated to be below15%.Effects due to nonuniform acceptance of the TPC were estimated to be below2%and are corrected for in the analysis.A significant contribution to the systematic error is coming from the uncertainty in the v2measurement,which is used as an estimate of the reaction plane resolution.The v2 estimate is obtained from the2-and4-particle cumulant analyses[20],which are affected in different ways by non-flow effects andflowfluctuations.For this analysis,v2was taken as the average of the two values,with half of the difference between v2f2g and v2f4g being attributed as the systematic uncertainty.The values of this uncertainty range from9%for the20%–30%centrality to18%(24%)for the 50%–60%(60%–70%)centrality class.The differences in the results from the four independent analysis methods (described below)were also considered as part of the system-atic uncertainty and were estimated to be3%for the 20%–30%and the50%–60%centrality bins and47%for the most peripheral centrality class.The contributions from all effects were added in quadrature to calculate the totalsystematic uncertainty.For the correlation between pairs of particles with the same charge it varies from 19%(28%)for the 20%–30%(50%–60%)centrality up to 55%for the 60%–70%centrality class.The correlations between oppo-site charged particles for 0%–60%centrality and for the same charge pairs for 0%–20%centrality are compatible with zero with a systematic error below 5:5Â10À5.Figure 1(a)presents the centrality dependence of the three-particle correlator,defined in Eq.(2).The correla-tions of the same charge pairs for the positive-positive and negative-negative combinations are found to be consistent within statistical uncertainties and are combined into one set of points,labeled same .The difference between the correlations of pairs with same and opposite charge indi-cates a charge dependence with respect to the reaction plane,as may be expected for the CME.To test the bias from the reaction plane reconstruction,four independent analyses were performed.The first analysis uses a cumu-lant technique [21],whereas for the three other analyses the orientation of the collision symmetry plane is estimated from the azimuthal distribution of charged particles in the TPC,and hits in the forward VZERO and ZDC detectors [22].There is a very good agreement between the results obtained with the event plane estimated from different detectors covering a wide range in pseudorapidity.This allows us to conclude that background sources due to corre-lations not related to the orientation of the reaction plane are negligible,with perhaps the exception of the peripheral collisions for the pairs of particles with opposite charge.Figure 1(b)shows the centrality dependence of the two-particle correlator h cos ð’ À’ Þi ,as defined in Eq.(3),which helps to constrain experimentally the P -even back-ground correlations.The statistical uncertainty is smaller than the symbol size.The two-particle correlations for the same and opposite charge combinations are always posi-tive and exhibit qualitatively similar centrality depen-dence,while the magnitude of the correlation is smaller for the same charged pairs.Our two-particle correlation results differ from those reported by the STARCollaboration for Au-Au collisions at ffiffiffiffiffiffiffiffis NN p ¼200GeV [8]for which negative correlations are observed for the same charged pairs.Figure 1(c)shows the h cosÁ’ cosÁ’ i and h sinÁ’ sinÁ’ i terms separately.For pairs of particles of the same charge,we observe that the h sinÁ’ sinÁ’ i correlations are larger than the h cosÁ’ cosÁ’ i ones.On the other hand,for pairs of opposite charge,the two terms are very close except for the most peripheral collisions.Further interpretation of the results presented in Fig.1(c)in terms of in-and out-of-plane correlations is complicated due to the significant nonflow contribution in h cos ð’ À’ Þi .Figure 2presents the three-particle correlator h cos ð’ þ’ À2ÉRP Þi as a function of the collision centrality com-pared to model calculations and results for RHIC energies.The statistical uncertainties are represented by the errorbars.The shaded area around the points indicates the systematic uncertainty based on the different sources described above.Also shown in Fig.2are STAR results [8].The small difference between the LHC and the RHIC data indicates little or no energy dependence for the three-particle correlator when changing from the collisionenergy of ffiffiffiffiffiffiffiffis NN p ¼0:2TeV to 2.76TeV .In Fig.2,the ALICE data are compared to the expectations from the HIJING model [23].The HIJING results for the three-particle correlations are divided by the experimentally〉)R P Ψ - 2βϕ + αϕ c o s (〈-0.50.5-3〉)βϕ-αϕ c o s (〈00.0020.0040.006centrality, %0.0020.003FIG.1(color online).(a)Centrality dependence of the correla-tor defined in Eq.(2)measured with the cumulant method and from correlations with the reaction plane estimated using the TPC,the ZDC,and the VZERO detectors.Only statistical errors are shown.The points are displaced slightly in the horizontal direction for visibility.(b)Centrality dependence of the two-particle corre-lator defined in Eq.(3)compared to the STAR data [8].The width of the solid red lines indicates the systematic uncertainty of the ALICE measurement.(c)Decomposition of the correlators into h cosÁ’ cosÁ’ i and h sinÁ’ sinÁ’ i terms.The ALICE results in (b)and (c)are obtained with the cumulant method.measured value of v 2(i.e.h cos ð’ þ’ À2’c Þi =v 2f 2g )as reported in [20]due to the absence of collective azimuthal anisotropy in this model.Since the points do not exhibit any significant difference between the correlations of pairs with same and opposite charge,they were averaged in the figure.The correlations from HIJING show a significant increase in the magnitude for very peripheral collisions.This can be attributed to correlations not related to the reaction plane orientation,in particular,from jets [8].The results from ALICE in Fig.2show a strong corre-lation for pairs with the same charge and simultaneously a very weak correlation for the pairs of opposite charge.This difference in the correlation magnitude depending on the charge combination could be interpreted as ‘‘quenching’’of the charge correlations for the case when one of the particles is emitted toward the center of the dense medium created in a heavy-ion collision [6,7].An alternative ex-planation can be provided by a recent suggestion [16]that the value of the charge-independent version of the corre-lator defined in Eq.(2)is dominated by directed flow fluctuations.The sign and the magnitude of these fluctua-tions based on a hydrodynamical model calculation for RHIC energies [16]appear to be very close to the mea-surement.Our results for charge-independent correlations are given by the shaded band in Fig.2.The thick solid line in Fig.2shows a prediction [13]for the same sign correlations due to the CME at LHC ener-gies.The model makes no prediction for the absolute magnitude of the effect and can only describe the energy dependence by taking into account the duration and time evolution of the magnetic field.It predicts a decrease of correlations by about a factor of 5from RHIC to LHC,which would significantly underestimate the observed magnitude of the same sign correlations seen at the LHC.At the same time in [7,12],it was suggested that the CME might have the same magnitude at the LHC and at RHIC energies.Figure 3shows the dependence of the three-particle correlator on the transverse momentum difference,j p T ; Àp T ; j ,the average transverse momentum,ðp T ; þp T ; Þ=2,and the pseudorapidity separation,j À j ,of the pair for the 30%-40%centrality range.The pairs of opposite charge do not show any significant dependence on the pseudorapidity difference,while there is a dependencecentrality, %〉)R P Ψ - 2βϕ + αϕ c o s (〈-0.6-0.4-0.200.20.40.6-3FIG.2(color online).The centrality dependence of the three-particle correlator defined in Eq.(2).The circles indicate the ALICE results obtained from the cumulant analysis.The stars show the STAR data from [8].The triangles represent the three-particle correlations [h cos ð’ þ’ À2’c Þi ]from HIJING [23]corrected for the experimentally measured v 2f 2g [20].Points are displaced horizontally for visibility.A model prediction for the same sign correlations incorporating the chiral magnetic effect for LHC energies [13]is shown by the solid line.The shaded band represents the centrality dependence of the charge-independent correlations.)| (GeV/c T,β - p T,α|p 〉)R P Ψ - 2βϕ + αϕc o s (〈-0.4-0.20.2-3))/2 (GeV/c T,β + p T,α(p |βη - αη = |η∆FIG.3(color online).The three-particle correlator defined in Eq.(2)as a function of (a)the transverse momentum difference,j p T ; Àp T ; j ,(b)the average transverse momentum,ðp T ; þp T ; Þ=2,and (c)the rapidity separation,j À j ,of the charged particle pair of same (closed symbols)and opposite (open symbols)sign.on j p T ; Àp T ; j (stronger)and ðp T ; þp T ; Þ=2(weaker).The correlations for pairs of particles of the same charge show no strong dependence on the p T difference,allowing one to exclude any type of short range correlations (e.g.quantum statistics correlations)as the main source of the effect.In addition,it is seen that the magnitude of the same charge correlations increases with increasing average p T of the pair.This observation is in contradiction to the initial expectations from theory [7]that the effect should originate from low p T particles.The dependence of the correlations on the j À j indicates a width of one unit in pseudor-apidity,beyond which the value of h cos ð’ þ’ À2ÉRP Þi is close to zero up to Á %1:5.Similar results were reported also at RHIC energies [8].At the moment there are no quantitative model calculations of the charge-dependent differential correlations.In summary,we have measured the charge-dependentazimuthal correlations in Pb-Pb collisions at ffiffiffiffiffiffiffiffis NN p ¼2:76TeV at the LHC using the ALICE detector.Both two-and three-particle correlations are reported.A clear signal compatible with a charge-dependent separation rela-tive to the reaction plane is observed.However,our results are not described by the only available quantitative model prediction of the CME for the LHC energy.The lack of realistic model calculations for the centrality and pair differential dependencies based on models incorporating CME and possible background contributions does not allow us to make a firm conclusion regarding the nature of the charge-dependent correlations originally observed at RHIC and now established at the LHC.The observation of a small collision energy dependence of the three-particle correlation and the simultaneous significant change in the two-particle correlations between top RHIC and LHC energies put stringent constraints on models built to interpret such correlations.Analyses of higher harmonic correlations are planned and may yield a better understanding of the com-plex charge-dependent correlations seen at LHC energies.The ALICE Collaboration would like to thank all its engi-neers and technicians for their invaluable contributions to the construction of the experiment and the CERN accelerator teams for the outstanding performance of the LHC complex.The ALICE Collaboration acknowledges the following fund-ing agencies for their support in building and running the ALICE detector:Calouste Gulbenkian Foundation from Lisbon and Swiss Fonds Kidagan,Armenia;ConselhoNacional de Desenvolvimento Cientı´fico e Tecnolo ´gico (CNPq),Financiadora de Estudos e Projetos (FINEP),Fundac ¸a˜o de Amparo a `Pesquisa do Estado de Sa ˜o Paulo (FAPESP);National Natural Science Foundation of China (NSFC),the Chinese Ministry of Education (CMOE),and the Ministry of Science and Technology of China (MSTC);Ministry of Education and Youth of the Czech Republic;Danish Natural Science Research Council,the Carlsberg Foundation,and the Danish National Research Foundation;The European Research Council under the EuropeanCommunity’s Seventh Framework Programme;Helsinki Institute of Physics and the Academy of Finland;French CNRS-IN2P3,the ‘‘Region Pays de Loire,’’‘‘Region Alsace,’’‘‘Region Auvergne,’’and CEA,France;German BMBF and the Helmholtz Association;General Secretariat for Research and Technology,Ministry of Development,Greece;Hungarian OTKA and National Office for Research and Technology (NKTH);Department of Atomic Energy and Department of Science and Technology of the Government of India;Istituto Nazionale di Fisica Nucleare (INFN)of Italy;MEXT Grant-in-Aid for Specially Promoted Research,Japan;Joint Institute for Nuclear Research,Dubna;National Research Foundation of Korea (NRF);CONACYT,DGAPA,Me´xico,ALFA-EC,and the HELEN Program (High-Energy Physics Latin-American–European Network);Stichting voor Fundamenteel Onderzoek der Materie (FOM)and the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO),Netherlands;Research Council of Norway (NFR);Polish Ministry of Science and Higher Education;National Authority forScientific Research-NASR (Autoritatea Nat ¸ionala˘pentru Cercetare S ¸tiint¸ifica ˘-ANCS);Federal Agency of Science of the Ministry of Education and Science of Russian Federation,International Science and Technology Center,Russian Academy of Sciences,Russian Federal Agency of Atomic Energy,Russian Federal Agency for Science and Innovations and CERN-INTAS;Ministry of Education of Slovakia;Department of Science and Technology,South Africa;CIEMAT,EELA,Ministerio de Educacio´n y Ciencia of Spain,Xunta de Galicia (Consellerı´a de Educacio ´n),CEADEN,Cubaenergı´a,Cuba,and IAEA (International Atomic Energy Agency);Swedish Research Council (VR)and Knut &Alice Wallenberg Foundation (KAW);Ukraine Ministry of Education and Science;United Kingdom Science and Technology Facilities Council (STFC);the United States Department of Energy,the United States National Science Foundation,the State of Texas,and the State ofOhio.[1]T.D.Lee,Phys.Rev.D 8,1226(1973);T.D.Lee andG.C.Wick,Phys.Rev.D 9,2291(1974).[2]P.D.Morley and I.A.Schmidt,Z.Phys.C 26,627(1985).[3] D.Kharzeev,R.D.Pisarski,and M.H.G.Tytgat,Phys.Rev.Lett.81,512(1998);D.Kharzeev and R.D.Pisarski,Phys.Rev.D 61,111901(2000).[4]T.Scha¨fer and E.V .Shuryak,Rev.Mod.Phys.70,323(1998).[5]S.S.Chern and J.Simons,Ann.Math.99,48(1974).[6] D.Kharzeev,Phys.Lett.B 633,260(2006);K.Fukushima, D.E.Kharzeev,and H.J.Warringa,Phys.Rev.D 78,074033(2008).[7] D.Kharzeev,L.D.McLerran,and H.J.Warringa,Nucl.Phys.A803,227(2008).[8] B.I.Abelev et al.(STAR Collaboration),Phys.Rev.Lett.103,251601(2009); B.I.Abelev et al.(STAR Collaboration),Phys.Rev.C 81,54908(2010).[9] B.Mu¨ller and A.Scha¨fer,Phys.Rev.C82,057902(2010).[10]S.Schlichting and S.Pratt,Phys.Rev.C83,014913(2011);S.Pratt,S.Schlichting,and S.Gavin,Phys.Rev.C84,024909(2011).[11] A.Bzdak,V.Koch,and J.Liao,Phys.Rev.C81,031901(2010);A.Bzdak,V.Koch,and J.Liao,Phys.Rev.C83, 014905(2011).[12] A.R.Zhitnitsky,Nucl.Phys.A853,135(2011);A.R.Zhitnitsky,Nucl.Phys.A886,17(2012).[13]V.D.Toneev and V.V oronyuk,arXiv:1012.1508.[14]S.V oloshin and Y.Zhang,Z.Phys.C70,665(1996);A.M.Poskanzer and S.A.V oloshin,Phys.Rev.C58,1671 (1998).[15]S.A.V oloshin,Phys.Rev.C70,057901(2004).[16] D.Teaney and L.Yan,Phys.Rev.C83,064904(2011).[17]K.Aamodt et al.(ALICE Collaboration),JINST3,S08002(2008).[18]K.Aamodt et al.(ALICE Collaboration),J.Phys.G30,1517(2004);K.Aamodt et al.(ALICE Collaboration), J.Phys.G32,1295(2006).[19]J.Alme et al.(ALICE Collaboration),Nucl.Instrum.Methods Phys.Res.,Sect.A622,316(2010).[20]K.Aamodt et al.(ALICE Collaboration),Phys.Rev.Lett.105,252302(2010).[21] A.Bilandzic,R.Snellings,and S.V oloshin,Phys.Rev.C83,044913(2011).[22]S.V oloshin, A.M.Poskanzer,and R.Snellings,inRelativistic Heavy Ion Physics,Landolt-Bornstein V ol.1 (Springer-Verlag,Berlin,2010),pp.554.[23]M.Gyulassy and X.N.Wang,mun.83,307(1994);X.N.Wang and M.Gyulassy,Phys.Rev.D44,3501(1991).B.Abelev,1J.Adam,2D.Adamova´,3A.M.Adare,4M.M.Aggarwal,5G.Aglieri Rinella,6A.G.Agocs,7 A.Agostinelli,8S.Aguilar Salazar,9Z.Ahammed,10N.Ahmad,11A.Ahmad Masoodi,11S.A.Ahn,12S.U.Ahn,13A.Akindinov,14D.Aleksandrov,15B.Alessandro,16R.Alfaro Molina,9A.Alici,17,18A.Alkin,19E.Almara´z Avin˜a,9J.Alme,20T.Alt,21V.Altini,22S.Altinpinar,23I.Altsybeev,24C.Andrei,25A.Andronic,26V.Anguelov,27J.Anielski,28C.Anson,29T.Anticˇic´,30F.Antinori,31P.Antonioli,17L.Aphecetche,32H.Appelsha¨user,33N.Arbor,34S.Arcelli,8A.Arend,33N.Armesto,35R.Arnaldi,16T.Aronsson,4I.C.Arsene,26 M.Arslandok,33A.Asryan,24A.Augustinus,6R.Averbeck,26T.C.Awes,36J.A¨ysto¨,37M.D.Azmi,11M.Bach,21A.Badala`,38Y.W.Baek,39,13R.Bailhache,33R.Bala,16R.Baldini Ferroli,18A.Baldisseri,40A.Baldit,39F.Baltasar Dos Santos Pedrosa,6J.Ba´n,41R.C.Baral,42R.Barbera,43F.Barile,22G.G.Barnafo¨ldi,7L.S.Barnby,44V.Barret,39J.Bartke,45M.Basile,8N.Bastid,39S.Basu,10B.Bathen,28G.Batigne,32B.Batyunya,46C.Baumann,33I.G.Bearden,47H.Beck,33I.Belikov,48F.Bellini,8R.Bellwied,49E.Belmont-Moreno,9G.Bencedi,7S.Beole,50I.Berceanu,25A.Bercuci,25Y.Berdnikov,51D.Berenyi,7 A.A.E.Bergognon,32D.Berzano,16L.Betev,6A.Bhasin,52A.K.Bhati,5J.Bhom,53L.Bianchi,50N.Bianchi,54 C.Bianchin,55J.Bielcˇı´k,2J.Bielcˇı´kova´,3A.Bilandzic,56,47S.Bjelogrlic,57F.Blanco,58F.Blanco,49D.Blau,15C.Blume,33M.Boccioli,6N.Bock,29S.Bo¨ttger,59A.Bogdanov,60H.Bøggild,47M.Bogolyubsky,61L.Boldizsa´r,7M.Bombara,62J.Book,33H.Borel,40A.Borissov,63S.Bose,64F.Bossu´,50M.Botje,56B.Boyer,65E.Braidot,66P.Braun-Munzinger,26M.Bregant,32T.Breitner,59T.A.Browning,67M.Broz,68R.Brun,6E.Bruna,50,16G.E.Bruno,22D.Budnikov,69H.Buesching,33S.Bufalino,50,16K.Bugaiev,19O.Busch,27 Z.Buthelezi,70D.Caballero Orduna,4D.Caffarri,55X.Cai,71H.Caines,4E.Calvo Villar,72P.Camerini,73 V.Canoa Roman,74G.Cara Romeo,17W.Carena,6F.Carena,6N.Carlin Filho,75F.Carminati,6A.Casanova Dı´az,54J.Castillo Castellanos,40J.F.Castillo Hernandez,26E.A.R.Casula,76V.Catanescu,25 C.Cavicchioli,6C.Ceballos Sanchez,77J.Cepila,2P.Cerello,16B.Chang,37,78S.Chapeland,6J.L.Charvet,40S.Chattopadhyay,10S.Chattopadhyay,64I.Chawla,5M.Cherney,79C.Cheshkov,6,80B.Cheynis,80V.Chibante Barroso,6D.D.Chinellato,81P.Chochula,6M.Chojnacki,57S.Choudhury,10P.Christakoglou,56 C.H.Christensen,47P.Christiansen,82T.Chujo,53S.U.Chung,83C.Cicalo,84L.Cifarelli,8,6,18F.Cindolo,17J.Cleymans,70F.Coccetti,18F.Colamaria,22D.Colella,22G.Conesa Balbastre,34Z.Conesa del Valle,6 P.Constantin,27G.Contin,73J.G.Contreras,74T.M.Cormier,63Y.Corrales Morales,50P.Cortese,85I.Corte´s Maldonado,86M.R.Cosentino,66F.Costa,6M.E.Cotallo,58E.Crescio,74P.Crochet,39E.Cruz Alaniz,9E.Cuautle,87L.Cunqueiro,54A.Dainese,55,31H.H.Dalsgaard,47A.Danu,88D.Das,64K.Das,64I.Das,65S.Dash,89A.Dash,81S.De,10G.O.V.de Barros,75A.De Caro,90,18G.de Cataldo,91J.de Cuveland,21A.De Falco,76D.De Gruttola,90H.Delagrange,32A.Deloff,92V.Demanov,69N.De Marco,16E.De´nes,7 S.De Pasquale,90A.Deppman,75G.D.Erasmo,22R.de Rooij,57M.A.Diaz Corchero,58D.Di Bari,22T.Dietel,28C.Di Giglio,22S.Di Liberto,93A.Di Mauro,6P.Di Nezza,54R.Divia`,6Ø.Djuvsland,23A.Dobrin,63,82T.Dobrowolski,92I.Domı´nguez,87B.Do¨nigus,26O.Dordic,94O.Driga,32A.K.Dubey,10A.Dubla,57L.Ducroux,80P.Dupieux,39M.R.Dutta Majumdar,10A.K.Dutta Majumdar,64D.Elia,91D.Emschermann,28。

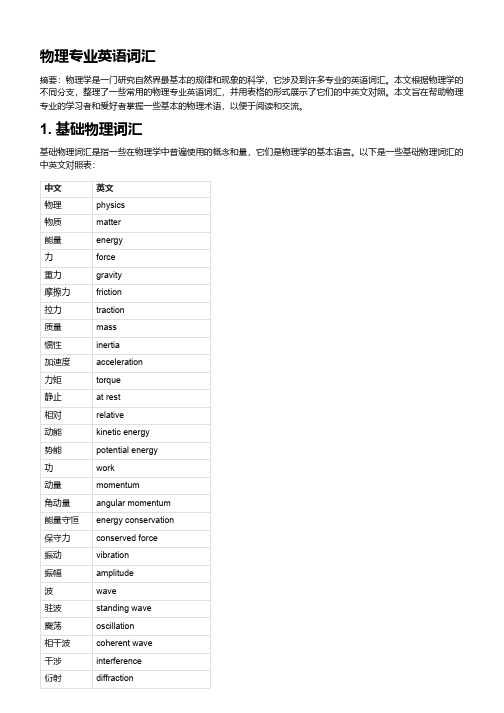
物理专业英语词汇摘要：物理学是一门研究自然界最基本的规律和现象的科学，它涉及到许多专业的英语词汇。

本文根据物理学的不同分支，整理了一些常用的物理专业英语词汇，并用表格的形式展示了它们的中英文对照。

本文旨在帮助物理专业的学习者和爱好者掌握一些基本的物理术语，以便于阅读和交流。

1. 基础物理词汇基础物理词汇是指一些在物理学中普遍使用的概念和量，它们是物理学的基本语言。

以下是一些基础物理词汇的中英文对照表：中文英文物理physics物质matter能量energy力force重力gravity摩擦力friction拉力traction质量mass惯性inertia加速度acceleration力矩torque静止at rest相对relative动能kinetic energy势能potential energy功work动量momentum角动量angular momentum能量守恒energy conservation保守力conserved force振动vibration振幅amplitude波wave驻波standing wave震荡oscillation相干波coherent wave干涉interference衍射diffraction轨道orbit速度velocity速率speed大小magnitude方向direction水平horizontal竖直vertical相互垂直perpendicular坐标coordinate直角坐标系Cartesian coordinate system极坐标系polar coordinate system2. 电学和磁学词汇电学和磁学是研究电荷、电流、电场、磁场等现象和规律的物理学分支，它们与光学、热学、原子物理等有着密切的联系。

以下是一些电学和磁学词汇的中英文对照表：中文英文电子electron电荷charge电流current电场electric field电通量electric flux电势electric potential导体conductor电介质dielectric绝缘体insulator电阻resistor电阻率resistivity电容capacitor3. 物理专业英语词汇物理专业英语词汇是指在物理学的学习和研究中经常使用的一些专业术语，它们涵盖了物理学的各个分支和领域，如力学、电磁学、光学、热学、量子力学等。

Toward Loop Level Study of Supersymmetric Model at Futuree+e−Linear ColliderMihoko M.Nojiri1KEK Theory Group,Oho1-1,Tsukuba,Ibaraki,305,JapanAbstract.In the case with a large splitting between the squark and slepton masses,thesupersymmetric identities which enforce the equality of the gauge and gaugino couplingsare violated in the effective theory below the squark mass threshold.We compute the fullone-loop(s)quark corrected slepton production cross-sections.Wefind that the one-loopcorrected slepton production cross-sections can depend on the squark mass strongly,upto9%×log10(M˜Q /m˜).We investigate the squark mass sensitivity of the slepton cross-section measurements at a future linear collider.For sneutrino production accessible at√s=500GeV there can be sensitivity to squark masses at or larger than1TeV.1.IntroductionSupersymmetry is an attractive possibility beyond the standard model.Because of the relations super-symmetry imposes among the dimensionless couplings,the quadratic divergences in the Higgs sector are cut-offby the superpartner mass scale.The cancellations stabilize the hierarchy between the Planck scale and the weak scale.The minimal supersymmetric standard model(MSSM)is consistent with gauge coupling unification suggested by grand unified theories.Also,it is interesting that one of the hallmarks of supersymmetry,a light Higgs boson(m h<∼130GeV),is favored by globalfits to precision electroweak dataIn this contribution we examine the prospect of testing supersymmetry via a precise measurement of the lepton-slepton-gaugino vertex.The linear collider provides a suitably clean experimental environ-ment[1,2,3,4,5].Among the relations which account for the cancellations of quadratic divergences, supersymmetry relates the lepton-slepton-gaugino coupling to the usual gauge coupling.Although bare(or)couplings enjoy the relations imposed by supersymmetry,the effective gauge and gaugino couplings are not equal because supersymmetry is broken.In particular,all non-singlet nondegenerate supermultiplets such as the quark-squark supermultiplets contribute to the split-ting.Hence,measurements of the type we consider here not only provide for detailed tests of supersym-metry,but can also elucidate important features of the scale and pattern of supersymmetry breaking [6,7,8,9,10].For example,the(s)quark contribution to the splitting of the U(1)and SU(2)gaugino/gauge (s)lepton couplings grows logarithmically with the squark mass,asδg Y g Y 11g2Y48π2lnM˜Qm˜,δg2g23g2216π2lnM˜Qm˜.(1)This correction is obtained by evolving the couplings according to the renormalization group equations(RGE’s)of the effective theory[11]below the squark mass threshold.When M˜Q /m˜10the correction1Address after Oct.1st.Yukawa Institute,Kyoto University,Kyoto,Japan.E-mail:nojirim@theory.kek.jp.This work is supported in part by Grant in aid for Science and Culture of Japan(07640428,09246232)e −e +˜ ˜∗(a)e −e +˜ ˜∗(b)Figure 1.Feynman graphs of the one-loop quarks-squark corrections to the processes e −e +→˜˜ ∗,for (a)s -channel and (b)t -channel amplitudes.to the SU(2)(U(1))coupling is about 2%(0.7%).This gives rise to an enhancement of the t -channel slepton or gaugino production cross-section of about 8%(2.8%).If large statistics are available and systematic errors can be controlled,we can (assuming the MSSM)constrain the squark mass scale by this measurement.We restrict our attention to the measurement of the first generation lepton-slepton-gaugino cou-pling at an e −e +linear collider.Much study has been undertaken to determine how accurately we can expect to measure these couplings[3,5,7,10].In Ref.[10],we perform a full one-loop calculation of the slepton production cross-section within the MSSM.We include only (s)quark loops in the calculation,because the correction is enhanced by a color factor and the number of generations.The remaining corrections are small,and if we did include them we expect our conclusions would not change.In this contribution,we only discuss our calculation only briefly in section 2.We point out that,to a good approximation,the one-loop t -channel amplitudes can be rewritten in the same form as the tree-level amplitudes,with the replacement of the tree-level parameters with renormalized effective parameters.Hence we introduce the effective coupling,the effective masses,and the effective mixing matrix.In section 3we discuss our numerical results,and show how well we can measure the squark loop correction to the coupling,and thereby constrain the squark mass,assuming both slepton and chargino production are possible.We show the statistical significance of the results by combining our knowledge of the superpartner masses and cross-sections.The uncertainty in the slepton mass measurement is quite important in this analysis.In the last section,section 4,we give our conclusions.2.calculationIn this section we discuss the calculation of the cross-section of e +e −→˜ i ˜ ∗j ,where ˜ i =(˜e −L ,˜e −R ,˜νe ),including one-loop (s)quark corrections.The full result is explicitly given in Ref.[10];here we restrict ourselves to outline the general features of the calculation.The tree level slepton productions proceed through s-channel exchange of Z and γ,and t-channel exchange of neutralinos or charginos (˜χi ).To evaluate the one-loop amplitude,we treat all the param-eters appearing in this tree-level expression as running DR quantities,and add the contributions from the one-loop diagrams (see Fig.1).Note that the (s)quark loop corrections do not give rise to external wave-function renormalization.To avoid a complexities of several gauge interactions,let us consider e +e −→˜e +R ˜e −R production.If the √s m Z ,the process approximately proceeds through s-channel exchange of B boson which couples to hypercharge,and t-channel exchange of ˜B ,superpartner of B boson.The s-channel amplitude below squark mass threshold is very well approximated by effective coupling g effY (Q =√s ).g Y(Q )in MSSM is related to g effY as αeffY =αDR (1+Σq (Q )+Σ˜q (Q ))where Σq (Q )and Σ˜q (Q )is the gauge two point function from quark and squark loops respectively and Q is renormalization scale.The g DR Y (Q )is equivalent to the t-channel coupling g ˜B (Q ),but we do not directly measure the coupling.The t-channel amplitude is the sum of tree level contribution and 1-loop contribution shown in Fig1.(b).TheΣq (Q ),Σ˜q (Q )Σq˜q (Q )αeffi αeff˜G i αi (Q )α˜G i (Q )≡(↔m Z ,m W ,e SM ,sin θeffW ...)gauge sector SUSY gaugino sectorFigure 2.Schematic figure of the correction to SUSY relationdifference S /Y ≡(g eff˜B −g effY )/g effY ≡(Σq ˜q −Σq −Σ˜q )(Q )/2is the correction to the SUSY relation(Fig.2).The leading logarithms of the corrections S /at Q =m ˜ are exactly those of Eq.(1),showing that the RGE approach of Ref.[11]gives the proper results.Although both s-channel and t-channel diagrams receive one loop corrections from squark and quark loops,only t-channel amplitude receive physically interesting correction.Notice in our approxi-mation,s-channel amplitude receives oblique correction of the gauge two point function only,which is common to the e +e −collision at Z pole.The measurement at Z pole fixes the s-channel amplitude of slepton production,thanks to the gauge symmetry.In Ref[10],we also how the one-loop corrected t -channel amplitude can be well approximated bya tree-level form.For e +e −→˜eR ˜e R ,we find M t RR =2¯v p / −4 i =1¯g 2e ˜e R ˜B N ∗i 1N i 1(p 2)p 2m 2i (p 2)P R u ,(2)where p is t-channel momentum and ¯g e ˜e R ˜B (p 2)is the effective bino coupling defined as ¯g e ˜e R ˜B (p 2)=ˆg Y (Q ) 1−12˜ΣL 11(Q,p 2) ,(3)and ˜ΣL 11(p 2)is the bino-bino component of the neutralino two-point function,and ˆgY (Q )is coupling.The N ij and m i are the effective neutralino mixing matrix and neutralino masses obtained by diagonal-izing the effective neutralino mass matrix Y ij .¯g i ,N ij ,and m i are physical scale independent quantities to O (α).¯m i (¯m i )is the pole mass of neutralinos.We also checked numerically the expression Eq.(2)reproduce the full result very well.3.Numerical results3.1.m ˜Q Dependence of Various Cross SectionsWe next show the numerical dependence of the one-loop corrected cross-sections of e −e +→˜ i ˜ ∗j (˜ i =(˜e −L ,˜e −R ,˜νe ))on the squark mass.We consider the case where the initial electron is completelylongitudinally polarized.We therefore treat the following eight modes,e −L e+→˜e −L ˜e +L ,˜e −R ˜e +R ,˜e −L ˜e +R ,˜νe ˜ν∗e ,e −R e +→˜e −L ˜e +L ,˜e −R ˜e +R ,˜e −R ˜e +L ,˜νe ˜ν∗e .(4)The production involves the t channel exchange of chargino and neutralino,which depends of gaugino mass parameter M 1,M 2,higgsino mass parameter µ,and tan β.We take the three pole masses (m ˜χ01,m ˜χ+1,m ˜χ03),and tan β(M Z )as inputs.We assume |µ| M Z ,in which case M eff1 m ˜χ01,M eff2 m ˜χ+1,and |µeff| m ˜χ03hold,where M eff1,M eff2,and −µeffare the (1,1),(2,2),and (3,4)elements of the effective neutralino mass matrix Y ij ,defined in [10].We show in Fig.3the M ˜Q dependence of the cross-sections for left handed electron beam.Here we normalize the cross-sections to the tree-level values defined in Ref.[10].The one-loop cor-rected cross-sections of the modes which have a t -channel contribution are similar to tree-level ones at1000M Q (GeV)0.951.001.051.10σ(c o r r )/σ(t r e e )(a)e −Le −L e +L~ ~νν*~~e −L e +R~ ~e −R e +R~ ~5000500~Figure 3.The M ˜Q dependence of the slepton production cross-sections.Input parametersare m ˜χ01=100GeV,m ˜χ+1=200GeV,m ˜χ03=300GeV,tan β(M Z )=4,m ˜ =200GeV,A =0,µ<0,and √s =500GeV.The corrected cross-sections are normalized by thetree-level cross-sections[10].M ˜Q <∼300GeV,but increase linearly with log M ˜Q .Because the effective masses are equal to the input pole masses,the squark mass dependence of the one-loop corrected cross-sections is primarily due to the difference between the effective theory gauge and gaugino couplings.See Eq.(2)The two channels which have ˜W contributions (e −L e +→˜e −L ˜e +L ,˜νe ˜ν∗e )show the largest M ˜Q depen-dence.The channel e −L e +→˜e −L ˜e +R ,show smaller M ˜Q dependence from ˜B contributions.Nevertheless,we found these M ˜Q dependences are significantly larger than the renormalization scale dependence ofthe corrected cross-sections (see Fig.2).In contrast,the remaining channels,which have only s -channel contributions,show very little M ˜Q dependence,as explained in Section 2.3.2.Determination of M ˜Q The sfermion and chargino/neutralino production cross-sections depend on M 1,M 2,µ,tan β,and the sfermion mass m ˜ .The cross-sections also depend on the effective fermion-sfermion-gaugino coupling ¯g f ˜f ˜χ,which is nicely parameterized by log M ˜Q .By constraining ¯g f ˜f ˜χwe can determine M ˜Q ,if the rest of the parameters are known accurately enough.It has been demonstrated that an accurate determination of m ˜χand m ˜ is indeed possible if sfermions ˜are produced and dominantly decay into a charged lepton and a chargino or neutralino ˜χ[1,2].The measurement of the end point energies determine the masses.Recently,Baer et al.[4]performed a MC study for the case that left-handed sfermions are produced and decay into a gaugino-like chargino or neutralinos.In their example called point 3,˜νe ˜ν∗e production is followed by ˜ν(∗)e →e ∓˜χ±1.The decay mode ˜νe ˜νe ∗→e −e +˜χ+1˜χ−1→e −e +µ2j (νµ2˜χ01)is background free and the measured electron endpoint energies allow for a 1%measurement of m ˜χ±1and m ˜ν.The results of Ref.[4]encourage us to consider their example point 3.The chosen parameter set corresponds to m ˜νe =207GeV,m ˜χ+1=96GeV,m ˜χ01=45GeV and m ˜χ03=270GeV,and the lightest chargino and neutralinos are gaugino-like.Their study suggests that we can take m ˜χ+1,m ˜χ01,and m ˜νe as well constrained input parameters.For 20fb −1of luminosity,their MC simulations show that at 68%CL,(δm ˜χ+1,δm ˜νe )=(1.5GeV,2.5GeV).In the following we estimate the statistical significance of the radiative correction to the production cross-section.We focus solely on the ˜νe production cross-section,because it is larger than 1pb for a left-handed electron beam,and larger than the other sparticle production cross-sections at √s =500GeV.We would first like to provide a feel for the sensitivity to the squark mass scale and tan βin the ideal case where we ignore the slepton and gaugino mass uncertainties.In Fig.4(left)we show the statistical significance of the loop correction by plotting contours of constant cross-section.Here we fix the sneutrino mass and determine µ,M 1and M 2by fixing the one-loop corrected masses m ˜χ01,m ˜χ03,and m ˜χ+1.We plot the contours corresponding to the number of standard deviations of the fluctuation of the accepted number of events.The 1-σfluctuation corresponds to N input ,where N input is ournominal value of the number of events at M ˜Q =1000GeV and tan β(M Z )=4.The accepted number of events N is given byN =A ·σ(e −Le +→˜νe ˜νe )× BR(˜νe →e ˜χ+1) 2×100fb −1.(5)Here we took BR(˜νe →e ˜χ+1)=0.6and overall acceptance A =0.28.The number of accepted eventsat our nominal point N input is about 12800for µ<0.Figure 4.(left):The constraint on M ˜Q and tan βcoming from σ(e −e +→˜νe ˜ν∗e →e −e +˜χ+1˜χ−1),withdtL =100fb −1.The central value is taken as M ˜Q =1000GeV and tan β(M Z )=4.m ˜χ03=270GeV,µ<0(right):∆χ2min vs.M ˜Q with µ<0and fixed tan β,m ˜χ01and m ˜χ03,but allowing m ˜χ+1and m ˜νe to vary freely.We show the contours for µ<0in Fig.4(left).If tan βis well measured,M ˜Q is constrained toM ˜Q =1000+370−280GeV at 1-σsignificance.If instead we assume the constraint 2<tan β<8,the mildtan βdependence yields 700<M ˜Q <1900GeV.In the case µ>0,the mixing of chargino gives rise to significant tan βdependence.Increasing the squark mass can be compensated for by decreasing tan β,and measuring sneutrino production then determines a region of the (M ˜Q ,tan β)plane.We now turn to the effect of the mass uncertainties.The sneutrino production cross-section depends on the masses m ˜νe ,m ˜χ01,m ˜χ03and m ˜χ+1.Of these masses the cross-section is most sensitive to the sneutrino mass.All of the same chirality scalar production cross-sections suffer from the strong β3˜ kinematic dependence.Near threshold this results in an especially large sensitivity to the final-state mass.Although a simple statistical scale-up of the results of Ref.[4]implies a sneutrino mass uncertainty of only 0.3%,this nevertheless leads to a significant degradation in our ability to constrain the squark mass scale.(Systematic errors might be the limiting factor here.)Note,however,that the measurement of the sneutrino mass in Ref.[4]was obtained by studying a small fraction of the total sneutrino decay modes.The mode they studied amounts to only about 4%of the total sneutrino ing other modes,such as e −e +4j (2˜χ01),might reduce the mass error even further.Because the ˜νe production cross-section is significantly larger than the other slepton cross-sections,isolating the various sneutrino signatures is less affected by SUSY backgrounds such as e −e +→˜e −L ˜e +L →e −e +4j (2˜χ01).Now we show the constraint on the squark mass M ˜Q after taking into account the uncertainty of the masses δm ˜νe and δm ˜χ+1for µ<0case.The effect of δm ˜χ03turns out to be negligible for the case,and we assume it is possible to distinguishsign of µby measuring heavier ino mass differences at √s >2m ˜χ03.[10].In Fig.4(right)we plot ∆χ2min against M ˜Q ,where ∆χ2min is a minimum of ∆χ2with respect to variations in m ˜χ+1and m ˜νe .The region of M ˜Q where 2min <1,2,...corresponds to 1,2,...-σerror of the squark mass when the chargino and sneutrino mass uncertainties are taken intoaccount.The sneutrino mass uncertainty reduces the sensitivity of the production cross-section to M ˜Q considerably,because the effect of increasing M ˜Q can be compensated for by a small increase in m ˜νe .On the other hand,we do not find any significant effect due to non-zero δm ˜χ+1.From Fig.4(right)we see that in this case,even with the sneutrino mass uncertainty,we canreasonably constrain the squark mass scale.For example,at the 1-σlevel with M ˜Q =1TeV,weconstrain M˜Q to1+1.2−0.5TeV,using the naive scale up(from20fb−1to100fb−1)of the statisticalerrors of Ref.[4].This corresponds to the difference between the gauge and gaugino effective couplings,δg2/g2=0.011±0.006.This can be compared to the estimate of the constraintδg2/g2=±0.02from the chargino production measurement[7].Such comparisons are sensitive to different choices of parameter space and other assumptions.If we reduce the mass uncertainties by a factor of2,wefind the interesting constraint600<M˜Q<1500GeV.4.conclusionsSupersymmetry is a beautiful symmetry which relates bosons and fermions.If we wish to determine whether this symmetry is realized in nature,the relations imposed between particles and their super-partners must be confirmed by experiment.Of course,discovering a particle with the quantum numbers of a superpartner is thefirst very important step in this procedure.An equally important test,though, is the confirmation of the hard relations imposed by supersymmetry,for example,the equivalence of the gauge and gaugino couplings.It has been argued that a next generation linear collider would be an excellent tool to verify supersymmetry in this respect.Production cross-sections such asσ(e−e+→˜ ˜ ∗)andσ(e−e+→˜χ−i˜χ+i) involve the t-channel exchange of gauginos or sleptons,so they depend on gaugino couplings.[5,3] In this paper,we approached this problem from a somewhat different direction.Because super-symmetry must be badly broken by soft breaking terms,the tree-level relations of the couplings are also broken,by radiative corrections.The corrections are logarithmically sensitive to the splitting of the supersymmetry multiplets.To quantify this,we have calculated the full one-loop correction due to(s)quark loops of the slepton production cross-sections.The difference between the effective lepton-slepton-gaugino couplings g eff˜G i and the effective gauge couplings g effi is given by a coupling factor timeslog M˜Q /m˜.We gave an explicit example which illustrates that the statistics at the future linear collider may be enough to constrain the squark mass scale through the measurement of the slepton production cross-section.We found,with1-σsignificance,M˜Q could be constrained to1+1.2−0.5TeV by the measurement ofthe sneutrino production cross-section.We found this constraint in theµ<0case where we took into account the errors(based on existing MC simulation)of the sneutrino and light chargino masses,but assumed tanβwas well constrained by other measurements.The mass of the sleptons and gauginos must be measured very precisely in order to successfully constrain the squark mass scale via production cross-section measurements.In order to determine the ultimate sensitivity of this procedure,a thorough study of the systematic uncertainties in the slepton mass measurements is necessary.It is important to note that the constraint on the squark mass scale can be stronger than the one presented in this paper.Here,we estimated the sensitively to squark mass scale by utilizing sneutrino production followed by its decay into a chargino and an electron.Depending on the spectrum and center-of-mass energy,there will typically be many other production processes which involve t-channel exchange of gauginos or sleptons,and all those amplitudes have log M˜Qcorrections.The constraint on the squark mass we have realized here could be unique in the sense that this information may not be available at the LHC.Even if the LHC squark production rate is large,the gluino could be produced in even larger numbers,creating a large irreducible background to the squark signal.A large gluino background could make the extraction of the squark mass from kinematical variables difficult.On the other hand,if information on the squark masses is obtained at the LHC,we would have rather accurate predictions for the gaugino couplings.In this case,the measurement of the production cross-sections we considered here would constrain new supersymmetry-breaking physics with standard model gauge quantum numbers.In a sense,the study proposed here is similar in nature to studies performed at LEP and SLC.The physics of gauge boson two-point functions has been studied extensively at LEP and SLC,and it has provided strong constraints on new physics.Similarly,a future LC and the LHC might provide precision studies of the gaugino two-point functions,to realize a supersymmetric version of new precision tests.References[1]JLC Group,JLC-1,KEK Report No.92–16(1992).[2]T.Tsukamoto et al.,Phys.Rev.D51,3153(1995).[3]J.L.Feng,M.E.Peskin,H.Murayama,X.Tata,Phys.Rev.D52,1418(1995).[4]H.Baer,R.Munroe,X.Tata,Phys.Rev.D54,6735(1996).[5]M.M.Nojiri,K.Fujii,T.Tsukamoto,Phys.Rev.D54,6756(1996).[6]H.-C.Cheng,J.L.Feng,N.Polonsky,hep-ph/9706438.[7]H.-C.Cheng,J.L.Feng,N.Polonsky,hep-ph/9706476.[8]L.Randall,E.Katz,S.Su,hep-ph/9706478and MIT–CTP–2646,inpreparation.[9] D.M.Pierce,S.Thomas,SLAC–PUB–7474,in preparation.[10]M.M.Nojiri,Damien M.Pierce and Youichi Yamada,Slepton Production as a Probe of the Squark MassScale,KEK-TH520,hep-ph/9707244.[11]P.H.Chankowski,Phys.Rev.D41,2877(1990).。

a rXiv:h ep-ph/944224v16Apr1994TMU-NT940401,hep-ph/9404224April 1994Roles of Diquarksin the Nucleon for the Deep Inelastic Scattering and the Non-leptonic Weak Transitions ∗Katsuhiko Suzuki †Department of Physics,Tokyo Metropolitan University Hachiohji,Tokyo 192,Japan Abstract :We study roles of quark-quark correlations in the baryons for the deep inelastic structure function and the ∆I =1/2rule of the non-leptonic weak hyperon decay.The quark-quark correlation is incorporated phenomenologically as diquarks within the Nambu and Jona-Lasinio model.The strong diquark correlations in the spin-0channel enhance the ∆I =1/2weak matrix elements,and account for the ∆I =1/2rule.The ratio of the nucleon structure functions F n 2(x )/F p 2(x )also comes to agree with experiment due to the diquark correlations.1Introduction −quark-quark correlations inside the nucleon Recently models of the baryons have attracted considerable interest.These models,e.g.MIT bag model and Skyrmion,possess some essential aspects of the low energy QCD,and give successful descriptions for static baryon properties such as masses and magneticmoments.However,these models do not take into account quark-quark correlations inside the baryon.In the QCD sum rule calculation,asymmetric momentum distributions in the proton are found,where the most part of the proton momentum is carried by the u-quark with its spin directed along the proton spin and the remaining small part is carried by the u-d quarks with combined spin-0[1].Instanton liquid model of the QCD vacuum also shows that the quark correlations in the spin-0and spin-1channels are completely different,due to the large attractive correlation in the spin-0channel [2].These results indicate that the quark-quark correlation in the spin-0channel is quite strong,and is of great importance to discuss the baryon structure.This strong correlation in the spin-0channelmay be understood as a close connection between the qq pair in the spin-0channel (¯ψc A iγ5ψc )and the pion (¯ψiγ5ψ),through a particle-antiparticle symmetry,i.e.Pauli-G¨u rsey symmetry [3,4].(Here,c A are the SU (3)color antitriplet operators,and ψc the charge conjugation of the quark field.)Due to the spontaneous breakdown of chiralsymmetry,the Goldstone pion is a collective state of the QCD vacuum.Hence,we expect that the strong correlation exists in the corresponding spin-0qq channel.In this study,we introduce”Diqurks”,i.e.correlated two quark states inside the baryons,to incorporate the quark-quark correlation in the phenomenological way[5]. Assuming the SU(6)spin-flavor symmetry,the baryon wave functions are written as products of diquarks and quarks.For example,the proton wave function is given by |p↑>=118[3S(ud)u↑+2A(uu)+d↓−√2A(ud)+u↓+A(ud)0u↑],(1) where S(ud)denotes the scalar(spin-0;0+),isospin-0diquark,and A(ij)κthe axial-vector (spin-1;1+)diquark with theflavor content i and j,and the helicityκ.These quantum numbers are determined by the antisymmetrization of the diquark wave function.In order to incorporate the non-perturbative quark-quark correlations,namely,structures of diquarks,we use the Nambu and Jona-Lasinio(NJL)model[6].This model demonstrates the spontaneous chiral symmetry breaking,and reproduces the SU(3)f meson properties very well with the parametersfixed by the pion and kaon properties[3].The constituent quark mass,the diquark mass,and the diquark-quark coupling constant are obtained by solving the Gap equation and the Bethe-Salpeter equation simultaneously.2∆I=1/2non-leptonic hyperon decay and diquark correlation The puzzle of the non-leptonic weak decay and the∆I=1/2rule has a long history.In the standard factorization approximation,theoretical calculations show serious disagreements with experiments(Table1).Although the renormalization group method for gluon exchange contributions indicates an enhancement of∆I=1/2amplitude and a suppression of∆I=3/2amplitude,this effect is too small.Recently,Stech and his collaborators pointed out that the scalar diquarks play a crucial role for the parity conserving part(P-wave)of∆I=1/2transitions[7].We consider a possible intermediate state contribution,which is the so called pole diagram as shown in Fig.1,where an initial hyperon B i changes to an intermediate state baryon B m by the weak interaction,and then B m emits a pion to produce afinal state baryon B f. The scalar diquark appears in the calculation of these weak transition matrix elements, since the effective weak Hamiltonian is rewritten by the diquark annihilation and creation operators by virtue of the Fierz transformation[7].H=G F sinθcosθ2{c1[¯uγµ(1−γ5)s][¯dγµ(1−γ5)u]+c2[¯uγµ(1−γ5)u][¯dγµ(1−γ5)s]+....=G F sinθcosθ2(c1−c2)2I=0,and(us)0+has I=1/2due to the Pauli principle.Therefore,the strong scalar diquark correlations enhance only the∆I=1/2weak matrix elements,and thus explain the∆I=1/ing the NJL model to calculate the diquark weak decay matrix elements,we obtain numerical results in Table1[8].The results of the factorization including the penguin contributions are listed in the second column,and the diquark contributions in the third column.In the forth column,the sum of the diquark and the factorization is listed,which is compared with experimental data indicated in thefifth column.The diquark process enhances largely the transition amplitudes,and the result is in a good agreement with experiment.Table1P-wave amplitude(×10−7)Σ++0.0037.037.041.8Σ+0 2.0524.526.526.7Σ−−−3.92 2.47−1.45−1.44Λ0−9.6012.021.622.4Ξ−−−2.4018.816.417.5ΩK0.00 6.59 6.59 5.37As a result,the proton and neutron structure functions are written asF p2(x)=29q V(x)+518Q V D(x)F n2(x)=16q V(x)+56Q V D(x),(3)where q S and q V are the quark distributions with the residual diquarks being the scalar and the axial-vector diquarks,respectively(Fig.2a).Q S D and Q V D are the quark distributions obtained by the scalar and the axial-vector diquark scattering processes,respectively (Fig.2b).Theflavor dependence of the structure functions arises from the difference of the distribution contents in this model.The correlations in the spin-0and spin-1diquarks affect the quark distributions,mainly through their masses.We note that this approach naturally reproduces the asymmetry of momentum distributions in the nucleon obtained by the QCD sum rule[1].To see this point,we calculate the momentum fraction carried by each quark.In the scalar channel,wefind<xq S>:<xQ S D>∼2:1,which is consistent with the result of ref.[1],while we get<xq V>:<xQ V D>∼1:1in the axial-vector channel.These results reflect the strength of the correlation in each channel. In the axial-vector channel,the quark correlation is so weak that the asymmetry of the momentum distribution is negligible.Our calculated quark distribution gives a boundary condition for the QCD pertur-bation at the low energy model scaleµ2∼1GeV2,at which the effective quark model is supposed to work[12].The distribution functions are evolved to the experimental high momentum scale with the help of the Altarelli-Parisi equation.The resulting ratio F n2(x)/F p2(x)is shown in Fig.2.The ratio F n2(x)/F p2(x)depends on the strength of the quark-quark correlation,and is the same value as the parton model prediction without the spin-0diquark correlations(dashed curve).If the correlation in the scalar channel is so strong as to reproduce the non-leptonic transitions,it is in a reasonable agreement with the data(solid curve),except for the small x region,where the sea quark effects dominate.4SummaryWe have studied the diquark correlation inside the baryon,and its contribution to the non-leptonic hyperon weak decay and the deep inelastic scattering.The diquark cor-relation,suggested by the QCD sum rule and the instanton liquid model,is the strongest in the spin-0and isospin-0channel.We comment on the result of the lattice QCD calcula-tion,in which the diquark-like clustering is not observed[13].At the present,such lattice simulations are performed within the quenched approximation.However,it is essential to include the light dynamical quark for the discussion of the hadron structure.Thus,the quenched approximation may be inadequate to study such diquark clusters.We have used the simple SU(6)diquark-quark model to incorporate the quark correlations within the NJL model.Such a diquark correlation enhances the∆I=1/2weak transition amplitudes,and reproduces the experimental data very well.The diquark correlations also produce the asymmetric momentum distribution inside the nucleon,as obtained in the QCD sum rule calculation.Due to this asymmetric distribution,the ratio of the nucleon structure functions becomes smaller than the naive parton model value at the large Bjorken x,and is consistent with experiment.Our results indicate the importance of the quark-quark correlation in the nucleon.The author wishes to thank Prof.H.Toki and Dr.T.Shigetani for their collabora-tions in this work.References[1]V.L.Chernyak and A.R.Zhitnitsky,Phys.Rep.112(1984)173[2]T.Schafer,E.V.Shuryak and J.J.M.Verbaarschot,Nucl.Phys.B412(1994)143[3]U.Vogl and W.Weise,Prog.Part.Nucl.Phys.27(1991)195,and references therein[4]K.Suzuki and H.Toki,Mod.Phys.Lett.A7(1992)2867[5]For a review,M.Anselmino et al.,Rev.Mod.Phys.65(1993)1199[6]Y.Nambu and G.Jona-Lasinio,Phys.Rev.122(1961)345[7]H.G.Dosch,M.Jamin and B.Stech,Z.Phys.C42(1989)167[8]K.Suzuki and H.Toki,Mod.Phys.Lett.A,in press[9]K.Suzuki,T.Shigetani,H.Toki,hep-ph/9310266,Nucl.Phys.A in press[10]H.Meyer and P.J.Mulders,Nucl.Phys.A528(1991)589[11]T.Shigetani,K.Suzuki,H.Toki,Phys.Lett.B308(1993)383;TMU preprint(1994),hep-ph/9402277[12]R.L.Jaffe and G.G.Ross,Phys.Lett.B93(1980)313[13]D.B.Leinweber,Phys.Rev.D47(1993)5090Figure CaptionsFig.1:Pole diagram for the non-leptonic hyperon decayFig.2:The forward scattering amplitude of the nucleon.The thin solid line represents the quark,and the shaded line the diquark.The nucleon and the virtual photon are depicted by the solid and the wavy lines.Fig.3:The ratio of the neutron-proton structure functions at Q2=15GeV2.The experi-mental data are taken from the EMC,BCDMS,and NMC experiments.The solid curve is obtained by taking into account the strong scalar diquark correlation.The dashed curve is the result where the channel difference of the diquark mass is neglected[9].Fig. 2a Fig.2bFig. 2B fFig. 1Fig. 3x。

a rXiv:h ep-ph/945231v15May1994Institute of Physics,Acad.of Sci.of the Czech Rep.PRA–HEP–94/3and hep-ph/9405231Nuclear Centre,Charles University May 5,1994Prague Feasibility of Beauty Baryon Polarization Measurement in Λ0J/ψdecay channel by ATLAS-LHC Julius Hˇr ivn´a ˇc ,Richard Lednick´y and M´a ria Smiˇz ansk´a Institute of Physics AS CR Prague,Czech Republic submitted to Zeitschrift f¨u r Physik CAbstractThe possibility of beauty baryon polarization measurement by cascade decay angu-lar distribution analysis in the channel Λ0J/ψ→pπ−l +l −is demonstrated.The error analysis shows that in the proposed LHC experiment ATLAS at the luminosity 104pb −1the polarization can be measured with the statistical precision better than δ=0.010for Λ0b and δ=0.17for Ξ0b .IntroductionThe study of polarization effects in multiparticle production provides an important infor-mation on spin-dependence of the quark confinement.Thus substantial polarization of the hyperons produced in nucleon fragmentation processes[1,2]as well as the data onthe hadron polarization asymmetry were qualitatively described by recombination quark models taking into account the leading effect due to the valence hadron constituents[3−6].Although these models correctly predict practically zero polarization ofΛandΩ−,they fail to explain the large polarization of antihyperonsΣ−recently discovered in Fermilab[7,8].The problem of quark polarization effects could be clarified in polarization measure-ments involving heavy quarks.In particular,an information about the quark mass de-pendence of these effects could be obtained[4,9].The polarization is expected to be proportional to the quark mass if it arises due to scattering on a colour charge[10−12]. The opposite dependence takes place if the quark becomes polarized due to the interac-tion with an”external”confiningfield,e.g.,due to the effect of spontaneous radiation polarization[13].The decrease of the polarization with increasing quark mass is expected also in the model of ref.[14].In QCD the polarization might be expected to vanish with the quark mass due tovector character of the quark-gluon coupling[10].It was shown however in Ref.[15] that the quark mass should be effectively replaced by the hadron mass M so that even the polarization of ordinary hadrons can be large.The polarization is predicted to be independent of energy and to vanish in the limit of both low and high hadron transverse momentum p t.The maximal polarization P max(x F)is reached at p t≈M and depends on the Feynman variable x F.Its magnitude(and in particular its mass dependence)is determined by two quark-gluon correlators which are not predicted by perturbative QCD.The polarization of charm baryons in hadronic reactions is still unmeasured due to the lack of sufficient statistics.Only some indications on a nonzero polarization were reported[16,17].For beauty physics the future experiments on LHC or HERA give an opportunity to obtain large statistical samples of beauty baryon(Λ0b,Ξ0b)decays intoΛ0J/ψ→pπ−l+l−,which is favorable mode to detect experimentally.Dedicated triggers for CP-violation effects in b-decays,like the high-p t one-muon trigger(LHC)[18] or the J/ψtrigger(HERA)[19]are selective also for this channel.Below we consider the possibility of polarization measurement of beauty baryonsΛ0b andΞ0b with the help of cascade decay angular distributions in the channelΛ0b(Ξ0b)→Λ0J/ψ→pπ−l+l−.1Polarization measurement method and an estimation of the statistical error.In the case of parity nonconserving beauty baryon(B b)decay the polarization causes the asymmetry of the distribution of the cosine of the angelθbetween the beauty baryon decay and production analyzers:w(cosθ)=1| p inc× p B b|,where p inc and p Bbare momenta of incident particle and B b in c.m.system.The asymmetry parameterαb characterizes parity nonconservation in a weak de-cay of B b and depends on the choice of the decay analyzer.In the two-body decay B b→Λ0J/ψit is natural to choose this analyzer oriented in the direction ofΛ0momentum pΛ0in the B b rest system.The considered decay can be described by4helicity ampli-tudes A(λ1,λ2)normalized to unity:a+=A(1/2,0),a−=A(−1/2,0),b+=A(−1/2,1) and b−=A(1/2,−1),|a+|2+|a−|2+|b+|2+|b−|2=1.(2) The difference ofΛ0and J/ψhelicitiesλ1-λ2is just a projection of B b spin onto the decay analyzer.The decay asymmetry parameterαb is expressed through these amplitudes in the formαb=|a+|2−|a−|2+|b+|2−|b−|2.(3) If P-parity in B b decay were conserved,then|a+|2=|a−|2,|b+|2=|b−|2so thatαb would be0.In the case of known and sufficiently nonzero value ofαb the beauty baryon polarization could be simply measured with the help of angular distribution(1)(see, e.g.,[20]).Due to lack of experimental information and rather uncertain theoretical estimates ofαb for the decayΛ0b→Λ0J/ψ[21]both the polarization andαb(or the decay amplitudes)should be determined simultaneously.This can be achieved with the2help of information onΛ0and J/ψdecays.Though it complicates the analysis,it shouldbe stressed that the measurement of the beauty baryon decay amplitudes could give valuable constrains on various theoretical models.Generally,such a measurement canbe done provided that at least one of the secondary decays is asymmetric and its decayasymmetry parameter is known[9].In our case it is the decayΛ0→pπ−with the asymmetry parameterαΛ=0.642.The angular distribution in the cascade decay B b→Λ0J/ψ→pπ−l+l−follows di-rectly from Eq.(6)of[9],taking into account that the only nonzero multipole parameters.It can be written in the formin the decay J/ψ→l+l−are T00=1and T20=110w(Ω,Ω1,Ω2)=1formula(4)integrated over the azimuthal anglesφ1,φ2would be in principle sufficient [9].In this case the number of free parameters is reduced to4(the phases don’t enter) and only a3-dimensionalfit is required.We will see,however,that the information on these angles may substantially increase the precision of the P b determination.To simplify the error analysis,we follow ref.[9]and consider here only the most unfavourable situation,when the parameters P2b,|a+|2−|a−|2and|b+|2−|b−|2are much smaller thanα2Λ.In this case the moments<F i>can be considered to be independent, having the diagonal error matrixW=13,19,115,145,16135,16135,2135,2135,245,245).(7)Here N is a number of B b events(assuming that the background can be neglected,see next section).The error matrix V of the vector a of the parameters a j,j=1,..7defined in (6)isV( a)=(A T W−1A)−1,(8) where the elements of the matrix A are A ij=d(f1i.f2i)V11=δ0N,(9)δ0=1α2Λ.[(2r0−1)2180+4r2015+(1−r0)(1+coshχ)10.(10)Hereδ0depends only on the relative contribution r0of the decay amplitudes with helicityλ2=0and on the relative phaseχ(Figs.1a,b).The maximal error on P b is δmax=4.7Nand it corresponds to the case when r0=1√√√,Σ∗b →Λ0b πand the electromagnetic decays Ξ0′b →Ξ0b γor Ξ0∗b →Ξ0b γ.The observable polarization P obs depends on the polarizations P B b of direct beauty baryons and their production fractions b B b (i.e.probabilities of the b-quark to hadronize to certain baryons B b ).In considered decays the beauty baryon Λ0b or Ξ0b retains −13)of the polarizationof a parent with spin 12+)(see Appendix).For P obs we get:P obs =b Λ0b P Λ0b + i (−13b Σ∗bi P Σ∗bi )3b Ξ0′b P Ξ0′b+1b Ξ0b +b Ξ0′b +b Ξ0∗b.(12)The summation goes over positive,negative and neutral Σb and Σ∗b .Assuming the polar-ization of the heavier states to be similar in magnitude to that of directly produced Λ0b or Ξ0b (P Λ0b or P Ξ0b )we may expect the observed polarization in an interval of (0.34−0.67)P Λ0bfor Λ0b and (0.69−0.84)P Ξ0b for Ξ0b.The polarization can be measured for Λ0b and Ξ0b baryons and for their antiparticles.Λ0b (Ξ0b )are unambigously distinquishable from their antiparticles by effective mass of pπ−system from Λ0→pπ−decay.The wrong assignment of antiproton and pion masses gives the kinematical reflection ofΞ0b is governed by b→dcc.HoweverΛ0fromΞ0b→Ξ0J/ψorΞ−b→Ξ−J/ψis produced in a weak hyperon decay,so this background can be efficiently reduced by the cut on the minimal distance d between J/ψandΛ0.A conservative cut d<1.5mm reduces this background by a factor≈0.05(Fig.3b).The background from B0d→J/ψK0when one ofπmesons is considered as a proton is negligible after the effective mass cuts on(pπ)and(pπJ/ψ)systems.Background from fake J/ψ′s,as it has been shown in[18],can be reduced to a low level by cuts on the distance between the primary vertex and the production point of the J/ψcandidate and the distance of closest approach between the two particles from the decay.These cuts also suppress the background from real J/ψ′s comming directly from hadronization.The number of producedΛ0b andΞ0b is calculated for the cross section of pp→busing the last segment of the hadron calorimeter by its minimum ionizing signature.-ForΛ0J/ψ→pπ−e+e−decay both electrons are required to have p e⊥>1GeV.The low threshold for electrons is possible,because of electron identification in the transition radiation tracker(TRT)[24].The events are required to contain one muon with a pµ⊥> 6GeV and|η|<1.6The second set of cuts corresponds to’offline’analysis cuts.The same cuts as for B0d→J/ψK0reconstruction[18]can be used(the only exception is the mass requirement forΛ0candidate,see the last of the next cuts):-The two charged hadrons fromΛ0decay are required to be within the tracking volume |η|<2.5,and transverse momenta of both to be greater than0.5GeV.-Λ0decay length in the transverse plane with respect to the beam axis was required to be greater than1cm and less than50cm.The upper limit ensures that the charged tracks fromΛ0decay start before the inner radius of TRT,and that there is a space point from the innermost layer of the outer silicon tracker.The lower limit reduces the combinatorial background from particles originating from the primary vertex.-The distance of closest approach between the two muon(electron)candidates forming the J/ψwas required to be less than320µm(450µm),giving an acceptance for signal of 0.94.-The proper time of theΛ0b decay,measured from the distance between the primary vertex and the production point of the J/ψin the transverse plane and the reconstructed p⊥ofΛ0b,was required to be greater than0.5ps.This cut is used to reduce the combina-torial background,giving the acceptance for signal events0.68.-The reconstructedΛ0and J/ψmasses were required to be within two standart de-viations of nominal values.The results on expectedΛ0b andΞ0b statistics and the errors of their polarization mea-surement are summarized in Table2.For both channels the statistics of reconstructed events at the luminosity104pb−1will be790000(220000)Λ0b and2600(720)Ξ0b,where the values are derived using UA1(CDF)results.For this statistics the maximal value of the statistical error on the polarization mea-surement,calculated from formulae(9)and(10),will be0.005(0.01)forΛ0b and0.09(0.17) forΞ0b.7ConclusionAt LHC luminosity104pb−1the beauty baryonsΛ0b andΞ0b polarizations can be measured with the help of angular distributions in the cascade decaysΛ0J/ψ→pπ−µ+µ−and Λ0J/ψ→pπ−e+e−with the statistical precision better than0.010forΛ0b and0.17for Ξ0b.AppendixThe polarization transfered toΛ0b,which was produced indirectly in strongΣb andΣ∗b decays,depends on the ratio∆| p inc× pΣb|,where p inc and pΣb are momenta of incident particle andΣb in c.m.system.Ω1=(θ1,φ1)are the polar and the azimuthal angles ofΛ0inΛ0b rest frame with the axes defined as z1↑↑ pΛ0b,y1↑↑ n× pΛ0b.After the transformation ofΩ1→Ω′1ofΛ0angles from the helicity frame x1,y1,z1to the canonical frame x,y,z with z↑↑ n and the integration over cosθandφ′1we get the distribution of the cosine of the angle between theΛ0momentum vector(Λ0b decay analyzer)and theΣb orΣ∗b production normal(which can be considered coinciding with theΛ0b production normal due to a small energy release in theΣb orΣ∗b decays):w(cosθ′1)∼1∓13(13(1References[1]K.Heller,Proceedings of the VII-th Int.Symp.on High Energy SpinPhysics,Protvino,1986vol.I,p.81.[2]L.Pondrom,Phys.Rep.122(19985)57.[3]B.Andersson et al.,Phys.Lett.85B(1979)417.[4]T.A.De Grand,H.I.Miettinen,Phys.Rev.D24(1981)2419.[5]B.V.Struminsky,Yad.Fiz.34(1981)1954.[6]R.Lednicky,Czech.J.Phys.B33(1983)1177;Z.Phys.C26(1985)531.[7]P.M.Ho et al.,Phys.Rev.Lett.65(1990)1713.[8]A.Morelos et al.,FERMILAB-Pub-93/167-E.[9]R.Lednicky,Yad.Fiz.43(1986)1275(Sov.J.Nucl.Phys.43(1986),817).[10]G.Kane,Y.P.Yao,Nucl.Phys.B137(1978)313.[11]J.Szwed,Phys.Lett.105B(1981)403.[12]W.G.D.Dharmaratna,Gary R.Goldstein,Phys.Rev.D41(1990)1731.[13]B.V.Batyunya et al.,Czech.J.Phys.B31(1981)11.[14]C.M.Troshin,H.E.Tyurin,Yad.Fiz.38(1983)1065.[15]A.V.Efremov,O.V.Teryaev,Phys.Lett.B150(1985)383.[16]A.N.Aleev et al.,Yad.Fiz.43(1986)619.[17]P.Chauvatet et al.,Phys.Lett.199B(1987)304.[18]The ATLAS Collaboration,CERN/LHCC/93-53,Oct.1993.[19]W.Hoffmann,DESY93-026(1993).[20]H.Albrecht et al.,DESY93-156(1993).9[21]A.H.Ball et al.,J.Phys.G:Nucl.Part.Phys.18(1992)1703.[22]UA1Collaboration,Phys.Lett.273B(1991)544.[23]CDF Collaboration,Phys.Rev.D47(1993)R2639.[24]I.Gavrilenko,ATLAS Internal Note INDET-NO-016,1992.[25]A.F.Falk and M.E.Peskin,SLAC-PUB-6311,1993.[26]R.Lednicky,DrSc Thesis,JINR-Dubna1990,p.174(in russian).10i f 2i011P ba +a ∗+−a −a ∗−−b +b ∗++b −b ∗−cos θ13P b αΛ−a +a ∗+−a −a ∗−+12b −b ∗−d 200(θ2)52b +b ∗+−1P b −a +a ∗++a −a ∗−−12b −b ∗−d 200(θ2)cos θ172b +b ∗+−1P b αΛ8P b αΛ3Im (a +a ∗−)sin θsin θ1sin 2θ2sin φ1102Re (b −b ∗+)sin θsin θ1sin 2θ2cos (φ1+2φ2)112Im (b −b ∗+)sin θsin θ1sin 2θ2sin (φ1+2φ2)−32Re (b −a ∗++a −b ∗+)sin θcos θ1sin θ2cos θ2cos φ213√P b αΛ−32Re (b −a ∗−+a +b ∗+)cos θsin θ1sin θ2cos θ2cos(φ1+φ2)15√P b αΛ16√P b−32Im (a −b ∗+−b −a ∗+)sin θsin θ2cos θ2sin φ218√αΛ−32Im (b −a ∗−−a +b ∗+)sin θ1sin θ2cos θ2sin(φ1+φ2)Table 1:The coefficients f 1i ,f 2i and angular functions F i in distribution (4).11Parameter Value forΛ0b CommentL[cm−2s−1]1033b(b→B b)0.08br(B b→Λ0J/ψ)2.210−2(0.610−2)J/ψ→µ+µ−0.06Λ0→pπ−0.641.110−4(0.310−3)0.060.64b)500µbN(µ+µ−pπ−)accepted1535000pµ⊥>6GeV,|η|<1.6(426000)pµ⊥>3GeV,|η|<2.5pπ,p⊥>0.5GeV,|η|<2.5740(210)2400(670)N(µeepπ−)reconstructed65000(18000)the maximum statistical error0.005on the polarization measurement(0.010)δ(P b)Table2:Summary on beauty baryon measurement possibilities for LHC experiment AT-LAS.The values in brackets correspond to the CDF result,while the analogical values without brackets to the UA1result.12Figure1:The maximal statistical error on the polarization measurementδ(P b)andδ0=N+1Figure 2:The Λ0J/ψeffective mass distribution:The peak at 5.62GeV is from Λ0b and background comes from J/ψfrom a b-hadron decay and Λ0either from the multiparticle production or from a b-hadron decay (a).The events that passed the cut on the transverse momenta (p T >0.5GeV )for p and π−from Λ0decay (b).14Figure 3:The Λ0J/ψeffective mass distribution:The peak at 5.84GeV is from Ξ0b →Λ0J/ψdecay.The background with the centre at ≈5.5GeV comes from Ξ0b →Ξ0J/ψ,Ξ0→Λ0π0and Ξ−b →Ξ−J/ψ,Ξ−→Λ0π−decays (a).The events that passed the cut on the minimal distance of J/ψand Λ0(d <1.5mm )(b).15。

a r X i v :h e p -l a t /0110033v 1 10 O c t 20011The Quest for Light Sea Quarks:Algorithms for the FutureW.Schroers a ∗,N.Eicker a ,M.D’Elia b ,Ph.de Forcrand c ,C.Gebert d ,Th.Lippert a ,I.Montvay d ,B.Orth a ,M.Pepe e ,K.Schilling aaDepartment of Physics,University of Wuppertal,D-42097Wuppertal,Germany b Dipartimento di Fisica dell’Universit`a di Genova and INFN,I-16146,Genova,ItalycInst.f¨u r Theoretische Physik,ETH H¨o nggerberg,CH-8093Z¨u rich,Switzerland d Theory Division,DESY,Notkestr.85,D-22603Hamburg,GermanyeLaboratoire de Physique Th´e orique Universit´e de Paris-Sud,Bˆa timent 210F-91405Orsay-CedexAs part of a systematic algorithm study,we present first results on a performance comparison between a multibosonic algorithm and the hybrid Monte Carlo algorithm as employed by the SESAM collaboration.The standard Wilson fermion action is used on 32×163lattices at β=5.5.1.IntroductionThe past six years have witnessed a number of large simulations of full QCD with two degen-erate sea quarks and Wilson like actions.All of them were based on the hybrid Monte Carlo algo-rithm (HMC)which has been systematically im-proved over the years.These simulations,how-ever,albeit being milestones for lattice QCD in the pre-Teracomputing age [1],suffer from severe restrictions that prevent them to be truly realis-tic:we need to go to lighter quark masses and operate with three flavors with masses eventually approaching the physical mass.This situation has been motivating research and development of alternative algorithms of the multibosonic variety (MBA)that promise in prin-ciple to overcome some of the restrictions of HMC mentioned.It has been shown that MBA can in-deed be geared to reach the efficiency of HMC [2]and encouraging results have been achieved with MBA for the treatment of finite density QCD [3],supersymmetric field theories [4]as well as the case of three dynamical fermion flavors [5].In this contribution we wish to describe our benchmarking of MBA,performed in the quest to achieve lighter quark masses than previouslyVolume:Ω=32×163,β=5.50.1590.1414.39(3)0.800(10)0.1600.1174.89(3)0.670(14)2two different quark mass settings,as given in ta-ble1.Note that both quark masses are from the regime of current full QCD simulations.3.Defining the MBA algorithmThe parameter space of MBA algorithms is large w.r.t.the HMC situation:MBA optimiza-tion proceeds(a)byfinding a not too high or-der polynomial approximating the inverse of the fermion matrix at the given working point,(b) by devising an efficient“trajectory”in form of an updating sequence for the degrees of freedom and (c)by exploiting a method to correct for the re-maining systematic error.Today,all MBAs use a noisy correction step for(c).For a detailed dis-cussion see e.g.ref.[7,8].For the construction of appropriate polyno-mials we followed the prescription proposed in ref.[9,10]which employs the GMRES algorithm tofind a non-hermitian approximation of the in-verse Wilson matrix with ultraviolet-filtering on a small sample of thermalized gaugefield config-urations.This was done to minimize the polyno-mial order and hence the number of bosonfields. Quadratically optimized polynomials[11]need about2−3times more bosonfields for similar acceptance rates.The other key element for the optimization of an MBA is the choice of“trajectory”,T,i.e.,the basic updating pattern.For that matter,one has to devise an appropriate blend of gauge and boson field updates.We have chosen the“trajectory”to beT=CO g(O b O g)5H b(O g O b)5O g,(2) with C being thefinal accept/reject correction step,O g(O b)a gauge(boson)field overrelax-ation sweep and H b a bosonfield global quasi-heat bath[12].The number of bosonfields is tuned such as to ensure a good acceptance rate in the ball-park of60−70%.As a result we obtained the values quoted in table2.4.ResultsThe determination of accurate autocorrelation times,τint,needs very long Monte Carlo time 0.1592460.3%0.8760.1604265.9%1.763κObserv.HMC MBA 0.160Plaq.0.56077(6)0.56067(5)(amπ)0.3041(36)0.3184(68)(amρ)0.4542(77)0.4674(81)3 0.159HMC352111.0(0.4)712(26)103<1620103<1620103MBA621744.7(3.4)786(60)103528103704103Table4Lengths of MC runs,estimated plaquette autocorrelation times and total cost,E ind,for producing one configuration decorrelated w.r.t.various observables,from HMC and MBA.From table4onefinds that E ind(plaq)is about equal for MBA and HMC at the larger quark mass.The total effort in the case of the HMC increases by a factor of8when stepping down in quark mass,while at the same time the cost for MBA‘only’rises by a factor of2.7.Conse-quently,the MBA has become almost a factor of three more efficient than HMC.5.ConclusionsWe have demonstrated in a realistic setting that MBA-type sampling techniques are not at all inferior to the state-of-the-art HMC techniques and appear to show superior scaling behavior in quark masses.We have established here a better scaling behavior of MBA,leading to a gain factor of almost three in favor of the particular MBA variant at currently reachable quark masses.It remains to be seen to what extent this encouraging result will pertain in the regime of smaller quark masses.The ultimate aim is to push full QCD simulation with Wilson like fermions below the point mπ/mρ≤0.5. Another point to check is whether the MBA variant considered in this paper with its non-hermitian approximation will remain operational for practical simulations in the deeper chiral regime.Because the GMRES method suffers from numerical instabilities for increasing orders n,one might have to take recourse—even on 32×163lattices—to128-bit precision.A more extended MBA study in this direction is in prepa-ration[13].AcknowledgmentsN.E.is supported under DFG grant Li701/3-1,M.P.by the European Community’s Human potential program under HPRN-CT-2000-00145 Hadrons/Lattice QCD,and W.S.by the DFG Graduiertenkolleg“Feldtheoretische Methoden in der Elementarteilchentheorie und Statistischen Physik”.The numerical productions were run on the APE-100systems installed at NIC Zeuthen. REFERENCES1.Th.Lippert,these proceedings; awa,ibid;H.Wittig,ibid.2. C.Alexandrou et al.,Phys.Rev.D61(2000)074503.3.S.Hands et al.,Eur.Phys.J.C17(2000)285.4.I.Campos et al.[DESY-M¨u nster Coll.],Eur.Phys.J.C11(1999)507.5. C.Gebert, F.Farchioni,I.Montvay,andW.Schroers,these proceedings.6.Th.Lippert,Habilitationsschrift,Univ.ofWuppertal,2001.7.P.de Forcrand,Parallel Computing25(1999)1341.8.W.Schroers,PhD-Thesis,Univ.of Wupper-tal,2001.9. A.Borrelli et al.,Nucl.Phys.B477(1996)809.10.P.de Forcrand,Nucl.Phys.Proc.Suppl.73(1999)822.11.I.Montvay,mun.109(1998)144.12.P.de Forcrand,Phys.Rev.E59(1999)3698.13.W.Schroers,N.Eicker,M.D’Elia,Ph.deForcrand,C.Gebert,Th.Lippert,I.Mont-vay,B.Orth,M.Pepe,and K.Schilling,in preparation.。

a r X i v :h e p -p h /9812285v 1 8 D e c 1998The Standard Model of Particle PhysicsMary K.Gaillard 1,Paul D.Grannis 2,and Frank J.Sciulli 31University of California,Berkeley,2State University of New York,Stony Brook,3Columbia UniversityParticle physics has evolved a coherent model that characterizes forces and particles at the mostelementary level.This Standard Model,built from many theoretical and experimental studies,isin excellent accord with almost all current data.However,there are many hints that it is but anapproximation to a yet more fundamental theory.We trace the development of the Standard Modeland indicate the reasons for believing that it is incomplete.Nov.20,1998(To be published in Reviews of Modern Physics)I.INTRODUCTION:A BIRD’S EYE VIEW OF THE STANDARD MODEL Over the past three decades a compelling case has emerged for the now widely accepted Standard Model of elementary particles and forces.A ‘Standard Model’is a theoretical framework built from observation that predicts and correlates new data.The Mendeleev table of elements was an early example in chemistry;from the periodic table one could predict the properties of many hitherto unstudied elements and compounds.Nonrelativistic quantum theory is another Standard Model that has correlated the results of countless experiments.Like its precursors in other fields,the Standard Model (SM)of particle physics has been enormously successful in predicting a wide range of phenomena.And,just as ordinary quantum mechanics fails in the relativistic limit,we do not expect the SM to be valid at arbitrarily short distances.However its remarkable success strongly suggests that the SM will remain an excellent approximation to nature at distance scales as small as 10−18m.In the early 1960’s particle physicists described nature in terms of four distinct forces,characterized by widely different ranges and strengths as measured at a typical energy scale of 1GeV.The strong nuclear force has a range of about a fermi or 10−15m.The weak force responsible for radioactive decay,with a range of 10−17m,is about 10−5times weaker at low energy.The electromagnetic force that governs much of macroscopic physics has infinite range and strength determined by the finestructure constant,α≈10−2.The fourth force,gravity,also has infinite range and a low energy coupling (about 10−38)too weak to be observable in laboratory experiments.The achievement of the SM was the elaboration of a unified description of the strong,weak and electromagnetic forces in the language of quantum gauge field theories.Moreover,the SM combines the weak and electromagnetic forces in a single electroweak gauge theory,reminiscent of Maxwell’s unification of the seemingly distinct forces of electricity and magnetism.By mid-century,the electromagnetic force was well understood as a renormalizable quantum field theory (QFT)known as quantum electrodynamics or QED,described in the preceeding article.‘Renormalizable’means that once a few parameters are determined by a limited set of measurements,the quantitative features of interactions among charged particles and photons can be calculated to arbitrary accuracy as a perturbative expansion in the fine structure constant.QED has been tested over an energy range from 10−16eV to tens of GeV,i.e.distances ranging from 108km to 10−2fm.In contrast,the nuclear force was characterized by a coupling strength that precluded a perturbativeexpansion.Moreover,couplings involving higher spin states(resonances),that appeared to be onthe same footing as nucleons and pions,could not be described by a renormalizable theory,nor couldthe weak interactions that were attributed to the direct coupling of four fermions to one another.In the ensuing years the search for renormalizable theories of strong and weak interactions,coupledwith experimental discoveries and attempts to interpret available data,led to the formulation ofthe SM,which has been experimentally verified to a high degree of accuracy over a broad range ofenergy and processes.The SM is characterized in part by the spectrum of elementaryfields shown in Table I.The matterfields are fermions and their anti-particles,with half a unit of intrinsic angular momentum,or spin.There are three families of fermionfields that are identical in every attribute except their masses.Thefirst family includes the up(u)and down(d)quarks that are the constituents of nucleons aswell as pions and other mesons responsible for nuclear binding.It also contains the electron and theneutrino emitted with a positron in nuclearβ-decay.The quarks of the other families are constituentsof heavier short-lived particles;they and their companion charged leptons rapidly decay via the weakforce to the quarks and leptons of thefirst family.The spin-1gauge bosons mediate interactions among fermions.In QED,interactions among elec-trically charged particles are due to the exchange of quanta of the electromagneticfield called photons(γ).The fact that theγis massless accounts for the long range of the electromagnetic force.Thestrong force,quantum chromodynamics or QCD,is mediated by the exchange of massless gluons(g)between quarks that carry a quantum number called color.In contrast to the electrically neutralphoton,gluons(the quanta of the‘chromo-magnetic’field)possess color charge and hence couple toone another.As a consequence,the color force between two colored particles increases in strengthwith increasing distance.Thus quarks and gluons cannot appear as free particles,but exist onlyinside composite particles,called hadrons,with no net color charge.Nucleons are composed ofthree quarks of different colors,resulting in‘white’color-neutral states.Mesons contain quark andanti-quark pairs whose color charges cancel.Since a gluon inside a nucleon cannot escape its bound-aries,the nuclear force is mediated by color-neutral bound states,accounting for its short range,characterized by the Compton wavelength of the lightest of these:theπ-meson.The even shorter range of the weak force is associated with the Compton wave-lengths of thecharged W and neutral Z bosons that mediate it.Their couplings to the‘weak charges’of quarksand leptons are comparable in strength to the electromagnetic coupling.When the weak interactionis measured over distances much larger than its range,its effects are averaged over the measurementarea and hence suppressed in amplitude by a factor(E/M W,Z)2≈(E/100GeV)2,where E is the characteristic energy transfer in the measurement.Because the W particles carry electric charge theymust couple to theγ,implying a gauge theory that unites the weak and electromagnetic interactions,similar to QCD in that the gauge particles are self-coupled.In distinction toγ’s and gluons,W’scouple only to left-handed fermions(with spin oriented opposite to the direction of motion).The SM is further characterized by a high degree of symmetry.For example,one cannot performan experiment that would distinguish the color of the quarks involved.If the symmetries of theSM couplings were fully respected in nature,we would not distinguish an electron from a neutrinoor a proton from a neutron;their detectable differences are attributed to‘spontaneous’breakingof the symmetry.Just as the spherical symmetry of the earth is broken to a cylindrical symmetry by the earth’s magneticfield,afield permeating all space,called the Higgsfield,is invoked to explain the observation that the symmetries of the electroweak theory are broken to the residual gauge symmetry of QED.Particles that interact with the Higgsfield cannot propagate at the speed of light,and acquire masses,in analogy to the index of refraction that slows a photon traversing matter.Particles that do not interact with the Higgsfield—the photon,gluons and possibly neutrinos–remain massless.Fermion couplings to the Higgsfield not only determine their masses; they induce a misalignment of quark mass eigenstates with respect to the eigenstates of the weak charges,thereby allowing all fermions of heavy families to decay to lighter ones.These couplings provide the only mechanism within the SM that can account for the observed violation of CP,that is,invariance of the laws of nature under mirror reflection(parity P)and the interchange of particles with their anti-particles(charge conjugation C).The origin of the Higgsfield has not yet been determined.However our very understanding of the SM implies that physics associated with electroweak symmetry breaking(ESB)must become manifest at energies of present colliders or at the LHC under construction.There is strong reason, stemming from the quantum instability of scalar masses,to believe that this physics will point to modifications of the theory.One shortcoming of the SM is its failure to accommodate gravity,for which there is no renormalizable QFT because the quantum of the gravitationalfield has two units of spin.Recent theoretical progress suggests that quantum gravity can be formulated only in terms of extended objects like strings and membranes,with dimensions of order of the Planck length10−35m. Experiments probing higher energies and shorter distances may reveal clues connecting SM physics to gravity,and may shed light on other questions that it leaves unanswered.In the following we trace the steps that led to the formulation of the SM,describe the experiments that have confirmed it,and discuss some outstanding unresolved issues that suggest a more fundamental theory underlies the SM.II.THE PATH TO QCDThe invention of the bubble chamber permitted the observation of a rich spectroscopy of hadron states.Attempts at their classification using group theory,analogous to the introduction of isotopic spin as a classification scheme for nuclear states,culminated in the‘Eightfold Way’based on the group SU(3),in which particles are ordered by their‘flavor’quantum numbers:isotopic spin and strangeness.This scheme was spectacularly confirmed by the discovery at Brookhaven Laboratory (BNL)of theΩ−particle,with three units of strangeness,at the predicted mass.It was subsequently realized that the spectrum of the Eightfold Way could be understood if hadrons were composed of three types of quarks:u,d,and the strange quark s.However the quark model presented a dilemma: each quark was attributed one half unit of spin,but Fermi statistics precluded the existence of a state like theΩ−composed of three strange quarks with total spin3A combination of experimental observations and theoretical analyses in the1960’s led to anotherimportant conclusion:pions behave like the Goldstone bosons of a spontaneously broken symmetry,called chiral symmetry.Massless fermions have a conserved quantum number called chirality,equalto their helicity:+1(−1)for right(left)-handed fermions.The analysis of pion scattering lengths andweak decays into pions strongly suggested that chiral symmetry is explicitly broken only by quarkmasses,which in turn implied that the underlying theory describing strong interactions among quarksmust conserve quark helicity–just as QED conserves electron helicity.This further implied thatinteractions among quarks must be mediated by the exchange of spin-1particles.In the early1970’s,experimenters at the Stanford Linear Accelerator Center(SLAC)analyzed thedistributions in energy and angle of electrons scattered from nuclear targets in inelastic collisionswith momentum transfer Q2≈1GeV/c from the electron to the struck nucleon.The distributions they observed suggested that electrons interact via photon exchange with point-like objects calledpartons–electrically charged particles much smaller than nucleons.If the electrons were scatteredby an extended object,e.g.a strongly interacting nucleon with its electric charge spread out by acloud of pions,the cross section would drop rapidly for values of momentum transfer greater than theinverse radius of the charge distribution.Instead,the data showed a‘scale invariant’distribution:across section equal to the QED cross section up to a dimensionless function of kinematic variables,independent of the energy of the incident electron.Neutrino scattering experiments at CERN andFermilab(FNAL)yielded similar parison of electron and neutrino data allowed adetermination of the average squared electric charge of the partons in the nucleon,and the result wasconsistent with the interpretation that they are fractionally charged quarks.Subsequent experimentsat SLAC showed that,at center-of-mass energies above about two GeV,thefinal states in e+e−annihilation into hadrons have a two-jet configuration.The angular distribution of the jets withrespect to the beam,which depends on the spin of thefinal state particles,is similar to that of themuons in anµ+µ−final state,providing direct evidence for spin-1√where G F is the Fermi coupling constant,γµis a Dirac matrix and12fermions via the exchange of spinless particles.Both the chiral symmetry of thestrong interactions and the V−A nature of the weak interactions suggested that all forces except gravity are mediated by spin-1particles,like the photon.QED is renormalizable because gauge invariance,which gives conservation of electric charge,also ensures the cancellation of quantum corrections that would otherwise result in infinitely large amplitudes.Gauge invariance implies a massless gauge particle and hence a long-range force.Moreover the mediator of weak interactions must carry electric charge and thus couple to the photon,requiring its description within a Yang-Mills theory that is characterized by self-coupled gauge bosons.The important theoretical breakthrough of the early1970’s was the proof that Yang-Mills theories are renormalizable,and that renormalizability remains intact if gauge symmetry is spontaneously broken,that is,if the Lagrangian is gauge invariant,but the vacuum state and spectrum of particles are not.An example is a ferromagnet for which the lowest energy configuration has electron spins aligned;the direction of alignment spontaneously breaks the rotational invariance of the laws ofphysics.In QFT,the simplest way to induce spontaneous symmetry breaking is the Higgs mech-anism.A set of elementary scalarsφis introduced with a potential energy density function V(φ) that is minimized at a value<φ>=0and the vacuum energy is degenerate.For example,the gauge invariant potential for an electrically charged scalarfieldφ=|φ|e iθ,V(|φ|2)=−µ2|φ|2+λ|φ|4,(3)√λ=v,but is independent of the phaseθ.Nature’s choice forθhas its minimum atspontaneously breaks the gauge symmetry.Quantum excitations of|φ|about its vacuum value are massive Higgs scalars:m2H=2µ2=2λv2.Quantum excitations around the vacuum value ofθcost no energy and are massless,spinless particles called Goldstone bosons.They appear in the physical spectrum as the longitudinally polarized spin states of gauge bosons that acquire masses through their couplings to the Higgsfield.A gauge boson mass m is determined by its coupling g to theHiggsfield and the vacuum value v.Since gauge couplings are universal this also determines the√Fermi constant G for this toy model:m=gv/2,G/2|φ|=212F=246GeV,leaving three Goldstone bosons that are eaten by three massive vector bosons:W±and Z=cosθw W0−sinθw B0,while the photonγ=cosθw B0+sinθw W0remains massless.This theory predicted neutrino-induced neutral current(NC)interactions of the typeν+atom→ν+anything,mediated by Z exchange.The weak mixing angleθw governs the dependence of NC couplings on fermion helicity and electric charge, and their interaction rates are determined by the Fermi constant G Z F.The ratioρ=G Z F/G F= m2W/m2Z cos2θw,predicted to be1,is the only measured parameter of the SM that probes thesymmetry breaking mechanism.Once the value ofθw was determined in neutrino experiments,the√W and Z masses could be predicted:m2W=m2Z cos2θw=sin2θwπα/QUARKS:S=1LEPTONS:S=13m3m Q=0m quanta mu1u2u3(2–8)10−3e 5.11×10−4c1c2c3 1.0–1.6µ0.10566t1t2t3173.8±5.0τ 1.77705/3g′,where g1isfixed by requiring the same normalization for all fermion currents.Their measured values at low energy satisfy g3>g2>g1.Like g3,the coupling g2decreases with increasing energy,but more slowly because there are fewer gauge bosons contributing.As in QED,the U(1)coupling increases with energy.Vacuum polarization effects calculated using the particle content of the SM show that the three coupling constants are very nearly equal at an energy scale around1016GeV,providing a tantalizing hint of a more highly symmetric theory,embedding the SM interactions into a single force.Particle masses also depend on energy;the b andτmasses become equal at a similar scale,suggesting a possibility of quark and lepton unification as different charge states of a singlefield.V.BRIEF SUMMARY OF THE STANDARD MODEL ELEMENTSThe SM contains the set of elementary particles shown in Table I.The forces operative in the particle domain are the strong(QCD)interaction responsive to particles carrying color,and the two pieces of the electroweak interaction responsive to particles carrying weak isospin and hypercharge. The quarks come in three experimentally indistinguishable colors and there are eight colored gluons. All quarks and leptons,and theγ,W and Z bosons,carry weak isospin.In the strict view of the SM,there are no right-handed neutrinos or left-handed anti-neutrinos.As a consequence the simple Higgs mechanism described in section IV cannot generate neutrino masses,which are posited to be zero.In addition,the SM provides the quark mixing matrix which gives the transformation from the basis of the strong interaction charge−1Finding the constituents of the SM spanned thefirst century of the APS,starting with the discovery by Thomson of the electron in1897.Pauli in1930postulated the existence of the neutrino as the agent of missing energy and angular momentum inβ-decay;only in1953was the neutrino found in experiments at reactors.The muon was unexpectedly added from cosmic ray searches for the Yukawa particle in1936;in1962its companion neutrino was found in the decays of the pion.The Eightfold Way classification of the hadrons in1961suggested the possible existence of the three lightest quarks(u,d and s),though their physical reality was then regarded as doubtful.The observation of substructure of the proton,and the1974observation of the J/ψmeson interpreted as a cp collider in1983was a dramatic confirmation of this theory.The gluon which mediates the color force QCD wasfirst demonstrated in the e+e−collider at DESY in Hamburg.The minimal version of the SM,with no right-handed neutrinos and the simplest possible ESB mechanism,has19arbitrary parameters:9fermion masses;3angles and one phase that specify the quark mixing matrix;3gauge coupling constants;2parameters to specify the Higgs potential; and an additional phaseθthat characterizes the QCD vacuum state.The number of parameters is larger if the ESB mechanism is more complicated or if there are right-handed neutrinos.Aside from constraints imposed by renormalizability,the spectrum of elementary particles is also arbitrary.As discussed in Section VII,this high degree of arbitrariness suggests that a more fundamental theory underlies the SM.VI.EXPERIMENTAL ESTABLISHMENT OF THE STANDARD MODELThe current picture of particles and interactions has been shaped and tested by three decades of experimental studies at laboratories around the world.We briefly summarize here some typical and landmark results.FIG.1.The proton structure function(F2)versus Q2atfixed x,measured with incident electrons or muons,showing scale invariance at larger x and substantial dependence on Q2as x becomes small.The data are taken from the HERA ep collider experiments H1and ZEUS,as well as the muon scattering experiments BCDMS and NMC at CERN and E665at FNAL.A.Establishing QCD1.Deep inelastic scatteringPioneering experiments at SLAC in the late1960’s directed high energy electrons on proton and nuclear targets.The deep inelastic scattering(DIS)process results in a deflected electron and a hadronic recoil system from the initial baryon.The scattering occurs through the exchange of a photon coupled to the electric charges of the participants.DIS experiments were the spiritual descendents of Rutherford’s scattering ofαparticles by gold atoms and,as with the earlier experi-ment,showed the existence of the target’s substructure.Lorentz and gauge invariance restrict the matrix element representing the hadronic part of the interaction to two terms,each multiplied by phenomenological form factors or structure functions.These in principle depend on the two inde-pendent kinematic variables;the momentum transfer carried by the photon(Q2)and energy loss by the electron(ν).The experiments showed that the structure functions were,to good approximation, independent of Q2forfixed values of x=Q2/2Mν.This‘scaling’result was interpreted as evi-dence that the proton contains sub-elements,originally called partons.The DIS scattering occurs as the elastic scatter of the beam electron with one of the partons.The original and subsequent experiments established that the struck partons carry the fractional electric charges and half-integer spins dictated by the quark model.Furthermore,the experiments demonstrated that three such partons(valence quarks)provide the nucleon with its quantum numbers.The variable x represents the fraction of the target nucleon’s momentum carried by the struck parton,viewed in a Lorentz frame where the proton is relativistic.The DIS experiments further showed that the charged partons (quarks)carry only about half of the proton momentum,giving indirect evidence for an electrically neutral partonic gluon.1011010101010FIG.2.The quark and gluon momentum densities in the proton versus x for Q 2=20GeV 2.The integrated values of each component density gives the fraction of the proton momentum carried by that component.The valence u and d quarks carry the quantum numbers of the proton.The large number of quarks at small x arise from a ‘sea’of quark-antiquark pairs.The quark densities are from a phenomenological fit (the CTEQ collaboration)to data from many sources;the gluon density bands are the one standard deviation bounds to QCD fits to ZEUS data (low x )and muon scattering data (higher x ).Further DIS investigations using electrons,muons,and neutrinos and a variety of targets refined this picture and demonstrated small but systematic nonscaling behavior.The structure functions were shown to vary more rapidly with Q 2as x decreases,in accord with the nascent QCD prediction that the fundamental strong coupling constant αS varies with Q 2,and that at short distance scales (high Q 2)the number of observable partons increases due to increasingly resolved quantum fluc-tuations.Figure 1shows sample modern results for the Q 2dependence of the dominant structure function,in excellent accord with QCD predictions.The structure function values at all x depend on the quark content;the increases at larger Q 2depend on both quark and gluon content.The data permit the mapping of the proton’s quark and gluon content exemplified in Fig.2.2.Quark and gluon jetsThe gluon was firmly predicted as the carrier of the color force.Though its presence had been inferred because only about half the proton momentum was found in charged constituents,direct observation of the gluon was essential.This came from experiments at the DESY e +e −collider (PETRA)in 1979.The collision forms an intermediate virtual photon state,which may subsequently decay into a pair of leptons or pair of quarks.The colored quarks cannot emerge intact from the collision region;instead they create many quark-antiquark pairs from the vacuum that arrange themselves into a set of colorless hadrons moving approximately in the directions of the original quarks.These sprays of roughly collinear particles,called jets,reflect the directions of the progenitor quarks.However,the quarks may radiate quanta of QCD (a gluon)prior to formation of the jets,just as electrons radiate photons.If at sufficiently large angle to be distinguished,the gluon radiation evolves into a separate jet.Evidence was found in the event energy-flow patterns for the ‘three-pronged’jet topologies expected for events containing a gluon.Experiments at higher energy e +e −colliders illustrate this gluon radiation even better,as shown in Fig.3.Studies in e +e −and hadron collisions have verified the expected QCD structure of the quark-gluon couplings,and their interference patterns.FIG.3.A three jet event from the OPAL experiment at LEP.The curving tracks from the three jets may be associated with the energy deposits in the surrounding calorimeter,shown here as histograms on the middle two circles,whose bin heights are proportional to energy.Jets1and2contain muons as indicated,suggesting that these are both quark jets(likely from b quarks).The lowest energy jet3is attributed to a radiated gluon.3.Strong coupling constantThe fundamental characteristic of QCD is asymptotic freedom,dictating that the coupling constant for color interactions decreases logarithmically as Q2increases.The couplingαS can be measured in a variety of strong interaction reactions at different Q2scales.At low Q2,processes like DIS,tau decays to hadrons,and the annihilation rate for e+e−into multi-hadronfinal states give accurate determinations ofαS.The decays of theΥinto three jets primarily involve gluons,and the rate for this decay givesαS(M2Υ).At higher Q2,studies of the W and Z bosons(for example,the decay width of the Z,or the fraction of W bosons associated with jets)measureαS at the100GeV scale. These and many other determinations have now solidified the experimental evidence thatαS does indeed‘run’with Q2as expected in QCD.Predictions forαS(Q2),relative to its value at some reference scale,can be made within perturbative QCD.The current information from many sources are compared with calculated values in Fig.4.4.Strong interaction scattering of partonsAt sufficiently large Q2whereαS is small,the QCD perturbation series converges sufficiently rapidly to permit accurate predictions.An important process probing the highest accessible Q2 scales is the scattering of two constituent partons(quarks or gluons)within colliding protons and antiprotons.Figure5shows the impressive data for the inclusive production of jets due to scattered partons in pp collisions reveals the structure of the scattering matrix element.These amplitudes are dominated by the exchange of the spin1gluon.If this scattering were identical to Rutherford scattering,the angular variable0.10.20.30.40.511010FIG.4.The dependence of the strong coupling constant,αS ,versus Q using data from DIS structure functions from e ,µ,and νbeam experiments as well as ep collider experiments,production rates of jets,heavy quark flavors,photons,and weak vector bosons in ep ,e +e −,and pt ,is sensitive not only to to perturbative processes,but reflectsadditional effects due to multiple gluon radiation from the scattering quarks.Within the limited statistics of current data samples,the top quark production cross section is also in good agreement with QCD.FIG.6.The dijet angular distribution from the DØexperiment plotted as a function ofχ(see text)for which Rutherford scattering would give dσ/dχ=constant.The predictions of NLO QCD(at scaleµ=E T/2)are shown by the curves.Λis the compositeness scale for quark/gluon substructure,withΛ=∞for no compositness(solid curve);the data rule out values of Λ<2TeV.5.Nonperturbative QCDMany physicists believe that QCD is a theory‘solved in principle’.The basic validity of QCD at large Q2where the coupling is small has been verified in many experimental studies,but the large coupling at low Q2makes calculation exceedingly difficult.This low Q2region of QCD is relevant to the wealth of experimental data on the static properties of nucleons,most hadronic interactions, hadronic weak decays,nucleon and nucleus structure,proton and neutron spin structure,and systems of hadronic matter with very high temperature and energy densities.The ability of theory to predict such phenomena has yet to match the experimental progress.Several techniques for dealing with nonperturbative QCD have been developed.The most suc-cessful address processes in which some energy or mass in the problem is large.An example is the confrontation of data on the rates of mesons containing heavy quarks(c or b)decaying into lighter hadrons,where the heavy quark can be treated nonrelativistically and its contribution to the matrix element is taken from experiment.With this phenomenological input,the ratios of calculated par-tial decay rates agree well with experiment.Calculations based on evaluation at discrete space-time points on a lattice and extrapolated to zero spacing have also had some success.With computing advances and new calculational algorithms,the lattice calculations are now advanced to the stage of calculating hadronic masses,the strong coupling constant,and decay widths to within roughly10–20%of the experimental values.The quark and gluon content of protons are consequences of QCD,much as the wave functions of electrons in atoms are consequences of electromagnetism.Such calculations require nonperturbative techniques.Measurements of the small-x proton structure functions at the HERA ep collider show a much larger increase of parton density with decreasing x than were extrapolated from larger x measurements.It was also found that a large fraction(∼10%)of such events contained afinal。

a r X i v :h e p -l a t /0512040v 1 27 D e c 2005BI-TP 2005/52BNL-NT-05/49TKYNT-05-30The isentropic equation of state of 2-flavor QCDS.Ejiri a ,F.Karsch b ,c ,ermann c and C.Schmidt baDepartment of Physics,The University of Tokyo,Tokyo 113-0033,Japan bPhysics Department,Brookhaven National Laboratory,Upton,NY 11973,USA cFakult¨a t f¨u r Physik,Universit¨a t Bielefeld,D-33615Bielefeld,Germany(Dated:February 1,2008)Using Taylor expansions of the pressure obtained previously in studies of 2-flavor QCD at non-zero chemical potential we calculate expansion coefficients for the energy and entropy densities up to O (µ6q )in the quark chemical potential.We use these series in µq /T to determine lines of constant entropy per baryon number (S/N B )that characterize the expansion of dense matter created in heavy ion collisions.In the high temperature regime these lines are found to be well approximated by lines of constant µq /T .In the low temperature phase,however,the quark chemical potential is found to increase with decreasing temperature.This is in accordance with resonance gas model calculations.Along the lines of constant S/N B we calculate the energy density and pressure.Within the accuracy of our present analysis we find that the ratio p/ǫfor T >T 0as well as the softest point of the equation of state,(p/ǫ)min ≃0.075,show no significant dependence on S/N B .PACS numbers:11.15.Ha,11.10.Wx,12.38Gc,12.38.MhI.INTRODUCTIONRecently studies of QCD thermodynamics on the lattice have successfully been extended to non-vanishing quark (or baryon)chemical potential using Taylor expansions [1,2]as well as reweighting techniques [3]around the limit of vanishing quark chemical potential (µq =0)and analytic continuations of numerical calculations performed with an imaginary chemical potential [4].The complementary approach at fixed baryon number [5,6]has also been used recently in simulations of 4-flavor QCD with light quarks [7].These calculations yield the additional contribution to the pressure that arises from the presence of a net excess of baryons over anti-baryons in a strongly interacting medium.We will further explore here the approach based on a Taylor expansion of the pressure and make use of our earlier calculations for 2-flavor QCD [2]to determine also the energy and entropy densities at non-vanishing baryon chemical potential.In a heavy ion collision a dense medium is created which after thermalization is expected to expand without further generation of entropy (S )and with fixed baryon number (N B )or,equivalently,with fixed quark number N q =3N B .During the isentropic expansion the ratio S/N B thus remains constant 1.The cooling of the expanding system then is controlled by the equation of state on lines of constant S/N B .From a knowledge of the energy density and pressure at non-vanishing quark chemical potential we can calculate trajectories in the µq -T phase diagram of QCD that correspond to constant S/N B and can determine the isentropic equation of state on these trajectories.This paper is organized as follows.In the next section we summarize the basic setup for calculating Taylor expansions for bulk thermodynamic observables and present a calculation of the Taylor expansion coefficients for energy and entropy densities at non-vanishing quark chemical potential up to O (µ6q ).We use these results in Section III to determine lines of constant S/N B and study the temperature dependence of pressure and energy density along these lines.Our conclusions are given in section IV.II.TAYLOR EXPANSION OF PRESSURE,ENERGY AND ENTROPY DENSITYThe analysis we are going to present in this paper is based on numerical results previously obtained in simulations of 2-flavor QCD on lattices of size 163×4with an improved staggered fermion action [1,2].In these calculations Taylor expansion coefficients for the pressure have been obtained up to O (µ6)for a fixed bare quark mass value (ˆm =0.1)which at temperatures close to the transition temperature (T 0)corresponds to a still quite large pion mass of about770MeV.However,in particular at temperatures above the QCD transition temperature the remaining quark mass dependence of thermodynamic observables is nonetheless small as deviations from the massless limit are controlled by the quark mass in units of the temperature,which is a small number.We closely follow here the approach and notation used in Ref.[2].We start with a Taylor expansion for the pressure in2-flavor QCD for non-vanishing quark chemical potentialµq(and vanishing isospin chemical potential,µI≡0),pV T3ln Z(T,µq)=∞n=0c n(T,m q) µqn!1∂(µq/T)nµq=0.(2)Here we explicitely indicated that the Taylor expansion coefficients c n depend on temperature as well as the quark mass2.In the context of lattice calculations it is more customary to think of this quark mass dependence in terms of a dependence on an appropriately chosen ratio of hadron masses characterizing lines of constant physics.We thus may replace m q by a ratio of pseudo-scalar(pion)and vector(rho)meson masses,m q≡(m P S/m V)2.Due to the invariance of the partition function under exchange of particle and anti-particle the Taylor expansion is a series in even powers ofµq/T;expansion coefficients c n vanish for odd values of n.From the pressure we immediately obtain the quark number density,n qV T3∂ln Z(T,µq)T n−1.(3)Using standard thermodynamic relations we also can calculate the difference between energy density(ǫ)and three times the pressure,ǫ−3pT n,(4) wherec′n(T,m q)=Td c n(T,m q)T4=∞n=0(3c n(T,m q)+c′n(T,m q)) µqT3≡ǫ+p−µq n qT n.(6)The expansion coefficients c n(T,m q)have been calculated in2-flavor QCD at several values of the temperature and for afixed value of the bare quark mass,ˆm=0.1[2].We note that the bare couplingˆm introduces an implicit temperature dependence ifˆm is keptfixed while the lattice cut-offis varied.The latter controls the temperature of the system on lattices of temporal extent Nτ,i.e.T−1=Nτa.The difference between derivatives taken atfixedˆm andfixed m q,however,is negligible at high temperature,where the quark mass dependence of bulk thermodynamic quantities is O((m q/T)2)and,of course,vanishes at all temperatures in the chiral limit as this also defines a line of constant physics.We thus approximate the derivative,Eq.5,by a derivative taken atfixedˆm which becomes exact in the chiral limit.These derivatives are evaluated usingfinite difference approximants.Alternatively we may expressderivatives of Taylor expansion coefficients with respect to T in terms of derivatives with respect to the bare lattice couplingsβ≡6/g2andˆm and rewrite Eq.5as,c′n(T,m q)=−a dβ∂β−adˆm∂ˆm.(7)Here the two latticeβ-functions,a dβ/d a and a dˆm/d a,have to be determined by demanding that the temperature derivative is taken along lines of constant physics[10,11].Theβ-function controlling the variation of the bare quark mass with the lattice cut-off,a dˆm/d a,is proportional to the bare quark massˆm and thus vanishes in the chiral limit [10].For small quark masses thefirst term in Eq.7thus gives the dominant contribution to c′n(T,m q).We have evaluated thisfirst term in Eq.7for n=2andfind that this approximation for c′2agrees within errors with the calculation of c′2fromfinite difference approximants.Only close to T0wefind differences of the order of10%.The expansion coefficients c n(T,m q)have been calculated in[2]forˆm=0.1at a set of16temperature values in the interval T/T0∈[0.81,1.98].From this set of expansion coefficients we have calculated the partial derivatives c′n at temperature T by averaging overfinite difference approximants for left and right derivatives at T.With this we have constructed the expansion coefficients for the energy and entropy densities,ǫn≡3c n(T,m q)+c′n(T,m q),s n≡(4−n)c n(T,m q)+c′n(T,m q).(8) Results for the2nd,4th and6th order expansion coefficients of energy and entropy densities obtained in the approxi-mation discussed above are shown in Fig.1.Also shown in thisfigure are the corresponding expansion coefficients for the pressure(p n≡c n).For temperatures larger than T/T0≃1.5all expansion coefficients satisfy quite well the idealgas relations,ǫSBn =3p SBnandǫSB2=3s SB2/2.As noted already in Ref.[2]results for the2nd and4th order expansioncoefficients are close to those of an ideal Fermi gas which describes the high temperature limit for the energy density of2-flavor QCD,ǫSBF10+3 µq2π2 µqN B =337π2T 2T+1T 3.(10)In the zero temperature limit,however,the resonance gas reduces to a degenerate Fermi gas of nucleons and the chemical potential approaches afinite value to obtainfinite baryon number and entropy,i.e.µq/T∼1/T.0.01.02.03.04.05.06.07.0-1.5-1.0-0.5 0.0 0.51.01.52.02.5-1.5-1.0-0.5 0.0 0.5 1.0 1.5FIG.1:The 2nd ,4th and 6th order Taylor expansion coefficients for pressure (p n ≡c n ),energy density (ǫn )and entropy density (s n )as functions of T /T 0.0.01.02.03.04.05.06.0FIG.2:The µq dependent contribution to energy density (filled symbols)and entropy density (open symbols)calculated in 4th order Taylor expansion.Data points for the entropy density have been shifted slightly for better visibility.Horizontal lines show the corresponding ideal gas values for the energy density.In Fig.3we show the values for µq needed to keep S/N B fixed.These lines of constant S/N B in the T -µq plane have been obtained by calculating the total entropy density for 2-flavor QCD from Eq.6using results for the pressure and energy density calculated at µq =0[9,12]and the corresponding µq dependent contributions shown in Fig.1.The ratio of s/T 3and n q /T 3obtained in this way is then solved numerically for µq /T .We find that isentropic expansion at high temperature indeed is well represented by lines of constant µq /T down to temperatures close to the transition,T ≃1.2T 0.In the low temperature regime we observe a bending of the isentropic lines in accordance with the expected asymptotic low temperature behavior.The isentropic expansion lines for matter created at SPS correspond to S/N B ≃45while the isentropes at RHIC correspond to S/N B ≃300.The energy range0.801.001.201.401.601.800.000.200.400.600.801.00µq /TT/T1502002503000 100 200 300 400 500 600 700 800 900T [MeV]FIG.3:Lines of constant entropy per quark number versus µq /T (left)and in physical units using T 0=175MeV to set the scales (right).In the left hand figure we show results obtained using a 4th (full symbols)and 6th (open symbols)order Taylor expansion of the pressure,respectively.Data points correspond to S/N B =300,150,90,60,45,30(from left to right).The vertical lines indicate the corresponding idealgas results,µq /T =0.08,0.16,0.27,0.41,0.54and 0.82in decreasing order of values for S/N B .For a detailed description of the right hand figure see the discussion given in the text.0.02.0 4.0 6.0 8.010.012.00.00.5 1.01.52.0 2.53.0 3.54.0FIG.4:The complete energy density (left)and pressure (right)evaluated on lines of constant S/N B using Taylor expansions up to 6th order in the quark chemical potential.Shown are results for S/N B =30,45,300.of the AGS which also corresponds to an energy range relevant for future experiments at FAIR/Darmstadt is well described by S/N B ≃30.These lines are shown in Fig.3(right)together with points characterizing the chemical freeze-out of hadrons measured at AGS,SPS and RHIC energies.These points have been obtained by comparing experimental results for yields of various hadron species with hadron abundances in a resonance gas [13,14].The solid curve shows a phenomenological parametrization of these freeze-out data [14].In general our findings for lines of constant S/N B are in good agreement with phenomenological model calculations that are based on combinations of ideal gas and resonance gas equations of state at high and low temperature,respectively [15,16].Our current analysis yields stable results for lines of constant S/N B also for temperatures T <∼T 0and values of the chemical potential µB ≃400MeV.This value of µB is larger than recent estimates for the location of the chiral critical point in 2-flavor [17]and (2+1)-flavor [18]QCD.We thus may expect modifications to our current analysis at temperatures below T 0once we include higher orders in the Taylor expansion and/or perform this analysis at smaller values of the quark mass.We now can proceed and calculate energy density and pressure on lines of constant entropy per baryon number using our Taylor expansion results up to O (µ6q ).In Fig.4we show both quantities for the parameters relevant for AGS (FAIR),SPS and RHIC energies.At high temperatures the relevant values of the quark chemical potential in an ideal quark gas are µq /T =0.82,0.54and 0.08,respectively.However,as can be seen from Fig.3at temperatures T <∼1.8T 0the required values for the chemical potentials are significantly smaller.In particular,for the AGS (FAIR)energies (S/N B =30)we find µq /T =0.77at T ≃1.8T 0.The 6th order Taylor expansion thus is still well behaved0.000.050.100.150.200.250.300.000.050.100.150.200.250.30FIG.5:Equation of state on lines of constant entropy per quark number versus T /T 0(left)and in physical units using T 0=175MeV to set the scale (right).Thesolidcurve in the right hand figure is the parametrization of the high temperature part of the equation of state given in Eq.12.at these values of the quark chemical potential.The dependence of ǫand p on S/N B cancels to a large extent in the ratio p/ǫ,which is most relevant for the analysis of the hydrodynamic expansion of dense matter.This may be seen by considering the leading O (µ2q )correction,p 3−1ǫ0 1+ c ′2ǫ0µq ǫ=11+0.5ǫfm 3/GeV.(12)We note,however,that this phenomenological parametrization is not correct at asymptotically large temperatures asit is obvious that Eq.12would lead to corrections to the ideal gas result p/ǫ=1/3that are proportional to T −4while perturbative corrections vanish only logarithmically as function of T .IV.CONCLUSIONSWe have determined Taylor expansion coefficients for the energy and entropy densities in 2-flavor QCD at non-zero quark chemical potential.At present these expansion coefficients have been determined from calculations performed at one value of the bare quark mass which gives a good description of QCD thermodynamics at high temperature.In this temperature regime lines of constant entropy per baryon are well described by lines of constant µq /T .On these isentropic lines we have determined the equation of state and find that the ratio of pressure and energy density shows remarkably little dependence on the ratio S/N B .The regime close to and below the transition temperature T 0is not yet well controlled in our current analysis.Smaller quark masses and the introduction of a non-vanishing strange quark mass,kept fixed in physical units,will be needed to explore this regime as well as the approach to the 3-flavor high temperature limit in more detail.AcknowledgmentsThe work of FK and CS has been supported by a contract DE-AC02-98CH1-886with the U.S.Department of Energy.FK and EL acknowledge partial support through a grant of the BMBF under contract no.06BI106.SE hasbeen supported by the Sumitomo Foundation under grant no.050408.[1]C.R.Allton,S.Ejiri,S.J.Hands,O.Kaczmarek,F.Karsch,ermann and C.Schmidt,Phys.Rev.D68(2003)014507.[2]C.R.Allton,M.D¨o ring,S.Ejiri,S.J.Hands,O.Kaczmarek,F.Karsch,ermann,K.Redlich,Phys.Rev D71(2005)054508.[3]Z.Fodor,S.D.Katz and K.K.Szabo,Phys.Lett.B568(2003)73;F.Csikor,G.I.Egri,Z.Fodor,S.D.Katz,K.K.Szabo and A.I.T´o th,JHEP0405(2004)046.[4]M.D’Elia and M.P.Lombardo,Phys.Rev.D70(2004)074509.[5]ler and K.Redlich,Phys.Rev.D35(1987)2524.[6]J.Engels,O.Kaczmarek,F.Karsch and ermann,Nucl.Phys.B558(1999)307.[7]S.Kratochvila and Ph.de Forcrand,PoS LAT2005(2005)167.[8]C.R.Allton,S.Ejiri,S.J.Hands,O.Kaczmarek,F.Karsch,ermann,Ch.Schmidt and L.Scorzato,Phys.Rev.D66(2002)074507.[9]F.Karsch,ermann,A.Peikert,Nucl.Phys.B605(2001)579.[10]T.Blum,L.K¨a rkk¨a inen,D.Toussaint and S.Gottlieb,Phys.Rev.D51(1995)5153.[11]A.AliKhan et al.(CP-PACS),Phys.Rev.D64(2001)074510.[12]A.Peikert,PhD thesis,Bielefeld,May2000.[13]J.Cleymans and K.Redlich,Phys.Rev.Lett.81(1998)5284J.Cleymans and K.Redlich,Phys.Rev.C60(1999)054908[14]J.Cleymans,H.Oeschler and K.Redlich,S.Wheaton,hep-ph/0511094.[15]C.M.Hung and E.Shuryak,Phys.Rev.C57(1998)1891.[16]V.D.Toneev,J.Cleymans,E.G.Nikonov,K.Redlich and A.A.Shanenko,J.Phys.G27(2001)827,nucl-th/0011029.[17]R.V.Gavai and S.Gupta,Phys.Rev.D71(2005)114014.[18]Z.Fodor and S.D.Katz,JHEP0404(2004)050.。