流体力学流体运动学

流体力学的基本理论和应用流体力学是研究流体运动规律的一门学科，其范围涉及气体、液体和等离子体等。

流体力学的研究对象是流体运动中各种物理量的变化规律，如速度、密度、压力、温度等。

它的研究领域广泛，从天气预报到飞机设计、石油勘探，都离不开流体力学的理论和应用。

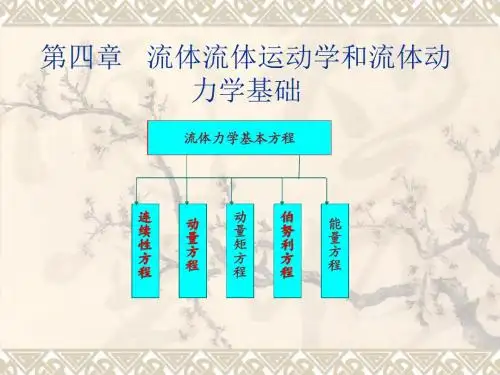
1. 流体力学的基本理论流体力学的基本理论包括流体的性质、流体方程、流体的运动学和动力学方程等。

1.1 流体的性质流体有四种基本性质，即密度、压力、温度和粘度。

密度是指单位体积内质量的大小，压力是单位面积受到的力的大小。

温度是流体内部分子热运动的平均程度，粘度是流体阻力大小的表征。

1.2 流体方程流体方程主要包括连续性方程和动量守恒方程。

连续性方程描述了质量守恒的规律，即在任何一个时间和空间点，通过一个截面进入的质量等于通过该截面流出的质量。

动量守恒方程描述了流体中动量守恒的规律。

1.3 流体的运动学流体的运动学研究的是流体在时间和空间上的运动规律。

就速度场而言，它可以用速度矢量场描述。

在三维空间中，一个流体速度场是指有三个分量的三维矢量场。

1.4 流体的动力学方程流体的动力学方程是研究流体运动的方程，包括质量守恒方程、动量守恒方程和能量守恒方程。

这些方程可以用于描述流体在空间中的各种运动方式。

2. 流体力学的应用流体力学的应用非常广泛，它不仅是科学研究领域中不可或缺的一部分，也是工程设计、生物医学和化学工程等领域必不可少的一门技术。

以下是几个流体力学应用领域：2.1 飞机设计飞机设计需要对空气流动进行深入研究。

流体动力学理论可以帮助设计人员优化飞机的翼型和发动机喷口设计，以减少空气阻力和提高飞机性能。

流体动力学还可以帮助研究飞行器的失速问题，并提出优质的控制方法。

2.2 汽车行驶汽车行驶的过程中，空气阻力会影响汽车的速度和燃油消耗。

通过流体力学研究，在设计汽车的外形和风阻系数时，可以优化方案以降低空气阻力。

2.3 气象预报气象预报是一项很重要的工作，流体力学理论可以用于研究气象现象，用以预测天气。

流体力学辅导材料3：第3章流体运动学【教学基本要求】1.了解描述流体运动的两种方法。

了解迹线与流线的概念。

掌握欧拉法质点加速度的表达式。

2.理解总流、过流断面、流量、断面平均流速的概念；理解定常流与非定常流、均匀流与非均匀流、渐变流与急变流、有压流与无压流。

3.熟练掌握总流的连续性方程。

4.理解无旋流与有旋流，掌握其判别方法。

5. 掌握流函数、速度势函数与速度的关系。

知道流网法、势流叠加法解平面势流的原理。

【学习重点】1.流线与迹线；质点加速度的欧拉表述法。

2.总流的连续性方程。

3.无旋流与有旋流的判别。

4.流函数、速度势与流速的关系。

【内容提要和学习指导】3.1 流动描述3.1.1 描述流动的两种方法描述流动的方法有拉格朗日法和欧拉法。

1. 拉格朗日（Lagrange）法：拉格朗日法以研究个别流体质点的运动为基础，通过对每个流体质点运动规律的研究来获得整个流体的运动规律。

这种方法又称为质点系法。

拉格朗日法的基本特点是追踪单个质点的运动。

此法概念明确，但复杂。

一般不采用拉格朗日法。

2. 欧拉（Euler）法：欧拉法是以考察不同流体质点通过固定的空间点的运动情况来了解整个流动空间内的流动情况，即着眼于研究各种运动要素的分布场。

这种方法又叫做流场法。

欧拉法中，流场中任何一个运动要素可以表示为空间坐标和时间的函数。

例如，在直角坐标系中，流速v是随空间坐标)yx和时间t而变化的，称为流速场。

,(z,用欧拉法描述流体运动时，质点加速度等于时变加速度和位变加速度之和，表达式为：⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+∂∂+∂∂+∂∂==∂∂+∂∂+∂∂+∂∂==∂∂+∂∂+∂∂+∂∂==z u u yu u xu u tu dtdu a z u u y u u x u u t u dt du a z u u y u u x u u t u dt du a z z z yz xz zy y z y y y x y yy x zx y x x x xx （3-6）3.1.2 迹线与流线在研究流动时，常用某些线簇图像表示流动情况。

流体力学知识点流体力学是研究流体（包括液体和气体）的运动规律以及流体与固体之间相互作用的学科。

它在许多领域都有着广泛的应用，如航空航天、水利工程、化工、生物医学等。

下面我们来一起了解一些流体力学的重要知识点。

一、流体的性质流体具有易流动性，即它们在微小的切应力作用下就会发生连续的变形。

流体的密度和黏度是两个重要的物理性质。

密度是指单位体积流体的质量。

对于均质流体，密度是一个常数；对于非均质流体，密度会随位置而变化。

例如，空气在不同高度的密度不同。

黏度则反映了流体内部的内摩擦力。

黏度大的流体，如蜂蜜，流动起来比较困难；而黏度小的流体，如水，流动相对容易。

二、流体静力学流体静力学主要研究静止流体的压力分布规律。

帕斯卡定律指出，在密闭容器内，施加于静止液体上的压力将以等值传递到液体各点。

这在液压系统中有着重要的应用。

另一个重要的概念是浮力。

当物体浸没在流体中时，它受到的浮力等于排开流体的重量。

这就是阿基米德原理。

例如，船舶能够漂浮在水面上，就是因为受到的浮力等于其自身的重量。

三、流体运动学流体运动学关注流体的运动方式和描述方法。

流线是用来描述流体流动的重要概念。

流线是在某一瞬时，在流场中画出的一条空间曲线，在该曲线上，流体质点的速度方向与曲线相切。

流量是指单位时间内通过某一截面的流体体积或质量。

四、流体动力学流体动力学研究流体运动与受力之间的关系。

伯努利方程是流体动力学中的一个关键方程，它表明在理想流体的稳定流动中，沿着一条流线，总水头（位置水头、压力水头和速度水头之和）保持不变。

例如，在水平管道中，流速大的地方压力小，流速小的地方压力大。

这可以解释为什么飞机机翼上方的流速快、压力低，从而产生升力。

五、黏性流体的流动实际流体都具有黏性。

在黏性流体的流动中，会产生内摩擦力，导致能量损失。

层流和湍流是两种常见的流动状态。

层流时，流体的质点作有规则的平行运动，各层之间互不干扰；而湍流时，流体的质点作不规则的随机运动。

流体力学知识点总结流体力学是一门研究流体（包括液体和气体）的运动规律以及流体与固体之间相互作用的学科。

它在许多领域都有着广泛的应用，如航空航天、水利工程、能源开发、生物医学等。

下面将对流体力学的一些重要知识点进行总结。

一、流体的物理性质1、密度和比容密度是指单位体积流体的质量，用ρ 表示。

比容则是单位质量流体所占的体积，是密度的倒数，用ν 表示。

2、压缩性和膨胀性压缩性是指流体在压力作用下体积缩小的性质，通常用体积压缩系数β 来表示。

膨胀性是指流体在温度升高时体积增大的性质，用体积膨胀系数α 来表示。

液体的压缩性和膨胀性通常较小，可视为不可压缩和不可膨胀流体；而气体的压缩性和膨胀性较为显著。

3、粘性粘性是流体内部产生内摩擦力以阻碍流体相对运动的性质。

粘性的大小用动力粘度μ 或运动粘度ν 来表示。

牛顿内摩擦定律指出，相邻两层流体之间的切应力与速度梯度成正比。

4、表面张力液体表面由于分子引力不均衡而产生的沿表面切线方向的拉力称为表面张力。

表面张力会使液体表面有收缩的趋势，在一些涉及小尺度流动的问题中需要考虑。

二、流体静力学1、静压强及其特性静止流体中任一点的压强大小与作用面的方位无关，只与该点的位置有关，即静压强各向同性。

2、欧拉平衡方程在静止流体中，单位质量流体所受的质量力和表面力平衡，由此可以导出欧拉平衡方程。

3、重力作用下的静压强分布在重力作用下，静止液体中的压强随深度呈线性增加，其计算公式为 p ＝ p0 ＋ρgh，其中 p0 为液面压强，h 为深度。

4、压力的表示方法绝对压强是以绝对真空为基准计量的压强；相对压强是以当地大气压为基准计量的压强。

真空度则是当绝对压强小于大气压时，相对压强为负值，其绝对值称为真空度。

5、作用在平面上的静水总压力对于垂直放置的平面，静水总压力的大小等于受压面面积与形心处压强的乘积，其作用点位于受压面的形心之下。

6、作用在曲面上的静水总压力将曲面所受静水总压力分解为水平方向和垂直方向的分力进行计算。