环形电流在空间一点产生的磁场强度

第五章 稳恒磁场设0x <的半空间充满磁导率为μ的均匀介质，0x >的半空间为真空，今有线电流沿z 轴方向流动，求磁感应强度和磁化电流分布。

解：如图所示令 110A I H e r = 220A IH e r= 由稳恒磁场的边界条件知，12t t H H = 12n n B B = 又 B μ= 且 n H H =所以 1122H H μμ= (1) 再根据安培环路定律H dl I ⋅=⎰得 12IH H rπ+= (2) 联立(1),(2)两式便解得，21120I I H r rμμμμπμμπ=⋅=⋅++012120I I H r rμμμμπμμπ=⋅=⋅++ 故， 01110IB H e r θμμμμμπ==⋅+ 02220IB H e rθμμμμμπ==⋅+ 212()M a n M M n M =⨯-=⨯ 220()B n H μ=⨯-00()0In e rθμμμμπ-=⋅⋅⨯=+ 222()M M M J M H H χχ=∇⨯=∇⨯=∇⨯0000(0,0,)zJ Ie z μμμμδμμμμ--=⋅=⋅++ 半径为a 的无限长圆柱导体上有恒定电流J 均匀分布于截面上，试解矢势A 的微分方程，设导体的磁导率为0μ，导体外的磁导率为μ。

？解： 由电流分布的对称性可知，导体内矢势1A 和导体外矢势2A 均只有z e 分量，而与φ，z 无关。

由2A ∇的柱坐标系中的表达式可知，只有一个分量，即 210A J μ∇=- 220A ∇= 此即101()A r J r r r μ∂∂=-∂∂21()0A r r r r∂∂=∂∂ 通解为 21121ln 4A Jr b r b μ=-++212ln A c r c =+ 当0r =时，1A 有限，有10b =由于无限长圆柱导体上有恒定电流J 均匀分布于截面上，设r a =时， 120A A ==,得202121ln 04Ja b c a c μ-+=+=)又r a =时，12011e A e A ρρμμ⨯∇⨯=⨯∇⨯，得 112c Ja a μ-=所以 2221220111,,224c Ja c Ja b Ja μμμ=-=-=所以， 22101()4A J r a μ=--221ln 2a A Ja rμ=写成矢量形式为 22101()4A J r a μ=--221ln 2a A Ja rμ=设无限长圆柱体内电流分布，0()z J a rJ r a =-≤求矢量磁位A 和磁感应B 。

Φ BS cos BS
s
一般情况 Φ s BdS
dS2
B
S 2
dS1
1
B1
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
B2
SB cosdS 0
磁场高斯定理
S B d S 0
物理意义：通过任意闭合曲面的磁通
量必等于零（故磁场是无源的）.
B B1 B2 B3
Bdl
l
0(I2 I3)
推广：
➢ 安培环路定理
n
B dl 0 Ii
i 1
n
安培环路定理
B dl 0 Ii
i 1
在真空的恒定磁场中，磁感强度 B沿任
一闭合路径的积分的值，等于 0乘以该闭合
路径所穿过的各电流的代数和.
注意
电流 I 正负的规定： I 与 L 成右螺旋
而与环路外电流无关。
3. B为环路上一点的磁感应强度，它与环路内外电流
都有关。
若
B
dl
0
并不一定说明环路上各点的 B 都为 0。
若 B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流，
应用 安培环路定理的应用举例
例1
求载流螺绕环内的磁场
解 （1）对称性分析：环内B 线为同心
B dl B 2r 0 I
B 0 I 1 2r r
I
r LR
r L
分布曲线
B
0 I 2R B r
B 1 r
o
R
r
例4 无限大均匀带电(线密度为i)平面的磁场
解 如图，作安培环路
abcda，应用安培环路 定理
b
l B d l 2a B dl

5
三、磁感应强度
描述磁场性质的基本物理量。 描述磁场性质的基本物理量。 1.磁感应强度的定义 1.磁感应强度的定义
×
q
r v r
× ×
B
当把运动电荷放在磁场中后， 当把运动电荷放在磁场中后， × × × 它会受到一种与其速度有关的力， 它会受到一种与其速度有关的力， × r q 洛仑兹力。 这个力称为洛仑兹力 这个力称为洛仑兹力。 × r× ×v × 当电荷运动速度与磁场方向一 当电荷运动速度与磁场方向一 × B× × × 致时电荷受力为 0 。 当运动电荷速度ቤተ መጻሕፍቲ ባይዱ磁场方向垂直时受到洛伦兹力 fL 最大。 最大。 定义： 定义：磁感应强度
2
r θ Idl
∴ dl = a csc θdθ r = a csc θ
2
2
l o
r
θ1
r dB ⊗ P x
a
µ0 Ia csc θ sin θdθ µ0 I dB = = sin θdθ 2 2 4π a csc θ 4πa µ0 I θ 2 µ0 I (cosθ1 − cosθ 2 ) sin θdθ = B = ∫ dB = ∫θ1 4πa 4πa 10
2
一、磁的基本现象
1.磁铁及其特性 1.磁铁及其特性 人造磁铁： S 人造磁铁： 特性： 特性：
S
I
N
天然磁铁----磁铁矿（Fe3O4） 天然磁铁----磁铁矿（ ----磁铁矿 N
N
I
v F
S N S 能吸引铁、 镍等物质--这种性质叫磁性。 --这种性质叫磁性 1）能吸引铁、钴、镍等物质--这种性质叫磁性。 具有两极且同性相斥，异性相吸。 2）具有两极且同性相斥，异性相吸。 3)目前还无法获得磁单极。 3)目前还无法获得磁单极。 目前还无法获得磁单极

环形电流产生的磁场强度计算公式咱们先来说说环形电流产生的磁场强度计算公式哈。

这环形电流产生磁场强度的计算，那可是物理学中的一个重要知识点。

打个比方，就像你在一个游乐场里坐摩天轮，这个环形电流就像是摩天轮的轨道，而产生的磁场强度就像是你在不同位置感受到的刺激程度。

要计算环形电流产生的磁场强度，咱们得用到一个公式：B = μ₀I /2R 。

这里面的 B 就是磁场强度，μ₀是真空磁导率，是个常数，就像你的生日一样固定不变，I 是环形电流的强度，而 R 则是环形电流的半径。

咱们来具体讲讲这个公式的用法。

比如说，有一个环形电流，电流强度是 5 安培，半径是 2 米。

那咱们就把数字带进公式里算算。

先把真空磁导率μ₀的值带进去，它约等于4π×10⁻⁷特斯拉·米/安培。

然后I 是 5 安培，R 是 2 米，这么一算，就能得出这个环形电流产生的磁场强度啦。

还记得有一次，我给学生们讲这个知识点的时候，有个学生就问我：“老师，这环形电流产生的磁场在生活中有啥用啊？”我当时就想了想，给他举了个例子。

我说：“你看咱们的手机，里面的好多零件运行可都离不开电磁原理，这环形电流产生的磁场知识说不定就在其中发挥着作用呢。

就像手机里的扬声器，声音的产生就和电流以及磁场有关系。

”再说说这个公式的推导过程，那也是有点意思的。

它可不是凭空冒出来的，而是通过一系列的物理实验和理论推导得出的。

这就好比你要搭一座桥，得先准备好材料，设计好结构，然后一步步搭建起来。

学习这个公式的时候，大家可别死记硬背，得理解着来。

多做几道相关的练习题，感受一下不同情况下磁场强度的变化。

比如说，电流增大了，磁场强度怎么变；半径变小了，磁场强度又会怎么变。

其实啊，物理学中的很多知识都是相互关联的。

就像这个环形电流产生的磁场强度计算公式，它和电磁感应、安培力等知识都有着千丝万缕的联系。

当你把这些知识都融会贯通的时候，你就会发现物理学的世界就像一个大拼图，每一块都能完美地拼在一起。

压力对磁感应强度的影响
压力的变化也会对物质的磁性质产生影响。在某些情况下 ，压力的增加可能会增强物质的磁性，而在另一些情况下 则可能会减弱磁性。
化学成分对磁感应强度的影响
不同化学成分的物质具有不同的磁性质。例如，铁、钴、 镍等金属具有铁磁性，而铜、铝等金属则具有抗磁性。因 此，化学成分的差异也会对磁感应强度产生影响。
1. 将电源、导线、 磁感应强度计等器 材按照实验需求进 行搭建和连接。
3. 使用磁感应强度 计测量导线周围的 磁感应强度，并记 录测量数据。
5. 对实验数据进行 整理和分析，得出 磁感应强度与电流 的关系。
数据记录表格模板提供
| 序号 | 电流大小（A） | 磁感 应强度（T） |
| --- | --- | --- |
音响喇叭
音响喇叭中的音圈就是一个电磁 铁，通过音频信号控制电流大小 ，从而驱动音圈振动发出声音。
门锁
一些电子门锁中使用了电磁铁作 为锁舌的驱动机构。当门锁通电 时，电磁铁产生吸力将锁舌吸合
，实现门锁的锁定或解锁。
电磁炉
电磁炉利用电磁感应原理加热食 物。当电磁炉中的线圈通电时， 产生交变磁场，使放置在炉面上 的铁锅产生涡流而发热，从而煮
磁性材料的作用
电磁铁中的铁芯通常采用容易磁化且磁导率高的软磁材料 ，如纯铁、硅钢等。当线圈通电时，铁芯被磁化并大大增 强磁场强度，从而实现电磁铁的吸力作用。
控制电流以调节磁场强度
电磁铁的磁场强度可以通过改变线圈中的电流大小来进行 调节。电流越大，产生的磁场越强，电磁铁的吸力也越大 。
电磁铁在日常生活中的应用举例
熟食物。
工业领域中电磁铁的应用举例
电机与发电机
电机与发电机是电磁铁在工业领域中最广泛的应用之一。电机利用 电磁感应原理将电能转换为机械能，而发电机则将机械能转换为电 能。

高中物理磁感应强度的知识点归纳高中物理磁感应强度的知识点归纳物理学（physics）是研究物质最一般的运动规律和物质基本结构的学科。

作为自然科学的带头学科，物理学研究大至宇宙，小至基本粒子等一切物质最基本的运动形式和规律，因此成为其他各自然科学学科的研究基础。

以下是店铺收集整理的高中物理磁感应强度的知识点归纳，欢迎大家分享。

高中物理磁感应强度的知识点归纳1磁感应强度(magnetic flux density)，描述磁场强弱和方向的物理量，是矢量，常用符号B表示，国际通用单位为特斯拉(符号为T)。

磁感应强度也被称为磁通量密度或磁通密度。

在物理学中磁场的强弱使用磁感应强度来表示，磁感应强度越大表示磁感应越强;磁感应强度越小，表示磁感应越弱。

磁感应强度的定义公式磁感应强度公式B=F/(IL)磁感应强度是由什么决定的?磁感应强度的大小并不是由F、I、L 来决定的，而是由磁极产生体本身的属性。

如果是一块磁铁，那么B的大小之和这块磁铁的大小和磁性强弱有关。

如果是电磁铁，那么B与I、匝数及有无铁芯有关。

很多文章都建议同学们采用类比的方法来理解各个物理量。

我们用电阻R来做个对比。

R的计算公式是R=U/I;可一个导体的电阻R大小并不是由U或者I来决定的。

而是由其导体自身属性决定的，包括电阻率、长度、横截面积。

同样，磁感应强度B也不是由F、I、L来决定的，而是由磁极产生体本身的属性。

如果同学们有时间，可以把静电场中电容的两个公式来对比着复习、巩固下。

B为矢量，方向与磁场方向相同，并不是在该处电流的受力方向，运算时遵循矢量运算法则(左手定则)。

描述磁感应强度的磁感线在磁场中画一些曲线，用(虚线或实线表示)使曲线上任何一点的切线方向都跟这一点的磁场方向相同(且磁感线互不交叉)，这些曲线叫磁感线。

磁感线是闭合曲线。

规定小磁针的北极所指的方向为磁感线的方向。

磁铁周围的磁感线都是从N极出来进入S极，在磁体内部磁感线从S极到N极。

环形电流在空间一点产生的磁场强度摘要：利用毕奥——萨法尔定律通过计算磁场的情况，得到环电流在整个空间的磁场分布表达式，其中运用了数学软件matlab 辅助求解！关键词：环形电流 磁场 矢量叠加 毕奥——萨法尔定律引言：了解书本上环形电流中心轴线上的磁场分布情况后，为了更深入了解环形电流在空间的磁场分布情况，现运用毕奥——萨法尔定律对其求解，再根据矢量叠加原理，将其最终结果在直角坐标系中的三个坐标轴上的分量分离了出来，且验证了空间分布公式在特殊情况下也适用！计算过程;1. 建立坐标系：设环半径为R ，以环心0为原点，环形电流所在平面为x0y 平面，以环中心轴为z 轴建立如图坐标系，则圆环的表达式为：222x y R += 在空间内任意选取一点p(x,y,z)，在环上任取一点11A(x ,y ,0)，则在A 点处的电流元Idl 满足关系式：Idl IR(isin jcos )d βββ=-+ （1）而P,A 两点的矢径为：r (x R c o s )i (y R s i n ββ=-+-+ （2）xz y p(x,y,z)R β 11A(x ,y ,0)将（1）（2）式代入毕奥——萨法尔定律：03Idl rdB 4r μπ⨯= （3）得P 点的磁感应强度为:00332222IR Idl r zi cos z jsin (R x cos ysin )k B d 4r 4(R y z 2yR sin )μμβββββππβ⨯++--==++-⎰⎰（4） 则令：20x 302222IR zi cos B d 4(R y z 2yR sin )πμββπβ=++-⎰20y 302222IR z jsin B d 4(R y z 2yR sin )πμββπβ=++-⎰ （5） 20z 302222IR (R x cos ysin )k B d 4(R y z 2yR sin )πμβββπβ--=++-⎰这就是环形电流在空间产生的磁场在空间的分布分量情况!特别地当p(x,y,z)在环的中心轴线上即z 轴上时，其坐标为p(0,0,z)，代入（5）组式，得到：20x 30222IR zi cos B d 4(R z )πμββπ=+⎰20y 30222IR z jsin B d 4(R z )πμββπ=+⎰20z 30222IR Rk B d 4(R z )πμβπ=+⎰利用matlab 分别输入以下程序并得相应结果：（其中0U 表示0μ，A 表示β）由求解结果显示得到：z 轴上的点磁通分量为：x y 20Z 223/2B 0B 0IR B k 2(R x )μ==-=+当p 在环中心时，其坐标为p(0,0,0)，显然x y 0z B 0B 0I B 2Rμ===综上可知环形电流在空间形成的磁场表达式为:20x 302222IR zi cos B d 4(R y z 2yR sin )πμββπβ=++-⎰20y 302222IR z jsin B d 4(R y z 2yR sin )πμββπβ=++-⎰20z 302222IR (R x cos ysin )k B d 4(R y z 2yR sin )πμβββπβ--=++-⎰这组式子在特殊情况下也成立！。

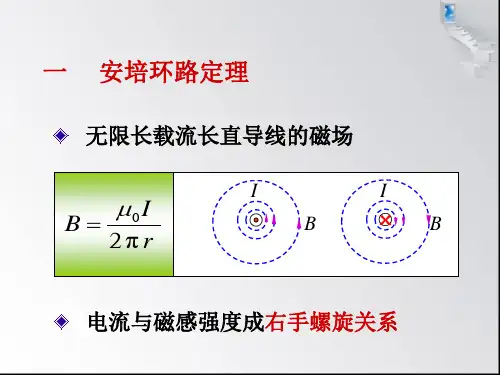
磁 场一、恒定电流的磁场1、直线电流的磁场通有电流强度为I 的无限长直导线，距导线为R 处的磁感应强度为：RIB πμ20=；如下图距通有电流强度为I 的有限长直导线为R 处的P 点的磁感应强度为：)cos (cos 40βαπμ+=RIB ----------------------------------①若P 点在通电直导线的延长线上，则R=0 α=0 β=π 无法直接应用上述式子计算，可进行如下变换lR d d 21)sin(2121=+βα 上式中1d 、2d 分别为P 点到A 、B 的距离，l 为直导线的长度所以：l d d R )sin(21βα+=代入①式得：)sin(cos cos 4210βαβαπμ++=d d Il B令2sin2cos2cos 2sin 22cos2cos2)sin(cos cos βαβαβαβαβαβαβαβα+-=++-+=++=y将α=0 β=π代入上式得0=y所以：在通电直导线的延长线上任意一点的磁感应强度为0=B2、微小电流元产生的磁场微小电流元的磁场，根据直线电流的磁场公式)cos (cos 40βαπμ+=rIB得：Ⅰ若α、β都是锐角，如左图，有：)cos (cos 40βαπμ+=r I B =)sin (sin 4210θθπμ∆+∆rI因1θ∆、2θ∆0→，所以≈∆+∆=)sin (sin 4210θθπμr I B )(4210θθπμ∆+∆rI所以：θπμ∆=rIB 40Ⅱ若α、β中有一个是钝角，如β（右图），则：]sin )[sin(cos 4)cos (cos 400000θθθθπμβαπμ-+∆=+=r Id I B -------------①00000sin sin cos cos sin sin )sin(θθθθθθθθ-∆+∆=-+∆因0→∆θ，所以：0000cos cos sin sin )sin(θθθθθθθ∆≈∆≈-+∆--------------------------------②②式代入①式得：θπμ∆=rIB40总上所述，电流元I 在空间某点产生的磁场为：θπμ∆=rIB 40，式中r 为电流元到该点的距离，θ∆为电流元端点与该点连线张开的角度。

磁场盘州市第七中学王富瑾一、磁场1、磁场是存在于磁体、电流和运动电荷周围的一种物质.永磁体和电流都能在空间产生磁场.变化的电场也能产生磁场。

2、基本特点:磁场对处于其中的磁体、电流和运动电荷有力的作用。

3、安培分子电流假说：安培提出：在原子、分子等物质微粒内部，存在着一种环形电流即分子电流，分子电流使每个物质微粒成为微小的磁体。

若这些微小磁铁排列有序，则该物体有磁性。

二、磁感应强度B1、定义:磁感应强度是表示磁场强弱的物理量，在磁场中垂直于磁场方向的通电导线，受到的磁场力F跟电流I和导线长度L的乘积IL的比值，叫做通电导线所在处的磁感应强度，定义式B=F/IL。

2、单位T（特斯拉），1T=1N/（A·m）。

3、标矢性：矢量。

通过该点的磁感线的切线方向，也是该点小磁针的北极（N）指向。

4、磁场中某位置的磁感应强度的大小及方向是客观存在的（仅取决于磁场本身），与放入的导线电流I的大小、导线的长短L无关，与电流受到的力也无关，即使不放入载流导体，它的磁感应强度也照样存在，因此不能说B与F成正比，或B与IL成反比。

5、若空间中存在多个磁场，则某位置的磁感应强度为各分磁场的磁感应强度的矢量和（平行四边形定则）。

三、磁感线1、在磁场中人为地画出一系列曲线，曲线的切线方向表示该位置的磁场方向，曲线的疏密能定性地表示磁场的弱强，这一系列曲线称为磁感线。

2、磁感线是闭合曲线：磁铁外部从N极出来，进入S极；在磁铁内部，由S极到N极。

3、磁感线永不相交4、磁感线的疏密表示磁场的强弱，即磁感应强度B的大小。

5、磁感线的切线方向即为磁感应强度B的反向，也是小磁针的北极指向（小磁针的北极要转向与磁感线切线一致的方向）6、常见磁场的磁感线的分布:7、地磁场:地球的磁场与条形磁体的磁场相似，其主要特点有三个:（1）地磁场的N极在地球南极附近，S极在地球北极附近。

（2）地磁场B的水平分量（Bx）总是从地球南极指向北极，而竖直分量（By）则南北相反，在南半球垂直地面向上，在北半球垂直地面向下。

判断题：1、电场中某点场强的方向，就是将点电荷放在该点所受电场力的方向。

(×)2、穿过某一个面的电力线条数就是通过该面的电通量。

(√)3、如果通过一个闭合面的电通量为零，则表示在该闭合面内没有净电荷。

(√)4、高斯面处的电场是由面内的电荷产生的，与面外的电荷无关。

(×)5、场强相等的区域，电势也处处相等；场强为零处，电势一定为零。

（×）6、电场力作正功，电势能增加。

（×）7、沿电场线的方向是电势降落的方向。

（√）8、在等势面上移动电荷，电场力不做功。

（√）9、平行板电容器的电容与电容器两极板带的电量成正比。

（×）10、地磁体的磁感应线是从北极发出终止于南极，因此，磁感应线是不闭合的。

(×)11、在稳恒电流产生的磁场中，一条闭合曲线上任意一点的磁感应强度只与穿过该闭合曲线的电流有关。

(×)12、在稳恒电流产生的磁场中，磁感应强度沿任意一条闭合曲线的积分只与穿过该闭合曲线的电流有关。

(√)13、一束电子在运动中发生了偏转，则它一定受到了洛仑兹力的作用。

(×) 14、导体线圈放置在变化的磁场中，则导体线圈一定有感应电流。

（×） 15、感应电流产生的磁场方向总是与原磁场方向相反。

（×） 16、引起动生电动势的非静电力是洛仑兹力。

（√）17、线圈的自感系数与互感系数都与通过线圈的电流无关。

（√）18、由麦克斯韦方程组可以知道变化的电场会产生磁场，同样，变化的磁场也会产生电场。

（√）填空题19、在边长为a 的正方形的四角，依次放置点电荷q 、2q 、4q -、2q ，则它的正中心的电场强度是2052qaπε。

20、有一半径为R 的细圆环, 环上有一微小缺口，缺口宽度为()d d R ，环上均匀带正电, 总电量为q ，如图1所示, 则圆心O 处的电场强度大小E =2308qd R πε ,场强方向为圆心O 点指向缺口的方向。

影响因素
交流电的频率和幅度会影响磁场的强 度和变化速度。频率越高，磁场变化 越快；幅度越大，磁场强度越强。
特殊形状导线（如螺线管）产生磁场方向
安培环路定理
对于长直螺线管，其内部的磁场可以看作是均匀的，且方向平行于螺线管的轴线。根据安培环路定理，可以计算 出螺线管内部的磁感应强度。
右手螺旋定则
对于螺线管产生的磁场方向，可以使用右手螺旋定则来判断。即如果电流沿顺时针方向流动，则磁场方向垂直于 螺线管平面向外；如果电流沿逆时针方向流动，则磁场方向垂直于螺线管平面向内。
环形电流的磁场方向
https://
REPORTING
• 环形电流基本概念 • 磁场方向判断方法 • 不同条件下磁场方向变化规律 • 实验验证与数据分析 • 环形电流在生活和工程应用举例 • 总结与展望
目录
PART 01
环形电流基本概念
REPORTING
WENKU DESIGN
https://
实验技术的改进
随着实验技术的不断进步，未来有望改进实验条件，提高 实验精度和可重复性，为环形电流磁场方向的研究提供更 加可靠的实验依据。
应用领域的拓展
随着科技的不断进步和社会需求的不断增长，未来环形电 流磁场方向有望在更多领域得到应用，推动相关技术的快 速发展。
THANKS
感谢观看
REPORTING
利用安培环路定理可以推导出环形电流的磁场分布，进而 确定磁场方向。
矢量合成法则
当空间中存在多个电流产生的磁场时，某点的磁场方向可以通过矢量合成法则来 确定。即该点的磁场方向是各个电流在该点产生的磁场方向的矢量和。
对于环形电流，可以将其看作由无数个直线电流段组成，每个电流段在空间某点 产生的磁场方向都可以用右手定则确定。然后利用矢量合成法则，将这些磁场方 向进行合成，得到环形电流在该点的总磁场方向。

圆环形电流的磁场分布福建省石狮市石光中学 陈龙法摘 要 本文详细推算出圆环形电流的磁场分布（包括磁标势、磁感应强度），证明了圆电流平面上圆内的磁感应强度为r 的单调增函数，且在圆心处磁感应强度有极小值。

设圆环形电流强度为I ，圆半径为R 0，以圆心为原点，过圆心垂直于圆面的轴为极轴，建立球坐标系。

如图所示。

用半径为R 0的球面把整个空间分成两个区域，在这两个区域内，磁场的标势分别满足拉普拉斯方程012=∇m φ （r<R 0）， 022=∇m φ （r>R 0）由于具有轴对称性，磁标势与方位角φ无关，所以满足边界条件有限−−→−→01r m φ， 有限−−→−∞→r m 2φ的通解可取为： ()θφcos 1n nnn m P ra ∑=（r<R 0） ⑴()θφcos 12nn n nm P rb ∑+=（r>R 0） ⑵ r=R 0的球面上，21m m φφ和满足边值关系：()φααφφe e f f m m r -=-=∇-∇⨯12 ⑶()012=∇-∇•m m r φφe ⑷解上列⑴⑵⑶⑷式得：()()f n n n n nn n n d dP R b d dP R aαθθθθ=-∑∑+-cos cos 2010⑸()()()0cos cos 11010=++∑∑--nnn n n n n nP R na P R b n θθ ⑹其中，面电流密度⎪⎭⎫ ⎝⎛-=20πθδαR I f ，I 是圆环中的电流强度 。

⎪⎭⎫ ⎝⎛-2πθδ可按连带勒让德函数展开：()()()()θθπθδcos !1!1212cos 2n nn n n P n n n P f '+-+==⎪⎭⎫⎝⎛-∑∑ ⑺)又 ()()θθθd dP P n n cos cos -='， ()002='k P ， ()()()()kk k k k P 22122!!1210+-='+ 于是⑸⑹式可化为：()()θθcos cos 100201nn nnn n n n n n P Rna R I P R b R a -+-∑∑-='⎪⎪⎭⎫ ⎝⎛-()()()0cos cos 1102=++∑∑-+nn n n n nn nP R na P Rb n θθ于是得到系数n n b a 和满足的方程：()()0121202010n n n n n P n n n R I R b R a '++-=-+- ⑻ 01120=+++n n n R a n n b ⑼ 解⑻⑼式，当n=2k 时，有：014022=-+k k k R a b 012214022=+++k k k R a k k b 这是关于k k b a 22和的齐次方程组，其系数行列式012211140140≠+-++k k R k kR 所以方程组只有零解，即022==k k b a ⑽当n=2k+1时，有：()()()()21201320122012!!2222341k k k k R IR b R a k k k k k k +++++++-=-022123401212=++++++k k k R a k k b解得：()()()1221201122!!21++++-=k k k k k k R Ia ⑾()()()()()21222012!222!2121k k k k IR b k k kk +++++-= ⑿ 由⑽⑾⑿及⑴⑵式，得到球内外的磁标势：()()()()θφcos 2!!21121212212011+++++∑-=k k k k k km P r k k R I（r<R 0） ⒀()()()()()θφcos 12!22!21122212222012+++++∑+-=k k kk k k m P r k k k IR （r>R 0） ⒁于是球内外的磁感应强度为：()()()()()()⎥⎦⎤⎢⎣⎡++⎪⎪⎭⎫ ⎝⎛-=∇-=+++∑θθθθμφμe e B r 1d dP P k R r k k R I k k kk kk m cos cos 122!!211212201220010 （r<R 0） ⒂ ()()()()()()()⎥⎦⎤⎢⎣⎡-+⎪⎭⎫ ⎝⎛++-=∇-=++++∑θθθθμφμe e B r d dP P k r R k k k R Ik k k k kkm cos cos 222!22!121121232012200202 （r>R 0） ⒃根据⒂⒃式，当2πθ=时，利用()0012=+k P ，()()()kk k k k d dP 22122)!(!121)(cos cos +-=+θθ便得到圆电流平面上圆内和圆外的磁感应强度为：()θμe B 1kk k R r a R Ir 20002∑⎪⎪⎭⎫⎝⎛=（r<R 0） ⒄ ()θβμe B 3200022+∑⎪⎭⎫⎝⎛=k k k r R R Ir (r>R 0) ⒅其中 ()[]()()442!212!12k k k a k k++=， ()[]()()442!222!12k k k k k ++=β 从⒄式知，()01>drr dB ，故圆电流平面上圆内的磁感应强度()r B 1为r 的单调增函数。

安培环路定理在电磁感应中的应用
电磁感应现象：电流通过导体产生磁场 安培环路定理：描述电流与磁场关系的定律 应用实例：电磁铁、变压器、电动机等 安培环路定理在电磁感应中的应用：分析电磁感应现象，解决实际问题
安培环路定理在电路分析中的应用
安培环路定理的定义：描述电流和磁场之间的关系 安培环路定理的应用：用于分析电路中的电流分布和磁场强度 安培环路定理在电路设计中的应用：优化电路设计，提高电路性能 安培环路定理在电磁场理论中的应用：研究电磁场的产生和传播规律
安培环路定ห้องสมุดไป่ตู้在物理教学中的作用
帮助学生理解磁 场与电流的关系
引导学生探索电 磁现象的本质
培养学生运用数 学工具解决物理 问题的能力
激发学生对电磁 学的兴趣和探索 精神
安培环路定理在其他领域的应用
电磁学：解释电磁感应现象，推导出电磁场方程 电路理论：分析电路中的电流分布和磁场强度 电磁波：描述电磁波的传播和能量转换 量子力学：解释电子在磁场中的运动和能级跃迁
感谢您的观看
汇报人：XX
上的电流为I=Idl*L，其中L为闭合曲线的长度
06 推 导 出 安 培 环 路 定 理 的 公 式 ： B = μ 0 / 4 π *
Idl×r/r^3，其中μ0为真空磁导率，r为电流元Idl和 P点之间的距离
安培环路定理的证明方法
假设一个电流元Idl，其磁场为Bdl 考虑一个闭合回路L，其边界为dl 根据安培环路定理，回路L内的电流会产生一个磁场B，其大小与电流Idl成正比 通过积分公式，将Bdl表示为电流Idl的函数，得到安培环路定理的证明方法
环形电流的磁场 对称性：关于环 心对称
环形电流的磁场变 化：随着电流的变 化而变化，具有动 态特性

物理磁场的知识点总结作为自然科学的带头学科，物理学讨论大至宇宙，小至基本粒子等一切物质最基本的运动形式和规律，因此成为其他各自然科学学科的讨论基础。

下面我给大家共享一些物理磁场的学问，盼望能够关心大家，欢迎阅读!物理磁场的学问一、磁场磁极和磁极之间的相互作用是通过磁场发生的。

电流在四周空间产生磁场，小磁针在该磁场中受到力的作用。

磁极和电流之间的相互作用也是通过磁场发生的。

电流和电流之间的相互作用也是通过磁场产生的。

磁场是存在于磁体、电流和运动电荷四周空间的一种特别形态的物质，磁极或电流在自己的四周空间产生磁场，而磁场的基本性质就是对放入其中的磁极或电流有力的作用。

二、磁现象的电本质1.罗兰试验正电荷随绝缘橡胶圆盘高速旋转，发觉小磁针发生偏转，说明运动的电荷产生了磁场，小磁针受到磁场力的作用而发生偏转。

2.安培分子电流假说法国学者安培提出，在原子、分子等物质微粒内部，存在一种环形电流-分子电流，分子电流使每个物质微粒都成为微小的磁体，它的两侧相当于两个磁极。

安培是最早揭示磁现象的电本质的。

一根未被磁化的铁棒，各分子电流的取向是杂乱无章的，它们的磁场相互抵消，对外不显磁性;当铁棒被磁化后各分子电流的取向大致相同，两端对外显示较强的磁性，形成磁极;留意，当磁体受到高温或猛烈敲击会失去磁性。

3.磁现象的电本质运动的电荷(电流)产生磁场，磁场对运动电荷(电流)有磁场力的作用，全部的磁现象都可以归结为运动电荷(电流)通过磁场而发生相互作用。

三、磁场的方向规定：在磁场中任意一点小磁针北极受力的方向亦即小磁针静止时北极所指的方向就是那一点的磁场方向。

四、磁感线1.磁感线的概念：在磁场中画出一系列有方向的曲线，在这些曲线上，每一点切线方向都跟该点磁场方向全都。

2.磁感线的特点：(1)在磁体外部磁感线由N极到S极，在磁体内部磁感线由S极到N极。

(2)磁感线是闭合曲线。

(3)磁感线不相交。

(4)磁感线的疏密程度反映磁场的强弱，磁感线越密的地方磁场越强。

圆环形电流的磁场分布福建省石狮市石光中学陈龙法摘 要本文详细推算岀圆环形电流的磁场分布（包括磁标势、磁感应强度） ，证明了圆电流平面上圆内的磁感应强度为r 的单调增函数，且在圆心处磁感应强度有极小值。

设圆环形电流强度为 I，圆半径为 R 。

，以圆心为原点，过圆心垂直于圆面的轴为极轴，建立球坐 标系。

如图所示。

用半径为 R o的球面把整个空间分成两个区域，在这两个区域内，磁场的标势分别满足拉普拉斯方程▽2°耐=0 (r<R o )，V 2°m2=° (r>R o )r=R o的球面上，' mi 和爲2满足边值关系:「m2 八二1〉fe r 「「m2 一 ' mi = 0解上列⑴⑵⑶⑷式得:P n cos i 亠 一 na n R°14P n cos 二-°n日—一 I ， I 是圆环中的电流强度 '、、2 丿二可按连带勒让德函数展n -1an R°djb n dP n COST萨—f开: 2n 1 n -1!平石比 fnPgep 2 (n +1!P n COS^由于具有轴对称性，磁标势与方位角 0无关，所以满足边界条件的通解可取为：a n r nP n COSTm2有限(r<R o)m2K借巳COSTr(r>R o)(r I )n 1 b n其中，面电流密度R or又P n COSJ「dP d0^，P2k 0 =0，卩2「1 0 = -1k! 2于是⑸⑹式可化为：Z a n R；' -R n^ Pn(cosT )=—占瓦na n R0’Pn(cos日)n i R0 J R0 n、n n12bn P n COST 、、n3n Ro J P n COS^ =0n R°n于是得到系数a n和b n满足的方程：n」b n a n R0 'VI.R0b「丄a n R^— 0n 1解⑻⑼式，当n=2k时，有：b2k -a2k R04k1 =0b2k氏a2kR T "这是关于a2k和b2k的齐次方程组，其系数行列式-R：k12k2k 1所以方程组只有零解，即a2k - b2k - 0当n=2k+1时，有:b2k 1 _ 1 k 1 _I 4k * 3 2k !£k 3一R0 2k 2 22k 1 k!2解得:a2k 1I 2k !R；k1 k!222k1(11)I 2n 12ka2k 1 R0b2k1 菩a2「R4k3-0b ik Ip 2k22k 12k!b 2k 1 - - I IR 02T72(2k+2p 2k41(k!)2由⑽(11)(12)及⑴⑵式，得到球内外的磁标势：于是球内外的磁感应强度为:2kR o k!222ki R o ?k 1P2ki C0"er/ 、2k 书一R o 2k 2k!222ki 7 _2k 2P2ki C妙er根据(15)(16)式，当 时，利用2便得到圆电流平面上圆内和圆外的磁感应强度为:2k 3(r>R o )从7式知，dBi「0 ,故圆电流平面上圆内的磁感应强度 drIB i r 为极小，有B i 0—，这正是用毕奥一萨伐尔定律求出的圆电流中心的磁感应强度。

eρ2 = cos ( <2 - <1) eρ1 + sin ( <2 - <1) e<1 (1) 同理 e<2 = - sin ( <2 - <1) eρ1 + cos ( <2 - <1) e<1 (2) 于是 :
收稿日期 :2004 - 12 - 01 作者简介 :朱平 (1957 —) ,男 ,云南江城人 ,思茅师范高等专科学校成教处副教授 ,主要从事大学物理学教学和科研工作.
关键词 :圆电流 ;磁场分布 ;椭圆积分 中图分类号 :O 441 文献标识码 :A 文章编号 :100020712 (2005) 0920013205
涉及椭圆积分的物理问题 , 分析和求解是困难 的. 因此 ,学者们总是从不同的角度 、采用不同的方 法来研究有关的问题[1～5] . 圆电流的磁场分布是电 磁学中一个重要而典型的椭圆积分问题. 在对这个 问题的研究中 ,文献[6 ]讨论了圆电流平面上圆电流 内部的磁场分布 ;文献[7 ]讨论了圆电流平面上的磁 场分布 ;文献[8 ]利用先求磁势矢再求磁感应强度的 方法讨论了亥姆霍兹的均匀磁场区 ; 文献[9 ]把小环 流与电偶极子进行类比 , 讨论了一些小环流的磁场 特点 ;文献[10 ]讨论了圆电流的磁矢势 ; 文献[11 ]在 直角坐标系中 , 利用圆电流磁场的空间对称性给出 了磁场分布. 本文在柱坐标系中 , 直接从磁场的计算 公式毕奥 - 萨伐尔定律出发 , 运用柱坐标系不同点 间的基矢关系和椭圆积分的理论 , 在更为普遍的情 况下 ,得到了圆电流空间磁场的分布函数. 通过具体 的计算得出圆电流空间磁场分布与方位角无关 , 具 有空间对称性. 并绘制出磁场的空间分布图 , 讨论了 圆电流平面上 、中心轴线以及远区的磁场. 比较系 统 、全面地分析讨论了圆电流的空间磁场分布 , 直观 地展示了圆电流磁场分布的特点 , 致使问题得到了 较好的解决.

安培环路定理求环形电流的磁感应强度公式下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!安培环路定理求环形电流的磁感应强度公式引言安培环路定理是电磁学中的重要定理之一，它描述了通过一个闭合路径的磁场强度等于该路径上电流的总和。