2020年河北中考数学一轮复习课件:§1.2 整式与因式分解
- 格式:pptx
- 大小:755.90 KB
- 文档页数:69



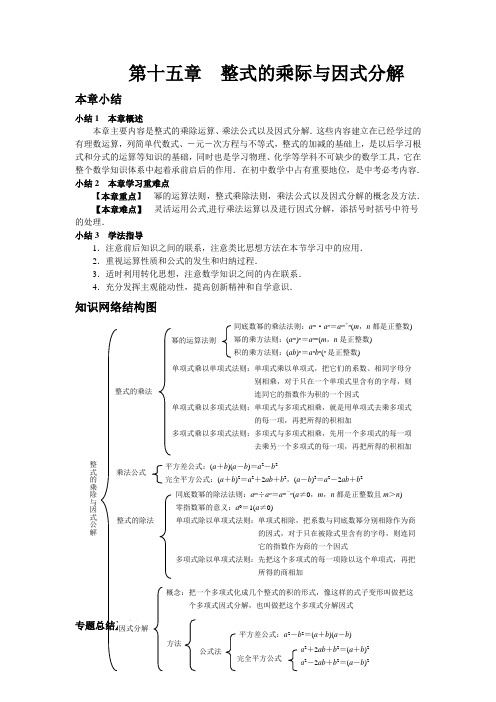
第十五章整式的乘际与因式分解本章小结小结1 本章概述本章主要内容是整式的乘除运算、乘法公式以及因式分解.这些内容建立在已经学过的有理数运算,列简单代数式、-元-次方程与不等式,整式的加减的基础上,是以后学习根式和分式的运算等知识的基础,同时也是学习物理、化学等学科不可缺少的数学工具,它在整个数学知识体系中起着承前启后的作用.在初中数学中占有重要地位,是中考必考内容.小结2 本章学习重难点【本章重点】幂的运算法则,整式乘除法则,乘法公式以及因式分解的概念及方法.【本章难点】灵活运用公式进行乘法运算以及进行因式分解,添括号时括号中符号的处理.小结3 学法指导1.注意前后知识之间的联系,注意类比思想方法在本节学习中的应用.2.重视运算性质和公式的发生和归纳过程.3.适时利用转化思想,注意数学知识之间的内在联系.4.充分发挥主观能动性,提高创新精神和自学意识.知识网络结构图专题1 幂的运算法则及其逆运用 【专题解读】同底数幂的乘法、除法、积的乘方、幂的乘方,它们都是整式运算的基础,作用非常大,在整个代数运算中起着奠基作用,幂的运算法则及其逆运用以及零指数幂都是中考必考内容.例1 计算2x 3·(-3x )2= .分析 本题是积的乘方与单项式乘法的综合运算,紧扣运算法则,即可求出.2x 3·(-3x )2=2x 3·9x 2=18x 5.故填18x 5.例2 计算[a 4(a 4-4a )-(-3a 5)2÷(a 2)3]÷(-2a 2)2. 分析 本题综合考查幂的四种运算法则,以及单项式乘以多项式、多项式除以单项式的法则.解:[a 4(a 4-4a )-(-3a 5)2÷(a 2)3]÷(-2a 2)2 =(a 8-4a 5-9a 10÷a 6)÷4a 4 =(a 8-4a 5-9a 4)÷4a 4 =14a 4-a -49.专题2 整式的混合运算【专题解读】幂的运算与整式的加减乘除混合运算是本章的核心内容,也是整个代数计算的重点.在进行混合运算时要注意:(1)确定运算顺序,先乘方,后乘除,最后加减,有括号先算括号内的或去括号;(2)计算要仔细认真,步步有依据,特别是要注意符号. 例3 计算[(a -2b )(2a -b )-(2a +b )2+(a +b )(a -b )-(3a )2]÷(-2a ). 分析 本题考查整式的混合运算.解:原式=(2a 2-ab -4ab +2b 2-4a 2-4ab -b 2+a 2-b 2-9a 2)÷(-2a ) =(-10a 2-9ab )÷(-2a ) =5a +29b . 【解题策略】本题综合考查了多项式乘以多项式、乘法公式、积的乘方、多项式除以单项式以及合并同类项,在计算的过程中,要注意符号问题及运算法则的应用. 专题3 因式分解 【专题解读】因式分解是整式乘法的逆运算,有两种基本方法:提公因式法和公式法.一般步骤是先提公因式,再用公式,最后检查是否分解彻底. 例4 分解因式.(1)m 3-m ; (2)(x +2)(x +3)+x 2-4.分析 (1)是二项式,提取公因式m 后,可以用平方差公式继续分解.(2)中把x 2-4先分解,然后再与(x +2)(x +3)一起提取公因式. 解:(1)m 3-m =m (m 2-1)=m (m +1)(m -1).(2)(x +2)(x +3)+x 2-4=(x +2)(x +3)+(x +2)(x -2)=(x +2)[(x +3)+(x -2)]=(x +2)(2x +1).【解题策略】 因式分解是十分灵活的题目,选用什么方法要结合题目特点,灵活选用. 二、思想方法专题 专题4 转化思想【专题解读】 转化思想是数学中的重要思想.利用这一思想,可以将复杂化为简单,将未知化为已知.整式的乘除法法则中多次用到转化思想. 例5 分解因式a 2-2ab +b 2-c 2.分析 本题表面上无法直接用提取公因式法或公式法分解.如果添加括号,将代数式进行恒等变形,就可以转化为能用公式法分解的多项式.解:a2-2ab+b2-c2=(a2-2ab+b2)-c2=(a-b)2-c2=(a-b+c)(a-b-c).专题5 整体思想【专题解读】整体思想是数学中常用的数学思想方法,利用此思想方法可以不求出每个字母的值而求出代数式的值,达到简化计算的目的,事半功倍.例6 (1)已知x+y=7,xy=12,求(x-y)2;(2)已知a+b=8,a-b=2,求ab的值.分析此题可充分利用公式的变形,并采取整体代入的方法求值.解:(1)∵x+y=7,∴x2+2xy+y2=49.∴x2+y2=49-2xy=49-2×12=25,(x-y)2=x2-2xy+y2=(x2+y2)-2xy=25-2×12=1.(2)∵a+b=8,∴a2+2ab+b2=64.①∵a-b=2,∴a2-2ab+b2=4.②①-②,得4ab=60,∴ab=15.【解题策略】(1)中把x2+y2以及xy当成了整体.(2)中把ab看做是一个整体.用整体代入法的前提是将已知的代数式和所求的代数式进行恒等变形,将其中的某些代数式化成数字,达到化简、求值的目的.2011中考真题精选1.(2011江苏连云港,3,3分)计算(x+2)2的结果为x2+□x+4,则“□”中的数为()A.-2 B.2 C.-4 D.4考点:完全平方式。


2020年中考数学第一轮复习第一章 数与式第四节 因式分解【基础知识回顾】一、因式分解的定义:1、把一个 式化为几个整式 的形式,叫做把一个多项式因式分解。
2、因式分解与整式乘法是运算,即:多项式 整式的积 【注意:判断一个运算是否是因式分解或判断因式分解是否正确,关键看等号右边是否为 的形式。
】二、因式分解常用方法:1、提公因式法:公因式:一个多项式各项都有的因式叫做这个多项式各项的公因式。
提公因式法分解因式可表示为:ma+mb+mc= 。
【注意:1、公因式的选择可以是单项式,也可以是 ,都遵循一个原则:取系数的 ,相同字母的 。
2、提公因式时,若有一项被全部提出,则括号内该项为 ,不能漏掉。
3、提公因式过程中仍然要注意符号问题,特别是一个多项式首项为负时,一般应先提取负号,注意括号内各项都要 。
】2、运用公式法:将乘法公式反过来对某些具有特殊形式的多项式进行因式分解,这种方法叫做公式法。
①平方差公式:a 2-b 2= ,②完全平方公式:a 2±2ab+b 2= 。
【注意:1、运用公式法进行因式分解要特别掌握两个公式的形式特点,找准里面的a 与b 。
如:x 2-x+14符合完全平方公式形式,而x 2- x+12就不符合该公式的形式。
】 三、因式分解的一般步骤1、 一提:如果多项式的各项有公因式,那么要先 。
2、 二用:如果各项没有公因式,那么可以尝试运用 法来分解。
3、 三查:分解因式必须进行到每一个因式都不能再分解为止。
【注意:分解因式不彻底是因式分解常见错误之一,中考中的因式分解题目一般为两步,做题时要特别注意,另外分解因式的结果是否正确可以用整式乘法来检验】【中考真题考点例析】考点一:因式分解的概念A .a (x-y )=ax-ayB .x +2x+1=x (x+2)+1C .(x+1)(x+3)=x 2+4x+3D .x 3-x=x (x+1)(x-1)考点二:因式分解例2. (2019山东东营)因式分解:x(x-3)-x+3= .对应练习2-1.(2019年济南)分解因式:244m m -+=_____.( ) ( )对应练习2-2.(2019年莱芜)分解因式:a 3﹣4ab 2= .考点三:因式分解的应用例1. 答案:6,1对应练习1-1. 答案:D考点二:因式分解例2. 答案:B对应练习2-1. 答案:2(2)m -对应练习2-2. 答案:a (a+2b )(a ﹣2b )考点三:因式分解的应用例3. 答案:4对应练习3-1. 答案:18【聚焦中考真题】一、选择题:1.(2019年山东临沂)将a 3b -ab 进行因式分解,正确的是( )A .a(a 2b -b)B .ab(a -1)2C .ab(a+1)(a -1)D .ab(a 2-1)2.(2019潍坊)下列因式分解正确的是( )A .3ax 2-6ax=3(ax 2-2ax)B .x 2+y 2=(-x+y)(-x -y)C .a 2+2ab -4b 2=(a+2b)2D .-ax 2+2ax -a=-a(x -1)23.(南昌)下列因式分解正确的是( ) A .x 2-xy+x=x (x -y ) B .a 3-2a 2b+ab 2=a (a -b )2C .x 2-2x+4=(x -1)2+3D .ax 2-9=a (x+3)(x -3)4.(张家界)下列各式中能用完全平方公式进行因式分解的是( )A .x 2+x+1B .x 2+2x-1C .x 2-1D .x 2-6x+95.(佛山)分解因式a 3-a 的结果是( )A .a (a 2-1)B .a (a-1)2C .a (a+1)(a-1)D .(a 2+a )(a-1)6.(恩施州)把x 2y-2y 2x+y 3分解因式正确的是( )A .y (x 2-2xy+y 2)B .x 2y-y 2(2x-y )C .y (x-y )2D .y (x+y )2二、填空题:7.(2019年威海)分解因式:2x 2-2x += .8.(2019年淄博)分解因式:=++x x x 6523 .A .3x -6x=x (3x-6)B .-a +b =(b+a )(b-a )C.4x2-y2=(4x+y)(4x-y)D.4x2-2xy+y2=(2x-y)233.(内江)若m-n=6,且m-n=2,则m+n= .参考答案一、选择题:1-5 CDBDC 6 C二、填空题:6.答案:()221 12x-7.答案:()()32++xxx8.答案:m(x+y)(x-y)9.答案:m(m-5)10.答案:B11.答案:2)2 (-ba12.答案:x(2-x)(2+x)13. 答案:5(x+2)(x -2)14. 答案:m(m+2)(m -2)15. 答案:b(a+2b)(a -2b)17. 答案:-91(3x+1)(3x -1)16. 答案:3(a+2b)(a -2b)17. 答案:2x(x -2)18. 答案:2m(m+2)(m -2)19. 答案:2(a+2b )(a -2b)20. 答案:22)(-x21. 答案:a(b+1)(b -1)22. 答案:(x -1)23. 答案:a(a -2)24. 答案:x(x+y)25. 答案:(a+3)(a -3)26. 答案:x -227. 答案:(x+y)(x -y)28. 答案:(x+3y)(x -3y)29. 答案:a(m+2n)(m -2n)30. 答案:))((22x y x y y x -+ 31. 答案:332. 答案:2433. 答案:x(x+1)(x -1)34. 答案:-31。
第2讲 整式及因式分解命题点1 代数式及其求值1.(2020·河北T12·2分)用一根长为a(单位:cm)的铁丝,首尾相接围成一个正方形,要将它按如图所示的方式向外等距扩1(单位:cm)得到新的正方形,则这根铁丝需增加(B)A .4 cmB .8 cmC .(a +4)cmD .(a +8)cm2.(2013·河北T9·3分)如图,淇淇和嘉嘉做数学游戏:假设嘉嘉抽到牌的点数为x ,淇淇猜中的结果应为y ,则y =(B) A .2 B .3 C .6 D .x +33.(2020·河北T18·3分)若a ,b 互为相反数,则a 2-b 2=0.4.(2012·河北T15·3分)已知y =x -1,则(x -y)2+(y -x)+1的值为1. 5.(2020·河北T18·3分)若mn =m +3,则2mn +3m -5mn +10=1. 命题点2 幂的运算6.(2020·河北T13·2分)若2n +2n +2n +2n=2,则n =(A)A .-1B .-2C .0D.14命题点3 整式的运算及求值7.(2012·河北T2·2分)计算(ab)3的结果是(C)A .ab 3B .a 3bC .a 3b 3D .3ab 8.(2020·河北T2·3分)下列运算正确的是(D)A .(-5)0=0B .x 2+x 3=x 5C .(ab 2)3=a 2b 5D .2a 2·a -1=2a 9.(2011·河北T4·2分)下列运算正确的是(D)A .2x -x =1B .x +x 4=x 5C .(-2x)3=-6x 3D .x 2y ÷y =x 210.(2020·河北T4·3分)下列运算正确的是(D)A .(12)-1=-12B .6×107=6 000 000C .(2a)2=2a 2D .a 3·a 2=a 511.(2020·河北T21·10分)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:(1)求所捂的二次三项式;(2)若x=6+1,求所捂二次三项式的值.解:(1)设所捂的二次三项式为A,根据题意,得A=x2-5x+1+3x=x2-2x+1.(2)当x=6+1时,A=(x-1)2=(6)2=6.12.(2020·河北T20·8分)嘉淇准备完成题目:化简:(x2+6x+8)-(6x+5x2+2).发现系数“”印刷不清楚.(1)他把“”猜成3,请你化简:(3x2+6x+8)-(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“”是几?解:(1)(3x2+6x+8)-(6x+5x2+2)=3x2+6x+8-6x-5x2-2=-2x2+6.(2)设“”是a,则原式=(ax2+6x+8)-(6x+5x2+2)=ax2+6x+8-6x-5x2-2=(a-5)x2+6.∵标准答案的结果是常数,∴a-5=0.解得a=5.13.(2020·河北T22·9分)发现:任意五个连续整数的平方和是5的倍数.验证:(1)(-1)2+02+12+22+32的结果是5的几倍?(2)设五个连续整数的中间一个为n ,写出它们的平方和,并说明是5的倍数.延伸:任意三个连续整数的平方和被3除的余数是几呢?请写出理由.解:验证:(1)∵(-1)2+02+12+22+32=1+0+1+4+9=15=5×3,∴(-1)2+02+12+22+32的结果是5的3倍.(2)由题意,得(n-2)2+(n-1)2+(n+1)2+(n+2)2+n2=5n2+10=5(n2+2).∵n为整数,∴五个连续整数的平方和是5的倍数.延伸:余数是2.理由:设中间的整数为n,则(n-1)2+n2+(n+1)2=3n2+2.∴任意三个连续整数的平方和被3除的余数是2.命题点4 乘法公式的应用14.(2020·河北T4·3分)将9.52变形正确的是(C)A.9.52=92+0.52B.9.52=(10+0.5)(10-0.5)C.9.52=102-2×10×0.5+0.52D.9.52=92+9×0.5+0.52命题点5 因式分解15.(2013·河北T4·2分)下列等式从左到右的变形,属于因式分解的是(D)A .a(x -y)=ax -ayB .x 2+2x +1=x(x +2)+1C .(x +1)(x +3)=x 2+4x +3D .x 3-x =x(x +1)(x -1)16.(2020·河北T3·2分)计算:852-152=(D)A .70B .700C .4 900D .7 000 17.(2011·河北T3·2分)下列分解因式正确的是(D)A .-a +a 3=-a(1+a 2) B .2a -4b +2=2(a -2b)C .a 2-4=(a -2)2D .a 2-2a +1=(a -1)2重难点1 幂的运算根据幂的运算法则,把a 6写成幂的运算形式,并说明依据哪种运算法则.(要求至少写出2种,且每种依据的运算不相同)例如:依据同底数幂的乘法可得,a 6=a 2·a 4.【自主解答】 解:答案不唯一,例如:依据同底数幂的乘法可得,a 6=a 3·a 3=a ·a 5……;依据同底数幂的除法可得,a 6=a 8÷a 2=a 7÷a ……;依据幂的乘方可得,a 6=(a 3)2=(a 2)3;依据单项式乘法可得,a 6=2a ·0.5a 5…….【变式训练1】(2020·保定二模)下列计算正确的是(D)A .a 4÷a 3=1B .a 4+a 3=a 7C .(2a 3)4=8a 12D .a 4·a 3=a 7【变式训练2】(2020·威海)已知5x =3,5y =2,则52x -3y=(D)A.34B .1C.23D.98方法指导我们把加减称为一级运算,乘除称为二级运算,乘方开方称为三级运算.幂的运算法则实质是把幂的运算转化为指数运算,因为指数本身处在高级位置,所以幂的运算转化为指数运算要降一级.如:同底数幂相乘(除)变为指数相加(减),幂的乘方变为指数相乘,积的乘方就是乘方对乘法的分配律,相当于乘法分配律升级. 重难点2 整式的运算(2020·邵阳)先化简,再求值:(a -2b)(a +2b)-(a -2b)2+8b 2,其中a =-2,b =12.【自主解答】解:原式=a 2-4b 2-a 2+4ab -4b 2+8b 2=4ab.当a =-2,b =12时,原式=-4.【变式训练3】【整体思想】若a 2-2a -3=0,代数式a 2·2-a 3的值是(D)A .0B .-a23C .2D .-12【变式训练4】(2020·河北考试说明)若m +n =2,mn =1,则m 2+n 2=2.【变式训练5】 【整体思想】(2020·临沂)已知m +n =mn ,则(m -1)(n -1)=1.方法指导先观察式子的结构特征,确定解题思路,结合数学思想:整体代入、降次、数形结合、逆向思维等,使解题更加方便快捷. 重难点3 因式分解把4a 2添上1项或2项,使它能够进行因式分解.(1)写出3个且要用三种不同的分解方法;(2)若要求能进行2步或2步以上分解,如何添加?请写出一个即可.【自主解答】 解:(1)答案不唯一,例如:4a 2+2a =2a(2a +1);4a 2+4a +1=(2a +1)2;4a 2-1=(2a -1)(2a +1). (2)答案不唯一,例如:①4a 2-4b 2=4(a 2-b 2)=4(a +b)(a -b);②4a 2-a 4=a 2(4-a 2)=a 2(2-a)(2+a);③4a 2-8ab +4b 2=4(a 2-2ab +b 2)=4(a -b)2.【变式训练6】 (2020·唐山乐亭县一模)下列各式由左到右的变形,属于因式分解的是(C)A .a(m +n)=am +anB .a 2-b 2-c 2=(a -b)(a +b)-c 2C .10x 2-5x =5x(2x -1)D .x 2-16+6x =(x +4)(x -4)+6x 【变式训练7】 (2020·河北中考预测)计算(919)2+2×919×89+(89)2的结果正确的是(A)A .100B .10 000C .1 000D .9 900【变式训练8】 (2020·唐山乐亭县七年级期末)2x 3y 2与12x 4y 的公因式是2x 3y .【变式训练9】 (2020·石家庄二模)分解因式:xy 2-2xy +x =x(y -1)2.【变式训练10】 【整体思想】(2020·苏州)若a +b =4,a -b =1,则(a +1)2-(b -1)2的值为12. 易错提示必须分解到每一个多项式都不能再分解为止.1.(2020·荆州)下列代数式中,整式为(A)A .x +1B.1x +1C.x 2+1D.x +1x2.(2020·河北中考预测)若(x +3)(x +n)=x 2+mx -15,则m 等于(A)A .-2B .2C .-5D .53.(2020·河北中考预测)下列各式中,计算结果为a 8的是(C)A .a 4+a 4B .a 4·a -2C .a 10÷a 2D .(-2a 4)24.(2020·包头)如果2xa +1y 与x 2yb -1是同类项,那么ab的值是(A)A.12B.32C .1D .35.(2020·淄博)若单项式am -1b 2与12a 2b n 的和仍是单项式,则n m的值是(C)A .3B .6C .8D .96.(2020·石家庄新华区二模)已知x 2+4mx +16是完全平方式,则m 的值为(C)A .2B .4C .±2D .±47.(2020·齐齐哈尔)我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予3a 实际意义的例子中,不正确的是(D)A .若葡萄的价格是3元/千克,则3a 表示买a 千克葡萄的金额B .若a 表示一个等边三角形的边长,则3a 表示这个等边三角形的周长C .将一个小木块放在水平桌面上,若3表示小木块与桌面的接触面积,a 表示桌面受到的压强,则3a 表示小木块对桌面的压力D .若3和a 分别表示一个两位数中的十位数字和个位数字,则3a 表示这个两位数8.(2020·青岛)计算(a 2)3-5a 3·a 3的结果是(C)A .a 5-5a 6B .a 6-5a 9C .-4a 6D .4a 69.【整体思想】(2020·邢台一模)若m -x =2,n +y =3,则(m -n)-(x +y)=(A)A .-1B .1C .5D .-510.(2020·河北考试说明)计算:552-152=(D)A .40B .1 600C .2 400D .2 80011.(2020·重庆)按如图所示的运算程序,能使输出的结果为12的是(C)A .x =3,y =3B .x =-4,y =-2C .x =2,y =4D .x =4,y =212.(2020·枣庄)如图,将边长为3a 的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长为2b 的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为(A)A .3a +2bB .3a +4bC .6a +2bD .6a +4b13.(2020·株洲)单项式5mn 2的次数为3.14.分解因式:m 3-9mn 2=m(m -3n)(m +3n).15.(2020·张家口一模)已知多项式A =(x +1)2-(x 2-4y).(1)化简多项式A ;(2)若x +2y =1,求A 的值.解:(1)A =(x +1)2-(x 2-4y)=x 2+2x +1-x 2+4y =2x +4y +1. (2)∵x +2y =1,由(1),得A =2x +4y +1=2(x +2y)+1, ∴A =2×1+1=3.16.(2020·唐山乐亭县七年级期末)下列说法:①(-2)101+(-2)100=-2100;②2 0182+2 018一定可以被2 019整除;③16.9×18+15.1×18能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的有(A)A .4个B .3个C .2个D .1个17.(2020·河北中考预测)若a 2-3ab =-5,b 2+ab =14,则a -b 的值为3或-3.18.(2020·河北中考预测)如图,已知大正方形的边长为a +b +c ,利用图形的面积关系可得:(a +b +c)2=a 2+b 2+c 2+2ab +2bc +2ac.当大正方形的边长为a +b +c +d 时,利用图形的面积关系可得:(a +b +c +d)2=a 2+b 2+c 2+d 2+2ab +2ac +2ad +2bc +2bd +2cd.一般地,n 个数的和的平方等于这n 个数的平方和加上它们两两乘积的2倍.根据以上结论解决下列问题:(1)若a +b +c =6,a 2+b 2+c 2=14,则ab +bc +ac =11;(2)从-4,-2,-1,3,5这五个数中任取两个数相乘,再把所有的积相加,若和为m ,求m 的值.解:∵-4-2-1+3+5=1,∴两边平方后得(-4-2-1+3+5)2=(-4)2+(-2)2+(-1)2+32+52+2m=55+2m=1.∴m=(1-55)÷2=-54÷2=-27.19.(2020·保定一模)若3×9m×27m=321,则m的值为(B)A.3 B.4 C.5 D.620.(2020·张家口一模)若x+3y=0,则2x·8y=1.21.(2020·河北模拟)在一次数学课上,李老师对大家说:“你任意想一个非零数,然后按下列步骤操作,我会直接说出你运算的最后结果.”(1)若小明同学心里想的是数5,请帮他计算出最后结果;(2)老师说:“同学们,无论你们心里想的是什么非零数,按照以上步骤进行操作,得到的最后结果都相等.”小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程.解:(1)第一步:(5+1)2-(5-1)2=20;第二步:20×25=500;第三步:500÷5=100.∴小明计算出最后结果为100.(2)∵[(a+1)2-(a-1)2]×25÷a=(a+1+a-1)(a+1-a+1)×25÷a=4a×25÷a=100,∴结论成立.。