当前位置：文档之家 › 误差的基本性质与处理

误差的基本性质与处理

  • 格式：pdf
  • 大小：194.84 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

误差理论与大数据处理实验报告材料

误差理论与大数据处理实验报告材料

标准文档误差理论与数据处理实验报告姓名：黄大洲学号：3111002350班级：11级计测1班指导老师：陈益民实验一 误差的基本性质与处理一、实验目的了解误差的基本性质以及处理方法二、实验原理（1）算术平均值对某一量进行一系列等精度测量，由于存在随机误差，其测得值皆不相同，应以全部测得值的算术平均值作为最后的测量结果。

1、算术平均值的意义：在系列测量中，被测量所得的值的代数和除以n 而得的值成为算术平均值。

设 1l ，2l ，…,n l 为n 次测量所得的值，则算术平均值121...nin i l l l l x n n=++==∑算术平均值与真值最为接近，由概率论大数定律可知，若测量次数无限增加，则算术平均值x 必然趋近于真值0L 。

i v = i l -xi l ——第i 个测量值，i =1,2,...,;n i v ——i l 的残余误差（简称残差）2、算术平均值的计算校核算术平均值及其残余误差的计算是否正确，可用求得的残余误差代数和性质来校核。

残余误差代数和为：11n niii i v l nx ===-∑∑当x 为未经凑整的准确数时，则有：1nii v==∑01）残余误差代数和应符合：当1n ii l =∑=nx ，求得的x 为非凑整的准确数时，1nii v =∑为零；当1nii l =∑>nx ，求得的x 为凑整的非准确数时，1nii v =∑为正；其大小为求x 时的余数。

当1n ii l =∑<nx ，求得的x 为凑整的非准确数时，1nii v =∑为负；其大小为求x 时的亏数。

2）残余误差代数和绝对值应符合： 当n 为偶数时，1ni i v =∑≤2n A; 当n 为奇数时，1nii v =∑≤0.52n A ⎛⎫- ⎪⎝⎭ 式中A 为实际求得的算术平均值x 末位数的一个单位。

（2）测量的标准差测量的标准偏差称为标准差，也可以称之为均方根误差。

1、测量列中单次测量的标准差2222121...nini nnδδδδσ=+++==∑式中 n —测量次数（应充分大）i δ —测得值与被测量值的真值之差211nii vn σ==-∑2、测量列算术平均值的标准差：x nσσ=三、实验内容：1．对某一轴径等精度测量8次，得到下表数据，求测量结果。

第2章 误差的基本性质与处理

第2章 误差的基本性质与处理

第二节 系统误差
二、系统误差的分类和特征
系统误差的特征是在同一条件下，多次测 量同一测量值时，误差的绝对值和符号保 持不变，或者在条件改变时，误差按一定 的规律变化。由系统误差的特征可知，在 多次重复测量同一值时，系统误差不具有 抵偿性，它是固定的或服从一定函数规律 的误差。从广义上讲，系统误差是指服从 某一确定规律变化的误差。
征
第二节 系统误差
（一）不变系统误差
固定系统误差是指在整个测量过程中，误差 的大小和符号始终是不变的。
如千分尺或测长仪读数装置的调零误差，量 块或其它标准件尺寸的偏差等，均为不变系 统误差。它对每一测量值的影响均为一个常 量，属于最常见的一类系统误差。
第二节 系统误差
i 1
j k 1
i 1
jK 1
i 1
jK 1
测量次数足够多时,
K
n
vi ' v j ' 0
i 1
j k 1
K
n
K
n
所以得： vi v j (li x) (l j x)
i 1
jK 1
i 1
j K 1
若Δ显著不为O，则有理由认为测量列存在线性系统误差。 这种校核法又称“马列科夫准则” 。
② 周期变化的系统误差 在整个测量 过程中，系统误差随某因素周期变化。
例如，仪表指针的回转中心与刻度盘中心有一
个偏心量 e ，则指针在任一转角 处引起的
读数误差为 L e。 s此in误 差变化规律符合正
弦曲线规律，当指针在 0 和 180 时误差为 零，而在 90 和 270 时误差绝对值达最大。
在此情况下，可用统计准则进行判断.若
n1
u vivi1 v1v2 v2v3 vn1vn 2 n 1 i 1

误差理论与数据处理第二章1.ppt

误差理论与数据处理第二章1.ppt

i 1
i 1
1
n
n
i
i 1
1 n
n i 1
li
L0
L0
1 n
n i 1
li
1 n
n
i
i 1
x
1 n
n
i
i 1
BEIJING UNIVERSITY OF TECHNOLOGY
北京工业大学机电学院
8/75
说明：
(1) n=1, δ1= x-L0=l1-L0即为随机误差定义
(2)
n=2，1
2
均值 x 定义为：
x
l1 l2 n
ln
1 n
n
li
i 1
BEIJING UNIVERSITY OF TECHNOLOGY
北京工业大学机电学院
7/75
3 x 与 L0之关系
对n个 i 求和，有
1 2 n l1 l2 ln nL0
=> 同除以n
n
n
i li nL0
BEIJING UNIVERSITY OF TECHNOLOGY
北京工业大学机电学院
6/75
(一) 算术平均值
1 随机误差的表示方法
设被测量真值L0(理想、理论)，一系列测量 值为l0，则测量值中随机误差δi为
i li L0 (i=1,2,3…，n) 2 算术平均值定义
设 l1,l2, ,ln 为n次测量所得结果，则算术平
1
2
x
L0
(3) n→∞时，由随机误差的特征(抵偿性)
有 x L0
1
n
n
i
i 1
0
即：如能对同一量测无限次时，就可得到不受随

《误差理论与数据处理》习题2及解答

《误差理论与数据处理》习题2及解答
试写出测量结果。③若手头无该仪器测量的标准差值的资料，试由②中 10 次重复测量的 测量值，写出上述①、②的测量结果。 【解】① 单次测量的极限误差以 3σ计算，δlimx=3σ=3×0.5=1.5(μm)=0.0015 (mm) 所以测量结果可表示为：26.2025±0.0015
(mm)
② 重复测量 10 次，计算其算术平均值为： x = 26.2025(mm). 取与①相同的置信度，则测量结果为：26.2025±3σ= 26.2025±0.0015 (mm). ③ 若无该仪器测量的标准差资料，则依 10 次重复测量数据计算标准差和表示测量结 果。选参考值 x0 = 26.202，计算差值 ∆x i = x i − 26.202 、 ∆ x 0 和残差ν i 等列于表中。 序 1 2 3 4 5 6 7 8 9 10 号
∑ν
i =1
i
n( n − 1)
= 1.253
0.0008 5× 4
= 0.000224 （mm）
σx =
σ
n
=
0.000255 5
= 0.000114 ； σ x =
'
σ'
n
=
0.000224 5
= 0.0001
⑤求单次测量的极限误差和算术平均值的极限误差 因假设测量值服从正态分布，并且置信概率 P=2Φ(t)=99%，则Φ(t)=0.495，查附录
∆ x0 = 1 10 ∑ ∆xi = 0.0005 10 i =1
νi
0 +0.0003 +0.0003 0 +0.0001 -0.0003 -0.0002 0 +0.0001 -0.0003
ν i2
0 9×10 9×10 0 1×10

误差理论及数据处理第二章-误差的基本性质与处理

误差理论及数据处理第二章-误差的基本性质与处理

第二章 误差的基本性质与处理2-1．试述标准差 、平均误差和或然误差的几何意义。

答：从几何学的角度出发，标准差可以理解为一个从 N 维空间的一个点到一条直线的距离的函数；从几何学的角度出发，平均误差可以理解为 N 条线段的平均长度； 2-2．试述单次测量的标准差 和算术平均值的标准差 ，两者物理意义及实际用途有何不同。

【解】单次测量的标准差σ表征同一被测量n 次测量的测量值分散性的参数，可作为测量列中单次测量不可靠性的评定标准。

2n δσ++=算术平均值的标准差xσ-是表征同一被测量各个独立列算术平均值分散性的参数，可作为算术平均值不可靠性的评定标准xσ-=在n ，当测量次数n 愈大时,算术平均值愈接近被测量的真值，测量精度也愈高。

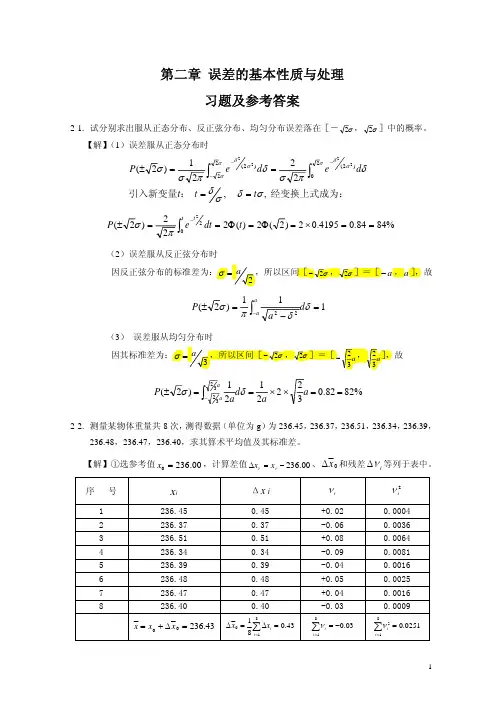
2-3试分析求服从正态分布、反正弦分布、均匀分布误差落在中的概率 【解】（1）误差服从正态分布时2222(2)(2)()P ed ed δδσσδδ--==引入新变量t:,t tδσδσ==,经变换上式成为： 22()2()20.41950.8484%t t P edt t -==Φ=⨯==⎰（2）误差服从反正弦分布时因反正弦分布的标准差为：σ=，所以区间[],,a a ⎡⎤=-⎣⎦,故:1()1aaP δπ+-==⎰（3） 误差服从均匀分布时因其标准差为：σ=,⎡⎤⎡⎤=⎢⎥⎣⎦⎣⎦，故111()20.8282%22P d a a δπ==⨯==⎰2-4．测量某物体重量共8次，测的数据(单位为g)为236.45，236.37，236.51，236.34，236.39，236.48，236.47，236.40，是求算术平均值以及标准差。

0.05(0.03)0.11(0.06)(0.01)0.080.070236.48236.43x +-++-+-+++=+=0.0599σ=0.0212x σ==2-5用別捷尔斯法、极差法和最大误差法计算2-4，并比较2-6测量某电路电流共5次，测得数据（单位为mA ）为168.41，168.54，168.59，168.40，168.50。

误差的基本性质与处理

误差的基本性质与处理
f ( ) d( ) 若误差区间为 [ , ]
1 0
f ( )
P[ ] 2(t )
2

得区间[ t , t ] 内的概率 P 2( t )
P

置信系数 置信概率 t 显著度 1 P 1 2( t )
14
四．不等精度测量的数据处理
为了得到更精确的测量结果或对比结果 而变更测量条件 不等精度测量 ① 测量次数
2.
3.
4.
系统误差的特殊性；
对系统误差的研究可以发现一些新事物。
19
定义： 在重复性条件下，对同一被测量进行 无限多次测量所得结果的平均值与被测量 的真值之差。 特征： 在同一测量条件下，多次测量同一量时， 误差的绝对值和符号保持恒定；或在条件改 变时，按某一确定的规律变化的误差。 产生原因： 测量装置的因素 测量方法的因素 测量环境的因素 测量人员的因素
Ⅱ：19.9990，20.0006，19.9995，20.0015，19.9994
均为 x 20.0000
标准差：

1 2 ... n
2 2
2
n


i 1
n
2 i
n
7
的物理意义:
大，数据分散，随机误差大，重复性差。
f ( )
小，小误差占优，数据集中，重复性好。
vi vi
使算术平均值增加或减小，对残差没 影响，只是引起误差分布曲线位置的平移， 而不影响分布曲线的形状。
23
2.
变值系统误差的影响 a. 对算术平均值的影响
x x
b. 对残差的影响
vi vi i
特点：1、具有确定规律性：测量过程中误差的大 小和符号固定不变，或按照确定的规律变化。 2、产生在测量开始之前：影响系统误差的因素在 测量开始之前就已经确定。 3、与测量次数无关：增加测量次数不能减小系统 误差对测量结果的影响。

《误差理论与数据处理(第6版)》费业泰 较全答案

《误差理论与数据处理》第一章 绪论1-1．研究误差的意义是什么简述误差理论的主要内容。

答： 研究误差的意义为：(1)正确认识误差的性质，分析误差产生的原因，以消除或减小误差； (2)正确处理测量和实验数据，合理计算所得结果，以便在一定条件下得到更接近于真值的数据；(3)正确组织实验过程，合理设计仪器或选用仪器和测量方法，以便在最经济条件下，得到理想的结果。

误差理论的主要内容：误差定义、误差来源及误差分类等。

1-2．试述测量误差的定义及分类，不同种类误差的特点是什么 答：测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质，可分为系统误差、随机误差、粗大误差。

！ 系统误差的特点是在所处测量条件下，误差的绝对值和符号保持恒定，或遵循一定的规律变化（大小和符号都按一定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定方式变化；粗大误差的特点是可取性。

1-3．试述误差的绝对值和绝对误差有何异同，并举例说明。

答：(1)误差的绝对值都是正数，只是说实际尺寸和标准尺寸差别的大小数量，不反映是“大了”还是“小了”，只是差别量；绝对误差即可能是正值也可能是负值，指的是实际尺寸和标准尺寸的差值。

+多少表明大了多少，-多少表示小了多少。

(2)就测量而言,前者是指系统的误差未定但标准值确定的，后者是指系统本身标准值未定1－5 测得某三角块的三个角度之和为180o 00’02”,试求测量的绝对误差和相对误差 解：绝对误差等于： @相对误差等于：1-6．在万能测长仪上，测量某一被测件的长度为 50mm ，已知其最大绝对21802000180''=-'''o o %000031.010*********.00648002066018021802≈=''''''⨯⨯''=''＝o误差为 1μm ，试问该被测件的真实长度为多少解： 绝对误差＝测得值－真值，即： △L ＝L －L 0 已知：L ＝50，△L ＝1μm ＝，测件的真实长度Ｌ0＝L －△L ＝50－＝（mm ） 1-7．用二等标准活塞压力计测量某压力得 ，该压力用更准确的办法测得为，问二等标准活塞压力计测量值的误差为多少解：在实际检定中，常把高一等级精度的仪器所测得的量值当作实际值。

误差的基本性质与处理解析

f ( ) 1
2
e
2 2 2
第一节 随机误差
第二章 误差的基本性质与处理
f ()
不同形状的分布曲线所 表征的含义是不同的。曲线 越陡，随机误差的分布就越 集中，表明测量精度就越高。

2 2 e 2
根据 可得
f ( )
1

2
f max
1

2
由此可知，当σ↑， f↓ max 曲线就平坦，随机误差的 分布就分散，测量精度低。
第一节 随机误差
2、或然误差ρ 将整个测量列的 n 个随机 误差分为个数相等的两半。 其中一半随机误差的数值落 在-ρ ~ +ρ范围内，而另一半 落在-ρ ~ +ρ范围以外。
第二章 误差的基本性质与处理
f ( ) d 0.5


2 0.6745 3
第一节 随机误差
第一节 随机误差
3、标准差的其它算法 (1) 别捷尔斯法
由
第二章 误差的基本性质与处理
v
2 i
n1


n
2 i
n n 2 i vi i vi n1 n1
1 n
将②式两边平方得 当n充分大时，
0 因此有
i 1 j 1 i j
n 1 n
x2 ③2 i
1 n
2
将①式平方后再相加， i 2 vi 2 n x 2
④
第一节 随机误差
③、④联立消去 x 2
x2
1 n2
2
第二章 误差的基本性质与处理
1 1 D ( x ) 2 nD ( l ) D ( l ) n n

第二章《误差理论与数据处理》

2 2 12 2 ...... n

n

i2
i 1
n
n
实际上真值一般情况下是 未知，在有限次测量下，用残 余误差代替随机误差可得到标 准差的估计值：
ˆ
v
i 1
n
2 i
n 1
该证明如下：
（一）构建残余误差与随机误差之间的关系：
i li L0
x

n
结论
在n次测量的等精度测量中，算术平均值 1 n 的标准差是单次测量标准差 n ， ， x 。但 也不是n越大越好，因为 n 要出较大的劳动， 而且 难保证测量条件的恒定，从而引入新 n 的误差。一般情况下去n=10为宜。
标准差的计算还有别捷尔斯法，极差法， 最大误差法等。
（4）别捷尔斯（Peters）法
1.253
v
i 1 n
ห้องสมุดไป่ตู้
n
i
n n 1
x 1.253
v
i 1
i
n
n 1
（4）极差法
等精度多次测量被测值 x1 ,x2 ,x3 ,......,xn 服从正态分布，在其中选取最大值 xmax 与最小 值 xmin，则两者之差称为极差：n xmax xmin 标准差的无偏估计： n
n1 n2
x1
i 1
1i
n1
n1
, x2
n2
i 1
2i
n2
,..., xm
m
l
i 1
nm
mi
nm
x ( l1i l2i ... lmi ) / ni
i 1 i 1 i 1 i 1

误差的基本性质与处理

误差的基本性质与处理第1章绪论1-1 研究误差的意义是什么？简述误差理论的主要内容。

答：研究误差的意义（1）正确认识误差的性质，分析误差产⽣的原因，以消除或减⼩误差。

（2）正确处理测量和实验数据，合理计算所得结果，以便在⼀定条件下得到更接近于真值的数据。

（3）正确组织实验过程，合理设计仪器或选⽤仪器和测量⽅法，以便在最经济的条件下，得到理想的结果。

误差理论的主要内容：（1）讨论形成误差的原因；（2）各类误差的特征及处理⽅法；（3）对测量结果进⾏评定。

1-2 试述测量误差的定义及分类，不同种类误差的特点是什么？答1：测量误差的定义：误差＝测得值－真值。

测量误差的分类：随机误差、系统误差和粗⼤误差。

各类误差的特点：（1）随机误差：服从统计规律，具有对称性、单峰性、有界性和抵偿性；（2）系统误差：不服从统计规律，表现为固定⼤⼩和符号，或者按⼀定规律变化；（3）粗⼤误差：误差值较⼤，明显地歪曲测量结果。

答2：测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质，可分为系统误差、随机误差、粗⼤误差。

系统误差的特点是在所处测量条件下，误差的绝对值和符号保持恒定，或遵循⼀定的规律变化（⼤⼩和符号都按⼀定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定⽅式变化；粗⼤误差的特点是可取性。

1-3 试述误差的绝对值与绝对误差有何异同，并举例说明。

答1：相同点：都是测量值与真值之差。

不同点：误差的绝对值都是正值，⽽绝对误差有正、有负，反映了测得值与真值的差异。

例：某长度的绝对误差为－0.05mm，⽽该误差的绝对值为|－0.05|mm＝0.05mm。

答2：(1)误差的绝对值都是正数，只是说实际尺⼨和标准尺⼨差别的⼤⼩数量，不反映是“⼤了”还是“⼩了”，只是差别量；绝对误差即可能是正值也可能是负值，指的是实际尺⼨和标准尺⼨的差值。

+多少表明⼤了多少，-多少表⽰⼩了多少。

(2)就测量⽽⾔,前者是指系统的误差未定但标准值确定的，后者是指系统本⾝标准值未定。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 1 1
α1 = 34D54′ +
2′ × 7 + 1′ × 2 = 34D55′36′′ 7 +1+ 2
υ1 = 24′′,υ2 = −96′′,υ3 = −36′′
∑ pυ
2 i i
= 7 × ( 24′′ ) + 1× ( −96′′ ) + 2 × ( −36′′ )
2 2 2
2
= 15840 × ( '')
例3 αi 34º56′ 对某一角度值，分两个测回进行测量，其权等于测量次数，测得值如下， 第一测回 pi 7 αi 34º55′40〞 34º55′30〞 34º55′20〞 34º54′ 1 34º55′0〞 第二测回 pi 3 2 1 1
34º55′70〞 34º55′10〞 34º55′ 2 34º55′50〞 试求该角度的最可信赖值及其标准差？ 解：第一测回的加权平均值及标准差
υ1 = 7′′,υ2 = −3′′,υ3 = −13′′,υ4 = −33′′, υ5 = −37′′,υ6 = −23′′,υ7 = −17′′ σ2 = σα =
2
∑ pυ ∑p
: 1
2
2
2 i i
m −1
i
=
3610 2 ( '') = 24.53′′ 7 −1
α2
= 7.76′′
两个测回的权比
x(1) = 10.0003, x( 2) = 10.0004, ⋅⋅⋅, x( 9) = 10.0007, x(10) = 10.001
今有两测得值 x(1) , x(10 ) 可怀疑，但由于
x − x(1) = 10.00055 − 10.0003 = 0.00025 x(10) − x = 10.001 − 10.00055 = 0.00045
或
σα = σα
2
p1 250 = 7.76′′ = 7.5′′ p1 + p2 269
例4 在万能测长仪上测量某校对量具。 重复测量 8 次， 测得值 （单位 mm） 为 150.0015， 150.0017，150.0016，150.0014，150.0013，150.0015，150.0016，150.0014。试分别以 99.73% 和 95%的概率确定测量结果 解：列表计算如下：
= −0.0005mm
加权算术平均值的标准差为
σL =
= =
最终测量结果为
∑ pυ ( m − 1) ∑ p
2 i 2
i 2 2
4 × ( 25 ) + 1× ( 35 ) + 25 × ( −5 ) ( 3 − 1)( 4 + 1 + 25) 4350 = 0.0009mm 60
L0 = L ± 3σ L = 1000.0020 ± 0.0027 mm
σ1 = σα =
1
∑ pυ ∑ pi
α1
2 i i
m −1
=
15840 ( '') = 88.99′′ 3 −1
= 28.14′′
第二测回的加权平均值及标准差
α 2 = 34D54′ +
= 34D55′33′′
40′′ × 3 + 30′′ × 2 + 20′′ × 1 + 70′′ × 1 + 10′′ × 1 + 50′′ × 1 3 + 2 +1+1+1+1+1
γ 0 (10, 0.05 ) = 0.477 γ 11 = 0.5 > γ 0 (10, 0.05 ) = 0.477
故表中第 9 个测得值含有粗大误差，应予剔除。 再判别最小值 x(1) ，计算统计量
γ 11
= 10.0003 − 10.0004 = 0.25 10.0003 − 10.0007
各组相应的残余误差为
υ1 = L1 − L = (1000.0045 − 1000.0020 ) mm
= +0.0025mm
υ2 = L2 − L = (1000.0055 − 1000.0020 ) mm
= +0.0035mm
υ3 = L3 − L = (1000.0015 − 1000.0020 ) mm
2
150.0015
-0.2 -0.1 0 +0.1 -0.1 0
x = ∑ xi / n = 1200.0120 / 8 = 150.0015mm
1
σ=
∑υ / ( n − 1) =
2 i 1
n
0.12 μ m ≈ 0.13μ m 8 −1
因测量次数 n 较小，应按 t 分布。 置信概率为 99.73%时， 置信概率为 95%时， 查 t 分布表得 则算术平均值的极限误差为
序号 1 2 3 4 5 6 7 8 9 10 n=10
xi μm
+0.5 +0.7 +0.4 +0.5 +0.3 +0.6 +0.5 +0.6 +1.0 +0.4
υi μm
-0.05 +0.15 -0.15 -0.05 -0.25 +0.05 -0.05 +0.05 +0.45 -0.15
υi2 μ m2
γ 11 =
则
x(1) − x(2) x(1) − x( n −1)
γ 11 = 0.25＜ γ 0 (10,0.05) = 0.477
L1 = 1000.0045mm, σ L1 = 0.5μ m L2 = 1000.0055mm, σ L2 = 1.0μ m L3 = 1000.0015mm, σ L3 = 0.2μ m
试求其最终测量结果。 解：已知各组标准差，即可确定各组的权：
p1 : p2 : p3 = = 1
σ
2 L1
:
x′ = 10.0005 σ ′ = 0.12
q(1) =
查表得
x′ − x(1)
σ′
=
10.0005 − 10.0003 ≈ 1.67 0.00012
q0 ( 9, 0.05 ) = 2.11
q(1) = 1.67 < q0 ( 9, 0.05 ) = 2.11
故可判别 γ 11 = 0.5 > γ 0 (10, 0.05 ) = 0.477 不含有粗大误差， 而各 q( i ) 皆小于 2.11， 故可认为 其余测得值也不含有粗大误差。 3） 按狄克松准则，将测得值从小到大顺序排列得
υi = xi − x (数据见上表)
（3） 求标准差
σ 10 =
∑υ
2 i
n −1
=
0.345 0.345 μm = μ m ≈ 0.2μ m 10 − 1 9
（4） 判断有无粗大误差 1）按罗曼诺夫斯基准则，首先怀疑第 9 各测得值含有粗大误差，将其剔除，根 据剩下的 9 个测得值计算算术平均值及标准差，得
1
σ
2
2 L2
:
1
2 σL
3
1
( 0.5) (1.0 ) ( 0.2 )
2
:
1
:
1
2
= 4 :1: 25
加权算术平均值为
q(1) =
x′ − x(1)
σ′
=
10.0005 − 10.0003 ≈ 1.67 0.00012
4 × 0.0030 + 1× 0.0040 ⎞ ⎛ L = ⎜1000.0015 + ⎟ mm 4 + 1 + 25 ⎝ ⎠ = 1000.0020mm
第二章
误差的基本性质与处理
例 题
例1 测量小轴直径共 10 次，得到一系列等精度测得值如下（单位 mm） ：25.0360， 25.0365，25.0362，25.0364，25.0367，25.0363，25.0366，25.0363，25.0366，25.0364。若 已排除了系统误差的影响和剔除了粗大误差， 试求其算术平均值及标准差， 并写出测量结果。 解： 列表计算如下： 序号 1 2 3 4 5 6 7 8 9 10 n=10 Di/mm 25.0360 25.0365 05.0362 25.0364 25.0367 25.0363 25.0366 25.0363 25.0366 25.0364 Vi / μ m -0.4 +0.1 -0.2 0 +0.3 -0.1 +0.2 -0.1 +0.2 0 Vi2/μm 0.16 0.01 0.04 0 0.09 0.01 0.04 0.01 0.04 0
xi / mm
1 2 3 4 5 6 7 8 ∑ 150.0015 150.0017 150.0016 150.0014 150.0013 150.0015 150.0016 150.0014 1200.0120mm
n
x / mm
υi / μ m
0 +0.2 +0.1
υi2 / μ m 2
0 0.04 0.01 0.04 0.01 0 0.01 0.01 0.12 μ m
p1 : p2 =
最可信赖值
1
2
1
σα σα
=
1
2
( 28.14′′ ) ( 7.76′′)
:
1
2
= 19 : 250
α = 34D55′′ + σα = σα
1
36′′ × 19 + 33′′ × 250 = 34D55′33.2′′ 19 + 250 p1 19 = 28.14′′ = 7.5′′ p1 + p2 269
2