第2章 误差的基本性质与处理

《误差理论与数据处理》第一章绪论1-1．研究误差的意义是什么？简述误差理论的主要内容。

答：研究误差的意义为：(1)正确认识误差的性质，分析误差产生的原因，以消除或减小误差；(2)正确处理测量和实验数据，合理计算所得结果，以便在一定条件下得到更接近于真值的数据；(3)正确组织实验过程，合理设计仪器或选用仪器和测量方法，以便在最经济条件下，得到理想的结果。

误差理论的主要内容：误差定义、误差来源及误差分类等。

1-2．试述测量误差的定义及分类，不同种类误差的特点是什么？答：测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质，可分为系统误差、随机误差、粗大误差。

系统误差的特点是在所处测量条件下，误差的绝对值和符号保持恒定，或遵循一定的规律变化（大小和符号都按一定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定方式变化；粗大误差的特点是可取性。

1-3．试述误差的绝对值和绝对误差有何异同，并举例说明。

答：(1)误差的绝对值都是正数，只是说实际尺寸和标准尺寸差别的大小数量，不反映是“大了”还是“小了”，只是差别量；绝对误差即可能是正值也可能是负值，指的是实际尺寸和标准尺寸的差值。

+多少表明大了多少，-多少表示小了多少。

(2)就测量而言,前者是指系统的误差未定但标准值确定的，后者是指系统本身标准值未定1－5 测得某三角块的三个角度之和为180o00’02”,试求测量的绝对误差和相对误差解：绝对误差等于：相对误差等于：1-6．在万能测长仪上，测量某一被测件的长度为 50mm，已知其最大绝对误差为 1μm，试问该被测件的真实长度为多少？解：绝对误差＝测得值－真值，即：△L＝L－L0已知：L＝50，△L＝1μm＝0.001mm，测件的真实长度Ｌ0＝L－△L＝50－0.001＝49.999（mm）1-7．用二等标准活塞压力计测量某压力得 100.2Pa，该压力用更准确的办法测得为100.5Pa，问二等标准活塞压力计测量值的误差为多少？解：在实际检定中，常把高一等级精度的仪器所测得的量值当作实际值。

误差理论与数据处理》习题及参考答案（第七版）第一章绪论1 — 5测得某三角块的三个角度之和为180°00' 02” ,试求测量的绝对误差1-8在测量某一长度时，读数值为 2.31m ，其最大绝对误差为 20 m ，试求其最大相对误差。

8.66 10-4%1-10检定2.5级（即引用误差为 2.5%）的全量程为100V 的电压表，发现 50V 刻度点的示值误差 2V 为最大误差，问该电压表是否合格？I 1 I 2 所以L 2=80mm 方法测量精度高。

1 — 13多级弹导火箭的射程为 10000km 时，其射击偏离预定点不超过0.1km ，优秀射手能在距离 50m 远处准确地射中直径为 2 cm 的靶心，试评述哪一个射和相对误差 解： 绝对误差等于: 相对误差等于: 180°00 02 180o 2222 180o 180 60 60 6480000.00000308641 0.000031%相对误差max绝对误差max测得值 100%20 10-62.31 100%最大引用误差某量程最大示值误差测量范围上限100%2100100% 2% 2.5%该电压表合格 1-12用两种方法分别测量L1=50mm L2=80mm 测得值各为50.004mm,80.006mm 。

试评定两种方法测量精度的高低。

相对误差 L 1：50mmI 150.004 50 50 100% 80.006 8080100% 0.008% 0.0075%击精度高? 解：多级火箭的相对误差为： ----------------------------0 10.00001 0.001% 10000射手的相对误差为：1cm°.°1m 0.0002 0.002% 50m 50m多级火箭的射击精度高。

1-14若用两种测量方法测量某零件的长度L1=110mm 其测量误差分别为11 m和9 m ;而用第三种测量方法测量另一零件的长度L2=150mm其测量误差为 12 m ，试比较三种测量方法精度的高低。

《误差理论与数据处理》(第七版)习题及参考答案第一章绪论1－5测得某三角块的三个角度之和为180o00’02”,试求测量的绝对误差和相对误差解：绝对误差等于： 180 o 00 02o 1802 相对误差等于： 2 o180180 2 60 60 ＝26480000.000003086410.000031%1-8在测量某一长度时，读数值为2.31m ，其最大绝对误差为20m ，试求 其最大相对误差。

相对误差max绝对误差 测得值 max 100%-6 20 102.31100%8.66 -4 10%1-10检定2.5级（即引用误差为2.5%）的全量程为100V 的电压表，发现 50V 刻度点的示值误差2V 为最大误差，问该电压表是否合格？ 最大引用误差某量程最大示值误差 测量范围上限100%2 100100%2%2.5%该电压表合格1-12用两种方法分别测量L1=50mm ，L2=80mm 。

测得值各为50.004mm ，80.6mm 。

试评定两种方法测量精度的高低。

相对误差50.450L 1:50mmI100%0.008%15080.680L2:80mmI100%0.0075%280I 1I 所以L 2=80mm 方法测量精度高。

21－13多级弹导火箭的射程为10000km时，其射击偏离预定点不超过0.lkm，优秀射手能在距离50m远处准确地射中直径为2cm的靶心，试评述哪一个射击精度高?解：多级火箭的相对误差为：0.12.320.001%10000射手的相对误差为：1cm0.01m8.6700020.002%50m50m多级火箭的射击精度高。

1-14若用两种测量方法测量某零件的长度L1=110mm，其测量误差分别为11和9m；而用第三种测量方法测量另一零件的长度L2=150mm。

m其测量误差为12m，试比较三种测量方法精度的高低。

相对误差I 11m1mm11080.7%I 9m2mm11050.50082%I 12m3mm15080.708%I3II第三种方法的测量精度最高21第二章误差的基本性质与处理2-6测量某电路电流共5次，测得数据（单位为mA）为168.41，168.54，1.，168.40，168.50。

第二章 误差的基本性质与处理2-1．试述标准差 、平均误差和或然误差的几何意义。

答：从几何学的角度出发，标准差可以理解为一个从 N 维空间的一个点到一条直线的距离的函数；从几何学的角度出发，平均误差可以理解为 N 条线段的平均长度； 2-2．试述单次测量的标准差 和算术平均值的标准差 ，两者物理意义及实际用途有何不同。

【解】单次测量的标准差σ表征同一被测量n 次测量的测量值分散性的参数，可作为测量列中单次测量不可靠性的评定标准。

2n δσ++=算术平均值的标准差xσ-是表征同一被测量各个独立列算术平均值分散性的参数，可作为算术平均值不可靠性的评定标准xσ-=在n ，当测量次数n 愈大时,算术平均值愈接近被测量的真值，测量精度也愈高。

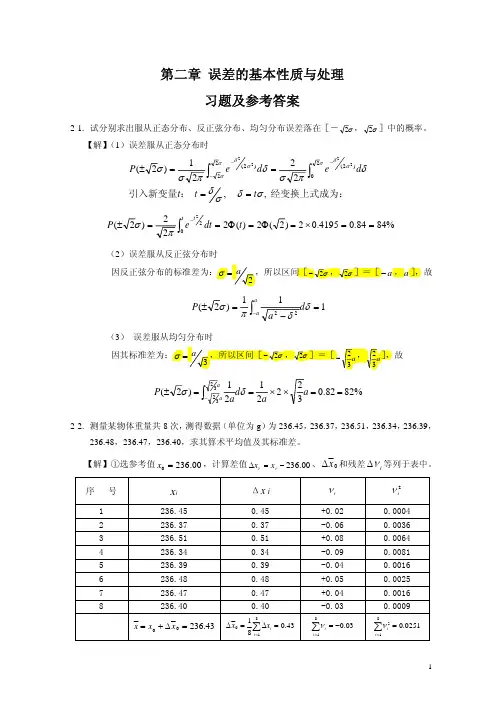
2-3试分析求服从正态分布、反正弦分布、均匀分布误差落在中的概率 【解】（1）误差服从正态分布时2222(2)(2)()P ed ed δδσσδδ--==引入新变量t:,t tδσδσ==,经变换上式成为： 22()2()20.41950.8484%t t P edt t -==Φ=⨯==⎰（2）误差服从反正弦分布时因反正弦分布的标准差为：σ=，所以区间[],,a a ⎡⎤=-⎣⎦,故:1()1aaP δπ+-==⎰（3） 误差服从均匀分布时因其标准差为：σ=,⎡⎤⎡⎤=⎢⎥⎣⎦⎣⎦，故111()20.8282%22P d a a δπ==⨯==⎰2-4．测量某物体重量共8次，测的数据(单位为g)为236.45，236.37，236.51，236.34，236.39，236.48，236.47，236.40，是求算术平均值以及标准差。

0.05(0.03)0.11(0.06)(0.01)0.080.070236.48236.43x +-++-+-+++=+=0.0599σ=0.0212x σ==2-5用別捷尔斯法、极差法和最大误差法计算2-4，并比较2-6测量某电路电流共5次，测得数据（单位为mA ）为168.41，168.54，168.59，168.40，168.50。

1、随机误差产生的原因（装环人）2、随机误差具有统计规律性对称性：绝对值相等的正误差和负误差出现的次数相等。

单峰性：绝对值小的误差比绝对值大的误差出现的次数多有界性：在一定的测量条件下，随机误差的绝对值不会超过一定界限。

抵偿性：随着测量次数的增加，随机误差的算术平均值趋向于零。

3、算术平均值非X=X1+X2+...+XiVi(残余误差)=Xi-非X4、标准差（1）单次测量的标准差（δi）标准差=根号下（δi平方和/n）标准差的估计值=根号下（Vi平方和/n-1）（贝塞尔公式）评定单次测量不可靠的参数或然误差p=2/3标准差的估计值平均误差θ=4/5标准差的估计值（2）算术平均值的标准差标准差非x=标准差/根号下n或然误差R=2/3算术平均值标准差非x平均误差T=4/5标准差非x5、极差法Wn=Xmax-Xmino=Wn/dn6、最大误差法真值可代替o=|δi|/Kn真值未知o=|Vi|/Kn'7、权的确定方法:按测量的次数确定权8、单位权化的实质是使任何一个量值乘以自身权数的平方根，得到新的量值权数为1。

9、系统误差产生的原因（装环方人）10、系统误差的特征（服从某一确定规律变化的误差）不变的系统误差线性变化的系统误差周期性变化的系统误差复杂规律变化的系统误差11、系统误差的发现方法实验对比法残余误差观察法残余误差校核法不同公式计算标准差比较法计算数据比较法秩和检验法t检验法12、系统误差的减小和消除（1）从产生误差的根源上消除系统误差（2）用修正方法消除系统误差（3）不变系统误差消除法（代替法抵消法交换法）（4）线性系统误差消除法（对称法）（5）周期性系统误差消除法（半周期法）13、粗大误差产生的原因测量人员的主观原因客观外界条件的原因14、防止与消除粗大误差的方法（1）设法从测量结果中发现和鉴别而加以剔除（2）加强测量者的工作责任心和以严格的科学态度对待测量工作（3）保证测量条件的稳定（4）采用不等精度测量方法（5）互相之间进行校核的方法15、判别粗大误差的准则3o准则（莱以特准则）罗曼诺夫斯基准则格罗布斯准则狄克松准则计算题测量某电路电流共5次，测得数据（单位位mA）为168.41 168.54 168.59 168.40 168.50 试求算术平均值及标准差或然误差和平均误差。

《误差理论与数据处理》(第七版)习题及参考答案第一章绪论1－5 测得某三角块的三个角度之和为 180o00’02”,试求测量的绝对误差和相对误差解：绝对误差等于：180o00'02 '-180o= 2 '相对误差等于：2 '180o =2 '＝180 ⨯ 60 ⨯ 60 '2 '648000 '= 0.00000308641 ≈ 0.000031%1-8 在测量某一长度时，读数值为 2.31m，其最大绝对误差为 20m，试求其最大相对误差。

相对误差max =绝对误差max⨯100% 测得值=20 ⨯10-6⨯2.31100%= 8.66 ⨯10-4%1-10 检定2.5 级（即引用误差为 2.5%）的全量程为 100V 的电压表，发现 50V 刻度点的示值误差 2V 为最大误差，问该电压表是否合格？最大引用误差=某量程最大示值误差⨯100% 测量范围上限=2100⨯100% = 2% < 2.5%该电压表合格1-12 用两种方法分别测量 L1=50mm，L2=80mm。

测得值各为 50.004mm，80.006mm。

试评定两种方法测量精度的高低。

相对误差L1:50mm L2:80mm I1 =I 2 =50.004 -505080.006 -8080⨯100% = 0.008%⨯100% = 0.0075%I 1 >I2所以L2=80mm 方法测量精度高。

1－13 多级弹导火箭的射程为 10000km 时，其射击偏离预定点不超过 0.lkm，优秀射手能在距离 50m 远处准确地射中直径为 2cm 的靶心，试评述哪一个射击精度高?解：多级火箭的相对误差为：0.110000= 0.00001 = 0.001% 射手的相对误差为：1cm 50m =0.01m50m= 0.0002 = 0.002%多级火箭的射击精度高。

1-14 若用两种测量方法测量某零件的长度 L1=110mm，其测量误差分别为±11m和±9m ；而用第三种测量方法测量另一零件的长度 L2=150mm。

《误差理论与数据处理》(第七版)习题及参考答案第一章 绪论1－5 测得某三角块的三个角度之和为180o00'02”,试求测量的绝对误差和相对误差 解：绝对误差等于： 相对误差等于:1-8在测量某一长度时，读数值为2。

31m,其最大绝对误差为20m μ,试求其最大相对误差。

%108.66 %1002.311020 100%maxmax 4-6-⨯=⨯⨯=⨯=测得值绝对误差相对误差1-10检定2。

5级（即引用误差为2.5%)的全量程为100V 的电压表，发现50V 刻度点的示值误差2V 为最大误差，问该电压表是否合格？%5.22%100%1002100%<=⨯=⨯=测量范围上限某量程最大示值误差最大引用误差该电压表合格1-12用两种方法分别测量L1=50mm,L2=80mm 。

测得值各为50.004mm ，80。

006mm 。

试评定两种方法测量精度的高低。

相对误差L 1:50mm 0.008%100%5050004.501=⨯-=IL 2:80mm 0.0075%100%8080006.802=⨯-=I 21I I > 所以L 2=80mm 方法测量精度高。

1－13 多级弹导火箭的射程为10000km 时，其射击偏离预定点不超过0.lkm,优秀射手能在距离50m 远处准确地射中直径为2cm 的靶心，试评述哪一个射21802000180''=-'''o o %000031.010*********.00648002066018021802≈=''''''⨯⨯''=''＝o击精度高？ 解：射手的相对误差为：多级火箭的射击精度高。

1—14若用两种测量方法测量某零件的长度L1=110mm ，其测量误差分别为m μ11±和m μ9±；而用第三种测量方法测量另一零件的长度L2=150mm.其测量误差为m μ12±，试比较三种测量方法精度的高低。

误差的基本性质与处理第1章绪论1-1 研究误差的意义是什么？简述误差理论的主要内容。

答：研究误差的意义（1）正确认识误差的性质，分析误差产⽣的原因，以消除或减⼩误差。

（2）正确处理测量和实验数据，合理计算所得结果，以便在⼀定条件下得到更接近于真值的数据。

（3）正确组织实验过程，合理设计仪器或选⽤仪器和测量⽅法，以便在最经济的条件下，得到理想的结果。

误差理论的主要内容：（1）讨论形成误差的原因；（2）各类误差的特征及处理⽅法；（3）对测量结果进⾏评定。

1-2 试述测量误差的定义及分类，不同种类误差的特点是什么？答1：测量误差的定义：误差＝测得值－真值。

测量误差的分类：随机误差、系统误差和粗⼤误差。

各类误差的特点：（1）随机误差：服从统计规律，具有对称性、单峰性、有界性和抵偿性；（2）系统误差：不服从统计规律，表现为固定⼤⼩和符号，或者按⼀定规律变化；（3）粗⼤误差：误差值较⼤，明显地歪曲测量结果。

答2：测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质，可分为系统误差、随机误差、粗⼤误差。

系统误差的特点是在所处测量条件下，误差的绝对值和符号保持恒定，或遵循⼀定的规律变化（⼤⼩和符号都按⼀定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定⽅式变化；粗⼤误差的特点是可取性。

1-3 试述误差的绝对值与绝对误差有何异同，并举例说明。

答1：相同点：都是测量值与真值之差。

不同点：误差的绝对值都是正值，⽽绝对误差有正、有负，反映了测得值与真值的差异。

例：某长度的绝对误差为－0.05mm，⽽该误差的绝对值为|－0.05|mm＝0.05mm。

答2：(1)误差的绝对值都是正数，只是说实际尺⼨和标准尺⼨差别的⼤⼩数量，不反映是“⼤了”还是“⼩了”，只是差别量；绝对误差即可能是正值也可能是负值，指的是实际尺⼨和标准尺⼨的差值。

+多少表明⼤了多少，-多少表⽰⼩了多少。

(2)就测量⽽⾔,前者是指系统的误差未定但标准值确定的，后者是指系统本⾝标准值未定。

第二章误差的基本性质与处理第一节随机误差一.随机误差的产生原因1)测量装置方面的因素2)环境方面的因素3)人员方面的因素二.正态分布若测量列中不包含系统误差和粗大误差，则该测量列中的随机误差一般具有以下几个特征：1)绝对值相等的正误差与负误差出现的次数相等，这称为误差的对称性。

2)绝对值小的误差比绝对值大的误差出现次数多，这称为误差的单峰性。

3)在一定测量条件下，随机误差的绝对值不会超过一定界限，这称为误差的有界性。

4)随着测量次数的增加，随机误差的算术平均值趋向于零，这称为误差的抵偿性。

服从正态分布的随机误差均具有以上4个特征。

，则测量列中的随机误差δi为设被测量的真值为Lδi=Ll0-（2--1）正态分布的分布密度f(δ)与分布函数F(δ)为f(δ)=e)2/(2221σδπσ- (2--2)δπσδδσδd eF ⎰∞--=)2/(2221)( (2--3)式中，δ为标准差（或称均方根误差）；e 为自然对数的底，其值为2.7182~~ 它的数学期望为⎰∞∞-==0)(δδδd f E(2--4)它的方差为 δδδσd f )(22⎰∞∞-= (2--5)其平均误差为 σσδδδθ547979.0)(≈==⎰∞∞-d f (2--6) 此外由21)(=⎰-δδd f pp可得或然误差为 p=0.6745σ≈σ32(2--7)三.算术平均值（一）算术平均值的意义设为n 次测量所得的值，则算术平均值为nlnl l l l x ni in ∑==++++=1321...... （2-8）一般情况下，被测量的真值为未知。

可用算术平均值，代替被测量的真值进行计算，则有 x l v i i -= （2-9），式中，为第i 个测得值，i =1,2，.... ，n ；i v 为i l 的残余误差（简称残差）。

任选一个接近所有测得值的数0l 作为参考值，计算出的每个测得值i l 与0l 的差值0l l l i i -=∆ i=1,2,......,n 因nlx ni i∑==1nlx ni i∑=∆=∆1则 x l x ∆+=0 （2--10） （二）算术平均值的计算校核根据式（2-9）求得的残余误差，其代数和为 x n l vni i ni i-=∑∑==11式中的算术平均值是根据（2-8）计算的，当求得的为未经凑整的准确数时，则有∑==ni i v 10 （2--11） 残余误差代数和为零是用来校核算术平均值及其残余误差计算的正确性。

《误差理论与数据处理》第一章 绪论1—1．研究误差的意义是什么?简述误差理论的主要内容.答： 研究误差的意义为：（1）正确认识误差的性质,分析误差产生的原因，以消除或减小误差;(2）正确处理测量和实验数据,合理计算所得结果,以便在一定条件下得到更接近于真值的数据；（3）正确组织实验过程,合理设计仪器或选用仪器和测量方法，以便在最经济条件下,得到理想的结果。

误差理论的主要内容:误差定义、误差来源及误差分类等. 1-2．试述测量误差的定义及分类,不同种类误差的特点是什么？答：测量误差就是测的值与被测量的真值之间的差；按照误差的特点和性质，可分为系统误差、随机误差、粗大误差。

系统误差的特点是在所处测量条件下,误差的绝对值和符号保持恒定,或遵循一定的规律变化（大小和符号都按一定规律变化）；随机误差的特点是在所处测量条件下，误差的绝对值和符号以不可预定方式变化； 粗大误差的特点是可取性。

1—3．试述误差的绝对值和绝对误差有何异同,并举例说明。

答：（1）误差的绝对值都是正数,只是说实际尺寸和标准尺寸差别的大小数量，不反映是“大了”还是“小了"，只是差别量;绝对误差即可能是正值也可能是负值，指的是实际尺寸和标准尺寸的差值。

+多少表明大了多少，-多少表示小了多少. （2）就测量而言,前者是指系统的误差未定但标准值确定的，后者是指系统本身标准值未定1－5 测得某三角块的三个角度之和为180o00’02”，试求测量的绝对误差和相对误差 解：绝对误差等于： 相对误差等于:1—6．在万能测长仪上，测量某一被测件的长度为 50mm ，已知其最大绝对误差为 1μm ，试问该被测件的真实长度为多少？解: 绝对误差＝测得值－真值，即: △L ＝L －L 0 已知:L ＝50，△L ＝1μm ＝0。

001mm ，测件的真实长度Ｌ0＝L －△L ＝50－0。

001＝49.999(mm ）1—7．用二等标准活塞压力计测量某压力得 100.2Pa ，该压力用更准确的办法测得为100。