七年级数学应用题专题---行程问题
- 格式:doc
- 大小:36.50 KB
- 文档页数:3

七年级数学方程应用题一、行程问题1. 例题:甲、乙两人从相距36千米的两地相向而行。
如果甲比乙先走2小时,那么他们在乙出发后2.5小时相遇;如果乙比甲先走2小时,那么他们在甲出发后3小时相遇。
甲、乙两人每小时各走多少千米?解析:设甲每小时走公式千米,乙每小时走公式千米。
根据“甲比乙先走2小时,他们在乙出发后2.5小时相遇”,可得到方程公式,即公式。
根据“乙比甲先走2小时,他们在甲出发后3小时相遇”,可得到方程公式,即公式。
将第一个方程公式两边同时乘以2,得到公式。
用公式减去公式,即公式,得到公式,解得公式。
把公式代入公式,得到公式,公式,公式,解得公式。
2. 练习:A、B两地相距20千米,甲从A地向B地前进,同时乙从B地向A地前进,2小时后二人在途中相遇,相遇后,甲返回A地,乙仍向A地前进,甲回到A地时,乙离A地还有2千米,求甲、乙二人的速度。
解析:设甲的速度为公式千米/小时,乙的速度为公式千米/小时。
根据“A、B两地相距20千米,2小时后二人在途中相遇”,可得方程公式,化简为公式。
甲返回A地仍用2小时,这2小时乙走了公式千米,可得方程公式,化简为公式。
将公式与公式相加,公式,得到公式,解得公式。
把公式代入公式,得公式,解得公式。
二、工程问题1. 例题:一项工程,甲单独做需要10天完成,乙单独做需要15天完成,两人合作4天后,剩下的部分由乙单独做,还需要几天完成?解析:设总工程为单位“1”,甲的工作效率为公式,乙的工作效率为公式。
两人合作4天的工作量为公式先计算括号内的值:公式。
那么公式。
剩下的工作量为公式。
乙单独完成剩下部分需要的时间为公式根据除法运算法则,公式(天)。
2. 练习:某工程,甲工程队单独做40天完成,若乙工程队单独做30天后,甲、乙两工程队再合作20天完成。
(1)求乙工程队单独做需要多少天完成?(2)将工程分两部分,甲做其中一部分用了x天,乙做另一部分用了y天,其中x、y均为正整数,且公式,求x、y的值。


行程问题无论怎么变化,都离不开“三个量,三个关系”:这三个量是:路程(s)、速度(v)、时间(t)三个关系:简单行程:路程=速度×时间相遇问题:路程和=速度和×时间追击问题:路程差=速度差×时间流水问题:顺水行程=(船速+水速)×顺水时间逆水行程=(船速-水速)×逆水时间顺水速度=船速+水速逆水速度=船速-水速静水速度=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2甲、乙两人分别从相距100 米的 A 、B 两地出发,相向而行,其中甲的速度是 2 米每秒,乙的速度是 3 米每秒。
一只狗从 A 地出发,先以 6 米每秒的速度奔向乙,碰到乙后再掉头冲向甲,碰到甲之后再跑向乙,如此反复,直到甲、乙两人相遇。
问在此过程中狗一共跑了多少米?1.甲、已两个车站相距168千米,一列慢车从甲站开出,速度为36千米/小时,一列快车从乙站开出,速度为48千米/小时。
(1)两列火车同时开出,相向而行,多少小时相遇?(2)慢车先开1小时,相向而行,快车开几小时与慢车相遇?2.甲、乙两人从同地出发前往某地。
甲步行,每小时走4公里,甲走了16公里后,乙骑自行车以每小时12公里的速度追赶甲,问乙出发后,几小时能追上甲?3.甲、乙两人练习50米短距离赛跑,甲每秒钟跑7米,乙每秒钟跑6.5米。
(1)几秒后,甲在乙前面2米?(2)如果甲让乙先跑4米,几秒可追上乙?4甲、乙两人在400米的环行形跑道上练习跑步,甲每秒跑5.5米,乙每秒跑4.5米。
a)乙先跑10米,甲再和乙同地、同向出发,还要多长时间首次相遇?b)乙先跑10米,甲再和乙同地,背向出发,还要多长时间首次相遇?c)甲、乙同时同地同向出发,经过多长时间二人首次相遇?d)甲先跑10米,乙再和甲同地、同向出发,还要多长时间首次相遇?5、一艘船在两个码头之间航行,水流速度是3千米每小时,顺水航行需要2小时,逆水航行需要3小时,求两码头的之间的距离?6、甲、乙两人在一条长400米的环形跑道上跑步,如果同向跑,每隔133分钟相遇一次,,如果反向跑,则每隔40秒相遇一次,已知甲比乙跑的快,求甲、乙两人的速度?7、甲、乙两人骑自行车,同时从相距65千米两地相向而行,甲的速度为17.5千米每小时,乙的速度为15千米每小时,经过了几小时两人相距32.5千米?1、甲乙两辆汽车同时从东西两地相向开出,甲车每小时行56千米,乙车每小时行48千米。

行程问题九大题型初中公式
在解决行程问题时,初中阶段主要涉及到的公式主要包括以下九大题型:
1. 相遇问题:
公式:总路程 = (甲速度 + 乙速度) × 相遇时间
2. 追及问题:
公式:追及时间 = 追及路程 / (快速 - 慢速)
公式:追及路程 = (快速 - 慢速) × 追及时间
3. 环形跑道上的相遇与追及:
公式:外圈路程 - 内圈路程 = 快者速度× 时间 - 慢者速度× 时间
4. 行程问题中的正反比例关系:
公式:路程一定,速度与时间成反比
5. 航行问题:
公式:顺水速度 = 静水速度 + 水流速度
公式:逆水速度 = 静水速度 - 水流速度
6. 火车过桥问题:
公式:车长 + 桥长 = 火车速度× 火车过桥时间
7. 流水问题:
公式:船速的(1 - 水速/船速)× 时间 = (顺水路程 / 顺水时间)× 时间
8. 行程问题中的比例关系:
公式:路程一定时,时间和速度成反比
9. 行程问题中的线性关系:
公式:速度一定时,路程和时间成正比
在解决具体问题时,需要根据问题的具体情况选择合适的公式进行计算。
同时,理解和掌握这些公式的含义和应用方法,对于提高解决实际问题的能力非常重要。

《一元一次方程:行程问题》解答题【基本知识】路程=速度×时间 时间=路程÷速度 速度=路程÷时间(1)相遇问题: 快行距+慢行距=原距(2)追及问题: 快行距-慢行距=原距(3)航行问题:顺水(风)速度=静水(风)速度+水流(风)速度逆水(风)速度=静水(风)速度-水流(风)速度抓住两码头间距离不变,水流速和船速(静不速)不变的特点考虑相等关系.行程问题:解行程问题的关键是抓住时间关系或路程关系,借助草图分析来解决问题.路程=速度×时间相遇路程=速度和×相遇时间追及路程=速度差×追及时间航行问题:顺水(风)速度=静水(风)速度+水流(风)速度逆水(风)速度=静水(风)速度-水流(风)速度水流速度=(顺水速度-逆水速度)÷2一、【求距离】1、七年级列队以每小时6千米的速度去甲地,小刚从队尾以每小时10千米的速度赶到队伍的排头后,又以同样的速度返回排尾,一共用了7.5分钟,求队伍的长。
【解】设队伍长度x 千米 ,等量:时间81164=+x x 52=∴x 答:略 2、队伍以每小时4千米的速度去甲地,小刚从队尾以每小时12千米的速度赶到队伍的排头后,又以同样的速度返回排尾,一共用了4.5分钟,求队伍的长。
【解】605.4168=+x x x = 0.4千米 3、队伍以每小时6千米的速度去甲地,小刚从队尾以每小时12千米的速度赶到队伍的排头后,又以同样的速度返回排尾,一共用了5分钟,求队伍的长。
【解】605186=+x x x = 0.375千米 4、一队学生从学校出发去部队军训,以每小时5千米的速度行进4.5千米时,一名通讯员以每小时14千米的速度从学校出发追赶队伍,他在离部队6千米处追上了队伍,设学校到部队的距离是x 千米,求x . 【解】565.4146--=-x x ∴ 13=x 5、已知某铁路桥长500m ,现在一列火车匀速通过该桥,火车从开始上桥到过完桥共用了30s ,整列火车完全在桥上的时间为20s ,则火车的长度为多少m ?【解】设火车的长度为x m ,根据火车的速度不变可得方程:2050030500x x -=+ 2(500+x )=3(500﹣x ) x =100. 答:火车的长度为100m .6、王先生计划骑车以每小时10千米的速度由A 地到B 地,这样便可在规定时间到达B 地,但他因事将原计划的出发时间推迟了10分钟,便只好以每小时12千米的速度前进,结果比规定时间早5分钟到达B 地,求A 、B 两地间的路程.【解】设由A 、B 两地的路程是 x 千米,则60560101210++=x x 解得:x=15,答:A 、B 两地间的路程是15千米 7、李明和王华步行同时从A 、B 两地出发,相向而行,在离A 地52米处相遇,到达对方出发点后,两人立即以原来的速度原路返回,又在离A 地44米处相遇,求A 、B 两地距离多少米?解:(行程问题,全是路程比与比例)设AB 相距x 千米李明 王华 路程和52 x -52 x2x -44 3x31344252==-∴x x x 8、某周末小明从家里到西湾公园去游玩,已知他骑自行车去西湾公园,骑自行车匀速的速度为每小时8千米,回家时选择乘坐公交车,公交车匀速行驶的速度为每小时40千米,结果骑自行车比公交车多用1.6小时,问他家到西湾公园相距多少千米?【解答】设小明家到西湾公园距离x 千米, 根据题意得:6.1408=-x x 解得:x =16. 答:小明家到西湾公园距离16千米.9、小张和父亲预定搭乘家门口的公交汽车赶往火车站,去家乡看望爷爷。

初一行程问题及解答1.轮船在两个码头之间航行,顺水航行需要4小时,逆水行驶需要5小时,水流的速度是2千米/时,求轮船在静水中的行驶速度用方程解应用题2.甲,乙两站相距360千米,一列慢车从甲站开出,每小时行驶48千米;一列快车从乙站开出,每小时行驶72千米,慢车先开出25分钟,两车相向而行,慢车开几小时与快车相遇用方程解应用题3.一个人从甲村走到乙村.如果他每小时走4千米,那么走到预定的时间,离乙村还有0.5千米;如果他每小时走5千米,那么比一定时间少用半小时就可以到达乙村.求预定时间是多少小时,甲村到一寸的路程是多少千米用方程解应用题4.一个自行车队进行训练,训练时所有队员都以35千米/小时的速度前进,突然一号队员以45千米/小时的速度独自行进,行进10千米后调转车头,仍以45千米/小时的速度往回骑,直到与其他队员会和.一号队员从离队开始到与队员重新会和,经过多长时间用方程解应用题5.某人骑自行车以每小时10千米的速度从甲地到乙地,返回时因事绕道而行,比去时多走8千米的路.虽然行车的速度增加到每小时12千米,但比去时还多用了10分钟.求甲、乙两地的距离.6.甲、乙两站相距380km,一列慢车从甲站开出,每小时行驶48km,一列快车从乙站开出,每小时行驶72km,慢车先开25分钟.两车相向而行,慢车开出多长时间后与快车相遇7.一队学生从学校出发去部队军训,行进速度是5千米/时,走了45千米时,一名通讯员按原路返回学校报信,然后他随即追赶队伍,通讯员的速度是14千米/时,他距部队6千米处追上队伍.问学校到部队的距离是多少8.某人原计划骑车以每小时12千米的速度由A第到B地,这样便可在规定的时间到达,但他因有事将原计划出发的时间推迟了20分钟,只好以每小时15千米的速度前进,结果比规定的时间早4分钟到B地,求AB两地距离.9.甲、乙两列火车相向而行,甲列车每小时行驶60千米,车长150米;乙列车每小时行驶75千米,车长120米.两车从车头相遇到车尾相离需多少时间10.矿山爆破为了确保安全,点燃引火线后人要在爆破前转移到3000米以外的安全地带,引火线燃烧的速度是0.8厘米每秒,人离开的速度是5米/秒,问引火线至少需要多少厘米11.甲,乙两人相距22.5千米,且分别以2.5km/h相向而行,同时甲所带的小狗以每小时7.5千米的速度奔向乙,小狗遇乙后立即回头奔向甲,遇甲后又奔向乙,……直到甲乙相遇,求小狗所走的路程.12.育红学校七年级的学生步行到郊区野营,一班的学生组成前队,步行速度为4千米/小时,二班的学生组成后队,速度为6千米/小时,前队出发一小时后后队才出发,,同时后队派一名联络员骑自行车在两队之间不断的来回联络,他骑自行车的速度为12千米/小时,问联络员骑了多少路答案1.设轮船静水中速度为X则x+24=x-25 得X=182.设为X小时相遇则72x+2548/60+48x=360 得X3.设预定时间为X4x+0.5=5x-0.5 得X甲乙距离:4x+0.54.设X则35x+x-10/4545=105.设甲乙两地的距离为x千米则:x/10=x+8/12-1/66x=5x+8-10x=30 所以甲乙两地之间的距离为30千米6.设慢车开出X小时后与快车相遇,则 48X+72X-25/60=380 X=41/127.设学校到部队的距离是X千米,则 X-6-45/514=X-6+45 X=1018.设AB两地距是X千米,则 X/12=X/15+20/60+4/60 X=249.设需X小时,则 60+75X=150+120/1000 X=0.00210.设需要X厘米,则 X/0.8=3000/5 X=48011.设小狗所走的路程为X千米,则 X/7.5=22.5/2.52 X=33.7512.设二班追上一班用了x小时,得:4x+1=6x13.解,得:x=2 联络员骑的路程为212=24千米。

行程问题1:甲、乙两地相距416千米,一辆汽车从甲地开往乙地,每小时行32千米,汽车开出半小时后,一辆摩托车从乙地开往甲地,速度是汽车的1.5倍,问摩托车开出几小时后才能与汽车相遇?2:甲、乙两人相距80千米,甲骑自行车每小时行20千米,乙骑摩托车每小时行60千米,摩托车在自行车后面,两人同时出发,同向行驶,问乙经过多少时间追上甲。
3:一只轮船,在甲、乙两地之间航行,顺水用8小时,逆水比顺水多30分钟,已知轮船在静水中速度是每小时26千米,求水流的速度。
4:自行车环城赛,一圈12千米,已知甲的速度是乙的5/7,两人同时同地出发后2小时30分相遇,问乙比甲每分钟快多少千米?5:一条山路,从山下到山顶,走了1小时还差1千米,从山顶到册下,50分钟可以走完,已知下山速度是上山速度的1.5倍,上山、下山每小时各走了多少千米?这条山路有多少千米?6:一架飞机在两个城市之间飞行,顺风时需要5小时30分钟,逆风时需要6小时,已知风速是每小时24千米,求两城市之间的距离?7:甲、乙两人骑自行车从相距75千米的两地相向而行,3小时后相遇,若甲比乙每小时多走2千米,求甲、乙的速度及各自所走的距离?8:一条环形跑道长400米,甲骑车,平均速度为550米/分,乙跑步平均速度为250米/分。
⑴两人同时同向从同地出发经过多少分钟两人再相遇。
⑵两人同时同地背向出发经过多少分钟相遇?9:甲、乙两人沿一公路自西向东前进,速度分别为3千米/小时和5千米/小时,甲于中午12时经过A地,乙于下午2时经过A地,则乙追上甲时离A地多远10:若敌我相距15千米,且敌军于1小时前以每小时4千米的速度逃跑,现我军以每小时7千米的速度追击,问几小时可以追上?11:甲骑自行车从A地出发,以每小时12千米的速度驶向B地,经过15分钟后,乙骑自行车从B地出发,以每小时14千米的速度驶向A地,两人相遇时,乙已超过中点1.5千米,求A、B两地距离。
12:一个学生用每小时5千米的速度前进,可以及时从家里返回学校,走了全程度的1/3,他搭上了速度是每小时20千米的公共汽车,因此比规定时间早2小时到达学校。

初一数学行程问题公式路程=速度×时间;路程÷时间=速度;路程÷速度=时间关键问题:确定行程过程中的位置路程相遇路程÷速度和=相遇时间相遇路程÷相遇时间= 速度和1、相遇问题:1)直线:甲的路程+乙的路程=总路程2)环形:甲的路程 +乙的路程=环形周长2、追及问题追及时间=路程差÷速度差速度差=路程差÷追及时间追及时间×速度差=路程差1)直线:距离差=追者路程-被追者路程=速度差X追及时间2)环形:快的路程-慢的路程=曲线的周长3、流水问题顺水行程=(船速+水速)×顺水时间逆水行程=(船速-水速)×逆水时间顺水速度=船速+水速逆水速度=船速-水速静水速度=(顺水速度+逆水速度)÷2水速:(顺水速度-逆水速度)÷21、甲乙齐自行车同时从相距80千米的两地相向而行,2小时相遇,甲比乙每小时多骑2.5千米,求乙的速度。
18.752、A、B两地相距230千米,甲队从A地出发,两小时后,乙队从B地出发与甲相向而行,乙队出发20小时后相遇,已知乙的速度比甲的速度每小时快1千米,求甲、乙的速度各是多少?5,63、甲、乙两车自西向东行驶,甲车速度是每小时48千米,乙车速度是每小时72千米,甲车开25分钟后乙车开出,吻几小时后乙车追上甲车。
5/64、甲乙两位同学练习赛跑,甲每秒跑7米,乙每秒跑6.5米(1)如果甲让乙先跑5米,几秒后可追上乙?10(2)如果加让一先跑1秒钟后,几秒钟后甲可以追上乙?13三辆汽车A、B、C各以不变的速度从甲地开往乙地.已知:B比C迟5分钟出发,出发后20分钟追上C;A比B迟10分钟,出发后50分钟追上C。
那么A出发多长时间追上B?解:设A,B,C三车速度分别为x,y,z由条件:(5+20)*z=20*y(10+5+50)*z=50*x设追上时间为t,则:(t+10)*y=t*x解之得:t=250有一项工程,甲单独做45天完成,乙单独做30天完成,乙先做25天,在合作完成。

七年级数学上册应用题行程问题详细解析行程问题是反映物体匀速运动的应用题,有"相向运动"(相遇问题)、"同向运动"(追及问题)和"相背运动"(相离问题)三种情况。
但它们反映出来的数量关系是相同的,都可以归纳为:速度×时间=路程。
【典型例题1】:甲、乙两车同时从相距960千米的两地相对而行,甲车每小时行90千米,途中因汽车故障甲车停了1小时,5小时后两车相遇。
乙车每小时行多少千米?【思路分析】:途中因汽车故障甲车停了1小时,5小时后两车相遇,则甲车实际行了5-1=4小时,行驶的路程为:90×4=360千米.已知全程为960千米,根据路程÷时间=速度可知乙的速度为:(960-360)÷5.综合算式为:[960-90×(5-1)]÷5。
解答::[960-90×(5-1)]÷5=[960-360]÷5=600÷5=120(千米);答:乙车每小时行120千米.【方法总结】:解决此类问题首先要弄清楚数量关系:乙车行驶的路程=两地的距离-甲车行驶的路程;还要明白由于故障,甲车停了1小时,实际上甲车少行驶了1小时,也就是说两车行驶的时间是不相等的,这是解决问题的关键;可以先根据“路程=速度×时间”计算出甲车行驶的路程,再根据“乙车行驶的路程=两地的距离-甲车行驶的路程”计算出乙车行驶的路程,最后利用“速度=路程÷实际”就可以计算出乙车的速度。
【典型例题2】:甲、乙两车分别从A、B两地同时开出,相向而行,经过6小时,甲车行了全程的75%,乙车超过中点16千米。
已知甲车比乙车每小时多行4千米。
求A、B两地相距多少千米?【思路分析】:甲车行了全程的75%,乙车超过中点16千米,即乙车行了全程的50%加上16千米,而6小时内,甲比乙多行6×4=24(千米),根据上述分析,全程的75%减去全程的50%,就等于(16+24)千米,或者:全程的50%加上16千米,再加上24千米,等于全程的75%。

行程问题1、行程类应用题基本关系:路程=速度×时间2、相遇问题:甲、乙相向而行,则:甲走的路程+乙走的路程=总路程。
3、追及问题:甲、乙同向不同地,则:追者走的路程=前者走的路程+两地间的距离。
甲、乙同向同地不同时,则:追者走的路程=前者走的路程4、环形跑道问题:①甲、乙两人在环形跑道上同时同地同向出发:快的必须多跑一圈才能追上慢的。
②甲、乙两人在环形跑道上同时同地反向出发:两人相遇时的总路程为环形跑道一圈的长度。
5、飞行(航行)问题、基本等量关系:①顺风(顺水)速度=无风(静水)速度+风速(水速)②逆风(逆水)速度=无风(静水)速度-风速(水速)顺风(水)速度-逆风(水)速度=2×风(水)速6、车辆(车身长度不可忽略)过桥问题:车辆通过桥梁(或隧道等),则:车辆行驶的路程=桥梁(隧道)长度+车身长度7、超车(会车)问题:超车过程中,车辆行驶路程等于车身长度和,相对速度为两车速度差。
会车过程中,车辆行驶路程等于车身长度和,相对速度为两车速度和。
在行程问题中,按照题意画出行程图,可以使问题的分析过程更直观,更容易理解。
特别是问题中运动状态复杂,涉及的量较多的时候,画行程图就成了理解题意的关键。
所以画行程图是我们必须学会的一种分析手段。
另外,由于行程问题中的基本量只有“路程”、“速度”和“时间”三项,所以,列表分析也是解决行程问题的一种重要方法。
追及问题1、甲、乙两地相距10km,A、B两人分别从甲、乙两地同时、同向出发,A在前,B在后,A的速度是每小时4km,B的速度是每小时5km,xh后A走了km,B走了km。
如果这时刚好B追上A,那么可列方程:。
2、甲、乙两人都从A地出发到B地,甲先走5km后乙再出发,甲速度是4km/h,乙速度是5km/h。
如果A、B两地相距xkm,那么甲先走的时间是h,乙走的时间是h,假如两人同时到达B地,那么可列方程:。
3、甲、乙两人同时以4km/h的速度从A地前往B地,走了2.5km后,甲要回去取一份文件。
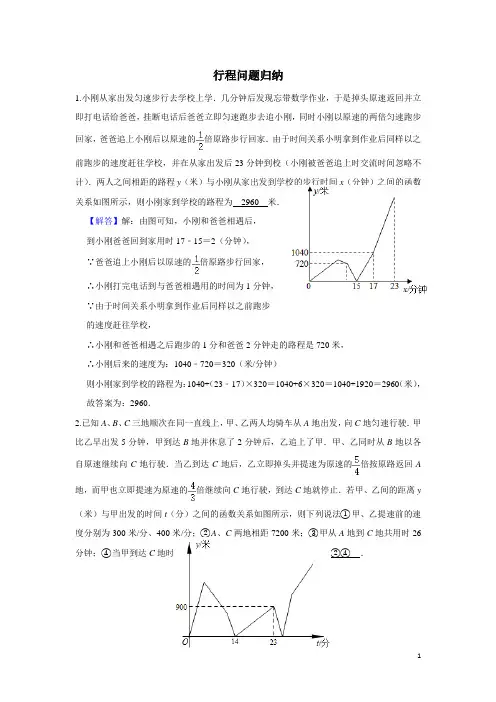
小中初数学教案等集合行程问题归纳1.小刚从家出发匀速步行去学校上学.几分钟后发现忘带数学作业,于是掉头原速返回并立即打电话给爸爸,挂断电话后爸爸立即匀速跑步去追小刚,同时小刚以原速的两倍匀速跑步回家,爸爸追上小刚后以原速的倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,并在从家出发后23分钟到校(小刚被爸爸追上时交流时间忽略不计).两人之间相距的路程y (米)与小刚从家出发到学校的步行时间x (分钟)之间的函数关系如图所示,则小刚家到学校的路程为 2960 米. 【解答】解:由图可知,小刚和爸爸相遇后,到小刚爸爸回到家用时17﹣15=2(分钟),∵爸爸追上小刚后以原速的倍原路步行回家, ∴小刚打完电话到与爸爸相遇用的时间为1分钟, ∵由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,∴小刚和爸爸相遇之后跑步的1分和爸爸2分钟走的路程是720米,∴小刚后来的速度为:1040﹣720=320(米/分钟)则小刚家到学校的路程为:1040+(23﹣17)×320=1040+6×320=1040+1920=2960(米),故答案为:2960. 2.已知A 、B 、C 三地顺次在同一直线上,甲、乙两人均骑车从A 地出发,向C 地匀速行驶.甲比乙早出发5分钟,甲到达B 地并休息了2分钟后,乙追上了甲.甲、乙同时从B 地以各自原速继续向C 地行驶.当乙到达C 地后,乙立即掉头并提速为原速的倍按原路返回A地,而甲也立即提速为原速的倍继续向C 地行驶,到达C 地就停止.若甲、乙间的距离y(米)与甲出发的时间t (分)之间的函数关系如图所示,则下列说法①甲、乙提速前的速度分别为300米/分、400米/分;②A 、C 两地相距7200米;③甲从A 地到C 地共用时26分钟;④当甲到达C 地时,乙距A 地6075米;其中正确的是 ①②④ .12x=(14﹣5)×(x+100),解得,x=300,则x+100=400,即甲、乙提速前的速度分别为300米/分、400米/分.故①正确;A、B两地之间的距离为:300×12=3600(米),A、C两地之间的距离为:400×(23﹣5)=7200(米),故②正确;∵当乙到达C地后,乙立即掉头并提速为原速的倍按原路返回A地,而甲也立即提速为原速的倍继续向C地行驶,∴后来乙的速度为:400×=500(米/分),甲的速度为300×=400(米/分),∴甲从A地到C地共用时:23+[7200﹣(23﹣2)×300]÷400=25(分钟),故③错误;∴当甲到达C地时,乙距A地:7200﹣(25﹣23)×500=6075(米),故④正确.综上所述,正确的有①②④.3.尊老助老是中华民族的传统美德,我校的小艾同学在今年元旦节前往家附近的敬老院,为老人们表演节目送上新年的祝福.当小艾同学到达敬老院时,发现拷音乐的U盘没有带,于是边打电话给爸爸边往家走,请爸爸能帮忙送来.3分钟后,爸爸在家找到了U盘并立即前往敬老院,相遇后爸爸将U盘交给小艾,小艾立即把速度提高到之前的1.5倍跑回敬老院,这时爸爸遇到了朋友,停下与朋友交谈了2分钟后,爸爸以原来的速度前往敬老院观看小艾的表演.爸爸与小艾的距离y(米)与小艾从敬老院出发的时间x(分)之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有240米.教案等集合练习9分钟的时候,小艾离敬老院的距离为:60×9=540(米),小艾最后回到敬老院的时间为:9+540÷(60×1.5)=15(分钟),当小艾回到敬老院时,爸爸离敬老院还有:540﹣(15﹣11)×75=240(米), 故答案为:240.4.甲、乙分别骑摩托车同时沿同一条路线从A 地出发B 地,已知A 、B 两地相距280km ,他们出发2小时的时候乙的摩托车坏了,乙立即开始修车,甲车继续行驶,当甲第一次与乙相遇时,乙还在修车,乙修好车继续按原速前往B 地.乙到达B 地小时后,甲车到达B 地.整个过程中,两人均保持各自的速度匀速行驶,甲、乙两人相距的路程y (千米)与甲出发的时间x (小时)之间的关系如图所示,则当乙车修好时,甲车距B 地的路程为 130 千米. 【解答】解:∵甲车速度==40千米/时,∴甲车走完全程时间==7小时,∴乙车速度=40+=70千米/时, 设乙车修了x 小时,由题意可得:70(﹣x )﹣40×=20,∴x =,∴当乙车修好时,甲车距B 地的路程=280﹣40×(2+)=130千米,5.十一黄金周,小明和小亮乘甲车从沙坪坝出发,以一定的速度匀速前往铁山坪体验“飞越丛林”.出发15分钟后,小明发现忘带身份证和钱包,便下车换乘乙车匀速回家去取(小明换车、取身份证和钱包的时间忽略不计),小亮仍乘甲车并以原速继续前行,小明回家取了身份证和钱包后,为节约时间,又立即乘乙车以原来速度的倍匀速按原路赶往铁山坪,由于国庆期间车流量较大,在小明乘乙车以加速后的速度匀速赶往铁山坪期间,甲车恰好因故在途中持续堵塞了5分钟,结果乙车先到达目的地.甲、乙两车之间的距离y (千米)与乙年数学测试题车行驶时间x (小时)之间的部分图象如图所示,则乙车出发小时到达目的地.【解答】解:设甲车的速度为a 千米/小时,乙车回家时的速度是b 千米/小时,a =b ,,设a =8m ,b =9m (m >0),由图象得乙车行驶小时两边相距千米, ﹣=, m =5,∴a =40,b =45,设t 小时两车相距3千米,=+3+(t ﹣)×40,t =,6.小亮和妈妈从家出发到长嘉汇观看国庆灯光秀,妈妈先出发,2分钟后小亮沿同一路线出发去追妈妈,当小亮追上妈妈时发现相机落在途中了,妈妈立即返回找相机,小亮继续前往长嘉汇,当小亮到达长嘉汇时,妈妈刚好找到了相机并立即前往长嘉汇(妈妈找相机的时间不计),小亮在长嘉汇等了一会,没有等到妈妈,就沿同一路线返回接妈妈,最终与妈妈会合,小亮和妈妈的速度始终不变,如图是小亮和妈妈两人之间的距离y (米)与妈妈出发的时间x (分钟)的图象;则小亮开始返回时,妈妈离家的距离为 575 米. 【解答】解:妈妈的速度为:100÷2=50(米/分),小亮的速度为:[100+50(12﹣2)]÷(12﹣2)=60(米/分),相遇时行走的路程为:12×50=600(米),观察图象在x =18时,小亮和妈妈的相距最大,可知是小亮到达长嘉汇所经历的时间,所以家到长嘉汇的距离为:60×(18﹣2)=960(米),由(18﹣12=6分钟)可知妈妈返回找到相机行走路程为6×50=300(米),此时设小亮在长嘉汇等妈妈的时间为t 分钟,由图象知小亮与妈妈会合所用时间为27﹣18=9分钟可建立方程如下: 60×(9﹣t )+50×9═960﹣(600﹣300),解得t =5.5(分钟), ∴小亮开始返回时,妈妈离家的距离为:50×(18+5.5﹣6×2)=575(米).小中初数学教案等集合向C 地赶去(中间拿文件的时间忽略不计).乙得知情况后决定先见到甲拿到文件再返回C 地办事.两人分别在C 地用了10分钟办完事后各自回出发地.已知甲、乙的速度始终保持不变,两人之间的距离y (单位:千米)与甲出发的时间x (单位:小时)的部分数关系如图所示,则当甲办完事再次返回到A 地时乙距B 地 50 千米. 【解答】解:乙的速度为:460﹣360=100(千米/时), 甲的速度为:(460﹣370﹣100×0.5)÷0.5=80(千米/时), 甲从出发到两人相遇所用时间为:(460﹣100)÷(80+100)+1=3(小时), ∴A 、C 两地距离为:80×(3﹣1)+(100﹣80)÷()=220(千米),甲从A 地到C 地的时间为:220÷80=2.75(小时), 甲从出发到返回所需时间为:1+2.75+=(小时),当甲办完事再次返回到A 地时, 乙与B 地的距离为:100×(﹣﹣)=50(米). 故答案为:50.8.某周末,大海和大成两家人同时开车从国奥村出发,以一定的速度匀速前往渝北统景镇风景区参加蹦极勇敢者挑战.出发15分钟后,大海发现忘带身份证,便掉头以另一速度匀速回国奥村去取(大海掉头、取身份证的时间忽略不计),大成仍以原速继续前行.大海回家取了身份证后,立即以返回速度的倍匀速按原路赶往统景镇,在大海以加速后的速度匀速赶往统景镇期间,大成在途中加油耽搁了5分钟,结果大海先到达目的地,两车之间的距离y (千米)与大成开车时间x (小时)之间的部分图象如图所示,则国奥村与统景镇相距 60 千米.测试题9a =8b ,, 设a =8m ,b =9m (m >0),()•8m ﹣()=, m =5,∴a =8m =40,b =9m =45,设x 小时,两车的距离是千米, 根据题意得:45×=+40(t ﹣)+,t =, 则国奥村与统景镇相距:(﹣)×=60(千米),9.暑假假期,小明和小亮两家相约自驾车从重庆出发前往相距172千米的景区游玩两家人同时同地出发,以各自的速度匀速行驶,出发一段时间后,小明家因故停下来休息了15分钟,为了尽快追上小亮家,小明家提高速度后仍保持匀速行驶(加速的时间忽略不计),小明家追上小亮家后以提高后的速度直到景区,小亮家保持原速,如图是小明家、小亮家两车之间的距离s (km )与出发时间t (h )之间的函数关系图象,则小明家比小亮家早到景区 6 分钟. 【解答】解:设出发时小明家的速度是a 千米/小时,小亮家的速度是b 千米/小时,且a >b ,由题意得:0.8(a ﹣b )=8,a =b +10,小明家因故停下来休息了15分钟,可知A (1.05,12),小亮的速度为:=80(千米/小时),∴小明家的速度是90千米/小时,设小明加速后的速度为m 千米/小时,根据题意得:×80=(﹣1.05)m +0.8×90,小中初数学m =100,﹣﹣1.05,=0.1(小时),=6(分), 即小明家比小亮家早到景区6分钟. 10.华师大一附中是各地中学生游学的向往之地,现有一组游学小分队从武汉站下车,计划骑自行车从武汉站到华中师大一附中,出发一段时间后,发现有贵重物品落在了武汉站,于是安排小李骑自行车以原速返回,剩下的成员速度不变向华中师大一附中前进.小李取回物后,改乘出租车追赶车队(取物品、等车时间忽略不计),小李在追赶上自行车队后仍乘坐出租车,再行驶10分钟后遭遇堵车,在此期间,自行车队反超出租车.拥堵30分钟后交通恢复正常,出租车以原速开往华中师大一附中,最终出租车和自行车队同时到达设自行车队和小李行驶时间为t 分钟,与武汉站距离s 千米,s 与t 的函数关系如图所示,则从第二次相遇到出租车堵车结束,经过了 22.5 分钟.【解答】解:自行车速度8÷30=(千米/分钟), 自行车到达终点用时为:20÷=75(分钟),出租车到达洪崖洞用时75﹣30﹣30=15(分钟); 出租车速度20÷15=(千米/分钟), 设自行车出发x 分钟第一次相遇,根据题意得 ,解得=37.5,设第二次相遇时间为y ,则, 解得y =52.5,75﹣52﹣5=22.5(分钟).所以第二次相遇后,出租车还经过了22.5分钟到达.。
七年级上册数学解方程应用题一、行程问题。
1. 甲、乙两人相距285米,相向而行,甲从A地每秒走8米,乙从B地每秒走6米,如果甲先走12米,那么甲出发几秒与乙相遇?- 解析:- 设甲出发t秒与乙相遇。
- 甲先走12米后,两人共同走的路程为(285 - 12)米。
- 甲的速度是每秒8米,乙的速度是每秒6米,根据路程 = 速度和×时间,可列方程(8 + 6)t=285 - 12。
- 化简得14t = 273,解得t=(273)/(14)=19.5秒。
2. 一辆汽车从A地到B地,若每小时行45千米,就要比原计划晚0.5小时到达;若每小时行50千米,就可比原计划提前0.5小时到达。
求A、B两地的距离。
- 解析:- 设原计划用x小时到达。
- 根据路程相等,可列方程45(x + 0.5)=50(x - 0.5)。
- 展开括号得45x+22.5 = 50x - 25。
- 移项得50x - 45x=22.5 + 25。
- 合并同类项得5x = 47.5,解得x = 9.5小时。
- 那么A、B两地的距离为50×(9.5 - 0.5)=450千米。
二、工程问题。
3. 一项工程,甲单独做需要10天完成,乙单独做需要15天完成,两人合作4天后,剩下的部分由乙单独做,还需要几天完成?- 解析:- 设还需要x天完成。
- 把这项工程的工作量看作单位“1”,甲的工作效率是(1)/(10),乙的工作效率是(1)/(15)。
- 两人合作4天的工作量为((1)/(10)+(1)/(15))×4,乙单独做x天的工作量为(1)/(15)x,可列方程((1)/(10)+(1)/(15))×4+(1)/(15)x = 1。
- 先计算((1)/(10)+(1)/(15))×4=((3 + 2)/(30))×4=(2)/(3)。
- 方程变为(2)/(3)+(1)/(15)x=1,移项得(1)/(15)x = 1-(2)/(3),(1)/(15)x=(1)/(3),解得x = 5天。
初一数学上册:一元一次方程解决应用题【行程问题】知识点1、行程问题中的三个基本量及其关系:路程=速度×时间时间=路程÷速度速度=路程÷时间2、行程问题基本类型相遇问题:快行距+慢行距=原距追及问题:快行距-慢行距=原距航行问题:顺水(风)速度=静水(风)速度+水流(风)速度逆水(风)速度=静水(风)速度-水流(风)速度抓住两码头间距离不变,水流速和船速(静不速)不变的特点考虑相等关系专项练习1、从甲地到乙地,某人步行比乘公交车多用3.6小时,已知步行速度为每小时8千米,公交车的速度为每小时40千米,设甲、乙两地相距x千米,则列方程为_____。
解:等量关系步行时间-乘公交车的时间=3.6小时列出方程是:X/8-X/40=3.62、某人从家里骑自行车到学校。
若每小时行15千米,可比预定时间早到15分钟;若每小时行9千米,可比预定时间晚到15分钟;求从家里到学校的路程有多少千米?解:等量关系(1)速度15千米行的总路程=速度9千米行的总路程(2)速度15千米行的时间+15分钟=速度9千米行的时间-15分钟方法一:设预定时间为x小/时,则列出方程是:15(x-0.25)=9(x+0.25)方法二:设从家里到学校有x千米,则列出方程是:X/15+15/60=X/9-15/603、与铁路平行的一条公路上有一行人与骑自行车的人同时向南行进。
行人的速度是每小时3.6km,骑自行车的人的速度是每小时10.8km。
如果一列火车从他们背后开来,它通过行人的时间是22秒,通过骑自行车的人的时间是26秒。
⑴行人的速度为每秒多少米?⑵这列火车的车长是多少米?等量关系:①两种情形下火车的速度相等②两种情形下火车的车长相等在时间已知的情况下,设速度列路程等式的方程,设路程列速度等式的方程。
解:⑴行人的速度是:3.6km/时=3600米÷3600秒=1米/秒骑自行车的人的速度是:10.8km/时=10800米÷3600秒=3米/秒⑵方法一:设火车的速度是X米/秒,则26×(X-3)=22×(X-1) 解得X=4方法二:设火车的车长是x米,则(X+22×1)/22=(X+26×3)/264、一次远足活动中,一部分人步行,另一部分乘一辆汽车,两部分人同地出发。
初中列方程解应用题(行程问题)专题行程问题是指与路程、速度、时间这三个量有关的问题。
我们常用的基本公式是:路程=速度×时间;速度=路程÷时间;时间=路程÷速度.行程问题是个非常庞大的类型,多年来在考试中屡用不爽,所占比例居高不下。
原因就是行程问题可以融入多种练习,熟悉了行程问题的学生,在多种类型的习题面前都会显得得心应手。
下面我们将行程问题归归类,由易到难,逐步剖析。
1. 单人单程:例1:甲,乙两城市间的铁路经过技术改造后,列车在两城市间的运行速度从h km /80提高到h km /100,运行时间缩短了h 3。
甲,乙两城市间的路程是多少?【分析】如果设甲,乙两城市间的路程为x km ,那么列车在两城市间提速前的运行时间为h x 80,提速后的运行时间为h x 100. 【等量关系式】提速前的运行时间—提速后的运行时间=缩短的时间. 【列出方程】310080=-x x .例2:某铁路桥长1000m ,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min ,整列火车完全在桥上的时间共s 40。
求火车的速度和长度。
【分析】如果设火车的速度为x s m /,火车的长度为y m ,用线段表示大桥和火车的长度,根据题意可画出如下示意图:【等量关系式】火车min 1行驶的路程=桥长+火车长;火车s 40行驶的路程=桥长-火车长 【列出方程组】⎩⎨⎧-=+=yx y x 100040100060举一反三:1.小明家和学校相距km 15。
小明从家出发到学校,小明先步行到公共汽车站,步行的速度为60min /m ,再乘公共汽车到学校,发现比步行的时间缩短了min 20,已知公共汽车的速度为h km /40,求小明从家到学校用了多长时间。
2.根据我省“十二五”铁路规划,连云港至徐州客运专线项目建成后,连云港至徐州的最短客运时间由现在的2小时18分钟缩短为36分钟,其速度每小时将提高km 260.求提速后的火车速度。
行程问题1、相遇问题:甲、乙相向而行:甲走的路程+乙走的路程=总路程2、追及问题:甲、乙同向不同地:追者走的路程=前者走的路程+两地间的距离3、环形跑道问题:(1)甲、乙两人在环形跑道上同时同地同向出发,快的必须多跑一圈才追上慢的。
(2)甲、乙两人在环形跑道上同时同地反向出发,两人第一次相遇跑的总路程=环形跑道一圈的长度。
4、飞行问题:基本等量关系:顺风速度= 无风速度+ 风速逆风速度= 无风速度-风速顺风速度-逆风速度= 风速×25、航行问题:基本等量关系:顺水速度= 静水速度+ 水速逆水速度= 静水速度-水速顺水速度-逆水速度=水速×2典型例题:(1)相遇问题:1、甲、乙两站间的路程为360千米,一列慢车从甲站开出,每小时行48千米,一列快车从乙站开出,每小时行72千米,已知快车先开25分钟,两车相向而行,慢车行驶多少时间两车相遇?2、A、B两地相距150千米。
一辆汽车以每小时50千米的速度从A地出发,另一辆汽车以每小时40千米的速度从B地出发,两车同时出发,相向而行,问经过几小时,两车相距30千米?(2)追及问题:1、甲从A地以6千米/小时的速度向B地行走,40分钟后,乙从A地以8千米/小时的速度追甲,结果在甲离B地还有5千米的地方追上了甲,求A、B两地的距离。
2、甲、乙两车都从A地开往B地,甲车每小时行40千米,乙车每小时行50千米,甲车出发半小时后,乙车出发,问乙车几小时可追上甲车?(3)航行问题:1、一轮船从甲码头顺流而下到达乙码头需要8小时,逆流返回需要12小时,已知水流速度是3千米/小时,求甲、乙两码头的距离。
2、甲乙两港相距120千米,A、B两船从甲乙两港相向而行6小时相遇。
A船顺水,B船逆水。
相遇时A船比B船多行走49千米,水流速度是每小时15千米,求A、B两船的静水速度。
3、一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的航速和两城之间的航程?(4)过桥问题:1、一列火车以每分钟1千米的速度通过一座长400米的桥,用了半分钟,则火车本身的长度为多少米?(5)隧道问题:1、火车用26秒的时间通过一个长256米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16秒的时间通过了长96米的隧道,求列车的长度。
初一应用题分类总结---------典型题型归类与解题思路(一)行程问题: 基本公式 时间×速度=距离行程问题包括相遇问题、追击问题、跑道赛跑、火车相遇、水中行船、时钟问题,还有相关的判断问题。
关键点:位置、距离、时间、速度。
清楚各点之间相关量的关系,忽略过程的细节。
1.从甲地到乙地,某人步行比乘公交车多用3.6小时,已知步行速度为每小时8千米,公交车的速度为每小时40千米,设甲乙两地相距x千米,则列方程为________________。
分析:行走问题,可以理解为追击问题时间等量关系 车行时间+3.6=人行时间 x÷40+3.6=x÷8 距离等量关系人行时间×人行速度=甲乙距离(x÷40+3.6)×8=x2.甲、乙两人在相距18千米的两地同时出发,相向而行,1小时48分相遇,如果甲比乙早出发40分钟,那么在乙出发1小时30分时两人相遇,求甲、乙两人的速度。
分析:相遇问题---相向而行(反方向) 甲距离+乙距离=某距离(1)甲乙两次的行走时间均已知,(2)两次行走的总距离均已知,(3)第一次甲乙时间同距离等量关系 第二次甲走+第二次乙走=18 ---(2)设甲速度x,乙的速度=距离÷第一次同时行走时间-x ---(3)x×(40+1时30)+(距离÷第一次同时行走时间-x)×1时30=18----单位应一致速度等量关系第二次甲40分钟路程÷40分钟=甲的速度第二次甲40分钟路程=总行程-第二次共同走过的行程第二次共同走过的行程=总行程×两次共同走过的时间比速度等量关系第一次共同行走时的速度=第二次行走时的速度18÷1小时48分=(18-x×40分)÷1小时30分 ----单位应一致3. 某人从家里骑自行车到学校。
若每小时行15千米,可比预定的时间早到15分钟;若每小时行9千米,可比预定的时间晚到15分钟;求从家里到学校的路程有多少千米?分析:行走问题。
行程问题
1:甲、乙两地相距416千米,一辆汽车从甲地开往乙地,每小时行32千米,汽车开出半小时后,一辆摩托车从乙地开往甲地,速度是汽车的1.5倍,问摩托车开出几小时后才能与汽车相遇?
2:甲、乙两人相距80千米,甲骑自行车每小时行20千米,乙骑摩托车每小时行60千米,摩托车在自行车后面,两人同时出发,同向行驶,问乙经过多少时间追上甲。
3:一只轮船,在甲、乙两地之间航行,顺水用8小时,逆水比顺水多30分钟,已知轮船在静水中速度是每小时26千米,求水流的速度。
4:自行车环城赛,一圈12千米,已知甲的速度是乙的5/7,两人同时同地出发后2小时30分相遇,问乙比甲每分钟快多少千米?
5:一条山路,从山下到山顶,走了1小时还差1千米,从山顶到册下,50分钟可以走完,已知下山速度是上山速度的1.5倍,上山、下山每小时各走了多少千米?这条山路有多少千米?
6:一架飞机在两个城市之间飞行,顺风时需要5小时30分钟,逆风时需要6小时,已知风速是每小时24千米,求两城市之间的距离?
7:甲、乙两人骑自行车从相距75千米的两地相向而行,3小时后相遇,若甲比乙每小时多走2千米,求甲、乙的速度及各自所走的距离?
8:一条环形跑道长400米,甲骑车,平均速度为550米/分,乙跑步平均速度为250米/分。
⑴两人同时同向从同地出发经过多少分钟两人再相遇。
⑵两人同时同地背向出发经过多少分钟相遇?
9:甲、乙两人沿一公路自西向东前进,速度分别为3千米/小时和5千米/小时,甲于中午12时经过A地,乙于下午2时经过A地,则乙追上甲时离A地多远?
10:若敌我相距15千米,且敌军于1小时前以每小时4千米的速度逃跑,现我军以每小时7千米的速度追击,问几小时可以追上?
11:甲骑自行车从A地出发,以每小时12千米的速度驶向B地,经过15分钟后,乙骑自行车从B地出发,以每小时14千米的速度驶向A地,两人相遇时,乙已超过中点1.5千米,求A、B两地距离。
12:一个学生用每小时5千米的速度前进,可以及时从家里返回学校,走了全程度的1/3,他搭上了速度是每小时20千米的公共汽车,因此比规定时间早2小时到达学校。
他家离学校多远?
13:一只轮船,航行于甲、乙两地之间,顺水用3小时,逆水比顺水多30分钟,已知轮船在静水中速度是每小时26千米,求水流的速度?
14:甲、乙两地相距128千米,一人骑自行车从甲地出发,每小时16千米,另一人骑摩托车从乙地出发,两人同时相向而行,已知摩托车速度是自行车的3倍,问多少小时后两人相遇?
15:A、B两地相距20千米,甲、乙两人分别从A、B两地同时出发,相向而行,2小时后两人在途中相遇,相遇后甲立即返回A地,乙仍向A地前进,待甲回到A地时,乙离A地还有2千米,求两人的速度各是多少?
16:一只轮船在甲、乙两地之间航行,顺水用4小时,逆水要5小时,已知水流速度是每小时3千米,求甲、乙两地之间的距离。
17:甲乙两站间的路程360km,一列慢车从甲站台开出,每小时行驶48km,一列快车从乙站台出发每小时行驶72km。
⑴快车先开25分钟,开车相向而行,快车开了几个小时与慢车相遇?
⑵如果慢车先开出25分钟,两车相向而行,慢车开了几小时与快车相遇?
⑶两列火车同时开出,相背而行,多少小时后两车相距840km
⑷两列火车同时开出同向而行,快车在慢车的后面,问经多少小时,快车能够追上慢车?
18:一列客车和一列货车在平行的轨道上同向行驶,客车的长度是200米,货车的长度是280米,客车与货车的速度之比是5﹕3,客车赶上货车的交叉时间是1分钟,求每个车的速度?若两用人才车相向而行,它们的交叉时间需要多少?
19.一列学生队伍长100米,通讯员在队尾,队伍以4米/秒的速度向前,有一通知通讯员需迅速传给排头,通讯员以6米/秒的速度跑到排头,通知完毕后又跑回队尾,通讯员从开始出发到又回到队尾共用了多少时间?(通知时间忽略不计)。