浙江高考历年真题之解析几何大题(理科)

普通高等学校招生全国统一考试（浙江卷）数学（理）试题解析一、选择题 （本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）设函数2,0,()()4,0.x x f x f x xα-≤⎧==⎨⎩若,则实数α=（A ）-4或-2 （B ）-4或2 （C ）-2或4 （D ）-2或2 【答案】B【解析】当0≤α时，4,42)(-==-=ααf ； 当0>α，4,42)(2===ααf .（2）把复数z 的共轭复数记作z ，i 为虚数单位，若z=1+I,则(1)z z +⋅= （A ）3-i （B ）3+i （C ）1+3i （D ）3 【答案】A【解析】∵i z +=1，∴i z -=1，∴i z z z z -=-+=•+3)1)(2()1(.(3)若某几何体的三视图如图所示，则这个几何体的直观图能够是【答案】D【解析】由正视图可排除A 、B 选项；由俯视图可排除C 选项. （4）下列命题中错误的是（A ）如果平面αβ⊥平面，那么平面α内一定存有直线平行于平面β （B ）如果平面不垂直于平面β，那么平面α内一定不存有直线垂直于平面β （C ）如果平面αγ⊥平面，平面βγ⊥平面，=l αβ⋂，那么l γ⊥平面 （D ）如果平面αβ⊥平面，那么平面α内所有直线都垂直于平面β 【答案】D【解析】若面⊥α面β，在面α内与面的交线不相交的直线平行平面β，故A 准确；B 中若α内存有直线垂直平面β，则βα⊥，与题没矛盾，所以B 准确；由面⊥面的性质知选项C 准确.（5）设实数,x y 满足不等式组250270,0x y x y x +-⎧⎪+-⎨⎪⎩＞＞≥，y ≥0，若,x y 为整数，则34x y +的最小值是（A ）14 （B ）16 （C ）17 （D ）19 【答案】B【解析】可行域如图所示联立⎩⎨⎧=-+=-+072052y x y x ，解之得⎩⎨⎧==13y x ，又∵边界线为虚线取不到，且目标函数线的斜率为43-，∴当y x z 43+=过点（4，1）时，有最小值16.（6）若02πα＜＜，02πβ-＜＜，1cos()43πα+=，cos()42πβ-=则cos()2βα+= （A）3 （B）3- （C）9 （D）9-【答案】C【解析】∵31)4cos(=+απ，20πα<<，∴332)4sin(=+απ，又∵33)24cos(=-βπ，02<<-βπ，∴36)24sin(=-βπ，∴)]24()4cos[()2cos(βπαπβα--+=+＝)24sin()4sin()24cos()4cos(βπαπβπαπ-++-+＝363323331⨯+⨯＝935. （7）若,a b 为实数，则“01m ab ＜＜”是11a b b a＜或＞的 （A ）充分而不必要条件 （B ）必要而不充分条件（C ）充分必要条件 （D ）既不充分也不必要条件 【答案】A【解析】当0,0>>b a 时，由10<<ab 两边同除b 可得ba 1<成立；当0,0<<b a 时，两边同除以a 可得a b 1>成立，∴“10<<ab ”是“b a 1<或a b 1>”的充会条件，反过来0<ab ，由b a 1<或ab 1>得不到10<<ab .（8）已知椭圆22122:1(0)x y C a b a b +=＞＞与双曲线221:14y C x -=有公共的焦点，2C 的一条渐近线与以1C 的长轴为直径的圆相交于,A B 两点，若1C 恰好将线段AB 三等分，则 （A ）2132a =（B ）213a = （C ）212b = （D ）22b = 【答案】 C【解析】由双曲线422y x -＝1知渐近线方程为x y 2±=，又∵椭圆与双曲线有公共焦点，∴椭圆方程可化为22x b ＋()225y b +＝()225b b +，联立直线与椭圆方程消y 得，()20552222++=b b b x，又∵1C 将线段AB 三等分，∴()3220552212222a b b b =++⨯+， 解之得212=b .（9）有5本不同的书，其中语文书2本，数学书2本，物理书1本.若将其随机的并排摆放到书架的同一层上，则同一科目的书都不相邻的概率[（A ）15 （B ）25 （C ）35 D 45【答案】B【解析】由古典概型的概率公式得522155222233232222=+-=A A A A A A A P .（10）设a ，b ，c 为实数，)1)1()(),)(()(22+++=+++=bx cx ax x g c bx x a x x f （.记集合S=()0,,()0,,x f x x R T x g x x R =∈==∈若S ，T 分别为集合元素S ，T 的元素个数，则下列结论不可能．．．的是 （A ）S =1且T =0 （B ）1T =1S =且 （C ）S =2且T =2 （D ）S =2且T =3 【答案】C【解析】当0===c b a 时，1=s 且 0||=T ；当0,0≠=b a 且042<-c b 时，1=s 且1||=T ；当04,02>-≠a b a 时，2=s 且3||=T .非选择题部分（共100分）二、填空题：本大题共7小题，每小题4分，共28分（11）若函数2()f x x x a =-+为偶函数，则实数a = 。

浙江高考历年真题之解析几何大题（教师版）1、（2005年）如图，已知椭圆的中心在坐标原点，焦点12,F F 在x 轴上，长轴12A A 的长为4，左准线l 与x 轴的交点为M ，|MA 1|∶|A 1F 1|＝2∶1． (Ⅰ)求椭圆的方程；(Ⅱ)若直线1l ：x ＝m (|m |＞1)，P 为1l 上的动点，使12F PF ∠ 最大的点P 记为Q ，求点Q 的坐标(用m 表示)．解析：(Ⅰ)设椭圆方程为()222210x y a b a b +=>>，半焦距为c ，则2111,a MA a A F a c c =-=- ，()2222224a a a c c a abc ⎧-=-⎪⎪⎪=⎨⎪=+⎪⎪⎩由题意,得 2,3,1a b c ∴=== ，221.43x y +=故椭圆方程为(Ⅱ) 设()0,,||1P m y m >，当00y >时，120F PF ∠=； 当00y ≠时，22102F PF PF M π<∠<∠<，∴只需求22tan F PF ∠的最大值即可设直线1PF 的斜率011y k m =+，直线2PF 的斜率021y k m =-， 002122222212002||tan 1121||1y k k F PF k k m y m y m -∴∠==≤=+-+-⋅- 201||m y -=时，12F PF ∠最大，(2,1,||1Q m m m ∴±->2、（2006年）如图，椭圆by a x 222+＝1（a ＞b ＞0）与过点A （2，0）、B(0,1)的直线有且只有一个公共点T ，且椭圆的离心率e=23。

(Ⅰ)求椭圆方程；(Ⅱ)设F 1、F 2分别为椭圆的左、右焦点，M 为线段AF 2的中点，求证：∠ATM=∠AF 1T 。

解析：（Ⅰ）过 A 、B 的直线方程为12xy += 因为由题意得⎪⎪⎩⎪⎪⎨⎧+-==+12112222x y b y a x 有惟一解，即0)41(2222222=-+-+b a a x a x a b 有惟一解, 所以2222(44)0(0),a b a b ab ∆=+-=≠故4422-+b a =0又因为e 32c =,即22234a b a -= ， 所以224a b = 从而得2212,,2a b == 故所求的椭圆方程为22212x y += （Ⅱ）由（Ⅰ）得62c =, 所以 1266((22F F -，从而M （1+46，0）由 ⎪⎩⎪⎨⎧+-==+12112222x y y x ，解得 121,x x == 因此1(1,)2T =因为126tan 1-=∠T AF ，又21tan =∠TAM ，62tan =∠2TMF ，得 1266112162tan -=+-=∠ATM ，因此，T AF ATM 1∠=∠ 3、（2007年）如图，直线y kx b =+与椭圆2214x y +=交于A B ，两点，记AOB △的面积为S ． （I ）求在0k =，01b <<的条件下，S 的最大值； （II ）当2AB =，1S =时，求直线AB 的方程．解析：（I ）设点A 的坐标为1()x b ，，点B 的坐标为2()x b ，．由2214x y +=，解得21,221x b =±- 所以222121||21112S b x x b b b b =-=-≤+-=，当且仅当22b =时，．S 取到最大值1． （Ⅱ）解：由2214y kx bx y =+⎧⎪⎨+=⎪⎩得222(41)8440k x kbx b +++-=2216(41)k b ∆=-+ ①｜AB 222212216(41)1|1241k b k x x kk -++-=+=+ ②又因为O 到AB 的距离221||1Sd AB k ===+ 所以221b k =+ ③ ③代入②并整理，得424410k k -+=，解得，2213,22k b ==， 代入①式检验，△＞0，故直线AB 的方程是2622y x =+或2622y x =-或2622y x =-+或2622y x =--． 4、（2008年）已知曲线C 是到点P （83,21-）和到直线85-=y 距离相等的点的轨迹。

解析几何高考真题一、单选题（共11题；共22分）1.（2020·新课标Ⅲ·理）设双曲线C ：x 2a 2−y 2b 2=1 （a>0，b>0）的左、右焦点分别为F 1 ， F 2 ， 离心率为 √5 ．P 是C 上一点，且F 1P ⊥F 2P ．若△PF 1F 2的面积为4，则a=（ ） A. 1 B. 2 C. 4 D. 82.（2020·新课标Ⅲ·理）设O 为坐标原点，直线x=2与抛物线C ：y 2=2px(p>0)交于D ，E 两点，若OD ⊥OE ，则C 的焦点坐标为（ ）A. （ 14 ，0）B. （ 12 ，0） C. （1，0） D. （2，0） 3.（2020·新课标Ⅱ·理）设O 为坐标原点，直线 x =a 与双曲线 C:x 2a2−y 2b 2=1(a >0,b >0) 的两条渐近线分别交于 D,E 两点，若 △ODE 的面积为8，则C 的焦距的最小值为（ ） A. 4 B. 8 C. 16 D. 32 4.（2020·天津）设双曲线 C 的方程为x 2a 2−y 2b 2=1(a >0,b >0) ，过抛物线 y 2=4x 的焦点和点 (0,b) 的直线为l ．若C 的一条渐近线与 l 平行，另一条渐近线与l 垂直，则双曲线C 的方程为（ ） A.x 24−y 24=1 B. x 2−y 24=1 C.x 24−y 2=1 D. x 2−y 2=15.（2019·天津）已知抛物线 的焦点为F ，准线为l.若与双曲线x 2a2−y 2b 2=1(a >0,b >0) 的两条渐近线分别交于点A 和点B ， 且 |AB|=4|OF| （O 为原点），则双曲线的离心率为（ ） A. √2 B. √3 C. 2 D. √56.（2020·北京）设抛物线的顶点为O ，焦点为F ，准线为l ．P 是抛物线上异于O 的一点，过P 作 PQ ⊥l 于Q ，则线段 FQ 的垂直平分线（ ）．A. 经过点OB. 经过点PC. 平行于直线 OPD. 垂直于直线 OP7.（2019·天津）已知抛物线 y 2=4x 的焦点为 F ，准线为 l ，若 l 与双曲线 x 2a 2−y 2b 2=1 (a >0,b >0) 的两条渐近线分别交于点 A 和点 B ，且 |AB|=4|OF| （ O 为原点），则双曲线的离心率为（ ）A. √2B. √3C. 2D. √5 8.（2019·全国Ⅲ卷理）双曲线 C:x 24−y 22=1 的右焦点为F,点P 在C 的一条渐近线上,O 为坐标原点,若|PO|=|PF|,则△PFO 的面积为（ ）A. 3√24B. 3√22C. 2√2D. 3√29.已知椭圆E:x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ．短轴的一个端点为M ，直线l:3x-4y=0交椭圆E 于A,B两点．若|AF+BF|=4，点M 到直线l 的距离不小于45 ， 则椭圆E 的离心率的取值范围是（ ）A. (0,√32] B. (0,34] C. [√32.1) D. [34,1)10.将离心率为e 1的双曲线c 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度，得到离心率为e 2的双曲线c 2 ， 则（ ）A. 对任意的a,b ， e 1>e 2B. 当a >b 时，e 1>e 2；当a <b 时，e 1<e 2C. 对任意的a,b ， e 1<e 2D. 当a >b 时，e 1<e 2；当a <b 时，e 1>e 211.将离心率为e 1的双曲线c 1的实半轴长a 和虚半轴长b (a ≠b )同时增加(m >0)个单位长度，得到离心率为e 2的双曲线c 2 ， 则（ ）A. 对任意的a,b,e 1>e 2B. 当a >b 时，e 1>e 2；当a <b 时，e 1<e 2C. 对任意的a,b,e 1<e 2D. 当a >b 时，e 1<e 2；当a <b 时，e 1>e 2二、填空题（共5题；共6分）12.（2020·新课标Ⅰ·理）已知F 为双曲线 C:x 2a2−y 2b 2=1(a >0,b >0) 的右焦点，A 为C 的右顶点，B 为C上的点，且BF 垂直于x 轴.若AB 的斜率为3，则C 的离心率为________.13.（2019·江苏）在平面直角坐标系 xOy 中，P 是曲线 y =x +4x (x >0) 上的一个动点，则点P 到直线x +y =0的距离的最小值是________. 14.（2019·浙江）已知椭圆x 29+y 25=1 的左焦点为F ，点P 在椭圆且在x 轴上方，若线段PF 的中点在以原点O 为圆心，|OF|为半径的圆上，则直线PF 的斜率是________ 15.（2018·北京）已知椭圆 M:x 2a 2+y 2b 2=1(a >b >0) ,双曲线 N:x 2m 2−y 2n 2=1 . 若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为________；双曲线N 的离心率为________16.（2017·江苏）在平面直角坐标系xOy 中，双曲线x 23﹣y 2=1的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是F 1 ， F 2 ， 则四边形F 1PF 2Q 的面积是________．三、解答题（共9题；共85分）17.（2020·新课标Ⅲ·理）已知椭圆 C:x 225+y 2m 2=1(0<m <5) 的离心率为√154，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线 x =6 上，且 |BP|=|BQ| ， BP ⊥BQ ，求 △APQ 的面积．18.（2020·新课标Ⅱ·文）已知椭圆C 1：x 2a 2+y 2b 2=1 (a>b>0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴重直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD|= 43 |AB|． （1）求C 1的离心率；（2）若C 1的四个顶点到C 2的准线距离之和为12，求C 1与C 2的标准方程．19.（2020·新课标Ⅰ·理）已知A 、B 分别为椭圆E ：x 2a 2+y 2=1 （a>1）的左、右顶点，G 为E 的上顶点，AG ⃗⃗⃗⃗⃗ ⋅GB ⃗⃗⃗⃗⃗ =8 ，P 为直线x=6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ． （1）求E 的方程； （2）证明：直线CD 过定点.20.（2020·新高考Ⅱ）已知椭圆C ： x 2a 2+y 2b 2=1(a >b >0) 过点M （2，3）,点A 为其左顶点，且AM 的斜率为 12 ， （1）求C 的方程；（2）点N 为椭圆上任意一点，求△AMN 的面积的最大值.21.（2019·天津）设椭圆x2a2+y2b2=1(a>b>0)的左焦点为F，左顶点为A，顶点为B.已知√3|OA|=2|OB|（O为原点）.（Ⅰ）求椭圆的离心率；（Ⅱ）设经过点F且斜率为34的直线l与椭圆在x轴上方的交点为p，圆C同时与x轴和直线l 相切，圆心C在直线x=4上，且OC∥AP，求椭圆的方程.22.（2019·全国Ⅲ卷文）已知曲线C：y= x22，D为直线y= −12上的动点，过D作C的两条切线，切点分别为A，B.（1）证明：直线AB过定点：（2）若以E(0，52)为圆心的圆与直线AB相切，且切点为线段AB的中点，求该圆的方程.23.（2019·全国Ⅲ卷理）已知曲线C: y=x22，D为直线y=- 12的动点，过D作C的两条切线，切点分别为A，B.（1）证明：直线AB过定点；（2）若以E（0，52）为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE的面积.24.（2019·全国Ⅱ卷文）已知F1,F2是椭圆C：x2a2+y2b2=1(a>b>0)的两个焦点，P为C上的点，O为坐标原点。

普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的. （1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （ ）A. ∅B. }2{C. }5{D. }5,2{ 【答案】B 【解析】.},2{},4,,3{},4,3,2{B A C A U u 选=∴==（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 【答案】A 【解析】..∴.1-,1∴,2),2),1.1-,1.22,0-∴22-)2222222A b a b a i bi a i bi a b a b a b a ab b a i abi b a bi a 选件综上，是充分不必要条不是必要条件，或（是充分条件，（或（=====+=+∴======∴===+=+（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm【答案】D 【解析】.138.93*3.186*3.363*4*3.935*34*6363*4*3D S S S S S S S S S S S 。

选几何体表面面积左面面积右面面积前后面面积，上底面面积几何体下底面面积右右前后上下左右前后上下=++++=∴=======+===4.为了得到函数()).∈(33R a a xx x f +=的图像，可以将函数x y 3sin 2=的图像（ ）A.向右平移4π个单位B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位【答案】D【解析】.12π3sin 2∴)12π(3sin 2)4π3sin(23cos 3sin D x y x x x x y 可以得到。

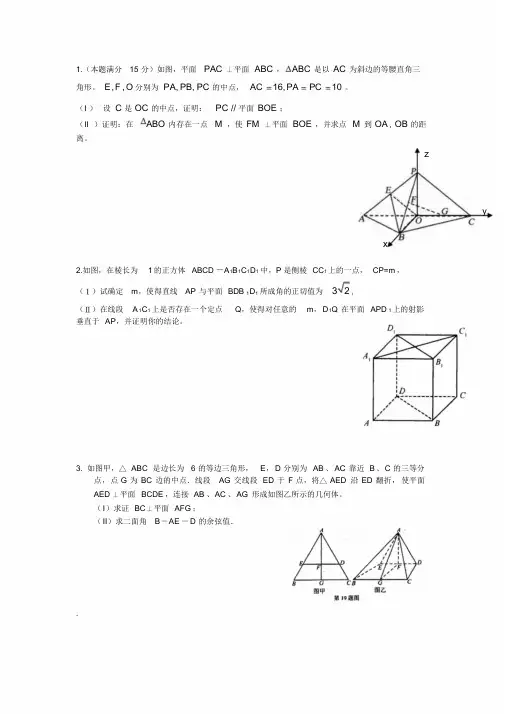
1.（本题满分15 分）如图，平面PAC ⊥平面ABC ，ABC 是以AC 为斜边的等腰直角三角形。

E,F ,O分别为PA, PB, PC 的中点，AC 16, PA PC 10 。

（I ）设 C 是OC 的中点，证明：PC // 平面BOE ；（II ）证明：在ABO 内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA , OB 的距离。

zyx2.如图，在棱长为 1 的正方体ABCD －A1B1C1D1 中，P 是侧棱CC1 上的一点，CP=m ，（Ⅰ）试确定m，使得直线AP 与平面BDB 1D1 所成角的正切值为 3 2 ；（Ⅱ）在线段A1C1 上是否存在一个定点Q，使得对任意的m，D1Q 在平面APD 1 上的射影垂直于AP，并证明你的结论。

3. 如图甲，△ABC 是边长为 6 的等边三角形，E，D 分别为AB 、AC 靠近B、C 的三等分点，点G 为BC 边的中点．线段AG 交线段ED 于F 点，将△AED 沿ED 翻折，使平面AED ⊥平面BCDE ，连接AB 、AC 、AG 形成如图乙所示的几何体。

（I）求证BC⊥平面AFG ；（II）求二面角B－AE －D 的余弦值．.4 在如图所示的几何体中，EA 平面ABC，DB 平面ABC，AC BC ，AC BC BD 2AE ，M是AB的中点．（1）求证：CM EM ；D（2）求CM与平面CDE所成的角ECAMB4.如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∥CF ，BCF CEF ，AD 3，E F 2．90D（Ⅰ）求证：AE ∥平面DCF ；AC （Ⅱ）当AB 的长为何值时，二面角 A EF C 的大小为60 ？BF E（第18 题）25.如图，在矩形ABCD 中，点E，F 分别在线段AB ，AD 上，AE=EB=AF= FD 4.沿直3线EF 将AEF 翻折成A' EF , 使平面A' EF 平面BEF.（I）求二面角A' FD C 的余弦值；（II ）点M ，N 分别在线段FD，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使 C与A' 重合，求线段FM 的长.6.如图，在三棱锥P-ABC 中，AB ＝AC，D 为BC 的中点，PO⊥平面ABC ，垂足O 落在线段AD 上，已知BC＝8，PO＝4，AO＝3，OD＝2（Ⅰ）证明：AP⊥BC；（Ⅱ）在线段AP 上是否存在点M ，使得二面角A-MC-B 为直二面角？若存在，求出AM 的长；若不存在，请说明理由。

复习: 电阻一定时,导体中的电流跟导体两端的电压成正比. 电压不变时，导体中的电流跟导体的电阻成反比. 上节课通过实验探究了电流与电压、电阻的关系: 以上实验结果综合起来得出结论，即欧姆定律。

结论是：欧姆于1787年3月16日生于德国巴伐利亚的埃朗根 。

1811年毕业于埃朗根大学并取得哲学博士学位， 1854年7月6日在慕尼黑逝世。

欧姆最重要的贡献是建立电路定律， 著作:《伽伐尼电路——数学研究》 为了纪念他在电路理论方面的贡献，电阻单位命名为欧姆。

导体中的电流跟导体两端的电压成正比，跟导体的电阻成反比。

I——电流——安培（A ）U——电压——伏特（V ） R——电阻——欧姆（Ω） （1）内容： （2）公式： （3）单位：I=U/R 欧姆定律是从实验中总结出来的规律，它适用于任何情况下的电流计算。

欧姆定律公式中各个物理量只能是同一导体在同一时刻所具有的量，也就是说不能用甲导体的电压、电阻去求乙导体的电流。

或用甲时刻的电压、电阻去求乙时刻的电流。

氖管 电阻 例题：试电笔内必须有一支很大的电阻，用来限制通过人体的电流。

现用一支试电笔，其中的电阻为880KΩ，氖管的电阻和人体的电阻都比这个小得多，可以不计。

使用时流过人体的电流是多少? 解题要求： 1、先读题，后画出电路图，再标出已知量、未知量 2、要换算单位的先换算 3、要对题目进行必要分析，后分步进行计算 4、解题过程中要先写出公式，再在公式中代入数据和单位，最后得结果。

5、每个物理量用自己的字母表示。

氖管 电阻 例题：试电笔内必须有一支很大的电阻，用来限制通过人体的电流。

现用一支试电笔，其中的电阻为880KΩ，氖管的电阻和人体的电阻都比这个小得多，可以不计。

使用时流过人体的电流是多少? 如果把安培换算成毫安，则 解： 已知:R ＝880KΩ R=880 KΩ I=? U ＝220V 分析：使用这支试电笔时，流过人体的电流是0.25mA,这个电流的大小对人体是安全的。

高二理科数学寒假网络课程（五）--浙江省高考中的解析几何大题浙江省近几年高考中，解析几何大题难度较大，作为压轴题能较好的区分学生的程度，题目新颖，变化多端，掌握起来没有固定套路。

2013年：椭圆,圆,直线综合.(1)求椭圆方程 (2)最值条件下求直线方程2012年：椭圆,直线综合. (1)求椭圆方程 (2)最值条件下求直线方程2011年：抛物线,圆,直线综合. (1)求点到准线距离 (2)求直线方程2010年：椭圆,圆,直线综合. (1)求直线方程 (2)求参数取值范围2009年：椭圆,抛物线,直线综合.(1)求椭圆方程 (2)求参数的最值（2013年浙江）如图，点P(0，－1)是椭圆C1：22221x ya b+=(a＞b＞0)的一个顶点，C1的长轴是圆C2：x2＋y2＝4的直径，l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D．(1)求椭圆C1的方程；(2)求△ABD面积取最大值时直线l1的方程．如图，点P (0，－1)是椭圆C 1：22221x y a b+=(a ＞b ＞0)的一个顶点，C 1的长轴是圆C 2：x 2＋y 2＝4的直径，l 1，l 2是过点P 且互相垂直的两条直线，其中l 1交圆C 2于A ，B 两点，l 2交椭圆C 1于另一点D ． (1)求椭圆C 1的方程；(2)求△ABD 面积取最大值时直线l 1的方程．解：(1)由题意得1,2.b a =⎧⎨=⎩ 所以椭圆C 的方程为24x ＋y 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，D (x 0，y 0)．由题意知直线l 1的斜率存在，不妨设其为k ， 则直线l 1的方程为y ＝kx －1.又圆C 2：x 2＋y 2＝4，故点O 到直线l 1的距离211d k =+，所以22243||2421k AB d k +=-=+. 又l 2⊥l 1，故直线l 2的方程为x ＋ky ＋k ＝0. 由220,44,x ky k x y ++=⎧⎨+=⎩ 得(4＋k 2)x 2＋8kx ＝0， 故0284kx k=-+. 所以|PD |＝22814k k ++. 设△ABD 的面积为S ，则S ＝12|AB |·|PD |＝228434k k ++， 所以S ＝2232134343k k +++≤22321613131324343k k =+⋅+，当且仅当102k =±时取等号． 所以所求直线l 1的方程为y ＝102x ±－1.（2012年浙江） 如图，椭圆C ：2222+1x y a b =(a ＞b ＞0)的离心率为12，其左焦点到点P (2，1)的距离为10．不过原点O 的直线l 与C 相交于A ，B 两点，且线段AB被直线OP 平分． (1)求椭圆C 的方程；(2) 求∆ABP 的面积取最大时直线l 的方程．如图，椭圆C ：2222+1x y a b =(a ＞b ＞0)的离心率为12，其左焦点到点P (2，1)的距离为10．不过原点O 的直线l 与C 相交于A ，B 两点，且线段AB 被直线OP 平分．(1)求椭圆C 的方程；(2) 求∆ABP 的面积取最大时直线l 的方程． (1)由题：12c e a ==； (1)左焦点(﹣c ，0)到点P (2，1)的距离为：22(2)1d c =++=10． (2)由(1) (2)可解得：222431a b c ===，，．∴所求椭圆C 的方程为：22+143x y =．(2)易得直线OP 的方程：y ＝12x ，设A (x A ，y A )，B (x B ，y B )，R (x 0，y 0)．其中y 0＝12x 0． ∵A ，B 在椭圆上，∴220220+12333434422+143A A A B A B AB A B A B B B x y x y y x x k x x y y y x y ⎧=⎪-+⎪⇒==-=-=-⎨-+⎪=⎪⎩． 设直线AB 的方程为l ：y ＝﹣32x m +(m ≠0)，代入椭圆：2222+143333032x y x mx m y x m ⎧=⎪⎪⇒-+-=⎨⎪+⎪⎩＝-．显然222(3)43(3)3(12)0m m m ∆=-⨯-=->． ∴﹣12＜m ＜12且m ≠0．由上又有：A B x x +＝m ，A B y y +＝233m -．∴|AB |＝1AB k +|A B x x -|＝1AB k +2()4A B A B x x x x +-＝1ABk +243m -．∵点P (2，1)到直线l 的距离为：31211ABABm m d k k -+-+==++．∴S ∆ABP ＝12d |AB |＝12|m ＋2|243m -，当|m ＋2|＝243m -，即m ＝﹣3 or m ＝0(舍去)时，(S ∆ABP )max ＝12．此时直线l 的方程y ＝﹣3122x +．(2011年浙江）已知抛物线1:C2x＝y，圆2:C22(4)1x y+-=的圆心为点M。

2013-2017年浙江高考理科数学历年真题之解析几何大题（教师版）1、（2013年）如图，点(0,1)P -是椭圆22122:1(0)x y C a b a b+=>>的一个顶点，1C 的长轴是圆222:4C x y +=的直径，12,l l 是过点P 且互相垂直的两条直线，其中1l 交2C 于,A B 两点，2l 交1C 于另一点D .(Ⅰ)求椭圆1C 的方程；ⅠⅠ()求ABD ∆面积取最大值时直线1l 的方程. (Ⅰ)解：依题意得21a b =⎧⎨=⎩ ，所以椭圆C 的方程为22 1.4x y += ⅠⅠ()设112200(,),(,),(,),A x y B x y D x y 由题意知直线1l 的斜率存在，不妨设为k ，则1l 的方程为1y kx =-.又圆222:4C x y +=，故点O 到直线1l的距离d =所以||AB ==又12l l ⊥，故直线2l 的方程为0x ky k ++=故028.4kx k =-+所以2||4PD k=+ 设ABD ∆的面积为S，则21||||24S AB PD k=⋅=+所以321313S =≤=当且仅当k =. 所求直线1l的方程为1y x =-.(第21题图)2、（2014年）如图，设椭圆(),01:2222>>=+b a by a x C 动直线l 与椭圆C 只有一个公共点P ，且点P 在第一象限.(Ⅰ)已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标；ⅠⅠ()若过原点O 的直线1l 与l 垂直，证明：点P 到直线1l 的距离的最大值为b a -.解析：（I ）设直线l 的方程为()0y kx m k =+<，由22221y kx mx y a b=+⎧⎪⎨+=⎪⎩，消去y 得，()22222222220b a k x a kmx a m a b +++-=，由于直线l 与椭圆C 只有一个公共点P ，故0∆=，即22220b m a k -+=，解得点P 的坐标为22222222,a km b m b a k b a k ⎛⎫- ⎪++⎝⎭， 由点P 在第一象限，故点P的坐标为22⎛⎫⎝； （II ）由于直线1l 过原点O ，且与l 垂直，故直线1l 的方程为0x ky +=，所以点P 到直线1l的距离d =，整理得22d =，因为22222b a k ab k+≥2222a b ≤=-，当且仅当2bk a=时等号成立， 所以点P 到直线1l 的距离的最大值为b a -.3、（2015年）已知椭圆222y x +=1上两个不同的点A , B 关于直线y =mx +21对称． (I)求实数m 的取值范围；(II)求△AOB 面积的最大值(O 为坐标原点)解: (I)设A (x 1, y 1), B (x 2, y 2), AB 的中点M (x 0, y 0), 则2x 0=x 1+x 2, 2y 0=y 1+y 2显然m ≠0, 故可设直线AB 的斜率k =2121x x y y --=m1-由222121=+y x ,222222=+y x , 相减得(x 1-x 2)(x 1+x 2)+2(y 1-y 2)(y 1+y 2)=0 即x 0m2-y 0=0 又点M (x 0, y 0)在直线y =mx +21上, ∴y 0=mx 0+21, 故得x 0=m 1-, y 0=21- 又点M 在椭圆1222=+y x 的内部, 故得41212+m <1, 解得m 2>32 因此, m >36或m <36- (此题用点差法最佳, 简明使得出错的几率小)法二: 设A (x 1, y 1), B (x 2, y 2), AB 的中点M (x 0, y 0), 则2x 0=x 1+x 2 显然m ≠0, 故可设直线AB 的方程为y =m1-x +b 由⎪⎩⎪⎨⎧=++-=22122y x bx m y 得(1+22m )x 2x m b 4-+2(b 2-1)=0有两个不等实根x 1, x 2,∴△=)1)(21(81622-+-b mm b >0 整理得m 2+2-m 2b 2>0 (*)且x 0=21(x 1+x 2)=222+m bm, y 0=m 1-x 0+b =222+m bm又∵点M (x 0, y 0)在直线y =mx +21上, ∴y 0=mx 0+21, 整理得bm =m m 222+-代入(*)式得m 2+22224)2(m m +->0 即4m 2-(m 2+2)>0, 解得m 2>32 因此, m >36或m <36- (其中也可得x 0=m 1-, y 0=21-)(II)由k =m 1-, 则0<k 2<23. 由(I)可得直线AB : y +21=k (x -k ) 即kx -y -k 221-=0∴原点O 到直线AB 的距离d =22121k k ++由⎪⎩⎪⎨⎧=+--=2221222y x k kx y 得x 2-2kx +21(2k 2+1)1222+-k =0 (利用|x 1-x 2|=∆)∴|AB |=21k +|x 1-x 2|=222222246121128)12(241k k k k k k k-++=+++-+故S △AOB =21|AB |d =8)21(841)46)(12(412222+--=-+k k k ≤22, 且0<k 2<23因此, 当k 2=21即m =2±时, △AOB 的面积S △AOB 有最大值224、（2016年）如图，设椭圆2221x y a+=()1a >.（1）求直线1y kx =+被椭圆截得的线段长（用a 、k 表示）；（2）若任意以点(0,1)A 为圆心的圆与椭圆至多有3个公共点，求椭圆离心率的取值范围. 解析：5、 (2017年)如图，已知抛物线x 2=y ，点A （-12，14），B （32，94），抛物线上的点p(x,y)(-12＜x ＜32)．过点B 作直线AP 的垂线，垂足为Q ．（1）求直线AP 斜率的取值范围； （2）求|PA|·|PQ|的最大值． 解析：。

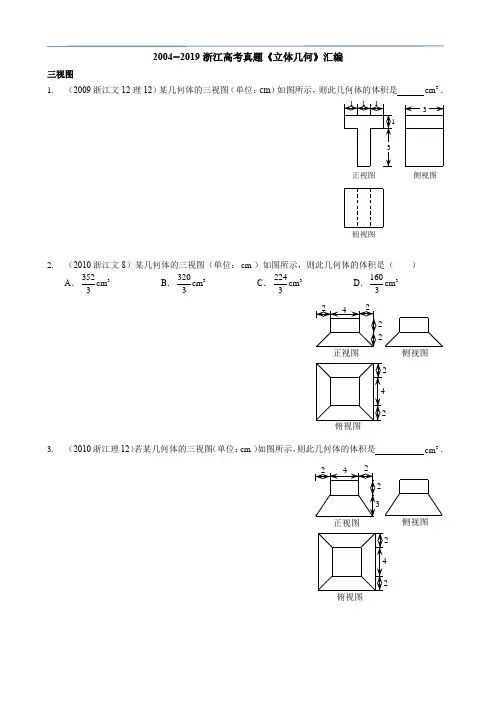
2004−2019浙江高考真题《立体几何》汇编三视图1. （2009浙江文12理12）某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．2. （2010浙江文8）某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（ ）A ．3352cm 3B ．3320cm 3C ．3224cm 3D ．3160cm 33. （2010浙江理12）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．侧视图俯视图正视图侧视图俯视图侧视图俯视图4. （2011浙江文7）某几何体的三视图如图所示，则这个几何体的直观图可以是（ ）5. （2011浙江理3）某几何体的三视图如图所示，则这个几何体的直观图可以是（ ）6. （2012浙江文3）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是（ ）A ．13cmB ．23cmC ．33cmD ．63cmDC BA侧视图俯视图正视图DCB A 侧视图俯视图正视图侧视图俯视图正视图7. （2012浙江理11）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积等于 3cm ．8. （2013浙江文5）已知某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（ ）A ．1083cmB ．1003cmC ．923cmD ．843cm9. （2013浙江理12）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于 3cm ．侧视图俯视图正视图俯视图侧视图正视图侧视图正视图3410. （2014浙江文3）某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（ ）A ．723cmB ．903cmC ．1083cmD ．1383cm11. （2014浙江理3）某几何体的三视图（单位：cm ）如图所示，则该几何体的表面积是（ ）A ．902cmB ．1292cmC ．1322cmD ．1382cm12. （2015浙江文2理2）某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（ ）A ．83cmB ．123cmC ．3233cmD ．403cm俯视图侧视图正视图俯视图侧视图正视图侧视图正视图13. （2016浙江理11）某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 2cm ，体积是 3cm ．14. （2016浙江文9）某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 2cm ，体积是 3cm ．15. （2017浙江3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（）A ．12π+B ．32π+C ．312π+D ．332π+俯视图正视图316. （2018浙江3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（ ）A ．2B ．4C ．6D ．817. （2019浙江4）祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V Sh 柱体，其中S 是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm ），则该柱体的体积（单位：3cm ）是（ ） A ．158B ．162C ．182D ．324俯视图正视图俯视图侧视图正视图点、直线、平面位置关系18. （2005浙江文7理6）设α，β为两个不同的平面，l ，m 为两条不同的直线，且l α⊂，m β⊂．有如下两个命题：①若αβ∥，则l m ∥；②若l m ⊥，则αβ⊥．那么（ ） A ．①是真命题，②是假命题 B ．①是假命题，②是真命题C ．①②都是真命题D ．①②都是假命题19. （2007浙江文7理6）若P 是两条异面直线l ，m 外的任意一点，则（ ）A ．过点P 有且仅有一条直线与l ，m 都平行B ．过点P 有且仅有一条直线与l ，m 都垂直C ．过点P 有且仅有一条直线与l ，m 都相交D ．过点P 有且仅有一条直线与l ，m 都异面20. （2008浙江文9）对两条不相交的空间直线a 与b ，必存在平面α，使得（ ）A ．a α⊂，b α⊂B ．a α⊂，b α∥C ．a α⊥，b α⊥D ．a α⊂，b α⊥21. （2009浙江文4）设α，β是两个不同的平面，l 是一条直线，以下命题正确的是（ ）A ．若l α⊥，αβ⊥，则l β⊂B ．若l α∥，αβ∥，则l β⊂C ．若l α⊥，αβ∥，则l β⊥D ．若l α⊥，αβ⊥，则l β⊥22. （2010浙江理6）设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是（ ）A ．若l m ⊥，m α⊂，则l α⊥B ．若l α⊥，l m ∥，则m α⊥C ．若l α∥，m α⊂，则l m ∥D ．若l α∥，m α∥，则l m ∥23. （2011浙江文4）若直线l 不平行于平面α，且l α⊄，则（ ）A ．α内的所有直线与l 异面B ．α内不存在与l 平行的直线C ．α内存在唯一的直线与l 平行D ．α内的直线与l 都想交24. （2011浙江理4）下列命题中错误的是（ ）A ．如果αβ平面⊥平面，那么平面α内一定存在直线平行于平面βB ．如果αβ平面不垂直于平面，那么平面α内一定不存在直线垂直于平面βC ．如果αγ平面⊥平面，βγ平面⊥平面，l αβ=，那么l γ⊥平面D ．如果αβ平面⊥平面，那么平面α内所有直线都垂直于平面β25. （2012浙江文5）设直线l 是直线，α，β是两个不同的平面．（ ）A ．若l α∥，l β∥，则αβ∥B ．若l α∥，l β⊥，则αβ⊥C ．若αβ⊥，l α⊥，则l β⊥D ．若αβ⊥，l α∥，则l β⊥26. （2013浙江文4）设m ，n 是两条不同的直线，α，β是两个不同的平面．（ ）A ．若m α∥，n α∥，则m n ∥B ．若m α∥，m β∥，则αβ∥C ．若m n ∥，m α⊥，则n α⊥D ．若m α∥，αβ⊥，则m β⊥27. （2014浙江文6）设m ，n 是两条不同的直线，α，β是两个不同的平面．（ ）A ．若m n ⊥，n α∥，则m α⊥B ．若m β∥，βα⊥，则m α⊥C ．若m β⊥，n β⊥，n α⊥，则m α⊥D ．若m n ⊥，n β⊥，βα⊥，则m α⊥28. （2015浙江文4）设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂．（ ）A ．若l β⊥，则αβ⊥B ．若αβ⊥，则l m ⊥C ．若l β∥，则αβ∥D ．若αβ∥，则l m ∥29. （2016浙江文2理2）已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足m α∥，n β⊥，则（ ） A ．m l ∥ B ．m n ∥C ．n l ⊥D ．m n ⊥30. （2018浙江6）已知平面α，直线m ，n 满足m α⊄，n α⊂，则“m n ∥”是“m α∥”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件小题31. （2004浙江文15）已知α平面⊥β平面，l αβ=，P 是空间一点，且P 到平行α，β的距离分别是1，2，则点P 到l 的距离为 ．32. （2004浙江理16）已知平面α和平面β相交于直线l ，P 是空间一点，P A ⊥α，垂足为A ，PB ⊥β，垂足为B ，且1PA =，2PB =，若点A 在β内的射影与点B 在α内的射影重合，则点P 到l 的距离为 ．33. （2004浙江文10理10）如图，在正三棱柱111ABC A B C -中，已知1AB =，D 在棱1BB 上，且1BD =，若AD 与平面11AA C C 所成的角为α，则sin α=（ ） ABCDDB 1A 1C 1CBA34. （2005浙江文12理12）设M ，N 是直角梯形ABCD 两腰的中点，DE ⊥AB 于E （如图）．现将△ADE沿DE 折起，使二面角A DE B --为45°，此时点A 在平面BCDE 内的射影为点B ，则M ，N 的连线与AE 所成角的大小等于 ．35. （2006浙江文8）如图，正三棱柱111ABC A B C -的各棱长都为2，E ，F 分别是AB ，11A C 的中点，则EF 的长是（ ） A ．2BCD36. （2006浙江理9）如图，O 是半径为1的球的球心，点A ，B ，C 在球面上，OA ，OB ，OC 两两垂直，E ，F 分别是大圆弧AB 与AC 的中点，则点E ，F 在该球面上的球面距离是（ ） A ．4π B ．3π C ．2π D．4B 1C 1A 1FE CBA37. （2006浙江文14）如图，正四面体ABCD 的棱长为1，平面α过棱AB ，且CD α∥，则正四面体上的所有点在平面α内的射影构成的图形面积是 ．38. （2006浙江理14）正四面体ABCD 的棱长为1，棱AB ∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 ．39. （2007浙江文17理16）已知点O 在二面角AB αβ--的棱上，点P 在α内，且45POB ∠=︒．若对于β内异于O 的任意一点Q ，都有45POQ ∠≥︒，则二面角AB αβ--的大小是 ．40. （2008浙江文15理14）如图，已知球O 的面上四点A ，B ，C ，D ，DA ⊥平面ABC ，AB ⊥BC ，DA AB BC ===O 的体积等于 ．BDACαBDACαDBCA41. （2008浙江理10）如图，AB 是平面α的斜线段．．．，A 为斜足．若点P 在平面α内运动，使得△ABP 的面积为定值，则动点P 的轨迹是（ ） A ．圆B ．椭圆C ．一条直线D ．两条平行直线42. （2009浙江理5）在三棱柱111ABC A B C -中，各棱长相等，侧棱垂直于底面，点D 是侧面11BB C C 的中心，则AD 与平面11BB C C 所成角的大小是（ ） A ．30° B ．45°C ．60°D ．90°43. （2009浙江理17）如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点，现将AFD △沿AF 折起，使平面ABD ⊥平面ABC ，在平面ABD 内过点D 作DK AB ⊥，K 为垂足，设AK t =，则t 的取值范围是 ．PABαKFDCBA44. （2012浙江理10）已知矩形ABCD ，1AB =，BC ．将△ABD 沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中，（ ）A ．存在某个位置，使得直线AC 与直线BD 垂直B ．存在某个位置，使得直线AB 与直线CD 垂直C ．存在某个位置，使得直线AD 与直线BC 垂直D ．对于任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直45. （2013浙江理10）在空间中，过点A 作平面π的垂线，垂足为B ，记()B f A π=．设α，β是两个不同的平面，对空间任意一点P ，()1Q f f P βα=⎡⎤⎣⎦，()2Q f f P αβ⎡⎤=⎣⎦，恒有12PQ PQ =，则（ ） A ．α平面与β平面垂直 B ．α平面与β平面所成的（锐）二面角为45° C ．α平面与β平面平行 D ．α平面与β平面所成的（锐）二面角为60°46. （2014浙江文10理17）如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练．已知点A 到墙面的距离为AB ，某目标点P 沿墙面上的射线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小．若15m AB =，25m AC =，30BCM ∠=︒，则tan θ的最大值是 ．（仰角θ为直线AP 与平面ABC 所成角）PMCB A47. （2015浙江文7）如图，斜线段AB 与平面α所成的角为60︒，B 为斜足，平面α上的动点P 满足30PAB ∠=︒，则点P 的轨迹是（ ）A ．直线B ．抛物线C ．椭圆D ．双曲线的一支48. （2015浙江理8）如图，已知ABC △，D 是AB 的中点，沿直线CD 将ACD △翻折成A CD '△，所成（ ） A ．A DB α'∠≤B ．A DB α'∠≥C ．A CB α'∠≤D ．A CB α'∠≥49. （2015浙江理13）如图，在三棱锥A BCD -中，3AB AC BD CD ====，2AD BC ==，点M ，N 分别为AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是 ．αPBAA'DCBAMNDCBA50. （2016浙江文14）如图，已知平面四边形ABCD ，3AB BC ==，1CD =，AD =90ADC ∠=︒．沿直线AC 将△ACD 翻折成△ACD'，直线AC 与BD'所成角的余弦的最大值是 ．51. （2016浙江理14）如图，在△ABC 中，2AB BC ==，120ABC ∠=︒．若平面ABC 外的点P 和线段AC 上的点D ，满足PD DA =，PB BA =，则四面体PBCD 的体积的最大值是 ．52. （2017浙江9）如图，已知正四面体D ABC -（所有棱长均相等的三棱锥），P ，Q ，R 分别为AB ，BC ，CA 上的点，AP PB =，2BQ CRQC RA==，分别记二面角D PR Q --，D PQ R --，D QR P --的平面角 为α，β，γ，则（ ） A ．γαβ<<B ．αγβ<<C ．αβγ<<D ．βγα<<D'DC APDCBARCQBP A D53. （2018浙江8）已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为1θ，SE 与平面ABCD 所成的角为2θ，二面角S AB C --的平面角为3θ，则（ ） A ．123θθθ≤≤ B ．321θθθ≤≤ C ．132θθθ≤≤ D ．231θθθ≤≤54. （2019浙江8）设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P AC B --的平面角为γ，则（ ） A ．,βγαγ<< B ．,βαβγ<< C ．,βαγα<< D ．,αβγβ<<大题55. （2004浙江文19）如图，已知正方形ABCD 和矩形ACEF所在的平面互相垂直，AB =1AF =，M 是线段EF 的中点． （1）求证：AM ∥平面BDE ； （2）求证：AM ⊥平面BDF ； （3）求二面角A DF B --的大小．M FEDCBA56. （2004浙江理19）如图，已知正方形ABCD 和矩形ACEF所在的平面互相垂直，AB =1AF =，M 是线段EF 的中点． （1）求证：AM ∥平面BDE ； （2）求二面角A DF B --的大小；（3）试在线段AC 上确定一点P ，使得PF 与BC 所成的角是60︒．57. （2005浙江文18）如图，在三棱锥P ABC -中，AB BC ⊥，12AB BC PA ==，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ．（1）求证：OD ∥平面PAB ；（2）求直线OD 与平面PBC 所成角的大小．58. （2005浙江理18）如图，在三棱锥P ABC -中，AB BC ⊥，AB BC kPA ==，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ． （1）求证：OD ∥平面PAB ；（2）当12k =，求直线PA 与平面PBC 所成角的大小；（3）当k 取何值时，O 在平面PBC 内的射影恰好为PBC △的重心？MFEDCBA59. （2006浙江文17）如图，在四棱锥P ABCD -中，底面为直角梯形，AD BC ∥，90BAD ∠=︒，PA ⊥底面ABCD ，且2PA AD AB BC ===，M ，N 分别为PC ，PB 的中点． （1）求证：PB DM ⊥；（2）求BD 与平面ADMN 所成角．60. （2006浙江理17）如图，在四棱锥P ABCD -中，底面为直角梯形，AD BC ∥，90BAD ∠=︒，PA ⊥底面ABCD ，且2PA AD AB BC ===，M ，N 分别为PC ，PB 的中点． （1）求证：PB DM ⊥；（2）求CD 与平面ADMN 所成的角．61. （2007浙江理19）在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC ⊥BC ，且2AC BC BD AE ===，M 是AB 的中点．（1）求证：CM EM ⊥；（2）求CM 与平面CDE 所成的角．62. （2007浙江文20）在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC BC ⊥，且2AC BC BD AE ===，M 是AB 的中点．（1）求证：CM EM ⊥；（2）求DE 与平面EMC 所成角的正切值．63. （2008浙江文20理18）如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∥CF ，90BCF CEF ∠=∠=︒，AD ，2EF =．（1）求证：AE DCF ∥平面；（2）当AB 的长为何值时，二面角A EF C --的大小为60°？64. （2009浙江文19）如图，DC ⊥平面ABC ，EB DC ∥，22AC BC EB DC ====，120ACB ∠=︒，P ，Q 分别为AE ，AB 的中点． （1）证明：PQ ACD ∥平面；（2）若AD 与平面ABE 所成角的正弦值．FEDCBA QPCDEBA65. （2009浙江理20）如图，平面PAC ⊥平面ABC ，ABC △是以AC 为斜边的等腰直角三角形，E ，F ，O 分别为P A ，PB ，AC 的中点，16AC =，10PA PC ==． （1）设G 是OC 的中点，证明：FG ∥平面BOE ；（2）证明：在ABO △内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA ，OB 的距离．66. （2010浙江文20）如图，在平行四边形ABCD 中，2AB BC =，120ABC ∠=︒，E 为线段AB 的中点，将ADE △沿直线DE 翻折成A DE '△，使平面A DE '⊥平面BCD ，F 为线段A C '的中点． （1）求证：BF ∥平面A DE '；（2）设M 为线段DE 的中点，求直线FM 与平面A DE '所成角的余弦值．67. （2010浙江理20）如图，在矩形ABCD 中，点E ，F 分别在线段AB ，AD 上，243AE EB AF FD ====， 沿直线EF 将AEF △翻折成A EF '△，使平面A EF '⊥平面BEF ． （1）求二面角A FD C '--的余弦值；（2）点M ，N 分别在线段FD ，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使C 与A '中和，求线段FM 的长．GF EPOCBAA'MFED CBANM A'F EDCB A68. （2011浙江文20）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上． （1）证明：AP BC ⊥；（2）已知8BC =，4PO =，3AO =，2OD =，求二面角B AP C --的大小．69. （2011浙江理20）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．已知8BC =，4PO =，3AO =，2OD =． （1）证明：AP BC ⊥；（2）在线段AP 上是否存在点M ，使得二面角A MC B --为直二面角？若存在，求出AM 的长；若不存在，请说明理由．70. （2012浙江文20）如图，在侧棱垂直底面的四棱柱1111ABCD A B C D -中，AD ⊥AB，AB =2AD =，4BC =，12AA =，E 是1DD 的中点，F 是平面11B C E 与直线1AA 的交点．（1）证明：（i ）11EF A D ∥；（ii ）111BA B C EF ⊥平面；（2）求1BC 与11B C EF 平面所成角的正弦值．OPDCBAOPDCBAD 1C 1B 1A 1EF B D CA71. （2012浙江理20）如图，在四棱锥P ABCD -中，底面是边长为的菱形，120BAD ∠=︒，且PA ABCD ⊥平面，PA =，M ，N 分别为PB ，PD 的中点．（1）证明：MN ∥平面ABCD ；（2）过点A 作AQ PC ⊥，垂足为点Q ，求二面角A MN Q --的平面角的余弦值．72. （2013浙江文20）如图，在四棱锥P ABCD -中，P A ⊥平面ABCD ，2AB BC ==，AD CD ==PA 120ABC ∠=︒．G 为线段PC 上的点． （1）证明：BD ⊥平面P AC ；（2）若G 为PC 的中点，求DG 与平面APC 所成的角的正切值；（3）若G 满足PC ⊥平面BGD ，求PGGC的值．73. （2013浙江理20）如图，在四面体A BCD -中，AD ⊥平面BCD ，BC CD ⊥，2AD =，BD =．M是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且3AQ QC =． （1）证明：PQ BCD ∥平面；（2）若二面角C BM D --的大小为60°，求BDC ∠的大小．QMNDABPGDB APQPMDBA74. （2014浙江文20）如图，在四棱锥A BCDE -中，平面ABC ⊥平面BCDE ，90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，AC =（1）证明：AC BCDE ⊥平面；（2）求直线AE 与平面ABC 所成角的正切值．75. （2014浙江理20）如图，在四棱锥A BCDE -中，平面ABC ⊥平面BCDE ，90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，AC（1）证明：DE ACD ⊥平面； （2）求二面角B AD E --的大小．76. （2015浙江文18）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，14AA =，1A 在底面ABC 的射影为BC 的中点，D 为11B C 的中点． （1）证明：11A D A BC ⊥平面；（2）求直线1A B 和平面11BB C C 所成的角的正弦值．BED CABED CAC 1B 1A 1DC BA77. （2015浙江理17）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，14AA =，1A 在底面ABC 的射影为BC 的中点，D 为11B C 的中点． （1）证明：11A D A BC ⊥平面；（2）求二面角11A BD B --的平面角的余弦值．78. （2016浙江文18）如图，三棱台ABC DEF -中，平面BCFE ⊥平面ABC ，90ACB ∠=︒，1BE EF FC ===，2BC =，3AC =．（1）求证：BF ⊥平面ACFD ；（2）求直线BD 与平面ACFD 所成角的余弦值．79. （2016浙江理17）如图，在三棱台ABC DEF -中，平面BCFE ⊥平面ABC ，90ACB ∠=︒，1BE EF FC ===，2BC =，3AC =．（1）求证：BF ⊥平面ACFD ；（2）求二面角B AD F --的平面角的余弦值．C 1B 1A 1DC BA80. （2017浙江19）如图，已知四棱锥P −ABCD ，△P AD 是以AD 为斜边的等腰直角三角形，BC ∥AD ，CD ⊥AD ，22PC AD DC CB ===，E 为PD 的中点． （1）证明：CE ∥平面P AB ；（2）求直线CE 与平面PBC 所成角的正弦值．81. （2018浙江19）如图，已知多面体111ABCA B C ，1A A ，1B B ，1C C 均垂直于平面ABC ，120ABC ∠=︒，14A A =，11C C =，12AB BC B B ===． （1）证明：1111AB A B C ⊥平面；（2）求直线1AC 与平面1ABB 所成的角的正弦值．82. （2019浙江19）如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，30BAC ∠=︒，11A A AC AC ==，E ，F 分别是AC ，11A B 的中点． （1）证明：EF BC ⊥；（2）求直线EF 与平面1A BC 所成角的余弦值．ED CBAPC 1B 1A 1CBAC 1B 1A 1FECBA。

解析几何高考真题一、单选题（共11题；共22分）1.（2020·新课标Ⅲ·理）设双曲线C ：x 2a 2−y 2b 2=1 （a>0，b>0）的左、右焦点分别为F 1 ， F 2 ， 离心率为 √5 ．P 是C 上一点，且F 1P ⊥F 2P ．若△PF 1F 2的面积为4，则a=（ ） A. 1 B. 2 C. 4 D. 82.（2020·新课标Ⅲ·理）设O 为坐标原点，直线x=2与抛物线C ：y 2=2px(p>0)交于D ，E 两点，若OD ⊥OE ，则C 的焦点坐标为（ ）A. （ 14 ，0）B. （ 12 ，0） C. （1，0） D. （2，0） 3.（2020·新课标Ⅱ·理）设O 为坐标原点，直线 x =a 与双曲线 C:x 2a2−y 2b 2=1(a >0,b >0) 的两条渐近线分别交于 D,E 两点，若 △ODE 的面积为8，则C 的焦距的最小值为（ ） A. 4 B. 8 C. 16 D. 32 4.（2020·天津）设双曲线 C 的方程为x 2a 2−y 2b 2=1(a >0,b >0) ，过抛物线 y 2=4x 的焦点和点 (0,b) 的直线为l ．若C 的一条渐近线与 l 平行，另一条渐近线与l 垂直，则双曲线C 的方程为（ ） A.x 24−y 24=1 B. x 2−y 24=1 C.x 24−y 2=1 D. x 2−y 2=15.（2019·天津）已知抛物线 的焦点为F ，准线为l.若与双曲线x 2a2−y 2b 2=1(a >0,b >0) 的两条渐近线分别交于点A 和点B ， 且 |AB|=4|OF| （O 为原点），则双曲线的离心率为（ ） A. √2 B. √3 C. 2 D. √56.（2020·北京）设抛物线的顶点为O ，焦点为F ，准线为l ．P 是抛物线上异于O 的一点，过P 作 PQ ⊥l 于Q ，则线段 FQ 的垂直平分线（ ）．A. 经过点OB. 经过点PC. 平行于直线 OPD. 垂直于直线 OP7.（2019·天津）已知抛物线 y 2=4x 的焦点为 F ，准线为 l ，若 l 与双曲线 x 2a 2−y 2b 2=1 (a >0,b >0) 的两条渐近线分别交于点 A 和点 B ，且 |AB|=4|OF| （ O 为原点），则双曲线的离心率为（ ）A. √2B. √3C. 2D. √5 8.（2019·全国Ⅲ卷理）双曲线 C:x 24−y 22=1 的右焦点为F,点P 在C 的一条渐近线上,O 为坐标原点,若|PO|=|PF|,则△PFO 的面积为（ ）A. 3√24B. 3√22C. 2√2D. 3√29.已知椭圆E:x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ．短轴的一个端点为M ，直线l:3x-4y=0交椭圆E 于A,B两点．若|AF+BF|=4，点M 到直线l 的距离不小于45 ， 则椭圆E 的离心率的取值范围是（ ）A. (0,√32] B. (0,34] C. [√32.1) D. [34,1)10.将离心率为e 1的双曲线c 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度，得到离心率为e 2的双曲线c 2 ， 则（ ）A. 对任意的a,b ， e 1>e 2B. 当a >b 时，e 1>e 2；当a <b 时，e 1<e 2C. 对任意的a,b ， e 1<e 2D. 当a >b 时，e 1<e 2；当a <b 时，e 1>e 211.将离心率为e 1的双曲线c 1的实半轴长a 和虚半轴长b (a ≠b )同时增加(m >0)个单位长度，得到离心率为e 2的双曲线c 2 ， 则（ ）A. 对任意的a,b,e 1>e 2B. 当a >b 时，e 1>e 2；当a <b 时，e 1<e 2C. 对任意的a,b,e 1<e 2D. 当a >b 时，e 1<e 2；当a <b 时，e 1>e 2二、填空题（共5题；共6分）12.（2020·新课标Ⅰ·理）已知F 为双曲线 C:x 2a2−y 2b 2=1(a >0,b >0) 的右焦点，A 为C 的右顶点，B 为C上的点，且BF 垂直于x 轴.若AB 的斜率为3，则C 的离心率为________.13.（2019·江苏）在平面直角坐标系 xOy 中，P 是曲线 y =x +4x (x >0) 上的一个动点，则点P 到直线x +y =0的距离的最小值是________. 14.（2019·浙江）已知椭圆x 29+y 25=1 的左焦点为F ，点P 在椭圆且在x 轴上方，若线段PF 的中点在以原点O 为圆心，|OF|为半径的圆上，则直线PF 的斜率是________ 15.（2018·北京）已知椭圆 M:x 2a 2+y 2b 2=1(a >b >0) ,双曲线 N:x 2m 2−y 2n 2=1 . 若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为________；双曲线N 的离心率为________16.（2017·江苏）在平面直角坐标系xOy 中，双曲线x 23﹣y 2=1的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是F 1 ， F 2 ， 则四边形F 1PF 2Q 的面积是________．三、解答题（共9题；共85分）17.（2020·新课标Ⅲ·理）已知椭圆 C:x 225+y 2m 2=1(0<m <5) 的离心率为√154，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线 x =6 上，且 |BP|=|BQ| ， BP ⊥BQ ，求 △APQ 的面积．18.（2020·新课标Ⅱ·文）已知椭圆C 1：x 2a 2+y 2b 2=1 (a>b>0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴重直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD|= 43 |AB|． （1）求C 1的离心率；（2）若C 1的四个顶点到C 2的准线距离之和为12，求C 1与C 2的标准方程．19.（2020·新课标Ⅰ·理）已知A 、B 分别为椭圆E ：x 2a 2+y 2=1 （a>1）的左、右顶点，G 为E 的上顶点，AG ⃗⃗⃗⃗⃗ ⋅GB ⃗⃗⃗⃗⃗ =8 ，P 为直线x=6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ． （1）求E 的方程； （2）证明：直线CD 过定点.20.（2020·新高考Ⅱ）已知椭圆C ： x 2a 2+y 2b 2=1(a >b >0) 过点M （2，3）,点A 为其左顶点，且AM 的斜率为 12 ， （1）求C 的方程；（2）点N 为椭圆上任意一点，求△AMN 的面积的最大值.21.（2019·天津）设椭圆x2a2+y2b2=1(a>b>0)的左焦点为F，左顶点为A，顶点为B.已知√3|OA|=2|OB|（O为原点）.（Ⅰ）求椭圆的离心率；（Ⅱ）设经过点F且斜率为34的直线l与椭圆在x轴上方的交点为p，圆C同时与x轴和直线l 相切，圆心C在直线x=4上，且OC∥AP，求椭圆的方程.22.（2019·全国Ⅲ卷文）已知曲线C：y= x22，D为直线y= −12上的动点，过D作C的两条切线，切点分别为A，B.（1）证明：直线AB过定点：（2）若以E(0，52)为圆心的圆与直线AB相切，且切点为线段AB的中点，求该圆的方程.23.（2019·全国Ⅲ卷理）已知曲线C: y=x22，D为直线y=- 12的动点，过D作C的两条切线，切点分别为A，B.（1）证明：直线AB过定点；（2）若以E（0，52）为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE的面积.24.（2019·全国Ⅱ卷文）已知F1,F2是椭圆C：x2a2+y2b2=1(a>b>0)的两个焦点，P为C上的点，O为坐标原点。