平行断面法和不平行断面法

储量计算中平行断面法公式的使用条件
平行断面法是一种有效的储量计算方法，在计算储量时可以得到准确可靠的结果。

它的使用条件有几方面：
1. 平行断面法需要被测采区的构造特征具有一定的相似性，即同一构造带任意两个断面的构造性质不同，但任意两断面之间的构造特征都是相同的。

2. 此外，平行断面法要求所采取的断面长度足够长，而且断面间必须保持一定的距离，以确保在计算储量时所采用的断面宽度是一致的。

3. 平行断面法要求断面宽度和断面之间的距离应该根据拉格朗日原理确定。

如果断面宽度和断面间的距离不能满足拉格朗日原理的要求，则该法的结果将无效。

4. 平行断面法的计算过程中还需要对断面粗略地进行等高计算，以便确定每条断面的储量，以及进行断面的整体赋值。

5. 除此之外，平行断面法还要求所采取的断面类型为连续断面，且断面之间没有显著的不同，这样才能全面反映构造带内储量变化状况。

以上是平行断面法公式使用的条件。

在使用该法之前，应该仔细核查每项条件，确保其满足计算可行性，从而得出准确可靠的储量计算结果。

矿量计算方法LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】资源量与储量计算方法储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD法等等。

（一）地质块段法计算步骤：首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表地质块段法储量计算表块段编号资源储量级别块段面积（m2）平均厚度(m）块段体积（m3）矿石体重（t/m3）矿石储量（资源量）平均品位（%）金属储量(t）备注需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

实习十一平行断面法储量计算一、实习目的通过本实习，熟悉断面法计算储量的一般原理，掌握平行断面法储量计算的程序、方法和具体步骤。

二、实习要求1．掌握坑、钻及断面、块段等平均品位的计算方法。

2．用方格法计算面积。

3．计算出一个块段的铜储量，本应按不同级别的矿石分别计算储量，但因实习时间所限。

暂不要求。

4．本次实习只要求计算能利用储量，暂不能利用储量的计算可留作同学们课外练习，进一步巩固所学的有关知识。

三、方法原理断面法计算储量，要求勘探工程有规律地布置，即沿垂直的或水平的剖面揭穿矿体，便于作出垂直的或水平的断面图（剖面图）。

应用若干个断面（或剖面）将矿体划分若干个块段，别计算这些块段的储量，然后将各块段的储量相加，即为矿体的总储量。

断面法是以勘探剖面（断面）图或中段平面图为基础的，它的实质是将剖面上的资料外推到控制范围中去。

根据断面是否彼此平行，可分为平行断面法和不平行断面法两种。

本次实习只应用平行断面法。

平行断面法的前提是勘探剖面（断面）之间是相互平行的，以两个断面间的块段作为储量计算基本单元，在断面图上根据既定的工业指标，先将矿体的边界圈定以后，利用求积仪或曲线仪，或采用透明方格纸、几何图形等方法，测量断面上矿体的面积，然后计算相邻断间各块段的体积。

再结合矿体各块段的平均品位和平均体重等参数，计算出各块段的矿石储和金属储量。

最后计算出总矿石储量和金属储量。

四、实习步骤1．应用透明方格纸测量第Ⅱ和第Ⅲ勘探线剖面图上能利用矿体的面积，并将测定结果经过比例尺换算后，填入表XI-3和表XI-4中。

2．计算块段的平均品位o应用上次实习计算的第Ⅱ剖面各勘探工程矿石的平均品位，并将这些值填入表11-1。

Ⅲ剖面各勘探工程矿石的平均品位，已在表XI-1中给出。

o用算术平均法计算断面的平均品位，将计算结果填入表XI-1。

o用加权平均法计算每一断面的平均品位，将计算结果填入表XI-2。

o根据以上计算结果，用算术平均法和加权平均法计算块段的矿石平均品位，完成表XI－3。

平行断面法与地质块段法地质学是一个广泛的领域，它涉及各种各样的技术和方法。

其中，平行断面法和地质块段法是两种被广泛应用的方法。

本文将讲解这两种方法的优点和应用情况。

一、平行断面法平行断面法是研究岩石和地质构造的一种方法。

它是通过将地质剖面在一定的间隔距离上作垂直切割，然后在连通的部位上绘制平行的线条，从而描绘出地质构造和岩石形成的情况。

平行断面法的主要优点在于可以显示岩石和地质构造在空间中的成型情况，使研究者可以更好地理解地球的构造、演化和地质历史。

在石油勘探和开发领域，平行断面法也被广泛应用。

它可以帮助研究者找到目标油气层，也可以提供有关岩石孔隙度、渗透率等重要参数的信息。

二、地质块段法地质块段法是一种在地质勘探、矿产勘探和土地利用规划中广泛应用的方法。

它是通过将区域内的地质面按照一定参数进行分割，然后在每一个地质块中进行详细的研究和分析，从而得到每一个地质块的地质特征和属性。

地质块段法的主要优点在于可以提高地质调查和矿产勘探的效率、可靠性和准确性。

它也是进行土地利用规划的一种有效的方法，可以帮助规划者更好地了解土地利用的可能性和风险。

三、应用情况平行断面法和地质块段法是地质学研究和勘探中常用的两种方法。

在石油勘探、矿物勘探、地震勘探等领域中被广泛应用。

两种方法的优点和适用情况不同，需要根据实际情况和研究目的进行选择和应用。

在石油勘探中，平行断面法可以帮助研究人员进行地质模拟和预测，预报油气储层的分布情况和产量。

地质块段法则可用于进行储油层及表面水矿化防治研究。

在矿物勘探中，平行断面法常用于矿床勘探、矿物矿化特征分析、矿物资源可持续性评价等方面。

地质块段法则常用于地质变形区水文地质背景研究、矿产资源预测和洞脉型矿体的富集规律研究。

在土地利用规划中，平行断面法可以用于地质遥感和数字地球建设中，帮助规划者更好地了解土地形成的背景和特征。

地质块段法则可用于近地面物质勘探、地下矿产资源分析等方面。

综上所述，平行断面法和地质块段法是两种常用的地质学研究方法。

（一）地质块段法计算步骤：1.首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；2.然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；3.所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表地质块段法储量计算表块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

缺点：误差较大。

当工程控制不足，数量少，即对矿体产状、形态、内部构造、矿石质量等控制严重不足时，其地质块段划分的根据较少，计算结果也类同其他方法误差较大。

（二）开采块段法开采块段主要是按探、采坑道工程的分布来划分的。

可以为坑道四面、三面或两面包围形成矩形、三角形块段；也可为坑道和钻孔联合构成规则或不甚规则块段。

同时，划分开采块段时，应与采矿方法规定的矿块构成参数相一致，与储量类别相适应。

该法的储量计算过程和要求与地质块段法基本相同。

凡在矿床勘探阶段，应用若干勘探剖面把矿床横切截为若干个块段，分别计算这些块段的储量，将各块段的储量合起来即矿体的总储量，这种方法称断面法或剖面法。

断面法还可分为垂直断面法、水平断面法及不平行断面法。

一、平行断面法平行断面法储量计算按以下步骤进行：（一）首先在各个勘探剖面图上测定矿体的面积；（二）其次，在两个勘探剖面面积之间计算矿体的体积。

为此，必须根据相邻两剖面矿体之相对面积差的大小来分别选择不同的公式进行计算。

当相邻两剖面上矿体之相对面积差＜40%时，一般选用梯形体积公式（图1），其公式为：式中：V－两剖面间矿体体积（立方米）；L－两相邻剖面之间距（米）；S1S2－两相邻剖面上的矿体面积（平方米）。

图1 相邻剖面间之梯形块段当相邻两剖面上矿体之相对面积差＞40%时，一般选用截锥体积公式计算体积（图2），其公式为：图2 相邻剖面间之锥块段在应用截锥公式，要进行开平方计算，实际计算较繁琐，为了简化计算，有人提出改用校正的梯形公式，其方法如下：假如使相邻两剖面的间距为L，则这些剖面间块段的体积V大致等于两剖面面积总和之半与某一修正系数F的乘积，即：修正系数F的大小等于该块段精确体积与近似体积之比：把F值代入公式中，则得：当S1＝S2时，则F＝1，因而。

在这种情况下，用近似公式也可得到精确的结果。

在S1或S2＝0时则F=2/3，这时V＝L/3·S成为规则角锥体体积公式。

现将F值公式作如下之改变：由上式可见，F值显然取决于剖面面积S1及S2之比的平方根，而不取决于这些面积的绝对值的大小。

此外，当S1与S2之值互换时，F值亦不受影响。

C·C·依扎值曲线图查出F值，故其体积公式为：断面平均面积当相邻的两剖面中只有一个剖面有面积，而另一剖面上矿体已尖灭，这时根据剖面上矿体面积形状不同，可分别选择楔形（图4）或锥形（图5）公式计算面积。

图4 楔形面积图5 锥形体积用楔形公式计算体积的公式为：用锥形公式计算体积的公式为：（三）计算各相邻两剖面间块段的矿石储量：式中：Q－块段的矿石储量；V－块段的矿石体积；－块段矿石平均体重。

凡在矿床勘探阶段,应用若干勘探剖面把矿床横切截为若干个块段,分别计算这些块段的储量,将各块段的储量合起来即矿体的总储量,这种方法称断面法或剖面法。

断面法还可分为垂直断面法、水平断面法及不平行断面法。

一、平行断面法平行断面法储量计算按以下步骤进行:(一)首先在各个勘探剖面图上测定矿体的面积;(二)其次,在两个勘探剖面面积之间计算矿体的体积。

为此,必须根据相邻两剖面矿体之相对面积差的大小来分别选择不同的公式进行计算。

当相邻两剖面上矿体之相对面积差＜40%时,一般选用梯形体积公式(图1),其公式为:式中:V－两剖面间矿体体积(立方米);L－两相邻剖面之间距(米);S1S2－两相邻剖面上的矿体面积(平方米)。

图1 相邻剖面间之梯形块段当相邻两剖面上矿体之相对面积差＞40%时,一般选用截锥体积公式计算体积(图2),其公式为:图2 相邻剖面间之锥块段在应用截锥公式,要进行开平方计算,实际计算较繁琐,为了简化计算,有人提出改用校正的梯形公式,其方法如下:假如使相邻两剖面的间距为L,则这些剖面间块段的体积V大致等于两剖面面积总与之半与某一修正系数F的乘积,即:修正系数F的大小等于该块段精确体积与近似体积之比:把F值代入公式中,则得:当S1＝S2时,则F＝1,因而。

在这种情况下,用近似公式也可得到精确的结果。

在S1或S2＝0时则F=2/3,这时V＝L/3·S成为规则角锥体体积公式。

现将F值公式作如下之改变:由上式可见,F值显然取决于剖面面积S1及S2之比的平方根,而不取决于这些面积的绝对值的大小。

此外,当S1与S2之值互换时,F值亦不受影响。

C·C·依扎克松利用上述关系,并使块段底面积之一,S1或S2等于1,编制了一个F值遇S1/S2＝α的关系表(表1)。

表1α＜1 α＞1 F值α＜1 α＞1 F值0、71 0、50 0、33 0、25 0、20 0、17 0、10 0、08 0、07 0、06 0、05 0、04 0、03 1、42、03、04、05、06、010、012、014、016、020、025、030、00、9950、9800、9550、9330、9150、9000、8590、8450、8330、8240、8090、7950、7850、0250、0200、0170、0140、0100、0070、0050、0030、0020、0020、0010、00140、050、060、070、0100、0140、0200、0300、0400、0500、0700、01000、00、7700、7600、7510、7450、7330、7240、7140、7060、7000、6960、6920、689表1表明,当S1与S2之比值α在0、71～1、4以内时,F值可略而不计,因为误差小于1%,尚未超出储量计算的一般精度范围。

资源量与储量计算方法资源量与储量计算方法储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD法等等。

（一）地质块段法计算步骤：1.首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；2.然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；3.所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表地质块段法储量计算表块段编号资源储量级别块段面积（m2）平均厚度(m）块段体积（m3）矿石体重（t/m3）矿石储量（资源量）平均品位（%）金属储量(t）备注12345678910需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

资源量与储量计算方法储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD法等等。

（一）地质块段法计算步骤：首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

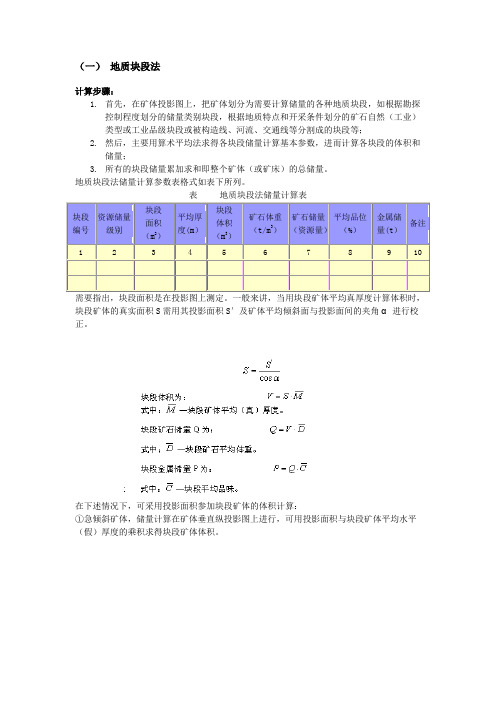
表?? 地质块段法储量计算表块段编号资源储量级别块段面积（m2）平均厚度(m）块段体积（m3）矿石体重（t/m3）矿石储量（资源量）平均品位（%）金属储量(t）备注?????????????????? 需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图???? 在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

（一）地质块段法计算步骤：1.首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；2.然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；3.所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表地质块段法储量计算表块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

缺点：误差较大。

当工程控制不足，数量少，即对矿体产状、形态、内部构造、矿石质量等控制严重不足时，其地质块段划分的根据较少，计算结果也类同其他方法误差较大。

（二）开采块段法开采块段主要是按探、采坑道工程的分布来划分的。

可以为坑道四面、三面或两面包围形成矩形、三角形块段；也可为坑道和钻孔联合构成规则或不甚规则块段。

同时，划分开采块段时，应与采矿方法规定的矿块构成参数相一致，与储量类别相适应。

该法的储量计算过程和要求与地质块段法基本相同。

（三）断面法定义：矿体被一系列勘探断面分为若干个矿段或称块段，先计算各断面上矿体面积，再计算各个矿段的体积和储量，然后将各个块段储量相加即得矿体的总储量，这种储量计算方法称为断面法或剖面法。

根据断面间的空间位置关系分为水平断面法和垂直断面法，凡是用勘探（线）网法进行勘探的矿床，都可采用垂直断面法；对于按一定间距，以穿脉、沿脉坑道及坑内水平钻孔为主勘探的矿床，一般采用水平断面法计算矿床资源量和储量。

根据断面间的关系分为平行断面法和不平行断面法。

1平行断面法无论是垂直平行断面法还是水平平行断面法，均是把相邻两平行断面间的矿段，作为基本储量计算单元。

首先在两断面图上分别测定矿体面积，然后计算块段的体积和储量。

体积（V）的计算有下述几种情况：1）设两断面上矿体面积为S1、S2，两断面间距为L（图4-7-4）则：图4-7-4 平行断面间的矿段图4-7-5 断面间内插断面（Sm）的三种求法示意图2）矿体边缘矿块只有一个矿体断面控制那么根据矿体形态及尖灭特点，用下述体积（V）计算公式：图4-7-6 矿体端部块段形态（a）锥形体；（b）楔形体断面法，在平均品位计算时，若需使用加权平均法计算，则单工程内线平均品位可用不同样品长度加权；断面上的面平均品位可用各取样工程长度或工程控制距离加权；块段的体积平均品位可用各断面面积加权；同中段或矿体的平均品位可用块段体积或矿石储量加权求得等。

储量计算表格式如表4-7-8所列。

表4-7-8 断面法储量计算表2 不平行断面法当相邻两断面（往往是改变方向处的两勘探线剖面）不平行时，块段体积的计算比较复杂，常采用辅助线（中线）法（图4-7-7），其公式为：图4-7-7 不平行断面间矿块（a）锥形体；（b）楔形体其他参数和块段矿石储量与金属储量计算同于平行断面法。

适用条件：断面法在地质勘探和矿山地质工作中应用极为广泛。

它原则上适用于各种形状、产状的矿体。

优点是能保持矿体断面的真实形状和地质构造特点，反映矿体在三维地质空间沿走向及倾向的变化规律；能在断面上划分矿石工业品级、类型和储量类别块段；不需另作图件，计算过程也不算复杂；计算结果具有足够的准确性。

储量计算的断面法凡在矿床勘探阶段，应用若干勘探剖面把矿床横切截为若干个块段，分别计算这些块段的储量，将各块段的储量合起来即矿体的总储量，这种方法称断面法或剖面法。

断面法还可分为垂直断面法、水平断面法及不平行断面法。

一、平行断面法平行断面法储量计算按以下步骤进行：（一）首先在各个勘探剖面图上测定矿体的面积；（二）其次，在两个勘探剖面面积之间计算矿体的体积。

为此，必须根据相邻两剖面矿体之相对面积差的大小来分别选择不同的公式进行计算。

当相邻两剖面上矿体之相对面积差＜40%时，一般选用梯形体积公式（图1），其公式为：式中：V－两剖面间矿体体积（立方米）；L－两相邻剖面之间距（米）；S1S2－两相邻剖面上的矿体面积（平方米）。

图1 相邻剖面间之梯形块段当相邻两剖面上矿体之相对面积差＞40%时，一般选用截锥体积公式计算体积（图2），其公式为：图2 相邻剖面间之锥块段在应用截锥公式，要进行开平方计算，实际计算较繁琐，为了简化计算，有人提出改用校正的梯形公式，其方法如下：假如使相邻两剖面的间距为L，则这些剖面间块段的体积V大致等于两剖面面积总和之半与某一修正系数F的乘积，即：修正系数F的大小等于该块段精确体积与近似体积之比：把F值代入公式中，则得：当S1＝S2时，则F＝1，因而。

在这种情况下，用近似公式也可得到精确的结果。

在S1或S2＝0时则F=2/3，这时V＝L/3·S成为规则角锥体体积公式。

现将F值公式作如下之改变：由上式可见，F值显然取决于剖面面积S1及S2之比的平方根，而不取决于这些面积的绝对值的大小。

此外，当S1与S2之值互换时，F值亦不受影响。

C·C·依扎克松利用上述关系，并使块段底面积之一，S1或S2等于1，编制了一个F值遇S1/S2＝α的关系表（表1）。

表1表1表明，当S1与S2之比值α在0.71～1.4以内时，F值可略而不计，因为误差小于1%，尚未超出储量计算的一般精度范围。

凡在矿床勘探阶段，应用若干勘探剖面把矿床横切截为若干个块段，分别计算 这些块段的储量，将各块段的储量合起来即矿体的总储量，这种方法称断面法或剖 面法。

断面法还可分为垂直断面法、水平断面法及不平行断面法。

一、平行断面法平行断面法储量计算按以下步骤进行：（一） 首先在各个勘探剖面图上测定矿体的面积；（二） 其次，在两个勘探剖面面积之间计算矿体的体积。

为此，必须根据相邻两剖面矿体之相对面积差的大小来分别选择不同的公式进行计算。

当相邻两剖面上矿体之相对面积差违厂 < 40%寸，一般选用梯形体积公式（图 1）,其公式为:式中：V -两剖面间矿体体积（立方米）； L —两相邻剖面之间距（米）； S 1S 2 -两相邻剖面上的矿体面积图1相邻剖面间之梯形块段S 严,算体积（图2），其公式为：当相邻两剖面上矿体之相对面积差 > 40%寸，一般选用截锥体积公式计（平方米）。

nI由上式可见，F 值显然取决于剖面面积 S 及S 2之比的平方根，而不取决于这些 面积的绝对值的大小。

此外，当 S i 与S 2之值互换时，F 值亦不受影响。

C- C •依扎相邻剖面间之锥块段在应用截锥公式，要进行开平方计算，实际计算较繁琐，为了简化计算，有人 提出改用校正的梯形公式，其方法如下：假如使相邻两剖面的间距为 L ,则这些剖面间块段的体积 V 大致等于两剖面面 积总和之半与某一修正系数 F 的乘积，即：V=P -. L （3） 2修正系数F 的大小等于该块段精确体积与近似体积之比:-2(1 +屆勺 3 q+Sj把F 值代入公式则得:当Si = S 时，则 F = 1,甘二墅鱼-L因而 2。

在这种情况下，用近似公式也可得到精确的结果。

在公式。

现将F 值公式作如下之改变:S i 或S 2= 0时则F=2/3，这时V = L/3 - S 成为规则角锥体体积J I4图2A磅（1+辔）=糾表1克松利用上述关系，并使块段底面积之一，S1或S2等于1,编制了一个F值遇S/S2 =a表1表明，当S与S2之比值a在0.71〜1.4以内时，F值可略而不计，因为误差小于1%尚未超出储量计算的一般精度范围。

资源量与储量计算方法（厚度*品味+厚度*品味）/厚度的总和加权平均储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD法等等。

（一）地质块段法计算步骤：1.首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；2.然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；3.所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表地质块段法储量计算表需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图；(c)、(d)—立体图1—矿体块段投影；2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

缺点：误差较大。

当工程控制不足，数量少，即对矿体产状、形态、内部构造、矿石质量等控制严重不足时，其地质块段划分的根据较少，计算结果也类同其他方法误差较大。

（三）断面法定义：矿体被一系列勘探断面分为若干个矿段或称块段，先计算各断面上矿体面积，再计算各个矿段的体积和储量，然后将各个块段储量相加即得矿体的总储量，这种储量计算方法称为断面法或剖面法。

根据断面间的空间位置关系分为水平断面法和垂直断面法，凡是用勘探（线）网法进行勘探的矿床，都可采用垂直断面法；对于按一定间距，以穿脉、沿脉坑道及坑内水平钻孔为主勘探的矿床，一般采用水平断面法计算矿床资源量和储量。

根据断面间的关系分为平行断面法和不平行断面法。

1平行断面法无论是垂直平行断面法还是水平平行断面法，均是把相邻两平行断面间的矿段，作为基本储量计算单元。

首先在两断面图上分别测定矿体面积，然后计算块段的体积和储量。

体积（V）的计算有下述几种情况：1）设两断面上矿体面积为S1、S2，两断面间距为L（图4-7-4）则：图4-7-4 平行断面间的矿段图4-7-5 断面间内插断面（Sm）的三种求法示意图2）矿体边缘矿块只有一个矿体断面控制那么根据矿体形态及尖灭特点，用下述体积（V）计算公式：图4-7-6 矿体端部块段形态（a）锥形体；（b）楔形体断面法，在平均品位计算时，若需使用加权平均法计算，则单工程内线平均品位可用不同样品长度加权；断面上的面平均品位可用各取样工程长度或工程控制距离加权；块段的体积平均品位可用各断面面积加权；同中段或矿体的平均品位可用块段体积或矿石储量加权求得等。

储量计算表格式如表4-7-8所列。

表4-7-8 断面法储量计算表 平台编号 勘探线或中段、矿体号 块段 号 矿石品级类型 储量级别 断面 上矿 体面 积 （m 2） 断面上平均品位 （%） 面积×品位 块段平均 品位（%） 断面间 距（m ） 块段 体积 （m3） 矿石 体重（t/m 3） 矿石储量 (t ） 金属储量 （t ） 备注 1 2 3 4 5 6 7 8 910 11 12 13 14 15 16 17 18 19 20 21 22 232 不平行断面法当相邻两断面（往往是改变方向处的两勘探线剖面）不平行时，块段体积的计算比较复杂，常采用辅助线（中线）法（图4-7-7），其公式为：图4-7-7 不平行断面间矿块（a）锥形体；（b）楔形体其他参数和块段矿石储量与金属储量计算同于平行断面法。

常用储量计算方法及其应用条件1）断面法：将矿体用若干个剖面截成若干个块段，分别计算每个块段的储量，然后将各块段的储量和起来既得到矿体的储量。

这种用断面划分块段求储量的方法叫断面法。

如果是用一系列垂直剖面划分块段而计算储量者，叫做垂直断面法；用以犀利水平断面划分块段计算储量者，叫水平断面法。

在垂直断面法中，如果断面与断面之间平行，称为平行断面法；若不平行则为不平行断面法。

平行断面法的优点在于断面图保持了矿体断面的真实形状，直观的反映了地质构造特征；储量计算时，可根据出量级别、矿石类型、工业品级等的要求任意划分块段，具有相当的灵活性。

任意形状的矿床都可用断面法。

因其优点较多，称为目前最常用的储量计算方法。

2)算术平均法：这种方法的基本特点是将整个矿体的各种参数都用简单算术平均法求得其平均值，从而计算矿体的储量。

他一般是利用水平投影图或垂直纵投影图来进行的，有时也在平行矿体倾斜面的投影图上进行。

算术平均法是所有储量计算方法中最简单的方法，也无须做复杂的图件。

因此，在矿点检查、矿区评价阶段常用这种方法计算。

当探矿工程数量较少，分布又不均匀，矿体各项指标值变化较大时，此法仅能得出粗略的计算结果。

此法没有按矿石类型、工业品级、储量级别等划分块段分别计算。

因此在勘探阶段很少用这种方法。

3）地质块断法：在计算方法上，地质块断法和算术平均法基本一样，所不同者仅在于它不是将整个矿体一起计算，而是按需要将矿体划分成若干块断，每个块断都用算术平均法计算出块断的储量。

有时根据指标值的变化特点，也用加权平均法计算。

所有块断储量之和即为全矿体的储量。

地质块断法具有算术平均法的所有优点，同时还弥补了算术平均法不能按需要划分块断的缺点。

它可以是用在任何大小、形状和产状的矿体上，特别是层状、似层状、透镜状矿体，而且勘查方法对它也没有影响。

因此，地质块断法成为目前勘探阶段储量计算的主要方法之一。

4）开采块断法：当矿体被坑道切割成许多开采块断时，常用此法计算储量。

煤矿勘查建设中煤炭储量的计算方法魏亮【摘要】对煤矿在建设以及生产各阶段煤炭储量的计算方法进行了分析介绍,主要包括地质地段法、剖面法、水平切面法、简单统计法四种计算方法,阐述了各种方法在计算时的注意事项及适用阶段,以提高煤炭储量计算的准确性.【期刊名称】《山西建筑》【年(卷),期】2014(040)016【总页数】2页(P75-76)【关键词】煤炭储量;计算;阶段;方法【作者】魏亮【作者单位】山西省煤炭地质水文勘查研究院,山西太原030006【正文语种】中文【中图分类】TD1630 引言煤炭储量计算方法很多，大约有二三十种，但在煤田地质勘查中常用的只有十多种，最常用的不过两三种。

固体矿产资源储量估算方法总的来说可概括为两类:几何图形法和地质统计学法。

其中几何图形法包括:算术平均法、地质地段法、等高线法、剖面法、水平面切面法、多角形法、三角形法和等值法。

其中，地质地段法和断面法(剖面法和水平面切面法)，在实际矿井建设生产中应用较多，其他估算方法应用相对较少，主要用于资源储量的概略估算，常用于地质勘探程度不高，工程分布有限，研究程度不足，只能用于供远景规划的资源量计算。

论文主要介绍地质地段法、断面法和地质统计学法。

1 地质地段法这是目前在煤炭储量计算中使用的最广的一种方法，见图1。

地质地段法是把一层煤利用各种要素分割成若干形状不同、大小不一的小块，分别计算每一块段的储量。

划分块段的主要因素有煤层的地质研究程度(如不同级别的划分)、煤层的厚度、构造因素(如断层、背向斜轴、煤层倾角大小，不同构造复杂程度等)、煤质特征(如按煤的不同牌号、灰分、硫分等)、开采技术条件(如地温、水文条件、含量、不同剥采比等)、开拓方式(如不同开采水平、分上下山等)。

图1 地质块段法计算储量时，把矿体当作一组密集的、大小不等的块体划分块段的原则就是各小块段内的指标一致或近似。

块段的多少是大不相同的，多则上百块，少则几块，它与勘查区范围的大小等许多因素有关。