2.4群的直积

直积运算规则
以下是 9 条关于直积运算规则：
1. 嘿，你知道吗，直积的元素可多啦！就像把两组东西一股脑儿地放在一起。

比如说集合 A 有 1、2，集合 B 有 3、4，那 A 和 B 的直积不就是(1,3)、(1,4)、(2,3)、(2,4)嘛！这多直观呀！
2. 哇塞，直积运算里每个元素都有自己独一无二的位置呢！就好像拼图的每一块都得在对的地方。

像两个集合拼起来形成的直积，可不是随随便便放的哟！
3. 嘿呀，直积运算可神奇了！它就像是搭建一个独特的城堡，用不同的部分组合起来。

比如给你两个集合，通过直积能创造出好多新的组合来呢！
4. 哎呀，你想想看，直积不就是把不同的元素搭配起来嘛，这多有意思呀！就像搭配衣服，不同的上衣和裤子能搭配出好多不同的造型呢，直积也是同理哟！
5. 哇，直积运算可以让简单的集合变得超级丰富咧！好比一只小蚂蚁变成了一个庞大的蚂蚁军团。

像集合 A 是红色、蓝色，B 是圆形、方形，它们的直积可就丰富多彩啦！
6. 嘿，直积就是把不同的东西交织在一起呀，产生奇妙的结果呢！比如一组数字和一组图形的直积，会带来好多新奇的组合哦。

7. 哎哟喂，直积运算规则其实不难理解啦！就像走一条路，跟着走就能弄清楚。

不同集合的直积，就是沿着特定的方式把它们组合起来嘛！
8. 哇哦，直积有时候就像变魔法一样！能把普通的东西变得很特别呢。

比如说两个普通的集合，一通过直积就变得不一般了呀。

9. 直积运算规则呀，真的是很特别呢！它让集合变得更有魅力更有趣啦！就好像给它们穿上了一件漂亮的外衣，变得光彩照人！我的观点结论就是，直积运算让数学变得更丰富多彩，更值得我们去深入探究和发现呀！。

群论是数学中一门重要的分支，研究的是代数结构中的群。

群是以二元运算（通常为乘法）定义的一种数学结构，满足封闭性、结合律、存在单位元和逆元的性质。

在群论中，有两个重要的概念，即群的基本定理和群的生成元。

首先，群的基本定理是群论中的核心定理之一。

它表明，对于任何有限群G，存在一个唯一的素数p以及正整数n₁,n₂,...,nk，使得G同构于n₁个阶为p的循环群、n₂个阶为p²的循环群、...、nk个阶为p^k的循环群的直积。

这个基本定理可以看作是将一个复杂的有限群分解为几个简单的循环群的直积的过程。

通过群的基本定理，我们可以更好地理解有限群的结构和性质，为解决许多数学问题提供了有力的工具。

其次，群的生成元是群论中的另一个重要概念。

对于给定的群G，如果存在元素a₁,a₂,...,an，它们的乘积可以得到G中的所有元素，那么称a₁,a₂,...,an是群G的生成元。

换句话说，生成元是通过群中的有限次操作可以生成整个群的元素。

生成元可以帮助我们更好地理解群的性质，特别是它们的元素之间的关系。

在许多实际问题中，通过寻找群的生成元，我们可以简化问题的复杂度，从而更容易解决。

在群的生成元的概念中，有一个重要的定理，即生成元的个数不唯一。

对于一个群G，它的生成元的个数可以是有限的也可以是无限的。

但是，存在一种特殊情况，即群G的所有生成元的个数都是有限的，这种情况下群G被称为有限生成群。

有限生成群在实际问题中具有重要的应用，如密码学、编码理论等领域。

除了有限生成群，还有一类特殊的群，即无限生成群。

无限生成群由无限多个生成元组成，通常被用来描述无穷集合中的对称性。

例如，无限群中的整数加法群Z和无限循环群C都是无限生成群。

总之，群论中的群的基本定理和群的生成元是群结构研究中的重要内容。

群的基本定理可以帮助我们理解有限群的结构和性质，而群的生成元则可以帮助我们处理复杂的群问题。

通过深入学习和应用群的基本定理和群的生成元，我们能够在数学和其他领域中更好地理解和解决问题。

第二章 群及其性质群论属于代数学的范畴，它所研究的是群这样一个代数系统。

所谓代数系统，就是一个具有满足一定法则的代数运算的集合。

一个群只有一种代数运算，我们把这种代数运算称为群的乘法，简称群乘。

群的定义：假设G 是由一些不同元素组成的集合，即G {} ,21,g g =。

在G 中各元素间定义了一种群乘规则 ( 连续操作，乘法、加法运算)， 如果G 对这种群乘规则满足以下条件：（1）满足封闭性。

G 中任意两个元素的乘积仍然属于G ，即 若G g g j i ∈∀,，则G g g g k j i ∈=。

（2）结合律成立。

G g g g k j i ∈∀,,，都有=k j i g g g )()(k j i g g g 。

（3）存在单位元E G ∈。

对Gg i ∈∀，都有ii i g E g Eg ==，所以E 又称为恒等操作。

（4）存在逆元。

对每个Gg i ∈, 存在一个唯一的逆元素Gg i ∈-1, 使i i g g 1-Eg g i i ==-1成立。

这时称集合G 对于所定义的群乘来说构成一个群。

这四个条件常被称为群公理。

单位元素的逆元是自身（E-1=E ）。

证明：因为1111)(g g =--，121)(-g g E g g ==--1112。

所以 E )()(21121g g g g -=211112g g g g --=。

群元的个数，称为群的阶（一般用符号g 来表示）。

若群G 的元素个数有限，则群G 称为有限群；若群G 的元素个数无限，则群G 称为无限群。

群的元素不但可以是数，而且可以是平移、转动、反射、置换、反演等物理操作。

最简单的操作是恒等操作，这种操作是指对事物什么也没有做。

我们需要恒等操作是为了满足群的数学条件。

群乘运算与元素有关。

如果群元是数，群乘就是通常的乘法或加法；如果群元是物理操作，群乘就是操作，先操作右边元素，再进行左边操作（与算符相似）。

群的乘法一般不具有可交换性，即对G g g ∈∀21,，一般说来21g g 12g g ≠。

自同构和直积-概述说明以及解释1.引言1.1 概述概述:自同构和直积是群论和代数学中重要的概念。

自同构指的是一个群与其自身之间存在一一对应的同构映射关系，直积则是将两个群的元素按照一定规则组合在一起得到一个新的群。

自同构和直积的研究在代数学和离散数学中具有重要的地位，它们不仅有着理论上的意义，也在实际中有着广泛的应用。

在本文中，我们将对自同构和直积这两个概念进行详细的介绍，并探讨它们之间的关系。

通过对这些概念的深入理解，我们可以更好地理解群论和代数结构中的各种问题，从而为进一步的研究和应用提供坚实的基础。

1.2 文章结构文章结构部分的内容应该包括本文的主要章节和内容概述。

在这里，我们可以简要介绍本文将分为引言、正文和结论三个部分。

在引言中将概述自同构和直积的概念，同时阐明本文的目的和意义。

在正文部分将详细介绍自同构和直积的定义、性质和相关定理，以及它们之间的关系。

最后在结论部分将总结自同构和直积在数学领域的重要性，并展望未来可能的研究方向。

整篇文章将围绕这些内容展开，希望可以为读者提供清晰的理解和启发。

1.3 目的本文旨在探讨自同构和直积在数学领域中的重要性和应用。

通过对自同构和直积的定义、性质和特点进行详细分析，我们希望读者能够深入了解这两个概念在代数学、几何学、拓扑学等领域中的重要作用。

通过对自同构和直积的关系进行讨论，我们将展示它们之间的联系和相互影响。

最终，我们将总结自同构和直积的重要性，并探讨它们在未来研究方向中的潜力应用，以期为数学领域的进一步发展提供启示。

2.正文2.1 自同构自同构是指一个结构与自身的同构映射。

在数学领域中，自同构通常指的是一个映射，它将一个结构映射到自身并保持结构的基本特征不变。

自同构在代数、拓扑、几何等领域都有重要应用。

在代数学中，自同构常常用来研究群、环、域等代数结构的性质。

一个群的自同构映射可以帮助我们理解群的对称性质，而一个环的自同构映射则可以揭示环的结构特征。

直积和直和
直积和直和是数学中的概念，用于描述两个或多个数学结构的组合方式。

直积通常用符号“×”表示，表示将两个结构按照一定的规则组合成一个新的结构；直和通常用符号“⊕”表示，表示将两个结构合并成一个新的结构。

以向量空间为例，设V和W分别为两个向量空间，则V×W是由所有形如(v,w)的元素组成的集合，其中v∈V，w∈W。

V×W中的加法和标量乘法分别定义为：
(v1,w1)+(v2,w2)=(v1+v2,w1+w2)；
k(v,w)=(kv,kw)。

而V⊕W是由所有形如v⊕w的元素组成的集合，其中v∈V，w∈W。

V⊕W中的加法和标量乘法分别定义为：
(v1⊕w1)+(v2⊕w2)=(v1+v2)⊕(w1+w2)；
k(v⊕w)=(kv)⊕(kw)。

可以看出，直积和直和的定义方式有些相似，但它们的组合方式和运算规则是不同的。

在不同的数学领域中，直积和直和的应用也有所不同，例如在代数学中常常用到直积，而在拓扑学中常常用到直和。

总之，直积和直和是数学中重要的概念，它们可以帮助我们更好地理解数学结构的组合方式和运算规则。

- 1 -。

直积的计算公式在数学中，直积是两个或多个集合的笛卡尔积的一个广义形式，它是一种很重要的基础概念。

直积在各种数学分支的表现都不相同，因此，它被广泛用于数学的各个领域，包括组合数学、代数学、几何学、拓扑学等。

直积的计算公式：设A={a1,a2,...,an}、B={b1,b2,...,bm}是两个非空集合，其直积为A×B={(a,b) | a∈A，b∈B}。

同理，设R={(x,y) | x∈A，y∈B}为A和B的直积，则R是一个由有序二元组(x,y)组成的集合。

R中的元素的个数n(A) ×n(B)，其中，n(A)和n(B)分别为集合A和B的元素个数。

例如，当A={1,2,3}，B={a,b}时，A与B的直积为{(1,a),(1,b)，(2,a),(2,b)，(3,a),(3,b)}。

直积的另一种表示形式是使用向量或矩阵的形式。

例如，若集合A和B都是有限域GF(p)上的向量空间，则A和B的直积可以表示为A⊗B={a⊗b | a∈A，b∈B}，其中⊗表示向量空间的张量积。

直积的此种表示形式在代数学、线性代数和量子力学等领域中应用广泛。

直积的计算公式可以用来计算两个或多个集合间的关系，例如可以使用直积计算关系的乘积或笛卡尔积，或者可以利用直积来计算不同集合间的同构关系。

同样地，直积也被用于计算拓扑空间和流形之间的笛卡尔积，以及多项式环和双线性映射之间的张量积。

在数学中，直积是一个非常基础的概念，在各个领域都有着广泛的应用。

因此，对于直积的基本定义和计算公式的理解，是数学学习的必要基础。

当我们能够熟练地应用直积的计算公式，我们就能更深入地理解和掌握数学中的各种概念和定理。

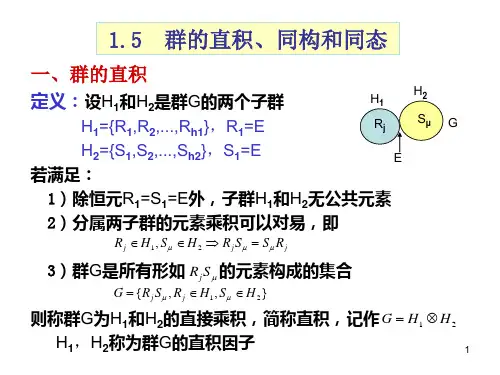
群的直积（Direct Product of Group ）群的直积是群论中的重要概念，也是研究群的重要手段之一，利用群的直积可以从已知的群构出新的群，可以用小群构造大群，也可以将一个群用它的子群来表示，这一节介绍子群的直积及其基本性质。

定义1 设12,G G 是群，121122{(,)|,)G a a a G a G =∈∈为集合G 1与G 2为的卡氏积（Cartesian product ）,在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G ⋅=∈。

则G 关于上述定义的乘法构成群，称为群G 1与G 2的外直积（external direct product ），记作21G G G ⨯=，G 1、G 2称为G 的直积因子(factor of the direct product)。

当G 1、G 2是加群时，G 1与G 2的外直积也可记作21G G ⊕。

定理1 设21G G G ⨯=是群G 1与G 2的外直积，则（1） G 是有限群的充分必要条件是G 1与G 2都是有限群，并且，当G 是有限群时，©©有||||||21G G G =；（2）G 是交换群的充分必要条件是G 1与G 2都是交换群。

（3）1221G G G G ⨯≅⨯； （4） 若令112112{(,)|,A a e a G e =∈为G 2的单位元}，则A 1是G 的子群，且11G A ≅；若令212222{(,)|,A e a a G e =∈为的单位元}，则A 2是G 的子群，且22G A ≅。

证明 （1）由卡氏积的性质显然。

（2）如果G 1和G 2都是交换群，则对任意的1212(,),(,),a a b b G ∈有),(),(),(),(),(),(2121221122112121a a b b a b a b b a b a b b a a ⋅===⋅，所以G 是交换群。

直积是指将两个或多个集合的元素按照一定规则进行组合，形成新的集合。

对于两个集合A 和B的直积，记作A ×B，其中A和B分别为两个集合。

直积的计算公式如下：A ×B = {(a, b) | a ∈A, b ∈B}其中，(a, b)表示一个有序对，a ∈A表示a是集合A中的一个元素，b ∈B表示b是集合B中的一个元素。

换句话说，直积A ×B包含了所有由A和B的元素组成的有序对。

例如，假设集合A = {1, 2}，集合B = {a, b, c}，则A ×B的计算结果为：A ×B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}这个结果表示了A和B的所有元素组成的有序对。

当计算两个集合的直积时，可以按照以下步骤进行：定义两个集合：首先，明确给定的两个集合A和B。

这些集合可以是数字、字符、对象或其他类型的集合。

创建直积集合：直积集合是由A和B的元素组成的有序对。

需要创建一个新的集合来容纳这些有序对。

遍历元素：对于集合A中的每个元素a，以及集合B中的每个元素b，生成一个由它们组成的有序对(a, b)。

添加有序对：将生成的有序对(a, b)添加到直积集合中。

完成直积计算：当遍历完集合A和B的所有元素后，直积计算完成。

下面是一个示例程序，用于计算集合A和B的直积：#include <stdio.h>int main() {int A[] = {1, 2, 3}; // 集合Achar B[] = {'a', 'b'}; // 集合Bint sizeA = sizeof(A) / sizeof(A[0]); // A的元素个数int sizeB = sizeof(B) / sizeof(B[0]); // B的元素个数// 创建直积集合int sizeProduct = sizeA * sizeB;int product[sizeProduct][2]; // 二维数组，存储有序对// 计算直积int index = 0; // 直积集合的索引for (int i = 0; i < sizeA; i++) {for (int j = 0; j < sizeB; j++) {product[index][0] = A[i]; // 第一个元素为A中的元素product[index][1] = B[j]; // 第二个元素为B中的元素index++;}}// 输出直积集合printf("直积集合：\n");for (int i = 0; i < sizeProduct; i++) {printf("(%d, %c)\n", product[i][0], product[i][1]);}return 0;}在这个示例程序中，集合A是一个包含整数的数组，集合B是一个包含字符的数组。

群的直积（Direct Product of Group ）群的直积是群论中的重要概念，也是研究群的重要手段之一，利用群的直积可以从已知的群构出新的群，可以用小群构造大群，也可以将一个群用它的子群来表示，这一节介绍子群的直积及其基本性质。

定义1 设12,G G 是群，121122{(,)|,)G a a a G a G =∈∈为集合G 1与G 2为的卡氏积（Cartesian product ）,在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G ⋅=∈。

则G 关于上述定义的乘法构成群，称为群G 1与G 2的外直积（external direct product ），记作21G G G ⨯=，G 1、G 2称为G 的直积因子(factor of the direct product)。

当G 1、G 2是加群时，G 1与G 2的外直积也可记作21G G ⊕。

定理1 设21G G G ⨯=是群G 1与G 2的外直积，则（1） G 是有限群的充分必要条件是G 1与G 2都是有限群，并且，当G 是有限群时，©©有||||||21G G G =；（2）G 是交换群的充分必要条件是G 1与G 2都是交换群。

（3）1221G G G G ⨯≅⨯； （4） 若令112112{(,)|,A a e a G e =∈为G 2的单位元}，则A 1是G 的子群，且11G A ≅；若令212222{(,)|,A e a a G e =∈为的单位元}，则A 2是G 的子群，且22G A ≅。

证明 （1）由卡氏积的性质显然。

（2）如果G 1和G 2都是交换群，则对任意的1212(,),(,),a a b b G ∈有),(),(),(),(),(),(2121221122112121a a b b a b a b b a b a b b a a ⋅===⋅，所以G 是交换群。

直积的计算公式直积是集合论中的一个重要概念。

在数学中，直积是指将两个集合的每个元素进行组合，生成一个新的集合的操作。

直积操作在许多数学分支中都有应用，如群论、环论、代数几何等。

对于集合A和集合B，它们的直积定义为一个新集合C，C中的元素是由A和B中的元素组成的有序对。

用数学符号表示为C = A × B。

直积可以推广到更多的集合之间。

下面是直积的计算公式：假设A = {a1, a2, a3}，B = {b1, b2, b3}，我们可以计算出A和B的直积C = A × B。

C的元素可以表示为C = {(a1, b1), (a1, b2), (a1, b3), (a2, b1), (a2, b2), (a2, b3), (a3, b1), (a3, b2), (a3, b3)}。

可以看出，C中的元素是由A和B中的元素两两组成的有序对。

其中，第一个元素来自于集合A，第二个元素来自于集合B。

如果A和B中的元素个数分别是m和n，则C中的元素个数即为m × n。

这是因为对于A中的每个元素，都可以和B中的每个元素配对，所以总共有m × n个配对。

当然，直积操作不仅限于两个集合的组合。

对于更多的集合，直积的计算公式类似。

对于集合A1, A2, ..., An，它们的直积可以表示为C = A1 × A2 × ... × An。

C的元素可以表示为C = {(a1, a2, ..., an) | a1 ∈ A1, a2 ∈ A2, ..., an ∈ An}。

可以看出，C中的元素是由A1, A2, ..., An中的元素按照一定顺序组合而成的n元组。

直积操作在数学中有许多重要的应用。

例如，群论中的直积可以用来构造新的群结构；环论中的直积可以用来构造新的环结构；代数几何中的直积可以用来描述多维几何空间等。

总结一下，直积是将两个或多个集合的元素进行组合生成一个新的集合的操作。

群的直积群的直积（Direct Product of Group ）群的直积是群论中的重要概念，也是研究群的重要手段之一，利用群的直积可以从已知的群构出新的群，可以用小群构造大群，也可以将一个群用它的子群来表示，这一节介绍子群的直积及其基本性质。

定义1 设12,G G 是群，121122{(,)|,)G a a a G aG =∈∈为集合G 1与G 2为的卡氏积（Cartesian product ）,在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G⋅=∈。

则G 关于上述定义的乘法构成群，称为群G 1与G 2的外直积（external direct product ），记作21G G G ⨯=，G 1、G 2称为G 的直积因子(factor of thedirect product)。

当G 1、G 2是加群时，G 1与G 2的外直积也可记作21G G ⊕。

定理1 设21G G G ⨯=是群G 1与G 2的外直积，则（1） G 是有限群的充分必要条件是G 1与G 2都是有限群，并且，当G 是有限群时，©©有||||||21G GG =；（2） G 是交换群的充分必要条件是G 1与G 2都是交换群。

11:A G →φ),(211e a a →则易知φ是一个同构映射，因此1A 是G 的子群，同理可证另一个结论。

例1 设>=<>=<b G a G21,分别是3阶和5阶的循环群，则21G G G ⨯=是一个15阶的循环群。

证明 首先，由定理1知，G 是一个15阶的交换群，设G b a c ∈=),(，),(21e e 是G 的单位元，则),(),,(225313e a c b e c ==，所以53,c c都不等于),(21e e ，可知ord c 5,3≠由拉格朗日定理知，ord c =15，即>=<c G 是15阶循环群。