电磁学 第二章 第九节
- 格式:ppt
- 大小:330.00 KB
- 文档页数:14
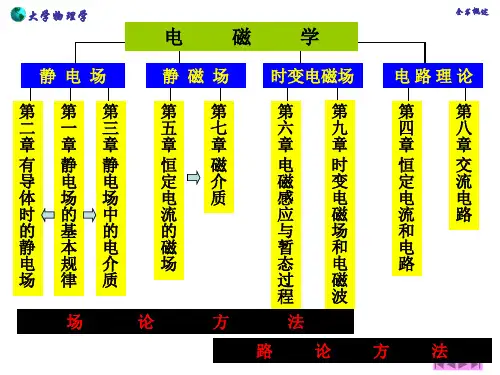




第二章 导体周围的静电场重点1、电场与物质相互作用:2、本章: 金属导体, 静电场3、根据: 高斯定理、环路定理§1 静电场中的导体1. 导体的电性质 (经典观点)导体静电平衡:无宏观电流, 电荷分布不再改变——静电场宏观电荷分布—带电2. 导体静电平衡条件E 内=E 外+E ’=03. 导体静电平衡时的性质导体内部无电荷,电荷在表面层(面密度σ)导体为等位体, 表面为等位面导体表面外附近电场 ⊥ 表面导体表面场强为: E 表=σε0n 4. 静电场问题的唯一性定理1 唯一性定理唯一性问题:(1)电荷自动调整,电场唯一吗?(2)边界条件确定, 域内电荷分布不变, 域内电场唯一吗?唯一性定理: 适当的物理条件确定之后,在给定区域V 内电场的稳定分布(静电平衡下的分布)是唯一的.适当的物理条件: U ⎪S or E n ⎪S 确定; V 内除导体外电荷分布确定;导体总电荷or 电位确定 2 唯一性定理意义(1)若有一个解就是 唯一的解.(2)指出决定解的因素.(3)V 外电荷分布改变(上述条件不变)则解不变3 唯一性定理简略证明(介绍)U ⎪S 给定的边界条件设在同一条件下有两解,证明两解相同对导体第一种情况的证明5. 例"猜出"可能的解, 就是唯一的真的解1. 已知孤立导体总电荷q ,求: 电荷分布σ(1)半径为R 的球体总电荷q“猜”:q 均匀分布在球的外表面上σ=q/4πR 2则:E 内=0是解,且唯一(2)无限大带电导体平板 “猜”:qE 总=σ/ε0=q/(2ε0S)E 总=0所猜即为解(3)一般形状 ——由实验测量2. 外电场中的中性导体匀强电场中的球形导体当σ(θ)=σ0cos θ 时, 导体内电场匀强为E’内= -σ0 z/3ε0 若σ0=3ε0 E 0 E 内=E 0+E ’=0 此即唯一解3. 外电场中的带电导体导体大平板A 、B, 面积S, 带电为Q A 、Q B . 设: 电荷在表面均匀分布 (σ1-σ2-σ3-σ4)/2ε0=0 (σ1+σ2+σ3-σ4)/2ε0=0 S(σ1+σ2)=Q A S (σ3+σ4)=Q B σ1=σ4=(Q A +Q B ) /2 σ2= -σ3=(Q A -Q B )/26. 电象法简介个别点电荷情况下,计算导体上感应电荷的一种简单方法——电象法 例1: 半径为R 的接地导体球,点电荷q 距导体球中心d.保持导体表面为零等位面, 球面外部的场不变, q’代替感应电荷对外部场的作用(1) 确定q’U(r=R)=q/(4πε0b)+q’/(4πε0b ’)=0R 1234b/b ’= -q/q’≡常数C由点G 和H 得:a=R 2/d q’= -Rq/d验证:b ’2=R 2+a 2-2Racos θ’=R 2(R 2+d 2-2Rdcos θ’)/d 2=R 2b 2/d 2即 b/b ’=d/R(2)计算电场由导体性质, 球内E 内=0球面外任意点P(r,θ)U P (r ) =04q πε(1/b-R/b ’d) E r = -∂U/∂r =04qπε[(r -dcos θ)/b 3-R(r -acos θ)/(b ’3d)]E θ= -1r(∂U /∂θ)=q 40πε d sin θ[1/b 3-(R/b ’d)3] E φ=0(3)表面上的电荷分布σ(R,θ) = -q(d 2-R 2)/[4πR(R 2+d 2-2Rd cos θ)3/2]q 感=⎰σ(R,θ)ds= -Rq/d=q’(4)作用到q 的力等于q’对q 的作用力∴F=qq’/4πε0(d -a)2=Rdq 2/4πε0(d 2-R 2)2§2利用导体构造和影响电场1. 静电透镜2. 闭合导体壳内外电场. 静电屏蔽1.q 外⊕σ外1 ⇒E 里=E 空=02 中性闭合导体壳部分屏蔽内部场(q 内的场)空腔 里 外3 接地闭合导体壳完全屏蔽内部场(q内的场) 3. 电容和电容器1. 电容概念导体电位与电量成正比,即U ∝ q ⇒电容概念电容C表达导体(组)容纳电荷的能力(1)孤立单导体U ∝ h ∝ q定义:常数C=qU为孤立导体电容例: 孤立导体球(R)设带电q, U=q/(4πε0R)C=q/U=4πε0R(2)带等量异号电荷的双导体设带电±q , ∆U ∝ qC=q/∆U2. 自屏蔽下的电容器实用的电容器都要屏蔽外界影响,为带等量异号电荷的双导体(1)球形电容器(球半径R1 ,壳内半径R2)C=4πε0R1R2/(R2-R1)(2) 圆柱形电容器(中心圆柱R1 , 壳体R2)C=2πε0L / [ln (R2/R1)](3)平行板电容器C=ε0S/d3. 电容器的串并联串联: Q相同V=∑V i等效电容C-1=∑ C i-1并联: V相同Q=∑Q i等效电容C=∑C i§3 静电能电荷观点: 带电体(点电荷系)具有电(势)能电场观点:电能储存在电场中静电场情况下,两种观点等效1. 点电荷系统静电能W取电荷相距无限远为电势能的零点W:从∞克服场力聚为现状所做功(积累能量)从现状分散到∞处场力所做功(放出能量)N个点电荷的系统依次将q1、q2、…、q N-1 移到∞ .W=q1U1(q2,…,q N)+…+q i U i(q i+1,…,q N) +…+q N-1U N-1(q N)依次将q N、q N-1、…q2移到∞ .W=q N U N(q1,…,q N-1)+…+q i U i(q1,…,q i-1) +…+q2U 2(q1)W= ∑12q i U iU i≡U i(q1,…,q N; -q i)2. 连续分布带电体静电能1.一般情况W=12⎰Udq说明:P0=∞对全部电荷积分U为全部电荷在dq处的电位W为全部电能(自能和互能) 2. 导体组W=∑12⎰Udq =∑12U i q i3. 电容器的静电能W=(q+U++q-U-)/2=12q∆U=12C∆U2例: 求半径R的均匀带电球体的静电能E=ρr/(3ε0) r<RE=q r/(4πε0r3)r>RU(r<R)=ρ(3R2-r2)/(6ε0)W=12⎰Udq=3q2/(20πεR)3. 互能与自能自能:带电体(子系统)具有的能量;互能: 带电体之间具有的能量两个带电体W=W自1+W自2+W互⎰q1U(q2)dq = ⎰q2 U(q1)dq =W互4. 电场的能量——场的观点真空中电场能量密度w =12ε0E2q112q2W= ⎰ wdV=⎰1ε0E2dV2例2. 均匀带电球体E内= qr/4πε0R3E外=q/4πε0r2 W = ⎰内ε0E内2dV/2+⎰外ε0E外2dV/2 =3q2/20πε0R。





电磁学第二章习题答案(总8页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除习题五(第二章 静电场中的导体和电介质)1、在带电量为Q 的金属球壳内部,放入一个带电量为q 的带电体,则金属球壳内表面所带的电量为 q ,外表面所带电量为 q +Q 。
2、带电量Q 的导体A 置于外半径为R 的导体 球壳B 内,则球壳外离球心r 处的电场强度大小204/r Q E πε=,球壳的电势R Q V 04/πε=。
3、导体静电平衡的必要条件是导体内部场强为零。
4、两个带电不等的金属球,直径相等,但一个是空心,一个是实心的。
现使它们互相接触,则这两个金属球上的电荷( B )。
(A)不变化 (B)平均分配 (C)空心球电量多 (D)实心球电量多5、半径分别R 和r 的两个球导体(R >r)相距很远,今用细导线把它们连接起来,使两导体带电,电势为U 0,则两球表面的电荷面密度之比σR /σr 为 ( B )(A) R/r (B) r/R (C) R 2/r 2 (D) 16、有一电荷q 及金属导体A ,且A 处在静电平衡状态,则( C )(A)导体内E=0,q 不在导体内产生场强; (B)导体内E ≠0,q 在导体内产生场强; (C)导体内E=0,q 在导体内产生场强; (D)导体内E ≠0,q 不在导体内产生场强。
7、如图所示,一内半径为a ,外半径为b 的金属球壳,带有电量Q ,在球壳空腔内距离球心为r 处有一点电荷q ,设无限远 处为电势零点。
试求: (1)球壳外表面上的电荷;(2)球心O 点处由球壳内表面上电荷产生的电势; (3)球心O 点处的总电势。
r AR Q·O · Q· b· O a rqB解: (1) 设球壳内、外表面电荷分别为q 1 , q 2,以O 为球心作一半径为R (a <R <b )的高斯球面S,由高斯定理01εqq dS E S +=⋅⎰⎰ ,根据导体静电平衡条件,当a <R <b 时,0=E。
电磁学习题第二章答案电磁学习题第二章答案电磁学习题是电磁学课程中的重要组成部分,通过解答学习题,可以帮助我们巩固理论知识,加深对电磁学的理解。
本文将为大家提供电磁学习题第二章的答案,希望对大家的学习有所帮助。
第一题:一根长为L的直导线,通以电流I,求其产生的磁场强度H。
答案:根据安培环路定理,直导线产生的磁场强度与电流成正比,与导线的长度成反比。
因此,直导线产生的磁场强度H与电流I和导线的长度L满足以下关系式:H = I / (2πL)其中,H为磁场强度,I为电流,L为导线长度。
第二题:一根直导线上通有电流I,求距离导线d处的磁感应强度B。
答案:根据比奥萨伐尔定律,距离直导线d处的磁感应强度B与电流I和距离d成正比。
因此,距离导线d处的磁感应强度B与电流I和距离d满足以下关系式:B = μ0I / (2πd)其中,B为磁感应强度,I为电流,d为距离导线的距离,μ0为真空中的磁导率,其值为4π×10^-7 T·m/A。
第三题:一根长为L的直导线,通以电流I,求距离导线d处的磁场强度H。
答案:根据比奥萨伐尔定律,距离直导线d处的磁感应强度B与电流I和距离d成正比。
而磁场强度H与磁感应强度B成正比。
因此,距离导线d处的磁场强度H与电流I、导线长度L和距离d满足以下关系式:H = μ0I / (2πd)其中,H为磁场强度,I为电流,L为导线长度,d为距离导线的距离,μ0为真空中的磁导率,其值为4π×10^-7 T·m/A。
第四题:一根长为L的直导线,通以电流I,求距离导线d处的磁场强度H和磁感应强度B。
答案:根据比奥萨伐尔定律,距离直导线d处的磁感应强度B与电流I和距离d成正比。
而磁场强度H与磁感应强度B成正比。
因此,距离导线d处的磁场强度H和磁感应强度B与电流I、导线长度L和距离d满足以下关系式:H = μ0I / (2πd)B = μ0I / (2πd)其中,H为磁场强度,B为磁感应强度,I为电流,L为导线长度,d为距离导线的距离,μ0为真空中的磁导率,其值为4π×10^-7 T·m/A。