最新小学五年级长方体正方体的奥数题

1、一个长方体的棱长之和是80厘米，如果把这个长方体平均截成两段，就成了两个大小相等的正方体，求：这个长方体的表面积和体积。

80÷2÷8=5（cm) 表面积：5X5X5X2=250（平方厘米）体积：5X5X5=125（立方厘米）答：这个长方体的表面积是250平方厘米，体积是125立方2、把3个完全相等的正方体拼成一个长方体，这个长方体的表面积是350平方厘米，每个正方体的表面积是多少平方厘米？350÷14X6=150（平方厘米）答：每个正方体的表面积是150平方厘米？3、把一个长方体的木块截成两段，就成了两个完全相等的正方体，这两个正方体的棱长之和比原来那个长方体的棱长之和增加40厘米，原来那个长方体的体积是多少立方厘米？40÷8=5（厘米）5X2=10（厘米）5X5X10=250（平方厘米）答：原来那个长方体的体积是250立方厘米4、把一个长、宽、高分别是7厘米、6厘米、5厘米的长方体截成两个长方体，使这两个长方体的表面积之和最大，这时表面积之和是多少平方厘米？（7X6+7X5+6X5）X2=214（平方厘米）214+6X7X2=298（平方厘米）答：这时表面积之和是298平方厘米5、一个长方体，前面和上面的面积之和是290平方厘米，这个长方体的长宽高都是质数，这个长方体的体积和表面积各是多少？290=29X10=29X（7+3）体积：29X7X3=609（立方厘米）表面积：（29X7+29X3+7X3）=672（平方厘米）答：这个长方体的体积j 609立方厘米，表面积是672平方厘米6、一个长方体的表面积是78平方厘米，底面积是15平方厘米，底面周长是16厘米，求长方体的体积。

78－15－15=48（平方厘米）48÷16=3（厘米）15×3=45（立方厘米）答：长方体的体积是45立方厘米7、一个长方体水箱，从里面量，长20厘米，宽30厘米，深35厘米，箱中水面高5厘米，放进一个棱长20厘米的正方体的铁块后，铁块顶面仍高于水面，这时水面的高多少厘米？20×30×5=3000（立方厘米）20×30－20×20=200（平方厘米）3000÷200=15（厘米）答：这时水面的高15厘米8、一个长方体木块，从下部和上部分别截去3厘米和2厘米的长方体后，成了一个正方体，表面积减少了120平方厘米，原长方体的体积是多少立方厘米？120÷（3+2）=24（平方厘米）24÷4=6（厘米）6+3+2=11（厘米）6×6×11=369（立方厘米）答：原长方体的体积是369立方厘米。

五年级下册数学长方体与正方体奥数练习题[共5篇]第一篇：五年级下册数学长方体与正方体奥数练习题长方体和正方体（二）【例题1】有一个长方体形状的零件，中间挖去一个正方体的孔（如图），你能算出它的体积和表面积吗？（单位：厘米）练习1：1.有一个形状如下图的零件，求它的体积和表面积。

（单位：厘米）。

2.有一个棱长是4厘米的正方体，从它的一个顶点处挖去一个棱长是1厘米的正方体后，剩下物体的体积和表面积各是多少？【例题2】一个正方体和一个长方体拼成了一个新的长方体，拼成的长方体的表面积比原来的长方体的表面积增加了100平方厘米。

原正方体的表面积是多少平方厘米？练习2：1.一根长80厘米，宽和高都是12厘米的长方体钢材，从钢材的一端锯下一个最大的正方体后，它的表面积减少了多少平方厘米？2.把4块棱长都是2分米的正方体粘成一个长方体，它们的表面积最多会减少多少平方分米？【例题3】一个棱长为6厘米的正方体木块，如果把它锯成棱长为2厘米的正方体若干块，表面积增加多少厘米？练习3：1.把27块棱长是1厘米的小正方体堆成一个大正方体，这个大正方体的表面积比原来所有的小正方体的表面积之和少多少平方厘米？2.有一个棱长是1米的正方体木块，如果把它锯成体积相等的8个小正方体，表面积增加多少平方米? 【例题4】有一个正方体木块，把它分成两个长方体后，表面积增加了24平方厘米，这个正方体木块原来的表面积是多少平方厘米？练习4：1.把三个棱长都是2厘米的正方体拼成一个长方体，这个长方体的表面积是多少平方厘米？2.有一个正方体木块，长4分米、宽3分米、高6分米，现在把它锯成两个长方体，表面积最多增加多少平方分米？3.有三块完全一样的长方体积木，它们的长是8厘米、宽4厘米、高2厘米，现把三块积木拱成一个大的长方体，怎样搭表面积最大？最大是多少平方厘米？【例题5】一个正方体的表面涂满了红色，然后如下图切开，切开的小正方体中：（1）三个面涂有红色的有几个？（2）二个面涂有红色的有几个？（3）一个面涂有红色的有几个？（4）六个面都没有涂色的有几个？练习5：1.把一个棱长是5厘米的正方体的六个面涂满红色，然后切成1立方厘米的小正方体，这些小正方体中，一面涂红色的、二面涂红色的、三面涂红色的以及六个面都没有涂色的各有多少个？2.把若干个体积相同的小正方体堆成一个大的正方体，然后在大正方体的表面涂上颜色，已知两面被涂上红色的小正方体共有24个，那么，这些小正方体一共有多少个？【例题4】一个长方体的长、宽、高分别是6厘米、5厘米和4厘米，若把它切割成三个体积相等的小长方体，这三个小长方体表面积的和最大是多少平方厘米？练习4：1.有三块完全一样的长方体木块，每块长8厘米、宽5厘米、高3厘米。

五年级奥数之长方体和正方体的表面积例1：一个长方体的棱长之和是48厘米，长是5厘米，宽是4厘米，求它的表面积。

这个长方体的高可以用48减去长和宽的和（5+4=9）得到，即39厘米。

根据长方体表面积的公式，它的表面积为2×(5×4+5×39+4×39)=518平方厘米。

例2：一个零件形状大小如下图，求它的表面积。

由于这个零件由一个长方体和两个正方体组成，可以分别计算它们的表面积再相加。

长方体的表面积为2×(5×4+5×3+4×3)=94平方厘米，正方体的表面积为6×(3×3)=54平方厘米，因此这个零件的表面积为94+54=148平方厘米。

例3：有一个长方体形状的零件。

中间挖去一个正方体的孔（如下图）。

求它的表面积。

（单位：厘米）由于这个零件由一个长方体和一个正方体孔组成，可以先计算长方体的表面积，再减去正方体孔的表面积。

长方体的表面积为2×(8×6+8×2+6×2)=208平方厘米，正方体孔的表面积为6×2×2=24平方厘米，因此这个零件的表面积为208-24=184平方厘米。

例4：下图中的立体图形是由14个棱长为5cm的立方体组成的，求这个立体图形的表面积。

首先可以将这个立体图形分解为一个长方体和两个正方体。

长方体的长、宽、高分别为5、5、10，表面积为2×(5×5+5×10+5×10)=300平方厘米。

正方体的边长为5，表面积为6×(5×5)=150平方厘米。

因此这个立体图形的表面积为300+150+150=600平方厘米。

例5：一个正方体的表面积为54平方厘米，如果一刀把它切成两个长方体，那么，这两个长方体表面积的和是多少平方厘米？一个正方体的表面积为6a^2，其中a为边长。

小学五年级奥数几何长方体和正方体经典例题详解精品学习网为您整理了：五年级奥数几何长方体和正方体经典例题详解欢迎大家阅读愉快!五年级奥数几何长方体和正方体经典例题详解1、一个零件形状大小如下图：算是一算，它的体积就是多少立方厘米，表面积就是多少平方厘米？(1)可以把零件沿虚线分成两部分来求它的体积，左边的长方体体积是10×4×2=80(立方厘米)，右边的长方体的体积是10×(6-2)×2=80(立方厘米)，整个零件的体积是80+80=160(立方厘米)。

10×4×2+10×(6-2)×2=160(立方厘米)(2)谋这个零件的表面积，看上去比较复杂，其实，朝上的两个面的面积和刚好与朝下的一个面的面积成正比;朝右的两个面的面积和刚好与朝左的一个面的面积成正比。

因此，此零件的表面积就是：(10×6+10×4+4×2×2)×2=232(平方厘米)练习(1)一个长5厘米、宽1厘米、高3厘米的长方体，被切去一块后(如下图)，剩下部分的表面积和体积各是多少?练(2)把一根长2米的长方体木料锯成1米短的两段，表面积减少2平方分米，谋这根木料原来的体积。

练习(3)有一个长8厘米，宽1厘米，高3厘米的长方体木块，在它的左右两角各切掉一个正方体(如下图)，求切掉正方体后的表面积和体积各是多少?2、存有一个长方体形状的零件。

中间挖去一个正方体的孔（如下图）。

你能算出来它的体积和表面积吗？（单位：厘米）(1)先求出长方体的体积，8×5×6=240(立方厘米)，由于挖去一个孔，所以体积减少2×2×2=8(立方厘米)，这个零件的体积是240-8=232(立方厘米)(2)长方体完备的表面积就是(8×5+8×6+5×6)×2=236(平方厘米)，但由于挖去一个孔，它的表面积增加了一个(2×2)平方厘米的面积，同时又减少了凹陷进来的5个(2×2)平方厘米的面,因此,这个零件的表面积就是236+(2×2)×4=252(平方厘米).练习(1)有一个形状如下图的零件，求它的体积和表面积。

图27—4五年级（长方体和正方体） 1、一个长方体木块，从下部和上部分别截去高为3厘米和2厘米的长方体后，便成为一个正方体，表面积减少了120平方厘米，原来长方体的体积是 立方厘米．2（1）有一个正方体，如果高增加4cm ，就成为一个长方体，这个长方体的表面积正好比原正方体的表面积增加80平方cm ，求原正方体的体积。

（2）一个长方体的高如果增加2cm ，就成为一个正方体，这时表面积就比原来增加了48平方cm 。

原来长方体的体积是（ ）？3.一个长方体的各条棱长的和是48厘米，并且它的长是宽的2倍，高与宽相等，那么这个长方体的体积是（ ） 4、一个长方体的表面积是33.66平方分米，其中一个面的长是2.3分米，宽是2.1分米，它的体积是_____立方分米.（结果以分数形式出现）5、在棱长为3cm 的正方体木块的每个面的中心上打一个直穿木块的洞，洞口呈边长为1cm 的正方形（见右图）。

求挖洞后木块的体积（ ）。

6.如图，从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长为2厘米的正方形，然后沿虚线折叠成长方体容器．这个容器的体积是（ ）立方厘米?7．一个长方体的棱长总和是48cm ，己知长是宽的1.5倍，宽是高的2倍，求它的体积（ ）。

8.一个正方体木块的表面积是96平方cm ，把它锯成体积相等的8个正方体小木块，每个小木块的表面积是 （ ）9..从一棱长10厘米正方体木块上挖去一长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是（ ）10..把一个长为12分米，宽为6分米，高为9分米的长方体木块锯成两个想同的小厂房体木块，这两个小长方体的表面积之和，比原来长方体的表面积增加了多少平方分米？11.把19个棱长为3厘米的正方体重叠起来，如下右图图27-4所示，拼成一个立体图形，求这个立体图形的表面积。

12..在一个长50厘米、宽40厘米、高10厘米的长方体容器中，盛有5厘米深的水。

现将一块石头放入水中，水面升高到8厘米处，这块石头的体积是多少立方厘米？13.在一个长24分米、宽9分米、高8分米的水槽中注入4分米深的水，然后放入一个棱长为6分米的铁块。

有关长方体和正方体的奥数题高分别是3厘米、4厘米、5厘米，求这两个立体图形的表面积和体积。

1.一个零件的形状如图所示，求它的体积和表面积。

该零件的体积为 60 立方厘米，表面积为 94 平方厘米。

2.一个长方体长 5 厘米，宽 1 厘米，高 3 厘米，被切去一块后剩下的部分的表面积为 38 平方厘米，体积为 12 立方厘米。

3.把一根长 2 米的长方体木料锯成 1 米长的两段，表面积增加了 2 平方分米，原来的木料体积为 8 立方米。

4.一个长方体形状的零件中间挖去一个正方体的孔，该零件的体积为 150 立方厘米，表面积为 194 平方厘米。

5.一个零件的形状如图所示，求它的体积和表面积。

该零件的体积为 48 立方厘米，表面积为 94 平方厘米。

6.一个正方体和一个长方体拼成了一个新的长方体，拼成的长方体的表面积比原来的长方体的表面积增加了 50 平方厘米。

原正方体的表面积为 54 平方厘米。

7.把 11 块相同的长方体砖拼成一个大长方体，每块砖的体积为 288 立方厘米，大长方体的表面积为 2184 平方厘米。

8.一个长方体的体积是 385 立方厘米，且长、宽、高都是质数，该长方体的表面积为 194 平方厘米。

9.一个长方体前面和上面的面积之和是 209 平方厘米，且长、宽、高都是质数。

该长方体的体积为 77 立方厘米，表面积为 214 平方厘米。

10.一个长方体和一个正方体的棱长之长相等，已知长方体长、宽、高分别为 3 厘米、4 厘米、5 厘米，两个立体图形的表面积分别为 94 平方厘米和 94 平方厘米，体积分别为 60 立方厘米和 27 立方厘米。

思维拓展训练：长方体和正方体-数学2024五年级下册1．求下图中大圆球的体积。

2．一个长方体，如果高增加4厘米，那么就变成一个正方体，这时表面积比原来增加128平方厘米，原来长方体的表面积是多少平方厘米？3．小强要用家里的一块长方形纸板做一个物品收纳盒。

这块纸板长20厘米，宽16厘米，四个角减去相同的小正方形（如图所示），就能围成无盖的长方体收纳盒。

（1）如果减去的小正方形的边长是5厘米，围成的长方体收纳盒的容积是多少？（2）减去的小正方形的边长还可以是多少厘米（长度取整厘米数）？这时围成的长方体收纳盒的表面积是多少？（3）如果用a厘米表示要减去的小正方形的边长，请你用字母公式表示出这个无盖长方体收纳盒的容积或表面积。

4．下图是李师傅为小明做的一个底面为正方形，内高是20厘米的无盖玻璃容器。

（1）把1升水倒入玻璃容器，水深10厘米，再把一个苹果沉入容器（苹果被水全部淹没），结果水面上升了3厘米，这个苹果的体积是多少立方厘米？（2）制作这个玻璃容器至少需要玻璃多少平方厘米？5．如下图，一个长、宽、高分别为30厘米、16厘米、21厘米的长方体容器中水位高度是10厘米，如果将另一个长方体（长、宽、高分别为16厘米、10厘米、36厘米的铁块竖直）放入左边的容器中（贴底面齐平），那么这个容器中的水会溢出吗？如果不溢出，那么容器中水位将上升至多少高度？如果溢出，那会溢出多少立方厘米的水量？6．笑笑家有甲、乙两个不同规格的带盖收纳盒，她想把家里散落的小包纸巾分别放入这两个收纳盒中（纸巾不能超过收纳盒的上沿且不能挤压）。

一小包纸巾的长、宽、高和收纳盒内部的长、宽、高如下图所示。

（单位：厘米）（1）甲收纳盒中最多可以放置多少包纸巾？（2）尽可能多地往乙收纳盒中放纸巾，你可以放置多少包？结合生活实际想一想，我（）笑笑的想法。

（填“同意”或“不同意”）如果同意，请你写出理由；如果不同意，尽可能多地往乙收纳盒中放纸巾，你可以放置多少包？写出你的思考过程，可以写一写，画一画。

小学五年级长方体正方体的练习题1、把一张长20厘米，宽16米的长方形纸裁成同样大小，面积尽可能大的正方形，纸没剩余，最多可裁多少个？2、两车同时从甲乙两地相对开出，甲每小时行48千米，乙车每小时行54千米，相遇时两车离中点36千米，甲乙两地相距多少千米？3、一块长40厘米、宽30厘米的长方形铁板，把它的四个角分别切掉边长为4厘米的正方形，然后焊接成一个无盖的盒子。

它的容积是多少升？4、楼房外壁用于流水的水管是长方体。

如果每节长15分米，横截面是一个长方形，长1分米，宽0.6分米。

做一节水管，至少要用铁皮多少平方分米？5.把一根长2米的长方体木料,平均截成3段,表面积增加了12平方米,原来长方体木料的体积是多少立方分米？6.一个长方体长16分米，高6分米,沿水平方向横切成俩个小长方体,表面积增加160平方分米,求原长方体体积？7.一个长方体如果高减少3厘米,正好成为一个正方体,表面积少36平方厘米,原长方体的体积？8.一个长方体高减2厘米成一个正方体,面积减少24平方厘米.原长方体的体积是多少立方厘米9.一个长方体木块，从上部和下部分别截去高为3厘米和2厘米的长方体，便成为一个正方体，表面积减少了120平方厘米，原来长方体的体积是多少立方厘米？10.一个长方体，如果高增加2厘米就成了一个正方体，而且表面积增加56平方厘米，求原长方体的体积？11.一段长方体木料，长1.2米如果锯短2厘米，它的体积就减少40立方厘米，求原长方体的体积？12.一个长方体，表面积是70平方分米,底面积是9.8平方分米,底面周长是12.6分米,这个长方体的高是多少？体积是多少？13.一个长方体的表面积为16000平方分米,底面是边长为40厘米的正方形,求长方体的体积是多少？14.将一块棱长20厘米的正方体铁块锻压成一块，100厘米长,2厘米厚的铁板，这个铁板的宽是多少？15.把一棱长30厘米的正方体钢坯,锻压成高和宽都是5厘米的长方体钢材.能锻造多长？16.把一个棱长5厘米的正方体钢材，锻压成长5厘米,宽4厘米的长方体钢材,钢材厚多少厘米？17、用两个长5cm，宽3cm，高4cm的长方体拼成一个大的长方体。

长方体与正方体一、走进来：大科学家伽里略说：“大自然用数学语言讲话。

这个语言的字母是：圆、三角形还有长方体及其它各种形体。

”圆、三角形等是平面图形；长方体、正方体等是立体图形平面图形是研究同一个平面内的各数量之间的关系；而立体图形研究的是若干个面内的数量和数量之间的关系。

长方体和正方体是我们最熟悉的几何体。

我国国家游泳中心就是一个巨大的长方体，它的长、宽、高分别为 177米、 177米、30米，又被称为“水立方”，2008年奥运会主要的游泳赛事将在这个巨大的长方体建筑内举行！本章我们将进一步认识长方体、正方体及其组合而成的立体图形的特征，学习其体积和表面积的计算方法和技巧。

提高作图能力、观察能力、计算能力和空间想象力。

二、一起做：【例1】有一个长6厘米，宽4厘米，高8厘米的长方体木块，表面被刷上了红油漆，把它截成棱长是2厘米的若干个小正方体教具，然后把各个小正方体教具中没有刷上红油漆面也刷上红油漆，问还要刷多少平方厘米的红油漆？提示：先画出图形，然后借助图形观察分析，弄清没有刷上红油漆的面处在大正方体的何位置。

【例2】老师为了考核同学们的空间想象能力，用若干个棱长为1cm的小正方体摆成如图所示的立体图形。

你能计算出这个立方体的体积和表面积吗？提示：求体积关键是数一数小正方体的个数，注意数正方体时要讲究顺序性。

数一数相对的面，看看你有什么发现？【例3】有一个六个面都涂满巧克力的长方体的大蛋糕，长4分米，宽4分米，高6分米，把它切成棱长是1分米的若干个小正方体蛋糕分给幼儿园的小朋友，问：（1）没有吃到巧克力的小朋友共有多少人？（2）吃到三个面、两个面、一个面涂有巧克力蛋糕的小朋友各有多少人？提示：动手画一画图，看看三面、二面、一面涂巧克力及没有涂巧克力的小正方各在长方体的什么位置。

相信你一定能发现其中的规律！【例4】在一个棱长为9厘米的正方体的钢坯上、下底面正中间打一个对穿孔，制成一个机器零件。

已知这个对穿孔是底面边长为2厘米的正方形，这个机器零件的体积和表面积各是多少？如果在前、后、左、右面正中间也各打一个同样的对穿孔，你能算出这个零件的体积和表面积吗？提示：你能画出相应的图形吗？体积的计算可采用相减的办法，当打三个对穿孔时需注意如何处理三个孔的交汇处的立方体。

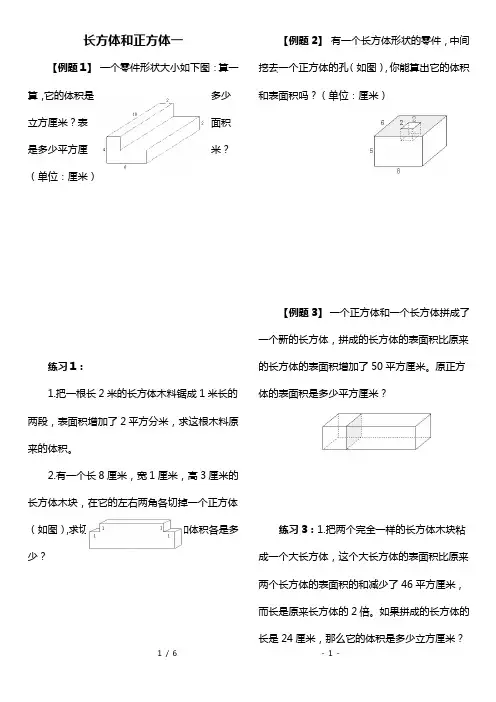
长方体和正方体一【例题1】一个零件形状大小如下图：算一算，它的体积是多少立方厘米？表面积是多少平方厘米？（单位：厘米）练习1：1.把一根长2米的长方体木料锯成1米长的两段，表面积增加了2平方分米，求这根木料原来的体积。

2.有一个长8厘米，宽1厘米，高3厘米的长方体木块，在它的左右两角各切掉一个正方体（如图），求切掉正方体后的表面积和体积各是多少？【例题2】有一个长方体形状的零件，中间挖去一个正方体的孔（如图），你能算出它的体积和表面积吗？（单位：厘米）【例题3】一个正方体和一个长方体拼成了一个新的长方体，拼成的长方体的表面积比原来的长方体的表面积增加了50平方厘米。

原正方体的表面积是多少平方厘米？练习3：1.把两个完全一样的长方体木块粘成一个大长方体，这个大长方体的表面积比原来两个长方体的表面积的和减少了46平方厘米，而长是原来长方体的2倍。

如果拼成的长方体的长是24厘米，那么它的体积是多少立方厘米？1 / 6 - 1 -2.一根长80厘米，宽和高都是12厘米的长方体钢材，从钢材的一端锯下一个最大的正方体后，它的表面积减少了多少平方厘米？3.把4块棱长都是2分米的正方体粘成一个长方体，它们的表面积最多会减少多少平方分米？【例题4】把11块相同的长方体砖拼成一个大长方体。

已知每块砖的体积是288立方厘米，求大长方体的表面积。

练习4：1.一块小正方体的表面积是6平方厘米，那么，由1000个这样的小正方体所组成的大正方体的表面积是多少平方厘米？2.一个长方体的体积是385立方厘米，且长、宽、高都是质数，求这个长方体的表面积。

3.有24个正方体，每个正方体的体积都是1立方厘米，用这些正方体可以拼成几种不同的长方体？用图画出来。

【例题5】一个长方体，前面和上面的面积之和是209平方厘米，这个长方体的长、宽、高以厘为为单位的数都是质数。

这个长方体的体积和表面积各是多少？练习5：1.有一个长方体，它的前面和上面的面积和是88平方厘米，且长、宽、高都是质数，那么这个长方体的体积是多少？2.一个长方体的长、宽、高是三个连续偶数，体积是96立方厘米，求它的表面积。

奥数专项训练长方体和正方体1.表面积与体积（五）【典型例题】一个正方体棱长为10分米，如果把这个正方体切割成棱长是2．5分米的小正方体，可以切成多少个？如果将这些小正方体排成一行，有多长？【举一反三】1．一个正方体棱长是1分米，如果把这个正方体切割成棱长是1厘米的小正方体，可以切成多少个？如果将这些小正方体排成一行，长多少米？2．一个正方体棱长是12厘米，如果把这个正方体切割成棱长是2厘米的小正方体，然后将这些小正方体排成一行，长多少米？3．一个长方体的长、宽、高分别是10厘米、8厘米、6厘米，如果把这个长方体切割成棱长是2厘米的小正方体，可以切成多少个？如果将这些小正方体排成一行，有多长？【拓展提高】一个集装箱，它的内尺寸是18×18×18，现在有一批货箱，它的外尺寸是1×4×9．这只集装箱能装多少只货箱？【奥赛训练】4．有一个长方体的盒子，从里面量长40厘米、宽12厘米、高7厘米．在这个盒子里放入长5厘米、宽4厘米、高3厘米的长方体木块，最多可以放几块？5．一个长方体容器内装满水，現在有大、中、小三个铁球，第一次把小球沉入水中；第二次把小球取出，把中球沉入水中；第三次把中球取出，把小球和大球一起沉入水中．已知每次从容器中溢出水量的情况是：第二次是第一次的3倍，第三次是第一次的2．5倍．间：大球的体积是小球的多少倍？6．一个长方体的长、宽、高都是两位数（其中长的值最大），并且它们的和是偶数．若这个长方体的体积是277、2380、3261、4125这四个数中的个，则这个长方体的长是多少？2.表面积与体积（六）【典型例题】如图所示，从一个棱长为10厘米的正方体木块中挖去ー个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？【举一反三】1．如图所示，从一个棱长为10厘米的正方体木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？2．如图所示，从一个棱长为10厘米的正方体木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？3．如图所示，从一个棱长为10厘米的正方体木块中挖去一个长10厘米宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？【拓展提高】如图所示，有一个棱长为12厘米的正方体木块，从它的上面、前面、左面中心分别凿穿一个边长为4厘米的正方形孔．那么，穿孔后木块的体积是多少立方厘米？【奥赛训练】4．从一个棱长为10厘米的正方体木块上，截去一个棱长为2厘米的小正方体，剩下部分的表面积是多少？（提示：可以从多角度考虑）5．一个棱长为1米的正方体木块，沿水平方向将它锯成3份，每份又锯成4长条，共得大大小小长方体12块．这12块小长方体的表面积总和是多少平方米？6．如图所示，有一个边长为5厘米的立方体本块，在它的每个角以及每条棱和每个面的中间各挖去一个边长为1厘米的小立方体（即图中画有阴影的那些小立方体）那么，余下部分的表面积是多少平方厘米？3.表面积与体积（七）【典型例题】在一个长15分米、宽12分米的长方体水箱中，有10分米深的水．如果在水中沉入ー个棱长为30厘米的正方体铁块，那么，水箱中水深多少分米？【举一反三】1．一个长方体容器，从里面量长5分米、宽4分米、高6分米，水深3分米如果把一块棱长为2分米的正方体铁块浸没于水中，水面将上升多少分米？2．一个正方体容器，从里面量棱长为2分米，向容器内倒入5升水，再把小块石头完全浸入水中，这时容器中的水深1．5分米，求石头的体积3．一个长方体容器的底面是一个边长为60厘米的正方形，容器里直立着一个高1米、底面边长为15厘米的长方体铁块，这时容器里的水深0．5米．如果把铁块取出，容器里水深多少厘米？【拓展提高】如图1，一个长方体容器，底面是一个边长为60厘米的正方形，容器里直立着一个高1米、底面边长为15厘米的长方体铁块，这时容器里的水深0．5米、如图2，现在把铁块轻轻向上提起24厘米后，那么，露出水面的铁块上被水浸湿的部分长多少厘米？【奥赛训练】4．某养鱼池长8米、宽5米、深1米，平时池中水面比池面低1分米，池内有两个边长为1分米的正方形出水口．如果平均每秒钟的排水速度是2米，那么，排完这池水需要多少分钟？5有一个长方体容器，从里面量长6分米、宽5分米、高5分米，里面注入了2分米深的水．如果把一块棱长是3分米的正方体铁块放入水中正方体铁块的一面与容器底面紧贴，水面上升多少分米？6．如图所示，在长、宽、高分别为10cm、10cm、6cm的长方体容器中盛有深4cm的水，若向容器中放入一个棱长为5cm的正方体铁块，那么，水深变为多少cm？4.表面积与体积（八）【典型例题】燕燕买了6盒外语听力磁带准备送给班里的贫困生，这种磁带从外面量，长12厘米、宽7厘米、高1厘米如果要求售货员包装一下，最少需要多少包装纸？（贴粘处不计）【举一反三】1．将两个长都是8厘米、宽都是6厘米、高都是5厘米的长方体拼成一个大长方体，这个大长方体表面积最大是多少平方厘米？2．有一个长、宽、高分别是5、4、3厘米的长方体，将它截成两个长方体，使这两个长方体的表面积之和最大．这时表面积之和是多少平方厘米？3．已知大正方体表面积是864平方厘米，把大正方体平均切割成27个正方体，求27个小正方体的表面积的和【拓展提高】一种长方体物品长17厘米、宽7厘米、高3厘米，现要把12件这样的物品拼成一个大长方体包装物．如何包装能使大长方体的表面积最小，最小是多少？【奥赛训练】4．用三块长5厘米、宽4厘米、高2厘米的长方体积木，把它们拼成个表面积最大的大长方体，这个大长方体的表面积是多少？5.如图所示，将9块相同的小长方体积木拼成了一个大长方体，已知每块小长方体的体积是48立方厘米，求大长方体的表面积6.将12件长9分米、宽7分米、高5分米的小长方体物品堆放成一个大长方体．这个大长方体的表面积最小是多少？。

五年级下册数学长方体与正方形体奥数练习题第一部分：长方体练题1. 问题：一个长方体的长是5cm，宽是3cm，高是2cm。

它的体积是多少？请用公式计算并写出答案。

问题：一个长方体的长是5cm，宽是3cm，高是2cm。

它的体积是多少？请用公式计算并写出答案。

答案：体积公式为：长 ×宽 ×高。

根据给定的值，可以计算体积：：体积公式为：长 ×宽 ×高。

根据给定的值，可以计算体积：5cm × 3cm × 2cm = 30cm³2. 问题：一个长方体的体积是54cm³，宽是2cm，高是3cm。

请问，它的长是多少？问题：一个长方体的体积是54cm³，宽是2cm，高是3cm。

请问，它的长是多少？答案：体积公式为：长 ×宽 ×高。

已知宽和高的值，可以通过体积公式求解长：：体积公式为：长 ×宽 ×高。

已知宽和高的值，可以通过体积公式求解长：54cm³ = 长 × 2cm × 3cm长 = 54cm³ / (2cm × 3cm) = 9cm3. 问题：一个长方体的长是8cm，高是4cm，体积是192cm³。

请问，它的宽是多少？问题：一个长方体的长是8cm，高是4cm，体积是192cm³。

请问，它的宽是多少？答案：体积公式为：长 ×宽 ×高。

已知长和高的值，可以通过体积公式求解宽：：体积公式为：长 ×宽 ×高。

已知长和高的值，可以通过体积公式求解宽：192cm³ = 8cm ×宽 × 4cm宽 = 192cm³ / (8cm × 4cm) = 6cm4. 问题：一个长方体的长是10cm，宽是6cm，体积是600cm³。

请问，它的高是多少？问题：一个长方体的长是10cm，宽是6cm，体积是600cm³。

10、号码分别为37、57、77、和97的四名运动员进行乒乓球比赛，规定每两人比赛的盘数是他们号码的和除以3的余数，那么打球盘数最多的运动员是几号？他打了多少盘？
11.一部书，甲、乙两个打字员需要10天完成，两人合打8天后，余下的由乙单独打，若这部书由甲单独打需要28天完成。问乙又干了几天完成？
12．在300米长的环形跑道上,甲、乙两人同时同向并排起跑，甲平均每秒跑5米，乙平均每秒跑4.4米。两人起跑后的第一次相遇在起跑线前多少米？
8、一个整数除以84的余数是46，那么他分别除以3、4、7所得的三个余数之和是多少？
9、甲、乙、丙、丁四个旅行团分别有游客69人、85人、93人、97人。现在要把四个旅行团分别进行分组，使每组都是A名游客，以便乘车前往参观旅游。已知甲、乙、丙三个团分成每组A人的若干组后，所剩下的人数相同，问丁旅行团分成每组A人的若干组后还剩下几人？
洗葱，切葱花
打蛋
搅拌蛋液和葱花
洗锅
烧热锅
烧热油
烧菜
1分钟
半分钟
1分钟
半分钟
半分钟
半分钟
2分钟
小晴做好这道菜至少需要分钟。
9、一项特殊的工作必须日夜有人值守，如果安排8人轮流值班，当值班人员为3人，那么，平均每人每天工作小时。
10、甲、乙两商店中某种商品的定价相同。甲商店按定价销售这种商品。销售额是7200
9、有一个棱长为9厘米的正方体，在每两个对面的中央钻一个边长为2厘米的正方形孔，且穿透，所得立体的体积是多少？
10、有甲、乙、丙三个正方体水池，它们内边长分别是5米、3米、1米，把两堆碎石分别沉没在乙、丙两个水池的水里，它们的水面分别升高了4厘米和2厘米。如果将这两堆碎石都沉没在甲水池的水里，甲水池的水面升高了多少厘米？

对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．cba H GF ED CB A①在六个面中，两个对面是全等的，即三组对面两两全等．(叠放在一起能够完全重合的两个图形称为全等图形．)②长方体的表面积和体积的计算公式是：长方体的表面积：2()S ab bc ca =++长方体；长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．板块一 长方体与正方体的表面积【例 1】 右图中共有多少个面？多少条棱？后面前面右面左面上面【考点】长方体与正方体 【难度】1星 【题型】解答【解析】 如右图所示，可以分前、后、左、右、上、下六个方向看这个立体图形．前、后看各有1个面，左面看有1个面，右面看有2个面，上面看有2个面，下面看有1例题精讲长方体与正方体（一）个面．所以共有1112218+++++=(个)面．前后方向的棱有6条，左右方向的棱有6条，上下方向的棱也有6条，所以共有棱66618++=(条)．【答案】8个面，18条棱【巩固】右图中共有多少个面？多少条棱？【考点】长方体与正方体【难度】1星【题型】解答【解析】9个面，21条棱．【答案】9个面，21条棱【例 2】如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？【考点】长方体与正方体【难度】2星【题型】解答【解析】我们从三个方向(前后、左右、上下)考虑，新几何体的表面积仍为原立方体的表面积：10⨯10⨯6=600．【答案】600【巩固】在一个棱长为50厘米的正方体木块，在它的八个角上各挖去一个棱长为5厘米的小正方体，问剩下的立体图形的表面积是多少？【考点】长方体与正方体【难度】2星【题型】解答【解析】对于和长方体相关的立体图形表面积，一般从上下、左右、前后3个方向考虑．变化前后的表面积不变：50⨯50⨯6=15000(平方厘米)．【答案】15000【例 3】如右图，有一个边长是5的立方体，如果它的左上方截去一个边分别是5，3，2的长方体，那么它的表面积减少了多少?【考点】长方体与正方体【难度】2星【题型】解答【解析】原来正方体的表面积为5⨯5⨯6=150．现在立体图形的表面积减少了前后两个面中的部分面，它们的面积为(3⨯2)⨯2=12，所以减少的面积就是12．【答案】12【例 4】如图，有一个边长是5的立方体，如果它的左上方截去一个边分别是5，3，2的长方体，那么它的表面积减少了百分之几?【考点】长方体与正方体【难度】2星【题型】解答【关键词】奥林匹克，初赛，10题【解析】原来正方体的表面积为 5 ×5×6=150，现在立体图形的表面积截了两个面向我们的侧面，它们的面积为(3×2)×2=12，12÷150=0.08=8％．即表面积减少了百分之八．【答案】百分之八【例 5】右图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）【考点】长方体与正方体【难度】2星【题型】解答【解析】原正方体的表面积是4⨯4⨯6=96(平方厘米)．每一个面被挖去一个边长是1厘米的正方形，同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分．总的来看，每一个面都增加了4个边长是1厘米的正方形．从而，它的表面积是：96+4⨯6=120平方厘米．【答案】120【例 6】如图，有一个边长为20厘米的大正方体，分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后，表面积变为2454平方厘米，那么挖掉的小立方体的边长是多少厘米？【考点】长方体与正方体【难度】2星【题型】解答【解析】大立方体的表面积是20⨯20⨯6=2400平方厘米．在角上挖掉一个小正方体后，外面少了3个面，但里面又多出3个面；在棱上挖掉一个小正方体后，外面少了2个面，但里面多出4个面；在面上挖掉一个小正方体后，外面少了1个面，但里面多出5个面．所以，最后的情况是挖掉了三个小正方体，反而多出了6个面，可以计算出每个面的面积：(2454-2400)÷6=9平方厘米，说明小正方体的棱长是3厘米．【答案】3【例 7】下图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞，第三个正方形小洞的挖法和前两个相同为14厘米，那么最后得到的立体图形的表面积是多少平方厘米？【考点】长方体与正方体【难度】3星【题型】解答【解析】我们仍然从3个方向考虑．平行于上下表面的各面面积之和：2⨯2⨯2=8(平方厘米)；左右方向、前后方向：2⨯2⨯4=16(平方厘米)，1⨯1⨯4=4(平方厘米)，1 2⨯12⨯4=1(平方厘米)，14⨯14⨯4=14(平方厘米)，这个立体图形的表面积为：816++4+1+14=1294(平方厘米).【答案】1 294【例 8】从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？(写出符合要求的全部答案)【考点】长方体与正方体【难度】3星【题型】解答【关键词】小学生数学报【解析】按图1所示沿一条棱挖，为592平方厘米；按图2所示在某一面上挖，为632平方厘米；按图3所示在某面上斜着挖，为648平方厘米；按图4所示挖通两个对面，为672平方厘米．图1 图2 图3 图4【答案】按图1所示沿一条棱挖，为592平方厘米；按图2所示在某一面上挖，为632平方厘米；按图3所示在某面上斜着挖，为648平方厘米；按图4所示挖通两个对面，为672平方厘米．图1 图2 图3 图4【例 9】一个正方体木块，棱长是15．从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体．这个木块剩下部分的表面积最少是多少？【考点】长方体与正方体【难度】4星【题型】解答【关键词】迎春杯【解析】截去一个小正方体，表面积不变，只有在截去的小正方体的面相重合时，表面积才会减少，所以要使木块剩下部分的表面积尽可能小，应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示)，这时剩下部分的表面积比原正方体的表面积减少最多．剩下部分的表面积最小是： 15⨯15⨯6-7⨯7⨯2=1252．想想为什么不是15⨯15⨯6-7⨯7-8⨯8 ？【答案】1252【例 10】 从一个长8厘米、宽7厘米、高6厘米的长方体中截下一个最大的正方体(如下图)，剩下部分的表面积之和是 平方厘米．68766【考点】长方体与正方体 【难度】3星 【题型】填空【解析】 可以将这个图形看作一个八棱柱，表面积和为：87662616661787292⨯-⨯⨯+⨯+++++++=（）（）(平方厘米)．也可以这样想：由于截去后原来的长方体的表面少了3个66⨯的正方形，而新图形凹进去的部分恰好是3个66⨯的正方形，所以新图形的表面积与原图形的表面积相等，为()8786762292⨯+⨯+⨯⨯=(平方厘米)．【答案】292【巩固】一个长、宽、高分别为21厘米、15厘米、12厘米的长方形，现从它的上面尽可能大的切下一个正方体，然后从剩余的部分再尽可能大的切下一个正方体，最后再从第二次剩余的部分尽可能大的切下一个正方体，剩下的体积是多少平方厘米？【考点】长方体与正方体 【难度】3星 【题型】解答【解析】 本题的关键是确定三次切下的正方体的棱长.由于21:15:127:5:4=，为了方便起见.我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体.因为754>>,容易知道第一次切下的正方体棱长应该是4厘米（如图），第二次切时，切下棱长为3厘米的正方体符合要求.第三次切时，切下棱长为2厘米的正方体符合要求. 剩下的体积应是()33321151212961107⨯⨯-++=（平方厘米）.【答案】1107【例 11】 一个正方体木块，棱长是1米，沿着水平方向将它锯成2片，每片又锯成3长条，每条又锯成4小块，共得到大大小小的长方体24块，那么这24块长方体的表面积之和是多少？【考点】长方体与正方体 【难度】3星 【题型】解答【解析】 锯一次增加两个面，锯的总次数转化为增加的面数的公式为：锯的总次数⨯2=增加的面数．原正方体表面积：1⨯1⨯6=6(平方米)，一共锯了(2-1)+(3-1)+(4-1)=6次， 6+1⨯1⨯2⨯6=18(平方米)．【答案】18【巩固】如右图，一个正方体形状的木块，棱长l米，沿水平方向将它锯成3片，每片又锯成4长条，每条又锯成5小块，共得到大大小小的长方体60块．那么，这60块长方体表面积的和是多少平方米?【考点】长方体与正方体【难度】3星【题型】解答【解析】我们知道每切一刀，多出的表面积恰好是原正方体的2个面的面积．现在一共切了(3-1)+(4-1)+(5-1)=9刀，而原正方体一个面的面积1⨯l=1(平方米)，所以表面积增加了9⨯2⨯1=18(平方米)．原来正方体的表面积为6⨯1=6(平方米)，所以现在的这些小长方体的表积之和为6+18=24(平方米)．【答案】24【巩固】一个表面积为256cm的长方体如图切成27个小长方体，这27个小长方体表面积的和是2cm．【考点】长方体与正方体【难度】3星【题型】填空【关键词】走美杯，六年级，初赛【解析】每一刀增加两个切面，增加的表面积等于与切面平行的两个表面积，所以每个方向切两刀后，表面积增加到原来的3倍，即表面积的和为2⨯=．563168(cm)【答案】168【例 12】右图是一个表面被涂上红色的棱长为10厘米的正方体木块，如果把它沿虚线切成8个正方体，这些小正方体中没有被涂上红色的所有表面的面积和是多少平方厘米？【考点】长方体与正方体【难度】3星【题型】解答【解析】10⨯10⨯6=600(平方厘米)．【答案】600【例 13】 有n 个同样大小的正方体，将它们堆成一个长方体，这个长方体的底面就是原正方体的底面．如果这个长方体的表面积是3096平方厘米，当从这个长方体的顶部拿去一个正方体后，新的长方体的表面积比原长方体的表面积减少144平方厘米，那么n 为多少？【考点】长方体与正方体 【难度】3星 【题型】解答【解析】 由于堆成的长方体的底面就是原来正方体的底面，说明这个长方体是由这些正方体一字排开组成的，从这个长方体的顶部拿去一个正方体，减少的面积相当于侧面的四个正方形的面积，所以正方体每个面的面积是144436÷=(平方厘米)．所堆成的长方体的表面积，包含底面的2个正方形和侧面的4n 个正方形，所以(3096362)14421n =-⨯÷=．【答案】21【例 14】 边长分别是3、5、8的三个正方体拼在一起，在各种拼法中，表面积最小多少？【考点】长方体与正方体 【难度】3星 【题型】解答【解析】 三个正方体两两拼接时，最多重合3个正方形面，其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形，边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形，三个正方形表面积和为6⨯3⨯3+6⨯5⨯5+6⨯8⨯8-2⨯2⨯3⨯3-2⨯5⨯5=502.【答案】502【例 15】 如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少？25块积木【考点】长方体与正方体 【难度】3星 【题型】解答【解析】 当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木，当拼成一个333⨯⨯的正方体时，表面积最小，现在要去掉2块小积木，只有在两个角上各去掉一块小积木，或在同一个角去掉两块相邻的积木时，表面积不会增加，该几何体表面积为54.【答案】54【例 16】 由六个棱长为1的小正方体拼成如图所示立体，它的表面积是 ．【考点】长方体与正方体 【难度】3星 【题型】填空【关键词】走美杯，4年级，决赛，第3题，8分【解析】 三视图法：表面积为：()454226++⨯=【答案】26【例 17】 将15个棱长为1的正方体堆放在桌子上，喷上红色后再将它们分开。

【思路导航】
铁块的体积是2×2×2=8（立方分米），把它浸入水中后，它就占了8立方分米的空间，因此，水上升的体积也就是8立方分米，用这个体积除以底面积（5×4）就能得到水上升的高度了。
有一个小金鱼缸，长4分米、宽3分米、水深2分米。把一块假山石浸入水中后，水面上升0.8分米。这块假山石的体积是多少立方分米？
【思路导航】
首先求出水的体积：30×20×6=3600（立方厘米）。当容器竖起来以后，水流动了，但体积没有变，这时水的形状是一个底面积是20×10=200平方厘米的长方体。只要用体积除以底面积就知道现在水的深度了。
01
有两个长方体水缸，甲缸长3分米，宽和高都是2分米；乙缸长4分米、宽2分米，里面的水深1.5分米。现把乙缸中的水倒进甲缸，水在甲缸里深几分米？
二、精讲精练
ห้องสมุดไป่ตู้
【例题1】 有两个无盖的长方体水箱，甲水箱里有水，乙水箱空着。从里面量，甲水箱长40厘米，宽32厘米，水面高20厘米；乙水箱长30厘米，宽24厘米，深25厘米。将甲水箱中部分水倒入乙水箱，使两箱水面高度一样，现在水面高多少厘米？
【思路导航】
由于后来两个水箱里的水面的高度一样，我们可以这样思考：把两个水箱并靠在一起，水的体积就是（甲水箱的底面积+乙水箱的底面）×水面的高度。这样，我们只要先求出原来甲水箱中的体积：40×32×20=25600（立方厘米），再除以两只水箱的底面积和：40×32＋30×24=2000（平方厘米），就能得到后来水面的高度。
02
有一块边长2分米的正方体铁块，现把它煅造成一根长方体，这长方体的截面是一个长4厘米、宽2厘米的长方形，求它的长。
练习4：
【例题5】
长方体不同的三个面的面积分别为10平方厘米、15平方厘米和6平方厘米。这个长方体的体积是多少立方厘米？

1、一个长方体的长、宽、高分别是5厘米、4厘米、3厘米，它的容积是多少立方厘米？A、20B、40C、60D、120（答案：C，解析：长方体的容积=长×宽×高=5×4×3=60立方厘米。

）2、一个正方体的棱长是6厘米，它的容积是多少立方厘米？A、216B、144C、108D、72（答案：A，解析：正方体的容积=棱长×棱长×棱长=6×6×6=216立方厘米。

）3、一个长方体的容积是120立方厘米，长是5厘米，宽是4厘米，那么它的高是多少厘米？A、5B、6C、7D、8（答案：B，解析：长方体的高=容积÷(长×宽)=120÷(5×4)=6厘米。

）4、一个正方体的容积是64立方厘米，那么它的棱长是多少厘米？A、4B、6C、8D、16（答案：A，解析：正方体的棱长=容积的立方根=64的立方根=4厘米。

）5、一个长方体的长、宽、高都扩大2倍，那么它的容积会扩大多少倍？A、2B、4C、6D、8（答案：D，解析：长方体的容积扩大倍数=长扩大倍数×宽扩大倍数×高扩大倍数=2×2×2=8倍。

）6、一个正方体的棱长扩大3倍，那么它的容积会扩大多少倍？A、3B、6C、9D、27（答案：D，解析：正方体的容积扩大倍数=棱长扩大倍数的立方=3的立方=27倍。

）7、一个长方体的容积是180立方厘米，如果它的长、宽、高都缩小一半，那么新的容积是多少立方厘米？A、180B、90C、45D、22.5（答案：C，解析：新的容积=原容积÷(长缩小倍数×宽缩小倍数×高缩小倍数)=180÷(2×2×2)=45立方厘米。

）8、一个正方体的容积是27立方厘米，如果它的棱长缩小到原来的三分之一，那么新的容积是多少立方厘米？A、27B、9C、3D、1（答案：C，解析：新的容积=原容积×(棱长缩小倍数的立方)=27×((1/3)的立方)=3立方厘米。

小学五年级奥数举一反三 第15周 长方体和正方体
(三)
知识要点
解答有关长方体和正方体的拼、切问题，除了要切 实掌握长方体、正方体的特征，熟悉计算方法，仔 细分析每一步操作后表面几何体积的等比情况外， 还必须知道：把一个长方体或正方体沿水平方向或 垂直方向切割成两部分，新增加的表面积等于切面 面积的两倍。
王牌例题3： 有一个正方体，棱长是3分米。如果按下图把它切成棱长是1 分米的小正方体，这些小正方体的表面积的和是多少？ 【思路导航】按题中要求切，一共可以切成的小正方体是 3×3×3=27（个）。由于每个小正方体的表面积是1×1×6=6 （平方分米），所以，这27个小正方体的表面积是6×27=162 （平方分米）。
王牌例题4： 一个正方体的表面涂满了红色，然后如下图切开，切开 的小正方体中： （1）三个面涂有红色的有几个？ （2）二个面涂有红色的有几个？ （3）一个面涂有红色的有几个？ （4）六个面都没有涂色的有几个？
【思路导航】按题中的要求切，切成的小正方体一共有 3×3×3=27个。 （1）三个面涂有红色的小正方体在大正方体的顶点处，共有8个； （2）二个面涂有红色的小正方体在大正方体的棱上，共有 1×12=12个； （3）一个面涂有红色的小正方体在大正方体的六个面上，共有 1×6=6个； （4）六个面都没有涂色的在大正方体的中间，有27－（8＋12＋ 6）=1个。
举一反三2
1.由16个棱长为2厘米的小正方体重叠而成的，求这个立体图形 的表面积。 2.把三个棱长都是2厘米的正方体拼成一个长方体， 这个长方体的表面积是多少平方厘米？ 3.有三块完全一样的长方体积木，它们长8厘米、宽4厘米、高2 厘米。现把三块积木拼成一个大的长方体，怎样搭表面积最大？ 最大是多少平方厘米？