第二章复变函数的积分.doc
- 格式:doc
- 大小:126.19 KB
- 文档页数:7



第二章 复变函数的积分在微积分学中,微分法与积分法是研究函数性质的重要方法。
同样,在复变函数中,积分法也跟微分法一样是研究复变函数性质十分重要的方法和解决实际问题的有力工具。
§2.1 复变函数积分的概念一、复变函数的积分设C 为平面上给定的一条光滑(或按段光滑)曲线。
若选定C 的两个可能方向中的一个作为正方向,那么就把C 理解为带有方向的曲线,称为有向曲线。
设曲线C 的两个端点为A 与B ,如果从A 到B 的方向作为C 的正方向,那么从B 到A 的方向就是C 的负方向,并把它记作-C 。
在今后的讨论中,常把两个端点中的一个作为起点,另一个作为终点。
除特殊声明外,正方向总是指从起点到终点的方向。
关于简单闭曲线的正方向是指当曲线上的点P 顺此方向沿该曲线前进时,临近P 点的曲线内部始终位于P 点的左方。
与之相反的方向就是曲线的负方向。
若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==,)(βα≤≤t (2.1) t 为实参数,则规定t 增加的方向为正方向,即由)(αz a =到)(βz b =的方向为正方向。
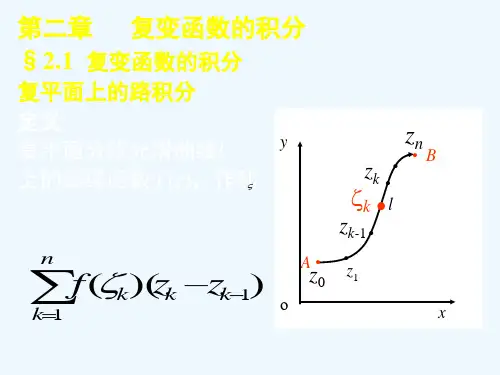
定义2.1 设函数)(z f w =定义在区域D 内,C 为区域D 内起点为A 终点为B 的一条光滑有向曲线,把曲线C 任意分成n 个弧段,设分点为:B z z z z z A n n ==-,...,,,1210 在每个小弧段上任取一点k ζ(图3.1),作和∑=∆=nk k k n z f S 1)(ζ其中1--=∆k k k z z z ,记=∆k s 的长度,}Δ{max 1k nk s δ≤≤=。
当n 无限增加,且δ趋于零时,如果不论对C 的分法及k ζ的取法如何,当n S 有唯一极限,那么称这个极限值为函数)(z f 沿曲线C 的积分,记作∑⎰=→=nk k kδCz ζf dz z f 1Δ)(lim )( (2.2)图2.1C 称为积分路径,⎰Cdz z f )(表示沿C 的正方向的积分,⎰-C dz z f )(表示沿C的负方向的积分。



Anhui University 在上一章学习了复变函数,重点介绍了解析函数的许多性质,这些性质都是在可导和可微的基础上得出的。
第2章复变函数积分()(,)(,) 若函数在区域内解析则有:f z u x y iv x y D =+1. 解析函数的调和性:解析函数的实部与虚部均满足二维拉普拉斯方程:(由C-R 条件可证明)。
220,0.xx yy xx yy u u u u v v v v ∆≡∇=+=∆≡∇=+=2. 解析函数的共轭性:解析函数的实部与虚部由C-R 方程联系,称为解析函数的共轭性。
具体说只要知道解析函数的实部或者虚部就可求得解析函数。
3. 解析函数的实部与虚部是彼此相互正交的曲线。
0),(),(=∇⋅∇y x v y x u为了深入理解复变函数,本章用积分理论来分析复变函数积分。
基本内容:1、掌握复积分的概念、性质和计算方法;2、掌握解析函数的基本定理-Cauchy定理及其应用;3、掌握解析函数的基本公式-Cauchy公式及其应用2.1 复数函数积分一. 复积分的定义1max 0()lim ()k n k k n C k z f z dz f z ζ→∞=∆→=∆∑∫记作:()w f z l =为被积函数,为积分路径。
二. 复积分存在的条件1max 0()lim ()k n k kn l k z f z dz f z ζ→∞=∆→=∆∑∫由上式可知:一个复积分的实质是两个实积分的和。
实积分存在的条件:(,)(,)分段光滑,,在上连续l u x y v x y l因此复积分存在的条件:分段光滑,在上连续。
()l f z l注1:所说的曲线总是指光滑或逐段光滑曲线。
注2:边界的正方向:规定当观察者沿曲线边界前进时,所围的区域始终在观察者的左手边,则前进的方向为正方向。
rzz<−单连通区域Rzzr<−<复连通区域正方向正方向三. 复积分的性质(1)()d ()d l lf z z f z z −=−∫∫反转积分路径:(2)()d ()d ;() l l kf z z k f z z k =∫∫为复常数(3)[()()]d ()d ()d ;l l l f z g z z f z z g z z ±=±∫∫∫121()(),,k n n k L l f z dz f z dz n l l l ==∑∫∫"(4),若曲线L由段线段组成被积函数的线性可叠加性积分路径的可叠加性(5)|()||()|||L L f z dz f z dz ≤⋅∫∫(6) , () () ()d ()d .设曲线的长度为函数在上满足那么l l l L f z l f z M f z z f z s ML ≤≤≤∫∫积分估值定理四. 计算方法1. 用定义计算2. 通过计算实积分结果表明:被积函数与积分路径有关。




第二章复变函数的积分
基本要求:
1.正确理解复变数函数路积分的概念;
2.深透理解柯西定理及孤立奇点的定义;
3.理解并会熟练运用柯西公式。
本章重点:
柯西定理,柯四公式和孤立奇点。
§2.1.复变函数的积分
1、复变函数积分
复数积分是复平面上的线积分。
设/是复平面上的一条由/到E点的光滑曲线,在曲线上复变函数./(Z)有定义,在曲线上任意分为段,曲线上各分点为
3是[Zk-\, Zk]段上的任意一点。
作和数
£/(彳)亿= £/(彳M
*=1 *=|
当斤无限增大,使每一Az&都趋于零时,如果这个和数的极限存在,且其值与各个点①的选取无关,则这极限值称为函数沿曲线由/到B的路积分:
"(Z心為tQ©曲
因
z = x + iy;/(z) = “(x,p) + j〃(x,y)
因此
J/(2)dz = J[〃(x,_y) + h(x,y)]d(x + ")
J ("dr - udy) + /|( zxh + udy)
即,复变函数的路积分归为两个实变函数的线积分。
2、复变函数积分的性质
由上一积分式知,复变积分具有实变函数线积分所具有的一般性质。
(1)常数因子可以移到积分号之外:
|J/'(z)dz =町/(z)dz A为常数
(2)函数的和的积分等于各个函数的积分之和:
[[•/;(z)*(z)+...4y;(z)]dz= “(z)血+(£(z)血+ ...+必⑵血
(3)反转积分路径,积分变号:
J /(z)dz = -ji /(z)dz 厂表示/的逆向
(4)全路径上的积分等于各段积分Z和:
j/(z)dz= j/(z)dz+ J /(2)血+ ...+ J /(Z)血
此外,还有经常用到的:
(5) |“(z)血卜J|/(z)||dz|
(6) \[f(z)dz\<MC,其中M为|/(z)|在/上的上界,C为/的长度。
例2・1求jRezdz, 1为(1)沿实轴由0—1,再平行虚轴1 — 1+7; (2)沿虚轴由0_>Z,再平行实轴z—l+j。
,(3)沿直线0 ->1+7。
解:(1)
JRezdz = Jxd(x + 少)=j(xd.r + /xdy) = J (xdv + ixdy)dz + J [xdx + ixdy)dz =(xdx + f idy = *
+ 7
(2)
JRczdz = Jxd (x + ") = |(xdr + ixdy) = | (xdv + Zrdy)dz+ j (xdr + ixdy)dz
I
I 1
)xdx =—
(3)因/的直线方程为兀二八因此
单连通区域:在区域中任何简单的闭合曲线,曲线内的点都属于该区域。
复连通区域(或称多连通区域):由多丁一条的闭曲线组成的区域。
简单说就是带“孔”的区域。
奇点:如果复变函数./(z)在某点不可导,这点就称为y(z)的奇点。
孤立奇点:如果复变函数比)在某个奇点的冇限小邻域上(不包括该奇点)是解析的,这奇点称为孤立奇点。
例如。
点是函数1/(Z- a)的孤立奇点。
柯西定理一:设求力是由回路/所围的闭单连通区域上的解析函数,则
“(z)dz = O
证:因
J / (z)血=J ("dr _ t)dy) +(txlr + z/dv)
设广⑵也是连续的,即単啟舉半都是连续函数。
因此上式右边两个积分ax uy ox oy
利用格林公式
J(Pdx + 0⑪)=J[(律dj坤
有:
由C —R条件,上式右边为零。
证毕。
推论一:单连通区域内,解析函数的积分值只与积分曲线的两端点有关,而与曲线的具体形状无关。
证:(略)
柯西定理二:如果复变函数./(z)是复连通区域上的单值解析函数,则
其中人4=1,2,...,〃)是复连通区域边界上各分段光滑的闭曲线。
证明:(略)
推论二:对于闭复通区域上的单值解析函数,沿外边界线逆时针方向的积分等于沿各内边界线逆时针方向积分之和。
推论三:闭单通或闭复通区域上的解析函数,当积分路径连续变形(或说不跳过“孔”)时,只要起点和终点不变,函数的积分值不变。
vdx^udy)
例2.2计算[亠z 。
z —a
解:。
点是一个奇点,被积函数在该点不可导。
考虑/绕和不绕。
点情况。
若冋 路不绕。
点,根据柯西定理,积分为零。
若/绕Q 点,考虑以。
点为圆心作一半 径为/?的圆周C,则在圆
周C 上,z = a + R* ,根据柯西定理则有:
f 1血一严(° +卅)_ F iR 尹(1。
_ [0 /不包围Q
^z-a _丄 —Re^ —_丄 Re i (p ~ iln /包围a
易证:J(Z-G )"dz = 0 (整数A7 工-1) 此例是很冇用的。
§2.3.不定积分
根据柯西定理,在单连通区域内的解析函数/(z)沿区域内任一段光滑曲线的 积分值只与起点
和终点有关。
因此,如果固定起点zo,而终点为z,则不定积分
『/(z )dz = F (z )
是区域内的一个单值解析函数(证明略),11
称F(z)为/⑵的原函数。
§2.4.柯西公式
1、柯西公式
设函数./(z)在以/为边界的闭区域上解析,点。
为区域内的一个点。
根据上 节例2.2,
有:
另外,如图,考虑如下积分,并根据柯西定理二的推论,我 们有: 因此,
J 占寸恃工厲护4
/(。
)=
2刃 1
2加
7 — a JC 7 — a
上式左边与园半径大小诜关,所以右边积分也不应依赖园的大小。
因此,可令£ —> Oo 又因为/(z)dz| < MC ,其中M 为在C 上的最大值,C 为园的周长。
在圆周上,z-a = £ 9因此有:
z-a
令 £-0,则有 J[z) =7(67),得: J/"!]% 也2”max|/(z)-/(a)| = 0
因此有:
卩⑺-心)“0 力 z-a
即:
z-a z-a
即:
/(a) = — f^-^dz = — f^^dz 2兀 i "z-a 2兀 i z-a
上式称为柯西积分公式,简称柯西公式。
2、几个重要推论
(1) 柯西公式
将柯西积分公式中的Q 是区域中任意一点,因此用Z 取代G 并将变量代换
以此类推: 上式也称为柯曲公式。
(2) 最大模定理(证明略)
若./U )是闭区域中的解析函数,则模I ./(勿的最大值在边界上。
以避免混淆,得:
因上式积分是在边界上进行, 因此上式可求导,因此有 因此ZH0,因此被积函数在积分威处处连续, /'(z) = 1! 2兀
i
• /⑷ /⑵一/⑷ dz<max /(Z )-
/(6Z )
(3)刘维定理(证明略)
若./U)在全平面解析,而且当ZTOO时,有界,则./U)是一个常数。
(4)均值定理(证明略)
解析函数Hz)在其解析区域内任一点a的函数值畑,等于在以a为圆心、完全位于区域内的任意一个园上的函数值的平均,即
(5)柯西不等式(证明略)
I7 1丿I 2兀 J/(g_z)* §2计'
其中M/z)|在边界上的最大值,/是边界的全长,〃是由z到边界点的最短距离。