得各物理量的量纲如下
- 格式:ppt
- 大小:1.33 MB
- 文档页数:49

有限元分析中的单位问题大多数有限元计算程序都不规定所使用的物理量的单位,不同问题可以使用不同的单位,只要在一个问题中各物理量的单位统一就可以。
但是,由于在实际工程问题中可能用到多种不同单位的物理量,如果只是按照习惯采用常用的单位,表面上看单位是统一的,实际上单位却不统一,从而导致错误的计算结果。
比如,在结构分析中分别用如下单位:长度– m;时间– s;质量– kg;力- N;压力、应力、弹性模量等– Pa,此时单位是统一的。
但是如果将压力单位改为MPa,保持其余单位不变,单位就是不统一的;或者同时将长度单位改为mm,压力单位改为MPa,保持其余单位不变,单位也是不统一的。
由此可见,对于实际工程问题,我们不能按照手工计算时的习惯来选择各物理量的单位,而是必须遵循一定的原则。
物理量的单位与所采用的单位制有关。
所有物理量可分为基本物理量和导出物理量,在结构和热计算中的基本物理量有:质量、长度、时间和温度。
导出物理量的种类很多,如面积、体积、速度、加速度、弹性模量、压力、应力、导热率、比热、热交换系数、能量、热量、功等等,都与基本物理量之间有确定的关系。
基本物理量的单位确定了所用的单位制,然后可根据相应的公式得到各导出物理量的单位。
具体做法是:首先确定各物理量的量纲,再根据基本物理量单位制的不同得到各物理量的具体单位。
基本物理量及其量纲:·质量m;·长度L;·时间t;·温度T。
导出物理量及其量纲:·速度:v = L/t;·加速度:a = L/t2;·面积:A = L2;·体积:V = L3;·密度:ρ= m/L3;·力:f = m·a = m·L/t2;·力矩、能量、热量、焓等:e = f·L = m·L2/t2;·压力、应力、弹性模量等:p = f/A = m/(t2·L) ;·热流量、功率:ψ= e/t = m·L2/t3;·导热率:k =ψ/ (L·T) = m·L/(t3·T);·比热:c = e/(m·T) = L2/(t2·T);·热交换系数:Cv = e/(L2·T·t) = m/(t3·T)·粘性系数:Kv = p·t = m/(t·L) ;·熵:S = e/T = m·l2/(t2·T);·质量熵、比熵:s = S/m = l2/(t2·T);在选定基本物理量的单位后,可导出其余物理量的单位,下面举两个常用的例子。

麦克斯韦方程组乃是由四个方程共同组成的:▪高斯定律描述电场是怎样由电荷生成。
电场线开始于正电荷,终止于负电荷。
计算穿过某给定闭曲面的电场线数量,即其电通量,可以得知包含在这闭曲面内的总电荷。
更详细地说,这定律描述穿过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。
▪高斯磁定律表明,磁单极子实际上并不存在于宇宙。
所以,没有磁荷,磁场线没有初始点,也没有终止点。
磁场线会形成循环或延伸至无穷远。
换句话说,进入任何区域的磁场线,必需从那区域离开。
以术语来说,通过任意闭曲面的磁通量等于零,或者,磁场是一个螺线矢量场。
▪法拉第感应定律描述含时磁场怎样生成(感应出)电场。
电磁感应在这方面是许多发电机的运作原理。
例如,一块旋转的条形磁铁会产生含时磁场,这又接下来会生成电场,使得邻近的闭循环因而感应出电流。
▪麦克斯韦-安培定律阐明,磁场可以用两种方法生成:一种是靠电流(原本的安培定律),另一种是靠含时电场(麦克斯韦修正项)。
在电磁学里,麦克斯韦修正项意味着含时电场可以生成磁场,而由于法拉第感应定律,含时磁场又可以生成电场。
这样,两个方程在理论上允许自我维持的电磁波传播于空间(更详尽细节,请参阅条目电磁波方程)。
自由空间:在自由空间里,不需要考虑介电质或磁化物质的问题。
假设源电流和源电荷为零,则麦克斯韦方程组变为:、、、。
对于这方程组,平面行进正弦波是一组解。
这解答波的电场和磁场相互垂直,并且分别垂直于平面波行进的方向。
电场与磁场同相位地以光速传播:。
仔细地观察麦克斯韦方程组,就可以发现这方程组很明确地解释了电磁波怎样传播于空间。
根据法拉第感应定律,时变磁场会生成电场;根据麦克斯韦-安培定律,时变电场又生成了磁场。
这不停的循环使得电磁波能够以光速传播于空间。
第一种表述:将自由电荷和束缚电荷总和为高斯定律所需要的总电荷,又将自由电流、束缚电流和电极化电流总合为麦克斯韦-安培定律内的总电流。
这种表述采用比较基础、微观的观点。

第一章习题解1-1.水流进高为h =0.2m 的两块宽平板之间的通道,如图1-52所示。
已知:通道截面具有速度分布2007575x u ..y =-。
求:通道截面平均速度U 。
解:由式(1-3)得通道截面平均速度()0.1220.0757.510.210.05m /s-⨯=⨯=⎰⎰x Au dA U =Ay dy1-2.如图1-53所示,在一密闭容器内装有水及油,密度分别为ρ水=998.1kg /m 3,,ρ油=850kg /m 3,油层高度h 1=350mm ,容器底部装有水银(ρ水银=13600 kg /m 3)液柱压力计,读数为R =700mm,水银面的高度差h 2=150mm ,求容器上方空间的压力p 。
解:在图1-53中,U 型管上取控制面Ⅰ,两侧压力相等。
由式(1-20)流体静力学的平衡定律得 ()1210油水水银p+ρgh +ρg R+h -h =p +ρgR将大气压50 1.013310Pa =⨯p 和其它已知数据代入上式,可得容器上方空间的压力51.8710Pa =⨯p1-3.如图1-54所示,已知容器 A 中水面上的压力为p A =1.25大气压,压力计中水银面的差值 h 1=0.2m ,h 2=0.25m ,h =0.5m, ρH 2O =1000kg/m 3,ρHg =13550kg/m 3。
求:容器B 中压力p B 。
解:在图1-54中,各U 型管上取控制面Ⅰ、Ⅱ,各控制面两侧压力相等。
设中间管中空气压力为p ,并忽略空气密度。
由式(1-20)流体静力学的平衡定律得 ()2A H O 1Hg 1B Hg 2⎧⎪⎨⎪⎩p +ρg h+h =p+ρgh p =p +ρgh ()()2B A H O 1Hg 12p =p +ρg h+h -ρg h +h将55A 1.25 1.013310 1.26710Pa =⨯⨯=⨯p 和其它已知数据代入上式,可得容器B 中压力4B 7.3810Pa =⨯p1-4.证明:单位时间单位面积动量的量纲与单位面积力的量纲相同。



第三节 量纲分析法量纲分析是20世纪初提出的, 在物理领域中建立数学模型的一种方法,它是在经验和实验的基础上, 利用物理定律的量纲齐次原则,确定各物理量之间的关系。
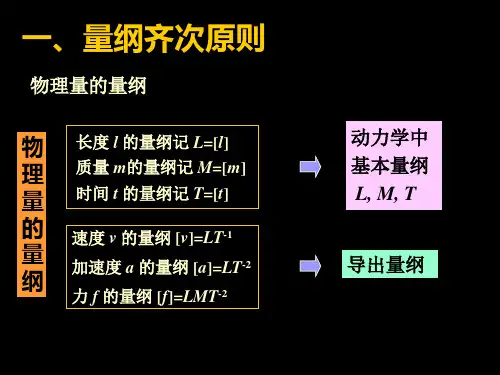
3.1 量纲齐次原则与Pi 定理许多物理量是有量纲的,有些物理量的量纲是基本的,另一些物理量的量纲则可以由基本量纲根据其定义或某些物理定律推导出来。
例如在动力学中,把长度l , 质量m 和时间t 的量纲作为基本量纲,记为[][][]T t M m L l ===,,; 而速度f v ,力的量纲可表示为[][]21,--==MLT f LT v .在国际单位制中,有7个基本量:长度、质量、时间、电流、温度、光强度和物质的量,它们的量纲分别为L 、M 、T 、I 、Θ、J 、和N ;称为基本量纲。
任一个物理量q 的量纲都可以表成基本量纲的幂次之积,[]ηξεδγβαJ N I T M L q Θ=量纲齐次性原则:用数学公式表示一个物理定律时,等式两端必须保持量纲一致。
量纲分析就是在保证量纲一致的原则下,分析和探求物理量之间关系;先看一个具体的例子,再给出量纲分析的一般方法。
例3—1: 单摆运动,质量为m 的小球系在长度为l 的线的一端,线的另一端固定,小球偏离平衡位置后,在重力mg 作用下做往复摆动,忽略阻力,求摆动周期t 的表达式。
解:在这个问题中有关的物理量有g l m t ,,,设它们之间有关系式3211αααλg l m t =---------------(3.1)其中32,,ααα为待定常数,入为无量纲的比例系数,取(3.1)式的量纲表达式有[][][][]321αααg l m t = 整理得:33212αααα-+=T LM T --------------(3.2)由量纲齐次原则应有⎪⎩⎪⎨⎧=-=+=12003321αααα ---------------(3.3)解得:,21,21,0321-===ααα 代入(3.1)得 glt λ= -------(3.4)(3.4)式与单摆的周期公式是一致的下面我们给出用于量纲分析建模的 Buckingham Pi 定理,定理:设n 个物理量n x x x ,,,21 之间存在一个函数关系()0,,,21=n x x x f --------------(3.5)[][]m x x 1为基本量纲,n m ≤。


七大基本量纲
七大基本量纲是国际单位制(SI)中定义的基本物理量的量纲。
它们是:
1. 长度(L):表示空间的尺寸和距离。
2. 质量(M):表示物体的惯性和重量。
3. 时间(T):表示事件发生的顺序和持续的时间。
4. 电流(I):表示电荷在导体中的流动。
5. 温度(θ):表示物体的热量和热能状态。
6. 物质的物质数量(N):表示物体中粒子数量的多少。
7. 光强度(J):表示光源的辐射功率。
这些基本量纲可以组合成其他衍生量纲,例如速度、加速度、力、功等。
SI单位制使用这些基本量纲和其衍生量纲来描述和测量物理现象。


§2.2 物理量的单位和量纲2.2.1 国际单位制(SI 制)在历史上, 由于物理量的单位制有很多种,世界各国往往按照各自的习惯,沿用不同的单位制,这不便于科学技术的交流和发展,而且也不规范。
鉴于这种情况,国际计量大会决议推行统一的国际单位制(Le Système International dùnités )简写为SI (注意是法文)。
我国也决定从1987年1月1日起,在各级学校的教科书中使用国际单位制。
国际单位制规定了7个具有严格定义的基本单位,见表2.1所示。
其中前三个单位:长度单位“米”、质量单位“千克”、时间单位“秒”是力学里的基本单位。
国际单位制除了规定7个基本单位之外,还有两个辅助单位,分别是平面角的单位弧度(rad )和立体角的单位球面度(sr )。
表2.1 国际单位制中的基本单位国际单位制规定的其它物理量所对应的单位,如力的单位牛顿、能量单位焦耳、电压单位伏特等等,都可以由这7个基本单位导出。
按照上述基本量和基本单位的规定,速度的单位是米每秒(1m s -⋅);角速度的单位是弧度每秒(1rad s -⋅);加速度的单位是米每二次方秒(2m s -⋅);力的单位是千克米每二次方秒(2kg m s -⋅⋅),称为 “牛顿”,简称“牛”(N )。
21N 1kg m s -=⋅⋅。
其它常见物理常数的名称、符号、数值和单位见附录B 。
2018年11月16日,第26届国际计量大会通过了关于修订国际单位制的决议。
国际单位制7个基本单位中的4个,即千克、安培、开尔文和摩尔将分别改由普朗克常数、基本电荷、玻尔兹曼常数和阿伏伽德罗常数来定义。
加之此前对“秒”、“米”和“坎德拉”的重新定义,至此组成国际计量单位制的7个基本单位均实现了由常数定义,全部告别了采用实物计量的历史。
为了便于读者理解,我们将力学中三个基本单位的新旧定义一并列出。
1. 秒,符号:s ,SI 的时间单位。
附录三物理量单位与量纲1.物理学中的单位制1.1 基本单位和导出单位物理学是一门实验科学,常需要对各种物理量进行必要的测量。
对一个物理量测量的结果一般包括所测定的数值和所需用的单位两个部分。
由于各个物理量之间存在一定的规律性联系,所以可不必对每个物理量的单位都独立地给予规定,而只需选择一组互相独立的物理量为基本量,并为每一个基本量规定一个基本单位。
至于其它的物理量,由于它们都可以由基本量通过有关的关系式(定义或定律)导出,因而称为导出量,与之所对应的单位则称为导出单位。
1.2 单位制由基本单位和一系列有关关系式得到的导出单位就制定了一套单位,这就构成了一定的单位制。
1.2.1 国际单位制(SI)为了国际上的贸易、工业及科学技术交往的需要,1875年在法国巴黎由17个国家的外长制定了米制公约。
米制公约规定:长度单位为米、质量单位为千克(公斤)、时间单位为秒,这种单位制被称为米⋅千克⋅秒制(英文简写为MKS制)。
随着电磁学、热力学、光学和微观物理学的发展,基本量由3个扩大到7个,在此基础上发展起来的单位制被称为国际单位制,这是在1960年的第11届国际计量大会上被首次予以确认的,并统一以SI表示。
在国际单位制中,将单位分为三大类:基本单位、导出单位和辅助单位。
其中基本单位有7个,它们分别为:(1)长度单位―――米(m)。
1889年第1届国际计量大会上批准以铂铱米尺(被称为国际米原器)的长度为1米。
1983年第17届国际计量大会上对米作了最新的定义:“米是1/299792458秒的时间间隔内光在真空中行程的长度”。
在通过“米”的定义的同时,还规定了复现新的米定义的三种方法(在此之前,应首先规定真空中的光速为c = 299792458m s-1):一是利用平面电磁波在真空中经过时间间隔∆t 所传播的距离l = c∆t的关系,从计量时间∆t得出l;二是利用频率为ν的平面电磁波在真空中的波长λ = c/ν的关系,从测量频率ν得出波长λ;三是可采用所规定的某种饱和吸收稳频激光的辐射,或某些光谱灯的辐射,通过测量其频率而得出波长。