二次函数复习课公开课.

格式：ppt
大小：224.50 KB
文档页数：4

下载文档原格式

二次函数图像与性质复习课件PPT课件一等奖新名师优质课获奖比赛公开课

方程的方程 ax2＋bx＋c＝0(a≠0)有两个相等的实数根；
关系 3.当 b2－4ac＜0 时抛物线与 x 轴___没__有_____交点，
方程 ax2＋bx＋c＝0(a≠0)没有实数根.
中考解读
考点聚焦
中考探究
当堂检测
第12课时┃ 二次函数旳图象与性质
考点 5 二次函数 y＝ax2＋bx＋c(a≠0)的图象特征与 a、b、 c 之间的关系
皖考解读
考点聚焦
皖考探究
当堂检测
第12课时┃ 二次函数旳图象与性质
解可设所求二次函数的解析式为 y＝a(x－1)2－1(a≠0)， ∵抛物线过原点(0，0)， ∴a(0－1)2－1＝0，解得 a＝1， ∴该函数解析式为 y＝(x－1)2－1，即 y＝x2－2x.
皖考解读
考点聚焦
皖考探究
当堂检测
第12课时┃ 二次函数旳图象与性质
二次函待定系数法确定二次函数的解析式分三种情况：
数解析 1.已知抛物线上任意三个点的坐标时，选用一般形式；
式的 2.已知抛物线顶点坐标时，选用顶点式；
确定 3.已知抛物线与 x 轴两个交点的坐标时，选用交点式.
中考解读
考点聚焦
中考探究
当堂检测
第12课时┃ 二次函数旳图象与性质
考点4 二次函数与一元二次方程
数)的图象与 x 轴的一个交点为(1，0)，则关于 x 的一元二次
方程 x2－3x＋m＝0 的两实数根是
(B )
A．x1＝1，x2＝－1 B．x1＝1，x2＝2
C．x1＝1，x2＝0 D．x1＝1，x2＝3
解析由于二次函数 y＝x2－3x＋m(m 为常数)的图象与 x 轴的一个交点为(1，0)，即 x＝1 是一元二次方程 x2 －3x＋m＝0 的根，代入得 12－3＋m＝0，m＝2，原方程为 x2－3x＋2＝0，解得 x1＝1，x2＝2，故选 B.

二十二-二次函数复习课PPT课件

一般式：解：设所求的二次函数为 y=a(x＋1)(x－1）
y=ax2+bx+c
由条件得：
y
两根式： y=a(x-x1)(x-x2)
点M( 0,1 )在抛物线上
所以：a(0+1)(0-1)=1
x o
顶点式： y=a(x-h)2+k
得： a=-1 故所求的抛物线解析式为 y=- (x＋1)(x-1)
.
23
4.求抛物线解析式的三种方法
例题精讲
例1.已知一个二次函数的图象过点（－1,10）、
（1,4）、（2,7）三点，求这个函数的解析式？
一般式：解：设所求的二次函数为 y=ax2+bx+c
y=ax2+bx+c
两根式： y=a(x-x1)(x-x2)
由条件得： a-b+c=10 a+b+c=4 4a+2b+c=7
有两个相等的
解
x1=x2=
b 2a
没有实数根
O
x
19
基础练习:
1.不与x轴相交的抛物线是(D )
A y=2x2 – 3
B y= - 2 x2 + 3
C y= - x2 – 3x D y=-2(x+1)2 - 3
2.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x
轴交点情况是( C )
（1）抛物线经过（2，0）（0，-2）（-1，0）三
点。
yx2 x2
（2）抛物线的顶点坐标是（6，-2），且与X轴
的一个交点的横坐标是8。
y1(x6 )221x26x 1 6

彭斌上课二次函数复习公开课(定稿)

(1)a确定抛物线的开口方向： a>0 a<0 (2)c确定抛物线与y轴的交点位置:
c>0 c=0 c<0
b x=- 2a
(3)a、b确定对称轴 ab>0 ab=0 Δ>0 Δ=0
的位置: ab<0 Δ<0
(4)Δ确定抛物线与x轴的交点个数：
(1)a确定抛物线的开口方向： a>0 a<0
y
(2)c确定抛物线与y轴的交点位置:
y y y y
O
x O x O
x O x
A B C D
答案: B
前进
快速反应（口答）
(题型四) 求函数解析式
根据下列条件选择合适的方法求二次函数解析式： 1、抛物线经过（2，0）（0，-2）（-2，3）三点。 2、抛物线的顶点坐标是（6，-2），且与X轴的一个交点的横坐标是8。 3、已知二次函数的图象与x轴交于(-1,0)和(6,0),并且经过点(2,12)。
解：∵二次函数的最大值是2 ∴抛物线的顶点纵坐标为2 又∵抛物线的顶点在直线y=x+1上 ∴当y=2时，x=1 ∴顶点坐标为（ 1 ， 2） ∴设二次函数的解析式为y=a(x-1)2+2 又∵图象经过点（3，-6）前进 ∴-6=a (3-1)2+2 ∴a=-2 ∴二次函数的解析式为y=-2(x-1)2+2 即： y=-2x2+4x
c>0
x
c=0
c<0
b x=- 2a
0
(3)a、b确定对称轴 ab>0 ab=0 Δ>0 Δ=0
的位置: ab<0 Δ<0
(4)Δ确定抛物线与x轴的交点个数：
y

二次函数复习-公开课

3
E
-1
2
l
4 12 x , x ，？) Q (x 7 7
过 P作 PQ 与 x轴垂直，交 AE于 Q ，设 P 点横坐标为 x .P Q 的长度为 l，
求 l关于 x 的函数关系式？并写出
y2
43
7
x
12 7
x的取值范围？当 P点运动到什么
位置时，线段 PQ的值最大，并求此时 P点的坐标；
y1 x 2 x 3
已知y 1
( a 1) x b x c
2
的图像,OA=OB，思考：
（1,4）
y2
(9 在抛物线的对称轴上（ 8) ）是否存在点 M，使得 △ ABM 是等腰三角形，若存在，求出点 M的坐标，若不存在，请说明理由；
2
1
x 1
3
已知
3
y 1 ( a 1) x b x c 的图像,OA=OB，思考：
(1, 4 )
2
(2)若该抛物线是由函数
y mx
2
n x p 图像向左
平移1个单位，再向下平移2个单位得到的，则m= -1 ,
-1
3
y1 x 2 x 3
2
n=
4
2
,p=
2
;
化为一般式
2
y x 4x 2
配方
y1 x 1 4
2
y1 x 2 4 2
向右
平移
y1 x 1 1 4

中考二次函数总复习-精品公开课获奖课件百校联赛一等奖课件

x
巩固一下吧！
下列函数中哪些是一次函数，哪些是二次函数？
(1) y 3 x 4
(3) y 1 2x
(5) y x2 x 1
(2) y x2 (4) y 2x2 1 3
x (6) y (x 1)2 (x 1)2
(7) y (x 2)2 3 (9) y x 2 1
x
(8) y 0.5x2 1 (10)x2 y2 5
y
(2)解:∵抛物线与x轴相交时
x2-2x-8=0
A
Bx
P
解方程得:x1=4, x2=-2
∴AB=4-(-2)=6 迈进
而P点坐标是(1,-9)
∴S△ABC=27
(二)根据函数性质鉴定函数图象之间旳位置关系
例3:在同一直角坐标系中，一次函数 y=ax+c和二次函数y=ax2+c旳图象大致为
y
y
y
3、解答题：
已知二次函数旳图象旳顶点坐标为（－2，－3），且图象过点（－3，－2）。（1）求此二次函数旳解析式；（2）设此二次函数旳图象与x轴交于A，B两点，O为坐标原点，求线段OA，OB旳长度之和。
能力训练
1、二次函数旳图象如图所示，则在下列各不等式中成立旳个数是____________
2.选择
(1) 抛物线y=x2-4x+3旳对称轴是___c__________.
A 直线x=1 B直线x= -1 C 直线x=2 D直线x= -2
(2)抛物线y=3x2-1旳______B__________ A 开口向上,有最高点 B 开口向上,有最低点 C 开口向下,有最高点 D 开口向下,有最低点
(3)顶点坐标是:(-2a ,
4ac-b2 4a

二次函数(复习课)课件

详细描述
伸缩变换包括横向伸缩和纵向伸缩。横向伸缩是指将图像在x轴方向上进行放大或缩小，纵向伸缩是指将图像在y轴方向上进行放大或缩小。具体来说，对于函数y=ax^2+bx+c，若图像在x轴方向上放大k倍，则新的函数为y=a(kx)^2+b(kx)+c；若图像在y轴方向上放大k倍，则新的函数为y=a(x)+b(x)/k+ck。通过这两种伸缩变换，我们可以得到原函数的放缩版函数。
02
二次函数的解析式
总结词
二次函数的一般形式是 $y = ax^2 + bx + c$，其中 $a neq 0$。
详细描述
一般式是二次函数的基本形式，它包含了二次函数的最高次项、一次项和常数项。通过一般式可以明确地看出函数的开口方向和开口大小，由系数 $a$ 决定。
VS
二次函数的顶点形式是 $y = a(x - h)^2 + k$，其中 $(h, k)$ 是函数的顶点坐标。
总结词
实际应用问题
总结词
与其他函数的综合
总结词
与几何图形的结合
01
02
03
04
05
06
总结词
详细描述
总结词与图像关系
这类问题需要探讨二次函数的系数与图像之间的关系，如开口大小、对称轴位置等。
一题多解法
这类问题通常有多种解法，需要灵活运用二次函数的性质和图像，寻找最简便的解法。
详细描述
二次函数具有对称性，其对称轴为直线$x = -frac{b}{2a}$。此外，二次函数的开口方向由系数$a$决定，当$a > 0$时，开口向上；当$a < 0$时，开口向下。顶点坐标为$left(-frac{b}{2a}, fleft(-frac{b}{2a}right)right)$。

二次函数复习课——公开课.ppt

如图根据图象解答下的图象二次函数xxycbxaxxcbxaxxacbxaxy??????????x11x231x3x2y2x28x6大大221yx?221yx??2321yx??2412yx???2512yx????2621yxx???20yaxhka????20yaxbxca????2723yxx????12??14二学会从解析式寻找函数信息开口顶点hk开口与y轴的交点0c顶点2424bacbaa??0001?10?121220yaxbxca????1求二次函数与y轴的交点2求二次函数与x轴的交点200yaxbxc????令240bacx?????函数与轴有两个交点240bacx?????函数与轴有一个交点240bacx?????函数与轴没有交点00cycyx轴必有交点与令??
(3)写出关于x的方程ax2 bx c 0的两个根：_x_1_=_1_,_x_2_=__3；（4)写出关于x的不等式ax2 bx c 0的解集为__1__<_x__<_3； (5)写出y随x的增大而减小的自变量x的取值范围：___x_>_2__.
二、学会从解析式寻找函数信息
(1) y x2 (2) y x2 1 (3) y 2(x 1)2 (4) y (x 1)2 2 (5) y (x 1)2 2
(0, 0) (0, 1) (1, 0)
(1, 2) (1, 2)
y a(x h)2 k(a 0)
开口顶点（h,k）
y ax2 bx c(a 0)
开口
(6)y x2 2x 1 (1,2) 与y轴的交点(0,c)
顶点 (7) y x2 2x 3 (1, 4)
( b , 4ac b2 ) 2a 4a
图象上有点A(x1, y1), B(x2 , y2 )，若

第22章《二次函数》复习课PPT课件(人教版)

形？若存在，求点N的坐标；若不存在，请说明理由
三、课堂练习
N M
N
重视知识归纳；重视基本概念；重视典型题型；重视每日小练；重视错题整理；避免盲目大意。
九年级数学
第22章《二次函数》复习（2）
定形图性义式象质
坦洲实验中学初三数学
一、知识回顾
归纳知识：
（1）开a口的向符上号：由抛物a线>0的开口y 方向确定
开口向下
（2）c的符号：
a<0
o
x
由抛物线与y轴的交点位置确定.
交点在y轴正半轴
c>0
y
交点在y轴负半轴
c<0
交点是坐标原点
c=0
ox
∴ OE=DE=1.5 即D(1.5,-1.5)
设直线OD为y=kx,代入D点坐标得y= -x
令x2-2x-3 = -x
二、典型例题
证明: b2-4ac=[-(2m-1)]2-4×1×(m2-m-2) =4m2-4m+1-4m2+4m+8 =9
即b2-4ac ＞0 ∴ 抛物线与x轴有两个不同的交点
三、课堂练习
C
一次函数y=ax+b经过的象限与a, b符号关系 A选项，经过一二四象限， a＜0, b＞0 B选项，经过一二三象限，a＞0, b＞0 C选项，经过一三四象限， a＞0, b＜0 D选项，经过一三四象限，a＞0, b＜0
三、课堂练习
·B
A2
6
三、课堂练习
-1·
·5
与x,y轴交点
-5·
二、典型例题
解：令x=0,解得y=m2-m-2 令y=0,得x2-(2m-1) x+m2-m-2=0 [x-(m-2)][x-(m+1)]=0

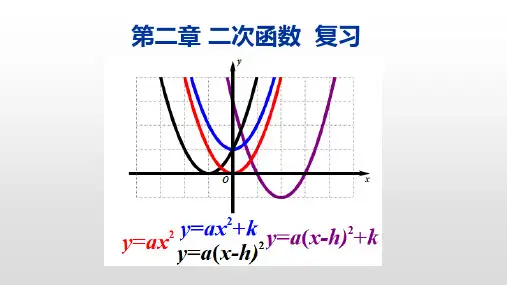
初中数学《二次函数》复习课名师教学PPT课件

3.某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y＝kx+b，且x＝65时，y＝55；x＝75时，y＝45；
(1)求一次函数的解析式；
(2)若该商场获得利润为W元，试写出利润W与销售单价x之间的关系；销售单价定为多少时，商场可获得最大利润，最大利润是多少元？
(3)若该商场所获得利润不低于500元，试确定销售单价x的范围.
二次函数在几何问题中的应用
1.为了节省材料，某水产养殖户利用水库的岸堤(岸堤足够长)为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等.设BC的长度为xm，矩形区域ABCD的面积为ym2.
A.图象关于直线x＝1对称 B.函数y=ax2+bx+c（a≠0）的最小值是-4 C.抛物线y=ax2+bx+c（a≠0）与x轴的两个交点的横坐标分别是-1，3 D.当x＜1时，y随x的增大而增大
2.已知函数y＝(k-3)x2+2x+1的图象与x轴有交点，则k的取值范围是（B）
A.k＜4 B.k≤4 C.k＜4且k≠3 D.k≤4且k≠3
1 x
2.已知函数y＝(m2+m)x2+mx+4为二次函数，则m的取值
范围是（ C）
A.m≠0 B.m≠－1 C.m≠0，且m≠－1 D.m＝－1
3.矩形的周长为24cm，其中一边为xcm（其中x＞0），面积为ycm2，则这样的矩形中y与x的关系可以写成（ B）
A.y＝x2 C. y＝12－x2
B.y＝(12－x)x D.y＝2(12－x)

公开课《二次函数复习课》教案

《二次函数复习》教学设计教学目标1、掌握二次函数的图象及其性质，能灵活运用数形结合知识解一些实际问题2、通过学生亲自经历巩固二次函数相关知识点的过程，体会数形结合思想、化归思想.3、经历探索二次函数相关题目的过程，培养学生的逻辑推理和直观形象和建模等核心素养。

教学重点和难点重点：二次函数图象及其性质，应用二次函数分析和解决简单的实际问题．难点：二次函数性质的灵活运用，能把相关应用问题转化为数学问题．教学过程一、观察图形，梳理基础知识（一）、二次函数的图象及其性质设计意图：通过一个具体二次函数，请学生说出尽可能多的结论，主要让学生回忆二次函数有关基础知识．同学们之间可以相互补充，体现团结协作精神．同时发展了学生的探究意识，培养了学生思维的广阔性．对应练习1. 抛物线y= 4(x+2)2+5的对称轴是______2. y= x2－4的图象与y轴的交点坐标是（）A（2，0） B（－2，0） C（0，4） D（0，－4）3.已知抛物线 y=0.3(x-4)2-3的部分图象,图象再次与x轴相交时的坐标是（）A（5，0） B（6，0）C（7，0） D（8，0）4. 二次函数图象如图，若点Ａ（-3，y1 ），Ｂ（-4，y2 ）是它的图象上两点，则 y1与 y2的大小关系是 ( ) Ａ． y1 ＜ y2 Ｂ． y1 ＝ y2 Ｃ． y1 ＞ y2 Ｄ．不能确定（二）由函数表达式到函数图象1、如何画出函数y=x2-2x-3的图象？2、如何做到快速、准确？3、五点定位法，怎样求出这五个点的坐标？4、粗略感知图象的位置——二次函数的系数a、b、c及b2-4ac对抛物线位置的影响5、二次函数的系数对它的图象有什么影响？设计意图: 由数到形，见“数”想到“形”，用数表达---------用形释义对应练习1.已知二次函数的图象如图，则abc 0.2.二次函数的图象如图所示，则下列关于a 、b 、c 的关系判断正确的是（）A ．ab ＜0 B. bc ＜0 C ．a+b ＋c ＞0 D ．a －b 十c ＜0（三）由函数图象到函数表达式的确定c bx ax y ++=2设计意图：由形到数，见“形”不忘“数”，由浅入深，循序渐进。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B
）
9.抛物线 y=ax2+bx+c 交 xD．下列结论： ①2a+b=0；②2c＜3b；③当 m≠1 时，a+b＜am2+bm；④当△ABD 是等腰直角三角形时，则 a= ；⑤当△ABC 是等腰三角形时，a 的值有 3 个．其中正确的有（
二次函数图像与性质
新课标教学网（）-海量教学资源欢迎下载！
活动一：如图是抛物线y=ax2+bx+c(a≠0) 的图像,请尽可能多的说出一些结论。
y
1
0
1
3
x
新课标教学网（）-海量教学资源欢迎下载！
活动二：归纳总结
名称
二次函数解析式（a≠0）
一般式
新课标教学网（）-海量教学资源欢迎下载！
活动四：难点突破
(1)活动一的图如果我们去掉点的坐标，试讨论与a,b,c有关的代数式的取值。
6
活动四：难点突破
（2）二次函数y=ax2+bx+c(a≠0)的图象
⑤⑥⑦⑧ 如右图所示，那么下列判断正确的有________
（填序号）
①abc>0 ②b2-4ac<0
3.如果将抛物线y=﹣x2﹣2向右平移3个单位，那么所得到的新抛物线的表达式是（ c ） A．y=﹣x2﹣5 B．y=﹣x2+1 C．y=﹣（x﹣3）2﹣2 D．y=﹣（x+3）2﹣2 4.对于抛物线y=﹣（x+2）2+3，下列结论中正确结论的个数为（ c ） ①抛物线的开口向下； ②对称轴是直线x=﹣2； ③图象不经过第一象限； ④当x＞2时，y随x的增大而减小． A．4 B．3 C．2 D．1
最大值 4a -海量教学资源欢迎下载！
o
y
x
o
3
x
活动三：考点梳理
1．下列函数中，二次函数是（ B ）
2.抛物线y=2（x+1）2﹣2与y轴的交点的坐标是（D ）
A．（0，﹣2） B．（﹣2，0）
C．（0，﹣1） D．（0，0）
新课标教学网（）-海量教学资源欢迎下载！
活动三：考点梳理
A）
A．①③④ B．①②④ C．①③⑤ D．③④⑤
新课标教学网（）-海量教学资源欢迎下载！
再见
新课标教学网（）-海量教学资源欢迎下载！ 13
③4a+b>0 ④a+b+c<0 ⑤a-b+c=0 ⑥4a+2b+c>0 ⑦a+b+2c>0 ⑧3a+c<0
新课标教学网（）-海量教学资源欢迎下载！
活动四：难点突破
(3)二次函数y=ax2+bx+c(a≠0)的图象
①④⑤⑥⑦ 如右图所示，那么下列判断正确的有________
B）
D．（﹣2，3）
C．（2，11）
2．抛物线 y=2（x+3）2﹣4 的顶点坐标是（
D）
A．（3，4） B．（3，﹣4） C．（﹣3，4） D．（﹣3，﹣4） 3．将抛物线 y=﹣ x2 向左平移 2 个单位长度，再向下平移 3 个单位长度，则平移后所得到的抛物线解析式是（ C A． B．） C． D．
顶点式直线 x=h (h , k)
交点式直线x=
y
y=ax2+bx+c
直线x=
y=a(x-h)2+k y=a(x-x1)(x-x2)
x1 x2 2
轴对称轴对称顶点坐标性增 a ＞0 减性 a ＜0
最值 a ＞0 a ＜0
b 2a b 4ac b 2 （ , ） 2a 4a
B．2 个 C．3 个 D．4 个
B
）
7．若二次函数 y=ax2+bx+c （a≠0）的图象如图所示，则下列结论正确的是（
C）
A．a＜0
B．c＞0 C．b=﹣2a D．b2﹣4ac＜0
新课标教学网（）-海量教学资源欢迎下载！
活动五：课堂达标
8．已知抛物线 y=ax2+bx+c （a＞0）的对称轴为 x=﹣1，交 x 轴的一个交点为（x1， 0），且 0＜x1＜1，则下列结论：①b＞0，c＜0；②a﹣b+c＞0；③b＜a；④3a+c ＞0；⑤9a﹣3b+c＞0，其中正确的命题有几个（ A．2 B．3 C．4 D．5
B
）
A．4 个 B．3 个 C．2 个 D．1 个
新课标教学网（）-海量教学资源欢迎下载！
活动五：课堂达标
6．二次函数 y=ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线 x=2，下列结论： ①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④当 x＞﹣1 时，y 的值随 x 值的增大而增大．其中正确的结论有（ A．1 个
在对称轴左侧,y随x的增大而减小，在对称轴右侧,y随x的增大而增大。在对称轴左侧,y随x的增大而增大，在对称轴右侧,y随x的增大而减小。
b 当x= 时, 当 x=h 时, 2 a 4ac b 2 y最小值= y最小值=k 4a b 当x= 2 a 时, 当x=h时， 4ac b 2 y最大值= 新课标教学网（） y =k
新课标教学网（）-海量教学资源欢迎下载！
活动五：课堂达标
4．如图，若 a＜0，b＞0，c＜0，则抛物线 y=ax2+bx+c 的大致图象为（
B）
A．
B．
C．
D．
5.二次函数 y=ax2+bx+c 的图象如图所示，则 abc，b2﹣4ac，2a+b，a+b+c 这四个式子中，值为正数的有（
（填序号）
①abc>0 ②b2-4ac<0
③2a+b>0 ④a+b+c<0 ⑤a-b+c>0 ⑥4a+2b+c<0 ⑦a+b+2c<0 ⑧3a+c<0
新课标教学网（）-海量教学资源欢迎下载！
活动五：课堂达标
1．二次函数 y=x2+2x+3 的顶点为（ A．（1，6） B．（-1，2）