流体力学作业讲解

2．在现实生活中可视为牛顿流体的有水 和空气 等。

3．流体静压力和流体静压强都是压力的一种量度。

它们的区别在于：前者是作用在某一面积上的总压力；而后者是作用在某一面积上的平均压强或某一点的压强。

4．均匀流过流断面上压强分布服从于水静力学规律。

5．和液体相比，固体存在着抗拉、抗压和抗切三方面的能力。

7．流体受压，体积缩小，密度增大 的性质，称为流体的压缩性 ；流体受热，体积膨胀，密度减少 的性质，称为流体的热胀性 。

8．压缩系数β的倒数称为流体的弹性模量 ，以E 来表示12．液体静压强分布规律只适用于静止、同种、连续液体。

13．静止非均质流体的水平面是等压面，等密面和等温面。

14．测压管是一根玻璃直管或U 形管，一端连接在需要测定的容器孔口上，另一端开口，直接和大气相通。

16．作用于曲面上的水静压力P 的铅直分力z P 等于其压力体内的水重。

17．通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。

18． 流线不能相交（驻点处除外），也不能是折线，因为流场内任一固定点在同一瞬间只能有一个速度向量，流线只能是一条光滑的曲线或直线。

20．液体质点的运动是极不规则的，各部分流体相互剧烈掺混，这种流动状态称为紊流。

21．由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv '，其中kv '称为上临界速度，k v 称为下临界速度。

23．圆管层流的沿程阻力系数仅与雷诺数有关，且成反比，而和管壁粗糙无关。

25．紊流过渡区的阿里特苏里公式为25.0)Re68(11.0+=d k λ。

26．速度的大小、方向或分布发生变化而引起的能量损失，称为局部损失。

29．湿周是指过流断面上流体和固体壁面接触的周界。

31．串联管路总的综合阻力系数S 等于各管段的阻抗叠加。

32．并联管路总的综合阻力系数S 与各分支管综合阻力系数的关系为3211111s s s s ++=。

管嘴与孔口比较,如果水头H 和直径d 相同，其流速比V 孔口/V 管嘴等于82.097.0,流量比Q 孔口/Q 管嘴等于82.060.0。

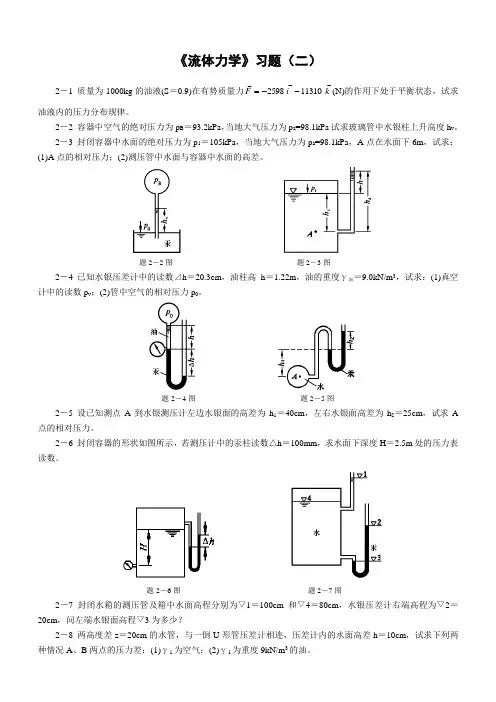
《流体力学》习题（二）2－1 质量为1000kg 的油液(S ＝0.9)在有势质量力k i F 113102598--=(N)的作用下处于平衡状态，试求油液内的压力分布规律。

2－2 容器中空气的绝对压力为p B ＝93.2kPa ，当地大气压力为p a =98.1kPa 试求玻璃管中水银柱上升高度h v 。

2－3 封闭容器中水面的绝对压力为p 1＝105kPa ，当地大气压力为p a =98.1kPa ，A 点在水面下6m ，试求：(1)A 点的相对压力；(2)测压管中水面与容器中水面的高差。

题2－2图 题2－3图 2－4 已知水银压差计中的读数⊿h ＝20.3cm ，油柱高h ＝1.22m ，油的重度γ油＝9.0kN/m 3，试求：(1)真空计中的读数p v ；(2)管中空气的相对压力p 0。

题2－4图 题2－5图 2－5 设已知测点A 到水银测压计左边水银面的高差为h 1＝40cm ，左右水银面高差为h 2＝25cm ，试求A 点的相对压力。

2－6 封闭容器的形状如图所示，若测压计中的汞柱读数△h ＝100mm ，求水面下深度H ＝2.5m 处的压力表读数。

题2－6图 题2－7图 2－7 封闭水箱的测压管及箱中水面高程分别为▽1＝100cm 和▽4＝80cm ，水银压差计右端高程为▽2＝20cm ，问左端水银面高程▽3为多少？2－8 两高度差z ＝20cm 的水管，与一倒U 形管压差计相连，压差计内的水面高差h ＝10cm ，试求下列两种情况A 、B 两点的压力差：(1)γ1为空气；(2)γ1为重度9kN/m 3的油。

题2－8图题2－9图2－9 有一半封闭容器，左边三格为水，右边一格为油(比重为0.9)。

试求A、B、C、D四点的相对压力。

2－10 一小封闭容器放在大封闭容器中，后者充满压缩空气。

测压表A、B的读数分别为8.28kPa和13.80kPa，已知当地大气压为100kPa，试求小容器内的绝对压力。

流 体 力 学习题解答及习题课第2章2-1 解：A B p p gh ρ=+ 则()()4442.710 2.9100.421.36109.807e a a v A B Hg e v p p p p p p h g g p p m g ρρρ+---==+⨯+⨯===⨯⨯2-2 解：111a p gh p gh ρρ++煤水＝ 则：()11a p p gh ρρ=+-水煤 同理：222a p gh p gh ρρ++煤水＝ 则：()22a p p gh ρρ=+-水煤而：12p p gH ρ=+煤 则：()()12a a p gh p gh gH ρρρρρ+-=+-+水煤水煤煤可得：第一章 流体及其主要物理性质例1：已知油品的相对密度为0.85，求其重度。

解：3/980085.085.0m N ⨯=⇒=γδ例2：当压强增加5×104Pa 时，某种液体的密度增长0.02%，求该液体的弹性系数。

解：0=+=⇒=dV Vd dM V M ρρρρρd dV V -=Pa dp d dp V dV E p84105.2105%02.01111⨯=⨯⨯==-==ρρβ例3：已知：A ＝1200cm 2，V ＝0.5m/sμ1＝0.142Pa.s ，h 1＝1.0mm μ2＝0.235Pa.s ，h 2＝1.4mm 求：平板上所受的内摩擦力F绘制：平板间流体的流速分布图及应力分布图 解：（前提条件：牛顿流体、层流运动）dy du μτ= ⎪⎪⎩⎪⎪⎨⎧-=-=⇒2221110h u h u V μτμτ 因为 τ1＝τ2 所以sm h h Vh u h uh u V /23.02112212211=+=⇒=-μμμμμN h uV A F 6.411=-==μτ第二章 流体静力学例1：如图，汽车上有一长方形水箱，高H ＝1.2m ，长L ＝4m ，水箱顶盖中心有一供加水用的通大气压孔，试计算当汽车以加速度为3m/s 2向前行驶时，水箱底面上前后两点A 、B 的静压强（装满水）。

第二章 流体的平衡2.2 给出如下体力场，分别在均质或正压流体斜压流体情况下说明流场能否静止：()()()();1222222k y xy x j x zx z i z yz y f++++++++=()k r r kf,23-=为常数，r 是内径。

[解答] （1）流体平衡的基本方程为P F b ∇=ρ对于正压流体（含均质流体）平衡的必要条件是体力有势，即体力无旋0=⨯∇b F 。

对于斜压流体在有势力作用下不可能处于平衡态。

()()()k y x j x z i z y y xy x x zx z zyz y z y x kji F b -+-+-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++++∂∂∂∂∂∂=⨯∇222222222则当z y x ==时，正压流体平衡；当不满足此条件时，斜压流体才有可能平衡。

（2）0003=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-∂∂∂∂∂∂=⨯∇r k r k ji F b ϑθ，∴正压流体平衡，斜压流体不能平衡。

2.3 图示一种酒精和水银的双液测压计，细管上端为大气压时酒精液面高度为零，当细管上端的表压为p 时，酒精的液面下降h,试用321,,d d d 和h 来表示p 。

酒精和水银密度均为已知。

[解答] 设开始时酒精液面高度（即液面上端距酒精水银的分界面）为H ，则有流体静力学规律知，分界面即等压面，从而有H g P gH P atm atm ∆+=+mercury alcohol ρρ（1）施加表压P 后，同理可得 )()(21mercury 1alcohol h h H g P h h H g P P atm atm ++∆+=+-++ρρ（2）其中1h 为分界面下降高度，2h 为水银面上升高度，由液体排开体积相等得：()2222312221444h d d h d h d -==πππ（3）解之得h d d d h h d d h 222321222211,-==（4）()(),12-并将（4）代入得)()(21mercury 1alcohol h h g h h g P ++-=ρρ)11()1(22232221mercury 2221alcohol d d d ghd d d gh -++-=ρρ 2.4 如图的微测压计用来测量两容器E 和B 中的气体压强差，试用21,,,ρρδd 表示,B E p p -并说明当横截面积,A a 〈〈，而且两种液体1ρ和2ρ相近似，很小的B E p p -就能引起很大的液面高差d ，从而提高了测量精度。

第一章 绪论1-2 水的容重3=9.71/γKN m ，s Pa μ•10×599.0=3，求它的运动黏度ν。

解：===γgμρμν 6.05x10-7s m /2 1-5. 水平方向运动的木板，其速度1 m/s ，平板浮在油面上δ= 10mm ，油的动力黏度μ为0.09807pa.s 。

求作用于平板单位面积上的阻力。

解：dudyτμ= 板间间隙较小，速度分布近似认为直线分布du vdy δ==100 1/s dudyτμ==0.09807x100=9.807N/m 2(Pa)1-7一底面积为40cm x 45crn ，高为1 cm 的木块，质量为5Kg ，沿着涂有润滑油的斜面等速向下运动。

已知s m v /1=，mm δ1=，重力加速度g 取9.82/s m 。

求润滑油的动力黏度。

解：沿斜面受力平衡有：dydu Aμθmg =sin 即，310×11×)5.0×4.0(×=135×8.9×5μ得：s Pa μ•105.0=1-11 体积为53m 的水，在温度不变的情况下，当压强从1at 增加到5at 时，体积减少1L ，求水的压缩系数及弹性模量。

解：N m dp V dV β/10×1.5=10×8.9×)1-5(×5001.0--=/-=210429/10×9.1=1=m N βE第二章 流体静力学2-2. 水的容重为9.807KN/m 3,水银的容重为133.38 KN/m 3，在封闭管端完全真空的情况一下，水银柱差Z 2=50mm ,求盛水容器液面绝对压强p 1和水面高度Z 1。

（10分） 解：10sy 20133.380.05 6.6696669p p Z Kpa paγ=+=+⨯==1266690.686809.8071000sp Z m mmγ====⨯2-5. 在封闭水箱中，水深h=1.5m 的A 点上安装有一压力表，水的容重为9.807KN/m 3，其中表距A 点Z=0.5m 压力表读数为4.9KN/m 2，求水面相对压强及其真空度。

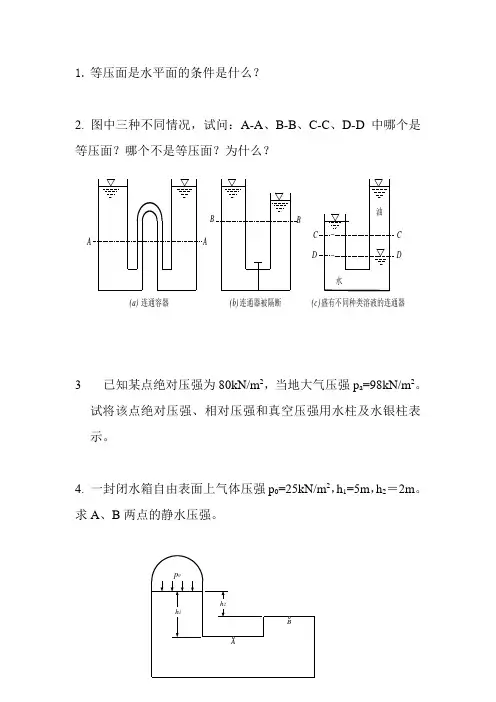
C (c) 盛有不同种类溶液的连通器DC D水油BB (b) 连通器被隔断AA(a) 连通容器1. 等压面是水平面的条件是什么？2. 图中三种不同情况，试问：A-A 、B-B 、C-C 、D-D 中哪个是等压面？哪个不是等压面？为什么？3 已知某点绝对压强为80kN/m 2，当地大气压强p a =98kN/m 2。

试将该点绝对压强、相对压强和真空压强用水柱及水银柱表示。

4. 一封闭水箱自由表面上气体压强p 0=25kN/m 2，h 1=5m ，h 2＝2m 。

求A 、B 两点的静水压强。

速？答：与流线正交的断面叫过流断面。

过流断面上点流速的平均值为断面平均流速。

引入断面平均流速的概念是为了在工程应用中简化计算。

8．如图所示，水流通过由两段等截面及一段变截面组成的管道，试问：(1)当阀门开度一定，上游水位保持不变，各段管中，是恒定流还是非恒定流？是均匀流还是非均匀流？(2)当阀门开度一定，上游水位随时间下降，这时管中是恒定流还是非恒定流？(3)恒定流情况下，当判别第II 段管中是渐变流还是急变流时，与该段管长有无关系？9 水流从水箱经管径分别为cmd cm d cm d 5.2,5,10321===的管道流出，出口流速sm V /13=，如图所示。

求流量及其它管道的断面平均流速。

解：应用连续性方程（1）流量：==33A v Q 4.91s l /103-⨯(2) 断面平均流速s m v /0625.01= , s m v /25.02= 。

10如图铅直放置的有压管道，已知d 1=200mm ，d 2=100mm ，断面1-1处的流速v 1=1m/s 。

求（1）输水流量Q ；（2）断面2-2处的平均流速v 2；（3）若此管水平放置，输水流量Q 及断面2-2处的速度v 2是否发生变化？（4）图a 中若水自下而上流动，Q 及v 2是否会发生变化？解：应用连续性方程 （1）4.31=Q s l / （2）s m v /42= （3）不变。

流体力学标准化作业（三）——流体动力学本次作业知识点总结1.描述流体运动的两种方法 （1）拉格朗日法；（2）欧拉法。

2.流体流动的加速度、质点导数流场的速度分布与空间坐标(,,)x y z 和时间t 有关，即(,,,)u u x y z t =流体质点的加速度等于速度对时间的变化率，即Du u u dx u dy u dza Dt t x dt y dt z dt ∂∂∂∂==+++∂∂∂∂投影式为x x x x x x y z y y y y y x y zz z z z z x y zu u u u a u u u t x y z u u u u a u u u t x y z u u u u a u u u t x y z ∂∂∂∂⎧=+++⎪∂∂∂∂⎪∂∂∂∂⎪=+++⎨∂∂∂∂⎪⎪∂∂∂∂=+++⎪∂∂∂∂⎩或 ()du ua u u dt t ∂==+⋅∇∂在欧拉法中质点的加速度du dt 由两部分组成， ut∂∂为固定空间点，由时间变化引起的加速度，称为当地加速度或时变加速度，由流场的不恒定性引起。

()u u⋅∇为同一时刻，由流场的空间位置变化引起的加速度，称为迁移加速度或位变加速度，由流场的不均匀性引起。

欧拉法描述流体运动，质点的物理量不论矢量还是标量，对时间的变化率称为该物理量的质点导数或随体导数。

例如不可压缩流体，密度的随体导数D D u t tρρρ∂=+⋅∇∂（） 3.流体流动的分类（1）恒定流和非恒定流 （2）一维、二维和三维流动 （3）均匀流和非均匀流 4.流体流动的基本概念 （1）流线和迹线流线微分方程x y zdx dy dz u u u ==迹线微分方程x y zdx dy dz dt u u u === （2）流管、流束与总流（3）过流断面、流量及断面平均流速体积流量 3(/)A Q udAm s =⎰ 质量流量 (/)mAQ udAkg s ρ=⎰断面平均流速 AudA Qv AA==⎰（4）渐变流与急变流 5. 连续性方程（1）不可压缩流体连续性微分方程0y x zu u u x y z∂∂∂++=∂∂∂ （2）元流的连续性方程121122dQ dQ u dA u dA =⎧⎨=⎩ （3）总流的连续性方程1122u dA u dA =6. 运动微分方程（1）理想流体的运动微分方程（欧拉运动微分方程）111xx x x x y z yy y y x y z zz z z x y z u u u u p X u u u x t x y zu u u u p Y u u u x t x y z u u u u p Z u u u x t x y z ρρρ∂∂∂∂∂⎫-=+++⎪∂∂∂∂∂⎪∂∂∂∂⎪∂-=+++⎬∂∂∂∂∂⎪⎪∂∂∂∂∂-=+++⎪∂∂∂∂∂⎭矢量表示式1()uf p u u tρ∂+∇=+⋅∇∂ （2）粘性流体运动微分方程（N-S 方程）222111x x x x x x y z y y y y y x y z z z z z z x y z u u u u pX u u u u x t x y zu u u u pY u u u u x t x y z u u u u p Z u u u u x t x y z νρνρνρ∂∂∂∂∂⎫-+∇=+++⎪∂∂∂∂∂⎪∂∂∂∂⎪∂-+∇=+++⎬∂∂∂∂∂⎪⎪∂∂∂∂∂-+∇=+++⎪∂∂∂∂∂⎭矢量表示式 21()uf p u u u tνρ∂+∇+∇=+⋅∇∂ 7.理想流体的伯努利方 （1）理想流体元流的伯努利方程22p u z C g gρ++=（2）理想流体总流的伯努利方程221112221222p v p v z z g g g gααρρ++=++8.实际流体的伯努利方程 （1）实际流体元流的伯努利方程2211221222wp u p u z z h g g g g ρρ++=+++（2）实际流体总流的伯努利方程2211122212w 22p v p v z z h g g g gααρρ++=+++10.恒定总流的动量方程()2211F Q vv ρββ=-∑投影分量形式()()()221122112211xx x y y y z z z F Q v v F Q v v F Q v v ρββρββρββ⎫=-⎪⎪=-⎬⎪=-⎪⎭∑∑∑标准化作业(5)——流体运动学选择题1. 用欧拉法表示流体质点的加速度a 等于( )。

第二章2-1.已知某种物质的密度ρ=2.94g/cm3，试求它的相对密度d。

解：d=ρ/ρw=2.94（g/cm3）/1（g/cm3）=2.942-2.已知某厂1号炉水平烟道中烟气组分的百分数为α（co2）=13.5%，a(SO2)=0.3%，a(O2)=5.2%，a(N2)=76%，a(H2O)=5%。

试求烟气的密度。

2-3.上题中烟气的实测温度t=170℃，实测静计压强Pe=1432Pa，当地大气压强Pa=10058Pa。

试求工作状态下烟气的密度和运动粘度。

2-4.当压强增量为50000Pa时，某种液体的密度增长0.02%，试求该液体的体积模量。

2-5.绝对压强为3.923×10^5Pa的空气的等温体积模量和等熵体积模量各等于多少？2-6. 充满石油的油槽的压强为4.9033×10^5Pa,今由槽中排出石油40kg，使槽压强降到9.8067×10^4Pa，设石油的体积模量K＝1.32×10^9 Pa。

试求油槽的体积。

2-7. 流量为50m3/h，温度为70℃的水流入热水锅炉，经加热后水温升到90℃，而水的体胀系数αV=0.000641/℃，问从锅炉中每小时流出多少立方米的水？2-8. 压缩机压缩空气，绝对压强从9.8067×104Pa升高到5.8840×105Pa，温度从20℃升高到78℃，问空气体积减少了多少？2-9. 动力粘度为2.9×10^-4Pa·S，密度为678kg/m3的油，其运动粘度等于多少？解：V=u/ρ=2.9×10^-4/678=4.28×10^-7m²/s2-10. 设空气在0℃时的运动粘度ν0=13.2×10-6m2/s,密度ρ0=1.29kg/m3。

试求在150℃时空气的动力粘度。

2-11. 借恩氏粘度计测得石油的粘度为8.5oE,如石油的密度为ρ=850kg/m3,试求石油的动力粘度。

第一章 绪论1-2 水的容重3=9.71/γKN m ，s Pa μ•10×599.0=3，求它的运动黏度ν。

解：===γgμρμν 6.05x10-7s m /2 1-5. 水平方向运动的木板，其速度1 m/s ，平板浮在油面上δ= 10mm ，油的动力黏度μ为0.09807pa.s 。

求作用于平板单位面积上的阻力。

解：dudyτμ= 板间间隙较小，速度分布近似认为直线分布du vdy δ==100 1/s dudyτμ==0.09807x100=9.807N/m 2(Pa)1-7一底面积为40cm x 45crn ，高为1 cm 的木块，质量为5Kg ，沿着涂有润滑油的斜面等速向下运动。

已知s m v /1=，mm δ1=，重力加速度g 取9.82/s m 。

求润滑油的动力黏度。

解：沿斜面受力平衡有：dydu Aμθmg =sin 即，310×11×)5.0×4.0(×=135×8.9×5μ得：s Pa μ•105.0=1-11 体积为53m 的水，在温度不变的情况下，当压强从1at 增加到5at 时，体积减少1L ，求水的压缩系数及弹性模量。

解：N m dp V dV β/10×1.5=10×8.9×)1-5(×5001.0--=/-=210429/10×9.1=1=m N βE第二章 流体静力学2-2. 水的容重为9.807KN/m 3,水银的容重为133.38 KN/m 3，在封闭管端完全真空的情况一下，水银柱差Z 2=50mm ,求盛水容器液面绝对压强p 1和水面高度Z 1。

（10分） 解：10sy 20133.380.05 6.6696669p p Z Kpa paγ=+=+⨯==1266690.686809.8071000sp Z m mmγ====⨯2-5. 在封闭水箱中，水深h=1.5m 的A 点上安装有一压力表，水的容重为9.807KN/m 3，其中表距A 点Z=0.5m 压力表读数为4.9KN/m 2，求水面相对压强及其真空度。