工程光学等厚干涉Matlab仿真

5.使用MATLAB进行等倾干涉动态模拟仿真5.1. 界面设计GUI界面设计]6[主要包括以下几个步骤：第一步构思草图，编排控件的布局。

打开MATLAB程序，在FILE菜单中选择NEW GUI，打开guide设计界面模板，界面模板左边的各个控件可以直接用鼠标拖到编辑框。

第二步设置各控件的属性。

如设置各个控件的标识（Tag），字体等。

第三步各个控件代码的设计。

关键是OpeningFcn(初始界面函数)和控件的CallBack（回调函数）代码的设计。

初始界面函数即设定各参数的初始值，可根据实际情况设定。

回调函数是核心，是对界面控件触发时的事件响应函数。

根据需要，等倾干涉条纹的动态模拟图形用户界面使用了2个按钮（Push Button），标识为绘图和退出，用鼠标点击任一项目，则会执行相应的功能；4个静态文本框（Static Text）用于输入波长，厚度及各自的单位；2个滑动条（Slider），用鼠标拖动相应的滑动条就可以改变波长和厚度的大小；1个坐标轴对象（Axes）用于显示仿真结果。

界面如图4。

图 4 仿真界面5.2 演示控件的回调函数演示控件的功能是通过其回调程序来实现的，用户界面设计完成之后，选中控件用鼠标双击，在弹出的菜单中选择Viewbacks,在其子菜单中选择CallBack，就可以进入回调程序编辑器中，在编辑器中编写控件代码，使图形界面完成约定的功能。

演示控件的回调函数代码为：lambda=get(handles.slider1,'value');d=get(handles.slider2,'value');f=200;n=1;N=300;xmax=10;ymax=10;x=linspace(-xmax,xmax,N);y=linspace(-ymax,ymax,N);for i=1:Nfor j=1:Nr(i,j)=sqrt(x(i)^2+y(j)^2);B(i,j)=cos(pi*(2*n*d*cos(asin(n*sin(atan(r(i,j)/f)))))/lambda).^2;endendNCLevels=255;Br=4*B*NCLevels;colormap(gray(NCLevels));image(x,y,Br);axes(handles.axes1)5.3改变参数对比相邻亮条纹间距变化规律用户通过调节平台的滑动条，分别改变入射波长，厚度影响等倾干涉的两个参数，可以分别得到不同的干涉图样。

基于Matlab的光学实验仿真基于Matlab的光学实验仿真一、引言光学是研究光的传播、反射、折射和干涉等现象的学科，广泛应用于光学器件、光通信等领域。

在光学实验中，通过搭建实验装置来观察和研究光的行为，以验证光学理论并深入理解光的特性。

然而，传统的光学实验不仅设备复杂，成本高昂，而且需要大量的实验时间和实验设计。

因此，基于计算机仿真的方法成为了一种重要的补充和替代。

Matlab作为一种强大的数值计算和仿真工具，具有强大的数学运算能力和友好的图形界面，被广泛应用于科学研究和工程设计。

在光学实验中，Matlab可以模拟光的传播、折射、干涉等各种光学现象，使得研究人员可以在计算机上进行光学实验，加速实验过程并提高实验效率。

二、光的传播仿真在光学实验中，光的传播是一项重要的研究内容。

通过Matlab的计算能力，我们可以模拟光线在不同介质中的传播情况，并观察其光程差、折射等现象。

光的传播可以用波动光学的理论来描述，其中最经典的是亥姆霍兹方程。

在Matlab中，我们可以利用波动光学的相关工具箱，通过求解亥姆霍兹方程来模拟光的传播。

例如，我们可以模拟光在一特定系统中的衍射效应。

在Matlab中，衍射效应可以通过菲涅尔衍射和弗雷涅尔衍射来模拟。

我们可以设定特定的光源和障碍物，通过Matlab的计算能力计算光的传播、衍射和干涉等现象，得到不同条件下的衍射效应，并可视化展示。

三、光的折射仿真光的折射是光学领域中的另一个重要现象，研究光的折射对于理解光在不同介质中的传播行为至关重要。

通过Matlab的仿真，我们可以模拟光的折射行为，并研究不同介质对光的影响。

在Matlab中，我们可以利用光学工具箱中的折射相关函数，输入光线的入射角度、折射率等参数，模拟光线在不同介质中的折射行为。

通过改变不同介质的折射率、入射角度等参数，我们可以观察到光的全反射、折射偏折等现象，并进行定量分析和比较。

四、光的干涉仿真光的干涉是光学领域的重要研究课题之一，通过模拟光的干涉行为，可以深入理解光的相干性、波动性质等特性。

基于Matlab的光学实验仿真一、本文概述随着科技的快速发展，计算机仿真技术已成为科学研究、教学实验以及工程应用等领域中不可或缺的一部分。

在光学实验中，仿真技术能够模拟出真实的光学现象，帮助研究者深入理解光学原理，优化实验设计，提高实验效率。

本文旨在探讨基于Matlab的光学实验仿真方法，分析Matlab在光学实验仿真中的优势和应用，并通过具体案例展示其在光学实验仿真中的实际应用效果。

通过本文的阐述，读者将能够了解Matlab在光学实验仿真中的重要作用，掌握基于Matlab的光学实验仿真方法，从而更好地应用仿真技术服务于光学研究和实验。

二、Matlab基础知识Matlab，全称为Matrix Laboratory，是一款由美国MathWorks公司出品的商业数学软件，主要用于算法开发、数据可视化、数据分析以及数值计算等领域。

Matlab以其强大的矩阵计算能力和丰富的函数库，在光学实验仿真领域具有广泛的应用。

Matlab中的变量无需预先声明，可以直接使用。

变量的命名规则相对简单，以字母开头，后面可以跟字母、数字或下划线。

Matlab支持多种数据类型，包括数值型（整数和浮点数）、字符型、逻辑型、结构体、单元数组和元胞数组等。

Matlab的核心是矩阵运算，它支持多维数组和矩阵的创建和操作。

用户可以使用方括号 [] 来创建数组或矩阵，通过索引访问和修改数组元素。

Matlab还提供了大量用于矩阵运算的函数，如矩阵乘法、矩阵转置、矩阵求逆等。

Matlab具有强大的数据可视化功能，可以绘制各种二维和三维图形。

在光学实验仿真中，常用的图形包括曲线图、散点图、柱状图、表面图和体积图等。

用户可以使用plot、scatter、bar、surf和volume 等函数来创建这些图形。

Matlab支持多种控制流结构，如条件语句（if-else）、循环语句（for、while）和开关语句（switch）。

这些控制流结构可以帮助用户编写复杂的算法和程序。

《基于Matlab的光学实验仿真》篇一一、引言光学实验是物理学、光学工程和光学科学等领域中重要的研究手段。

然而，实际的光学实验通常涉及到复杂的光路设计和精密的仪器设备，实验成本高、周期长。

因此，通过基于Matlab的光学实验仿真来模拟光学实验，不仅能够为研究提供更方便的实验条件，而且还可以帮助科研人员更深入地理解和掌握光学原理。

本文将介绍基于Matlab的光学实验仿真的实现方法和应用实例。

二、Matlab在光学实验仿真中的应用Matlab作为一种强大的数学计算软件，在光学实验仿真中具有广泛的应用。

其强大的矩阵运算能力、图像处理能力和数值模拟能力为光学仿真提供了坚实的数学基础。

1. 矩阵运算与光线传播Matlab的矩阵运算功能可用于模拟光线传播过程。

例如，光线在空间中的传播可以通过矩阵的变换实现，包括偏振、折射、反射等过程。

通过构建相应的矩阵模型，可以实现对光线传播过程的精确模拟。

2. 图像处理与光场分布Matlab的图像处理功能可用于模拟光场分布和光束传播。

例如，通过傅里叶变换和波前重建等方法，可以模拟出光束在空间中的传播过程和光场分布情况，从而为光学设计提供参考。

3. 数值模拟与实验设计Matlab的数值模拟功能可用于设计光学实验方案和优化实验参数。

通过构建光学系统的数学模型，可以模拟出实验过程中的各种现象和结果，从而为实验设计提供依据。

此外，Matlab还可以用于分析实验数据和优化实验参数，提高实验的准确性和效率。

三、基于Matlab的光学实验仿真实现方法基于Matlab的光学实验仿真实现方法主要包括以下几个步骤：1. 建立光学系统的数学模型根据实际的光学系统，建立相应的数学模型。

这包括光路设计、光学元件的参数、光束的传播等。

2. 编写仿真程序根据建立的数学模型，编写Matlab仿真程序。

这包括矩阵运算、图像处理和数值模拟等步骤。

在编写程序时，需要注意程序的精度和效率，确保仿真的准确性。

3. 运行仿真程序并分析结果运行仿真程序后，可以得到光束传播的模拟结果和光场分布等信息。

工程光学仿真实验报告1、杨氏双缝干涉实验1杨氏干涉模型杨氏双缝干涉实验装置如图1所示: S 发出的光波射到光屏上的两个小孔S1 和S2 , S1 和S2 相距很近,且到S 等距;从S1 和S2 分别发散出的光波是由同一光波分出来的,所以是相干光波,它们在距离光屏为 D 的屏幕上叠加,形成一定的干涉图 样; 图 杨氏双缝干涉假设S 是单色点光源,考察屏幕上某一点P ,从S1 和S2 发出的光波在该点叠加产生的光强度为:I = I1 + I2 + 2 I1 I2 cos δ 1-1式中, I1 和I2 分别是两光波在屏幕上的光强度, 若实验装置中S1 和S2 两个缝大小相等, 则有I1 = I2 =I0 1-2δ= 2πr2 - r1/λ1-3 1-3 2221)2/(D y d x r +++= 1-4 2222)2/(D y d x r ++-= 1-5可得 xd r r 22122=- 1-6因此光程差：12r r -=∆ 1-7则可以得到条纹的强度变化规律- 强度分布公式：]/)([cos 1220λπd r r I I -= 1-8 （2）仿真程序clear;Lambda=650; %设定波长,以Lambda 表示波长Lambda=Lambda1e-9;d=input '输入两个缝的间距 '; %设定两缝之间的距离,以d 表示两缝之间距离d=d;Z=; %设定从缝到屏幕之间的距离,用Z 表示yMax=5LambdaZ/d;xs=yMax; %设定y 方向和x 方向的范围Ny=101;ys=linspace-yMax,yMax,Ny;%产生一个一维数组ys,Ny 是此次采样总点数%采样的范围从- ymax 到ymax,采样的数组命名为ys%此数组装的是屏幕上的采样点的纵坐标for i=1:Ny %对屏幕上的全部点进行循环计算,则要进行Ny 次计算L1=sqrtysi-d/2.^2+Z^2;L2=sqrtysi+d/2.^2+Z^2; %屏上没一点到双缝的距离L1和L2Phi=2piL2-L1/Lambda; %计算相位差Bi,:=4cosPhi/2.^2; %建立一个二维数组,用来装该点的光强的值end %结束循环NCLevels=255; %确定使用的灰度等级为255级Br=B/NCLevels; %定标:使最大光强4. 0对应于最大灰度级白色subplot1,4,1,imagexs,ys,Br; %用subplot 创建和控制多坐标轴colormapgrayNCLevels; %用灰度级颜色图设置色图和明暗subplot1,4,2,plotB:,ys; %把当前窗口对象分成2块矩形区域 %在第2块区域创建新的坐标轴%把这个坐标轴设定为当前坐标轴%然后绘制以 b : , ys 为坐标相连的线title '杨氏双缝干涉';3仿真图样及分析a 双缝间距2mmb 双缝间距4mmc 双缝间距6mmd 双缝间距8mm图改变双缝间距的条纹变化由上面四幅图可以看出,随着双缝之间的距离增大,条纹边缘坐标减小,也就是条纹间距减小,和理论公式d D e /λ=推导一致;如果增大双缝的缝宽,会使光强I 增加,能够看到条纹变亮;二、杨氏双孔干涉实验1、杨氏双孔干涉杨氏双孔干涉实验是两个点光源干涉实验的典型代表;如图2所示;当光穿过这两个离得很近小孔后在空间叠加后发生干涉,并在像屏上呈现出清晰的明暗相间的条纹;由于双孔发出的波是两组同频率同相位的球面波, 故在双孔屏的光射空间会发生干涉; 于是, 在图2中两屏之间的空间里,如果一点P 处于两相干的球面波同时到达波峰或波谷的位置, 叠加后振幅达到最高, 图 杨氏双孔干涉表现为干涉波的亮点; 反之, 当P 处处于一个球面波的波峰以及另一个球面波的波谷时候,叠加后振幅为零,变现是暗纹;1r 为S1到屏上一点的距离, 2221)2/(D y d x r +++= 2-1,2r 为S2到屏上这点的距离,2222)2/(D y d x r ++-= 2-2,如图2,d 为两孔之间的距离,D 为孔到屏的距离;由孔S1和孔S2发出的光的波函数可表示为 )ex p(1111ikr r A E = 2-3 )ex p(2212ikr r A E =2-4 则两束光叠加后 21E E E += 2-5干涉后光强 **E E I = 2-62、仿真程序clear;Lambda=63210^-9; %设定波长,以Lambda 表示波长d=; %设定双孔之间的距离D=1; %设定从孔到屏幕之间的距离,用D 表示A1=; %设定双孔光的振幅都是1A2=;yMax=1; %设定y 方向的范围xMax=yMax/500; %设定x 方向的范围N=300; %采样点数为Nys=linspace-yMax,yMax,N;%Y 方向上采样的范围从-ymax 到ymaxxs=linspace-xMax,xMax,N;%X 方向上采样的范围从-xmax 到xmaxfor i=1:Nfor j=1:N %对屏幕上的全部点进行循环计算,则要进行NN 次计算 r1i,j=sqrtxsi-d/2^2+ysj^2+D^2;r2i,j=sqrtxsi+d/2^2+ysj^2+D^2; %屏上一点到双孔的距离r1和r2E1i,j=A1/r1i,jexp2pi1jr1i,j/Lambda;%S1发出的光的波函数E2i,j=A2/r2i,jexp2pi1jr2i,j/Lambda;%S2发出的光的波函数Ei,j=E1i,j+E2i,j; %干涉后的波函数Bi,j=conjEi,jEi,j; %叠加后的光强endend %结束循环NCLevels=255; %确定使用的灰度等级为255级Br=B/NCLevels; %定标:使最大光强4. 0对应于最大灰度级白色imagexs,ys,Br; %仿真出图像colormap 'hot';title '杨氏双孔';（3）干涉图样及分析1改变孔间距对干涉图样的影响d=1mm d=3mm图 改变孔间距对干涉的影响如图,分别是孔间距为1mm 和3mm 的干涉图样,可以看出,随着d 的增加,视野中干涉条纹增加,条纹变细,条纹间距变小;2）改变孔直径的影响图 孔直径对干涉的影响如图,这里改变孔直径指的是改变光强,不考虑光的衍射;孔直径变大,光强变大,可以看出,干涉条纹变亮;3、平面波干涉(1)干涉模型根据图可以看出,这是两个平行光在屏上相遇发生干涉,两束平行光夹角为θ;它们在屏上干涉叠加,这是平面波的干涉;两束平行波波函数为：)ex p(111ikr A E = 3-1)ex p(222ikr A E = 3-2两束光到屏上一点的光程差为θsin y =∆ 3-3 图 平行光干涉垂直方向建立纵坐标系,y 是屏上点的坐标;那么屏上点的光强为)cos(2212221∆++=k A A A A I 3-4式中A1和A2分别是两束光的振幅;（2）仿真程序clear;Lambda=; %设定波长Lambda=Lambda1e-9;t=input '两束光的夹角'; %设定两束光的夹角A1=input '光一的振幅'; %设定1光的振幅A2=input '光二的振幅'; %设定2光的振幅yMax=10Lambda;xs=yMax; %X 方向和Y 方向的范围N=101; %设定采样点数为Nys=linspace-yMax,yMax,N; %Y 方向上采样的范围从- ymax 到ymaxfor i=1:N %循环计算N 次phi=ysisint/2; %计算光程差Bi,:=A1^2+A2^2+2sqrtA1^2A2^2cos2piphi/Lambda;%计算光强end %结束循环 NCLevels=255; %确定使用的灰度等级为255级Br=BNCLevels/6; %定标:使最大光强4. 0对应于最大灰度级白色subplot1,4,1,imagexs,ys,Br; %用subplot 创建和控制多坐标轴colormapgrayNCLevels; %用灰度级颜色图设置色图和明暗subplot1,4,2,plotB:,ys; %把这个坐标轴设定为当前坐标轴%然后绘制以 b : , ys 为坐标相连的折线（3）干涉图样及分析1)改变振幅比对干涉图样的影响a 振幅比1：1b 振幅比1:2图不同振幅比的干涉图样由图看出,振幅比从1:1变成1:2后,干涉条纹变得不清晰了;干涉叠加后的波峰波谷位置没有变化,条纹间距没有变化,但是叠加后的波振幅变小了,即不清晰;2）改变平行光夹角对干涉图样的影响a 两束光夹角60度b 两束光夹角90度图平面波不同夹角的干涉图样图是两束平行光夹角为60度和90度的干涉条纹,由于夹角不同,光程差不同,改变叠加后光波波峰波谷位置,因此干涉明条纹和暗条纹的位置和间距不同;4、两点光源的干涉（1）干涉模型如图,S1和S2是两个点光源,距离是d;两个点光源发出的光波在空间中相遇发生干涉;在接收屏上,发生干涉的两束波叠加产生干涉条纹;S2与屏距离是z,S1与屏的距离是d+z;两个点光源的干涉是典型的球面波干涉,屏上一点到S1 图 点光源干涉 和S2的距离可以表示为 2221)(z d y x r +++= 4-1 2222z y x r ++= 4-2则 )ex p(1111ikr r A E = 4-3 )ex p(2222ikr r A E = 4-4 其中A1和A2分别是S1、S2光的振幅;干涉后的光为21E E E += 4-5因此干涉后光波光强为**E E I = 4-6（2）仿真程序clear;Lambda=650; %设定波长Lambda=Lambda1e-9;A1=2; %设定S1光的振幅A2=2; %设定S2光的振幅d=input '输入两点光源距离'; %设定两个光源的距离z=5; %设定S2与屏的距离xmax= %设定x 方向的范围ymax=; %设定y 方向的范围N=200; %采样点数为Nx=linspace-xmax,xmax,N;%X 方向上采样的范围从-xmax 到xmax,采样数组命名为x y=linspace-ymax,ymax,N;%Y 方向上采样的范围从-ymax 到ymax,采样数组命名为y for i=1:Nfor k=1:N %对屏幕上的全部点进行循环计算,则要进行NN 次计算 l1i,k=sqrtd+z^2+ykyk+xixi; %计算采样点到S1的距离l2i,k=sqrtz^2+ykyk+xixi; %计算采样点到S2的距离E1i,k=A1/l1i,kexp2pi1j.l1i,k/Lambda;%S1复振幅E2i,k=A2/l2i,kexp2pi1j.l2i,k/Lambda;%S2复振幅Ei,k=E1i,k+E2i,k; %干涉叠加后复振幅Bi,k=conjEi,k.Ei,k;%干涉后光强endendNclevels=255; %确定使用的灰度等级为255级Br=BNclevels; %定标imagex,y,Br; %做出干涉图像colormap 'hot';title '双点光源干涉';3干涉图样及分析改变点光源的间距对干涉图样的影响ad=1mbd=2mcd=3m图改变点光源间距的干涉图样 图是根据图仿真干涉出的图样,S1和S2之间距离分别为1m 、2m 、3m,由图样可以看出,随着d 的增加,光程差变大,视野内的干涉圆环逐渐增多,圆环之间的距离变小;5、 平面上两点光源干涉（1）干涉模型S1和S2是平面上的两个点光源,距离为d,两个光源发出的光相遇发生干涉,产生干涉条纹;以S1所在处为原点建立平面直角坐标系,平面上任意一点到S1、S2的距离是 221y x r += 5-1 图 平面两点光源干涉222)(y d x r +-= 5-2S1和S2发出的都是球面波,可表示为)ex p(1111ikr r A E = 5-3 )ex p(2222ikr r A E =5-4 式中A1和A2分别是S1、S2的振幅;干涉叠加后的波函数为21E E E += 5-5因此干涉后光波光强为**E E I = 5-62仿真程序clear;Lambda=650; %设定波长Lambda=Lambda1e-9;A1=; %设定S1光的振幅d1S 2SA2=; %设定S2光的振幅d= %设定两个光源的距离xmax=; %设定x 方向的范围ymax=; %设定y 方向的范围N=500; %采样点数为Nx=linspace-xmax,xmax,N;%X 方向上采样的范围从-xmax 到xmax,采样数组命名为x y=linspace-ymax,ymax,N;%Y 方向上采样的范围从-ymax 到ymax,采样数组命名为y for i=1:Nfor k=1:N %对屏幕上的全部点进行循环计算,则要进行NN 次计算 r1i,k=sqrtykyk+xixi; %计算采样点到S1的距离r2i,k=sqrtykyk+xi-dxi-d; %计算采样点到S2的距离E1i,k=A1/r1i,kexp2pij.r1i,k/Lambda;%S1复振幅E2i,k=A2/r2i,kexp2pij.r2i,k/Lambda;%S2复振幅Ei,k=E1i,k+E2i,k; %干涉叠加后复振幅Bi,k=conjEi,k.Ei,k; %干涉后光强endend %结束循环Nclevels=255; %确定使用的灰度等级为255级Br=BNclevels/4; %定标imagex,y,Br;colormap 'hot';title '并排双点光源干涉';（3）干涉图样及分析1）聚散性对干涉图样的影响a 会聚b 发散图聚散性对干涉的影响两个点光源并排放置,在靠近点光源的观察屏上看到的干涉条纹是一组放射状的条纹,并且强度从中心向四周减弱,光源的聚散性对干涉图样没有影响;2改变两光源间距对干涉的影响ad=4um bd=8um图两光源间距对干涉的影响从图可以看出,视野中条纹逐渐多了;随着间距变小,干涉条纹宽度变小,条纹间距变小;6、平行光与点光源干涉图 图 图1平面波和球面波干涉如图,三幅图都是点光源和平行光的干涉,平面光入射的角度不同;平行光与点光源相遇在空间中产生干涉,在屏上形成干涉条纹;点光源与屏的距离为z,屏上坐标为x,y 的一点与点光源的距离是2221z y x r ++= 6-1由点光源发出的光波表示为 )ex p(1111ikr r A E = 6-2 平行光可以表示为)sin /ex p(22θikz A E = 6-3式中θ表示平行光与屏的夹角;两束光发生干涉叠加后,干涉光复振幅21E E E += 6-4则光强**E E I = 6-52仿真程序clear;Lambda=650; %设定波长,以Lambda 表示波长Lambda=Lambda1e-9; %变换单位A1=1; %设定球面波的振幅是1A2=1; %设定平面波的振幅是1xmax=; %设定x 方向的范围ymax=; %设定y 方向的范围t=input '输入角度'; %设定平行光和屏的夹角z=1; %设定点光源和屏的距离N=500; %N 是此次采样点数x=linspace-xmax,xmax,N; %X 方向上采样的范围从-xmax 到ymaxy=linspace-ymax,ymax,N; %Y 方向上采样的范围从-ymax 到ymaxfor i=1:N %对屏幕上的全部点进行循环计算,则要进行NN 次计算 for k=1:Nl1i,k=sqrtykyk+xixi+z^2; %表示屏上一点到点光源的距离E1i,k=A1/l1i,kexp2pij.l1i,k/Lambda;%球面波的复振幅E2i,k=A2exp2pij.z1/sint/Lambda; %平面波的复振幅Ei,k=E1i,k+E2i,k; %屏上点的振幅Bi,k=conjEi,k.Ei,k; %屏上每个采样点的光强end %结束循环end %结束循环Nclevels=255; %确定使用的灰度等级为255级Br=BNclevels/4; %定标:使最大光强4. 0对应于最大灰度级 imagex,y,Br; %干涉图样colormap 'hot'; %设置色图和明暗（3）仿真图样及分析平行光入射角度对干涉图样的影响a90=θ b 45=θ c 135=θ图平行光入射角度对干涉的影响图分别是平行光与屏夹角为90度、45度、135度的情况,斜入射与垂直入射相比,干涉圆环更大;而角度互补的两种入射方式,区别在于中心是明还是暗;由图可以看出,斜入射135度的平行光与点光源干涉,干涉图样中心是暗斑;7、平行光照射楔板 （1）图的楔板 L=63010^-9;alfa=pi/20000;H=; %波长630nm,倾角e-4,厚5mm n=; %折射率N= a2=axes'Position',,,,; %定位在绘图中的位置x,y=meshgridlinspace0,,200; %将5mm5mm 区域打散成200200个点h=tanalfax+H; %玻璃厚度Delta=2hn+L/2； %光程差In=+cosDeltapi2/L/2; %光强分布按比例缩小到0-1imshowIn %生成灰度图图 图 λ=630nm ,θ=pi/20000λ=430nm ,θ=pi/20000 λ=630nm ,θ=pi/30000图 图可见增大波长或者减小楔角会使干涉条纹间距加大;（2）牛顿环L=63010^-9;R=3; %波长630nm 曲率半径3Ma2=axes'Position',,,,; %定位在绘图中的位置x,y=meshgridlinspace,,200; %将5mm5mm 区域打散成200200r2=x.^2+y.^2; %r2为各个点距中心的距离^2矩阵h=R-sqrtR^2-r2 %空气薄膜厚度Delta=2h+L/2 %光程差In=+cosDeltapi2/L/2; %光强分布按比例缩小到0-1 imshowIn %生成灰度图λ=630nm ,R=3M图图λ=430nm ,R=3M λ=630nm ,R=10M图图增大波长或者增大球的曲率半径会使牛顿环半径增大;3圆柱曲面干涉L=63010^-9;R=3; %波长630nm,曲率半径3Ma2=axes'Position',,,,; %定位在绘图中的位置x,y=meshgridlinspace,,200; %将5mm5mm区域打散成200200r2=x.^2+0y.^2; % r2为各个点距中心的距离^2矩阵h=R-sqrtR^2-r2 %空气薄膜厚度Delta=2h+L/2 %光程差In=+cosDeltapi2/L/2; %光强分布按比例缩小到0-1 imshowIn %生成灰度图λ=630nm ,R=3M图图λ=430nm ,R=3M λ=630nm ,R=10M图图可见增大波长或者增大圆柱底面的半径会使干涉条纹变宽;（4）任意曲面L=63010^-9;R=3; %波长630nm 曲率半径3Ma2=axes'Position',,,,; %定位在绘图中的位置x,y=meshgridlinspace,,200; %将5mm5mm区域打散成200200r2=x.^2+y.^2; %r2为各个点距中心的距离^2矩阵h=sinr23000 %空气薄膜厚度Delta=2h+L/2 %光程差In=+cosDeltapi2/L/2; %光强分布按比例缩小到0-1 imshowIn曲面函数：z=sin3000x^2+y^2图图8、等倾干涉（1）平行平板干涉图图 如图,扩展光源上一点S 发出的一束光经平行平板的上、下表面的反射和折射后,在透镜后焦平面P 点相遇产生干涉;两支光来源于同一光线,因此其孔径角是零;在P 点的强度是： )cos(22121∆++=k I I I I I8-1其中光程差2/cos 22λθ+=∆nh 8-2 光程差越大,对应的干涉级次越高,因此等倾条纹在中心处具有最高干涉级次; λλ02/2m nh =+ 8-30m 一般不一定是整数,即中心不一定是最亮点,它可以写成q m m +=10,式中1m 是最靠近中心的亮条纹的整数干涉级,第N 条亮条纹的干涉级表示为]1[1+-N m ;如图2,其角半径记为N 1θ则 q N hn n +-=11'1λθ 8-4 上式表明平板厚度h 越大,条纹角半径就越小;条纹角间距为12'12θλθh n n =∆ 8-5 表明靠近中心的条纹稀疏,离中心越远的条纹越密,呈里疏外密分布;（2）仿真程序xmax=;ymax=; %设定y 方向和x 方向的范围Lamd=452e-006; %设定波长,以Lambda 表示波长h=2; %设置平行平板的厚度是2mmn=input '输入折射率'; %设置平行平板的折射率,以n 表示f=50; %透镜焦距是50mmN=500; %N 是采样点数x=linspace-xmax,xmax,N;%X 方向采样的范围从-ymax 到ymax,采样数组命名为x y=linspace-ymax,ymax,N;%Y 方向采样的范围从-ymax 到ymax,采样数组命名为y for i=1:N %对屏幕上的全部点进行循环计算,则要进行NN 次计算 S S Sfor j=1:Nri,j=sqrtxixi+yjyj; %平面上一点到中心的距离ui,j=ri,j/f; %角半径ti,j=asinnsinatanui,j; %折射角phii,j=2nhcosti,j+Lamd/2; %计算光程差Bi,j=4cospiphii,j/Lamd.^2;%建立一个二维数组每一个点对应一个光强end%结束循环end%结束循环Nclevels=255; %确定使用的灰度等级为255级Br=B/Nclevels; %定标:使最大光强4. 0对应于最大灰度级白色imagex,y,Br; %做出函数Br的图像colormapgrayNclevels; %用灰度级颜色图设置色图和明暗（3）干涉图样及分析折射率变化对干涉图样的影响an= bn= cn=图折射率变化对干涉的影响观察上面三幅图,分别是折射率、、时候的干涉图样;由图可以看出,等倾干涉的条纹间距是不相等的,靠近中心处比较稀疏,外部比较密集;随着折射率的增大,视野内的条纹变少,条纹间距变大,条纹更稀疏;。

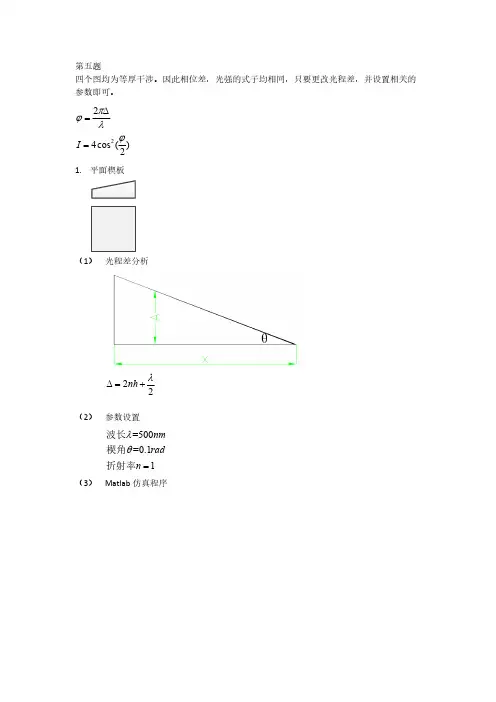
文章编号: 1007-2934( 2014) 04-0097-03 基 于 Matlab 的牛顿环白光干涉实验仿真王蕴杰( 青海师范大学 ，青海 西宁 810008)摘 要: 根据色度学原理，利用 M a t l a b 仿真出了牛顿环白光干涉场的分布图，并给出了程序代码，仿真结果形象直观，效果良好。

关 键 词: 干涉; 牛顿环; M a t l a b ; 计算机仿真 中图分类号: O411-3 文献标志码: A光的干涉现象对于由光的微粒说到光的波动 说的推进起到了重大作用。

干涉现象是波的相干 迭加的必然结果，其现象证明了光的波动性。

利 用计算机模拟光的干涉，可以不受仪器、场地的限 制，实验 效 果 形 象、直 观［1］。

同 时 计 算 机 仿 真 实验可以方便的改变实验参数，从而反映出不同条 件下的实验现象和结果，方便了实验教学的开展。

由于白光源难于控制和白光的干涉场光强较弱， 白光的干涉现象观察有一定的难度。

文章中根据 色度学原理，应用 M a t l a b 仿真了实验室中牛顿环 的白光等厚干涉现象［2-3］。

板之间形成很薄的空气层。

如果有光从上向下照射，那么从空气层的上下表面反射出的两束光线 1、2 将产生干涉。

由于空气层厚度相同的各点位 于以透镜顶点 O 为圆心半径 r 的圆周上，因此干 涉条纹是以 O 为圆心的若干同心圆。

当 光 源 发 出的许多波长的光发生干涉时，就会形成彩色的 干涉条纹。

这种干涉现象的发现者是牛顿，故该 装置被称为牛顿环［4］。

1． 2 色度学原理色光的三基色是指红、绿、蓝 三 色，任 何 颜 色 的光可以通过红、绿、蓝三色按照不同的比例合成 产生，这是色度学的最基本原理，即三基色原理。

因此，可将白光分解为红、绿、蓝三基色，白光产生 的干涉条纹可认为是由红、绿、蓝三基色的相干单 色光波所产生干涉条纹的非相干叠加。

由“C I E ( 国际照明委员会) 1931-ＲG B 系统”的规定，白光 可被分解为波长分别为 700 nm 、546． 1 nm 、435． 8 nm 的红、绿、蓝三基色光。

基于matlab 的几个干涉实验模拟------------吴旭普摘要：根据干涉原理对牛顿环，杨氏双缝和迈克尔逊干涉仪原理进行分析得到各种参数的关系，采用计算机模拟方法并通过软件matlab 编程并运行得到干涉图样 关键词：干涉 matlab 牛顿环 杨氏干涉 迈克尔逊干涉仪 一．牛顿环干涉模拟 1.建模如图，牛顿环是一种分振幅法产生干涉的装置，由一光平玻璃和一曲率很大的平凸透镜构成，平玻璃和平凸透镜之间形成了一个空气劈尖，且其等厚轨迹是以接触点为圆心的一系列同心圆，所以干涉条纹的形状也是明暗相间的同心圆。

在编制程序之前，我们需要对决定干涉条纹特征的光程差、相位差与干涉条纹半径r ，光波波长和平凸透镜的曲率半径R 之间的曲率半径R 之间的关系。

对于形成牛顿环干涉处的空气层厚度e ，两相干光的光程差为: 22e λ∆=+由几何关系：因为R>>e ,所以略去故得:所以两相干光的相位差为：=两相干光的干涉光强为：其中分别是反射光1和反射光2的光强，为使问题简单化设平凸透镜和平板玻璃的反射率均为15%，并且设两反射光的光强近似相等，均设为最终牛顿环干涉的光强为2.程序编写Clear all %清除内存lamd=600e-9; %设定入射光波长 R=10; %设定牛顿环曲率 rm=1e-2; %设定干涉条纹区域 x=0:0.0001:rm; y=rm:-0.0001:0; [X,Y]=meshgrid(x,y); r2=X.^2+Y.^2;phi=2*pi*(r2/R+lamd/2)/lamd; %相位差I=4*cos(phi./2).^2; %第一象限干涉光强 N=255; %设定灰度等级Ir2=(I/4.0)*N; %最大光强为最大灰度Ir1=fliplr(Ir2); %矩阵对称操作Ir3=flipud(Ir1);Ir4=flipud(Ir2);Ir=[Ir1 Ir2;Ir3 Ir4]; %构造图像矩阵figureimage(Ir,'XData',[-0.02,0.02],'YData',[0.02,-0.02]); %画干涉条纹colormap(gray(N));axis squareTitle（“牛顿环干涉光强”）3．运行程序与结果分析如图2，模拟结果与实验一致，通过以上推倒可知牛顿环条纹与相位差有很大联系。

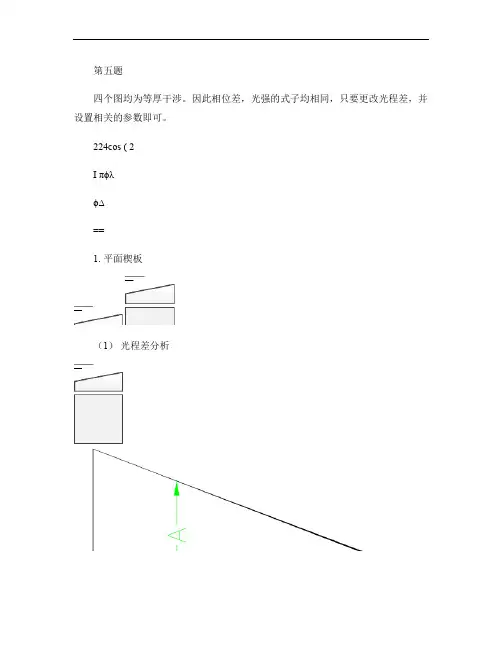
第五题
四个图均为等厚干涉。

因此相位差，光强的式子均相同，只要更改光程差，并设置相关的参数即可。

224cos ( 2
I πϕλ
ϕ∆
==
1. 平面楔板
（1）光程差分析
22nh λ∆=+
（2）参数设置 =500=0.11 nm
rad n λθ=波长楔角折射率（3） Matlab 仿真程序
（4）仿真结果
2. 柱面楔板
（1）光程差分析
22222
y x R y A y h h nhA λ
+=⇒==-=∆=+ （2）参数设置
=500=4.51
nm
R mm n λ=波长平行平板距柱面圆心透镜距离h=0.5mm柱面透镜半径折射率（3） Matlab 仿真程序
（
4）仿真结果
3. 球面楔板
（1）光程差分析
2
222000( 222
r R R h r h R
A R h h nhA λ=-+⇒==--∆=-
（2）参数设置
=500=4.51
nm
R mm
n λ=波长平行平板距球面球心透镜距离h=0.5mm球面透镜半径折射率
（3） Matlab 仿真程序
（4）仿真结果
4. 不规则柱面楔板
（1）光程差分析
以柱面楔板干涉为基础，将以常数R 为半径的柱面更改为2(100 0.1R x x =+的二
次曲线，即可满足题目要求。

（2）参数设置波长平行平板距柱面圆心透镜距离h=0.5mm 折射率（3） Matlab 仿真程序（4）仿真结果。