表面涂色的正方体探索规律完整版
- 格式:docx
- 大小:82.15 KB
- 文档页数:6
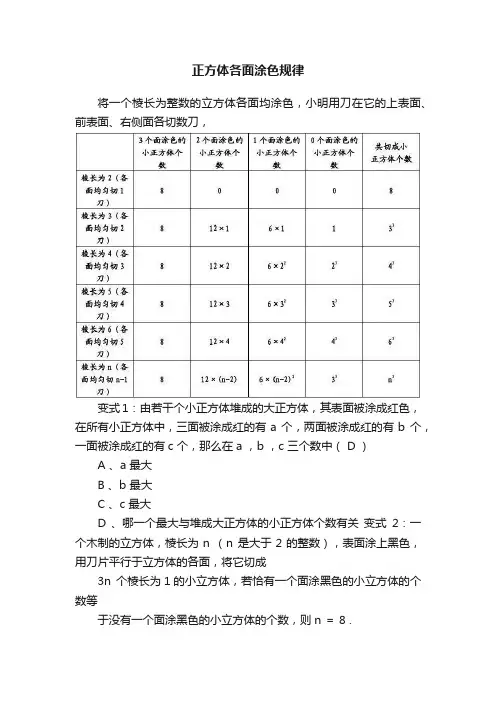
正方体各面涂色规律
将一个棱长为整数的立方体各面均涂色,小明用刀在它的上表面、前表面、右侧面各切数刀,
变式1:由若干个小正方体堆成的大正方体,其表面被涂成红色,在所有小正方体中,三面被涂成红的有a 个,两面被涂成红的有b 个,一面被涂成红的有c 个,那么在a ,b ,c 三个数中( D )
A 、a 最大
B 、b 最大
C 、c 最大
D 、哪一个最大与堆成大正方体的小正方体个数有关变式2:一个木制的立方体,棱长为n (n 是大于2的整数),表面涂上黑色,用刀片平行于立方体的各面,将它切成
3n 个棱长为1的小立方体,若恰有一个面涂黑色的小立方体的个数等
于没有一个面涂黑色的小立方体的个数,则n = 8 .
变式3:将一个正方体木块表面涂上红色, 如果每面等距离地切4刀, 则可以得到 _8__ 个三面红色的小正方体, __36__ 个两面红色的小正方体, __54__ 个一面红色的小正方体, __27__ 个没有涂色的小正方体; 如果要得到各面都没有涂色的小正方体1000个, 则每面至少需切__11_ 刀.
变式4:由若干个单位立方体组成一个较大的立方体,然后把这个大立方体的某些面上涂上油漆,油漆干后,把大立方体拆开成单位立方体,发现有45个单位立方体上任何一面都没有漆。
那么大立方体被涂过油漆的面数是( C )
A :2
B :3
C :4
D :5。




正方体涂色块数的规律正方体是一种非常基础且常见的几何体,它具有六个面,每个面都是一个正方形。
在进行涂色的时候,我们可以根据几何特征和规律来确定涂色块的数量。
我们可以从最简单的情况开始探讨。
当正方体只有一个面时,也就是只有一个正方形,此时涂色块的数量为1。
当正方体有两个面时,也就是正方体的两个相邻面被涂成了不同的颜色,此时涂色块的数量为2。
接下来,我们考虑正方体有三个面的情况。
我们可以将正方体的六个面依次编号为1、2、3、4、5、6。
在这种情况下,我们可以发现涂色块的数量为3。
具体来说,编号为1的面和编号为2的面是相邻的,编号为3的面与它们相邻,所以这三个面的涂色块数量为3。
当正方体有四个面时,涂色块的数量为4。
我们可以将正方体的六个面按照某种方式排列,使得四个面两两相邻。
这样一来,我们可以将涂色块的数量分为两组,每组的数量都为2,因此总的涂色块数量为4。
当正方体有五个面时,涂色块的数量为5。
同样,我们可以将正方体的六个面按照某种方式排列,使得五个面两两相邻。
这样一来,我们可以将涂色块的数量分为两组,一组的数量为3,另一组的数量为2,因此总的涂色块数量为5。
当正方体有六个面时,涂色块的数量为6。
此时,正方体的每个面都是相邻的,所以涂色块的数量就是正方体的面的数量,即6。
从以上的分析可以看出,正方体涂色块的数量与正方体的面的数量是一致的。
因此,对于任意一个正方体来说,涂色块的数量就是6。
正方体涂色块数的规律可以总结为:涂色块的数量等于正方体的面的数量。
这个规律适用于任意大小的正方体,无论是边长为1的小正方体,还是边长为x的大正方体,其涂色块的数量都是6。
在实际生活中,这个规律可以应用于许多场景。
比如在建筑设计中,设计师可以根据正方体涂色块数的规律,来确定建筑物表面的装饰图案的数量和布局。
在教育教学中,教师可以利用这个规律,帮助学生更好地理解和掌握几何体的特征和性质。
正方体涂色块数的规律简洁明了,易于理解和应用。


大小正方體表面塗色規律壹、摘要許多規律性數學問題,往往透過具體物的操作,例如小積木的操作。
生活中常見物體表面塗色問題,本研究結合此兩元件,探尋由小積木組成不同邊長正方體表面塗色時,6至0個面被塗色積木數的規律性。
研究結果發現:1.六面塗色正方體之排列:6面、5面、4面被塗色有0個積木(n>1),3面被塗色有8個積木(n>1),2面被塗色有12(n-2)個積木(n≧2),1面被塗色有6(n-2)2個積木(n≧2),0面被塗色有(n-2)個積木(n≧2)。
2.五面塗色正方體之排列(底部不塗色):6面、5面、4面被塗色有0個積木(n>1),3面被塗色有4個(n>1),2面被塗色有【4(n-1)+4(n-2)】個積木(n >1),1面被塗色有【4(n-1)(n-2)+(n-2)2】個積木(n≧2),0面被塗色有【(n-2)2(n-1)】個積木(n≧2)。
貳、研究動機:上學期某次數學課,老師要我們用1立方公分的白色積木疊成5×4×3和7×3×2的長方體,再把長方體的6個面塗色,並進一步計算3個面、2個面、1個面以及0個面被塗到顏色的白色積木各有多少個。
我們發現塗到3個面的白色積木都是8個,而塗到2個面、1個面、0個面的白色積木數是乎也存在某些規則,我們心裡產生了一些疑問。
學期初,老師要我們做科展時,我們決定探究我們的疑問,但長方體的邊長並沒有規則性,所以我們決定用1立方公分的白色積木疊成不同邊長正方體,並進一步探究不同面數被塗到顏色的白色積木數之規律性。
參、研究目的:一、能利用1立方公分的白色積木疊成不同邊長正方體。
二、能歸納整理出不同邊長六面塗色正方體中,6至0個面被塗色積木數的規律性。
三、能歸納整理出不同邊長五面塗色正方體(底部不塗色) 中,6至0個面被塗色積木數的規律性。
四、訓練學生的思考,將抽象的思考和具體的操作合而為一。
五、啟發學生從生活中發現數學、運用數學。




表面涂色的正方体探索
规律
HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】
六年级数学上册第一单元
表面涂色的正方体(探索规律)
主备人:宋新教学内容:
教科书第26-27页。
教学目标:
1.在经历把表面涂色的正方体切成若干个同样大的小正方体,探索表面涂色的小正方体的各种情况以及其中隐含的简单规律的过程。
2.在学习活动中培养自己的合作能力、空间想象能力和思维能力。
3.在探索数学规律的过程中,感受数学的结构美,获得成功发现数学规律的愉悦体验,激发学习数学的兴趣。
教学重点:
探索表面涂色的小正方体的各种情况以及其中隐含的简单规律的过程。
教学难点:
发现其中隐含的简单规律。
教学准备:
自主学单。
教学过程:
一、创设情境激活经验
出示一个表面涂色的正方体模型,问:一个表面涂色的正方体,每条棱都平均分成2份,能切成多少个同样大的小正方体每个小正方体有几个面涂色
如果把正方体的每条棱都平均分成3份、4份、5份……结果会怎样?
二、自主学习获取经验
学生借助教材完成自主学习单上的学习内容:
自学课本第26-27页。
1.如果像这样把正方体切开,能切成多少个小正方体切成的小正方体中,3面涂色、2面涂色、1面涂色的各有多少个分别在什么位置再在下表中填出来。
2.如果把这个正方体的每条棱平均分成4份、5份……再切成同样大的小正方体,结果会怎样?先在图中找一找,再把结果填入下表。
3.填写第27页上的表格。
4.观察上表,你能发现什么规律?有几条写几条?
5.如果用n表示把大正方体的棱平均分的份数,用α、b分别表示2面涂色和1面涂争的小正方个数,你能用式子分别表示n和α、b的关系吗?
α= ,b= 。
6.回顾探索和发现规律的过程,说说你的体会。
三、合作学习交流经验
1.小组交流。
(组间交流)
学生完成【自主学习】后小组交流讨论。
小组内先结对子交流,对有争议的内容提交全组交流,小给交流后还存在疑问的,可以在题号前打上“”,在大组交流时可以提出来讨论。
2.大组汇报。
(全班交流)
指名带自主学习单到展台全班交流。
四、教师指导完善经验
教师根据学生大组交流的情况相机进行指导,并了解全班同学在自主学习过程中存在的问题,及时给予帮助,确保90%以上的学生达成目标。
1. 题1引导学生讨论小正方体表面涂色的情况一共有几种,分别是哪几种。
2. 题2要注意引导学生结合直观图说清楚得到每种表面涂色小正方体个数的方法。
3. 题4、5引导学生用自己的语言说清楚归纳和发现规律的思考过程,写出规律的字母表达式。
五、反思构建内化经验
请同学们拿出自主学习单,看我们刚才自主学习的内容,把你认为重要的内容标注出来,把新的收获在上面写一写,然后把你学习到的和小组内同学交流。
教学反思:
经验课堂自主学习六年级数学(上册)第一单元
学习内容:表面涂色的正方体
班级:姓名:
自主学习
学生借助教材完成自主学习单上的学习内容:
自学课本第26-27页。
1.如果像这样把正方体切开,能切成个小正方体。
切成的小正方体中,3面涂色有个、2面涂色有个、1面涂色的有个。
分别在什么位置?再在下表中填出来。
2.如果把这个正方体的每条棱平均分成4份、5份……再切成同样大的小正方体,结果会怎样?先在图中找一找,再把结果填入下表。
3.填写第27页上的表格。
4.观察上表,你能发现什么规律有几条写几条
5.如果用n表示把大正方体的棱平均分的份数,用α、b分别表示2面涂色和1面涂争的小正方个数,你能用式子分别表示n和α、b的关系吗?
α= ,b= 。
6.回顾探索和发现规律的过程,说说你的体会。