当前位置：文档之家 › 机器人概论 第三章机械手的运动 ppt课件

机器人概论 第三章机械手的运动 ppt课件

  • 格式：ppt
  • 大小：1.29 MB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

第1章 工业机器人概论PPT课件

第1章 工业机器人概论PPT课件

控制系统
17
第1章 工业机器人概论
工业机器人技术基础
■工业机器人示教器
示教器是人机交互的一个接口，也称示教盒或示教编程器，主要由液晶屏和可供 触摸的操作按键组成。操作时由控制者手持设备，通过按键将需要控制的全部信 息通过与控制器连接的电缆送入控制柜中的存储器中，实现对机器人的控制。示 教器是机器人控制系统的重要组成部分，操作者可以通过示教器进行手动示教， 控制机器人到达不同位姿，并记录各个位姿点坐标，也可以利用机器人语言进行 在线编程，实现程序回放，让机器人按编写好的程序完成轨迹运动。
随着工业机器人的应用越来越广泛，我国也在积极推动我国机器人产业的发展。
尤其是进入“十三.五”以来，国家出台的《机器人产业发展规划（2016-2020）》对机
器人产业进行了全面规划，要求行业、企业搞好系列化、通用化、模块化设计，积极
推进工业机器人产业化进程。
9
第1章 工业机器人概论
工业机器人技术基础
4
第1章 工业机器人概论
工业机器人技术基础
1.1 工业机器人定义及其发展 工业机器人定义 定义虽不同，但有一定的共性： 工业机器人是由仿生机械结构，电机、减速机和控制系统组成的，用于从 事工业生产，能够自动执行工作指令的机械装置。它可以接受人类指挥， 也可以按照预先编排的程序运行，现代工业机器人还可以根据人工智能技 术制定的原则和纲领行动。 一般情况下，工业机器人应该具有四个特征： 1. 特定的机械结构； 2. 从事各种工作的通用性能； 3. 具有感知、学习、计算、决策等不同程度的智能； 4. 相对独立性。
量22.5万台，亚洲的销量占到2/3，中国市场的机器人销量近45500台，增长35%。到目
前为止，全球的主要机器人市场集中在亚洲、澳洲、欧洲、北美，其累计安装量已超

第三章机器人运动学PPT课件

第三章机器人运动学PPT课件
（2）矩阵与数相乘：该数与矩阵各元素相乘。
（3）矩阵与矩阵相乘： （4） 矩阵的转置：把矩阵的行换成同序数的列，记为
7. 矩阵的逆（逆矩阵） 8. 分块矩阵：分块后的矩阵与普通矩阵的运算相同。
9. 正交矩阵：如果
，则A为正交矩阵。它满足：
如果
是正交矩阵，则
行列式和矩阵的区别：矩阵是按一定方式排成的数表；行列式是 一个数。
三、矢量的点积（内乘积或标量积）
其中θ是a和b两矢量间的夹角，如图3-2所示。 令b=i （i为b方向上的单位矢量），则
图3-2标量积
换句话说：一个矢量在另一个矢量上的投影等于该矢量与另一矢量 方向上单位矢量的点积。
再令a=j （j 为a方向上的单位矢量），则
即两矢量方向上单位矢量的点乘等于两矢量夹角的余弦。
二、坐标旋转
图3-6 坐标旋转
如图3-6，{B}与{A}有共同的坐标原点，但方位不同。令
和
分别是{A}和{B}中的单位主矢量，点P 在两
坐标系中各坐标轴上的坐标分量分别为：
和
所以有 利用点乘的性质和上式共同求解得
将
代入上面三式中并写成矩阵形式得
上式简写为： 此式称为坐标旋转方程。其中旋转矩阵 表示了坐标系{B}相 对于{A}的方位，正好与刚体姿态的描述相同。同理也可得
和 APCO APBO
进而有
例3.2 已知坐标系{B}初始位姿与{A}重合，首先{B}相对{A}的zA轴
转30°，再沿{A}的xA轴移动10个单位，并沿{A}的
,求 。
解：
zB zA
OB OA
xA30oxB
yB 30o
yA
zA zB
OA
(10,5,0)
xA

机器人 第三章 课件

机器人 第三章 课件

机器人技术基础第三章操作臂运动学第三章操作臂运动学1.连杆参数与连杆坐标系2.连杆变换与运动学方程3.XHK 5140换刀机械手的运动学方程4.PUMA 560机器人的运动学方程5.PUMA 560机器人的运动学反解6.腕部三轴相交时的封闭解7.运动学反解的有关问题8.关节空间和操作空间连杆参数与连杆坐标系连杆及其序号关节及其序号关节的种类关节的轴线机械手的结构节拍中间连杆中间连杆的几何描述方法连杆的功能连杆的几何特征尺寸及特征参数a，α例3.1相连中间连杆的连接描述方法转动关节中θ为变量，d为常量。

移动关节中d 为变量，θ为常量。

连杆参数与关节变量第i-1连杆，需要有4个参数：a i-1，αi-1，di-1，θi-1描述。

称为连杆参数。

其中3个为常数，1个为变量。

关节变量qi-1。

n杆机械手，将会有3n常量，n个变量。

n个变量为：q1，q2，… ，q i-1，… ，q n。

记为：[q1，q2，… ，qi-1，… ，qn]T称为：关节向量q，或驱动向量q。

驱动向量q的线性代数空间称为驱动空间，驱动空间是n维空间。

连杆坐标系x 轴的位置：两z 轴相交，两z 轴平行。

两个相邻坐标系之间的关系。

连杆坐标系下连杆参数的正负规定。

连杆1为中间连杆，连杆1的坐标系1可确定，坐标系1在连杆1上，当连杆1运动时坐标系1一起运动。

规定：当t =0时坐标系1的位置为坐标系0的位置，坐标系0的位置永远不动，坐标系0是静止坐标系。

末连杆n规定：当t =0时x n-1的位置为xn的位置。

之后，当qn 变化时xn的位置变化。

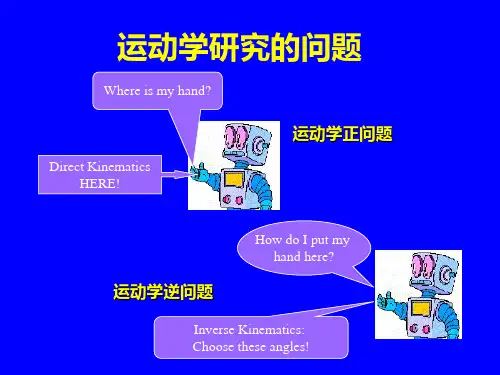
PUMA 560机器人的运动学方程。

最新机械手-图文PPT课件

最新机械手-图文PPT课件

Robofeeder3、4
Robofeeder3－4主要功能为： 将对中台上调整好位置的板料， 放入第一台压机模腔内；
其由四个伺服电机驱动： 1、轴传送运动 2、轴手臂直线运动 3、轴手臂旋转运动 4、轴端拾器杆旋转运动
区别与Robofeeder1、2： 考虑到左右前门，左右中门
为一模两件。在第二序或第三序 时中间切断。后序翻边时，两件 间距加大。故增加两侧气缸，实 现可伸展，完成压件安放；
• 功能与主治：清热泻火，散风止痛。用于 头痛眩晕，目赤耳鸣，咽喉肿痛，口舌生 疮，牙龈肿痛，大便燥结。
• 用法用量：口服，一次1丸，一日2次。 • 注意事项
牛黄上清丸的功效与作用/doc-view-1300.html
• 1、忌食辛辣食物。 • 2、孕妇慎用。 • 3、不宜在服药期间同时服用温补性中成药。 • 4、有心律失常、心脏病、肝病、肾病等慢
对中台有自己独自的轨道，其进 出的准确控制，由一个激光测距 仪完成；
高速拆垛机械手
高速拆垛机械手主要作用为上料用； 可以拾取两侧板料小车上的料板。单侧 拾取板料时，另一侧的安全保护栅榄升 起。
由两个伺服电机驱动其完成Y轴，横 向运动；Z轴，竖直运动，拾取板料。
Z Y
Robofeeder1
Robofeeder1主要功能为： 将对中台上调整好位置的板料， 放入第一台压机模腔内；
机械手-图文
EDSTACKER
线头部分：
板料小车:运送板料； 高速拆垛机械手：负责把板料放到
磁性传送带上；
磁性传送带:负责运送板料； 双料回收箱:负责回收拆垛手误操
作拿起的双板料，由 第一部分传送带反转 送出；
扫描仪:采集板料图像传送到计算机 对中台:对中台的侧移和旋转完成

机械手运动分析介绍课件

机械手运动分析介绍课件
集成化：机械手将与其他设备集成，实现自 动化生产线
柔性化：机械手将具备更高的灵活性和适应 性，满足不同场景的需求
发展趋势分析
智能化：机械手将具备自主学习和 决策能力，提高工作效率
集成化：机械手将与其他设备集成， 实现自动化生产线
轻量化：机械手将采用更轻便的材 料和结构，提高运动速度和灵活性
环保化：机械手将采用环保材料和 节能技术，降低能耗和污染
传感器与反馈：设计合适的传感器，如位置传感器、力传 感器等，实现对机械手运动状态的实时监测与反馈
控制参数优化：通过实验和仿真，优化控制参数，提高 机械手的运动精度和稳定性
控制策略实现
01
控制算法：PID控制、模糊控制、 神经网络控制等
02
传感器：位置、速度、加速度等 传感器
03
驱动系统：电机、液压、气动等 驱动系统
并联型机械手：基于并联机构，适用 0 5 于高速、高精度的运动和操作任务
复合型机械手：结合多种机械手的 0 6的应用领域
01
工业自动化：用于生产 线上的物料搬运、装配、 焊接等操作
02
医疗领域：用于手术、 康复治疗、辅助诊断等
03
服务行业：用于餐厅、 酒店、商场等场所的服 务机器人
机械手可以提高生产效率，降低 人工成本，提高产品质量
机械手的分类
直角坐标机械手：基于直角坐标系， 0 1 适用于简单的搬运和装配任务
圆柱坐标机械手：基于圆柱坐标系， 0 2 适用于旋转和摆动任务
球坐标机械手：基于球坐标系，适 0 3 用于空间内的任意方向运动
关节型机械手：基于关节结构，适 0 4 用于复杂的运动和操作任务
发展趋势展望
智能化：机械手将具备 自主学习和决策能力， 提高工作效率

机器人手部结构详解精品PPT课件

机器人手部结构详解精品PPT课件

5．异形吸盘：
结构特点：
可用来吸附鸡蛋、 锥颈瓶等物件。 扩大了真空吸盘 在机器人上的应 用。
6．喷气式吸盘：
工作原理：
压缩空气进入喷嘴后，利用伯努利效应，当压缩 空气刚进入时，由于喷嘴口逐渐缩小，致使气流 速度逐渐增加。当管路截面收缩到最小处时，气 流速度达到临界速度，然后喷嘴管路的截面逐渐 增加，使与橡胶皮碗相连的吸气口处，造成很高 的气流速度而形成负压。
43
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
讲师：XXXXXX XX年XX月XX日
当手爪夹紧和松开物体时，手指作回转运动。当 被抓物体的直径大小变化时，需要调整手爪的位 置才能保持物体的中心位置不变。
平动型：
手指由平行四杆机构传动，当手爪夹紧和松开物 体时，手指姿态不变，作平动。
平移型：
当手爪夹紧和松开工件时，手指作平移运动，并 保持夹持中心的固定不变，不受工件直径变化的 影响。
手部可能还有一些电、气、液的接口： 由于手部的驱动方式不同造成。对这 些部件的接口一定要求具有互换性。
2．手部是末端操作器：
可以具有手指，也可以不具有手指； 可以有手爪，也可以是专用工具。
末端操作器图例（1）：
每个手指有三个或 四个关节。技术关 键是手指之间的协 调控制。
末端操作器图例（2）：
2．设有检测开关的手爪装置：
工作原理：
手爪装有限位开 关5和7。在指爪 4沿垂直方向接 近工件6的过程 中，限位开关检 测手爪与工件的 相对位置。当工 件接触限位开关 时发信号，汽缸 通过连杆3驱动
指爪夹紧工件。
4．上料吸盘（1）：

第3章_机器人运动学

第3章_机器人运动学
T6 = A1 A2 A3 A4 A5 A6
(3.1)
一个六连杆机械手可具有六个自由度，每个连 杆含有一个自由度，并能在其运动范围内任意 定位与定向。
机器人学基础 2
3.1 机器人运动方程的表示 3.1.1 运动姿态和方向角 机械手的运动方向
原点由矢量p表示。 接近矢量a：z向矢量 方向矢量o：y向矢量 法线矢量n：它与矢量 图3.1 矢量n,o,a和p o和a一起构成一个右手 矢量集合，并由矢量的交乘所规定：n = o × a。
9
3.1 机器人运动方向的表示
3.1.2 运动位置和坐标
用球面坐标表示运动位置 用球面坐标表示手臂运动位置矢量的方法。这个方法 对应于沿轴平移，再绕轴旋转角，最后绕轴旋转角， 如图3.4(b)所示，即为：
Sph(α , β , r ) = Rot ( z ,α ) Rot ( y , β )Trans (0,0, r )
(3.9)
式中，Sph 表示球面坐标组合变换。
3.1 机器人运动方向的表示
10
3.1 机器人运动方程的表示
3.1.3 连杆变换矩阵及其乘积 广义连杆 相邻坐标系间及其相应连杆可以用齐次变换矩阵来表 示。要求出操作手所需要的变换矩阵，每个连杆都要 用广义连杆来描述。在求得相应的广义变换矩阵之后， 可对其加以修正，以适合每个具体的连杆。
cθ1 sθ 0 T1 = 1 0 0
cθ 3 sθ 2 T3 = 3 0 0
− sθ1 cθ1 0 0
− sθ 3 cθ 3 0 0
0 0 1 0
0 0 0 1
cθ 2 0 1 T2 = − sθ 2 0
− sθ 2 0 − cθ 2 0
3.1 机器人运动方向的表示 13

机器人学基础_第3章_机器人运动学

机器人学基础_第3章_机器人运动学
机械手的运动姿态往往由 一个绕轴x ，y 和 z 的旋转 序列来规定。这种转角的 序列，称为欧拉（Euler） 角。 欧拉角: 用一个绕 z 轴 旋转ф角，再绕新的 y 轴 y’旋转θ角，最后绕新的 z 轴z’’旋转ψ角来描述任 图3.2 欧拉角的定义 何可能的姿态。 欧拉变换Euler可由连乘三个旋转矩阵来求得，即 Euler (φ ,θ ,ψ ) = Rot ( z , φ ) Rot ( y,θ ) Rot ( z ,ψ ) （3.3）
Kinematics treats motion without regard to the forces that cause it. Within the science of kinematics one studies the position, velocity, acceleration, and all higher order derivatives of the position variables (with respect to time or any other variable). 从几何学 几何学的观点来处 几何学 理手指位置 手指位置P与关节变量 关节变量 手指位置 L1, L2, θ1 和 θ 2的关系称为 运动学(Kinematics)。 运动学
(3.9)
3.1 Representation of Kinematics Equation of Manipulator
17
3.1 Representation of Kinetic Equation of Robot Manipulator
3.1 Representation of Kinematics Equation of Manipulator
12
3.1.1 Kinetic Pose and Oriented Angle Roll, Pitch, Yaw to represent motion pose

机器人技术基础课件第三章-机器人运动学精选全文完整版

机器人技术基础课件第三章-机器人运动学精选全文完整版
03T 01T12T 23T
如此类推，对于六连杆机器人，有下列矩阵：
06T 01T 12T 23T 34T 45T 56T
3.2 3.2 机械手运动学方程
26
0 6
T
3.1.4 连杆变换矩阵及其乘积
06T 01T12T 23T 34T 45T 56T
机器人运动学方程
此式右边表示了从固定参考系到手部坐标系的各连杆
一个六连杆机械手可具有六个自由度，每个连杆含 有一个自由度，并能在其运动范围内任意定位与定向。 其中三个自由度用于规定位置，而另外三个自由度用 来规定姿态。
8
3.1.1 连杆坐标系
机械手的运动方向
机器人手部的位置和姿态也可以
用固连于手部的坐标系{B}的位姿
来表示
关节轴为ZB， ZB轴的单位方向 矢量α称为接近矢量，指向朝外。
(1) 坐标系｛i-1｝绕xi-1轴转角αi-1，使Zi－1与Zi平行，算子为Rot(x, αi-1) ； (2) 沿Xi-1轴平移ai-1，使Zi－1和Zi共线， 算子为Trans(ai-1,0,0)； (3)绕Zi轴转角θi; 使得使Xi－1与Xi平行, 算子为Rot(z,θi)；
(4) 沿Zi轴平移di。使得i-1系和i系重合, 算子为Trans(0,0,di)。
3.2.1 机器人正运动学方程
连杆 i 1
2
3
连杆长 度ai-1
0
a0
a1
连杆偏距 di 0
0
d2
连杆扭角 αi-1 00
00
-900
关节角 θi
θ1(00) θ2(00) θ3(00)
3.2.1 机器人正运动学方程
该3自由度机器人的运动学方程为：

机械手臂教材ppt课件

机械手臂教材ppt课件

三、机器手臂的组成
手臂由以下几部分组成： （1）运动元件。如油缸、气缸、齿条、凸轮等是驱
动手臂运动的部件。 （2）导向装置。是保证手臂的正确方面及承受由于
工件的重量所产生的弯曲和扭转的力矩。 （3）手臂。起着连接和承受外力的作用。手臂上的
零部件，如油缸、导向杆、控制件等都安装在手臂上。 此外，根据机械来自运动和工作的要求，如管路、冷却
多轴机械手臂研发方面，多轴式机械手臂广泛应用于汽车製造 商、汽车零组件与电子相关产业。机械手臂可以提昇产品技术 与品质，而这些初期工作大多可以藉由机械手臂来完成。
近年来，各先进国家为了提昇台机器人的技术水准，都会推广 机器人产业与创立相关联盟，并且特别针对工业以外的领域进 行推广，例如：医疗、服务、生活方面…等。
机械手臂教材
目录
一、演进与发展 二、种类与原理
三、组成 四、应用于发展
一.演进与发展
1921年捷克科幻作家卡雷尔·恰佩克的《罗素姆的万 能机器人》最早出现机器人。 1956年第一台专门应用于产业生产使用的机械手臂 则是由具有「机械手臂之父」之称的约瑟夫·恩格伯 格（Joseph F. Engelberger）所发明的。利用乔治·迪 沃尔（George Devol）所授权的专利技术，研发出第 一台工业用机械手臂，名为「Unimate」。
装置、行程定位装置和自动检测装置等，一般也都装 在手臂上。所以手臂的结构、工作范围、承载能力和 动作精度都直接影响机械手的工作性能。
四、应用与发展
机械手臂在产业自动化的应用已经相当广泛，主要是使用于人 工无法进行或者会耗费较多时间来做的工作，机械手臂在精度 与耐用性上可以减少许人为的不可预知问题。
乔治·迪沃尔
1963年日本不二輸送机工业株式会社制造出专门 使用在栈板装载（Palletizing）的机械手臂，研发出 针对栈板专用的搬运工具。 1973年德国库卡机器人集团（KUKA Robot Group） 就研发出第一台采用机电驱动的6轴机械手臂。

机械手课件

机械手课件
竞争压力加大
随着机械手市场的不断发展，竞争也日益激烈， 企业需要不断提高产品质量和技术水平以保持竞 争优势。
机遇与挑战并存
虽然市场需求变化带来了挑战，但也为企业提供 了更多的发展机遇，如开发新的应用领域、拓展 新的市场等。
企业战略转型与可持续发展路径探讨
转型发展路径
01
企业需要从传统的生产型企业向技术研发和服务型企业转型，
加强技术研发和人才培养，提高核心竞争力。
பைடு நூலகம்
可持续发展路径
02
企业需要注重环保和可持续发展，采用绿色制造技术和清洁能
源，降低对环境的影响，提高企业的社会责任感。
合作发展路径
03
企业需要加强与高校、科研机构等的合作，共同推动机械手技
术的发展和应用，实现互利共赢。
THANKS
感谢观看
常见故障排除方法及技巧分享
故障诊断
通过观察机械手运行状态、听声音、闻气味等方 式，判断机械手可能出现的故障。
排除方法
针对不同故障，采取相应的方法进行排除，如更 换损坏部件、调整参数等。
技巧分享
分享一些常见的故障排除技巧，如如何快速找到 故障点、如何避免常见故障等。
安全操作规范和注意事项
安全操作规范
柔性化技术
柔性机械手的出现，使得机械手能够适应更多种类的工件和工作环 境，提高了生产效率。
模块化技术
模块化设计使得机械手更加易于维护和升级，同时也能够根据不同 的需求进行定制。
市场需求变化带来的挑战机遇分析
1 2 3
市场需求多样化
随着消费者对产品质量和个性化的需求不断提高 ，机械手需要满足更多样化的市场需求。
严格遵守机械手操作规程，确保操作 过程安全可靠。

机器人学基础_第3章机器人运动学

机器人学基础_第3章机器人运动学

移动连杆坐标系的建立
移动连杆坐标系的规定：
• 坐标轴Zi：与i+1关节的轴线重合； • 坐标轴Xi：沿移动关节i轴线与关节i+1轴线的公垂线,指向i+1关节； • 坐标轴Yi：按右手直角坐标系法则确定； • 坐标原点Oi： （1）当关节i轴线和关节i+1轴线相交时，取交点； （2）当关节i轴线和关节i+1轴线异面时，取两轴线的公垂线与关节i轴
动到使其原点与连杆i坐标系原点重合的地方。 • (4) 绕Xi旋转αi角，使Zi–1转到与Zi同一直线上。 • 连杆i–1的坐标系经过上述变换与连杆i的坐标系
重合。如果把表示相邻连杆相对空间关系的矩阵 称为A矩阵，那么根据上述变换步骤，从连杆i到 连杆i–1的坐标变换矩阵Ai为
•
(3.13)
• 同理，对联轴器的齐次坐标变换矩阵有 •
• 手部的位置矢量为固定参考系原点指向手 部坐标系{B}原点的矢量P，手部的方向矢 量为n、o、a。于是手部的位姿可用4 4 矩阵表示为
•
•
nX oX a X PX
T
nY
oY
aY
PY
nZ 0
oz 0
aZ 0
PZ 1
• 思考：
• ①说明位姿矩阵的左上角3×3矩阵的几何 意义。
• ②分别说明n, o, a, P的几何意义。
a1 = l 1 =100
a2 = l 2 =100
旧课复习与总结
转动连杆坐标系的建立
• 坐标轴Zi：与i+1关节的轴线重合； • 坐标轴Xi：沿连杆i两关节轴线的公垂线,指向i+1关节； • 坐标轴Yi：按右手直角坐标系法则确定； • 坐标原点Oi： （1）当关节i轴线和关节i+1轴线相交时，取交点； （2）当关节i轴线和关节i+1轴线异面时，取两轴线的公垂

人工智能工业机器人机械手臂科研PPT模板ppt通用模板

人工智能工业机器人机械手臂科研PPT模板ppt通用模板
请替换文字内容
请替换文字内容，修改文字内容，也可以直接复制你的内容到此。请替换文字内容，修改文字内容，也可以直接 复制你的内容到此。请替换文字内容，修改文字内容，也可以直接复制你的内容到此。请替换文字内容，修改文 字内容，也可以直接复制你的内容到此。请替换文字内容，修改文字内容，也可以直接复制你的内容到此。
标题文本
标题文本预设
此部分内容作为 文字排版占位显 示 （建议使用主
题字体）
标题文本预设
此部分内容作为 文字排版占位显 示 （建议使用主
题字体）
标题文本预设
此部分内容作为 文字排版占位显 示 （建议使用主
题字体）
标题文本预设
此部分内容作为文字排版占位显示 （建议使用主题字体）
标题文本预设
此部分内容作为文字排版占位显示 （建议使用主题字体）
此部分内容作为文字排版占位显 示（建议使用主题字体）。
标题文本预设
此部分内容作为文字排版占位显示（建议使 用主题字体）
点击添加相关标题文字
ADD RELATED TITLE WORDS
75%
在此处添加详细描述文本，尽量与标题文本语言风格相符合，语言描述尽量简洁生动，尽可 能概括出段落内容。在此处添加详细描述文本，尽量与标题文本语言风格相符合，语言描述 尽量简洁生动，尽可能概括出段落内容。
请替换文字内容 请替换文字内容
2016 65%
02 请替换文字内容 请替换文字内容，修改文字内容，也可以直接复制你的内容 到此。请替换文字内容，修改文字内容
此部分内容作为文字排版占位显示（建议使
标用题主文题字本体预）设
如需更改请在（设置形状格式）菜单下（文 本选项）中调整
此部分内容作为文字排版占位显示（建议使

工业机器人课件第三章 机器人运动学

工业机器人课件第三章 机器人运动学

T3= A1 A2 A3
称这些A矩阵的乘积为T矩阵，其前置上标若为0，则可省略。对于六 连杆机械手，有下列T矩阵
T6= A1 A2 A3 A4 A5 A6
手爪坐标系
机械手的运动方向 原点由矢量p表示。 接近矢量a：z轴设在手指接近物体的方向，称为接近矢量 方向矢量o：y轴设在两手指的连线方向，称为方位矢量 法线矢量n：x轴由右手系确定， 即 n = o a ，称为法向矢量。
0 sin i cos i 0
0 0 0 1
对于在第i坐标系中的点ri在第i—1坐标系中表示为:
ri 1 i 1Ai ri
确定第i坐标系相对于机座坐标系的位置的齐次变换矩阵i-1Ti是 各齐次变换矩阵Ai的连乘积，可表示成
0
Ti A1 A2 A3 A4 A5 A6 A j
பைடு நூலகம்
cos i sin cos i i 1 sin i sin i 1 0
例 建立右图所示机器人相邻坐标 系间的转换矩阵 解：建立的坐标系如右图，这是二维坐 标系(在三维空间中，各坐标系的z轴垂 直于纸面)，其相邻坐标系的变换矩阵 为
A1 Rz ,Tx ,l1
第三章 机器人运动学
§ 3.1 机器人运动方程的表示
机器人的机械手看作是一系列由关节连接起来的连杆构成的。为机 械手的每一连杆建立一个坐标系，并用齐次变换来描述这些坐标系间 的相对位置和姿态。通常把描述一个连杆与下一个连杆间相对关系的 齐次变换叫做A矩阵。一个A矩阵就是一个描述连杆坐标系间相对平移 和旋转的齐次变换。如果A1表示第一个连杆对于基系的位置和姿态， A2表示第二个连杆相对于第一个连杆的位置和姿态，则第二个连杆在 基系中的位置和姿态可由下列矩阵的乘积给出 T2= A1 A2 同理，若A3表示第三个连杆相对于第二个连杆的位置和姿态，则有

机器人技术概论PPT完整全套教学课件精选全文完整版

机器人技术概论PPT完整全套教学课件精选全文完整版
一、 机器人的诞生
由于当时技术条件的限制，这些玩偶都是身高一米的巨型玩具。现在保留下来的最早的机器人是瑞士努萨蒂尔历史博物馆里的少女玩偶，它制作于二百年前，两只手的十个手指可以按动风琴的琴键弹奏音乐，现在还定期演奏供参观者欣赏，展示了古代人的智慧。
19世纪中叶自动玩偶分为2个流派，即科学幻想派和机械制作派，并各自在文学艺术和近代技术中找到了自己的位置。1831年歌德发表的《浮士德》，塑造了人造人“荷蒙克鲁斯”。1870年霍夫曼出版了以自动玩偶为主角的作品《葛蓓莉娅》。1883年科洛迪的《木偶奇遇记》问世。1886年《未来的夏娃》问世。在机械制作方面，1893年摩尔制造了“蒸汽人”，“蒸汽人”靠蒸汽驱动双腿沿圆周走动。
二、 现代机器人
图1-5所示为水下机器人。将机器人技术（如传感技术、智能技术、控制技术等）扩散和渗透到各个领域形成了各式各样的新机器——智能化机器，如仿生机器人、可重构机器人等。当前与信息技术的交互和融合又产生了“软件机器人”“网络机器人”等新名词，这也说明了机器人所具有的创新活力。
“工欲善其事，必先利其器”，人类在认识自然、改造自然、推动社会进步的过程中，不断地创造出各种各样为人类服务的工具，其中许多具有划时代的意义。作为20世纪自动化领域的重大成就，机器人已经和人类社会的生产、生活密不可分。世间万物，人力是第一资源，这是任何其他物质不能替代的。我们完全有理由相信，像其他许多科学技术的发明发现一样，机器人也将成为人类的好助手、好朋友。
按机械结构
和串联机器人相比较，并联机器人具有以下特点：
（1） 无累积误差，精度较高；（2） 驱动装置可置于定平台上或接近定平台的位置，这样运动部分重量轻，速度快，动态响应好；（3） 结构紧凑，刚度高，承载能力大；（4） 完全对称的并联机构具有较好的各向同性；（5） 工作空间较小。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

机械手的运动
3.1 机械手运动的表示方法
3.1.2 机械手的机构和运动学 正运动学与逆运动学 θ f 1(r)
2 1ta 1 nx y ta 1 n L 1L 2L s2ci2 n o 2 s co1s(x22 yL 21 )L 2L1 2L2 2
机械手的运动
3.1 机械手运动的表示方法
3.2.3 齐次变换 利用上式的确步骤： 1）建立连杆坐标系，并用
连杆长度和关节变量， 求相邻坐标系的位姿关系 2）求相邻坐标系的齐次变换 矩阵； 3）利用上式求总变换
机械手的运动
3.2 手爪位置和关节变量的关系
3.2.3 齐次变换
Bp1 0 0 ,
BR 1 C S1 1
S1 C 1
1p20 L1,
3.2.3 齐次变换
C1 S1 0C2 S2 L11 0 L2
B TE S1 C1
0S2 C2
0 0 1
0
0 0 10 0 1 0 0 1
C1C2 S1S2 S1C2 C1S2
0
C1S2 S1C2 S1S2 C1C2 0
L2 (C1C2 S1S2 ) L1C1
L2 (S1C2
J J 1 J 2 , J i R 2 1
J 1 L 1 L C 1 1 S 1 L 2 L C 2 1 S 12 2 ,
J 2 L 2 L C 2 1 S 1 2 2
rJ11J22
则J1、J2分别为单位关节速度 在手爪位置产生的速度分量。即 由图中的PE,1,PE,2反时针转动 90度而成
x 1 L 1 S 1 L 2 S 1,2 y 1 L 1 C 1 L 2 C 1,2
x 2 L 2 S 12 y 2 L 2 C 12
J L1L C 11 S 1 L2 L C 21 S122
L2S12 L2S12
机械手的运动
3.3 雅可比矩阵
3.3.2 关节速度和手爪速度的几何学关系
sin /(2) 0 cos/2 () pE,21
1L2C12 0L2S12
L2L C 21S2 12J2
机械手的运动
3.4 手爪力和关节驱动力的关系
3.4.1 虚功原理
F AxAF BxB0
x A L A, x B L B
(F A L A F B L B ) 0
第三章 机械手的运动
3.1 机械手运动的表示方法 3.2 手爪位置和关节变量的关系 3.3 雅可比矩阵 3.4 手爪力和关节驱动力的关系 3.5 机械手运动方程式的求解
机械手的运动
3.1 机械手Βιβλιοθήκη 动的表示方法3.1.1 机械手的结构
机械手的运动
3.1 机械手运动的表示方法
3.1.2 机械手的机构和运动学
C1S2 )
L1S1
1
C1 2 S12
0
S12 C12
0
L1C1 L2C12
L1S1
L2 S1 2
1
机械手的运动
3.3 雅可比矩阵
3.3.1雅可比矩阵的定义
机器人正运动学方程：r f(θ) ，这里
rr1r2,,rmTRm1 θ12,,nTRn1
其中：r 1 f 1 ( 1 2 , ,n )
3.1.3 运动学、静力学、动力学的关系
机械手的运动
3.2 手爪位置和关节变量的关系
3.2.1 手爪位置和姿态的表示方法 ΣB 基坐标系 ΣE 手爪坐标系 BpE∈R3x1:手爪坐标系
原点在基坐标中的 位置向量 BRE ∈R3x3:坐标变换 矩阵
B R E B e x ,B e y ,B e z
( j 1 , 2 , , m )
n>m:冗余机器人
机械手的运动
3.3 雅可比矩阵
3.3.1雅r可比J矩θ阵 的定义
rifi(1,2, n)
ri fi11 fi22 finn
f1
Jf (θ) 1
θT fm
1
f1
n1
fm
n
Rmn
f1
r1 rm
1
f
m
1 m
机械手的运动
3.3 雅可比矩阵
3.3.2 关节速度和手爪速度的几何学关系
cos/2 () si n/(2)
si n/(2) 0 cos/2 () pE,1 1
1L1C 1L2C 12 0 L1S1L2S12
L1L C 11 S 1 L2 L C 21 S1 22 J1
cos/2 () sin /(2)
1
drJdθ J：雅可比矩阵
机械手的运动
3.3 雅可比矩阵
3.3.1雅可比矩阵的定义 例：两自由度机械手的雅可比矩阵
xL1C 1L2C 12
yL1S1L2S12
C 1 c 1 ; S o 1 s1 s ; C i 1 n c 21 o 2 ) S 1 s ; s 2( 1 i2 ) n(
1BppBTE
Epp 1
BTE 0BTRE
BpE 1
Bpp 1
BT111pp
BT1 0BTR1
Bp1 1
1pp 1
1T2
2pp 1
12pP2TE
Epp 1
1T2 10RT 2
1p2
1
2TE 02RT E
2pE
1
BT EBT 11T 22T E
机械手的运动
3.2 手爪位置和关节变量的关系
1R2C S2 2
S2 C2
2pE0 L2,
2RE1 010
机械手的运动
3.2 手爪位置和关节变量的关系
3.2.3 齐次变换
C1 S1 0
B T1 S1 C1
0
0 0 1
C2 S2 L1
1T2 S2 C2
0
0 0 1
1 0 L2
2 TE 0 1
0
0 0 1
机械手的运动
3.2 手爪位置和关节 变量的关系
回转关节 棱柱关节 关节变量 手爪姿态 运动学
机械手的运动
3.1 机械手运动的表示方法
3.1.2 机械手的机构和运动学 手爪位置r;关节变量θ
有：
rxy, θ12
x L 1 co 1 L s 2 co 1 s 2 )(
y L 1 si1 n L 2 si1 n2 ) (
写为：r f (θ) 运动学方程式。
机械手的运动
3.2 手爪位置和关节变量的关系
3.2.3 齐次变换 两个坐标系中位姿关系：
B p p B R EEp p B p E
1BppBTE
Epp 1
BTE 0BT RE
BpER33 1
上式称为齐次变换矩阵
机械手的运动
机械手的运动
3.2 手爪位置和关节变量的关系
3.2.3 齐次变换
对二自由度机械手