康普顿散射
- 格式:doc
- 大小:408.50 KB
- 文档页数:6

康普顿散射现象康普顿散射现象是指入射光子与物质中自由电子相互作用,发生能量转移并改变方向的现象。
这种现象是由美国物理学家康普顿在20世纪初发现的,后来被广泛应用于各种领域,如医学、物理学、天文学等。
康普顿散射现象的本质是能量守恒和动量守恒。
当入射光子与物质中自由电子相互作用时,光子的能量和动量会被转移给电子,从而使光子的波长发生变化,即发生散射。
这种散射过程是随机的,因此入射光子的方向也会改变。
康普顿散射现象的重要性在于它可以用来测量物质中的自由电子密度和能量。
在医学领域,康普顿散射现象被广泛应用于X射线成像。
X射线是一种高能量的电磁波,可以穿透人体组织,因此可以用于检查内部器官的情况。
当X射线穿过人体组织时,会发生康普顿散射现象,从而使X射线的强度和方向发生变化。
通过测量散射后的X 射线的能量和方向,可以推断出物质中的自由电子密度和能量。
在物理学领域,康普顿散射现象被用于研究物质的结构和性质。
通过测量入射光子的能量和方向以及散射后的光子的能量和方向,可以推断出物质中的自由电子密度和能量,从而了解物质的结构和性质。
在天文学领域,康普顿散射现象被用于研究宇宙射线的来源和性质。
宇宙射线是一种高能量的粒子,可以穿透地球大气层,因此可以用于研究宇宙的物理现象。
当宇宙射线进入地球大气层时,会与大气层中的分子发生康普顿散射现象,从而使宇宙射线的强度和方向发生变化。
通过测量散射后的宇宙射线的能量和方向,可以推断出宇宙射线的来源和性质。
总之,康普顿散射现象是一种重要的物理现象,被广泛应用于各种领域。
通过研究康普顿散射现象,可以了解物质的结构和性质,推断出宇宙射线的来源和性质,以及进行医学成像等应用。


康普顿散射现象康普顿散射现象是一种物理现象,它是指X射线或伽马射线与物质相互作用时,光子能量的一部分被散射,而散射光子的能量和方向都与原来的光子不同。
康普顿散射现象的发现,不仅为物理学家提供了一种研究原子核和电子的有效手段,而且也在医疗诊断和工业领域有着广泛的应用。
康普顿散射现象的发现可以追溯到20世纪初期,当时的物理学家康普顿和威尔逊在研究X射线与物质相互作用时,发现了一个非常奇特的现象。
他们发现,当X射线与物质相互作用时,光子的能量会发生变化,而且散射的光子的能量和方向都与原来的光子不同。
这个现象被称为康普顿散射现象。
康普顿散射现象的原理是:当X射线或伽马射线与物质相互作用时,光子会与物质中的电子相互作用,电子会吸收一部分光子的能量,并发生散射。
散射后的光子的能量和方向都与原来的光子不同,这是因为散射过程中电子的动能也发生了变化。
康普顿散射现象的发现,不仅为物理学家提供了一种研究原子核和电子的有效手段,而且也在医疗诊断和工业领域有着广泛的应用。
康普顿散射现象在医疗诊断中有着广泛的应用。
医生们利用X射线的康普顿散射现象来进行各种疾病的诊断。
例如,医生们可以通过X射线的康普顿散射现象来检测骨骼的损伤和病变。
此外,医生们还可以利用X射线的康普顿散射现象来检测肿瘤和其他内部器官的异常情况。
这些应用都是建立在康普顿散射现象的基础上的。
康普顿散射现象在工业领域也有着广泛的应用。
工业生产中,康普顿散射现象可以被用来检测材料的缺陷和质量。
例如,工业生产中常常需要检测金属材料中的裂纹和疏松区域,这时就可以利用X射线的康普顿散射现象来检测。
此外,康普顿散射现象还可以被用来检测工业生产过程中的污染物和放射性物质。
康普顿散射现象的研究也为科学家们提供了研究原子核和电子的有效手段。
康普顿散射现象的研究可以帮助科学家们了解物质的结构和性质。
例如,科学家们可以利用康普顿散射现象来研究原子核的结构和电子的运动轨迹。
这些研究对于物理学的发展和应用都有着重要的意义。

h /c m o vcos / .12h cos /c康普顿散射实验报告、实验目的1. 学会康普顿散射效应的测量技术;2. 验证康普顿散射的 丫光子能量及微分截面与散射角的关系。
、实验原理1 •康普顿散射康普顿效应是射线与物质相互作用的三种效应之一。
康普顿效应是入射光子与物质原子中的核外电子产生非 弹性碰撞而被散射的现象。
碰撞时,入射光子把部分能量 转移给电子,使它脱离原子成为反冲电子, 而散射光子的 能量和运动方向发生变化。
当入射光子与电子发生康普顿效应时,如图 1所示, 其中h v 是入射Y 光子的能量,h v 是散射Y 光子的能量, 堤散射角, e 是反冲电子,①是反冲角。
由于发生康普顿散射的 丫光子的能量比电子的束缚能要大得多, 子中的电子作用时, 可以把电子的束缚能忽略, 看成是自由电子, 静止的,动能为 0 ,只有静止能量 m o c 2。
散射后,电子获得速度 E mc 2 m o c " !/ 1 2,动量为mv 用相对论的能量和动量守恒定律就可以得到 所以入射的丫光子与原 并视散射发生以前电子是 v ,此时电子的能量 2,其中 v/c , c 为光速。
m 0c 2 hm 0c 2/ 12h(1)式中,h v/c 是入射丫光子的动量,hv' /是散射丫光子的动量。
h sin /c m o vsin / , 12(3)由式(1)、(2)、( 3)可得出散射此式就表示散射 丫光子能量与入射 丫光子的能量h h1 一 (1 cos )m °c丫光子能量、散射角的关系。
(4)2 •康普顿散射的微分截面康普顿散射的微分截面的意义是: 一个能量为hv 的入射丫光子与原子中的一个核外电子作用后被散射到 B 方向单位立体角里的几率(记作d_・,单位:cm 2/单位立体角)为 d式中r o =2.818 x 113cm ,是电子的经典半径,式(5)通 常称为“克来茵一仁科”公式,此式所 描述的就是微分截面与入射 丫光子能量及散射角的关系。

康普顿散射动量转移原则及能量方向康普顿散射是一种重要的粒子物理现象,它发生在高能光子与电子之间的相互作用过程中。
康普顿散射动量转移原则和能量方向是描述康普顿散射过程的重要规律和性质。
本文将详细介绍康普顿散射动量转移原则和能量方向的基本概念、原理以及相关应用。
首先,我们来了解一下康普顿散射的基本过程。
康普顿散射是由于高能光子与自由电子发生相互作用而引起的散射现象。
当高能光子碰撞到自由电子时,光子会失去一部分能量,并改变方向。
这个过程中,光子被散射到较大的角度,并且会转移一部分动量给电子。
在康普顿散射中,动量转移原则是指散射后的光子和电子之间交换的动量差。
根据动量守恒定律,散射前后的总动量应保持不变。
因此,光子失去的动量必然转移到了电子上。
动量转移原则描述了康普顿散射中光子和电子之间动量的转移关系。
接下来,让我们来了解一下康普顿散射中能量的转移方向。
根据能量守恒定律,散射前后的总能量应保持不变。
在康普顿散射中,光子失去的能量被转移给了电子,并且散射后的光子的能量减小,而电子的能量增加。
因此,能量的转移方向是从光子向电子转移。
康普顿散射动量转移原则和能量方向的研究不仅在理论物理领域具有重要地位,而且在实际应用中也有广泛的应用价值。
首先,深入研究康普顿散射的动量转移原则和能量方向有助于增强人们对基本粒子相互作用的理解。
通过研究康普顿散射过程,可以揭示物质内部微观结构的特征和性质。
其次,在医学领域,康普顿散射动量转移原则和能量方向的理论研究与实践应用相结合,可以为放射疗法和医学成像技术等提供重要的指导。
康普顿散射被广泛应用于医学成像技术中,如正电子发射断层扫描(PET)和单光子发射计算机断层扫描(SPECT)等。
这些技术利用康普顿散射过程中能量的转移方向来获取图像信息,从而实现对人体内部器官结构和功能的非侵入性检测。
此外,康普顿散射动量转移原则和能量方向的研究还对材料科学领域具有重要意义。
康普顿散射被用于通过测量散射光子的能量损失来研究材料的电子结构和晶格动力学行为。


为什么光子可以引起康普顿散射?
光子可以引起康普顿散射是因为光子和物质中的自由电子之间存在相互作用,导致光子的能量和动量发生改变。
康普顿散射是一种光子与自由电子碰撞后的散射过程。
当一个入射光子与自由电子相互作用时,光子的能量和动量一部分以散射光子的形式被转移给了电子,而散射光子的能量和动量发生了变化。
这个过程可以使用能量和动量守恒定律来解释。
根据能量守恒定律,入射光子的能量等于散射光子的能量加上电子的动能。
根据动量守恒定律,入射光子的动量等于散射光子的动量加上电子的动量。
康普顿散射的散射角度和散射光子能量的变化可以通过科曼普顿公式来描述。
根据这个公式,散射光子的能量与入射光子的能量和散射角度有关。
特别地,入射光子的能量越高,散射角度的改变越明显。
因此,光子可以引起康普顿散射的原因是光子和自由电子之间存在相互作用,并且这个相互作用导致光子的能量和
动量发生改变。
康普顿散射是光与物质相互作用的重要现象之一,也将影响电磁辐射的传播和相互作用特性。

康普顿散射现象康普顿散射现象是物理学中的一个重要现象,它是指入射光子与物质原子相互作用时,光子的能量部分转移给原子中的自由电子,导致光子的散射。
康普顿散射现象最早是由美国物理学家康普顿在20世纪20年代发现的。
他利用X射线对物质进行研究时,发现X射线的散射角度与入射角度不同,而且散射光子的能量也有所改变。
通过对散射光子的能量和角度的测量,康普顿成功地解释了这一现象。
他提出了一个简单的公式来描述康普顿散射的能量转移,这个公式成为了现代物理学中的基本公式之一。
康普顿散射的机制非常复杂,它涉及到光子与原子中的自由电子发生相互作用的过程。
当一个光子进入物质时,它会与物质中的原子相互作用。
光子的电磁波场会激发原子中的自由电子,导致电子发生振动。
这个过程会导致光子的能量部分转移给电子,使得光子的波长增加,频率降低。
最终,散射光子的能量和波长会与入射光子不同。
康普顿散射现象在物理学中有着广泛的应用。
它可以用来研究物质的结构和组成,也可以用来测量物质的密度和厚度。
康普顿散射还可以用来研究宇宙射线和天体物理学中的一些问题。
此外,康普顿散射还被用于医学影像学中,例如X射线断层扫描(CT)和正电子发射断层扫描(PET)等技术中。
康普顿散射现象的研究也带来了一些重要的物理学理论。
例如,康普顿散射的能量转移过程是量子力学中的重要问题之一。
量子力学中的康普顿效应理论可以用来描述光子与物质相互作用的量子力学过程。
此外,康普顿散射现象也与相对论物理学有关。
康普顿效应的解释需要引入相对论量子力学的概念,例如质量能量关系和动量守恒等。
总之,康普顿散射现象是物理学中的一个重要现象,它不仅带来了重要的物理学理论,还有着广泛的应用价值。
未来,随着科学技术的不断发展,康普顿散射现象的研究将会更加深入,为我们认识世界带来更多的启示。

发现:•1922年,美国物理学家康普顿在研究石墨中的电子对X射线的散射时发现,有些散射波的波长比入射波的波长略大,他认为这是光子和电子碰撞时,光子的一些能量转移给了电子,康普顿假设光子和电子、质子这样的实物粒子一样,不仅具有能量,也具有动量,碰撞过程中能量守恒,动量也守恒。
短波长电磁辐射射入物质而被散射后,在散射波中,除了原波长的波以外,还出现波长增大的波,散射物的原子序数愈大,散射波中波长增大部分的强度和原波长部分的强度之比就愈小。
按照这个思想列出方程后求出了散射前后的波长差,结果跟实验数据完全符合,这样就证实了他的假设。
这种现象叫康普顿效应。
康普顿效应发现过程在1923年5月的《物理评论》上,A.H.康普顿以《X射线受轻元素散射的量子理论》为题,发表了他所发现的效应,并用光量子假说作出解释。
他写道(pton,Phys.Rev.,21(1923)p.):“从量子论的观点看,可以假设:任一特殊的X射线量子不是被辐射器中所有电子散射,而是把它的全部能量耗于某个特殊的电子,这电子转过来又将射线向某一特殊的方向散射,这个方向与入射束成某个角度。
辐射量子路径的弯折引起动量发生变化。
结果,散射电子以一等于X射线动量变化的动量反冲。
散射射线的能量等于入射射线的能量减去散射电子反冲的动能。
由于散射射线应是一完整的量子,其频率也将和能量同比例地减小。
因此,根据量子理论,我们可以期待散射射线的波长比入射射线大”,而“散射辐射的强度在原始X射线的前进方向要比反方向大,正如实验测得的那样。
”为什么散射光中还有与入射光波长相同的谱线? 是由于光子与原子碰撞,原子质量很大,光子碰撞后,能量不变,散射光频率不变。
1. 散射波长改变量lD的数量级为10-12m,对于可见光波长l~10-7m,lD<<l,所以观察不到康普顿效应。
解释:他发现其中包含有两种不同频率的成分,一种频率(或波长)和原来人射的X射线的频率相同,而另一种则比原来人射的父射线的频率小。

康普顿散射效应名词解释
嘿,朋友们!今天咱来唠唠康普顿散射效应。
这玩意儿啊,就好像是一场奇妙的光线“变戏法”。
你看啊,光平时就直直地跑,对吧?可在康普顿散射效应这里,情况就变得有趣啦!就好比一个小球本来沿着直线滚动,突然碰到了一些特别的东西,然后它的运动方向就发生了改变。
在康普顿散射效应里,光子就像是这个小球,当它和物质中的电子发生碰撞的时候,光子不仅把一部分能量给了电子,自己的运动方向也变了!这多神奇呀!
咱可以想象一下,光子就像个调皮的小精灵,本来开开心心地往前飞,结果遇到电子这个“小捣蛋”,被撞得晕头转向,方向都搞不清啦!这可不是瞎编哦,科学家们通过各种实验观察到了这个现象呢。
而且啊,康普顿散射效应可重要了呢!它让我们对光和物质的相互作用有了更深的理解。
就好像我们了解了一个人的小脾气,以后跟他打交道就更有数啦!通过研究它,我们能知道很多关于物质结构和光的性质的秘密。
它在很多领域都有大用处呢!比如在医学上,帮助医生更好地了解人体内部的情况;在物理学研究中,让科学家们能探索更多未知的奥秘。
这就像是一把神奇的钥匙,能打开好多知识的大门。
康普顿散射效应不就是在提醒我们,这个世界充满了奇妙和惊喜吗?就像生活中那些突然出现的小意外,也许会让我们措手不及,但也可能会带来意想不到的收获呀!所以啊,别小瞧了这些看似深奥的科学知识,它们其实和我们的生活息息相关呢。
总之,康普顿散射效应就是这么一个既有趣又重要的现象,它就像隐藏在科学世界里的一颗璀璨宝石,等待着我们去发现和欣赏它的光芒。
我们可得好好琢磨琢磨它,说不定能从里面找到更多的宝藏呢!。
康普顿效应科技名词定义中文名称:康普顿效应英文名称:Compton effect其他名称:康普顿散射(Compton scattering)定义:短波电磁辐射(如X射线,伽玛射线)射入物质而被散射后,除了出现与入射波同样波长的散射外,还出现波长向长波方向移动的散射现象。
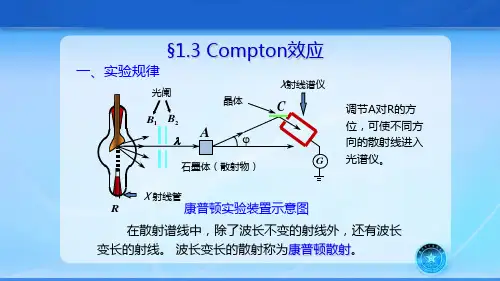
所属学科:大气科学(一级学科);大气物理学(二级学科)本内容由全国科学技术名词审定委员会审定公布康普顿效应实验原理图1923年,美国物理学家康普顿在研究x射线通过实物物质发生散射的实验时,发现了一个新的现象,即散射光中除了有原波长l0的x光外,还产生了波长l>l0 的x光,其波长的增量随散射角的不同而变化。
这种现象称为康普顿效应(compton effect)。
用经典电磁理论来解释康普顿效应遇到了困难。
康普顿借助于爱因斯坦的光子理论,从光子与电子碰撞的角度对此实验现象进行了圆满地解释.我国物理学家吴有训也曾对康普顿散射实验作出了杰出的贡献。
目录康普顿效应 compton effect对康普顿散射现象的研究经历了一、二十年才得出正确结果。
康普顿效应第一次从实验上证实了爱因斯坦提出的关于光子具有动量的假设。
这在物理学发展史上占有重要的位置。
光子在介质中和物质微粒相互作用时,可能使得光向任何方向传播,这种现象叫光的散射.康普顿效应1922年,美国物理学家康普顿在研究石墨中的电子对X射线的散射时发现,有些散射波的波长比入射波的波长略大,他认为这是光子和电子碰撞时,光子的一些能量转移给了电子,康普顿假设光子和电子、质子这样的实物粒子一样,不仅具有能量,也具有动量,碰撞过程中能量守恒,动量也守恒.按照这个思想列出方程后求出了散射前后的波长差,结果跟实验数据完全符合,这样就证实了他的假设。
这种现象叫康普顿效应。
编辑本段发现1922~1923年康普顿研究了X射线被较轻物质(石墨、石蜡等)散射后光的成分,发现散射谱线中除了有波长与原波长相同的成分外,还有波长较长的成分。
康普顿散射公式简便推导康普顿散射是一种重要的量子力学现象,其公式推导是量子力学课程中的经典教学内容之一。
本文将介绍一种简便的康普顿散射公式推导方法。
首先,我们需要了解康普顿散射的基本概念。
康普顿散射是指高能光子与自由电子相互作用后,光子的波长发生变化的现象。
在康普顿散射过程中,光子的能量和动量都被转移给了电子,因此,散射后光子的能量和动量会有所变化。
接下来,我们可以通过以下步骤推导康普顿散射公式:1. 假设入射的光子具有能量$E$,波长$lambda$,动量$p$,自由电子静止质量为$m_0$。
2. 光子与电子相互作用后,光子的能量减小为$E'$,波长变为$lambda'$,动量为$p'$。
3. 应用能量动量守恒定律,得到以下方程:$E + m_0 c^2 = E' + sqrt{(p'c)^2 + (m_0c^2)^2}$$p = p' costheta + sqrt{(frac{E'}{c} + frac{E}{c} -2p'costheta)(frac{E'}{c} - frac{E}{c})}$其中,$theta$为散射角度。
4. 应用康普顿散射能量差公式,得到:$Delta E = E - E' = frac{h}{m_0 c}(1 - costheta)$ 其中,$h$为普朗克常数。
5. 应用康普顿散射波长差公式,得到:$Delta lambda = lambda' - lambda = frac{h}{m_0 c}(1 - costheta)$6. 将公式中的电子静止质量$m_0$替换为电子的动能$T = mc^2 - m_0 c^2$,得到最终的康普顿散射公式:$Delta lambda = frac{h}{mc}(1 - costheta)$通过以上步骤,我们得到了康普顿散射公式的简便推导方法。
康普顿效应康普顿效应,也称为康普顿散射,是描述X射线通过物质时发生散射现象的一种物理现象。
这一现象是由于X射线与物质中的自由电子发生碰撞而发生的。
康普顿效应是近代物理学的重要发现之一,对现代物理学的发展产生了重要影响。
康普顿效应是由美国物理学家康普顿于1923年发现的。
他在实验中发现,当X射线入射到物质中时,会与物质中的自由电子发生碰撞,从而使X射线发生能量和波长的变化。
这一现象被称为康普顿效应。
康普顿效应证实了光的粒子性质,并为验证爱因斯坦的光量子假设提供了实验证据。
康普顿效应的实验装置通常包括一个X射线源、一个散射物体(通常是金属),以及一个能观测到散射后X射线的探测器。
实验过程中,X射线源会发射出一束高能量的X射线,入射到散射物体上。
与散射物体内的自由电子发生碰撞后,X射线的能量和波长会发生变化,并且出射角度也会发生改变。
观测到的散射射线的能量和角度分布可以用来研究康普顿效应。
康普顿效应可以用普朗克常数和电子质量来描述。
根据康普顿效应的理论,入射X射线和散射X射线的波长差值与散射角度有关,可以通过以下公式表示:Δλ = λ' - λ = h/mc * (1 - cosθ)其中,Δλ为散射射线的波长差值,λ'和λ分别为散射射线和入射射线的波长,h为普朗克常数,m为电子质量,c为光速,θ为散射角度。
这个公式成为康普顿公式,它对于解释X射线在物质中发生散射的现象起到了重要作用。
康普顿效应的发现对现代物理学的发展有着重要的意义。
首先,康普顿效应证实了光的粒子性质,支持了光的粒子-波动二象性,进一步验证了爱因斯坦的光量子假设。
其次,康普顿效应为核物理的发展打下了基础。
康普顿效应的发现表明,X射线是由高能量的光子组成的,提供了进一步研究核物理和相对论物理的线索。
此外,康普顿效应还在医学领域起到了重要作用,主要应用于X射线的成像和辐射治疗。
总之,康普顿效应的发现揭示了X射线在物质中发生散射的基本规律,证实了光的粒子性质,并为现代物理学的发展提供了重要线索。
光电效应,康普顿散射,对的产生能量排序
光电效应、康普顿散射、对的产生是量子力学中的三个重要概念,它们反映了光子和物质之间相互作用时能量的转化过程。
根据这些过程中所需要的能量大小,我们可以将它们排序如下:
1. 光电效应:
光电效应是指当光子的能量大于金属的逸出功时,金属表面会发射出电子。
发生光电效应所需的能量最小,只需要足以使电子从金属表面逸出即可。
2. 康普顿散射:
康普顿散射是光子与自由电子之间的相互作用过程。
在这个过程中,光子会将一部分能量传递给电子,使电子获得动能。
所需的能量比光电效应大,因为不仅要使电子逸出,还要赋予它一定的动能。
3.对的产生:
对的产生是指在高能量的电磁辐射或粒子与物质相互作用时,光子的能量可以转化为一对粒子-反粒子(如电子-正电子对)的产生。
这需要最高的能量,因为它涉及到质量的创造。
根据Einstein的著名公式E=mc^2,产生一个粒子-反粒子对需要的最小能量等于它们静止质量的总和乘以光速的平方。
根据所需的能量大小,这三个过程的排序为:光电效应< 康普顿散射< 对的产生。
klein-nishina 公式与康普顿散射公式
Klein-Nishina公式和康普顿散射公式都是描述光子与物质相互作用的物理学公式。
其中,康普顿散射公式描述了x射线光子与靶材中的电子发生碰撞后的散射过程,而Klein-Nishina公式则描述了康普顿散射的微分截面与入射γ光子能量及散射角的关系。
Klein-Nishina公式的表达式为:
式中Z=13,r0=2.818×10-13cm,是电子的经典半径。
此式所描述的就是微分截面与入射γ光子能量及散射角的关系。
康普顿散射公式的表达式为:
当时,说明x-射线光子在穿过靶材时,没有撞到电子,光子仍沿原来入射的方向传播没变,实验中对应的就是那些散射波长没有变化的散射线;当,波长差会随着增大而增加;当,;当,波长差有最大的值。
这些公式在物理学和相关领域中都有广泛的应用。
康普顿散射名词解释
康普顿散射是指一种物理现象,即高能光子(如X射线或伽马
射线)与物质中的自由电子相互作用后,光子的能量和动量发生改变,并改变方向的过程。
这个现象由美国物理学家康普顿于1923年
首次提出并解释。
在康普顿散射过程中,入射的高能光子与物质中的自由电子发
生碰撞,光子的一部分能量和动量转移给电子,使电子获得动能,
并改变方向。
这个过程中,光子的波长增加,即发生了能量的损失,这是由于能量和动量守恒定律的结果。
康普顿散射的散射角度与光
子能量和电子质量有关。
康普顿散射在物理学、天体物理学和核物理学等领域具有重要
的应用。
它被广泛用于测量物质中的自由电子密度、研究物质的结
构和成分,以及探测高能光子的能谱等。
康普顿散射的理论基础是
量子电动力学和相对论,它为我们理解光子与物质相互作用的基本
机制提供了重要的实验证据。
康普顿散射 实验报告一、实验目的1. 学会康普顿散射效应的测量技术;2. 验证康普顿散射的γ光子能量及微分截面与散射角的关系。
二、实验原理1.康普顿散射康普顿效应是射线与物质相互作用的三种效应之一。
康普顿效应是入射光子与物质原子中的核外电子产生非弹性碰撞而被散射的现象。
碰撞时,入射光子把部分能量转移给电子,使它脱离原子成为反冲电子,而散射光子的能量和运动方向发生变化。
当入射光子与电子发生康普顿效应时,如图1所示,其中hν是入射γ光子的能量,hν′是散射γ光子的能量,θ是散射角,e 是反冲电子,Φ是反冲角。
由于发生康普顿散射的γ光子的能量比电子的束缚能要大得多,所以入射的γ光子与原子中的电子作用时,可以把电子的束缚能忽略,看成是自由电子,并视散射发生以前电子是静止的,动能为0,只有静止能量m 0c 2。
散射后,电子获得速度v ,此时电子的能量2220/1E mc m c β==-,动量为20/1mv m v β=-,其中/v c β=,c 为光速。
用相对论的能量和动量守恒定律就可以得到22200/1m c h m c h νβν'+=-+ (1) 20/cos /1cos /h c m v h c νβνθ'=Φ-+ (2)式中,hν/c 是入射γ光子的动量,hν′/c 是散射γ光子的动量。
20sin /sin /1h c m v νθβ'=Φ- (3)由式(1)、(2)、(3)可得出散射γ光子的能量201(1cos )h h h m cνννθ'=+- (4)此式就表示散射γ光子能量与入射γ光子能量、散射角的关系。
2.康普顿散射的微分截面康普顿散射的微分截面的意义是:一个能量为hv 的入射γ光子与原子中的一个核外电子作用后被散射到θ方向单位立体角里的几率(记作()d d σθΩ,单位:cm 2/单位立体角)为图1 康普顿散射示意图 反冲电子散射光子入射光子220()()(sin )2r d h h h d h h h σθνννθννν''=+-'Ω (5) 式中r 0=2.818×10-13cm ,是电子的经典半径,式(5)通 常称为“克来茵一仁科”公式,此式所描述的就是微分截面与入射γ光子能量及散射角的关系。
本实验采用NaI(Tl)闪烁谱仪测量各散射角的散射γ光子能谱,用光电峰峰位及光电峰面积得出散射γ光子能量hv ,并计算出微分截面的相对值0()/()/d d d d σθσθΩΩ。
3.散射γ光子的能量h ν'及微分散射截面的相对值0()/()/d d d d σθσθΩΩ的实验测定原理(1)散射γ光子的能量h ν'的测量①对谱仪进行能量刻度,作出能量—道数的曲线。
②由散射γ光子能谱光电峰峰位的道数,在步骤①中所作的能量—道数刻度曲线上查出散射γ光子的能量hv′。
注意:实验装置中已考虑了克服地磁场的影响,光电倍增管已用圆筒形坡莫合金包住。
即使这样,不同θ角的散射光子的能量刻度曲线仍有少量的差别。
(2)微分散射截面的相对值0()/()/d d d d σθσθΩΩ的测量根据微分散射截面的定义,当有N 0个光子入射时,与样品中N e 个电子发生作用,在忽略多次散射自吸收的情况下,散射到θ方向Ω立体角里的光子数N (θ)应为0()()e d N N N f d σθθ=ΩΩ(6) 式中f 是散射样品的自吸收因子,我们假定f 为常数,即不随散射γ光子能量变化。
由图1可以看出,在θ方向上,NaI 晶体对散射样品(看成一个点)所张的立体角Ω=S /R 2,S 是晶体表面面积,R 是晶体表面到样品中心的距离,则N (θ)就是入射到晶体上的散射γ光子数。
我们测量的是散射γ光子能谱的光电峰计数N p (θ),假定晶体的光电峰本征效率为εf (θ),则有()()()p f N N θθεθ= (7)已知晶体对点源的总探测效率()ηθ与能量的关系(见表一)和晶体的峰总比R (θ)与能量的关系(见表二)。
设晶体的总本征效率为ε(θ),则有()()()f R εθθεθ= (8) ()()4ηθεθπΩ=(9) 由式(8)和(9)可得4()()()f R πεθθηθ=Ω(10) 将式(10)和(7) 则有4()()()()p N N R πθθθηθ=Ω(11) 将式(6)和 (11) 则有0()4()()()p e d N R N N f d σθπθθηθ=ΩΩΩ(12) 由式(12)可得0()()4()()p e N d d R N N fθσθπθηθ=Ω (13) 这里需要说明:η(θ)、R (θ)、ε(θ)、εf(θ) 都是能量的函数,但在具体情况下,入射γ光子具有单一能量,散射γ光子的能量就取决于θ。
为简便起见,我们都将它们写成了θ的函数。
式(13)给出了微分截面()d d σθΩ与各参量的关系,若各量均可测或已知,则微分截面可求。
实际上有些量无法测准(如N 0、N e 等),但它们在各个散射角θ下都保持不变,所以只能求得微分截面的相对值0()/()/d d d d σθσθ⎛⎫Ω ⎪Ω⎝⎭。
在此过程中,一些未知量都消掉了。
例如,设散射角θ=20º时的微分散射截面相对值为1,则由式(3.9-13)不难得到其它散射角θ的微分散射截面与20º时值之比为0000()()()//()/()()()()p p N N d d d d R R θθσθσθθηθθηθΩ=Ω (14) 由式(14)可看出,实验测量的就是N p (θ )和N p (θ0 )(θ=20º时)。
由表一和表二给出的数据,用内插法求出R (θ),η(θ),R (θ0 ),η(θ0),就可以求出微分散射截面的相对值。
注意:N p (θ)和N p (θ0)的测量条件必须相同。
表二 距点源10cm ,Ф40×40mmNaI(Tl)对点源的峰总比R (θ)与能量关系三、实验仪器本实验是由137Cs 放射源射出γ光子,经准直孔打在实验台上的铝散射棒上,产生的散射光子用NaI(T1)探测器接收,然后输出的脉冲信号,经线性放大器适当放大脉冲幅度,送到微机多道,测出散射光子的能谱。
NaI(T1)探测器能够以散射棒为中心而转动,这样不断改变散射角θ ,就可以测到不同θ角度下的散射光子能谱。
仪器装置见图2。
主要装置有:1.康普顿散射实验台一套:含台面主架、导轨、铅屏蔽块及散射用铝棒(Ф= 20mm)。
2.放射源:一个约10mCi的137Cs放射源,密封安装在铅室屏蔽体内;作刻度用的60Co放射源一个及小铅盒。
3.闪烁探测器:碘化钠晶体为声Ф40×40mm;光电倍增管型号为CRI05。
4.配套电子学插件:盒式高、低压电源;线形脉冲放大器,型号BH1224。
5.微机多道系统一套:含4096ADC和PHA接口二合一卡,计算机PHA仿真软件等。
四、实验内容与结果1. 按照仪器框图连接检查仪器,预热30分钟。
2. 双击桌面上的UMS图标,进入程序。
3. 能量刻度(取下散射棒,调整探测器位置,使θ= 0°)(1)打开137Cs源,调节探测器高压电源和线性放大器至推荐值,使0.662MeV光电峰峰位在多道的合适测量位置,测谱并寻峰,定出光电峰及各参数。
(2)关闭137Cs源,放上60Co源,在与(1)相同的实验条件下测量60Co的γ光子能图2 康普顿散射实验方块图谱,并定出1.1MeV和1.33MeV两峰对应参数。
(3)根据测得的三个峰,作能量刻度曲线。
实验记录表一能量刻度(θ=0)jSTQSKt。
0v1XaQj。
放射源137Cs 60CoE(Mev)0.662 1.173 1.332 光电峰峰位(道)400 711 800能量刻度曲线4. 测量不同散射角时的散射光子能谱,观察微分散射截面和散射峰能量随散射角的变化。
插上散射铝棒,设置合适的测量时间(根据源强及对峰技术的不确定度要求而定),记录在相同测量时间内不同散射角时光电峰的峰位、峰面积、上下道位置。
建议散射角分别取:θ=20°,40°,60°,80°,100°,120°。
5.测量上述散射角的本底谱。
取下散射棒,记下和步骤4中相同时间内相同道数区间的本底面积。
实验记录表二散射能谱的光电峰峰位和面积θ光电峰峰位(道)总峰面积本底面积净峰面积测量时间(秒)6. 导出微分散射截面与散射角θ的关系,以及散射光子的能量与散射角θ的关系。
由步骤3得到的能量刻度曲线在较为精确的范围内都满足线性关系,因此进行直线拟合,得到光电峰峰位和能量的函数关系为: =0.001670.006E x -。
根据各光电峰峰位的道数值在能量刻度曲线上用上述函数关系找出对应的散射光子能量的实验值E ,再由此能量在R (θ)-E 和η(θ)-E 曲线上找出对应的R (θ)、η(θ)值,计算出散射光子微分截面的实验值0()/()/d d d d σθσθ'⎛⎫Ω ⎪Ω⎝⎭。
表三表四120 0.2250.204-9.3349650.1794 0.1821 1.51利用表五,作关系曲线:137Cs的散射γ光子能量与散射角θ的关系137Cs的散射γ光子的微分散射截面与散射角θ的关系从实验数据看出误差略大,分析可能的原因有:1、仪器在测量过程中,散射γ光子峰位产生漂移。
2、R(θ)、η(θ)引用的参照数据,与该实验的条件不完全一致。
且实际用作图法读取关系值的时候存在误差3、能量刻度曲线标定引起的误差。
4、实验选取的光电峰峰位道数不准而产生的峰面积计数误差。