图乘法例题

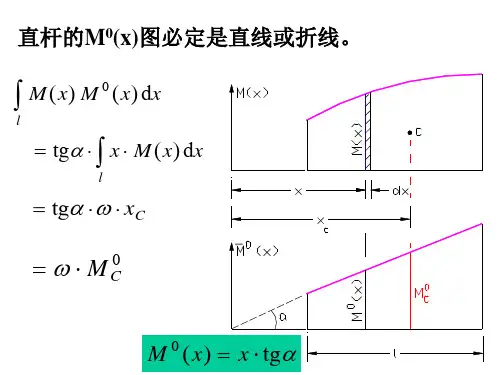
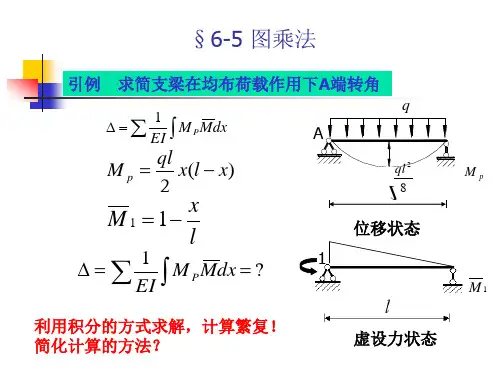
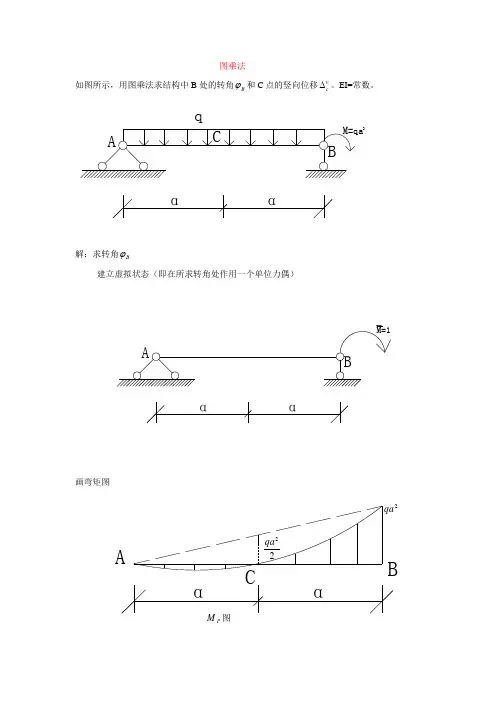
图乘法如图所示，用图乘法求结构中B 处的转角B ϕ和C 点的竖向位移vc ∆。

EI=常数。

ααCBAM=qa2q解：求转角B ϕ建立虚拟状态（即在所求转角处作用一个单位力偶）ααBAM=1画弯矩图P M 图ααCBA2qa 22qaααBAM 图根据公式cy EIω∆=∑ω为P M 图的面积c y 为P M 图的形心所对应的M 图的竖标的弯矩值232112(22)2323cB y qa qa a qa a EI EI EIωϕ==⨯⨯-⨯⨯=∑() 结果为正，说明方向与所设单位力偶的方向相同求位移vc ∆ 建立虚拟状态αα注：求转角和求位移的公式一样，公式中的力是广义的力（可以是集中力或力偶），位移是广义的位移（可以是位移和转角）。

1画弯矩图ααCBAP M 图BAααM 图2241125(22)222322824v ccy a qa qa a qa a a EI EI EIω∆==-⨯⨯⨯-⨯⨯⨯⨯⨯=-∑( ) 结果为负，说明所求位移方向与所设虚拟单位力的方向相反注：M 图和P M 图中可以用其中一个的面积去乘以这个的形心所对的另一个在该形心位置上的弯矩值，也就是说M 和P M 中至少有一个为直线图形即可，比如本题中就是用M 的面积去乘以其形心所对的P M 中三角形的弯矩值总结：求转角和求位移所用的公式相同只是求转角作用的虚拟单位力是力偶，求位移用的虚拟单位力是集中力2qa 22qa 2a。

1.2.3图乘法图乘法是关于的简化计算方法。

在一定的应用条件下，图乘法可给出该积分的数值解，而且是精确解。

适用条件（1）杆件为直杆；（2）EI为常数（等截面）；（3）和图中至少应有一个直线图形。

对于等截面直杆所构成的梁和刚架，都能同时满足以上三个条件，因而均可采用弯矩图图乘的方法，简称图乘法。

算位移的公式（1-15）式中为、图中某一图形的面积；为与该截面形心对应的另一个图形的竖标。

这样，就将较为复杂的积分运算问题简化为求图形的面积、形心和标距等几何运算问题。

三）几种常见图形的面积的形心位置在图1-15中，给出了位移计算中几种常见图形的面积公式和形心位置。

图1-15【注意】在所示的各次抛物线图形中，抛物线“顶点”处的切线都是与基线平行的。

这种图形可称为抛物线标准图形。

应用图中有关公式时，应注意这个特点。

（四）图乘法计算位移必须注意的几个问题（1）必须取自直线图形。

（2）与若在杆件同侧时，其乘积取正号；反之，取负号。

（3）如果两个图形都是直线图形，则可取自其中任何一个图形。

（4）如果图是曲线图形，图是折线图形，则应分段互乘，最后叠加。

（5）如果图形比较复杂（由不同类型的多个荷载作用绘出），其面积和形心位置不便确定时，则可利用“区段叠加法”的逆运算，将其分解为几个简单的标准图形，并将它们分别与另一个图形图乘，最后叠加。

（6）如果杆件EI分段变化时，可分段图乘，最后叠加。

（7）如果EI沿杆长连续变化或是曲杆和拱结构，则必须用积分计算位移。

（1）绘实际荷载作用下的图；（2）根据所求位移，加相应单位力，绘图；（3）代入式（1-15）求位移：【注意】根据计算结果的正负号，判定位移的实际方向，并在计算值之后所加的圆括号中，标明其实际方向。