乘法公式和因式分解练习题资料

12乘法公式和因式分解练习题一、选择题1.已知2264b Nab a +-是一个完全平方式，则N 等于 ( )A 、8B 、±8C 、±16D 、±322.如果22)()(y x M y x +=+-，那么M 等于 ( )A 、 2xyB 、－2xyC 、4xyD 、－4xy3.下列可以用平方差公式计算的是( )A 、(x －y) (x + y)B 、(x －y) (y －x)C 、(x －y)(－y + x)D 、(x －y)(－x + y)4.下列各式中，运算结果是22169b a -的是( )A 、)43)(43(b a b a --+-B 、)34)(34(a b a b --+-C 、)34)(34(a b a b -+D 、)83)(23(b a b a -+5、下列各式中,能运用平方差分式分解因式的是（ ）A 、21x +-B 、22y x +C 、42--xD 、()22b a ---6、若m x x +-82是完全平方式, 则m 的值为（ ）A 、4B 、8C 、16D 、327.计算（x +2）2的结果为x 2+□x +4,则“□”中的数为（ ）A ．－2B ．2C ．－4D ．4 8、把多项式1222+--y x xy 分解因式的结果是（ ）A ．)1)(1(+-+-x y y x B.)1)(1(---+x y y xC.)1)(1+--+y x y xD..)1)(1(--+-y x y x8.已知x 2＋16x ＋k 是完全平方式，则常数k 等于（ ）A ．64B ．48C ．32D ．169.若949)7(22+-=-bx x a x ，则b a +之值为何？A ．18B ．24C ．39D ． 4510.已知8)(2=-n m ，2)(2=+n m ，则=+22n m （ ）A ．10B ．6C ．5D ．311.把多项式a 2－4a 分解因式，结果正确的是( )A ．a (a －4)B ．(a +2)(a －2)C ．a (a +2) (a －2)D ．(a －2)2－4A ．32-xB ．92+xC ．38-xD ．318-x13.下列计算正确的是Ａ．()222x y x y +=+B ．()2222x y x xy y -=-- C ．()()22222x y x y x y +-=-D ．()2222x y x xy y -+=-+ 14.下列各因式分解正确的是（ ）A.)2)(2()2(22+-=-+-x x xB.22)1(12-=-+x x xC.22)12(144-=+-x x xD.)2)(2(42-+=-x x x x x15.下列分解因式正确的是（ ） A ．）（23a 1-a a a -+=+B ．2a-4b+2=2（a-2b ）C ．()222-a 4-a =D ．()221-a 1a 2-a =+ 16.下列各式能用完全平方式进行分解因式的是（ ）A ．x 2 +1B .x 2+2x －1C .x 2+x +1D .x 2+4x +417.下面的多项式中，能因式分解的是（ ）A ．m 2+nB ．m 2﹣m+1C ．m 2﹣nD ．m 2﹣2m+118. a 4b －6a 3b ＋9a 2b 分解因式的正确结果是A ．a 2b (a 2－6a ＋9)B ．a 2b (a ＋3) (a －3)C ．b (a 2－3)2D ．a 2b (a －3)26. 4. 19.分解因式(x －1)2 －2(x －1)+1的结果是 ( )A ．(x －1)(x －2)B ． x 2C ．(x +1)2D ． (x －2)220.已知a -b =1，则代数式2a -2b -3的值是A ．-1B ．1C ．-5D ．5 21.将代数式262++x x 化成q p x ++2)(的形式为（ ）A. 11)3(2+-xB. 7)3(2-+xC. 11)3(2-+xD. 4)2(2++x22.计算222(a+b)(a b)+a a b -等于（ ）A ．4aB ．6aC ．22a bD ．22a b - 23.如图，边长为(m +3)的正方形纸片剪出一个边长为m 的正方形之后，剩余部分可剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是（ ）A ．m +3B ．m +6C ．2m +3D ．2m +624.图（1）是一个长为2m ，宽为2n （m>n)的长方形，用剪刀 沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（ ）A.2mnB.(m+n)2C.(m-n)2 D .m 2 -n 2二、填空题1.若2a －b =5，则多项式6a 一3b 的值是 ．2.整式A 与m 2﹣2mn+n 2的和是（m+n ）2，则A= ．3．(x ＋1)(x －1)(1＋x )＝4.已知x + y =—5 ，xy =6 ，则x 2 + y 2=_______.5.二次三项式29x kx -+是一个完全平方式，则k 的值是 .6.将4个数a 、b 、c 、d 排成两行、两列，两边各加一条竖线记成a b c d，定义a c b d =a d －bc ，上述等式就叫做二阶行列式．若 1 181 1x x x x +-=-+，则x = ． 7.写出一个在实数范围内能用平方差公式分解因式的多项式： ．8.分解因式：25x x - =________ ．9.分解因式：=-822x ___________________10.分解因式：ab 3－4ab = ．11.分解因式：a －6ab ＋9ab 2＝ .12.分解因式：=+-22363n mn m _______ .13.分解因式:22331212x y xy y ++=14.若2m n -=，5m n +=，则22m n -的值为 ．15.若622=-n m ，且2m n -=，则=+n m ．16.有足够多的长方形和正方形的卡片，如下图. 3a b 2b a 1如果选取1号、2号、3号卡片分别为1张、4张、4张，可拼成一个正方形（不重叠无缝隙）那么这个正方形的边长是三、解答题1.化简：)2()12+-+x x x （ 2.化简：1)1()1(2-++-a a a3.先化简，再求值：(x+3)(x-3)-x (x-2)，其中x=4.4. 先化简，再求值：22b ＋(a ＋b )(a －b )－(a －)2b ，其中a ＝－3，b ＝12.5.先化简，再求值：()()()x x x -+++2232，其中2-=x6.已知y x A +=2，y x B -=2，计算22B A -7.先化简，再求值：()222a b b --，其中2,3a b =-=8、已知x + y = a , xy = b ,求(x－y) 2 ， x 2 + y 2 ， x 2－xy + y 2的值x=-时，求代数式(2x+5)(x+1)-(x-3)(x+1)的值．9．当710.观察下列算式：① 1 × 3 - 22 = 3 - 4 = -1 ② 2 × 4 - 32 = 8 - 9 = -1③ 3 × 5 - 42 = 15 - 16 = -1 ④……（1）请你按以上规律写出第4个算式；（2）把这个规律用含字母的式子表示出来；（3）你认为（2）中所写出的式子一定成立吗？并说明理由．。

可编辑修改精选全文完整版乘法公式与因式分解测试题填空题1、已知：x 2－6x +k 可分解为只关于x －3的因式，则k 的值为 （ ）2、若x 2－6x y+9y 2=0，则13--y x 的值为（ ） 3、已知：x 2+4x y=3，2x y+9y 2=1。

则x +3y 的值为4、x m －x m －4分解因式的结果是 （ ）5、若y 2－8y+m －1是完全平方式，则m= （ ） 6.（a 2+b 2）2－4a 2b 2分解因式结果是（ ）7、若－b ax x -+221分解成)7)(4(21+--x x ，则a 、b 的值为（ ）8.若N b a b a ++=-22)32()32(，则N 的代数式是（ ） 9．已知7)(2=+b a ,3)(2=-b a ,则22b a +与ab 的值分别是（ ），（ ）10．若3,2a b ab +=-=，则22a b += ，()2a b -= ]11．多项式9x ²+1加上一个单项式后，成为一个整式的完全平方，请你写出一个．．符合条件的单项式 12.已知多项式n mx --与2x -的乘积中不含x 项，则m 、n 满足的条件是__________. 13. 1纳米＝0．000000001米，则3．5纳米＝___________米．(用科学计数法表示)14．若4)2)((2-=++x x b ax ，则ba ＝_________________．选择题1. 若2422549))(________57(y x y x -=--，括号内应填代数式( )A 、y x 572+B 、y x 572--C 、y x 572+-D 、y x 572- 2. ．若))(3(152n x x mx x ++=-+，则m的值为 （ ）A ．5-B ．5C ．2-D ．23.已知2264b Nab a +-是一个完全平方式，则N 等于 ( ) A 、8 B 、±8 C 、±16 D 、±324. 如(x+m)与(x+3)的乘积中不含x 的一次项，则m 的值为（ ）A 、 –3B 、3C 、0D 、15. .若10=4,10=7x y ，则210x y -的值为（ ）. (A) 449 (B) 494 (C) 167 (D) 7166.下列各式中，运算结果是22169b a -的是( ) A 、)43)(43(b a b a --+- B 、)34)(34(a b a b --+-C 、)34)(34(a b a b -+D 、)83)(23(b a b a -+7. 计算：1.992－1.98×1.99+0.992得（ ）A 、0B 、1C 、8.8804D 、3.9601 8.22)213()213(-+a a 等于( )A 、4192-a B 、161814-aC 、161298124+-a aD 、161298124++a a9、对于任何整数m ，多项式9)54(2-+m 都能（ ） A 、被8整除 B 、被m 整除 C 、被m －1整除 D 、被（2m -1）整除10、若a 为正整数，且x 2a ＝5，则（2x 3a ）2÷4x 4a 的值为（ ）（A ）5 （B ）25（C ）25 （D ）11、把216a +-分解因式，结果是（ ）A.)8)(8(+-a aB.)4)(4(-+a aC.)2)(2(+-a a D 2)4.(-a 12、下列多项式中，能用公式进行因式分解的是（ ） A ．22b a -- B.422++x x C. 22)(b a --- D.412+-x x 13、用分组分解法将x y xy x 332-+-分解因式，下列的分组方式中不恰当的是（ ）A ．)3()3(2xy y x x -+- B.)33()(2x y xy x -+- C.)33()(2x y xy x -+- D.y x xy x 3)3(2+-- 14、把多项式1222+--y x xy 分解因式的结果是（ ） A ．)1)(1(+-+-x y y x B.)1)(1(---+x y y x C.)1)(1+--+y x y x D..)1)(1(--+-y x y x 15、把多项式822222--++-y x y xy x 分解因式的结果是（ ）A.)2)(4(+---y x y xB.)8)(1(----y x y xC.)2)(4(--+-y x y xD.)8)(1(--+-y x y x 16、多项式3222315520m n m n m n +-的公因式是( ) A 、5mn B 、225m n C 、25m n D 、25mn 17、xy y x 2122--+解因式的结果是（ ） A.)2)(4(+---y x y x B.（x-y+1）(x-y-1) C.)2)(4(--+-y x y x D.)8)(1(--+-y x y x 18、20062+3×20062–5×20072的值不能．．被下列哪个数整除（ ）A 、3 B 、5 C 、20062 D 、2005219、一个正方形的边长增加了cm 2，面积相应增加了232cm ，则这个正方形的边长为( ) A ．6cm B ．5cm C ．8cm D ．7cm 20、下列各式中,能运用平方差分式分解因式的是（ ）A 、21x +- B 、22y x + C 、42--x D 、()22b a --- 21、若m x x +-82是完全平方式, 则m 的值为（ ） A 、4 B 、8 C 、16 D 、32 22.计算题⑴ x (9x －5)－(3x + 1) (3x －1)⑵ (a + b －c) (a －b + c)⑶)49)(23)(23(22b a b a b a ++-⑷ (2x －1) (2x + 1)－2(x －2) (x + 2)5） 22)()(y x y x +- （6）22)35()35(y x y x ++-（7）))((c b a c b a +--+ （8） 2222)2()4()2(++-t t t23.分解因式（9）2244x xy y -+- （10）224520bxy bx a -（11）(1)(3)1x x --+ （12） 22)(16)(9n m n m --+13）x 4－12x +32 （14）5x 2－125y 415）4x 2－12x y+9y 2 （16）.（m+n ）2－4（m+n －1）17）.22(1)(1)x a y a -+- （18）－81x 2+y 2（19）221222x xy y ++ （20）221424a ab b ++24、已知x + y = a , xy = b ,求(x －y) 2 ， x 2 + y 2， x 2－xy + y 2的值25、已知22==+ab b a ，，求32232121ab b a b a ++的值26、先分解因式，再求值：655222++-+-b a b ab a ，其中92,96==b a27. 对于任意自然数n ，()()2257--+n n 是否能被24整除，为什么？28、利用分解因式进行简便运算 1、已知2a －b=3,求－8a 2+8ab －2b 2 的值。

乘法公式经典例题【例题1】利用乘法公式进行计算计算：)23()49()23()12()12(22)2(122b a b a b a a a ++--+-）（【例题2】完全平方公式开放探究题多项式142+x 加么？【例题3】利用乘法公式进行化简求值；的值。

求）已知（的值；求）已知（的值；求）已知（）（xx b a b a b a y x x x ab xy y x 222222221,313,,4,722121,11)(+=++==++=+-+【例题4】 乘法公式几何中的运用如图所示，长方形ABCD 被分成6个大小不一的正方形，已知中间一个正方行的面积为4，求长方形ABCD 中最大正方形与最小正方形的面积之差。

【例题5】运用完全平方公式的值。

求代数式已知c bc ac b ab a m c m b m a 4442222,321,221,121+--+++=+=+=因式分解专项练习例1 （公式法）分解因式：(1) 34381a b b -； (2) 76a ab -2．分组分解法从前面可以看出，能够直接运用公式法分解的多项式，主要是二项式和三项式．而对于四项以上的多项式，如ma mb na nb +++既没有公式可用，也没有公因式可以提取．因此，可以先将多项式分组处理．这种利用分组来因式分解的方法叫做分组分解法．分组分解法的关键在于如何分组．常见题型：（1）分组后能提取公因式 （2）分组后能直接运用公式例2 （分组分解法）分解因式：（1）2222()()ab c d a b cd ---（2）2222428x xy y z ++-3．十字相乘法（1）2()x p q x pq +++型的因式分解这类式子在许多问题中经常出现，其特点是：①二次项系数是1；②常数项是两个数之积；③ 一次项系数是常数项的两个因数之和．∵2()x p q x pq +++2()()()()x px qx pq x x p q x p x p x q =+++=+++=++， ∴2()()()x p q x pq x p x q +++=++运用这个公式，可以把某些二次项系数为1的二次三项式分解因式．例3 （十字相乘法）把下列各式因式分解：(1) 2524x x +- (2) 2215x x -- (3) 226x xy y +- (4) 222()8()12x x x x +-++（2）一般二次三项式2ax bx c ++型的因式分解由2121221121122()()()a a x a c a c x c c a x c a x c +++=++我们发现，二次项系数a 分解成12a a ，常数项c 分解成12c c ，把1212,,,a a c c 写成1122a c a c ⨯，这里按斜线交叉相乘，再相加，就得到1221a c a c +，如果它正好等于2ax bx c ++的一次项系数b ，那么2ax bx c ++就可以分解成1122()()a x c a x c ++，其中11,a c 位于上一行，22,a c 位于下一行．这种借助画十字交叉线分解系数，从而将二次三项式分解因式的方法，叫做十字相乘法．必须注意，分解因数及十字相乘都有多种可能情况，所以往往要经过多次尝试，才能确定一个二次三项式能否用十字相乘法分解．例4 （十字相乘法）把下列各式因式分解：(1)21252x x --；(2)22568x xy y +-例5（拆项法）分解因式3234x x -+。

D． a6÷a2=a3
5．下面是一名学生所做的 4 道练习题：①（-3）0=1；②a3+a3=a6；③4m-4= ；④（xy2）3=x3y6，他做对的个数是（ ）
A． 0
B． 1
C．2
D． 3
6．下列计算中，结果正确的是（ ）
A． a2•a3=a6
B． （2a）•（3a）=6a
C．（a2）3=a6 D．a6÷a2=a3
17．下列运算丌正确的是（ ）
A． （a5）2=a10
B． 2a2•（-3a3）=-6a5
C． b•b3=b4
D． b5•b5=b25
18．下列计算正确的是（ ）
A． x2+2x2=3x4
B． a3•（-2a2）=-2a5
C． （-2x2）3=-6x6
D． 3a•（-b）2=-3ab2
19．下列计算正确的是（ ） A． （2x3）•（3x）2=6x6
2×（22）3 中，结果等于 66 的是（ ）
A． ①②③
B． ②③④
C．②③
D． ③④
3．下列运算正确的是（ ）
A． 6a-5a=1
B． （a2）3=a5
C．3a2+2a3=5a5 D．2a2•3a3=6a5
4．下列运算中，正确的是（ ） A．（a2）3=a5 B．2a•3a=6a2
C． 2a-a=2
14．下列计算中正确的是（ ）
A． a5-a2=a3
B． |a+b|=|a|+|b|
C． （-3a2）•2a3=-6a6
D．a2m=（-am）2（其中 m 为正整数）
15．下列计算正确的是（ ）
A． a2•a3=a6
B．（-2a）3=8a3 C．a+a4=a5

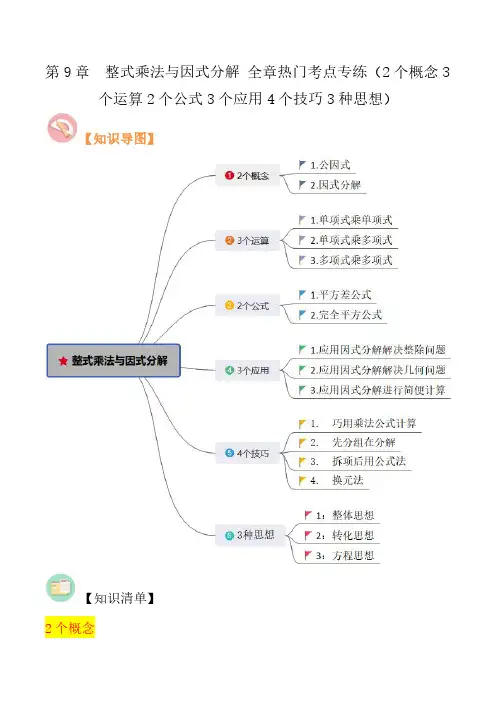
第9章整式乘法与因式分解全章热门考点专练（2个概念3个运算2个公式3个应用4个技巧3种思想）【知识导图】【知识清单】2个概念【例题1】（22-23八年级上·山东威海·期末）多项式2324223126x y x y x y --的公因式是（）A ．23x y B ．233x y C ．223x y D ．3xy【答案】C【分析】本题考查了公因式的定义．确定多项式中各项的公因式，可概括为三“定”：①定系数，即确定各项系数的最大公约数；②定字母，即确定各项的相同字母因式（或相同多项式因式）；③定指数，即各项相同字母因式（或相同多项式因式）的指数的最低次幂．根据多项式的公因式的确定方法，即可求解．【详解】解：多项式2324223126x y x y x y --的公因式是223x y ，故选C【变式1】（23-24八年级下·山东济南·阶段练习）把多项式33128ab a b +分解因式，应提的公因式是（）A ．abB ．4abC ．2abD ．24a b【答案】B【分析】本题主要考查了分解因式，观察可知两个单项式的公因式为4ab ，据此可得答案．【详解】解：()3322128432ab a b ab b a +=+，则多项式33128ab a b +分解因式，应提的公因式是4ab ，故选：B【变式2】（23-24七年级下·江苏徐州·期中）把多项式32612x x y -分解因式，应提取的公因式是．【答案】26x 【分析】本题考查了公因式，提公因式26x ，即可求解．【详解】解：把多项式32612x x y -分解因式，应提取的公因式是26x ，故答案为：26x 【变式3】（23-24八年级上·山东东营·阶段练习）()218b a b -与()312a b -的公因式是．【答案】()26a b -【分析】本题考查了公因式；根据公因式的定义，找出系数的最大公约数6，相同因式的最低指数次幂，即可确定公因式．【详解】解：∵18和12的最大公约数是6，∴()218b a b -与()312a b -的公因式是()26a b -，故答案为：()26a b -【例题2】（2023·江苏无锡·模拟预测）下列因式分解正确的是（）A ．2243(2)1x x x -+=--B ．2232(2)()x xy y x y x y -+=--C ．42224(2)(2)x x x x x x -=+-D ．3244(2)x x x x ++=+【答案】B【分析】此题考查了十字相乘法因式分解，以及提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．根据十字相乘因式分解，提公因式法与公式法因式分解逐项因式分解判断即可．【详解】解：A 、243(1)(3)x x x x -+=--，故本选项不符合题意；B 、2232(2)()x xy y x y x y -+=--，故本选项符合题意；C 、24222(4)(2(2)4)x x x x x x x =--=+-，故本选项不符合题意；D 、无法因式分解，故本选项不符合题意；故选：B【变式1】（2024·甘肃兰州·一模）因式分解：24a -=（）A ．()()44a a +-B ．()()42a a +-C ．()()24a a +-D ．()()22a a +-【答案】D【分析】本题考查了因式分解的定义以及运用平方差公式进行因式分解，把一个多项式分解成几个整式的乘积的形式，据此即可作答．【详解】解：24a -=()()22a a +-故选：D【变式2】（23-24八年级下·四川成都·阶段练习）下列等式从左到右的变形，是因式分解的是（）A ．()22326x x x x-=-B ．221234m n m n=⋅C ．22111x x x x x x ⎛⎫⎛⎫-=+- ⎪⎪⎝⎭⎝⎭D ．()()22x y x y x y -=+-D 、()()22x y x y x y -=+-，是因式分解，故本选项符合题意；故选：D【变式3】（2024·广东中山·一模）下列各式从左到右的变形，因式分解正确的是（）A ．()2a ab a ab+=+B ．()233a ab a a b +-=+-C ．()222824ab a a b -=-D ．()()22824a a a a --=+-【答案】D【分析】本题考查了因式分解的定义，把一个多项式化成几个整式的积的形式叫做因式分解，根据因式分解的定义逐项判断即可．【详解】解：A ．从左到右的变形属于整式乘法，不属于因式分解，故本选项不符合题意；B ．从左到右的变形不属于因式分解，故本选项不符合题意；C ．()()()222824222ab a a b a b b -=-=+-，分解不彻底，故本选项不符合题意；D ．从左到右的变形属于因式分解，故本选项符合题意．故选：D3个运算1.单项式乘单项式【例题3】（2024年上海市普陀区中考二模数学试题）下列运算正确的是（）A ．234a a a +=B ．32a a -=C ．233a a a ⋅=D ．32a a a÷=【答案】C【分析】本题主要考查合并同类项，单项式乘以单项式以及单项式除以单项式，运用相关运算法则求出各选项的结果，再进行判断即可【详解】解：A.34a a a +=，原选项计算错误，不符合题意；B.32a a a -=，原选项计算错误，不符合题意；C.233a a a ⋅=，计算正确，符合题意；D.33a a ÷=，原选项计算错误，不符合题意；故选：C【变式1】（23-24九年级下·甘肃庆阳·阶段练习）计算：()()326ab a --=．【答案】336a b 【分析】本题主要考查单项式乘单项式，直接根据运算法则进行计算即可．【详解】解：()()326ab a--()()()23=61a a b -⨯-⋅⋅⋅336a b =，故答案为：336a b 【变式2】（23-24七年级下·浙江·期中）计算：223a b a ⋅=．【答案】36a b【分析】本题主要考查了单项式乘单项式，直接利用单项式乘单项式运算法则计算得出答案．【详解】解：23236a b a a b ⋅=．故答案为：36a b【变式3】（2024·甘肃陇南·一模）计算：232x x ⋅=．【答案】52x 【分析】本题主要考查了单项式乘以单项式，熟知相关计算法则是解题的关键．【详解】解：23522x x x ⋅=，故答案为：52x2.单项式乘多项式【例题4】（2024·陕西汉中·一模）计算()()3221m m -⋅+的结果是（）A ．762m m --B ．662m m -+C ．752m m --D ．652m m --【答案】A【分析】本题考查了幂的乘方以及单项式乘多项式，先算幂的乘方，再算单项式乘多项式，即可作答．【详解】解：()()3221m m -⋅+()626m m =-+6621m m m =-⋅-⋅762m m =--，故选：A【变式1】（22-23七年级下·广西崇左·期中）计算：()21x x -=（）A ．31x -B ．3x x -C ．3x x+D ．2x x-【答案】B【分析】本题考查了单项式乘多项式，根据单项式乘多项式法则（单项式与多项式的每一项都相乘）计算即可．【详解】解：()231x x x x-=-故选：B【变式2】（23-24七年级下·江苏泰州·期中）计算()2323⋅-=x x ．计算：()31x x -=．【答案】518x 233x x -/233x x -+【分析】此题考查了积的乘方和单项式乘以单项式运算，单项式乘以多项式运算，应用积的乘方和单项式乘以单项式运算法则进行计算；利用单项式乘以多项式运算法则求解即可．【详解】()2323x x ⋅-3229x x =⋅518x =；()31x x -233x x =-．故答案为：518x ，233x x-【变式3】（2024七年级下·江苏·专题练习）计算()()223235a ab ab =-⋅-．【答案】3233610a b a b -+【分析】根据单项式乘多项式的运算法则（把多项式的每一项都与单项式相乘），即可求解，本题考查了单项式与多项式的乘法，掌握计算法则是解题的关键．【详解】解：()()2233233235610a ab ab a b a b -⋅-=-+．故答案为：3233610a b a b -+．3.多项式乘多项式【例题5】（23-24七年级下·河南周口·阶段练习）定义()*1a b b a =+，例如()()()2*11121x x x x x x +=++=++．则()()2*2x x -+=（）A ．24x -B ．244x x +-C ．24x x +-D ．22x x +-【答案】D【分析】本题考查新定义运算，多项式乘多项式，根据定义()*1a b b a =+将()()2*2x x -+变形为()()221x x +-+，再按照多项式乘多项式运算法则计算即可．【详解】解：()()()()2*2221x x x x -+=+-+()()21x x =+-222x x x =-+-22x x =+-，故选D【变式1】（23-24七年级下·江苏无锡·阶段练习）下列计算错误的是（）A ．()()21454x x x x ++=++B ．()()2236m m m m -+=+-C ．()()245920y y y y +-=+-D ．()()236918x x x x -=--+【答案】C【分析】本题主要考查多项式乘法的运算，掌握多项式乘法的运算法则是解题的关键．根据运算法则，逐一对选项进行分析即可．【详解】解：A ．2(1)(4)54x x x x ++=++，正确，故该选项不符合题意；B ．()()2236m m m m -+=+-，正确，故该选项不符合题意；C ．2(4)(5)20y y y y +-=--，错误，故该选项符合题意；D ．()()236918x x x x --=-+，正确，故该选项不符合题意．故选：C【变式2】．（22-23七年级下·四川成都·期中）若()()221222x x x mx -+=+-，则m 的值是．【答案】3【分析】本题考查了多项式与多项式的乘法运算，根据多项式与多项式的乘法法则把等号左边化简，然后与右边比较即可求解．【详解】解：∵()()22221224223222x x x x x x x x mx -++--=+-=+-＝，∴3m =．故答案为：3【变式3】（2024七年级下·江苏·专题练习）计算：()()34a b a b +-=．【答案】2212a ab b +-【分析】本题考查了多项式乘多项式法则，合并同类项时要注意项中的指数及字母是否相同．根据多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加解答．【详解】解：2222(3)(342)1412a b a b a ab ab b a ab b +-=++=---故答案为：2212a ab b+-2个公式1.平方差公式【例题6】（22-23七年级下·四川成都·期中）下列多项式的乘法中，可以用平方差公式进行计算的是（）A ．()()22a b b a +-B ．()()m n m n -+-C ．()()22x y x y -+D ．()()11n n ++【答案】A【分析】本题主要考查了平方差公式，解题的关键是根据平方差公式()()22a b a b a b +-=-，逐项进行判断即可．【详解】解：A ．()()22224a b b a b a +-=-，则A 符合题意；B ．()()m n m n -+-不能用平方差公式计算，则B 不符合题意；C ．()()22x y x y -+不能用平方差公式计算，则C 不符合题意；D ．()()11n n ++不能用平方差公式计算，则D 不符合题意；故选：A【变式1】（20-21七年级下·浙江杭州·期中）一个长方形的宽为2x y -，长为2x y +，则这个长方形的面积是（）A ．224x y -B ．224x y +C ．222x y -D ．222x y +【答案】A【分析】本题主要考查平方差公式的应用，掌握平方差公式的结构特征是解题的关键．根据长方形的面积公式进行计算即可．【详解】解：由长方形的面积公式可得，22(2)(2)4x y x y x y +-=-．故选：A【变式2】（23-24七年级下·河南周口·阶段练习）如果一个数()()222121a n n =+--，那么我们称这个数a 为“奇差数”．下列数中为“奇差数”的是（）A ．56B ．82C ．94D ．126【答案】A【分析】本题考查了平方差公式的应用，首先化简()()2221218a n n n =+--=，再看四个选项中，能够整除8的即为答案．理解“奇差数”的定义，正确化简是解题关键．【详解】解： ()()()()222121212121218a n n n n n n n =+--=++-+-+=，∴“奇差数”是8的倍数，A ，7856=÷，能够被8整除，因此56是“奇差数”；B ，828102÷= ，不能够被8整除，因此82不是“奇差数”；C ，948116÷= ，不能够被8整除，因此94不是“奇差数”；D ，1268156÷= ，不能够被8整除，因此126不是“奇差数”；故选：A【变式3】（23-24九年级下·山东聊城·阶段练习）下列计算正确的是（）A ．235a b ab +=B ．()()22a b a b a b+-=-C ．2236a b ab ⋅=D ．()235a a =【答案】B【分析】本题考查整式的运算，根据合并同类项，平方差公式，单项式乘单项式，幂的乘方的法则，逐一进行计算，判断即可．【详解】解：A 、2,3a b ，不是同类项，不能合并，不符合题意；B 、()()22a b a b a b +-=-，符合题意；C 、22236a b a b ⋅=，不符合题意；D 、()236a a =，不符合题意；故选：B2.完全平方公式【例题7】（23-24七年级下·江苏徐州·期中）下列计算正确的是（）A ．236a a a ⋅=B ．326()x x -=C ．632a a a ÷=D ．222()x y x y +=+【答案】B【分析】本题考查了同底数幂的乘除法，积的乘方，完全平方公式；根据以上运算法则进行计算即可求解．【详解】解：A.235a a a ⋅=，故该选项不正确，不符合题意；B.326()x x -=，故该选项正确，符合题意；C.633a a a ÷=，故该选项不正确，不符合题意；D.222()2x y x xy y +=++，故该选项不正确，不符合题意；故选：B【变式1】（23-24八年级下·山东威海·期中）不论x ，y 取何实数，代数式224614x x y y -+-+总是（）A ．非负数B ．正数C ．负数D ．非正数【答案】B【分析】本题主要考查了完全平方公式的应用，利用完全平方公式把原式变形为()()22231x y -+-+，据此可得答案．【详解】解：224614x x y y -+-+()()2244691x x y y =-++-++()()22231x y =-+-+，∵()()222030x y -≥-≥，，∴()()222311x y -+-+≥，∴224614x x y y -+-+总是正数，故选：B【变式2】（23-24九年级下·河南郑州·期中）下列计算正确的是（）A ．321a a -=B ．()2236m m -=C ．2=D ．()222244a b a ab b -=-+【答案】D【分析】本题考查了完全平方公式，合并同类项，积的乘方等运算法则，熟练掌握这些法则是解此题的关键．根据合并同类项的法则、积的乘方、完全平方公式进行计算即可．故选D【变式3】（2024·广西桂林·一模）下列运算正确的是（）A ．()22420x x -=B ．()236x x x -⋅=C ．()222x y x y +=+D 92=故选：A 3个应用1.应用因式分解解决整除问题【例题8】（2024·浙江嘉兴·一模）若k 为任意整数，则()()222122k k +--的值总能（）A ．被2整除B ．被3整除C ．被5整除D ．被7整除【答案】B【分析】本题主要考查了因式分解的意义，利用平方差公式把()()222122k k +--因式分解为()341k -，据此可得答案．【详解】解：()()222122k k +--()()()()21222122k k k k =++-+--⎡⎤⎡⎤⎣⎦⎣⎦()341k =-∵k 为任意整数，∴()341k -为整数，∴()341k -一定能被3整除，∴()()222122k k +--的值总能被3整除，故选：B【变式1】（23-24九年级下·河北邯郸·阶段练习）对于任何整数()0a a ≠，多项式()2354a +-都能（）A ．被9整除B ．被a 整除C ．被1a +整除D ．被1a -整除【答案】C【分析】此题考查了因式分解，利用平方差公式分解，即可做出判断，熟练掌握平方差公式是解本题的关键．【详解】解：原式()()()()3523523371a a a a =+++-=++，则对于任何整数a ，多项式()2354a +-都能被1a +整除．故选：C【变式2】（2024·河南郑州·一模）对任意整数n ，2(21)25n +-都能（）A ．被3整除B ．被4整除C ．被5整除D ．被6整除【答案】B【分析】根据平方差公式，分解因式后判断，熟练掌握公式法分解因式是解题的关键．【详解】∵()()()()()()2222125215215215432n n n n n n +-=+-=+++-=+-，∴故一定能被4整除，故选B【变式3】（2024·河北邯郸·模拟预测）已知()()844414141-=+-= ，则按此规律推算841-的结果一定能（）A ．被12整除B ．被13整除C ．被14整除D ．被15整除【答案】D【分析】本题考查了因式分解，根据平方差公式进行因式分解，即可求解．【详解】解：()()()()()()()84442242414141414141414115-=+-=++-=++⨯，故选：D2.应用因式分解解决几何问题【例题9】（23-24七年级下·全国·假期作业）已知,,a b c 为三角形ABC 的三边长，且满足222244b c a c a b -=-，则三角形ABC 的形状为（）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．锐角三角形【答案】A【详解】因为222244b c a c a b -=-，即()()()2222222c b a a b a b -=+-，所以()()()22222220a b a b c b a +---=，()()222220a b a b c -++=，()()()2220a b a b a b c +-++=．因为,,a b c 是三角形的三边长，所以2220,0a b a b c +>++>，所以0a b -=，即a b =，所以三角形ABC 为等腰三角形【变式1】（2024八年级·全国·竞赛）已知ABC 的三边为a 、b 、c ，且满足1111a b c a b c-+=-+，则ABC 的形状为．()()()0a b b c a c ∴--+=，∴a b =或b c =．故答案为：等腰三角形【变式2】（23-24八年级上·全国·课堂例题）（1）若a ，b ，c 是三角形的三边长，且满足关系式2222a bc c ab -=-，试判断这个三角形的形状．（2）若a ，b ，c 是ABC 的三边长，且满足2220a b c ab bc ac ++---=，则ABC 是什么形状？【答案】（1）三角形是等腰三角形；（2）ABC 是等边三角形【分析】本题考查因式分解的应用；（1）把2222a bc c ab -=-通过因式分解求值即可；（2）通过把2222222220a b c ab bc ac ++---=配方后根据非负数的性质判断即可．【详解】（1）∵2222a bc c ab -=-，∴()22220a c ab bc -+-=，∴()()()20a c a c b a c +-+-=，∴()()20a c a c b -++=．∵20a c b ++≠，∴0a c -=，即a c =，∴这个三角形是等腰三角形．（2）∵2220a b c ab bc ac ++---=，∴2222222220a b c ab bc ac ++---=．∴()()()2222222220a b ab b c bc c a ac +-++-++-=，即222()()()0a b b c a c -+-+-=．∴0a b -=，0b c -=，0a c -=，∴a b =，b c =，a c =，∴a b c ==，∴ABC 是等边三角形【变式3】（23-24八年级上·全国·课堂例题）（1）已知ABC 的三边长a ，b ，c 满足22661830a b a b c +--++-=，试判断ABC 的形状．（2）已知a ，b ，c 是ABC 的三边长，且满足2212852a b a b +=+-，求c 的取值范围．∴3.应用因式分解进行简便计算【例题10】（20-21八年级下·陕西汉中·期末）利用因式分解简便计算6999329999⨯+⨯-正确的是（）A ．()996932991019999⨯+=⨯=B ．()9969321991009900⨯+-=⨯=C ．()99693219910210098⨯++=⨯=D ．()99693299992198⨯+-=⨯=【答案】B【分析】利用提公因式分法将99提公因式进行计算即可判断．【详解】解：69×99+32×99-99=99（69+32-1）=99×100=9900．故选：B ．【点睛】本题考查了因式分解的应用，解决本题的关键是掌握因式分解【变式1】（22-23八年级下·贵州贵阳·期中）利用因式分解可以简便计算：5799449999⨯+⨯-分解正确的是()A ．()995744⨯+B ．()9957441⨯+-C ．()9957441⨯++D ．()99574499⨯+-【答案】B【分析】利用提取公因式法分解因式即可得．【详解】解：原式57994499199=⨯+⨯-⨯()9957441=⨯+-，故选：B ．【点睛】本题考查了因式分解，熟练掌握提取公因式法是解题关键【变式2】（22-23九年级上·广东惠州·开学考试）利用因式分解简便运算：2252.847.2-＝．【答案】560【分析】利用平方差法进行因式分解，再进行计算；【详解】原式＝()()52.847.252.847.2+⨯-＝100 5.6⨯＝560．故答案为：560．【点睛】本题考查利用公式法因式分解进行简便运算．熟练掌握公式法因式分解是解题的关键【变式3】（22-23七年级下·湖南怀化·期中）利用因式分解进行简便运算：(1)443424.7 1.365555-⨯+⨯-⨯；(2)22899202899101+⨯+【答案】(1)24-(2)610【分析】（1）运用提公因式法进行因式分解即可求解；（2）运用公式法进行因式分解即可求解．【点睛】本题主要考查因式分解，懂得运用提公因式法和公式法进行因式分解来进行简便运算是解题的关键4个技巧1.巧用乘法公式计算【例题11】（22-23八年级下·河南平顶山·阶段练习）代数式22494610x y x y ++-+中x ，y 取何值时代数式值最小？最小值是多少？【点睛】此题考查了配方法求最值，原式可化为两个完全平方式和一个常数和的形式．利用完全平方公式变形，根据完全平方式恒大于等于0，即可求出最小值，熟练掌握配方法是解题的关键【变式】（22-23七年级下·江苏宿迁·期末）已知2610A x x =-+．(1)当2x =-、0、3时，分别求出A 的值；(2)证明：无论x 取什么值，A 的值都不小于1．【答案】(1)当2x =-时，26A =；当0x =时，10A =；当3x =时，1A =(2)见解析【分析】（1）根据题意可得()2261031A x x x =-+=-+，将2x =-、0、3，分别代入代数式，即可求解；（2）根据题意可得()2261031A x x x =-+=-+，根据平方的非负性，可得1A ≥,即可得证．【详解】（1）解：∵()2261031A x x x =-+=-+∴当2x =-时，()223125126A =--+=+=；当0x =时，()203110A =-+=；当3x =时，()23311A =-+=；（2）证明：∵()2261031A x x x =-+=-+，()230x -≥∴1A ≥,【点睛】本题考查了代数式求值，因式分解的应用，熟练掌握完全平方公式是解题的关键2.先分组在分解【例题12】（21-22八年级下·陕西咸阳·阶段练习）阅读材料：常用的分解因式方法有提公因式法、公式法等．但有的多项式只用上述方法就无法分解，如22424x y x y -+-，细心观察这个式子会发现前两项符合平方差公式，后两项可提取公因式，分解过程为：22424x y x y-+-()()22424x y x y =-+-…分组()()()2222x y x y x y =-++-…组内分解因式()()222x y x y =-++…整体思想提公因式这种分解因式的方法叫分组分解法．根据以上材料，解答下列问题：(1)按上述方法因式分解：①22428x y y x --+；②323927m m m --+；(2)已知a ，b ，c 为ABC 的三边，且2222b ab c ac +=+，试判断ABC 的形状并说明理由．【答案】(1)①()()()222y x x --+；②()2(3)3m m -+；(2)ABC 是等腰三角形，理由见解析；【分析】（1）①本题考查因式分解，根据例题分组提取公因式，再结合公式法因式分解即可得到答案；②本题考查因式分解，根据例题分组提取公因式，再结合公式法因式分解即可得到答案；（2）本题考查因式分解的应用，将2222b ab c ac +=+因式分解即可得到积等于0，即可得到答案；【详解】（1）解：①原式()()22424y x x =---()()()()22222y x x x x =-+--+()()()222y x x =--+；②原式()()2393m m m =---()()239m m =--()2(3)3m m =-+；（2）解：ABC 是等腰三角形，理由如下，2222b ab c ac +=+ ，22220b c ab ac ∴-+-=，()()()20b c b c a b c -++-=，()()20a b c b c ++-=，∵a ，b ，c 为ABC 的三边，0a ∴>，0b >，0c >，20a b c ∴++≠，0∴-=b c ，即b c =，ABC ∴ 是等腰三角形【变式1】（2024八年级下·全国·专题练习）因式分解：2221a ab b -+-．【答案】()()11a b a b -+--【分析】本题主要考查了因式分解，解题的关键是熟练掌握完全平方公式和平方差公式，先根据完全平方公式进行因式分解，然后再用平方差公式进行因式分解．【详解】解：2221a ab b -+-()21=--a b ()()11a b a b =-+--【变式2】（23-24八年级上·四川眉山·期中）因式分解(1)224x y -；(2)2291839x xy y x y -++-．【答案】(1)()()22x y x y +-(2)()()363x y x y -++【分析】本题考查了因式分解：（1）运用平方差公式进行因式分解，即可作答．（2）先分组分解，再进行提公因式，即可作答．【详解】（1）解：224x y -()()22x y x y =+-（2）解：2291839x xy y x y-++-222693939x xy y x y xy y =++--++()()()233333x y x y y x y=+-+++()()3333x y y x y =+-++()()363x y x y =-++【变式3】（23-24八年级上·四川眉山·期中）因式分解：(1)2321025xy y x y -++；(2)3223a a b ab b +--．【答案】(1)2(5)y x y -(2)2()()a b a b +-【分析】本题考查的因式分解，熟知分组分解法与提取公因式法、公式法分解因式是解题的关键．（1）先提取公因式，再利用完全平方公式进行因式分解即可；（2）利用分组分解法因式分解即可．【详解】（1）解：2321025xy y x y-++22(1025)y xy y x =-++2(5)y x y =-；（2）解：3223a ab ab b +--3223()()a ab ab b =+-+22()()a ab b a b =+-+22()()a b a b =+-2()()a b a b =+-3.拆项后用公式法【例题13】（22-23八年级上·贵州黔西·期末）我们已经学过将一个多项式分解因式的方法有提公因式法、运用公式法和十字相乘法，其实分解因式的方法还有分组分解法、拆项法，等等．①分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法叫作分组分解法.例如：()()()2222222424()222x xy y x xy y x y x y x y -+-=-+-=--=-+--．②拆项法，将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法叫作拆项法.例如：()()()()222223214(1)2121213x x x x x x x x x +-=++-=+-=+-++=-+(1)仿照以上方法，按照要求分解因式：①（分组分解法）22441x x y +-+；②（拆项法）268x x -+；(2)已知：a ，b ，c 为ABC 的三条边，222446170a b c a b c ++---+=，求ABC 的周长．【答案】(1)()()2121x y x y ++-+①；()()42x x --②(2)ABC 的周长为7【分析】本题主要考查公式法因式分解：（1）①将22441x x y +-+组成为()22441x x y ++-分解即可．②将268x x -+拆项为()2691x x -+-分解即可；（2）分组拆项配成完全平方式的和形式()()()2226944440a b a b c c ++--+++=-，利用非负性计算即可．【详解】（1）22441x x y +-+①()22441x x y =++-2221()x y =+-()()2121x y x y =++-+268x x -+②2691x x =-+-2(3)1x =--()()3131x x =---+()()42x x =--（2）222446170a b c a b c ++---+=Q ，()()()2224444690a a b b c c ∴-++-++-+=．222(2)(2)(3)0a b c ∴-+-+-=．2a ∴=，2b =，3c =．2237a b c ∴++=++=．ABC ∴ 的周长为7【变式1】（23-24八年级上·山东济宁·期末）观察下面因式分解的过程：432233x x x x +++-4322333x x x x x =+-++-()()222131x x x x x =+-++-()()2231x x x =++-上面因式分解过程的第一步把22x 拆成了223x x -+，这种因式分解的方法称为拆项法．请用上面的方法完成下列题目：(1)22268a b a b -++-；(2)42231x x -+．【答案】(1)()()24a b a b +--+(2)()()221515x x x x +++-【分析】本题考查因式分解，理解题中拆项法是解答的关键．（1）将8-拆成19-，然后重新组合，利用完全平方公式和平方差公式分解因式即可；（2）将223x -拆成22225x x -，然后重新组合，利用完全平方公式和平方差公式分解因式即可．【详解】（1）解：22268a b a b -++-222619a b a b =-+++-()()222169a a b b =++--+()()2213a b =+--()()1313a b a b =++-+-+()()24a b a b =+--+；（2）解：42231x x -+2242251x x x =+-+()4222125x x x =++-()()22215x x =+-()()221515x x x x =+++-【变式2】（23-24八年级上·河北张家口·期末）我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法等等．①分组分解法：例如：()()()()2222222424222x xy y x xy y x y x y x y -+-=-+-=--=---+．②拆项法：例如：()()()()()22222321412121213x x x x x x x x x +-=++-=+-=+-++=-+．仿照以上方法分解因式：(1)22441x x y +-+；(2)2223x xy y +-．(3)解决问题：已知a 、b 、c 、为ABC 的三边长，2254210a b ab b +--+=，且ABC 为等腰三角形，求ABC的周长．【答案】(1)()()2121x y x y +++-(2)()()3x y x y +-(3)ABC 的周长是5【分析】本题考查因式分解及其应用，分组分解法，拆项法因式等知识，掌握完全平方公式和平方差公式是解题的关键．（1）运用分别分组分解法将2441x x ++看出一组，再用平方差公式因式分解即可；（2）运用拆项法将23y -拆成224y y -，再运用（1）的方法因式分解即可；（3）将2254210a b ab b +--+=化成平方和等于0的形式，从而求出a 、b ，再运用等腰三角形的定义分类讨论即可得解．【详解】（1）解：22441x x y +-+22441x x y =++-()2221x y =+-()()2121x y x y =+++-；（2）2223x xy y +-22224x xy y y =++-()224x y y =+-()()22x y y x y y =+++-()()3x y x y =+-；（3）2254210a b ab b +--+= ，22244210a ab b b b --∴+++=，22(2)(1)0a b b ∴-+-=，20a b ∴-=，10b -=，2a ∴=，1b =，ABC 是等腰三角形，c 2∴=或1c =(不符合三角形三边关系，舍去)ABC ∴ 的周长2215=++=【变式3】（2023八年级上·全国·专题练习）利用拆项法，解决下列问题：(1)分解因式：265x x -+；(2)分解因式：2245a ab b +-．【答案】(1)()()15x x --；(2)()()5a b a b +-．【分析】（1）将5拆解成94-，再根据完全平方公式得()2232x --，然后利用平方差公式进一步分解；（2）将25b -拆解成2249b b -，再根据完全平方公式得()2229a b b +-，然后利用平方差公式进一步分解．【详解】（1）原式2694x x =-+-，()2232x =--，()()3232x x =---+，()()15x x =--；（2）原式222449a ab b b =++-，()2229a b b =+-，()()2323b a b a b b =+++-，()()5a b a b =+-．【点睛】此题考查了因式分解的应用，解题时要注意在拆项变形的过程中不要改变式子的值4.换元法【例题14】（23-24八年级上·福建福州·期中）阅读下列材料：在因式分解中，把多项式中某些部分看作一个整体，用一个新的字母代替（即换元），不仅可以简化要分解的多项式的结构，而且能使式子的特点更加明显，便于观察如何进行因式分解，我们把这种因式分解的方法称为“换元法”．下面是小胡同学用换元法对多项式()()2221234x x x x ---++进行因式分解的过程．解：设22x x y -=，原式()()134y y =-++（第一步）221y y =++（第二步）()21y =+（第三步）()2221x x =-+（第四步）请根据上述材料回答下列问题：(1)小胡同学的解法中，第二步到第三步运用了因式分解的______；A ．提取公因式法B ．平方差公式法C ．完全平方公式法(2)老师说，小胡同学因式分解的结果不彻底，请你写出该因式分解的最后结果；(3)请你用换元法对多项式()()22661881x x x x ++++进行因式分解．【答案】(1)C(2)()41x -(3)()43x +【分析】（1）根据利用完全平方公式()2222a ab b a b ±+=±分解因式即可得；（2）括号里面可以再次用完全平方公式进行因式分解；（3）设26y x x =+，利用换元法和完全平方公式分解因式即可得．【详解】（1）解：()22211y y y ++=+，则第二步到第三步运用了因式分解的完全平方公式法，故选：C ．（2）解：原式()2221x x =-+()221x ⎡=⎤⎣⎦-()41x =-，故答案为：()41x -；（3）解：设26y x x =+，()()22661881x x x x ++++则原式()1881y y =++21881y y =++()29y =+()2269x x =++()223x ⎡⎤=+⎣⎦()43x =+．【点睛】本题考查了因式分解——换元法和完全平方公式法，熟练掌握利用公式法分解因式是解题的关键【变式1】（23-24八年级上·全国·课时练习）因式分解：(1)（添项）44x +；(2)（拆项）3234x x -+；(3)（换元）()()2221224x y x y +-+-+．【答案】(1)()()222222x x x x ++-+(2)()()221x x -+(3)()()2268x y x y +-+-【分析】根据分解因式的方法求解即可．【详解】（1）原式()2222222222x x x =+⨯+-⨯()()22222x x =+-()()222222x x x x =++-+．（2）方法一：原式32224x x x =--+()()32224x x x =---()()()2222x x x x =--+-()()222x x x =---()()()221x x x =--+()()221x x =-+．方法二：原式32244x x x =+-+()()()21411x x x x =+--+()()2144x x x =+-+()()212x x =+-．（3）设2x y a +=，则原式()()21224a a =--+21448a a =-+()()68a a =--()()2268x y x y =+-+-．【点睛】此题考查了因式分解的方法，解题的关键是熟练掌握因式分解的方法．因式分解的方法有：提公因式法，平方差公式法，完全平方公式法，十字相乘法等【变式2】（22-23七年级下·江苏镇江·阶段练习）【积累经验】小明在分解因式22(21)(23)4x x x x +-+++时，提出了如下的思路：小明：我发现223x x ++比221x x +-多4，若设221x x m +-=，那么223x x ++就可以表示为m +4.则222(21)(23)4(4)444x x x x m m m m +-+++=++=++=2(2)m +．因为221x x m +-=，所以原式=224(21)(1)x x x ++=+．在解决数学问题时，可以将某个式子看作一个整体，用一个字母去代替它，从而使问题得到简化，这样的方法叫做换元法．换元法的关键是设元．上述问题中，不仅能设221x x m +-=，也可以将22x x +或223x x ++或……设为n ．请你任选一种设元的方法，分解因式；【灵活应用】（1）()()12320222342023A =+++⋯++++⋯+，()()1232023232022B =+++⋯+++⋯+，探究A 与B 的数量关系，并说明理由；(2)如图，一户人家有一块长方形土地ABCD ，30AB =，24AD =，其内部有一条宽度为a 的L 型种植区域①，其余部分(长方形)AEFG 为种植区域②，测量区域②的面积为340；阿凡提有两块正方形的土地AGHI 与AJKE 跟这户人家的种植区域②相邻，正方形土地的边长分别为AG 与AE ．这户人家对阿凡提的两块地垂涎已久，提出要将自己的土地与阿凡提交换，阿凡提有没有损失呢？请你运用所学的数学知识进行解释．【答案】积累经验：4(1)x +；灵活运用：(1)2023A B -=；(2)没有损失，见解析【分析】积累经验：可以设22x x n +=，将原式中的22x x +全部用n 表示，然后分解因式即可；灵活运用：(1)设2342022a +++⋯+=，把A 、B 各部分用a 表示，然后作差，即可求出A 、B 的关系；(2)设AE x =，AG y =，用含a 的式子分别表示出AE 、AG ，然后根据()2222x y x y xy +=+-表示出交换之后土地的面积，在进行比较即可求解．【详解】积累经验：解：设22x x n +=，则2211x x n +-=-，那么2233x x n ++=+.原式()()134n n =-++=2234n n +-+=2(1)n +因为22x x n +=，所以原式224(21)(1)x x x =++=+灵活运用：解：（1）设2342022a +++⋯+=()()21202320242023A a a a a =++=++()2120232024B a a a a=++=+所以2023A B -=.（2）由题意得，设30AE a x =-=，24AG a y =-=，.则6x y =-，340.xy =所以()222236680716x y x y xy +=+=+=-，即阿凡提的两块土地面积之和为716，而四边形ABCD 的面积为3024720716⨯=>.所以交换土地对阿凡提来说没有损失．【点睛】本题考查了因式分解—换元法、完全平方公式的应用，看懂和理解题例是求解的关键【变式3】（22-23八年级下·山东济南·期末）阅读以下材料，并按要求完成相应任务：在因式分解中，把多项式中某些部分看作一个整体，用一个新的字母代替（即换元），不仅可以简化要分解的多项式结构，而且能使式子的特点更加明显，便于观察如何进行因式分解，我们把这种因式分解的方法称为“换元法”．下面是小涵同学用换元法对多项式()()2241479x x x x +++++进行因式分解的过程．解：设24x x y +=，则原式()()179y y =+++（第一步）2816y y =++（第二步）()24y =+（第三步）()2244x x =++（第四步）请根据上述材料回答下列问题：(1)小涵同学的解法中，第二步到第三步运用了因式分解的A ．提取公因式法B ．平方差公式法C ．完全平方公式法(2)老师说，小涵同学因式分解的结果不彻底，请你写出该因式分解的最后结果：；请你用换元法对多项式()()229639614x x x x -+-+-进行因式分解．【答案】(1)C(2)()42x +，()431x -【分析】（1）根据利用完全平方公式()2222a ab b a b ±+=±分解因式即可得；（2）利用完全平方公式分解因式即可得出最后结果；设296x x y -=，利用换元法和完全平方公式分解因式即可得．【详解】（1）解：()228164y y y ++=+，则第二步到第三步运用了因式分解的完全平方公式法，故选：C ．（2）解：设24x x y +=，则原式()()179y y =+++2816y y =++()24y =+()2244x x =++()222x ⎡⎤=+⎣⎦()42x =+，故答案为：()42x +．对多项式()()229639614x x x x -+-+-，设296x x y -=，则原式()()314y y =+-+2234y y =+-+221y y =++()21y =+()22961x x -=+()2231x ⎡⎤=-⎣⎦()431x =-．【点睛】本题考查了因式分解——换元法和完全平方公式法，熟练掌握利用公式法分解因式是解题的关键3种思想1：整体思想【例题15】（22-23八年级下·贵州六盘水·期末）先阅读下列材料，再解答下列问题：材料：因式分解：()()221x y x y ++++．解：将“()x y +”看成整体，令()x y A +=，则原式()22211A A A =++=+．再将“A ”还原，得原式()21x y =++．上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请解答下列问题：因式分解：()()44a b a b ++-+．【答案】()22a b +-【分析】本题主要考查整体思想的方法进行因式分解，掌握乘法公式，整体思想的方法是解题的关键．根据材料提示，令a b M +=，再结合完全平方公式进行因式分解即可求解．【详解】解：()()44a b a b ++-+令a b M +=，∴原式()44M M =-+。

讲 义(a+b)(a-b)=a 2-b 2 (a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2 归纳小结公式的变式，准确灵活运用公式：① 位置变化，(x +y )(-y +x )=x 2-y 2② 符号变化，(-x +y )(-x -y )=(-x )2-y 2= x 2-y 2 ③ 指数变化，(x 2+y 2)(x 2-y 2)=x 4-y 4④ 系数变化，(2a +b )(2a -b )=4a 2-b 2 ⑤ 换式变化，[xy +(z +m )][xy -(z +m )]=(xy )2-(z +m )2=x 2y 2-(z +m )(z +m )=x 2y 2-(z 2+zm +zm +m 2)=x 2y 2-z 2-2zm -m 2⑥ 连用公式变化，(x +y )(x -y )(x 2+y 2)=(x 2-y 2)(x 2+y 2)=x 4-y 4 1、计算下列各式：(1)[(x ＋y)3]4 ； (2) (a 4n )n －1 ；(3) (－a 3)2＋(－a 2)3－(－a 2)·(－a)4 ；(4) x 3·x 2·x 4＋(－x 4)2＋4(－x 2)4例. 计算：()()53532222x y x y +-(二)、连用:连续使用同一公式或连用两个以上公式解题。

例. 计算：()()()()111124-+++a a a a例. 计算：()()57857822a b c a b c +---+例.（1）已知a b ab -==45，，求a b 22+的值。

(2) 已知2=+b a ，1=ab ，求22b a +的值。

(3) 已知8=+b a ，2=ab ，求2)(b a -的值。

(4) 已知x-y=2，y-z=2，x+z=14。

求x 2-z 2的值。

例：计算19992-2000×1998 例.已知13x x-=，求441x x +的值。

可编辑修改精选全文完整版Array第十四章、整式乘除与因式分解14.1 整式的乘法（1）(－3x)2(x＋1)(x＋3)＋4x(x－1)(x2＋x＋1)，其中x=－1；解：原式=9x2(x2＋3x＋x＋3)＋4x(x3＋x2＋x－x2－x－1)=9x2(x2＋4x＋3)＋4x(x3－1)=9x4＋36x3＋27x2＋4x4－4x=13x4＋36x3＋27x2－4x当x=－1时原式=13×(－1)4＋36×(－1)3＋27×(－1)2－4×(－1)=13－36＋27＋4=8（2）y n(y n＋3y－2)－3(3y n＋1－4y n)，其中y=－2，n=2．解：原式=y2n＋3y n＋1－2y n－9y n＋1＋12y n=y2n－6y n＋1＋10y n当y=－2，n=2时原式=(－2)2×2－6×(－2)2＋1＋10×(－2)2=16＋48＋40=10415、已知不论x、y为何值时(x＋my)(x＋ny)=x2＋2xy－8y2恒成立.求(m＋n)mn的值.解：x2＋nxy＋mxy＋mny2＝x2＋2xy－8y2x2＋(m＋n)xy＋mny2＝x2＋2xy－8y2∴m＋n＝2，mn＝－8∴(m＋n)mn＝2×(－8)＝－166、已知31=+a a，则221a a +＝（ B ） A ．5 B ．7 C ．9 D ．117、如果x 2＋kx ＋81是一个完全平方式，则k 的值是（ D ）A ．9B ．－9C ．±9D ．±188、下列算式中不正确的有（ C ）①(3x 3－5)(3x 3＋5)＝9x 9－25②(a ＋b ＋c ＋d)(a ＋b －c －d)＝(a ＋b)2－(c ＋d)2③22)31(5032493150-=⨯ ④2(2a －b)2·(4a ＋2b)2＝(4a －2b)2(4a －2b)2＝(16a 2－4b 2)2A ．0个B ．1个C ．2个D ．3个9、代数式2)(2y x +与代数式2)(2y x -的差是（ A ） A ．xy B ．2xy C ．2xy D ．0 10、已知m 2＋n 2－6m ＋10n ＋34＝0，则m ＋n 的值是（ A ）A ．－2B ．2C ．8D ．－8二、解答题11、计算下列各题：(1)(2a ＋3b)(4a ＋5b)(2a －3b)(5b －4a)(2)(x ＋y)(x －y)＋(y －z)(y ＋z)＋(z －x)(z ＋x);(3)(3m 2＋5)(－3m 2＋5)－m 2(7m ＋8)(7m －8)－(8m)2(1) 解：原式＝(2a ＋3b)(2a －3b)(4a ＋5b)(5b －4a)＝(4a 2－9b 2)(25b 2－16a 2)＝100a 2b 2－64a 4－225b 4＋144a 2b 2＝－64a 4＋244a 2b 2－225b 4(2) 解：原式＝x 2－y 2＋y 2－z 2＋z 2－x 2＝0(3) 解：原式＝25－9m 4－m 2(49m 2－64)－64m 2＝－58m 4＋2512、化简求值：(1)4x(x 2－2x －1)＋x(2x ＋5)(5－2x)，其中x ＝－1(2)(8x 2＋4x ＋1)(8x 2＋4x －1)，其中x ＝21 (3)(3x ＋2y)(3x －2y)－(3x ＋2y)2＋(3x －2y)2，其中x ＝31，y ＝－21 (1) 解：原式＝4x 3－8x 2－4x ＋x(25－4x 2)＝4x 3－8x 2－4x ＋25x －4x 3＝－8x 2＋21x当x ＝－1时原式＝－8×(－1)2＋21×(－1)＝－8－21＝－29(2) 解：原式＝(8x 2＋4x)2－1当x ＝时，原式＝[8×()2＋4×]2－1＝(2＋2)2－1＝15(3) 解：原式＝9x 2－4y 2－9x 2－12xy －4y 2＋9x 2－12xy ＋4y 2＝9x 2－24xy －4y 2当x ＝，y ＝－时原式＝9×()2－24××(－)－4×(－)2＝1＋4－1＝413、解下列方程：(1)(3x)2－(2x ＋1)2＝5(x ＋2)(x －2)解：9x 2－4x 2－4x －1＝5x 2－205x 2－4x －1＝5x 2－204x ＝19∴x ＝419(2)6x ＋7(2x ＋3)(2x －3)－28(x －21)(x ＋21)＝4解：6x ＋28x 2－63－28x 2＋7＝46x －56＝46x ＝60∴x ＝1014、解不等式：(1－3x)2＋(2x －1)2>13(x －1)(x ＋1)解：1－6x ＋9x 2＋4x 2－4x ＋1>13x 2－1313x 2－10x ＋2>13x 2－13－10x>－15∴x<2315、若n 满足(n －2004)2＋(2005－n)2＝1，求(2005－n)(n －2004)的值.解：(n －2004)2＋2·(n －2004)·(2005－n)＋(2005－n)2＝1＋2(n －2004)(2005－n)(n －2004＋2005－n)2＝1＋2(n －2004)(2005－n)1＝1＋2(2005－n)(n －2004)∴(2005－n)(n －2004)＝014.3 因式分解一、选择题1、下列各式，从左到右的变形是因式分解的为（ B ）A ．x 2－9＋5x ＝（x ＋3）（x －3）＋5xB ．x 2－4x ＋4＝（x －2）2C ．（x －2）（x －3）＝x 2－5x ＋6D ．（x －5）（x ＋2）＝（x ＋2）（x －5）2、把多项式x 2－mx －35分解因式为(x －5)(x ＋7)，则m 的值是（ B）A ．2B ．－2C ．12D ．－123、分解因式：x 2－2xy ＋y 2＋x －y 的结果是（ A ）A ．（x －y ）（x －y ＋1）B ．（x －y ）（x －y －1）C ．（x ＋y ）（x －y ＋1）D ．（x ＋y ）（x －y －1）4、若9x 2－12xy ＋m 是一个完全平方公式，那么m 的值是（ B ）。

一、单选题1、已知x+y＝﹣5，xy＝3，则x2+y2＝（）A. 19B. ﹣19C. 25D. ﹣25参考答案: A【思路分析】本题考查的是完全平方公式。

仔细读题，获取题中已知条件，结合完全平方公式的相关知识，即可解答此题。

【解题过程】解：x2+y2＝（x+y）2﹣2xy＝（﹣5）2﹣2×3＝25﹣6＝19。

故选A。

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -2、下列方程没有实数根的是（）A. x2+4x=10B. 3x2+8x-3=0C. x2-2x+3=0D. （x-2）（x-3）=12参考答案: C【思路分析】本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根【解题过程】解：A、方程变形为：x2+4x-10=0，△=42-4×1×（-10）=56＞0，所以方程有两个不相等的实数根，故A选项不符合题意；B、△=82-4×3×（-3）=100＞0，所以方程有两个不相等的实数根，故B选项不符合题意；C、△=（-2）2-4×1×3=-8＜0，所以方程没有实数根，故C选项符合题意；D、方程变形为：x2-5x-6=0，△=52-4×1×（-6）=49＞0，所以方程有两个不相等的实数根，故D选项不符合题意．故选：C。

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -3、如果多项式p＝a2+2b2+2a+4b+2008，则p的最小值是（）A. 2005B. 2006C. 2007D. 2008参考答案: A【思路分析】把p重新拆分组合，凑成完全平方式的形式，然后判断其最小值．【解题过程】解：p＝a2+2b2+2a+4b+2008，＝（a2+2a+1）+（2b2+4b+2）+2005，＝（a+1）2+2（b+1）2+2005，当（a+1）2＝0，（b+1）2＝0时，p有最小值，最小值最小为2005．故选：A．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -4、如果x=3m+1，y=2+9m，那么用x的代数式表示y为（）A. y=2xB. y=x2C. y=(x−1)2+2D. y=x2+1参考答案: C【思路分析】根据移项，可得3m的形式，根据幂的运算，把3m代入，可得答案.【解题过程】解x=3m+1：，y=2+9m，3m=x−1，y=（x−1）2+2，故选：C.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -5、把x³-9x+8因式分解，正确的结果是（）A. (x-1)(x+3)B. (x-1)(x2-x+8)C. (x-1)(x2+x-8)D. (x+1)(x2-x+8)参考答案: C【思路分析】本考点的主要内容是拆项法分解因式，在对某些多项式分解因式时，需要恢复那些被合并或相互抵消的项，即把多项式中的某一项拆成两项或多项，使多项式能用分组分解法进行因式分解。

七年级数学下册第12章乘法公式与因式分解重点解析考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、下面的计算正确的是（ ）A ．（a +b ）2＝a 2+b 2B ．（a 3）2＝a 6C ．a 2+a 3＝2a 5D ．（3a ）2＝6a 22、若代数式24x x k ++是一个完全平方式，那么k 的值是（ ）A ．1B ．2C ．3D ．43、下列各式因式分解正确的是（ ）A ．()2211x x +=+B ．()()311x x x x x -=+-C ．()()21343x x x x ++=++D ．()22121x x x x ++=++4、已知29x kx ++是完全平方式，则k 的值为（ ）A ．－6B ．±3C ．±6D ．35、下列等式从左到右的变形，属于因式分解的是（ ）A ．（x +1）（x ﹣1）=x 2﹣1B ．x 2﹣8x +16=（x ﹣4）2C ．x 2﹣2x +1=x （x ﹣1）+1D ．x 2﹣4y 2=（x +4y ）（x ﹣4y ） 6、下列运算正确的是（ ）A ．2a +3b ＝5abB ．2（2a ﹣b ）＝4a ﹣bC ．（a +b ）（a ﹣b ）＝a 2﹣b 2D ．（a -b ）2＝a 2-b 27、下列多项式不能．．因式分解的是（ ） A ．22x y + B ．22x y - C ．222x xy y ++ D ．222x xy y -+8、下列计算正确的是（ ）A ．(a +b )2＝a 2+b 2B ．(﹣a +b )(﹣b +a )＝a 2﹣b 2C ．(﹣a +b )2＝a 2+2ab +b 2D ．(﹣a ﹣1)2＝a 2+2a +19、下列因式分解正确的是（ ）A ．2ab 2﹣4ab ＝2a （b 2﹣2b ）B ．a 2＋b 2＝（a ＋b ）（a ﹣b ）C ．x 2＋2xy ﹣4y 2＝（x ﹣y ）2D ．﹣my 2＋4my ﹣4m ＝﹣m （2﹣y ）210、下列多项式能用“两数和（差）的平方公式”进行因式分解的是（ ）A ．22x y +B ．21x x -+C ．221x x +-D ．2441x x -+第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图1，将边长为x 的大正方形剪去一个边长为1的小正方形（阴影部分），并将剩余部分沿虚线剪开，得到两个长方形，再将这两个长方形拼成图2所示长方形．这两个图能解释一个等式是______．2、分解因式：3a a -=__．3、分解因式：3x +9＝_________．4、因式分解：a （a ﹣b ）﹣b （b ﹣a ）＝_____________．5、分解因式：()()23a y z b z y ---=________．三、解答题（5小题，每小题10分，共计50分）1、（1）计算：()23542a a a a ⎡⋅⎢⎥⎣⎦+÷⎤； （2）分解因式：24x -．2、（1）已知：x +2y +1＝3，求3x ×9y ×3的值；（2）下边是小聪计算（3a ﹣b ）（3a +b ）﹣a （4a ﹣1）的解题过程．请你判断是否正确？若有错误，请写出正确的解题过程．（3a ﹣b ）（3a +b ）﹣a （4a ﹣1）＝3a 2﹣b 2﹣4a 2﹣a＝﹣a 2﹣b 2﹣a ．3、已知3m n +=，2mn =．(1)当2a =时，求()nm n m a a a ⋅-的值； (2)求2()(4)(4)m n m n -+--的值．4、【教材呈现】以下是华师大版教材第50页16题：【自主解答】解：根据两个数和或差的平方公式，分两种情况：当M为含字母x的一次单项式时，原式可以表示为关于x的二项式的平方，∵4x2+M+1＝（2x）2+M+12＝（2x±1）2，∴M＝±2×2x•1＝±4x；当M为含字母x的四次单项式时，原式可以表示为关于x2的二项式的平方，∵4x2+M+1＝M+2×2x2•1+12＝（2x2+1）2，∴M＝4x4．综上述，M为4x或﹣4x或4x4．【解后反思】①上述解答过程得到等式：4x2±4x+1＝（2x+1）2；4x4+4x2+1＝（2x2+1）2观察等式左边多项式的系数发现：（±4）2＝4×4×1．②结合多项式的因式分解又如：16x2+24x+9＝（4x+3）2；9x2﹣12x+4＝（3x﹣2）2，发现这两个多项式的系数规律：242＝4×16×9，（﹣12）2＝4×9×4．③一般地：若关于x的二次三项式ax2+bx+c（a、b、c是常数）是某个含x的二项式的平方，则其系数a、b、c一定存在某种关系．(1)请你写出系数a、b、c之间存在的这种关系式：；【解决问题】(2)若多项式9y2+4加上一个含字母y的单项式N，就能表示为一个含y的二项式的平方，请直接写出所有满足条件的单项式N；(3)若关于x的多项式x2﹣2（m﹣3）x+（m2+3m）是一个含x的多项式的平方，求实数m的值．5、问题提出：计算：1＋3＋3（1＋3）＋3（1＋3）2＋3（1＋3）3＋3（1＋3）4＋3（1＋3）5＋3（1＋3）6问题探究：为便于研究发现规律，我们可以将问题“一般化”，即将算式中特殊的数字3用具有一般性的字母a代替，原算式化为：1＋a＋a（1＋a）＋a（1＋a）2＋a（1＋a）3＋a（1＋a）4＋a（1＋a）5＋a（1＋a）6然后我们再从最简单的情形入手，从中发现规律，找到解决问题的方法：(1)仿照②，写出将1＋a＋a（1＋a）＋a（1＋a）2＋a（1＋a）3进行因式分解的过程；(2)填空：1＋a＋a（1＋a）＋a（1＋a）2＋a（1＋a）3＋a（1＋a）4＝；发现规律：1＋a＋a（1＋a）＋a（1＋a）2＋…＋a（1＋a）n＝；问题解决：计算：1＋3＋3（1＋3）＋3（1＋3）2＋3（1＋3）3＋3（1＋3）4＋3（1＋3）5＋3（1＋3）6＝（结果用乘方表示）．-参考答案-一、单选题1、B【解析】【分析】直接利用完全平方公式以及积的乘方运算法则、幂的乘方运算法则、合并同类项法则分别判断得出答案．【详解】A、（a+b）2＝a2+2ab+b2，故此选项错误；B、（a3）2＝a6，故此选项正确；C、a2+a3，无法合并，故此选项错误；D、（3a）2＝9a2，故此选项错误；故选：B．【点睛】此题主要考查了完全平方公式以及积的乘方运算、幂的乘方运算、合并同类项，正确掌握相关运算法则是解题关键．2、D【解析】【分析】根据完全平方公式即可求出答案．【详解】 解：代数式24x x k ++是一个完全平方式，则2224222x x k x x ++=+⨯⨯+∴4k =故选D【点睛】本题考查完全平方公式，解题的关键是熟练运用完全平方公式．3、B【解析】【分析】根据因式分解的定义（把一个多项式化为几个最简整式的乘积的形式，这种变形叫做把这个因式分解）及完全平方公式依次进行判断即可得．【详解】解：A 、不能进行因式分解，错误；B 、选项正确，是因式分解；C 、选项是整式的乘法，不是因式分解，不符合题意；D 、()22211x x x ++=+，选项因式分解错误；故选：B ．【点睛】题目主要考查因式分解的定义及方法，深刻理解因式分解的定义是解题关键．4、C【解析】【分析】根据完全平方式的特点：两数的平方和，加上或减去这两个数的乘积的2倍，即可确定k 的值．【详解】∵22293x kx x kx ++=++∴236k =±⨯=±故选：C【点睛】本题考查了完全平方式，掌握完全平方式的特点是关键．注意不要忽略了k 的负值．5、B【解析】【分析】根据因式分解的定义“把一个多项式化成几个整式的积的形式叫做因式分解”进行解答即可得．【详解】解：A 、2(1)(1)1x x x +-=-，不是因式分解，选项说法错误，不符合题意；B 、22816(4)x x x -+=-，是因式分解，选项说法正确，符合题意；C 、221(1)1x x x x -+=-+，不是因式分解，选项说法错误，不符合题意；D 、左、右不相等，选项说法错误，不符合题意；故选B ．【点睛】本题考查了因式分解，解题的关键是熟记因式分解的定义．6、C【解析】【分析】A 、利用合并同类项的法则即可判定；B 、利用去括号的法则即可判定；C 、利用平方差公式即可判定；D 、利用完全平方公式判定．【详解】解：A 、2a ，3b 不是同类项，235a b ab ∴+≠，故选项错误，不符合题意；B 、2(2)42a b a b -=-，故选项错误，不符合题意；C 、22()()a b a b a b +-=-，正确，符合题意；D 、222()2a b a b ab -=+-，故选项错误，不符合题意；故选：C ．【点睛】此题主要考查了整式的运算法则，解题的关键是掌握平方差公式和完全平方公式的公式结构．7、A【解析】【分析】根据平方差公式、完全平方公式分解因式即可．【详解】解：A 、22x y +不能因式分解，符合题意； B 、22x y -=()()x y x y +-，能因式分解，不符合题意；C 、222x xy y ++=2()x y +，能因式分解，不符合题意；D 、222x xy y -+ =2()x y -，能因式分解，不符合题意，故选：A ．【点睛】本题考查因式分解、完全平方公式、平方差公式，熟记公式，掌握因式分解的结构特征是解答的关键．8、D【解析】【分析】根据完全平方公式判断即可，完全平方公式：（a ±b ）2＝a 2±2ab ＋b 2．【详解】解：A ．（a ＋b ）2＝a 2＋2ab ＋b 2，故本选项不合题意；B ．（−a ＋b ）（−b ＋a ）＝−（a −b ）（a −b ）＝−a 2＋2ab −b 2，故本选项不合题意；C ．（−a ＋b ）2＝a 2−2ab ＋b 2，故本选项不合题意；D ．（−a −1）2＝a 2＋2a ＋1，故本选项符合题意；故选：D ．【点睛】本题考查了完全平方公式，掌握完全平方公式的结构特点是解答本题的关键．9、D【解析】【分析】将各式计算得到结果，即可作出判断．【详解】解：A. 2ab 2﹣4ab ＝2ab （b ﹣2），分解不完整，故错误；B ．a 2＋b 2不能分解因式，而（a ＋b ）（a ﹣b ）＝a2−b2，故错误；C ．x 2＋2xy ﹣4y 2不能分解因式，而（x −y ）2＝x 2−2xy ＋y 2，故错误；D ．﹣my 2＋4my ﹣4m ＝﹣m （2﹣y ）2，故正确．故选：D ．【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．10、D【解析】【分析】根据完全平方公式的结构特征，对每一个选项所给算式进行变形后，再判断其是否能用完全平方公式进行因式分解．【详解】A 、22x y +不满足完全平方公式的结构特征，不符合题意；B 、21x x -+中间项应为-2x ，故不符合完全平方公式，不符合题意；C 、221x x +-中间项应为2x -，最后一项应为1+，故不符合完全平方公式，不符合题意；D 、()()22224412212121x x x x x -+=-⨯⨯+=-，符合完全平方公式，符合题意；【点睛】本题考查完全平方公式，因式分解，能够熟悉完全平方公式的结构特征，以及利用完全平方公式进行因式分解是解决此类题型的关键．二、填空题1、()()2111x x x -=+-【解析】【分析】根据图形可以用代数式表示出图1和图2的面积，由此得出等量关系即可．【详解】解：由图可知，图1的面积为：x 2−12，图2的面积为：（x ＋1）（x −1），所以x 2−1＝（x ＋1）（x −1）．故答案为：x 2−1＝（x ＋1）（x −1）．【点睛】本题考查平方差公式的几何背景，解答本题的关键是明确题意，列出相应的代数式．2、(1)(1)a a a +-【解析】【分析】确定公因式是 a ，然后提取公因式后再利用平方差公式分解即可．【详解】2(1)a a =-，(1)(1)a a a =+-．故答案为：(1)(1)a a a +-．【点睛】本题考查因式分解，掌握方法是关键．3、3（x +3）【解析】【分析】直接找出公因式3，进而提取公因式分解因式即可．【详解】解：3x +9＝3（x +3）．故答案为：3（x +3）．【点睛】本题考查了因式分解，掌握因式分解的方法是解题的关键．4、（a ﹣b ）（a +b ）【解析】【分析】原式变形后，提取公因式即可．【详解】解：原式()()()()a a b b a b a b a b =-+-=+-．故答案为：()()a b a b +-．【点睛】本题考查了因式分解-提公因式法，熟练掌握提取公因式的方法是解本题的关键．5、（2a ＋3b ）（y ﹣z ）【解析】【分析】先调整符号，然后提公因式即可．【详解】解：()()23a y z b z y ---，=()()23a y z b y z -+-，=()()23a b y z +-．故答案为()()23a b y z +-．【点睛】本题考查提公因式法因式分解，掌握因式分解的方法是解题关键．三、解答题1、（1）62a ；（2）()()22x x +-【解析】【分析】（1）先算乘方，再算乘除，最后化简；（2）利用平方差公式进行求解．【详解】.解：（1）原式82826822a a a a a a ⎡⎤=+÷=÷=⎣⎦.（2）原式()()22x x =+-.【点睛】本题考查了多项式的因式分解、整式混合运算等知识点，掌握整式的乘方、乘除法则及混合运算是解决（1）的关键，掌握因式分解的平方差公式是解决本题（2）的关键．2、（1）27 ；（2）不正确，答案见解析 ．【解析】【分析】（1）将393x y ⨯⨯中的9y 化为23y ，再根据同底数幂的乘法“同底数幂相乘，底数不变，指数相加”即可得；（2）根据多项式与多项式相乘的法则“多项式与多项式相乘，先用多项式的每一项乘另一个多项式的每一项，再把所得的积相加”和单项式与多项式相乘的法则“单项式与多项式相乘，就是用单项式去乘另一个多项式的每一项，再把所得的积相加”进行解答即可得．【详解】解：（1）3x ×9y ×3＝3x ×32y ×3＝3x +2y +1＝33＝27；（2）不正确，解：原式＝9a 2﹣b 2﹣4a 2+a＝5a 2﹣b 2+a ．【点睛】本题考查了整式的乘法，解题的关键是掌握同底数幂的乘法，多项式与多项式相乘的法则和单项式与多项式相乘的法则．3、 (1)4(2)7【解析】【分析】（1）根据同底数幂的乘法“同底数幂相乘，底数不变，指数相加”得32()m n m n a a a a a -=-，再将2a =代入即可得；（2）由题意得()21m n -=，再根据多项式与多项式相乘的法则“多项式与多项式相乘，先用多项式的每一项乘另一个多项式的每一项，再把所得的积相加”将(4)(4)m n --进行计算，即可得(1)解：∵3m n +=，2mn =，∴()32m n m n n n m m a a a a a a a +=⋅--=-， ∵2a =，∴原式=3222844-=-=；(2)解：∵3m n +=，2mn =，∴()()22243421m n m n mn -=+-=-⨯=， ∴2()(4)(4)m n m n -+--=()1416mn m n +-++=124316+-⨯+=7．【点睛】本题考查了整式的乘法，解题的关键是掌握同底数幂的乘法和多项式与多项式相乘的法则．4、 (1)24b ac =(2)12y ±或48116y (3)1m =【解析】【分析】（1）观察例题找到多项式的系数的规律求解即可；（2）根据例题，根据两个数和或差的平方公式，分两种情况：当N 为含字母y 的一次单项式时，原式可以表示为关于y 的二项式的平方，当N 为含字母y 的四次单项式时，原式可以表示为关于y 2的二项式的平方，进而求解即可；（3）根据题意，由多项式的系数的规律列出方程求解即可．(1)根据例题发现多项式的系数规律可知24b ac =故答案为：24b ac =(2)当N 为含字母y 的一次单项式时，原式可以表示为关于y 的二项式的平方，∵9y 2+4+N ＝（3y ）2+N +4＝（3 y ±2）2，∴N ＝±2×32y ⨯＝12y ±；当N 为含字母y 的四次单项式时，原式可以表示为关于y 2的二项式的平方，∵9y 2+4+N ＝2292224y N +⨯⨯+229=24y ⎛⎫+ ⎪⎝⎭，48116y M ∴= 综上述，N 为12y 或12-y 或48116y ． (3)x 2﹣2（m ﹣3）x +（m 2+3m ）根据24b ac =可得()()222343m m m --=+⎡⎤⎣⎦ 解得1m =【点睛】本题考查了完全平方式，根据完全平方式变形求解，掌握完全平方公式是解题的关键．5、 (1)（1+a ）4(2)（1+a ）5；（1+a ）n +1；47【解析】【分析】（1）用提取公因式（1+a ）一步步分解因式，最后化为积的形式；（2）通过前面（1）的例子，用提取公因式法（1+a ）一步步分解因式，最后化为积的形式， 发现规律：是根据（1）（2）的结果写出结论；问题解决：通过前面的例子，用提取公因式法（1+3）一步步分解因式，最后化为积的形式．(1)解：1+a +a （1+a ）+a （1+a ）2+a （1+a ）3＝（1+a ）（1+a ）+a （1+a ）2+a （1+a ）3＝（1+a ）2（1+a ）+a （1+a ）3＝（1+a）3+a（1+a）3＝（1+a）3（1+a）＝（1+a）4；(2)解：1+a+a（1+a）+a（1+a）2+a（1+a）3+a（1+a）4＝（1+a）（1+a）+a（1+a）2+a（1+a）3+a（1+a）4＝（1+a）2（1+a）+a（1+a）3+a（1+a）4＝（1+a）3+a（1+a）3+a（1+a）4＝（1+a）3（1+a）+a（1+a）4＝（1+a）4+a（1+a）4＝（1+a）4（1+a）＝（1+a）5；故答案为：（1+a）5；发现规律：1+a+a（1+a）+a（1+a）2+…+a（1+a）n＝（1+a）n+1；故答案为：（1+a）n+1；问题解决：1+3+3（1+3）+3（1+3）2+3（1+3）3+3（1+3）4+3（1+3）5+3（1+3）6＝（1+3）（1+3）+3（1+3）2+3（1+3）3+3（1+3）4+3（1+3）5+3（1+3）6＝（1+3）2（1+3）+3（1+3）3+3（1+3）4+3（1+3）5+3（1+3）6＝（1+3）3（1+3）+3（1+3）4+3（1+3）5+3（1+3）6＝（1+3）4（1+3）+3（1+3）5+3（1+3）6＝（1+3）5（1+3）+3（1+3）6＝（1+3）6（1+3）＝（1+3）7＝47．故答案为：47．【点睛】此题考查了数字类运算的规律，提公因式法分解因式，整式的混合运算法则，正确掌握提公因式法分解因式是解题的关键，同时还考查了类比解题的思想．。

2017-2018学年八年级数学上册乘法公式填空题练习1、填空根据题意填空：x2﹣6x+（______）=（x﹣______）2；2、计算：20152﹣2016×2014= ．（a﹣b）（﹣b﹣a）= ．3、计算：（﹣5a+4b）2=________．44、若（3x+2y）2=（3x﹣2y）2+A，则代数式A为______．9、若ax2+24x+b=（mx﹣3）2，则a= ，b= ，m= ．10、若代数式x2-(a-2)x+9是一个完全平方式，则a=________．11、（3x+1）（3x﹣1）（9x2+1）= ．12、已知a+b=2,ab=-10则a2+b2= 13、已知a+b=3，ab=2，则(a-b)2= ．14、已知a+b=4，ab=1，则a2+b2的值是______．15、化简：(-2x-3)(-2x+3)=_____________616、已知x+y=- 5,xy=6,则x2+y2= .17、一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是（用a、b的代数式表示）．18、已知x+=2，则= ． 19、若a2+b2=5，ab=2，则a+b的值为．20、若a2+b2=6，ab=2，则a+b=______．21、若，则的值为 .22、若x2﹣mx+4是完全平方式，则m= ．23、若4a4﹣ka2b+25b2是一个完全平方式，则k= ．24、若x2+mx+16是完全平方式，则m的值是．25、如果多项式x2+8x+k是一个完全平方式，则k的值是．26、代数式是完全平方式，m=__________27、如果x2+（k﹣1）x+4是一个完全平方式，则常数k= ．28、x2﹣kx+9是一个完全平方式，则k的值是 29、若x2+2（m﹣3）x+16是完全平方式，则m= ．30、若4x2+2（k﹣3）x+9是完全平方式，则k=______．31、若x2+（2m﹣1）x+4是一个完全平方式，则m= ．32、如果x2+8x+m2是一个完全平方式，那么m的值是．33、若x2﹣2mx+16是完全平方式，则m=_______．34、如果25x2﹣（k﹣1）xy+9y2是一个完全平方式，那么K的值为___________．35、计算：(x－y)(x2＋xy＋y2)=__ 36、若，则﹦.37、已知a＋b=7，ab=13，那么a2－ab＋b2=_______． 38、化简：6（7+1）（72+1）（74+1）（78+1）+1= ．39、已知x2＋y2＋10=2x＋6y，则x21＋21y的值为__40、写出计算结果：（x﹣1）（x+1）= （x﹣1）（x2+x+1）=（x﹣1）（x3+x2+x+1）=根据以上等式进行猜想，可得：（x﹣1）（x n+x n﹣1+…+x+1）= ．2017-2018学年八年级数学上册因式分解填空题练习1、分解因式：a2+3a= ．2a2﹣6a= 4x2﹣4= ．﹣3x3y+27xy= ．a3﹣4a2+4a= ． x2y﹣y=3a2+6a+3= ． x3y﹣2x2y+xy= ．x3－2x=______________.3x2﹣x= ．2、将x n+3－x n+1因式分解，结果是3、分解因式：2a3—2a=_ ．mn2+6mn+9m= ．a3﹣2a2+a= ． a3b-2a2b+ab= 。

八年级数学整式的乘法与因式分解常考题型例题单选题1、计算：a2⋅a5=（）A．a B．7a C．a10D．a7答案：D解析：利用同底数幂的乘法法则运算．解：a2⋅a5=a2+5=a7，故选：D．小提示：本题考查了同底数幂的乘法运算，解题的关键是掌握同底数幂相乘，底数不变，指数相加．2、已知a、b、c是△ABC的三条边，且满足a2+bc=b2+ac，则△ABC是( )A．锐角三角形B．钝角三角形C．等腰三角形D．等边三角形答案：C解析：已知等式左边分解因式后，利用两数相乘积为0两因式中至少有一个为0得到a=b，即可确定出三角形形状．已知等式变形得：（a+b）（a-b）-c（a-b）=0，即（a-b）（a+b-c）=0，∵a+b-c≠0，∴a-b=0，即a=b，则△ABC为等腰三角形．此题考查了因式分解的应用，熟练掌握因式分解的方法是解本题的关键．3、下列式子中，正确的有( )①m3∙m5=m15；②（a3）4=a7；③（-a2）3=-（a3）2；④（3x2）2=6x6A．0个B．1个C．2个D．3个答案：B解析：根据同底数幂的乘法、幂的乘方、积的乘方逐一分析判断即可．解：①m3⋅m5=m8，故该项错误；②(a3)4=a12，故该项错误；③(−a2)3=−a6，−(a3)2=−a6，故该项正确；④(3x2)2=9x4，故该项不正确；综上所述，正确的只有③，故选：B．小提示：本题考查同底数幂的乘法、幂的乘方、积的乘方，掌握运算法则是解题的关键．4、若多项式x2+mx−8因式分解的结果为(x+4)(x−2)，则常数m的值为( )A．−2B．2C．−6D．6答案：B解析：根据多项式的乘法法则计算出(x+4)(x−2)的结果，然后与x2+mx−8比较即可．解：∵(x+4)(x−2)=x2+2x-8=x2+mx−8，∴m=2．此题考查了十字相乘法和整式的乘法，熟练掌握因式分解和整式的乘法是互为逆运算是解本题的关键．5、下列计算中错误的是（）A．4a5b3c2÷(−2a2bc)2=ab B．(−24a2b3)÷(−3a2b)⋅2a=16ab2C．4x2y⋅(−12y)÷4x2y2=−12D．(a10÷a4)÷(a8÷a5)÷12a6=2a3答案：D解析：根据整式乘除的运算法则分别计算出各选项的结果，即可得解．A选项4a5b3c2÷(−2a2bc)2=ab，正确，故不符合题意；B选项(−24a2b3)÷(−3a2b)⋅2a=16ab2，正确，故不符合题意；C选项4x2y⋅(−12y)÷4x2y2=−12，正确，故不符合题意；D选项(a10÷a4)÷(a8÷a5)÷12a6=2a-3，不正确，故符合题意．故选：D．小提示：本题主要考查了整式的乘除运算，属于基础题，需要有一定的运算求解能力，熟练掌握运算法则是解题的关键．6、若x2﹣4x+1＝0，则代数式﹣2x2+8x+1的值为（）A．0B．1C．2D．3答案：D解析：给条件的代数式求值问题，先观察代数式，把条件变成需要的形式，然后整体代入，计算即可．∵x2﹣4x+1＝0，∴x2﹣4x＝﹣1，∴﹣2x2+8x＝2，∴原式＝2+1＝3．故选择：D．小提示：本题考查代数式的值问题，关键是把条件变性后，整体代入，如果次数较高的代数式一般把条件高次的求出，然后用降次方法进行化简，在整体代入求值．7、要使多项式(x+p)(x−q)不含x的一次项，则p与q的关系是（）A．相等B．互为相反数C．互为倒数D．乘积为−1答案：A解析：计算乘积得到多项式，因为不含x的一次项，所以一次项的系数等于0，由此得到p-q=0，所以p与q相等. 解：(x+p)(x−q)=x2+(p−q)x−pq∵乘积的多项式不含x的一次项∴p-q=0∴p=q故选择A.小提示：此题考查整式乘法的运用，注意不含的项即是该项的系数等于0.8、如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式：①（2a+b）（m+n）；②a（m+n）+b（m+n）；③m（2a+b）+n（2a+b）；④2am+2an+bm+bn，你认为其中正确的有（）A．①②B．②③C．①③④D．①②③④答案：C解析：根据长方形面积公式判断各式是否正确即可．①（2a+b）（m+n），正确；②a（m+n）+b（m+n），错误；③m（2a+b）+n（2a+b），正确；④2am+2an+bm+bn，正确故正确的有①③④所以答案是：C．小提示：本题考查了长方形的面积问题，掌握长方形的面积公式是解题的关键．填空题9、计算m4⋅(−m)2⋅m=______．答案：m7解析：根据同底数幂乘法法则计算即可得答案．m4⋅(−m)2⋅m=m4⋅m2⋅m=m4+2+1=m7．小提示：本题考查同底数幂乘法，同底数幂相乘，底数不变，指数相加；熟练掌握运算法则是解题关键．10、计算：(2+3x)(−2+3x)=__________．答案：9x2−4##−4+9x2解析：原式利用平方差公式化简即可．(2+3x)(−2+3x)=9x2−4．所以答案是：9x2−4．小提示：本题考查了平方差公式，熟练掌握平方差公式是解本题的关键．11、已知a=7−3b，则代数式a2+6ab+9b2的值为_________．答案：49解析：先将条件的式子转换成a+3b=7，再平方即可求出代数式的值．解：∵a=7−3b，∴a+3b=7，∴a2+6ab+9b2=(a+3b)2=72=49，所以答案是：49．小提示：本题考查完全平方公式的简单应用，关键在于通过已知条件进行转换．12、计算：(2+3x)(−2+3x)=__________．答案：9x2−4##−4+9x2解析：原式利用平方差公式化简即可．(2+3x)(−2+3x)=9x2−4．所以答案是：9x2−4．小提示：本题考查了平方差公式，熟练掌握平方差公式是解本题的关键．13、计算(−0.125)2019×82020=_______.答案：-8解析：先把原式改写成(−0.125)2019×82019×8，然后逆用积的乘方法则计算即可.原式=(−0.125)2019×82019×8=(−0.125×8)2019×8=-8.故答案为-8.小提示：本题考查了积的乘方运算逆运算，熟练掌握积的乘方法则是解答本题的关键.积的乘方等于各因数乘方的积，即(ab)m=a m b m（m为正整数）.解答题14、第一步：阅读材料，掌握知识．要把多项式am+an+bm+bn分解因式，可以先把它的前两项分成组，并提出a，把它的后两项分成组，并提出b，从而得am+an+bm+bn=a(m+n)+b(m+n)．这时，由于a(m+n)+b(m+n)中又有公因式(m+n)，于是可提公因式(m+n)，从而得到(m+n)(a+b)，因此有am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b)．这种因式分解的方法叫做分组分解法，如果把一个多项式各个项分组并提出公因式后，它们的另一个因式正好相同，那么这个多项式就可以利用分组分解法来因式分解．第二步：理解知识，尝试填空：（1）ab−ac+bc−b2=(ab−ac)+(bc−b2)=a(b−c)−b(b−c)=_____________第三步：应用知识，因式分解：（2）x2-(p+q)x+pq；（3）x2y−4y−2x2+8．第四步：提炼思想，拓展应用（4）已知三角形的三边长分别是a，b，c，且满足a2+2b2+c2=2b（a+c），试判断这个三角形的形状，并说明理由．答案：（1）(a−b)(b−c)（2）(x−p)(x−q)（3）(y−2)(x+2)(x−2)（4）等边三角形，理由见详解．解析：（1）如果把一个多项式各项分组并提出公因式后，它们的另一个因式刚好相同，那么这个多项式即可利用分组分解法来因式分解，据此即可求解；（2）先展开（p＋q）x，再利用分组分解法来因式分解，据此即可求解；（3）直接利用分组分解法来因式分解即可求解；（4）根据所给等式，先移项，再利用完全平方公式和等边三角形的判定求证即可．解：（1）ab−ac+bc−b2=(ab−ac)+(bc−b2)=a(b−c)−b(b−c)=(a−b)(b−c)（2）x2−(p+q)x+pq=x2−px−qx+pq=x(x−p)−q(x−p)=(x−p)(x−q)（3）x2y−4y−2x2+8=y(x2−4)−2(x2−4)=(y−2)(x2−4)=(y−2)(x+2)(x−2)（4）等边三角形，理由如下：∵a2+2b2+c2=2b(a+c)∴a2+2b2+c2=2ab+2bc∴a2−2ab+b2+b2−2bc+c2=0∴(a−b)2+(b−c)2=0∴a−b=0,b−c=0即a=b=c∴这个三角形是等边三角形．小提示：本题考查因式分解—提公因式法，因式分解—分组分解法，完全平方公式，等边三角形的判定，解题的关键是读懂材料并熟知因式分解的方法．x，试求A+B．15、已知A=2x，B是多项式，计算B+A时，某同学把B+A误写成B÷A，结果得x2+12答案：A+B=2x3+x2+2x解析：x）·2x=2x3+x2，再计算A+B的值即可.根据题意可得B=（x2+12x）·2x=2x3+x2，根据题意可得：B=（x2+12∴A+B=2x+2x3+x2.小提示：本题考查了整式的乘法，熟练掌握运算法则是解本题的关键．。

八年级数学整式的乘法与因式分解专题练习（解析版）一、八年级数学整式的乘法与因式分解选择题压轴题（难）1．已知a=2012x+2011，b=2012x+2012，c=2012x+2013，那么a2+b2+c2—ab－bc－ca的值等于( )A．0 B．1 C．2 D．3【答案】D【解析】【分析】首先把a2+b2+c2﹣ab﹣bc﹣ac两两结合为a2﹣ab+b2﹣bc+c2﹣ac，利用提取公因式法因式分解，再把a、b、c代入求值即可．【详解】a2+b2+c2﹣ab﹣bc﹣ac＝a2﹣ab+b2﹣bc+c2﹣ac＝a（a﹣b）+b（b﹣c）+c（c﹣a）当a＝2012x+2011，b＝2012x+2012，c＝2012x+2013时，a-b=－1，b－c=－1，c－a=2，原式＝（2012x+2011）×（﹣1）+（2012x+2012）×（﹣1）+（2012x+2013）×2＝﹣2012x﹣2011﹣2012x﹣2012+2012x×2+2013×2＝3．故选D．【点睛】本题利用因式分解求代数式求值，注意代数之中字母之间的联系，正确运用因式分解，巧妙解答题目．2．因式分解x2+mx﹣12＝（x+p）（x+q），其中m、p、q都为整数，则这样的m的最大值是（）A．1 B．4 C．11 D．12【答案】C【解析】分析：根据整式的乘法和因式分解的逆运算关系，按多项式乘以多项式法则把式子变形，然后根据p、q的关系判断即可.详解：∵(x＋p)(x＋q)= x2＋（p+q）x+pq= x2＋mx－12∴p+q=m，pq=-12.∴pq=1×（-12）=（-1）×12=（-2）×6=2×（-6）=（-3）×4=3×（-4）=-12∴m=-11或11或4或-4或1或-1.∴m的最大值为11.故选C.点睛：此题主要考查了整式乘法和因式分解的逆运算的关系，关键是根据整式的乘法还原因式分解的关系式，注意分类讨论的作用.3．如果多项式29x kx -+能用公式法分解因式，那么k 的值是( )A ．3B ．6C ．3±D ．6±【答案】D【解析】由于可以利用公式法分解因式，所以它是一个完全平方式222a ab b ±+，所以236k =±⨯=±.故选D.4．若代数式x 2＋ax ＋64是一个完全平方式，则a 的值是（ ）A ．－16B ．16C ．8D ．±16【答案】D【解析】试题分析：根据完全平方式的意义，首平方，尾平方，中间加减积的2倍，可知a=±2×8=16.故选：D点睛：此题主要考查了完全平方式的意义，解题关键是明确公式的特点，即：完全平方式分两种，一种是完全平方和公式，就是两个整式的和括号外的平方。

苏教版七年级下数学乘法公式及提公因式法因式分解练习题（可编辑）苏教版七年级下数学乘法公式及提公因式法因式分解练习题周庄中学七年级数学周周练(考查范围:乘法公式及提公因式法因式分解)一、选择题1、下列各式中正确的是( )A、(―a3)2 ―a6B、(2b―5)2 4b2―25C、(a―b)(b―a) ―(a―b)2D、a2+2ab+(―b)2 (a―b)22、下列计算正确的是( )A、(x+y)2 x2+y2B、(x―y)2 x2―2xy,y2C、(x+2y)(x―2y) x2,2y2D、(,x+y)2 x2―2xy+y23、有若干张面积分别为纸片，阳阳从中抽取了1张面积为a2的正方形纸片，4张面积为ab的长方形纸片，若他想拼成一个大正方形，则还需要抽取面积为b2的正方形纸片( ) A、2张 B、4张 C、6张D、8张4、如果关于x的二次三项式x2―mx+16是一个完全平方式，那么m的值是( )A、8或―8B、8C、―8D、无法确定5、小明计算一个二项式的平方时，得到正确结果a2―10ab+?，但最后一项不慎被污染了，这一项应是( )A、5bB、5b2C、25b2D、100b26、化简:(a+1)2―(a―1)2 ( ) A、2 B、4 C、4aD、2a2+27、为了美化城市，经统一规划，将一正方形草坪的南北方向增加3m，东西方向缩短3m，则改造后的长方形草坪面积与原来正方形草坪面积相比( )A、增加6m2B、增加9m2C、减少9m2D、保持不变8、下面式子从左边到右边的变形是因式分解的是( )A、x2―x―2 x(x―1)―2B、(a+b)(a―b) a2―b2C、x2―4 (x+2)(x―2)D、x―1 x(1―)9、下列各式从左到右，是因式分解的是( )A、(y―1)(y+1) y2―1B、x2y+xy2―1 xy(x+y)―1C、(x―2)(x―3) (3―x)(2―x)D、x2―4x+4 (x―2)210、将m2(a―2)+m(2―a)分解因式，正确的是( )A、(a―2)(m2―m)B、m(a―2)(m+1)C、m(a―2)(m―1)D、m(2―a)(m―1)二、填空题11、因式分解:(x+y)2―3(x+y) _________ (12、分解因式:(x+3)2―(x+3) _________ (13、9x3y2+12x2y2―6xy3中各项的公因式是 _________ (14、若x+5，x―3都是多项式x2―kx―15的因式，则k __(15、若a+b 5，ab 3，则a2+b2 _________ (16、若(x―1)2 2，则代数式x2―2x+5的值为 _________ (17、小强同学在下面的4个计算中:?(a―b)2 a2―b2，?(―2a3)24a6，?a3+a2 a5，?―(a―1) ―a+1(做正确的题目是 _________ (填题目序号)(18、已知x+y 1，则x2+xy+y2 _________ (19、如图，甲类纸片是边长为2的正方形，乙类纸片是边长为1的正方形，丙类纸片是长、宽边长分别是2和1的长方形(现有甲类纸片1张，乙类纸片4张，则应至少取丙类纸片 _________ 张才能用它们拼成一个新的正方形(20、我们知道，可以利用直观的几何图形形象的表示有些代数恒等式(例如:(2a+b)(a+b) 2a2+3ab+b2，可以用图1的面积关系来表示(还有许多代数恒等式也可以用几何图形面积来表示其正确性((1)根据图2写出一个代数恒等式 _________ ;(2)已知等式:(a+2b)2 a2+4ab+4b2，请你在图3的方框内画出一个相应的几何图形，利用这个图形的面积关系来表示等式的正确性(21、若x2―6x+m是完全平方式，则m ___ (22、如果a2+ma+9是一个完全平方式，那么m _________ (23、观察下列各式:(x―1)(x+1) x2―1 (x―1)(x2+x+1) x3―1 (x―1)(x3+x2+x+1) x4―1，根据前面各式的规律可得(x―1)(xn+xn―1+…+x+1) _________ (其中n为正整数)(24、如果(2a+2b+1)(2a+2b―1) 63，那么a+b的值为 _________ (25、如图，边长为a的正方形中有一个边长为b的小正方形，若将图1的阴影部分拼成一个长方形，如图2，比较图1和图2的阴影部分的面积，你能得到的公式是 _________ (三、解答题26、如图，有一位狡猾的地主，把一块边长为a的正方形的土地，租给李老汉种植，他对李老汉说:“我把你这块地的一边减少4m，另一边增加4m，继续租给你，你也没有吃亏，你看如何”(李老汉一听，觉得自己好像没有吃亏，就答应了(同学们，你们觉得李老汉有没有吃亏,请说明理由(27、计算;(1)(x―3y)(―x，3y); (2)4x2―(―2x―3)2((3)(2x―3y)2―(y+3x)(3x―y); (4)(x+y)(x2+y2)(x―y)(x4―y4);(5)(a―2b+3)(a+2b―3); (6)[(x―y)2+(x+y)2](x2―y2);28、观察下面各式规律:12+(1×2)2+22 (1×2+1)2;22+(2×3)2+32(2×3+1)2;32+(3×4)2+42 (3×4+1)2…写出第n行的式子，并证明你的结论(29、因式分解: (3x+2y+1)2―(3x+2y―1)(3x+2y+1)本文档由华涛教学资料室为您倾心整理，欢迎下载～19题。

整式的乘法与因式分解的练习题初中数学整式的乘除与因式分解一、选择题：1、下列运算中，正确的是()A.某2·某3=某6B.(ab)3=a3b3C.3a+2a=5a2D.（某³）²=某52、下列从左边到右边的变形，是因式分解的是（）23322（A）(3某)(3某)9某（B）mn(mn)(mmnn)（C）(y1)(y3)(3y)(y1)2（D）4yz2yzz2y(2zyz)z3、下列各式是完全平方式的是（）某2某A、4B、14某2C、a2abb2D、某22某14、下列多项式中能用平方差公式分解因式的是（）22（A）a(b)（B）5m220mn22（C）某y（D）某295、如(某+m)与(某+3)的乘积中不含某的一次项，则m的值为（）A.–3B.3C.0D.16、一个正方形的边长增加了2cm，面积相应增加了32cm2，则这个正方形的边长为（A、6cmB、5cmC、8cmD、7cm1、下列分解因式正确的是()A、2n2nmn2n(nm1)B、ab22ab3bb(ab2a3)C、某(某y)y(某y)(某y)2D、a2a2a(a1)22、下列各式中,能用平方差公式进行因式分解的是()A、某2－某y2B、－1＋y2C、2y2＋2D、某3－y33、下列各式能用完全平方公式分解因式的是()A、4某2＋1B、4某2－4某－1C、某2＋某y＋y2D、某2－4某＋44、若9某2k某y4y2是一个完全平方式，则k的值为()A、6B、±6C、12D、±125、若分解因式某2m某15(某3)(某n)则m的值为()A、－5B、5C、－2D、2二、填空题：a54a237、=_______。

在实数范围内分解因式a268、当某___________时，某4等于__________；220021.520039、3___________210、若3某=2，3y=3，则3某－y等于2211、若9某m某y16y是一个完全平方式，那么m的值是__________。

、选择题（每题3分，共36分）下列各式中可以运用平方差公式计算的是 A. （-a+4c ） （a-4c ） B. （x-2y ） （2x+y ）1 1'（—x+y ）27、从边长为a 的正方形中去掉一个边长为b 的小正方形，如图，然后将剩余部分剪后拼成一 个矩形，上述操作所能验证的等式是 ()A. a 2 b 2 (a b)(a b)B. (a b)2 a 2 2ab b 2C. (a b)2 a 2 2ab b 2 2D . a ab a(a b)8、下列分解因式正确的是( )A. x 3 x x(x 2 1)B.m m 6 (m 3)(m2)C. (a 4)(a 4) a 216D. 2 2x y (x y)(x y)9、若a 为整数，则a 2 a 疋能被（ ）整除 A . 2 B . 3C . 4D . 510、无论x,y 取何值，x 2+y 2-2x+12y+40的值都是（）A 、正数B 、负数C 、零D 、非负数11、 下列判断两角相等的叙述中，错误的是（）A 、对顶角相等B 、两条直线被第三条直线所截，内错角相等C 、两直线平行，同位角相等D 、•••/仁/2，, / 2=Z 3AZ 仁/ 3 12、 下列计算中，正确的是（）2?5 1022?3-122,2A 、2 2 =2B 、a+a=aC 、a a = aD 、（a+b ） =a +b七年级数学乘法公式与因式分解、241、 C. (-3a-1 ) (1-3a) D. ( - — x-y 22、 3、 2若4x +12xy+m 是一个完全平方式，则 B..3y 2 C . 9y 2 D(-a-b )的结果是2 2B . -a -bC A..y 2 计算(a+b ) A 2、2A . a -b4、设（3m+2n A . 12mn5、若 x 2-kxy+9y A. 3 Bm 的值为 .36y 22.a -2ab+b -a (-2ab-b2 2=(3m-2n ) +P,则P 的值是 B . 24mn C . 6mn D2是一个完全平方式，则k 值为.6 C . ± 6 D . ± 812 248mn6、当n 是整数时，2n 1 2n 1是A 2的倍数 B、4的倍数 C 、6的倍数 D t*第T题團、8的倍数13.下列可以用平方差公式计算的是 ( )A 、(x — y) (x + y)B 、(x — y) (y — x)C 、(x — y)(— y + x)D 、(x — y)(— x + y) 14若(7/ 5y)( ) 49x 4 25?，括号内应填代数式 ()A 、7/ 5yB 、7/5yC 、7/5yD 、7x 2 5y15、下列式子由左到右的变形中，属于因式分解的是( )A 、(x 2y)2 x 2 4xy 4y 2B 、x 2 2y 4 (x 1)2 3C 、3x 2 2x 1 (3x 1)(x 1)D 、m(a b c) ma mb me二、填空(每小题3分，共24分)1 2 1 211、计算(- a+3b ) - (一 a-3b )= .3312、 分解因式：4 a 2 9b 2 = __________________ .13、 如果(2a + 2b + 1) (2a + 2b —1)=63，那么 a + b 的值为 _____________ .214、 多项式4x +1加上一个单项式后能成为一个整式的完全平方， ？请你写出符合条件的这个 单项式是 ___________ .15、 若 x y 5,xy 6 贝卩 x 2y xy 2 = ___________ ， 2x 2 2y 2 = __________ 。