第四章齿轮机构学时8知识要点：本章重点讲解，内容较多，包含齿轮传动类型、渐开线性质、直齿参数计算、根切现象、变位齿轮、轮系计算，了解斜齿轮、蜗杆传动§1概述齿轮传动是精密机械中应用最广泛的传动机构。
主要用途是：1）传递任意两轴间的运动和转矩。
2）变换运动的方式：转动与移动相互转换。
3）变速——实现低速的相互转换。
在机器中通常是用来实现减速，而在仪器仪表中，还常用于增速，以实现传动放大作用。
优点：传动比恒定，精度小；尺寸小，结构紧凑；效率高，寿命长。
缺点：制造和安装的精度要求高，费用比较昂贵。
§2齿廓啮合的基本定律齿轮传动是主动轮轮齿的齿廓，依次推动从动轮轮齿的齿廓实现的。
其基本要求是瞬时传动比应保持恒定。
否则，当主动轮以等角速转动时，从动轮的角速度将发生变化，产生惯性力，从而影响齿轮的强度；同时还引起振动，影响齿轮的传动精度。
如图8-2的一对相互啮合的齿轮，主动轮1以角速度ω1顺时针转动，从动轮2以角速度ω2逆时针回转。
齿廓C1、C2在任意点K接触，在此点的线速度分别为υK1、υK2。
υK2K1为两齿廓接触点间的相对速度。
过K点作两齿廓C1、C2的公法线NN，两齿廓连续接触传动，则υK1、υK2在NN上分速度相等，否则两齿廓将会压坏或分离，即1122111222K K K KKKCOS COSO KO Kυαυαυωυω==•=•所以12212211KKO KCOSiO KCOSωαωα==过O1、O2分别作公法线NN的垂线，得交点图8-1齿廓啮合基本定理N 1、N 2，则2222K O KCOS O N α=，O1K 1111K O KCOS O N α=。
而△O 1PN 1∽△O 2PN 2，最后可得 1222122111O N O Pi O N O Pωω===要使i 12为定值，则O 2P/O 1P 为常数。
而O 1O 2为定长，故P 点应为定点，即节点P 。
齿轮啮合基本定律：不论两齿轮在任何位置接触，过接触点（啮合点）的公法线必须与两齿轮的连心线交于一定点P 。
从理论上讲，用作共轭齿廓曲线很多，但从设计、制造、安装、互换性、使用上考虑，常用的有渐开线、摆线、修正摆线等。
目前，绝大多数用渐开线齿廓。
§3渐开线齿廓曲线一、渐开线的形成及其性质 （一）渐开线的形成如图8-3所示，当一直线NK上任一点K 的轨迹AK 的基圆，其半径用r b 表示；直线角θk 称为渐开线AK 段的展角。
（二）渐开线的性质1 N A NK=2圆的切点N 转动，故发生线上K K 点速度方向应沿渐开线在K 相垂由直，此可知，发生线NK 所以渐开线的法线必与基圆相切。
3）发生线与基圆的切点N 是渐开线上K 点的曲率中心，而线段NK 为其曲率半径。
渐开线在基圆上A 点处的曲率半径等于零。
4）渐开线的形状取决于基圆的大小。
如图8-4所示，基圆愈小，渐开线愈弯曲；基圆愈大，渐开线愈平直，齿条的齿廓就是这种直线齿廓。
5）因渐开线是从基圆开始向外展开，故基圆以内无渐开线。
二、渐开线方程式如图8-3所示，若以OA 为极坐标轴，则渐开线上任意点K 的坐标可由向径r k 和极角（展角）θk 来表示。
又当以此渐开线作为齿轮的齿廓并且与其共轭齿廓在K 点啮合时，则此齿廓在K 点所受正压力的方向（即齿廓曲线在该点的法线）与K 点速度方向线之间的夹角，称为渐开线在K 点的压力角，用αk 表示。
由ΔONK 可知： r k =r b /cos αk θk =tan αk -αk由上式可知，展角θk 是随压力角αk 的大小而变化的。
只要知道了渐开线上各点的压力角αk ，该点的展角θk 就可以用上式求出。
所以，称展角θk 为压力角αk 的渐开线函数，工程上常用inv αk 表示θk ，即θk =inv αk =tan αk -αk综上所述，可得渐开线的极坐标方程式为r k =r b /cos αk θk =inv αk =tan αk -αk不同压力角的渐开线函数可查表。
三、渐开线齿廓满足啮合基本定律的证明如图8-5，C 1、C 2为一对互相啮合齿轮渐开线齿廓，基圆半径分别为r b1、r b2。
当在任一点K 啮合时，过K 点作公法线N 1N 2，由渐开线的性质可知：此公法线必同时与两齿廓的基圆相切，即N 1N 2为两轮基圆的内公切线，并与连心线O 1O 2相交于P 点。
由于基圆的大小和位置是不变的，所以无论这两个齿轮在任何位置啮合，如K ‘点，则过K ’点作两齿廓的公法线，都将于N 1N 2重合，因两基圆只有一条内公切线。
说明N 1N 2是一条定直线，故与连心线O 1O 2的交点P 必为一定点，符合轮齿啮合基本定律，其瞬时传动比为一常数。
1222122111O N O P i O N O Pωω====常数。
以O 1、O 2为圆心，P 点为交点的两圆称为 节圆。
§4渐开线齿轮各部分的名称、符号和几何尺寸的计算一、 齿轮各部分名称和符号图8-6a 所示为直齿圆柱外齿轮的一部分，其各部分的名称和符号如下： 顶齿圆：过所有顶齿端的圆称为顶齿圆，半径用r a 表示，直径用d a 表示。
齿根圆：过所有齿槽底的圆称为齿根圆，半径用r f 表示，直径用d f 表示。
齿槽宽：相邻两齿间的空间称为齿槽，沿任意圆周所量得的齿槽的弧线长度称为该圆周上的齿槽宽，用e k表示。
齿厚：沿任意圆周所量得的轮齿的弧线长度称为该圆周上的齿厚，用s k表示。
齿距：沿任意圆周所量得的相邻两齿上对应点之间的弧长，称为该圆上的齿距用p k表示。
同一圆周内p k = s k + e k图8-2齿轮各部分名称和符号分度圆：为了作为计算齿轮各部分尺寸的基准，在齿顶圆与齿根圆之间规定一直径为d （半径为r）的圆，并把这个圆称为齿轮的分度园。
分度圆上的齿厚、齿槽宽和齿距分别用s、e和p表示，而且p=s+e。
标准齿轮s=e。
模数：分度圆直径显然与齿距p和齿数z有关。
且有d=z p/π令p/π=m，并把这个比值叫做模数，用m表示，单位为mm。
于是得 d=mz（分度圆直径）为便于计算、制造、检验和互换使用，模数已标准化（见表8-1）表8-1 标准模数系列2.选用模数时应优先采用第一系列，括号内的模数尽可能不用。
分度圆压力角：cosαk= r b/r k由上式可见，对于同一齿廓上，r k不同αk亦不同，即渐开线齿廓在不同的圆周上有不同的压力角。
通常所说的齿轮压力角是指分度圆上的压力角，用α表示，于是有cosα＝r b/r或r b＝rcosα将分度圆上的压力角规定为标准值，一般取α=20。
（或15。
）至此，可以给分度圆下一个完整的定义：分度圆就是齿轮上具有标准模数和标准压力角的圆。
齿顶高：轮齿在分度圆和齿顶圆之间的径向高度，用h a表示。
h a=h a*m齿根高：轮齿在分度圆和齿根圆之间的径向高度，用h f表示。
h f=（h a*+C*）m式中h a*为齿顶高系数；C*为顶隙系数。
当模数m≥1时，h a*=1，C*=0.25当模数m<1时，h a*=1，C*=0.35齿宽：轮齿在齿轮轴向的宽度，用b表示。
二、标准直齿圆柱齿轮几何尺寸的计算（见表8-2）（一）齿轮2 压力角 α020α=3 分度圆直径 d d 1=mz 1 d 2=mz 24 齿顶高 h a 正常齿：h a =m,短齿：h a =0.8m5 齿根高 h f 正常齿：h f =1.25m(m ≥1时)；短齿：h f =1.1m h f =1.35m(m <1时)6 全齿高 h 正常齿：h=2.25m(m ≥1时)；短齿：h=1.9m h=2.35m(m <1时)7 顶隙c正常齿：c=0.25m(m ≥1时)；短齿：c=0.3m c=0.35m(m <1时) 8 齿顶圆直径 d a d a1= d 1+2 h a =m(z 1+2h a *)d a2= d 2±2 h a =m(z 2±2h a *)①9 齿根圆直径 d f d f1= d 1-2 h f =m(z 1-2h a *-2c*)d f2= d 2±2 h f =m(z 2±2h a *±2c*)①10 基圆直径 d b d b1=d 1cos α d b2d 2os α 11 齿距 p p=πm12 齿厚 s 2ms π=13 齿间宽e2me π= 14 标准中心距 a 2121()1()22m z z a d d ±=±=① 15齿宽b一般取b=（6~12）m ，常取b=10m①上面符号用于外啮合齿轮，下面符号用于内啮合齿轮。
（二）齿条齿条可看成是齿数为无穷多的齿轮，基圆半径无穷大，渐开线齿廓变成直线齿廓。
主要特点：1） 由于齿廓是直线齿廓，所以齿廓上各点的法线是平行的。
2） 由于齿条作直线移动，齿廓上各点的速度大小和方向一致，故齿廓上各点的压力角相同，其大小等于齿廓的倾斜角α，即齿形角，标注值200或150。
3） 由于齿条上各齿同侧齿廓是平行的，所以不论在分度线上、齿顶线上或与其平行的其它直线上的齿距均相等，即 m p •=π。
齿条的基本尺寸可参照标准直齿圆柱齿轮几何尺寸的计算公式进行计算。
5渐开线直齿圆柱齿轮传动一、 啮合过程分析如图8-9所示。
设齿轮１为主动轮，齿轮２为从动轮。
当两轮的一对齿开始啮合时，必是主动轮的齿根推动从动轮的齿顶；因而开始啮合点是从动轮的齿顶与啮合线Ｎ1N 2的交点B 2； 同理，主动轮的齿顶与啮合线Ｎ1N 2的交点B 1为这对齿开始分离的点（即终止啮合点）。
线段B 1B 2为啮合点的实际轨迹，故称为实际啮合线。
当齿高增大时，实际啮合线B 1B 2向外延伸。
但因基圆以内没有渐开线，故实际啮合线不能超过极限点Ｎ1和N 2，线段Ｎ1N 2成为理论啮合线。
α’称为啮合角。
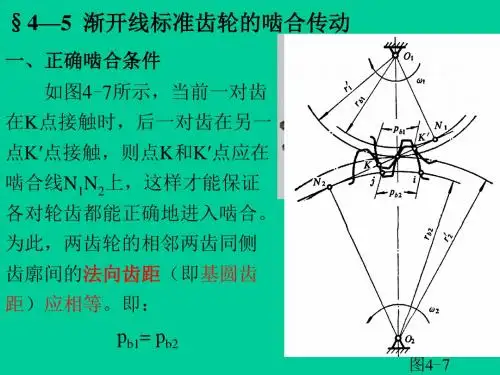
二、正确啮合条件前述一对渐开线齿廓沿啮合线啮合时能够保证瞬时传动比为常数， 212211b b r o p i r o p ωω===12 一对齿轮要实现正确啮合应具备条件？如图8-10所示，应使两齿轮的相邻两齿同侧齿廓在啮合线上的距离相等（''1122K K K K =），即两齿轮的法向齿距应相等。
而法向点距=基节，要使两轮正确啮合， 必须使 P b1= P b2，即： P 1cos α1= P 1cos α1=πm 1 cos α1P 2cos α2= P 2cos α2=πm 2cos α2 m 1 cos α1= m 2cos α2由于齿轮的模数和压力角已标准化，所以必须使m 1=m 2= m α1=α2=α 上式表明，渐开线齿轮正确啮合条件是两轮分度圆上的模数、压力角分别相等，这也是渐开线齿轮互换的条件。
