经典控制理论——第七章3..
- 格式:ppt
- 大小:469.50 KB
- 文档页数:50






控 制教学目的:明确控制职能的地位,了解控制类型与过程,掌握控制的方法。
教学要求:阐明控制基本原理与原则,明确控制的要求。
教学内容:控制概述、控制原则与程序。
教学重点:控制类型与程序教学课时:4第一节 控制内涵一.控制的含义一般意义的控制就是指引导一个动态系统达成预定状态。
例:空调器对室内温度的控制。
管理学中的控制是指按照既定目标和标准,对组织活动进行监督、测量,发现偏差并分析原因,采取措施使组织活动符合既定要求的过程。
二.控制的必要性控制是管理工作的最重要职能之一,是保证组织计划与实际运作动态相适应的管理职能。
管理控制的必要性是由以下原因决定的:(1)环境的变化(2)管理权力的分散(3)工作能力的差异三.控制原理控制理论中有下列基本原理:(1)任何系统都是由因果关系链接在一起的元素的集合。
元素之间的这种关系就叫耦合。
(2)为了控制耦合系统的运行,必须确定系统的控制标准Z 。
控制标准Z 的值是不断变化的某个参数S 的函数,即Z=f(S)。
(3)可以通过对系统的调节来纠正系统输出与标准值Z 之间的偏差,从而实现对系统的控制。
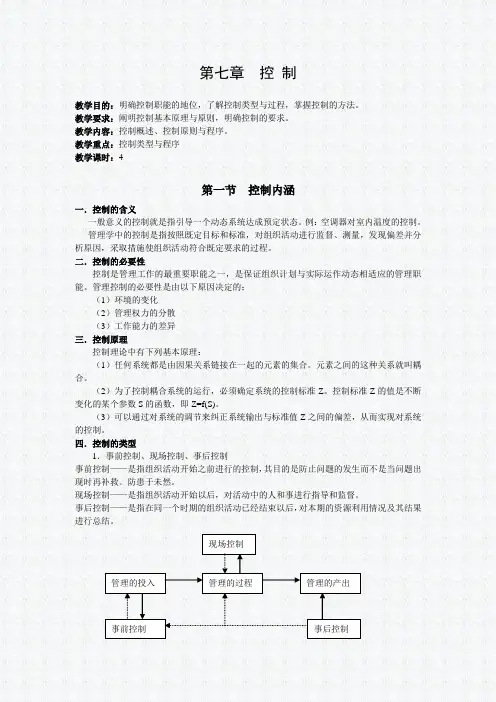
四.控制的类型1.事前控制、现场控制、事后控制事前控制——是指组织活动开始之前进行的控制,其目的是防止问题的发生而不是当问题出现时再补救。
防患于未然。
现场控制——是指组织活动开始以后,对活动中的人和事进行指导和监督。
事后控制——是指在同一个时期的组织活动已经结束以后,对本期的资源利用情况及其结果进行总结。
管理的投入 管理的过程 管理的产出 事前控制 现场控制 事后控制信息流向纠正措施2.集中控制与分散控制集中控制——对组织的重大项目与事务成立专门的控制机构,进行重点控制。
分散控制——对日常的一般性、常规性事务则由各部门、各岗位及全体员工自行控制。
3.战略控制与战术控制战略控制——即对战略规划的控制。
战术控制——即对经营战术活动的控制。
4.程序控制与跟踪控制程序控制——又叫计划控制,是一种将预先编制好的内容和步骤作为受控系统的输入,从而对整个管理过程予以控制的方式。


目录第一章自动控制系统的基本原理第一节控制系统的工作原理和基本要求第二节控制系统的基本类型第三节典型控制信号第四节控制理论的内容和方法第二章控制系统的数学模型第一节机械系统的数学模型第二节液压系统的数学模型第三节电气系统的数学模型第四节线性控制系统的卷积关系式第三章拉氏变换第一节傅氏变换第二节拉普拉斯变换第三节拉普拉斯变换的基本定理第四节拉普拉斯逆变换第四章传递函数第一节传递函数的概念与性质第二节线性控制系统的典型环节第三节系统框图及其运算第四节多变量系统的传递函数第五章时间响应分析第一节概述第二节单位脉冲输入的时间响应第三节单位阶跃输入的时间响应第四节高阶系统时间响应第六章频率响应分析第一节谐和输入系统的定态响应第二节频率特性极坐标图第三节频率特性的对数坐标图第四节由频率特性的实验曲线求系统传递函数第七章控制系统的稳定性第一节稳定性概念第二节劳斯判据第三节乃奎斯特判据第四节对数坐标图的稳定性判据第八章控制系统的偏差第一节控制系统的偏差概念第二节输入引起的定态偏差第三节输入引起的动态偏差第九章控制系统的设计和校正第一节综述第二节希望对数幅频特性曲线的绘制第三节校正方法与校正环节第四节 控制系统的增益调整 第五节 控制系统的串联校正 第六节 控制系统的局部反馈校正 第七节 控制系统的顺馈校正第一章 自动控制系统的基本原理定义:在没有人的直接参与下,利用控制器使控制对象的某一物理量准确地按照预期的规律运行。
第一节 控制系统的工作原理和基本要求 一、 控制系统举例与结构方框图例1. 一个人工控制的恒温箱,希望的炉水温度为100C °,利用 表示函数功能的方块、信号线,画出结构方块图。
图1人通过眼睛观察温度计来获得炉内实际温度,通过大脑分析、比较,利用手和锹上煤炭助燃。
煤炭给定的温度100 C手和锹眼睛实际的炉水温度比较图2例2. 图示为液面高度控制系统原理图。
试画出控制系统方块图 和相应的人工操纵的液面控制系统方块图。


典型信号(单位)阶跃函数(Step function ) 0,)(1≥t t室温调节系统和水位调节系统(单位)斜坡函数(Ramp function ) 速度 0,≥t t (单位)加速度函数(Acceleration function )抛物线0,212≥t t (单位)脉冲函数(Impulse function ) 0,)(=t t δ正弦函数(Simusoidal function )Asinut ,当输入作用具有周期性变化时。
============================================================================设线性定常系统由下述n 阶线性常微分方程描述:)()()()()()()()(1111011110t r b t r dt db t r dt d b t r dt d b tc a t c dt da t c dtd a t c dt d a m m m m m m n n n n n n ++⋅⋅⋅++=++⋅⋅⋅++------系统传递函数为:)()()()()(11101110s N s M a s a s a s a b s b s b s b s R s C s G n n n n m m m m =++⋅⋅⋅++++⋅⋅⋅++==----传递函数与微分方程之间有关系)()()(s R s C s G =如果将dtdS ⇔置换 微分方程传递函数⇔ ============================================================================传递函数的极点和零点对输出的影响)()()()()(11*jnj imi P S Z S K s N s M s G --==∏∏== i Z ),,2,1(m i ⋅⋅⋅= 为传递函数的零点j P ),,2,1(n j ⋅⋅⋅= 为传递函数的极点 极点是微分方程的特征跟,因此,决定了所描述系统自由运动的模态。
经典控制理论在20世纪30到40年代,奈奎斯特、伯德、维纳等人的著作为自动控制理论的初步形成奠定了基础;二次大战以后,又经过众多学者的努力,在总结了以往的实践和关于反馈理论、频率响应理论并加以发展的基础上,形成了较为完整的自动控制系统设计的频率法理论。
1948年又提出了根轨迹法。
至此,自动控制理论发展的第一阶段基本完成。
这种建立在频率法和根轨迹法基础上的理论,通常被称为经典控制理论。
经典控制理论以拉氏变换为数学工具,以单输入-单输出的线性定常系统为主要的研究对象。
将描述系统的微分方程或差分方程变换到复数域中,得到系统的传递函数,并以此作为基础在频率域中对系统进行分析和设计,确定控制器的结构和参数。
通常是采用反馈控制,构成所谓闭环控制系统。
经典控制理论具有明显的局限性,突出的是难以有效地应用于时变系统、多变量系统,也难以揭示系统更为深刻的特性。
当把这种理论推广到更为复杂的系统时,经典控制理论就显得无能为力了,这是因为它的以下几个特点所决定。
1.经典控制理论只限于研究线性定常系统,即使对最简单的非线性系统也是无法处理的;2.经典控制理论只限于分析和设计单变量系统,采用系统的输入-输出描述方式,这就从本质上忽略了系统结构的内在特性,也不能处理输入和输出皆大于1的系统。
实际上,大多数工程对象都是多输入-多输出系统,尽管人们做了很多尝试,但是,用经典控制理论设计这类系统都没有得到满意的结果;3.经典控制理论采用试探法设计系统。
即根据经验选用合适的、简单的、工程上易于实现的控制器,然后对系统进行分析,直至找到满意的结果为止。
虽然这种设计方法具有实用等很多优点,但是,在推理上却是不能令人满意的,效果也不是最佳的,人们自然提出这样一个问题,即对一个特定的应用课题,能否找到最佳的设计。
综上所述,经典控制理论的最主要的特点是:线性定常对象,单输入单输出,完成镇定任务。
即便对这些极简单的对象、对象描述及控制任务,理论上也尚不完整,从而促使现代控制理论的发展:对经典理的精确化、数学化及理论化。