2020年上海市金山区高考数学二模试卷(有答案解析)

2020年上海市金山区高考数学二模试卷一、填空题（本大题共有12题，满分54分，第1～6题每题4分，第7～12题每题5分）考生应在答题纸的相应位置直接填写结果1．（4分）集合{|03}A x x =<<，{|||2}B x x =<，则A B =I ． 2．（4分）函数12y x -=的定义域是 ．3．（4分）i 是虚数单位，则||1ii-的值为 ． 4．（4分）已知线性方程组的增广矩阵为113()02a ，若该线性方程组的解为1()2，则实数a = ．5．（4分）已知函数21()||11x f x =，则1(0)f -= ． 6．（4分）已知双曲线2221(0)x y a a-=>的一条渐近线方程为20x y -=，则实数a = ．7．（5分）已知函数1()sin 11xf x lg x x-=+++．若()4f m =，则()f m -= ．8．（5分）数列{}n a 通的项公式*11,2132n nn na n N n ⎧=⎪⎪=∈⎨⎪⎪⎩…，前n 项和为n S ，则lim n n S →∞= ． 9．（5分）甲、乙、丙三个不同单位的医疗队里各有3人，职业分别为医生、护士与化验师，现在要从中抽取3人组建一支志愿者队伍，则他们的单位与职业都不相同的概率是 ．（结果用最简分数表示）10．（5分）若点集22{(,)|1}A x y x y =+„，{(,)|22B x y x =-剟，11}y -剟，则点集12{(,)|Q x y x x x ==+，12y y y =+，1(x ，1)y A ∈，2(x ，2)}y B ∈所表示的区域的面积是 ．11．（5分）我们把一系列向量(1i a i =u u r ，2，⋯，)n 按次序排成一列，称之为向量列，记作{}i a u u r，已知向量列{}i a u u r 满足1(1,1)a =u u r ，11111(,)(,)(2)2n n n n n n n a x y x y x y n ----==-+u u r …，设n θ表示向量n a uu r 与1n a -u u u r 的夹角，若2n n n b θπ=对任意正整数n ，log (12)a a ⋯+>-恒成立，则实数a 的取值范围是 ．12．（5分）设*n N ∈，n a 为(2)(1)n n x x +-+的展开式的各项系数之和，16,2m t t R =-+∈，1222[][][]([]333n n n na a ab x =++⋯+表示不超过实数x 的最大整数），则22()()n n t b m -+-的最小值为 ．2x二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确答案，考生应在答题纸的相应位置，将代表正确选项的小方格涂黑13．（5分）已知直角坐标平面上两条直线方程分别为1111:0l a x b y c ++=，2222:0l a x b y c ++=，那么“11220a b a b =是“两直线1l ，2l 平行”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件14．（5分）如图，若一个水平放置的图形的斜二测直观图是一个底角为45︒且腰和上底均为1的等腰梯形，则原平面图形的面积是( )A 22+ B 12+ C ．22D ．12+15．（5分）在正方体1111ABCD A B C D -中，下列结论错误的是( )A ．221111111()3A A A D A B A B ++=u u u r u u u u r u u u u r u u u u rB ．1111()0AC A B A A -=u u u u r u u u u r u u u rgC ．向量1AD u u u u r 与1A B uuu r的夹角是120︒D ．正方体1111ABCD A B C D -的体积为1||AB AA AD u u u r u u u r u u u rg g16．（5分）函数()f x 是定义在R 上的奇函数，且(1)f x -为偶函数，当[0x ∈，1]时，()f x x =，若函数()()g x f x x m =--有三个零点，则实数m 的取值范围是( ) A ．11(,)44-B ．(12,21)-C ．11(4,4)()44k k k Z -+∈D ．(412,421)()k k k Z ++∈三、解答题（本大满分76分）本天题共有5题，下列必频在答题纸相应编号的规定区城内写出必要的步骤，17．（14分）已知四棱锥P ABCD -，PA ⊥底面ABCD ，1PA =，底面ABCD 是正方形，E是PD 的中点，PD 与底面ABCD所成角的大小为6π． （1）求四棱锥P ABCD -的体积；（2）求异面直线AE 与PC 所成角的大小（结果用反三角函数值表示）．18．（14分）已知函数2()2cos 3sin 2xf x x =． （1）求函数()f x 在区间[0，]π上的单调增区间； （2）当11()5f α=，且236ππα-<<，求sin(2)3πα+的值． 19．（14分）随着疫情的有效控制，人们的生产生活逐渐向正常秩序恢复，位于我区的某著名赏花园区重新开放．据统计研究，近期每天赏花的人数大致符合以下数学模型*:n N ∈ 以611200150016()30032400728234006502936n n n f n n n n -+⎧⎪⎪=+⎨⎪-⎪⎩g剟剟剟表示第n 个时刻进入园区的人数； 以0115()4005000162882002936n g n n n n ⎧⎪=-⎨⎪⎩剟剟剟表示第n 个时刻离开园区的人数； 设定每15分钟为一个计算单位，上午8点15分作为第1个计算人数单位，即1n =；8点30分作为第2个计算单位，即2n =；依此类推，把一天内从上年8点到下午5点分成36个计算单位（最后结果四含五入，精确到整数）．（1）试分别计算当天12:30至13:30这一小时内，进入园区的人数(19)(20)(21)(22)f f f f +++和离开园区的游客人数(19)(20)(21)(22)g g g g +++；（2）请问，从12点（即16)n =开始，园区内游客总人数何时达到最多？并说明理由．20．（16分）已知动直线l 与与椭圆22:12y C x +=交于1(P x ，1)y ，2(Q x ，2)y 两不同点，且OPQ ∆的面积2OPQ S ∆=O 为坐标原点． （1）若动直线l 垂直于x 轴．求直线l 的方程；。

解析几何一、直线1、【2020年闵行区二模第3题】若直线10ax by ++=的方向向量为(1,1)，则此直线的倾斜角为 【答案：4π】 2、【2020年黄浦区二模第4题】若直线1:350l ax y +-=与2:210l x y +-=互相垂直，则实数a 的值为 【答案： 6- 】3、【2020年金山区二模第13题】已知直角坐标平面上两条直线的方程分别为1111:0l a x b y c ++=，2222:0l a x b y c ++=，那么“11220a b a b =”是“两直线1l 、2l 平行”的( )． （A ）充分非必要条件 （B ）必要非充分条件 （C ）充要条件 （D ）既非充分又非必要条件 【答案：B 】4、【2020年徐汇区二模第8题】已知直线(2)(1)30a x a y ++--=的方向向量是直线(1)(23)20a x a y -+++= 的法向量，则实数a 的值为 .【答案：11或- 】5、【2020年松江区二模第13题】若为坐标原点，是直线上的动点，则的最小值为（ ） (A)(B)(C)(D)【答案：B 】6、【2020年金山区二模第12题】设*n ∈N ，n a 为()(2)1nn x x +-+的展开式的各项系数之和，162m t =-+，，1222...333n n n a a na b ⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦（[x ]表示不超过实数x 的最大整数），则()22()n n t b m -+-的最小值为___________.O P 20-+=x y OP 2R t ∈【答案：95解析：赋值法，令1x =，∴32nnn a =-，∴(32)2[][][()]333n n nn n nna n n n -==-⋅， 可用计算器分析2()3n n ⋅单调性及范围，可知2()(0,1)3n n ⋅∈，∴[]13n n na n =-，∴(1)2n n n b -=，22()()n n t b m -+-的 几何意义为点(,)n n b 到点(,)t m 的距离的平方，如图所示， 当3n =时，点(3,3)到直线162y x =-+的距离最小， ∴min 22512d ==+，即2min95d =。

2020 金山 高三二模一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 集合{|03}A x x =<<，{|||2}B x x =<，则A B =I 2. 函数12y x-=的定义域是3. i 是虚数单位，则i||1i-的值为 4. 已知线性方程组的增广矩阵为11302a ⎛⎫⎪⎝⎭，若该线性方程组的解为12⎛⎫⎪⎝⎭，则实数a =5. 已知函数21()11x f x =，则1(0)f -=6. 已知双曲线2221x y a-=(0)a >的一条渐近线方程为20x y -=，则实数a =7. 已知函数1()lgsin 11xf x x x-=+++，若()4f m =，则()f m -= 8. 数列{}n a 的通项公式1,1,21,32n nn na n ⎧=⎪⎪=⎨⎪≥⎪⎩，n ∈*N ，前n 项和为n S ，则lim n n S →∞=9. 甲、乙、丙三个不同单位的医疗队里各有3人，职业分别为医生、护士与化验师，现在要从中抽取3人组建一支志愿者队伍，则他们的单位与职业都不相同的概率是 （结果用最简分数表示） 10. 若点集22{(,)|1}A x y x y =+≤，{(,)|22,11}B x y x y =-≤≤-≤≤，则点集12121122{(,)|,,(,),(,)}Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积是11. 我们把一系列向量i a u r (1,2,,)i n =⋅⋅⋅按次序排成一列，称为向量列，记作{}i a u r ，已知向量列{}i a u r满足1(1,1)a =u u r ，11111(,)(,)2n n n n n n n a x y x y x y ----==-+u u r (2)n ≥，设n θ表示向量1n a -u u u r 与n a u u r 夹角，若2n n n b θπ=，对任意正整数nlog (12)a a ⋅⋅⋅>-恒成立，则实数a 的取值范围是 12. 设n ∈*N ，n a 为(2)(1)n n x x +-+的展开式的各项系数之和，162m t =-+，t ∈R ，1222[][][]333n n n na a ab =++⋅⋅⋅+（[]x 表示不超过实数x 的最大整数），则22()()n t b m -+-的最小值为二. 选择题（本大题共4题，每题5分，共20分）13. 已知直角坐标平面上两条直线的方程分别为1111:0l a x b y c ++=，2222:l a x b y c ++0=，那么“11220a b a b =”是“两直线1l 、2l 平行”的（ ） A . 充分非必要条件 B . 必要非充分条件 C . 充要条件 D . 既非充分又非必要条件14. 如图，若一个水平放置的图形的斜二测直观图是一个底角为45°且腰和上底均为1的等腰梯形，则原平面图形的面积是（ ） A .22+ B . 12+ C . 22+ D . 12+ 15. 在正方体1111ABCD A B C D -中，下列结论错误的是（ ）A. 221111111()3A A A D A B A B ++=u u u r u u u u r u u u u r u u u u r B . 1111()0A C A B A A ⋅-=u u u r u u u u r u u u r 、C .向量1AD u u u u r 与1A B uuu r的夹角是0120D .正方体1111ABCD A B C D -的体积为1AB AA AD ⋅⋅u u u r u u u r u u u r16. 函数()f x 是定义在R 上的奇函数，且(1)f x -为偶函数，当[0,1]x ∈时，()f x x =，若函数()()g x f x x m =--有三个零点，则实数m 的取值范围是（ ）A . 11(,)44- B . (12,21)--C . 11(4,4)44k k -+(Z k ∈) D . (412,421)k k +-+-(Z k ∈)三. 解答题（本大题共5题，共14+14+14+16+18=76分）17. 已知四棱锥P ABCD -，PA ⊥底面ABCD ，1PA =，底面ABCD 是正方形，E 是PD 的中点，PD 与底面ABCD 所成角的大小为6π. （1）求四棱锥P ABCD -的体积； （2）求异面直线AE 与PC 所成角的大小. （结果用反三角函数值表示）18. 已知函数2()2cos 3sin 2xf x x =+.（1）求函数()f x 在区间[0,]π上的单调递增区间； （2）当11()5f α=，且236ππα-<<，求sin(2)3πα+的值.19. 随着疫情的有效控制，人们的生产生活逐渐向正常秩序恢复，位于我区的某著名赏花园区重新开放，据统计研究，近期每天赏花的人数大致符合以下数学模型（*N n ∈）：以611200150016()30032400728234006502936n n n f n n n n -+≤≤⎧⎪⎪=⋅+≤≤⎨⎪-≤≤⎪⎩表示第n 个时刻进入园区的人数，以0115()4005000162882002936n g n n n n ≤≤⎧⎪=-≤≤⎨⎪≤≤⎩表示第n 个时刻离开园区的人数.设定每15分钟为一个计算单位，上午8点15分作为第1个计算人数单位，即1n =，8点30分作为第2个计算单位，即2n =，依次类推，把一天内从上午8点到下午5点分成36个计算单位（最后结果四舍五入，精确到整数）.（1）试分别计算当天12：30至13：30这一小时内，进入园区的游客人数(19)(20)f f +(21)(22)f f ++和离开园区的游客人数(19)(20)(21)(22)g g g g +++；（2）请问，从12点（即16n =）开始，园区内游客总人数何时达到最多？并说明理由.20. 已知动直线l 与椭圆22:12y C x +=交于11(,)P x y 、22(,)Q x y 两不同点，且△OPQ的面积2OPQ S =V ，其中O 为坐标原点.（1）若动直线l 垂直于x 轴，求直线l 的方程；（2）证明2212x x +和2212y y +均为定值；（3）椭圆C 上是否存在点D 、E 、G ，使得三角形面积2ODE ODG OEG S S S ===V V V ？若存在，判断△DEG 的形状，若不存在，请说明理由.21. 若无穷数列{}n a 满足：存在*N k ∈，对任意的0n n ≥（*N n ∈），都有n k n a a d +-=（d 为常数），则称{}n a 具有性质0(,,)Q k n d .（1）若无穷数列{}n a 具有性质(3,1,0)Q ，且11a =，22a =，33a =，求234a a a ++的值；（2）若无穷数列{}n b 是等差数列，无穷数列{}n c 是公比为正数的等比数列，151b c ==，5181b c ==，n n n a b c =+，判断{}n a 是否具有性质0(,,0)Q k n ，并说明理由；（3）设无穷数列{}n a 既具有性质1(,2,)Q i d ，又具有性质2(,2,)Q j d ，其中*,N i j ∈，i j <，i 、j 互质，求证：数列{}n a 具有性质1(,2,)j iQ j i d i--.金山区2019学年第二学期质量监控高三数学试卷评分参考答案一、填空题（本大题共有12题，满分54分，第1–6题每题4分，第7–12题每题5分） 考生应在答题纸相应编号的空格内直接填写结果．1．02（，） ；2．0+∞（，）；3．2 ； 4．2；5．0；6．127．-2；8．74；9．114；10．20+π；11．10,3（）；12．95 二、选择题（本大题共4小题，满分20分，每小题5分）每题有且只有一个正确选项．考生应在答题纸的相应位置，将代表正确选项的小方格涂黑． 13．B ；14．C ；15．D ；16．C.三、解答题（本大题共有5题，满分76分）解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．17．(本题满分14分，第1小题满分7分，第2小题满分7分)解：(1)由PA ⊥底面ABCD ，得PD 与底面ABCD 所成角为PDA ∠， …………………3分由=6PDA π∠，得AD = ……………………………………………………4分所以2113V AD PD =⨯=; ……………………………………………………………………7分 (2)解法一：取CD 中点F ，连接,EF AF ，因为//EF PC ，所以AEF ∠就是所求角（或其补角） 10分由计算得1,AE AF EF ===，222cos 2AE EF AF AEF AE EF +-∠==⋅所以，异面直线所成角为其补角，大小为. ………………………………………14分解法二：如图建系（图略），得())10,0,1,,0,22P CE ⎛⎫⎪ ⎪⎝⎭， …………………10分设异面直线所成角为θ ，则cos 7||||AE PC AE PC θ⋅==u u u r u u u ru u u r u u u r所以，异面直线所成角大小为arccos7. ………………………………………14分 18．(本题满分14分，第1小题满分7分，第2小题满分7分)解：(1)()1cos 2sin 16f x x x x π⎛⎫=++=++ ⎪⎝⎭， ……………………………3分 22,262k x k k Z πππππ-+≤+≤+∈，22233k x k ππππ-+≤≤+， ………5分所以，当[0,]x π∈ 时，函数单调递增区间是[0,]3π; ……………………7分(2)1132sin 1,sin ,6565ππαα⎛⎫⎛⎫++=+= ⎪ ⎪⎝⎭⎝⎭ ………………………9分 因为,36263πππππαα2-<<-<+< ，所以cos 06πα⎛⎫+> ⎪⎝⎭，4cos 65πα⎛⎫+= ⎪⎝⎭， …11分因而3424sin 2sin 22sin cos 236665525ππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=+=++=⨯⨯= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦………14分 19．(本题满分14分，第1小题满分6分，第2小题满分8分) 解：(1)进入园区人数为(19)(20)(21)(22)f f f f +++1314151611111111300[3333]24004=⨯++++⨯14738≈（人）， …………………3分离开园区的人数(19)(20)(21)(22)=12800g g g g +++（人）； ………………6分 （2）当时，园内游客人数递增；当时，园内游客人数递减， …8分 ①当1628n ≤≤时，661111()()30032400(4005000)30034007400n n f n g n n n ---=⋅+--=⋅-+，由计算器计算可得：当1622n ≤≤时，()()0f n g n ->，进入园区游客人数多于离开园区游客人数，总人数越来越多; 当2328n ≤≤时，()()0f n g n -<，进入园区游客人数少于离开游客人数，总人数将变少；…10分()()()()222282.9130,2323161.30f g f g -=>-=-< ………………11分②当2936n ≤≤时，由()()65015200f n g n n -=-+递减，且其值恒为负数．进入园区游客人数少于离开游客人数，总人数将变少． ………………13分综上，当天下午13：30时（22n =）园区内的游客人数最多人. ………………14分20．(本题满分16分，第1小题满分4分，第2小题满分6分，第3小题满分6分)解：(1)直线l 垂直于x 轴时，,P Q 两点关于x轴对称，由111|||2y |22S x =⋅=与2211=12y x +，…2分 可得2112x =，所以，直线l的方程为2x =± ； ……………………………………4分(2) 若直线l 垂直于x 轴时，由（1）知，22121x x +=，22122y y +=均为定值 ……………5分若直线l 与x 轴不垂直时，设直线l 的方程为y kx m =+ ，0)()(≥-n g n f 0)()(<-n g n f联立2212y x y kx m ⎧+=⎪⎨⎪=+⎩，消去y 得：222(2)220k x kmx m +++-=， 则12221222222km x x k m x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩，由∆>0 得222m k <+， …………………6分由122|||2PQ x x k=-=+，d =21|||222m S PQ d k ===+V得()()242222244220,22m mkk m k -+++==+ 满足∆>0， ……………8分()()()()()22222222212121222222242222122k m m k m k x x x x x x k k -++++=+-===++， ………9分()()2222121222222y y x x +=-+-=，综上，2212=1x x + 和2212=2y y + 均为定值; ……………10分(3) 椭圆C 上不存在点,,D E G，使得三角形面积ODE ODG OEG S S S ===V V V ,………11分 假设存在()()()112233,,,,,,D x y E x y G x y 由（2）得2222221223311,1,1x x x x x x +=+=+= ，得22212312x x x ===同理，2221231y y y ===, ………13分 所以,,D E G只能在12⎛⎫±± ⎪ ⎪⎝⎭这4个点中任取3个不同点，而这三点的两两连线中必有一条过原点，不构成三角形，所以产生矛盾，假设不成立.所以，椭圆C 上不在点,,D E G . …………16分21．(本题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分)解：(1) 由30,1n n a a n +-=≥ …………1分 知411a a ==，所以2346a a a ++=； …………………4分(2) 设等差数列{}n b 公差为d ， 等比数列{}n c 的公比为q ，则由题意，411111481b c q b d c ⎧==⎨+==⎩解得11811,,1203c b d q =⎧=⎧⎪⎨⎨==⎩⎪⎩52019,3nn n b n c -=-=， …………………7分532019n n a n -=+-，对任意0n n ≥，()520331n k n k n a a k --+-=+-不恒为0，所以，不具有性质()0,,0Q k n .…………………………………………10分（解法二：说明从第二项起单调递增） (3) 由题意得12(1)2(2)n i n n j n a a d n a a d ++-=⎧≥⎨-=⎩，，， …………………………………………12分由（1）得1n ji n a a jd +=+ （3） 由（2）得2n ij n a a id +=+ （4）(3)(4)- 得21,2,jd d n i=≥ …………………………………………15分 由（1）得()1+,2n j n j i a a d n +--=≥ （5）， 由(2)(5)- 得211,2n j i n j ia a d d d n i+---=-=≥ 即数列{}n a 具有性质1,2,j i Q j i d i -⎛⎫- ⎪⎝⎭.{}n a {}n a。

上海金山区高考数学二模试卷Modified by JACK on the afternoon of December 26, 20202018年上海市金山区高考数学二模试卷副标题题号一二三总分得分一、选择题（本大题共4小题，共分）1.若向量a⃗=(2, 0)，b⃗ =(1, 1)，则下列结论中正确的是( )．A. a⃗b⃗ =1B. |a⃗|=|b⃗ |C. (a⃗b⃗ )⊥b⃗D. a⃗ ∥b⃗2.椭圆的参数方程为{x=5cosθy=3sinθ(θ为参数)，则它的两个焦点坐标是( )．A. (±4, 0)B. (0, ±4)C. (±5, 0)D. (0, ±3)3.如图几何体是由五个相同正方体叠成的，其三视图中的左视图是( )．4.A.B.C.D.5.若对任意x∈(12,1)，都有x1+x2x2=a0+a1x+a2x2+…+a n x n+…，则a2+a3的值等于( )．A. 3B. 2C. 1D. -1二、填空题（本大题共12小题，共分）6.函数y=3sin(2x+π3)的最小正周期T=___________．7.函数y=lg x的反函数是_____．8.已知集合P={x| (x+1)(x–3)<0}，Q={x| |x| > 2}，则P∩Q=______．9.函数y=x+9x，x∈(0，+∞)的最小值是________．10.计算：limn→∞[12+14+18+⋯+(12)n]=________．11.记球O1和O2的半径、体积分别为r1、V1和r2、V2，若V1V2=827，则r1r2=________．12.若某线性方程组对应的增广矩阵是(m421m m)，且此方程组有唯一一组解，则实数m的取值范围是________．13.若一个布袋中有大小、质地相同的三个黑球和两个白球，从中任取两个球，则取出的两球中恰是一个白球和一个黑球的概率是_______．14.(1+2x)n的二项展开式中，含x3项的系数等于含x项的系数的8倍，则正整数n=_______．15.平面上三条直线x–2y+1=0，x–1=0，x+ky=0，如果这三条直线将平面划分为六个部分，则实数k的取值组成的集合A= .16.已知双曲线C：x29y28=1，左、右焦点分别为F1、F2，过点F2作一直线与双曲线C的右半支交于P、Q两点，使得∠F1PQ=90°，则△F1PQ的内切圆的半径r =________．17.若sin2018α–(2–cosβ)1009≥(3–cosβ–cos2α)(1–cosβ+cos2α)，则sin(α+β2)=__________．三、解答题（本大题共5小题，共分）18.在四棱锥P–ABCD中，底面ABCD是边长为6的正方形，PD⊥平面ABCD，PD=8．19.20.21.22.(1) 求PB与平面ABCD所成角的大小；23.24.(2) 求异面直线PB与DC所成角的大小．25.26.27.28.29.30.31.复数z=(12√32i)2是一元二次方程mx2+nx+1=0(m、n∈R)的一个根．32.33.(1) 求m和n的值；(2) 若(m+ni)u+u=z(u∈C)，求u．35.已知椭圆Γ：x24+y23=1的右焦点为F，过点F且斜率为k的直线与椭圆Γ交于A(x1, y1)、B(x2, y2)两点(点A在x轴上方)，点A关于坐标原点的对称点为P，直线PA、PB分别交直线l：x=4于M、N两点，记M、N两点的纵坐标分别为y M、y N．36.37.38.39.(1) 求直线PB的斜率(用k表示)；40.41.(2) 求点M、N的纵坐标y M、y N (用x1, y1表示) ，并判断y M×y N是否为定值？若是，请求出该定值；若不是，请说明理由．42.43.44.45.47.48.49. 已知数列{a n }满足：a 1=2，a n +1=12a n +2．50. (1) 证明：数列{a n –4}是等比数列；51. (2) 求使不等式a n ma n+1m<23成立的所有正整数m 、n 的值； 52. (3) 如果常数0 < t < 3，对于任意的正整数k ，都有a k+1ta k t <2成立，求t 的取值范围．53.54.55.56.57.58. 59. 若函数y =f (x )对定义域内的每一个值x 1，在其定义域内都存在唯一的x 2，使f (x 1)f (x 2)=1成立，则称该函数为“依赖函数”．60. (1) 判断函数g (x )=2x 是否为“依赖函数”，并说明理由；61. (2) 若函数f (x )=(x –1)2在定义域[m ，n ](m >1)上为“依赖函数”，求实数m 、n 乘积mn 的取值范围；62. (3) 已知函数f (x )=(x –a )2 (a <43)在定义域[43，4]上为“依赖函数”．若存在实数x ∈[43，4]，使得对任意的t ∈R ，有不等式f (x )≥–t 2+(s –t )x +4都成立，求实数s 的最大值．63.64.65.66.67.答案和解析1.【答案】C【解析】【分析】根据向量数量积运算公式和向量平行、垂直的充要条件，对各项逐个加以判别，即可得到本题答案．本题给出两个向量的坐标，判断几个式子的正确性，着重考查了向量数量积运算公式和向量平行、垂直的充要条件等知识，属于基础题．【解答】解：对于B因为||==，||=，所以||与||不相等，故B项不正确；对于A，=2，得A项不正确；对于C，-=（1，-1），则()=0，所以（+），因此C项正确；对于D，不存在实数λ，使=λ成立，得D项不正确．故选C.2.【答案】A【解析】【分析】本题考查圆锥曲线的参数方程与普通方程的互化，考查椭圆的简单几何性质，属于基础题.将参数方程化成普通方程，写出焦点坐标即可.【解答】解：椭圆的参数方程为(θ为参数)，所以椭圆的标准方程为半焦距故焦点坐标为(±4，0).故选A.3.【答案】A【解析】【分析】本题考查几何体的三视图，难度一般.【解答】解：下面两个正方形，上面一个正方形.根据几何体的三视图，它的左视图应该是下面两个正方形，上面一个正方形.故选A.4.【答案】B【解析】【分析】本题考查了二项式定理的应用问题,解题时应根据多项式相乘原理求出某项的系数,是基础题目.根据题意,=a0+a1x+a2x2+…+a n x n+…化为,利用系数相等,列出方程,求出,,,,,的值计算即可.【解答】解:对任意时,都有=a0+a1x+a2x2+…+a n x n+…，即,,且,解得,,,,,，故答案为-2.5.【答案】π【解析】【分析】本题考查给出三角函数表达式求函数的最小正周期，着重考查了函y=Asin （ωx+φ）的周期公式的知识，属于基础题.将题中的函数表达式与函数y=Asin （ωx+φ）进行对照，可得ω=2，由此结合三角函数的周期公式加以计算，即可得到函数的最小正周期.【解答】解：∵函数表达式为y=3sin（2x+），∴ω=2，可得最小正周期T=||=||=π.故答案为π.6.【答案】y=10x【解析】【分析】本题考查反函数，属于基础题.同底的对数函数和指数函数互为反函数.【解答】解：函数y=lgx的反函数是.故答案为.7.【答案】(2,3)【解析】【分析】根据交集的定义即可求解.【解答】解：所以故答案为（2,3）.8.【答案】6【解析】【分析】本题主要考查利用基本不等式求最值, 利用基本不等式，注意当a=b时，等号成立，从而求得最小值.【解答】解：因为x∈(0，+∞)，由基本不等式得：,即,所以当x=3时，y的最小值为6，故答案为6.9.【答案】1【解析】【分析】本题zhuy主要考查等比数列的求和，考查极限的求法，属于基础题.【解答】解：===1.故答案为1.10.【答案】23【解析】【分析】本题考查球的体积.【解答】解：由已知得：，又，所以，所以，故答案为.11.【答案】m≠±2【解析】【分析】本题的考点是二元一次方程组的矩阵形式，主要考查二元线性方程组的增广矩阵的涵义，计算量小，属于较容易的题型．根据题意得到二元线性方程组的表达式，此方程组有唯一一组解，则两直线不平行也不重合，求解即可.【解答】解：由二元线性方程组的增广矩阵为，可得到二元线性方程组的表达式，因为此方程组有唯一一组解，所以两直线不平行也不重合，故∴m≠±2?，故答案为m≠±2.12.【答案】35【解析】【分析】此题考查的知识点是古典概型，其中计算出所有取法的基本事件总数，及两个球中恰有一个白球的基本事件个数，是解答本题的关键.根据已知中口袋中装有大小相同的3个黑球，2个白球，从中任取两个球，我们易计算出所有取法的基本事件总数，及两个球中恰有一个白球的基本事件个数，代入古典概型公式，即可得到答案.【解答】解：∵口袋中装有大小相同的3个黑球，2个白球，分别计为A，B，C，1，2，则任取两个球共有：（A，B），（A，C），（A，1），（A，2）、（B，C），（B，1），（B，2），（C，1），（C，2），（1，2）共10种，其中恰有一个白球共有（A，1），（A，2），（B，1），（B，2），（C，1），（C，2），共种，故取出的两个球中至少有一个白球的概率P=.故答案为.13.【答案】5【解析】【分析】本题主要考查了利用二项展开式的通项公式求解指定的项，解题的关键是熟练掌握通项，属于基础试题.由题意可得T r+1=C n r（2x）r=2r C n r x r分别令r=3，r=1可得含x3，x项的系数，从而可求.【解答】解：由题意可得二项展开式的通项，T r+1=C n r（2x）r=2r C n r x r令r=3可得含x3项的系数为：8C n3，令r=1可得含x项的系数为2C n1∴8C n3=8×2C n1∴n=5故答案为5.14.【答案】{–1，0，–2}【解析】【分析】三条直线将平面划分为六部分，则直线x+ky=0过另外两条直线的交点，或这条直线与另外两条直线平行，由此求出k的值．【解答】解：若是三条直线两两相交，且交点不重合，则这三条直线把平面分成7部分；如果这三条直线将平面划分为六部分包括两种情况能够成立，①是x+ky=0过另外两条直线的交点，由x?2y+1=0和x?1=0的交点是(1,1)，解得k=?1；②是这条直线与另外两条直线平行，此时k=0或2，综上,k的取值集合是{0,1,2}.故答案为{1,0,2}.15.【答案】2【解析】【分析】本题考查双曲线的概念和标准方程，涉及直角三角形的内切圆，属中高档题. 设PF1=s,则PF2=s-2a,设QF1=t,则QF2=t-2a,在Rt△F1PF2中，利用勾股定理求得s的值，即可算出内切圆半径【解答】解：双曲线C：，，设PF1=s,则PF2=s-2a,设QF1=t,则QF2=t-2a,所以,即,所以,解得或s=-2,∴内切圆半径,故答案为2. 16.【答案】±1 【解析】 【分析】本题考查三角恒等变换，三角函数的有界性等知识点，属于基础题， 首先通过化简处理，再利用三角函数的有界性，将不等式化为等式处 理. 【解答】 解：由已知得，∵左边，右边，∴， ∴，∴，， ∴，，∴，∴.故答案为±1.17.【答案】解：(1)连BD ，因为PD ⊥平面ABCD ，则∠PBD 就是PB 与平面ABCD 所成的角， 在△PBD 中，tan ∠PBD =?2√23，所以∠ PBD =arctan 2√23， 所以PB 与平面ABCD 所成的角的大小为arctan2√23； (2)因为AB ∥DC ，所以∠PBA 就是异面直线PB 与DC 所成的角， 因为PD ⊥平面ABCD ，所以AB ⊥PD ，又AB ⊥AD ，所以AB ⊥PA ， 在Rt △PAB 中，PA =10，AB =6， 所以tan ∠PBA =53，∠PBA =arctan 53，异面直线PB 与DC 所成角的大小为arctan 53．【解析】本题考查四棱锥的知识，考查线面成角和异面直线所成角的大小的求法，考查运算求解能力，考查函数与方程思想，是中档题．（1）由PD⊥平面ABCD，则∠PBD就是PB与平面ABCD所成的角即可求出；（2）由AB∥DC，得∠PBA就是异面直线PB与DC所成的角，由此能求出异面直线PB与DC所成角的大小．18.【答案】解：(1)因为z=(12√32i)2=12√32i，所以z=12＋√32i，由题意知：z、zˉ是一元二次方程mx2+nx+1=0(m、n∈R)的两个根，由{nm =(12√32i)+(12+√32i)1 m =(12√32i)(12+√32i)，解之得：{m=1 n=1，(2)设u=c+di(c,d∈R)，则(1+i)(c–di)+(c+di)=12√32i，2c+d+ci=12√32 i,则有{2c＋d=12c=√32，解得{c=√32d=12＋√3，所以u=√32＋(√312)i．【解析】(1)化简可得，则，根据z、是一元二次方程mx2+nx+1=0(m、n∈R)的两个根，利用根与系数的关系求解；(2)设u=c+di(c,d∈R)，则，,利用复数相等的充要条件则有，求解即可.19.【答案】解：(1)设直线AB方程为y=k(x1)，联立{y =k(x1)x 24＋y 23=1，消去y ，得(4k 2＋3)x 28k 2x ＋4k 212=0， 因为A(x 1,y 1)、B(x 2,y 2)，且{x 1＋x 2=8k 24k 2＋3x 1x 2=4k 2124k 2＋3， 又P(x 1,y 1)，所以k PB =y 1＋y 2x1＋x 2=k(x 11)＋k(x 21)x 1＋x 2=34k ，；(2)又直线PA 的方程为y =y1x 1x ，则y M =4y 1x 1，由题意可知，k =y1x 11，直线PB 的方程为y +y 1=3(x 11)4y 1(x +x 1)，则y N =3(x 11)(4＋x 1)4y 1y 1，x 124＋y 123=1，y M ×y N =3(x 11)(4＋x 1)x 14y 12x 1=3x 12＋4y 12＋9x 112x 1=–9，综上，乘积y M ×y N 为定值–9． 【解析】本题主要考查了椭圆与直线的关系，(1)设直线AB 方程为，联立，消去，得，再由韦达定理即可k PB ；(2)又直线的方程为，则，由题意可知，，直线的方程为y+y 1=(x+x 1)，则，，即可求出y M ×y N 为定值–9．20.【答案】（1）证明：由a n +1=12a n +2， 所以a n +1–4 =12(a n –4 )，且a 1–4=–2，故数列{a n –4}是以–2为首项，12为公比的等比数列； （2）解：由（1）题，得a n –4=–2(12)n1，得a n =4(12)n2， 于是4(12)n2m 4(12)n1m <23，当m ≥4时，4(12)n2m 4(12)n1m >1，无解，因此，满足题意的解为{m =1n =1或{m =2n =1或{m =3n =2；（3）解：①当k =1时，由3t2t <2，解得0<t <1或2<t <3， ②当k ≥2时，a n =4(12)n23，故分母a n t >0恒成立， 从而，只需a k +1–t <2(a k –t )对k ≥2，k ∈N *恒成立，即t <2a k –a k +1对k ≥2，k ∈N *恒成立， 故t <(2a k –a k +1)min ， 又2a k a k ＋1=43(12)k1，故当k =2时，(2a k a k ＋1)min =52，所以t <52， 综上所述，t 的取值范围是(0,1)∪(2,52)． 【解析】本题考查了数列的函数特征和等比数列的判定与证明，是中档题. （1）由a n+1=a n +2，所以a n+1–4 =(a n –4 )，即可得证等比数列；（2）由(1)题，得，于是，求解即可；（3）分k=1和k≥2两种情况分别由数列的函数特征求解即可.21.【答案】解：(1) 对于函数g (x )=2x 的定义域R 内任意的x 1，取x 2= –x 1， 则g (x 1)g (x 2)=1，且由g (x )=2x 在R 上单调递增，可知x 2的取值唯一， 故g (x )=2x 是“依赖函数”；(2) 因为m >1，f (x )=(x –1)2在[m ，n ]递增， 故f (m )f (n )=1，即(m –1)2(n –1)2=1， 由n >m >1，得(m –1) (n –1) =1，故n =mm1， 由n >m >1，得1<m <2，从而mn =m 2m1=m1＋1m1＋2在m ∈(1,2)上单调递减，故mn ∈(4,＋∞)；(3) 因a <43，故f(x)=(xa)2在[43,4]上单调递增， 从而f(43)f(4)=1，即(43a)2(4a)2=1， 进而(43a)(4a)=1， 解得a =1或a =133(舍)，从而，存在x ∈[43,4]，使得对任意的t ∈R ，不等式(x1)2t 2＋(st)x ＋4都成立，即t 2＋xt ＋x 2(s ＋2)x30恒成立，由Δ=x 24[x 2(s ＋2)x3]0，得4(s ＋2)x3x 212，由x ∈[43,4]，可得4(s ＋2)3x 12x，又y =3x12x在x ∈[43,4]单调递增， 故当x =4时，(3x12x )max=9，从而4(s ＋2)9，解得s 14， 故实数s 的最大值为14． 【解析】(1) 取x 2= –x 1，则g(x 1)g(x 2)=1，且由g(x)=2x 在R 上单调递增，可知x 2的取值唯一，根据新定义可得g(x)=2x 是“依赖函数”；(2) m>1，f(x)=(x –1)2在[m ，n]递增，故f(m)f(n)=1，即(m –1)2(n –1)2=1，从而在上单调递减，故可得；(3) 因，故在上单调递增，从而解得，原不等式即即恒成立，由，且在单调递增，故当时，，从而，求解即可．。

上海市金山区2020届高三二模数学试卷2020.5一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1.集合{|03}A x x ，{|||2}B x x ，则A B 2.函数12y x的定义域是3.i 是虚数单位，则i||1i的值为 4.已知线性方程组的增广矩阵为11302a ，若该线性方程组的解为12，则实数a 5.已知函数21()11x f x ，则1(0)f6.已知双曲线2221x y a(0)a 的一条渐近线方程为20x y ，则实数a7.已知函数1()lg sin 11xf x x x，若()4f m ，则()f m8.数列{}n a 的通项公式1,1,21,32n nn na n，n *N ，前n 项和为n S ，则lim n n S9.甲、乙、丙三个不同单位的医疗队里各有3人，职业分别为医生、护士与化验师，现在要从中抽取3人组建一支志愿者队伍，则他们的单位与职业都不相同的概率是 （结果用最简分数表示）10.若点集22{(,)|1}A x y x y ，{(,)|22,11}B x y x y ，则点集12121122{(,)|,,(,),(,)}Q x y x x x y y y x y A x y B 所表示的区域的面积是11.我们把一系列向量i a (1,2,,)i n 按次序排成一列，称为向量列，记作{}i a，已知向量列{}i a 满足1(1,1)a ，11111(,)(,)2n n n n n n n a x y x y x y (2)n ，设n 表示向量1n a 与n a 夹角，若2n n n b，对任意正整数n ，log (12)a a恒成立，则实数a 的取值范围是12.设n *N ，n a 为(2)(1)n n x x 的展开式的各项系数之和，162m t ，t R ，1222[][][]333n n n na a ab （[]x 表示不超过实数x 的最大整数），则22()()n t b m 的最小值为二. 选择题（本大题共4题，每题5分，共20分）13.已知直角坐标平面上两条直线的方程分别为1111:0l a x b y c ，2222:l a x b y c 0 ，那么“11220a b a b ”是“两直线1l 、2l 平行”的（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件14.如图，若一个水平放置的图形的斜二测直观图是一个底角为45°且腰和上底均为1的等腰梯形，则原平面图形的 面积是（ ）A.22B.12C. 2D. 115.在正方体1111ABCD A B C D 中，下列结论错误的是（）A. 221111111()3A A A D A B A B B. 1111()0A C A B A AC. 向量1AD 与1A B的夹角是120°D. 正方体1111ABCD A B C D 的体积为1||AB AA AD16.函数()f x 是定义在R 上的奇函数，且(1)f x 为偶函数，当[0,1]x 时，()f x 若函数()()g x f x x m 有三个零点，则实数m 的取值范围是（）A. 11(,)44B. (11)C. 11(4,4)44k k (Z k )D. (411)k k (Z k )三. 解答题（本大题共5题，共14+14+14+16+18=76分）17.已知四棱锥P ABCD ，PA 底面ABCD ，1PA ，底面ABCD 是正方形，E 是PD 的中点，PD 与底面ABCD 所成角的大小为6.（1）求四棱锥P ABCD 的体积； （2）求异面直线AE 与PC 所成角的大小. （结果用反三角函数值表示）18.已知函数2()2cos 2xf x x . （1）求函数()f x 在区间[0,] 上的单调递增区间； （2）当11()5f，且236 ，求sin(23的值. 19.随着疫情的有效控制，人们的生产生活逐渐向正常秩序恢复，位于我区的某著名赏花园区重新开放，据统计研究，近期每天赏花的人数大致符合以下数学模型（*N n ）：以611200150016()30032400728234006502936n n n f n n n n表示第n 个时刻进入园区的人数，以0115()4005000162882002936n g n n n n表示第n 个时刻离开园区的人数.设定每15分钟为一个计算单位，上午8点15分作为第1个计算人数单位，即1n ，8点30分作为第2个计算单位，即2n ，依次类推，把一天内从上午8点到下午5点分成36个计算单位（最后结果四舍五入，精确到整数）.（1）试分别计算当天12：30至13：30这一小时内，进入园区的游客人数(19)(20)f f(21)(22)f f 和离开园区的游客人数(19)(20)(21)(22)g g g g ；（2）请问，从12点（即16n ）开始，园区内游客总人数何时达到最多？并说明理由.20.已知动直线l 与椭圆22:12y C x 交于11(,)P x y 、22(,)Q x y 两不同点，且△OPQ 的面积2OPQ S ，其中O 为坐标原点.（1）若动直线l 垂直于x 轴，求直线l 的方程；（2）证明2212x x 和2212y y 均为定值；（3）椭圆C 上是否存在点D 、E 、G ，使得三角形面积2ODE ODG OEG S S S ？ 若存在，判断△DEG 的形状，若不存在，请说明理由.21.若无穷数列{}n a 满足：存在*N k ，对任意的0n n （*N n ），都有n k n a a d （d 为常数），则称{}n a 具有性质0(,,)Q k n d .（1）若无穷数列{}n a 具有性质(3,1,0)Q ，且11a ，22a ，33a ，求234a a a 的值； （2）若无穷数列{}n b 是等差数列，无穷数列{}n c 是公比为正数的等比数列，151b c ，5181b c ，n n n a b c ，判断{}n a 是否具有性质0(,,0)Q k n ，并说明理由；（3）设无穷数列{}n a 既具有性质1(,2,)Q i d ，又具有性质2(,2,)Q j d ，其中*,N i j ，i j ，i 、j 互质，求证：数列{}n a 具有性质1(,2,)j iQ j i d i.参考答案一. 填空题1.(0,2)2.(0,)3.24.25.06.127.28.749.11410.20 11. 1(0,)312.95二. 选择题 13.B 14.C15.D16.C三. 解答题17.（1）1；（2）arccos7. 18.（1）[0,3 ；（2）2425.19.（1）14738，12800；（2）13点30分.20.（1）2x；（2）1，2；（3）不存在. 21.（1）6；（2）不具有；（3）略.。

高考数学二模试卷题号一二三总分得分一、选择题（本大题共4小题，共20.0分）1.在长方体ABCD-A1B1C1D1中，下列计算结果一定不等于0的是（ ）A. B. C. D.2.在我国南北朝时期，数学家祖暅在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”．其意思是，用一组平行平面截两个几何体，若在任意等高处的截面面积都对应相等，则两个几何体的体积必然相等．根据祖暅原理，“两几何体A、B的体积不相等”是“A、B在等高处的截面面积不恒相等”的（）条件A. 充分不必要B. 必要不充分C. 充要D. 既不充分也不必要3.设F1、F2是双曲线C：（a＞0，b＞0）的两个焦点，P是C上一点，若|PF1|+|PF2|=6a，∠PF1F2是△PF1F2的最小内角，且∠PF1F2=30°，则双曲线C的渐近线方程是（ ）A. x±y=0B. x±y=0C. x±2y=0D. 2x±y=04.若实数a、b满足，则的取值范围是（ ）A. [-2，0]B.C.D.二、填空题（本大题共12小题，共54.0分）5.函数的定义域是______．6.函数y=（sin x+cos x）2的最小正周期是______．7.若关于x、y的线性方程组的增广矩阵为，该方程组的解为，则m+n的值是______8.二项式（x+1）7的展开式中含x3项的系数值为______．9.已知全集U=R，集合，则∁U P=______．10.若z1=1+i，z2=a-i，其中i为虚数单位，且R，则|z2|=______11.方程（t为参数，t∈R）所对应曲线的普通方程为______12.在Rt△ABC中，∠C=90°，AC=4，则=______．13.若生产某种零件需要经过两道工序，在第一、二道工序中生产出废品的概率分别0.01、0.02，每道工序生产废品相互独立，则经过两道工序后得到的零件不是废品的概率是______（结果用小数表示）14.已知函数f（x）=sin x和的定义域都是[-π，π]，则它们的图象围成的区域面积是______15.若集合A={x|x2-（a+2）x+2-a＜0，x∈Z}中有且只有一个元素，则正实数a的取值范围是______16.正方形ABCD的边长为2，对角线AC、BD相交于点O，动点P满足，若，其中m、n∈R，则的最大值是______三、解答题（本大题共5小题，共76.0分）17.已知△ABC中，，，．求：（1）角C的大小；（2）△ABC中最小边的边长．18.如图，已知点P在圆柱OO1的底面圆O上，AB为圆O的直径，圆柱OO1的侧面积为16π，OA=2，∠AOP=120°．（1）求三棱锥A1-APB的体积；（2）求直线A1P与底面PAB所成角的大小．19.从金山区走出去的陈驰博士，在《自然-可持续性》杂志上发表的论文中指出：地球正在变绿，中国通过植树造林和提高农业效率，在其中起到了主导地位．已知某种树木的高度f（t）（单位：米）与生长年限t（单位：年，t∈）满足如下的逻辑斯蒂函数：，其中e为自然对数的底数．设该树栽下的时刻为0．（1）需要经过多少年，该树的高度才能超过5米？（精确到个位）（2）在第几年内，该树长高最快？20.已知椭圆Γ：，过点D（-1，0）的直线l：y=k（x+1）与椭圆Γ交于M、N两点（M点在N点的上方），与y轴交于点E．（1）当m=1且k=1时，求点M、N的坐标；（2）当m=2时，设，，求证：λ+μ为定值，并求出该值；（3）当m=3时，点D和点F关于坐标原点对称，若△MNF的内切圆面积等于，求直线l的方程．21.若数列{a n}、{b n}满足|a n+1-a n|=b n（n∈N*），则称{b n}为数列{a n}的“偏差数列”．（1）若{b n}为常数列，且为{a n}的“偏差数列”，试判断{a n}是否一定为等差数列，并说明理由；（2）若无穷数列{a n}是各项均为正整数的等比数列，且a3-a2=6，{b n}为数列{a n}的“偏差数列”，求的值；（3）设，{b n}为数列{a n}的“偏差数列”，a1=1，a2n≤a2n-1且a2n≤a2n+1，若|a n|≤M对任意n∈N*恒成立，求实数M的最小值．答案和解析1.【答案】D【解析】解：如图，以D为原点，分别以DA，DC，DD1所在直线为x，y，z轴建立空间直角坐标系，设长方体的长宽高分别为a，b，c则A（a，0，0），B（a，b，0），C（0，b，0），D（0，0，0），B1（a，b，c），C1（0，b，c），D1（0，0，c），∴=（-a，0，c），=（-a，0，-c），=（-a，-b，c），=（-a，b，0），=（0，b，0），=（-a，0，0），∴•=a2-c2，当a=c时，•=0，•=a2-b2，当a=b时，•=0，•=0，•=a2≠0，故选：D．以D为原点，分别以DA，DC，DD1所在直线为x，y，z轴建立空间直角坐标系，根据向量的运算和向量的数量积的关系即可判断本题考查了向量的数量积，建立坐标系是关键，属于基础题2.【答案】A【解析】【分析】本题考查了阅读能力、原命题与其逆否命题的真假及充分必要条件，属中档题.先阅读题意，再由原命题与其逆否命题的真假及充分必要条件可得解.【解答】解：由已知有”在任意等高处的截面面积都对应相等”是“两个几何体的体积必然相等“的充分不必要条件，结合原命题与其逆否命题的真假可得：“两几何体A、B的体积不相等”是“A、B在等高处的截面面积不恒相等”的充分不必要条件，故选：A．3.【答案】B【解析】解：设|PF1|＞|PF2|，则|PF1|-|PF2|=2a，又|PF1|+|PF2|=6a，解得|PF1|=4a，|PF2|=2a．则∠PF1F2是△PF1F2的最小内角为30°，∴|PF2|2=|PF1|2+|F1F2|2-2|PF1|•|F1F2|cos30°，∴（2a）2=（4a）2+（2c）2-2×4a×2c×，同时除以a2，化简e2-2e+3=0，解得e=，∴c=，∴b==，∴双曲线C：=1的渐近线方程为y==±，即=0．故选：B．设|PF1|＞|PF2|，由已知条件求出|PF1|=4a，|PF2|=2a，e=，进而求出b=，由此能求出双曲线C：=1的渐近线方程．本题考查双曲线的渐近线方程的求法，是中档题，解题时要认真审题，要熟练掌握双曲线的简单性质．4.【答案】D【解析】解：作出不等式组对应的平面区域如图：（阴影部分）：则=，的几何意义为阴影部分的动点（a，b）到定点原点连线的斜率的取值范围．由图象可知当点位于B时，直线的斜率最大，当点位于A时，直线的斜率最小，由，解得B（，），∴BO的斜率k=3，由可得A（1，1），OA的斜率k=1，∴1≤z≤3，则==（k-）2-∈．故选：D．作出不等式对应的平面区域，利用线性规划的知识，利用的几何意义即可求出的取值范围．本题主要考查线性规划的应用，利用z的几何意义是解决本题的关键，利用数形结合是解决线性规划问题中的基本方法．5.【答案】{x|x≥4}【解析】解：∵函数，∴x-4≥0，可得x≥4，∴函数的定义域为：{x|x≥4}，故答案为：{x|x≥4}；函数关系中主要有二次根式．根据二次根式的意义，被开方数是非负数，进行求解；函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数．6.【答案】π【解析】解：函数y=（sin x+cos x）2=1+2sin x cosx=1+sin2x，故它的最小正周期等于=π，故答案为：π．利用同角三角函数的基本关系，二倍角公式可得函数y=1+sin2x，根据最小正周期等于求出结果．本题主要考查同角三角函数的基本关系，二倍角公式的应用，正弦函数的周期性及其求法，属于基础题．7.【答案】10【解析】解：由题意，可根据增广矩阵的定义还原成线性方程组为：．∵方程组的解为，∴m=-2，n=12．∴m+n=10．故答案为：10．本题可先根据增广矩阵的定义还原成线性方程组，然后将方程组的解为代入方程组得到m、n的值，即可得到m+n的值．本题主要考查增广矩阵的定义，根据方程组的解得出参数的值．本题属基础题．8.【答案】35【解析】解：二项式（x+1）7的展开式的通项公式为T r+1=•x7-r，令7-r=3，求得r=4，可得展开式中含x3项的系数值为=35，故答案为：35．先求得二项式展开式的通项公式，再令x的幂指数等于3，求得r的值，即可求得含x3项的系数值．本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．9.【答案】（-∞，1]【解析】解：由P中y=，0＜x＜1，得到y＞1，即P=（1，+∞），∵全集U=R，∴∁U P=（-∞，1]．故答案为：（-∞，1]求出P中y的范围确定出P，根据全集U=R，求出P的补集即可．此题考查了补集及其运算，熟练掌握补集的定义是解本题的关键．10.【答案】【解析】解：=a+i，则z1•=（1+i）（a+i）=a-1+（a+1）i，若R，则a+1=0，即a=-1，则z2=a-i=-1-i，则|z2|==，故答案为：根据复数的运算法则结合复数为实数求出a的值，结合复数模长的公式进行计算即可．本题主要考查复数模长的计算，结合复数的运算法则进行化简是解决本题的关键．11.【答案】y=-x2+2x+2【解析】解：由方程消去参数t可得y=3-（x-1）2，化简得y=-x2+2x+2，故意答案为：y=-x2+2x+2．由方程消去参数t可得y=3-（x-1），再化简可得．本题考查了参数方程化成普通方程，属基础题．12.【答案】16【解析】解：Rt△ABC中，C=90°，AC=4，则•=||•||•cos A=||•||==16，故答案为16．由题意可得•=||•||•cos A=||•||，由此可得结果．本题主要考查两个向量的数量积的运算，一个向量在另一个向量上的投影，属于中档题．13.【答案】0.9702【解析】解：生产某种零件需要经过两道工序，在第一、二道工序中生产出废品的概率分别0.01、0.02，每道工序生产废品相互独立，则经过两道工序后得到的零件不是废品的概率：p=（1-0.01）（1-0.02）=0.9702．故答案为：0.9702．利用对立事件概率计算公式和相互独立事件概率乘法公式能求出经过两道工序后得到的零件不是废品的概率．本题考查概率的求法，考查对立事件概率计算公式和相互独立事件概率乘法公式等基础知识，考查运算求解能力，是基础题．14.【答案】【解析】解：的图象为圆心为O半径为π的圆的上半部分，∵y=sin x是奇函数，∴f（x）在[-π，0]上与x轴围成的面积与在[0，π]上与x轴围成面积相同，则两个函数图象之间围成的面积等价为圆的上半部分的面积S==，故答案为：作出f（x）与g（x）的图象，结合图象的对称性进行求解即可．本题主要考查区域面积的计算，作出两个函数的图象，利用图象的对称性，利用割补法是解决本题的关键．比较基础．15.【答案】【解析】解：∵x2-（a+2）x+2-a＜0 且a＞0∴x2-2x+2＜a（x+1）令f（x）=x2-2x+2；g（x）=a（x+1）∴A={x|f（x）＜g（x），x∈Z}∴y=f（x）是一个二次函数，图象是确定的一条抛物线；而y=g（x）一次函数，图象是过一定点（-1，0）的动直线．又∵x∈Z，a＞0．数形结合，可得：．故答案为：（，]因为集合A中的条件是含参数的一元二次不等式，首先想到的是十字相乘法，但此题行不通；应该把此不等式等价转化为f（x）＜g（x）的形式，然后数形结合来解答，需要注意的是尽可能让其中一个函数不含参数．此题主要考查集合A的几何意义的灵活运用，利用数形结合的数学思想来解决参数取值范围问题．16.【答案】1【解析】解：建立如图所示的直角坐标系，则A（-1，-1），B（1，-1），D（-1，1），P（，），所以=（+1，sinθ+1），=（2，0），=（0，2），又，所以，则=，其几何意义为过点E（-3，-2）与点P（cosθ，sinθ）的直线的斜率，设直线方程为y+2=k（x+3），点P的轨迹方程为x2+y2=1，由直线与圆的位置关系有：，解得：，即的最大值是1，故答案为：1由平面向量的坐标运算得：则A（-1，-1），B（1，-1），D（-1，1），P（，），所以=（+1，sinθ+1），=（2，0），=（0，2），又，所以，则=，其几何意义为过点E（-3，-2）与点P（cosθ，sinθ）的直线的斜率，由点到直线的距离得：设直线方程为y+2=k（x+3），点P的轨迹方程为x2+y2=1，由点到直线的距离有：，解得：，即的最大值是1，得解本题考查了平面向量的坐标运算、直线与圆的位置关系及点到直线的距离，属难度较大的题型17.【答案】解：（1）∵C=π-（A+B），tan A=，tan B=，∴tan C=-tan（A+B）=-=-1，又∵0＜C＜π，∴C=；（2）由tan A==，sin2A+cos2A=1且A∈（0，），得sin A=．∵，∴BC=AB•=．即最小边的边长为．【解析】（1）利用tan C=-tan（A+B）=-，求出内角C的大小；（2）先求出sin A=，再利用，求出最小边的边长．本题考查正弦定理的应用，考查和角的正切公式，考查学生的计算能力，比较基础．18.【答案】解：（1）由题意，S侧=2π•2•AA1=16π，解得AA1=4，在△AOP中，OA=OP=2，∠AOP=120°，所以，在△BOP中，OB=OP=2，∠BOP=60°，所以BP=2，∵AB是圆O的直径，∴AP⊥BP．∴．（2）因为AA1⊥底面PAB，所以∠APA1是直线A1P与底面PAB所成的角，在Rt△APA1中，，，即直线A1P与底面PAB所成角的大小为．【解析】（1）根据侧面积公式计算圆柱的高，在底面中，根据等腰三角形知识求出AP ，BP，带入棱锥的体积公式计算体积；（2）在Rt△AA1P中计算∠A1PA．本题考查了棱锥的体积计算，直线与平面所成角的计算，属于中档题．19.【答案】解：（1）令≥5，解得t≥4+2ln5≈7.2，即需要经过8年，该树的高度才能超过5米；（2）当t∈时，=，设e-0.5t+2=u，则u∈（0，e2]，．令，则．上式当且仅当时，g（u）取得最大值．此时，u=e-0.25，即e-0.5t+2=e-0.25，解得t=4.5．由于要求t为正整数，故树木长高最快的t可能值为4或5，又，，所以，该树在第四年内或第五年内长高最快．【解析】本题主要考查函数的应用问题，利用作差法判断函数的最值是解决本题的关键．考查学生的计算能力．属于中档题.（1）解不等式f（t）≥5即可;（2）利用作差法求出f（t）-f（t-1）的表达式，判断函数的单调性和最值即可．20.【答案】解：（1）当m=k=1时，联立，解之得：或，即M（0，1），N（，）；证明：（2）当m=2时联立，消去y得：（3k2+2）x2+6k2x+3k2-6=0，设M（x1，y1），N（x2，y2），则，由，，且点E的横坐标为0，得x1=λ（x1+1）、x2=μ（x2+1）．从而，则==，即λ+μ为定值3；解：（3）当m=3时，椭圆Γ：，假设存在直线l：y=k（x+1）满足题意，则△MNF的内切圆的半径为，又D（-1，0）、F（1，0）为椭圆Γ的焦点，故△MNF的周长为8，从而，消去y，得（4k2+3）x2+8k2x+4k2-12=0，设M（x1，y1）、N（x2，y2），则．故，即．由（2），得，化简，得17k4+k2-18=0，解得k=±1，故存在直线l：y=±（x+1）满足题意．【解析】（1）代值联立方程组．解得即可求出，（2）联立方程，利用韦达定理，以及向量的知识可得从而，化简整理即可证明，（3）假设存在直线l：y=k（x+1）满足题意，则△MNF的内切圆的半径为，根据韦达定理，弦长公式，三角形的面积公式，即可求出k的值本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、韦达定理、三角形面积计算公式、考查了推理能力与计算能力，属于难题．21.【答案】解：（1）{a n}不一定为等差数列，如，则b n=2为常数列，但{a n}不是等差数列，（2）设数列{a n}的公比为q，则由题意，a1、q均为正整数，因为a3-a2=6，所以a1q（q-1）=6=1×2×3，解得或，故或（n∈N*），①当时，，，==；②当时，，，==；综上，的值为或；（3）由a2n≤a2n-1且a2n≤a2n+1得，=故有：，，……，累加得：==，又a1=1，所以，当n为奇数时，{a n}单调递增，a n＞0，，当n为偶数时，{a n}单调递减，a n＜0，，从而|a n|≤，所以M≥，即M的最小值为．【解析】（1）{a n}不一定为等差数列，如；（2）设数列{a n}的公比为q，解方程可得首项和公比，由等比数列的通项公式和求和公式，计算可得所求值；（3）由累加法可得数列{a n}的通项公式，讨论n为奇数或偶数，求得极限，由不等式恒成立思想可得M的最小值．本题考查新定义的理解和运用，考查等差数列和等比数列的通项公式和求和公式，考查分类讨论思想方法，化简运算能力，属于难题．。

上海市金山区2020年第二学期高三质量测试数学试卷(文理合卷)(满分：150分，完卷时间：120分钟)一、填空题(本大题有12小题，每小题5分，共计60分) 1、函数y = sin2x 的最小正周期是 。

2、(理)函数y=lg(x 2–2x +4)的单调递减区间是 。

(文)不等式：|x –4|≤6的解是 。

3、函数f (x )＝2x +1(x ≥1)的反函数f –1(x )= 。

4、(理)已知f (x )为奇函数，且当x >0时f (x )=x (x –1)，则f (–3)= 。

(文)下面3个关于算法的叙述：(1)一个程序的算法步骤是可逆的；(2)完成一件事情的算法不止一种；(3)设计算法要本着简单方便的原则。

其中叙述正确．．的序号是 。

5、关于x 的不等式：x x x 1<2的解是 。

6、(理)计算：11131)1(913112141211lim ---∞→-+++-++++n n n n ΛΛ= 。

(文)计算：]31)1(2719131[lim 1n n n -∞→-+++-Λ= 。

7、(理)如果(x +x1)n (n ∈N *)展开式中各项系数的和等于32，则展开式中第3项是 。

(文)如果(x +1)n (n ∈N *)展开式中各项系数的和等于32，则展开式中第3项是 。

8、(理)已知直线l 的参数方程为：⎪⎪⎩⎪⎪⎨⎧-=+=t y t x 232211(t 为参数)，则直线l 的倾斜角的大小为 。

(文)圆柱侧面展开图是一个边长为2的正方形，则其体积为 。

9、(理)设地球的半径约为6371千米，在赤道圈上有两点A 、B ，这两点的经度差为120o ，则A 、B 两点的球面距离是 (千米)。

(计算结果精确到1千米)(文)已知目标函数k =3x+y ，且x 、y 满足以下条件：⎪⎩⎪⎨⎧≥≥≥+-0304y x y y x ，则k 的最大值为 。

10、(理)有一种叫做“天天彩”的彩票，每注售价2元，中奖的概率为1%，如果每注奖的奖金为50元，那么购买一注彩票的期望收益是 (元)。

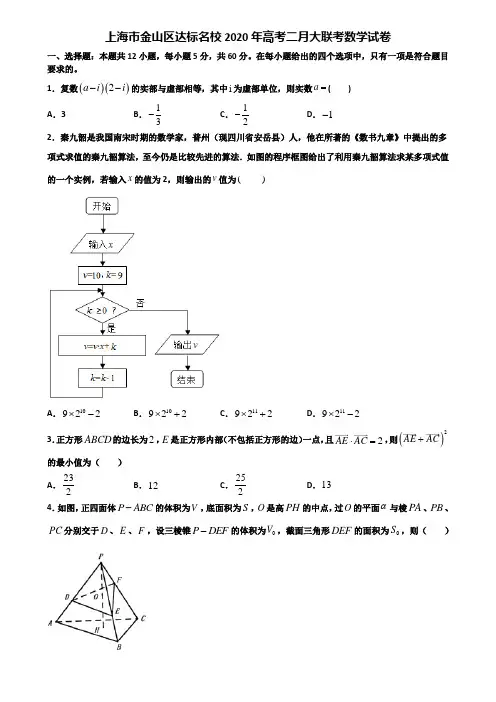
上海市金山区达标名校2020年高考二月大联考数学试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．复数()()2a i i --的实部与虚部相等，其中i 为虚部单位，则实数a =( ) A ．3B ．13-C ．12-D ．1-2．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x 的值为2，则输出的v 值为( )A ．10922⨯-B ．10922⨯+C ．11922⨯+D ．11922⨯-3．正方形ABCD 的边长为2，E 是正方形内部（不包括正方形的边）一点，且2AE AC ⋅=，则()2AE AC +的最小值为（ ） A ．232B ．12C ．252D ．134．如图，正四面体P ABC -的体积为V ，底面积为S ，O 是高PH 的中点，过O 的平面α与棱PA 、PB 、PC 分别交于D 、E 、F ，设三棱锥P DEF -的体积为0V ，截面三角形DEF 的面积为0S ，则（ ）A ．08V V ≤，04S S ≤B ．08V V ≤，04S S ≥C ．08V V ≥，04S S ≤D ．08V V ≥，04S S ≥5．已知正四面体的内切球体积为v ，外接球的体积为V ，则Vv=（ ） A ．4B ．8C ．9D ．276．已知平面向量,,a b c ，满足||2,||1,b a b c a b λμ=+==+且21λμ+=，若对每一个确定的向量a ，记||c 的最小值为m ，则当a 变化时，m 的最大值为（ ） A ．14B ．13C ．12D ．17．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果，哥德巴赫猜想的内容是：每个大于2的偶数都可以表示为两个素数的和，例如：422=+，633=+，835=+，那么在不超过18的素数中随机选取两个不同的数，其和等于16的概率为（ ） A ．121B ．221C ．115D ．2158．如图，这是某校高三年级甲、乙两班在上学期的5次数学测试的班级平均分的茎叶图，则下列说法不正确的是（ ）A ．甲班的数学成绩平均分的平均水平高于乙班B ．甲班的数学成绩的平均分比乙班稳定C ．甲班的数学成绩平均分的中位数高于乙班D ．甲、乙两班这5次数学测试的总平均分是1039．已知三棱锥A BCD -的所有顶点都在球O 的球面上，AD ⊥平面,120ABC BAC ︒∠=，2AD =，若球O 的表面积为20π，则三棱锥A BCD -的体积的最大值为（ ） A ．33B ．33C 3D ．310．已知集合{}2|2150A x x x =-->，{}|07B x x =<<，则()R A B 等于( )A ．[)5,7-B ．[)3,7-C ．()3,7-D ．()5,7-11．复数z 的共轭复数记作z ，已知复数1z 对应复平面上的点()1,1--，复数2z :满足122z z ⋅=-.则2z 等于（ ）A ．2B ．2C ．10D ．1012．已知()32z i i =-，则z z ⋅=（ ） A ．5B ．5C ．13D ．13二、填空题：本题共4小题，每小题5分，共20分。