龚政辉-RS码及其编译码算法
- 格式:pdf
- 大小:211.65 KB
- 文档页数:34



一.RS 码RS 码是有限域GF (p^m )上,码长为n=p^m-1的本原BCH 码,它是多进制的BCH 码。
RS 码不但可以纠正随机错误、突发错误以及二者的组合,而且可以用来构造其它码类。
在计算机中数据是以二进制的形式存在,所以p 通常取值为2。
RS 码的参数:符号取自GF(2^m),纠t 个错的RS(n,k)码的定义如下: 符号大小m .表示符号比特数为m 位。
码块总长度为n 个符号,其中信息长度k 个符号,校验位长度K=n —k 个符号。
RS 码的纠错能力是出码块中的冗余数据校验码的长度K 决定的。
在码块中的错误位置事先并不知道的情况下,RS(n ,k)码可以纠正t=K /2个错误符号。
显然t 值越大,RS 码的纠错能力越强,但与之相对应的是更复杂的算法,更长的运算时间,更低效的数据传输率。
RS 码既可以纠随机错又可以纠突发错。
但RS 码中采用符号这一特性使得它特别适用于产生突发错的场合。
因为不论一个符号中错了多少位,在RS 解码过程中。
它只会被认为是产生了一个符号错。
一个可以纠t 个符号的RS 码,它至少可以纠一个(t-1)m+1个连续比特组成的突发错,而当随机错恰好都不在同一个符号中时只能纠正t 个比特的随机错。
二.RS 码编码对于GF(2^m)来说,若域中非零元素a 的级是2^m-1,则将a 称为本原域元素。
设符号取自GF(2^m),纠t 个错的RS(n,k)码,它的最小距离d=2t+1,则由本原域元素a 的2t 个连续根 ,0αm ,α120-+t m 作为g(x)的根来构造生成多项式g(x)=(x+αm 0)(x+α10+m ))(012αm t x +-+通常情况下取通常取m 0 = 0或m 0 = 1只要将信息码多项式m(x)=m m x m x k k 0111+++-- 乘以x k n -次,然后以g(x)为模,求出余式q(x)便可以得到系统码。
q (x )= m(x) x k n -modg(x)=q q x q x k n k n 0111+++---- C(x)= m(x) x k n -+ q (x )例 构造能纠正2个错误,码长为15符号的RS 码n=15,t=2可得m=4,k=11,d=5.因此RS 码为(15,11)码,生成多项式为g(x)=(x+α)(x+α2)(x+α3)(x+α4) =αααα103263134++++x x x x假设待发送的信息码组为m(x)=x x m x x ααα963102)(++=则编码后的码组多项式为C(x)= m(x) x k n -+ m(x) x k n -modg(x)=ααααα133359103142+++++x x x x x编码的实现:1)首先构造有限域,RS 码的性质和运算法则均定义在Galois 域上,Galois 域是能进行加减乘除运算的有限个元素的封闭集合,它的加减运算符合结合律、交换律和分配律。

RS码在旋转头数字磁记录器中的应用研究
周云生
【期刊名称】《遥测遥控》
【年(卷),期】1995(016)002
【摘要】本文讨论了数字磁记录器的差错控制方案以及RS码在旋转头数字磁记录器中的应用。
简介RS码译码器的实现原理和方法。
本文所介绍的原理与方法对BCH码译码也适用的。
文中给出了用EPLD实现的RS码译码器的结构.经实验测试,该译码器的速度可以达到47Mb/s,并成功地用于旋转头数字磁记录器(模样机)中。
文章最后提出了RS码编译码器设计中有关问题与建议。
【总页数】7页(P14-20)
【作者】周云生
【作者单位】航天工业总公司七0四所
【正文语种】中文
【中图分类】TN946
【相关文献】
1.RS码在旋转头数字磁记录器中的应用研究 [J], 周云生
2.多重偏置在RS码软判译码中的应用研究 [J], 张春蕾
3.交叉交织RS码在旋转头数字磁记录器中的应用 [J], 李立忠;侯著胜
4.RS码技术在PDF417码纠错码编译码中的应用研究 [J], 李建勋;解建仓;张栓新;智勇
5.交叉产我织RS码在旋转数字磁器中的应用 [J], 李立忠;李乐民
因版权原因,仅展示原文概要,查看原文内容请购买。

RS码译码算法及其实现的研究RS码译码算法及其实现的研究摘要:纠错编码在信息传输中起到了至关重要的作用,其中纠错码是最常用的一种编码方式。
RS码作为一种具有高纠错能力的纠错码,被广泛应用于存储介质、数字通信和数据传输等领域。
本文将详细介绍RS码的编码和译码原理,以及RS 码译码算法的研究进展和实现方法。
一、引言在现代通信系统中,由于信道和介质的不完美性,信息传输过程中常常伴随着噪声和错误,导致数据传输错误率的增加。
为了提高数据传输的可靠性和冗余性,人们引入了纠错码,用于在数据传输过程中对错误进行修正。
二、RS码的原理RS码全称为Reed-Solomon码,是一种基于有限域的纠错码。
RS码利用了有限域GF(q)上的多项式编码理论,通过在数据流中引入冗余位进行编码和译码,从而实现错误的检测和纠正。
1. 编码原理RS码的编码原理是将信息数据流进行多项式编码,然后再添加纠错码,生成一个较长的编码后数据流进行传输。
具体编码流程如下:(1)将n个信息符号划分为m个长度为t的子串,其中m = n / t,t为RS码的最小距离;(2)将每个子串看作一个特定的数字,代入t-1次幂相乘的多项式中;(3)将每个子串多项式求模,得到t-1阶多项式;(4)在多项式后方添加r个纠错码位,使整个编码构成一个长度为t+r的新多项式;(5)重复以上步骤,直到对所有信息子串进行编码处理。
2. 译码原理RS码的译码原理是利用多项式除法实现。
译码时,首先接收到一个由编码器生成的编码后数据流,然后通过解码器进行解码,恢复原始信息数据流。
具体译码流程如下:(1)通过接收到的数据流计算相应的符号多项式;(2)使用Berlekamp-Massey算法,计算出多项式的最小生成多项式,从而确定修正多项式;(3)对错误位置进行定位,然后使用Forney算法计算纠错多项式;(4)使用译码器获得纠正后的数据流。
三、RS码的译码算法研究进展1. 经典的译码算法目前,根据实际应用需求,已经提出了许多RS码译码算法。

Data Matrix将有效信息(数字字母等)编码成0~255内的数字表示(编码方式参考:/wiki/Data_Matrix)。
为了及时发现数据传输时的错误,使用RS编解码来进行错误检测校验。
RS码可以看成伽罗华域GF(2^m)上的元素,dm码的元素0~255正好对应伽罗华域GF(2^8)上的256个元素。
通过编码时添加冗余信息,可以有效校验数据是否正确传输。
以下为文献概要:1) 介绍如何生成GF(2^m)域,伽罗华域的加法运算为异或运算,乘法运算为指数相加后mod(2^m)。
2) 实例分析如何编码及纠错。
(实际上就是求解多项式方程组的过程,在实际工程算法中运用到的钱氏搜索法(Chien Search),Berlekamp-Massey 算法都是为了快速求解方程组,从而纠错)。
3) 附录部分为GF(2^8)上的元素列表。
13.2 RS编码和纠错算法13.2.1. GF(2m)域RS(Reed-Solomon)码在伽罗华域(Galois Field,GF)中运算的,因此在介绍RS码之前先简要介绍一下伽罗华域。
CD-ROM中的数据、地址、校验码等都可以看成是属于GF(2m) = GF(28)中的元素或称符号。
GF(28)表示域中有256个元素,除0,1之外的254个元素由本原多项式P(x)生成。
本原多项式的特性是得到的余式等于0。
CD-ROM用来构造GF(28)域的是(13-1)而GF(28)域中的本原元素为α = (0 0 0 0 0 0 1 0)下面以一个较简单例子说明域的构造。
[例13.1]构造GF(23)域的本原多项式假定为α定义为= 0的根,即α3+α+1 = 0和α3= α+1GF(23)中的元素可计算如下:0mod(α3+α+1) = 0α0mod(α3+α+1) = α0= 1α1mod(α3+α+1) = α1α2mod(α3+α+1) = α2α3mod(α3+α+1) = α+1α4mod(α3+α+1) = α2+αα5mod(α3+α+1) = α2+α1+1α6mod(α3+α+1) = α2+1α7mod(α3+α+1) = α0α8mod(α3+α+1) = α1……用二进制数表示域元素得到表13-01所示的对照表表13-01 GF(23)域中与二进制代码对照表,GF(23)域元素二进制对代码0(000)α0(001)α1(010)α2(100)α3(011)α4(110)α5(111)α6(101)这样一来就建立了GF(23)域中的元素与3位二进制数之间的一一对应关系。

RS码及其编译码算法指导教员:雷 菁姓 名:龚 政 辉第一章 引言本文介绍符号取自)GF里的里德-所罗门码(Reed-Solomon(qCode,以下简称RS码)。
RS码是非二进制BCH码的一个最常用的子类,而BCH码是大家所熟悉的。
虽然RS码属于BCH码,但是它却是由Reed和Solomon于1960年采用完全不同的方法独立构造出来的。
RS码的最小距离等于它的奇偶校验符号数加一。
RS码在纠正随机符号错误和随机突发错误方面非常有效,因此被广泛应用于通信和数据存储系统中以便进行差错控制,应用领域涵盖从深空通讯到高密度磁盘等多方面。
以RS码作为外码,简单二进制码作为内码的级联方式在降低译码复杂度的同时,能够提供很高的数据可靠性。
但与二进制BCH码不同,RS码的译码需要同时确定符号错误的的位置和取值,所以它的译码更为复杂而编码算法是大体一致的。
第二章 循环纠错码的基本理论2.1 有限域(Galoias 域)基本概念及相关结论有限域(Galoias 域)就是域中元素的个数是有限的,元素的个数称为域的阶。
q 阶有限域,用()GF q 表示。
如果q 为一个素数,则集合{}0,1,2,,1q − 在模q 加法和乘法下,构成一个q 阶有限域()GF q 。
有限域在编码理论中具有重要的地位,下面给出Galoias 域的几个基本概念和相关结论。
定义1 在域()GF q 中,满足0ne =的最小正整数n 称为域的特征,e 为域的单位。
定义2以q 为特征的域是()m GF q ,1,2,m =…,称()GF q 是()m GF q 的基域,()m GF q 为()GF q 的扩域。
域中一切非零元素的特征都等于域的特征,且域的特征一定为素数。
非零元素构成的乘法群的阶定义为域中该元素的级。
若α为域()GF q 中的n 级元素,则称α为n 次单位原根。
若某一元素α的级为1q −,则称α为本原域元素。
域的特征表明了域中加法运算的循环性,而域的级则表明了域中乘法运算的循环性。

一种rs码的快速译码方法万用码(RS码)的快速译码方法是一种表达和传输信息的常用方法,它可以把原始信息进行编码,并且可以把编码过的信息转换成原始信息。
万用码有两种传输:串行传输和并行传输。
在串行传输中,每个比特都是以一种特定的序列顺序传输;而在并行传输中,多个比特同时以异步的方式发送,也就是说,多个比特可以在同一时间段内传输,因此提高传输速度。
万用码的比特长度为1~128个比特,具有自适应性,并可以满足多种应用需求,因此在计算机系统中得到了广泛的应用。
万用码的优势在于它可以提供高速率的数据传输能力和可靠的译码能力,同时也可以支持传输长距离的信息。
万用码是一种编码方式,它可以把有限集转换成另一种有限集的字符,以便于识别和恢复原始信息。
它的实现原理是通过使用两个不同的状态序列来表示字符,状态序列的有效长度为0~8。
万用码译码是一种复杂的任务,它要求数据信号必须严格按照一定顺序输入,而且必须同时遵循一定的状态序列。
译码可以分为两个步骤:先把传输的比特流进行解码,再把解码的结果恢复成原信息。
为了把比特流解码,通常需要引入RS译码器,它可以动态地把传输的比特流解码成原有的信息,而译码过程也可以基于时序图的原理来实现,也就是说,在时序图中,万用码每个比特都可以被恢复成它原有的状态序列,从而可以得到完整的信息。
万用码译码技术不仅仅适用于数据传输,而且也广泛用于计算机程序开发、信号处理技术以及语音信号传输技术等领域。
万用码的译码算法和把原始信息转换成比特流信息的编码算法一起形成一个完整的信息系统,可以把原始信息以最低的成本实现最大速率的传输。
总之,万用码是一种快速译码的方法,在计算机系统中已经得到了广泛的应用,它可以实现高速率数据传输,提高传输效率,并有效地把原始信息转换成比特流信息,从而使数据传输更加安全可靠。

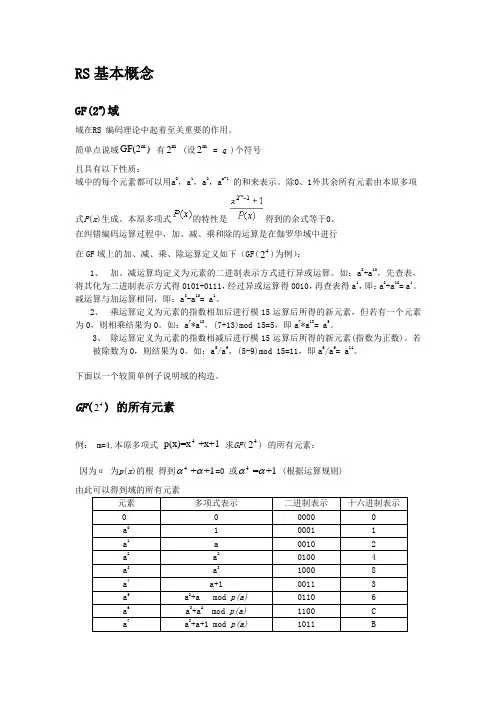
RS 基本概念GF(2m )域域在RS 编码理论中起着至关重要的作用。
简单点说域m GF(2)有m2(设m2= q )个符号且具有以下性质:域中的每个元素都可以用a 0,a 1,a 2,a m-1的和来表示。
除0、1外其余所有元素由本原多项式P (x )生成。
本原多项式的特性是得到的余式等于0。
在纠错编码运算过程中,加、减、乘和除的运算是在伽罗华域中进行 在GF 域上的加、减、乘、除运算定义如下(GF(42)为例):1、 加、减运算均定义为元素的二进制表示方式进行异或运算。
如:a 8+a 10,先查表,将其化为二进制表示方式得0101+0111,经过异或运算得0010,再查表得a 1,即:a 8+a 10= a 1。
减运算与加运算相同,即:a 8-a 10= a 1。
2、 乘运算定义为元素的指数相加后进行模15运算后所得的新元素,但若有一个元素为0,则相乘结果为0。
如:a 7*a 13,(7+13)mod 15=5,即a 7*a 13= a 5。
3、 除运算定义为元素的指数相减后进行模15运算后所得的新元素(指数为正数)。
若被除数为0,则结果为0。
如:a 5/a 9,(5-9)mod 15=11,即a 5/a 9= a 11。
下面以一个较简单例子说明域的构造。
GF (42) 的所有元素例:m=4,本原多项式 4p(x)=x +x+1求GF (42) 的所有元素:因为α为p (x )的根得到4 ++1αα=0 或4=+1αα (根据运算规则)符号(n,k)RSGF(2)域中,符号(n,k)RS的含义如下:在介绍之前需要说明一些符号。
在4m表示符号的大小,如m = 8表示符号由8位二进制数组成n表示码块长度,k表示码块中的信息长度K=n-k = 2t表示校验码的符号数t表示能够纠正的错误数目RS的编码算法GF(2)域上的RS(15,11)码,码长n=15字符,码元长k=11本项目RS纠错算法选择在4字符,码距d=5,纠错能力t=2字符,每字符为4bits,即一个码组合7.5字节。

RS(255,223)码的编译码软件实现
刘悦;刘明业;尚振宏
【期刊名称】《计算机应用与软件》
【年(卷),期】2006(23)11
【摘要】为了实现RS(255,223)的软件编码和译码,在对纠错技术进行研究的基础上,采用高级语言设计了此码的编码和译码算法.实验表明,软件实现的RS纠错编译码算法是高效的.
【总页数】3页(P46-47,116)
【作者】刘悦;刘明业;尚振宏
【作者单位】北京理工大学,北京,100081;济南大学,山东,济南,250022;北京理工大学,北京,100081;昆明理工大学,云南,昆明,650093
【正文语种】中文
【中图分类】TP3
【相关文献】
1.基于DCME算法的RS(255,223)码的译码器实现 [J], 包涛;张会生;许家栋
2.符合CCSDS标准的RS(255,223)码译码器的FPGA实现及其性能测试 [J], 石俊峰;王宇;孙辉先
3.RS(255,223)编译码器的设计与FPGA实现 [J], 向征;刘兴钊
4.高级在轨系统RS(255,223)码解交织器的设计与实现 [J], 刘佳玲
5.基于MEA算法的RS(255,223)码的译码软件实现 [J], 包涛;张会生;许家栋;毛得明
因版权原因,仅展示原文概要,查看原文内容请购买。
RS码及其编译码算法指导教员:雷 菁姓 名:龚 政 辉第一章 引言本文介绍符号取自)GF里的里德-所罗门码(Reed-Solomon(qCode,以下简称RS码)。
RS码是非二进制BCH码的一个最常用的子类,而BCH码是大家所熟悉的。
虽然RS码属于BCH码,但是它却是由Reed和Solomon于1960年采用完全不同的方法独立构造出来的。
RS码的最小距离等于它的奇偶校验符号数加一。
RS码在纠正随机符号错误和随机突发错误方面非常有效,因此被广泛应用于通信和数据存储系统中以便进行差错控制,应用领域涵盖从深空通讯到高密度磁盘等多方面。
以RS码作为外码,简单二进制码作为内码的级联方式在降低译码复杂度的同时,能够提供很高的数据可靠性。
但与二进制BCH码不同,RS码的译码需要同时确定符号错误的的位置和取值,所以它的译码更为复杂而编码算法是大体一致的。
第二章 循环纠错码的基本理论2.1 有限域(Galoias 域)基本概念及相关结论有限域(Galoias 域)就是域中元素的个数是有限的,元素的个数称为域的阶。
q 阶有限域,用()GF q 表示。
如果q 为一个素数,则集合{}0,1,2,,1q − 在模q 加法和乘法下,构成一个q 阶有限域()GF q 。
有限域在编码理论中具有重要的地位,下面给出Galoias 域的几个基本概念和相关结论。
定义1 在域()GF q 中,满足0ne =的最小正整数n 称为域的特征,e 为域的单位。
定义2以q 为特征的域是()m GF q ,1,2,m =…,称()GF q 是()m GF q 的基域,()m GF q 为()GF q 的扩域。
域中一切非零元素的特征都等于域的特征,且域的特征一定为素数。
非零元素构成的乘法群的阶定义为域中该元素的级。
若α为域()GF q 中的n 级元素,则称α为n 次单位原根。
若某一元素α的级为1q −,则称α为本原域元素。
域的特征表明了域中加法运算的循环性,而域的级则表明了域中乘法运算的循环性。
下面给出几个有限域的相关结论。
定理1在()GF q 中,每一个非0元素均满足110q x −−=。
定理2在特征为q 的域中,恒有()q q q x a x a −=−,式中,a 是域中的任一元素。
定理3有限域()GF q 中的1q −个非零元素构成一个循环群,它其中至少有一个本原元,它的其它元素分别为这个本原元的j 次幂构成0,1,,2j q =− 。
2.2 有限域上的多项式有限域GF(q)上的n 次多项式定义为:1110(),()0,1,2,,n n n n i f x f x f x f x f f GF p i n −−=++++∈= … (2.1)定理4给定任意两个多项式(),()f x g x 为()GF q 上的多项式,一定存在有唯一的多项式()q x 和()r x 使()()()()0()()()0f x q x g x r x r x g x or r x =+≤∂<∂= (2.2) 定义3 设()f x 是次数大于零的多项式,如若除了常数和常数本身的乘积以外,再不能被域()GF q 上的其它多项式除尽,则称()f x 为域()GF q 上的既约多项式。
定理5 每一个首一多项式()f x 必可分解为首一既约多项式之积,并且当不考虑因式的顺序时,这种分解是唯一的,即:1212()()()()s i f x p x p x p x ααα= (2.3) 式中,()i p x 为首一既约多项式,i α是某一正整数,1,2,,i s = 。
定义4 若()(),(),,()f x g x k x 是同时除尽多项式(),(),,()f x g x k x 的次数最高的首一多项式,则称()(),(),,()f x g x k x 是(),(),,()f x g x k x 的最大公因式,用()(),(),,()f x g x k x 表示之。
定理6多项式的欧几里德算法()(),()()()()()f x g x A x f x B x g x =+ (2.4) 式中()()0()()(),()0()()(),()A x g x f x g x B x f x f x g x ≤∂<∂−∂≤∂<∂−∂定义5若()GF q 上的多项式上()a x 、()b x 被同一多项式()f x 除时有相同的余式:12()()()()0()()()()()()a x q x f x r x r x f x b x q x f x r x =+≤∂<∂=+ (2.5)则称()a x 、()b x 关于()f x 同余,记为()()()mod ()a x b x f x ≡ (2.6) 定理7若(0)n >次首一多项式()f x 在域()GF q 上既约,则由模()f x 所组成的多项式剩余类环是一个有n q 个元素的有限域()n GF q 。
定理8 设()f x 为()GF q 上的多项式,若q 特征域的的元素ω是方程()0f x =的根,则对于一切自然数n 、nq ω也必是()f x 的根。
定义6系数取自()GF q 上,且以()m GF q ω∈为根的所有首一多项式中,必有一个次数最低的,称它为ω的最小多项式。
定理9在q 特征有限域中的每一个元素ω,皆存在有唯一的最小多项式,记为()m x ,则它具有如下性质:(1)()m x 在()GF q 域上既约;(2)若()f x 也是21,,,,m p p p ωωωω− 上的多项式,且()0f ω=,则()|()m x f x 。
定理10 设ω为q 特征有限域()m GF q 中的n 级元素,而m 是q 关于模n 的方次数,则ω的最小多项式()m x 是m 次多项式,且10()()im p i m x x ω−==−∏ (2.7)定义7元素ω的最小多项式的次数,称ω为m 次域元素。
定义8系数取自()GF q 上的以()m GF q 中本原域元素为根的最小多项式,称为本原多项式。
定理11 若ω是q 特征有限域F 上的m 次域元素,则()GF q 上的次数小于m 的、ω的多项式的全体构成域F 上的m q 阶子域。
由于有限域的阶必是其特征的幂,而有限域的特征必是素数q 的幂m q 。
因此,若有一素数q ,则一定可以从()GF q 的多项式中选出一个m 次既约多项式()p x ,以它构造出一个m q 阶有限域()m GF q 。
并且该域包含了()GF q 上所有m 次既约多项式的全部根。
如果把()p x 的一个根称为α,则由定理11,可把m q 阶有限域中的每一个元素,表示成系数在()GF q 上且次数低于m 的α多项式。
2.3 BCH 码自1950年汉明发表了纠正单个错误的码以来,几乎过了10年的时间,才于1959年由霍昆格姆 (Hocquenghem), 1960年由博斯(Bose)和雷一查得胡里 (Ray-Chaudhuri)分别提出了纠正多个随机错误的循环码——BCH 码的构造方法。
BCH 码是目前所发现的一类很好的线性纠错码类,它的纠错能力很强,特别是在短和中等码长下,其性能接近理论值,并且构造方便,编码简单。
特别是它具有严格的代数结构,因此它在编码理论中起着重要的作用。
BCH 码是迄今为止研究得最为详尽,分析得最为透彻,取得成果也最多的码类之一。
BCH 码的定义:给定任一有限域()GF q 及其扩域()m GF q ,其中,q 是素数或素数的幂,m 为某一正整数。
若码元取自()GF q 上的一循环码,它的生成多项式()g x 的根集合中含有以下1δ−个连续根:{}00012,,,m m m R δααα++−⊇ (2.8) 时,则由()g x 生成的循环码称为q 进制BCH 码。
其中,()m GF q α∈是域中的n 级元素,0()(02)m i m GF q i αδ+∈≤≤−,0m 是任意非负整数。
如果生成多项式()g x 的根中,有一个()m GF q 域中的本原域元素,则1m n q =−,称这种码长1m n q =−的BCH 码为本原BCH 码;否则,称为非本原BCH 码。
()m GF q 中元素的级一定是1m q −的因子。
2.4 RS 码RS 码是一类有很强的纠错能力的码,是二进制BCH 码的多进制推广,也是一种典型的代数几何码,它首先由里得(Reed)和索洛蒙(Solomon)应用MS 多项式于1960年构造出来的,所以称为Reed-Solomon 码,简称RS 码。
RS 码的定义:()(2)GF q q ≠上,码长1N q =−的本原BCH 码称为RS 码。
RS 码是符号域和根域相一致的BCH 码。
长为1N q =−,设计距离为δ的RS 码,生成多项式00012()()()()m m m g x x x x δααα++−=−−− (2.9) 其中0m 是任意非负整数,α为()GF q 上的本原域元素。
由此生成了一个q 进制的[1,]q q δ−−RS 码,有最小距离δ。
RS 码最小距离等于校验元的个数加1,所以也称RS码为极大最小距离可分码,简称MDS 码。
任何一个()n k RS码,对任何k个符号位置,将只有一GF q上的(,)个与这个位置内k q种符号组合之一相对应的码字。
第三章 RS 码编码算法及其高速化 常用的RS 码编码方法可采用乘法电路或者除法电路来实现。
采用乘法电路编出的码为非系统码,而采用除法电路编出的为系统码。
因此,本文将只介绍用除法电路实现的系统码的典型编码算法。
这种算法实现结构简单,但需要全局时钟信号,因此限制了编码速度。
脉动(systolic)RS 编码算法,不需要全局时钟信号,可以实现高速编码。
因此,本章也将会对这种算法进行分析。
3.1 除法电路实现的RS 系统码典型编码算法设(2)m GF 域上的待编码的信息矢量为()120,,,k k m m m −− ,可用多项式表示为如下的形式:121210()k k k k m x m x m x m x m −−−−=++++ (3.1)首先确定(2)m GF 上的一个本原域元素α,构成生成多项式: 000121()()()()m m m t g x x x x ααα++−=−−− (3.2) 其中,t 为设计的纠错符号个数,0m 为任意非负整数。
把2()t x m x 除以()g x ,所得余式是一个次数小于等于21t −次多项式()r x ,计算式如下:()2()()mod ()t r x x m x g x ≡ (3.3) 于是2()()()t C x x m x r x =−能被()g x 整除,故是一个码多项式。
这样的RS 码字中,信息集中在码字的高k 位,称这种码为系统RS 码。