变位齿轮跨齿数计算公式的合理选择
- 格式:doc
- 大小:152.50 KB
- 文档页数:6

从斜齿轮齿宽可否进行公法线长度测量的验算结果看跨齿数选择合理的重要性中煤北京煤机公司退休职工 周万峰摘要:从变位斜齿轮的齿宽可否进行公法线长度测量的验算角度,论述因跨齿数不合理给斜齿轮所造成的不良后果,从而说明跨齿数选择合理的重要性。
关键词:变位斜齿轮,跨齿数,齿宽,公法线长度。
一 、概述大伙儿明白,目前讨论公法线长度的合理与否 ,都是从公法线的测量点(量具卡脚与齿廓的切点)是不是在齿廓的合理部位为起点的。
如测量点在齿高的中点部位那么说明公法线长度是合理的,如测量点在齿根部或齿顶部那么说明公法线长度是不合理的。
但是由于跨齿数多跨或少跨一齿给斜齿轮齿宽造成的不良的后果至今还未讨论过。
本文确实是从这点动身讨论跨齿数选择合理的重要性的。
这是其一。
其二,有些人可能以为:在计算公法线长度时跨齿数多一齿或少一齿是无关紧要的,这从目前形式多样、五花八门的变位齿轮的跨齿数计算公式所确信的跨齿数不尽相同就说明那个问题。
其实这种熟悉是不妥的:跨齿数多一齿或少一齿不仅会造成公法线长度的测量点在齿廓部位上的不合理,而且还会因齿宽大小问题给斜齿轮造成不良的后果。
众所周知,测量斜齿轮的公法线长度时轮齿必需有足够的宽度,不然公法线长度是无法测量的(见图1)。
知足公法线长度测量的有效齿宽目前不论斜齿轮变成与否都是按公式βsin kn W b >进行计算的。
但是该公式只适用于标准斜齿轮,对变位斜齿轮是不适用的。
图1 斜齿轮齿宽对测量公法线长度的阻碍如变位斜齿轮也用该公式计算,不仅理论上说不通,就在事实上有时也是不行的(见《变位斜齿轮知足公法线长度测量的有效齿宽的正确计算》一文)。
变位斜齿轮有效齿宽的验算公式应为:k kn W b βsin > (1)kn W ——斜齿轮的公法线长度;k β——斜齿轮公法线测量点所在圆的螺旋角。
由公式(1)知,齿宽可否进行公法线长度的测量是由kn W 和k β两个值决定的。
若是k kn W β或不合理(或kn W 和k β都不合理)不仅使公法线测量点在轮齿上的部位不合理,阻碍公法线长度测量的准确性,而且还将造成齿宽的不合理。

变位齿轮计算公式变位齿轮是一种特殊的齿轮传动装置,由于其特殊的设计结构,在很多工程领域中被广泛应用。
变位齿轮的计算涉及到很多参数和公式,下面将介绍1200字以上的变位齿轮计算公式。
1.变位齿轮的模数计算公式:变位齿轮的模数实际上是齿轮的基本参数之一,是计算齿轮尺寸和性能的重要依据。
模数的计算公式如下:m=(π*d)/(z+2)其中,m为模数,d为齿轮的总直径,z为齿数。
2.变位齿轮的齿宽计算公式:变位齿轮的齿宽决定了齿轮的受力和传动能力,齿宽的计算公式如下:bw = K * m其中,bw为齿宽,K为齿宽系数,m为模数。
3.变位齿轮的中心距计算公式:变位齿轮的中心距是指两个齿轮中心线之间的距离,中心距的计算公式如下:a=(m*(z1+z2))/2其中,a为中心距,m为模数,z1和z2分别为两个齿轮的齿数。
4.变位齿轮的齿数比计算公式:齿数比是指两个齿轮齿数的比值,齿数比的计算公式如下:i=z2/z1其中,i为齿数比,z1为主动齿轮的齿数,z2为从动齿轮的齿数。
5.变位齿轮的齿侧间隙计算公式:齿侧间隙表示两个齿轮侧面的距离,可以通过以下计算公式进行计算:cg = 0.25 * m * (z1 + z2) + c其中,cg表示齿侧间隙,m表示模数,z1和z2表示两个齿轮的齿数,c表示一个修正系数。
6.变位齿轮的分度圆直径计算公式:分度圆直径是指齿轮两齿间的直径,可以通过以下计算公式进行计算:d=m*z其中,d表示分度圆直径,m表示模数,z表示齿轮的齿数。
7.变位齿轮的螺旋角计算公式:螺旋角表示齿轮齿槽相对于圆柱面的旋转角度,可以通过以下计算公式进行计算:φ = tan^(-1)((cosα1/sinα1)+((z1+z2)/(2m*tanα1)))其中,φ表示螺旋角,α1表示变位齿轮的压力角,z1和z2分别表示两个齿轮的齿数,m表示模数。
8.变位齿轮的齿形因数计算公式:齿形因数是表示齿轮齿形的一个参数,可以通过以下计算公式进行计算:X = (2*m*(cosα1+cosα2))/(π*tan(α1+α2))其中,X表示齿形因数,m表示模数,α1和α2分别表示两个齿轮的压力角。

目前手册上的跨齿数计算公式大都是近似的,有误差的,并非精确的计算公式,因而有时影响跨齿数的合理性。
就是那些精确的公式,它们在角度变位中也是有不足之处的。
而且至今在手册上似乎还未见到有斜齿精确的跨齿数计算公式。
有人说:“手册上的5.01800+'=n z k α不就是标准斜齿轮跨齿数精确的计算公式吗?”不,它算出的也是近似值(文章后面进行验证)。
笔者已退休多年,精力尚可,因而对此进行了研究、探讨,于是给出一个高度、角度变位都是情况良好的公式。
公式为:5.01)cos sin 2(+--'=παααzinv m xm W k k (用于直齿) (1)5.01)cos sin 2(+'--'=παααn n n n n n n inv z m m x W k (用于斜齿) (1)公式中的'k W 和'n W 当为高度变位直齿时, bKd xm d W 22)2(-+='; 斜齿时, b bn n n d m x d W βcos )2(22-+='。
当为角度变位直齿时, b k d xm d W 22)9.1(-+=';斜齿时, 。
cos )9.1(22b bn n n d m x d W β-+='上列公式中:d ——分度圆直径; b d ——基圆直径;m ——模数,斜齿时为n m ;z —— 齿数;___z '斜齿轮的假想齿数,ntinv inv zz αα=' ; ___α压力角,斜齿轮法面压力角为n αx —— 变位系数,斜齿时法面变位系数为n x ; ___bβ斜齿轮基圆螺旋角;k W '——直齿轮的公法线长度原始计算值 ; n W '——斜齿轮的公法线长度原始计算值 。
2、公式(1)的由来公式(1)是怎么来的?其实它的来历很简单,就是由公法线长度计算公式变换而来的。
公法线长度计算公式为 :[] sin 2)5.0( cos ααπαm x zinv k m W k ++-= (直齿) (2)[] sin 2)5.0cos n n n n n n n m x inv z k m W ααπα+'+-=((斜齿) (2) 将公式(2)中的k 移到等号左边,将k W 和n W 移到等号右边(且变为k W '和n W ')即为公式(1)。

变位齿轮跨齿数计算公式的合理选择 中煤北京煤机公司退休职工 周万峰摘要:目前变位圆柱齿轮的跨齿数,教材、手册上大都给出的是用公式“πααxctg z k 25.01800++=”和“公法线长度 )(**kn k W W 表”进行选择。
其实该公式和该表并不是情况良好的公式和情况良好的选择用表。
本文对此进行了分析和论证,并推荐出情况良好的公式和给出合理的选择用表。
关键词:跨齿数,公法线长度,公法线长度测量点。
目前手册上对变位齿轮的跨齿数大都给出两种确定方法:一种是用公式计算,一种是查图表。
用公式计算绝大多数手册都给出的是下面的公式: απαctg x z k 25.01800++= (直齿) (1) n n n ctg x z k απα25.01800++'= (斜齿) (1) 用查表法手册大都给出的是“020 1====n n m m αα、的标准齿轮的公法线长度表 )(**k k W W ”(见表1)。
笔者认为:公式(1)并不是个情况良好的公式,表1也不是个跨齿数合理的选择用表。
下面进行分析和论证。
表1 公法线长度)(**kn k W W020 1='===αα,m m注:本表选自1991年版由徐灏任主编的《机械设计手册》第三卷“表23·2——13”。
该表跨齿数偏少,公法线的测量点靠近齿根,情况不良。
今天各家手册大都有这个表。
1、表1不是跨齿数合理的选择用表 今天各家手册都给出了表1这样的“公法线长度 )(**k k W W 表”,但该表并不是个公法线长度计算合理的选择用表:⑴ 该表是将“公法线长度”与“基圆弧长”混为一谈的。
该表称“ )(**kn k W W 为 1=m (或)1=n m 的标准齿轮的公法线长度”是不合理的。
对z=86这个齿轮而言,经验证当k=10、k=11时,它们对应的2020.32)(2497.29)(==****kn k kn k W W W W 和是这个标准齿轮的公法线长度;但当k=12、k=13时,它们对应的1060.38)(1540.35)(==****kn k kn k W W W W 和就不是这个标准齿轮的公法线长度了。

变位齿轮的计算方法1 变位齿轮的功用及变位系数变位齿轮具有以下功用:(1)避免根切;(2)提高齿面的接触强度和弯曲强度;(3)提高齿面的抗胶合和耐磨损能力;(4)修复旧齿轮;(5)配凑中心距。
对于齿数z=8~20的直齿圆柱齿轮,当顶圆直径d a=mz+2m+2xm时,不产生根切的最小变位系数x min,以及齿顶厚S a=0.4m和S a=0时的变位系数x sa=0.4m和x sa=0如表1所列。
2 变位齿轮的简易计算将变位齿轮无侧隙啮合方程式作如下变换:总变位系数中心距变动系数齿顶高变动系数表 1 齿数z=8~20圆柱齿轮的变位系数z x min x sa=0.4m x sa=08 910111213141516171819 200.53 0.47 0.42 0.36 0.30 0.24 0.18 0.12 0.06 0-0.05 -0.11 -0.170.180.220.270.310.350.390.430.460.500.530.560.590.620.560.630.700.760.820.880.930.981.031.081.131.181.23或Δy=xΣ-y式中:α——压力角,α=20°;α′——啮合角;z2、z1——大、小齿轮的齿数。
将上述三式分别除以,则得:由上述公式可以看出,当齿形角α一定时,x z、y z和Δy z均只为啮合角α′的函数。
在设计计算时,只要已知x z、y z、Δy z和α′四个参数中的任一参数,即可由变位齿轮的x z、y z、Δy z和啮合角α′的数值表(表2)中,查出其他三个参数,再进行下列计算。
一般齿轮手册上均列有此数值表。
式中正号用于外啮合,负号用于内啮合。
3 计算实例例1:已知一对外啮合变位直齿轮,齿数z1=18,z2=32,压力角α=20°,啮合角α′=22°18′,试确定总变位系数xΣ、中心距变动系数y及齿顶高变动系数Δy。

齿轮计算公式机械制图方面=>齿轮计算公式2009-10-26 11:521 齿轮模数:m=p/π齿轮模数 m=齿距 p 除以 3.14测绘时的简易计算 m=齿顶圆直径(外径)d 除以(齿数z+2)2 齿轮分度圆直径:d=mz分度圆直径d=模数m 乘以齿数z3 齿轮压力角:标准齿轮的压力角为20度压力角标准为20度其他还有14.5度17.5度15度25度和28度4 齿轮变位系数:用范成法加工齿轮时,刀具中心线不与齿轮的分度圆相切,刀具中心与齿轮的分度圆的距离除以模数所得的商就是齿轮的变位系数。
刀具中心线在齿轮的分度圆之外,为正变位,变位系数为正,反之为负。
注:一般一对齿轮啮合一大一小相差悬殊时,小齿轮要做正变位,大齿轮做负变位,以保证它们的使用寿命比较均衡5 齿轮跨齿数:k=zα/180+0.5跨齿数k=齿数x压力角/180+0.5 (注:必须四舍五入取整数)6 齿轮公法线长度直齿公式Wk=mcosα[(k-0.5)π+zinva] 简化为;Wk=m[2.9521*(k-0.5)+0.014z]斜齿公式Wk=mcosα[(k-0.5)π+zinva]+2xtanα α=20时tanα-α=0.01490438其中:α= 压力角标准为20度其他还有 14.5度17.5度15度25度和28度K = 跨齿数 X=变位系数invα=tan(α)-α7 齿轮齿跳 Fr一般为0.025 (表示各齿跳动公差)8 齿轮齿向Fβ一般为0.008 (表示各齿向公差)9 齿轮齿形 Ff 一般为0.008 (表示各齿形状大小公差)10 齿轮齿距p=πm m 模数11 齿轮齿顶高 ha=ha*m12 齿轮齿根高 hf=(ha*+c*)m13 齿轮齿顶圆直径 da=(d+2ha) d :分度圆直径 ha ;齿顶高14 齿轮齿根圆直径 df=d-2hf=(z-2ha-2ca*)m15 中心距 a=(d1+d2)/2=(z1+z2)m/2 d1和d2配对的两个齿轮分度圆直径;z1和z2两齿轮齿数。

变位圆柱齿轮跨测齿数的简便计算中煤北京煤机公司退休职工周万峰摘要:本文给出一个简便的跨齿数计算的经验公式,并验证了该公式确定的跨齿数是合理的。
关键词:变位齿轮,跨齿数,公法线长度。
1、推荐笔者的经验公式目前变位齿轮的跨齿数计算公式可谓形式多样,五花八门:有教科书上公式,有各种手册上公式,有参考书上的公式,还有近些年来杂志上发表的公式等等。
如果将它们汇集起来恐怕不下十数个之多。
但最常见的还是表1所列的几个公式。
表1 几个常见的变位齿轮的跨齿数计算公式序号用于直齿用于斜齿1234[]+0.5 []+0.5注:早先公式1多为教材所选用。
公式2《机修手册》选用。
公式3《齿轮手册》选用。
公式4多为《机械设计手册》选用。
不难看出,表1中的几个公式大都比较复杂:平方、开放、三角函数等等项目很多,计算起来十分不便。
而且有的公式有时确定的跨齿数也不合理。
有鉴于此,笔者通过分析研究,并进行了大量的算例计算以及反复验证后给出一个跨齿数计算的经验公式。
当压力角时,经验公式为:——齿数,斜齿时代入(,可查手册)。
——变位系数,斜齿时。
——与变位系数正负有关的系数。
当变位系数为正(时p=1.4,当变位系数为负(时p=1.9。
通过大量的算例验证后得知,当变位系数为负时,由经验公式确定的跨齿数与表1中的公式(4)确定的跨齿数是完全一样的(见表2)。
当变位系数为正时,经验公式与表1中的(2)、(3)、(4)确定的跨齿数绝大多数是相同的,只在极少数情况下两者的跨齿数不同。
但在不同的情况下,经验公式的情况比理论公式的情况还好些(见表3)。
这就说明经验公式确定的跨齿数是合理的。
表2 变位直齿轮跨齿数计算公式比较表()齿数z 变位系数x跨齿式计算值确定的跨齿数齿数z变位系数x跨齿数计算值确定的跨齿数经验公式理论公式经验公式理论公式经验公式理论公式经验公式理论公式14 0.40 2.61 2.63 3 3 56 -0.4 5.96 5.97 6 6 19 0.60 3.45 3.47 3 3 67 -0.52 6.95 6.96 7 7 24 0.70 4.14 4.18 4 4 80 -0.63 8.19 8.19 8 8 28 0.72 4.61 4.67 5 5 96 -0.7 9.83 9.85 10 10 52 1.0 7.67 7.80 8 8 124 -0.8 12.75 12.79 13 13 100 1.50 13.71 13.96 14 14 150 -1.20 14.89 14.90 15 15注:表2中的“理论公式”为表1中的公式(4)。

变位齿轮参数计算公式引言变位齿轮是一种常用的齿轮传动装置,可以实现不等速传动。
在实际设计和计算中,需要了解和确定变位齿轮的参数,以便满足传动需求。
本文将介绍一些常用的变位齿轮参数计算公式,帮助读者了解和计算变位齿轮的相关参数。
1. 转速比计算公式对于一个变位齿轮传动系统,转速比是一个重要的参数,表示两轴之间的转速比例关系。
通常以N1、N2分别表示第一齿轮的转速和第二齿轮的转速。
变位齿轮的转速比计算公式如下:转速比 = (N2 - N1) / N12. 锥齿轮的齿数计算公式对于一对变位齿轮中的锥齿轮,其齿数计算公式如下:Z = (Z1 * m1) / m2其中,Z为锥齿轮的齿数,Z1为直齿轮的齿数,m1为直齿轮的模数,m2为锥齿轮的模数。
3. 螺旋角计算公式螺旋角是变位齿轮的一个重要参数,表示齿轮齿线沿轴向的倾斜角度。
对于一对变位齿轮中的螺旋齿轮,其螺旋角的计算公式如下:β = atan(tan(α) - (m2 * (Z2 - Z1)) / (2 * π * a))其中,β为螺旋角,α为压力角,m2为齿数为Z2的螺旋齿轮的模数,Z1为另一齿轮的齿数,a为啮合齿轮的轴向分度圆半径。
4. 齿面距计算公式齿面距是变位齿轮的另一个重要参数,表示两个啮合齿轮齿面上同一点之间的距离。
对于一对变位齿轮中的两个螺旋齿轮,其齿面距的计算公式如下:h = m2 * b / cos(α)其中,h为齿面距,m2为螺旋齿轮的模数,b为螺旋齿轮的齿宽,α为压力角。
5. 压力角计算公式压力角是变位齿轮设计中的一个重要参数,表示齿形曲线的锋角与轴线的夹角。
通常使用以下计算公式得到压力角的值:cos(α) = (Z1 + Z2) / (2 * m2 * a)其中,α为压力角,Z1和Z2分别为两个啮合齿轮的齿数,m2为螺旋齿轮的模数,a为啮合齿轮的轴向分度圆半径。
结论本文介绍了几个重要的变位齿轮参数计算公式,包括转速比、锥齿轮的齿数、螺旋角、齿面距和压力角的计算公式。


齿轮变位系数公式
齿轮是机械传动中常用的元件,齿轮传动的稳定性和可靠性是机械传动的关键之一。
在齿轮传动中,齿轮的变位系数是一个重要的参数,它可以反映齿轮传动的稳定性和可靠性等性能指标。
齿轮变位系数是指齿轮轴线之间的垂直距离与模数的比值,通常用符号ε表示。
齿轮变位系数的计算公式如下:
ε = (y1 + y2) / (2m)
其中,y1和y2分别表示相邻两个齿轮齿数之差的绝对值,m为模数。
该公式适用于所有齿轮传动类型,包括直齿轮、斜齿轮、圆弧齿轮等。
齿轮变位系数的计算可以通过手算和计算机辅助设计软件进行。
在手算时,需要准确测量齿轮的齿数和模数,并应用齿轮变位系数公式进行计算。
在计算机辅助设计软件中,可以直接输入齿轮参数,软件会自动计算齿轮变位系数。
齿轮变位系数的大小对齿轮传动的稳定性和可靠性有着重要的影响。
当齿轮变位系数太大时,齿轮传动会出现过载、振动等问题,影响传动系统的性能;当齿轮变位系数太小时,齿轮传动会出现接触不良、噪声等问题,同样会影响传动系统的性能。
因此,在齿轮设计
和选择时,需要合理地选取齿轮变位系数,以保证传动系统的稳定性和可靠性。
齿轮变位系数是齿轮传动中一个重要的性能指标,它的大小对传动系统的稳定性和可靠性有着重要的影响。
齿轮变位系数的计算公式简单易用,可以帮助工程师准确地计算齿轮的变位系数,从而保证传动系统的性能。
变位齿轮跨齿数计算公式的合理选择
一、引言
在机械装配中,齿轮跨齿数计算是一个重要环节,它是确定行星齿轮
的精密联接、变位齿轮的曲率,以及传动齿轮的精确性能的关键步骤。
由
于此过程受齿轮的各种参数(转动惯量、分度圈、齿数、模数、内径等)
的影响,因此,必须采用正确的公式来确定齿轮跨齿数,以满足特定的齿
轮应用需求。
针对不同的齿轮应用,有不同的齿轮跨齿公式可供选择。
但是,由于
齿轮参数的复杂性,采用的公式必须具有足够的准确性、可靠性和适用性,以确保正确的齿轮跨齿。
1、传统的斯蒂尔公式
传统的斯蒂尔公式是计算齿轮跨齿数的一种有效方法,由英国工程师
和科学家Willard C.Stiehl提出。
该公式涉及到两种不同类型的齿轮,
即基本齿轮和参考齿轮,可计算出此类齿轮之间的跨齿数。
斯蒂尔公式可
用于满足许多齿轮应用的实践计算,但其准确性依赖于齿轮参数的精确度。
2、现代微分公式
在现代齿轮应用中,现代微分公式可用于计算不同类型的齿轮的跨齿数。
基本齿轮和参考齿轮之间的跨齿数可以用微分公式计算出来,但是它
的可靠性要比传统的斯蒂尔公式要高。
变位齿轮的计算方法变位齿轮是一种齿轮传动装置,它由两个或多个具有不同齿数的齿轮组成,通过啮合来传递动力和运动。
变位齿轮广泛应用于各种机械设备中,如汽车变速器、工程机械、纺织机械等。
在设计和计算变位齿轮时,需要考虑齿轮的齿数、模数、齿宽、啮合角等参数。
下面将介绍变位齿轮的计算方法。
一、齿轮齿数的选择:在变位齿轮传动设计中,首先要确定齿轮的齿数。
齿数的选择需要考虑传动比、装置的重量、运动平稳性等因素。
一般来说,齿数越多,传动比越大,装置越重,运动平稳性越差。
因此,需要在齿数和传动比之间进行权衡。
二、模数的确定:模数是变位齿轮设计中的一个重要参数,它决定了齿轮的尺寸和齿面强度。
模数的选择需要根据变位齿轮的工作条件和要求来确定。
通常情况下,模数应该使齿轮在满足强度要求的前提下,尽可能小,以减小齿轮的体积和重量。
三、齿宽的计算:齿宽是指齿轮齿面的有效工作宽度,它决定了变位齿轮传动的承载能力和寿命。
齿宽的计算需要考虑齿轮的载荷、齿数和模数等因素。
一般来说,齿宽应该使齿轮在满足强度要求的前提下,尽可能小,以减小齿轮的尺寸和重量。
四、啮合角的计算:啮合角是指变位齿轮齿面的啮合角度,它决定了齿轮传动的配合性能和工作平稳性。
啮合角的计算需要考虑齿轮的齿数、齿宽和模数等因素。
一般来说,啮合角应该使齿轮在满足配合性能要求的前提下,尽可能小,以减小齿轮的摩擦和磨损。
以上是变位齿轮的基本计算方法。
在实际设计和计算中,还需要考虑齿面的修形、齿轮的加工精度、齿轮的轴向力和径向力等因素。
设计变位齿轮需要综合考虑齿轮传动的强度、齿轮的尺寸和重量、齿轮的运动平稳性和配合性能等因素,以满足机械设备的要求。
变位齿轮几何参数计算变位齿轮是一种能够实现传动的机械装置,其特点是能够传递转矩和变速的功能。
变位齿轮几何参数计算是设计变位齿轮传动的重要步骤之一,本文将对变位齿轮几何参数计算进行详细介绍。
主要内容涵盖变位齿轮的基本概念、几何参数的计算方法以及相关的应用举例。
一、变位齿轮的基本概念变位齿轮是由一对轴平行并且具有相同模数的齿轮组成的,其中一只齿轮的齿数是固定不变的,称为定齿轮;另一只齿轮的齿数是可变的,称为动齿轮。
变位齿轮传动通过改变动齿轮的齿数来实现变速。
二、几何参数的计算方法1.变位齿轮的齿数计算变位齿轮的齿数计算需要确定定齿轮的模数和动齿轮的模数变化量。
固定的定齿轮齿数N1可根据传动比和任意选定的动齿轮齿数N2计算得到。
变位齿轮的齿轮传动比等于定齿轮的齿数除以动齿轮的齿数,即传动比i=N1/N22.变位齿轮的齿廓计算变位齿轮的齿廓计算需要根据变位齿轮的齿数、螺旋角和压力角来确定。
变位齿轮的齿形是沿齿轮直齿廓方向逐渐变化的。
在变位齿轮的齿廓计算中,首先需要确定变位齿轮的基圆半径和齿顶高,然后根据基圆半径和齿顶高计算齿根高和齿根圆半径。
最后,根据齿根高、齿根圆半径和变位齿轮的螺旋角、压力角来计算出齿廓。
三、相关应用举例1.变位齿轮传动装置的设计根据给定的传动比和传动功率,可以利用变位齿轮几何参数计算的结果设计出适合的变位齿轮传动装置,以实现所需的变速和传动效果。
2.变位齿轮传动的优化通过调整变位齿轮的几何参数,如齿数、齿廓等,可以优化传动装置的性能,比如降低传动中的噪音和振动,提高传动效率等。
3.变位齿轮的制造利用变位齿轮几何参数计算的结果可以指导齿轮的加工制造,保证制造出的变位齿轮符合设计要求。
总结:变位齿轮几何参数计算是设计变位齿轮传动的基本步骤之一,通过计算齿数和齿廓等参数可以实现变位齿轮传动的设计、优化和制造。
变位齿轮传动在机械装置中具有重要的应用和发展前景,对于提高传动效果和性能具有重要意义。
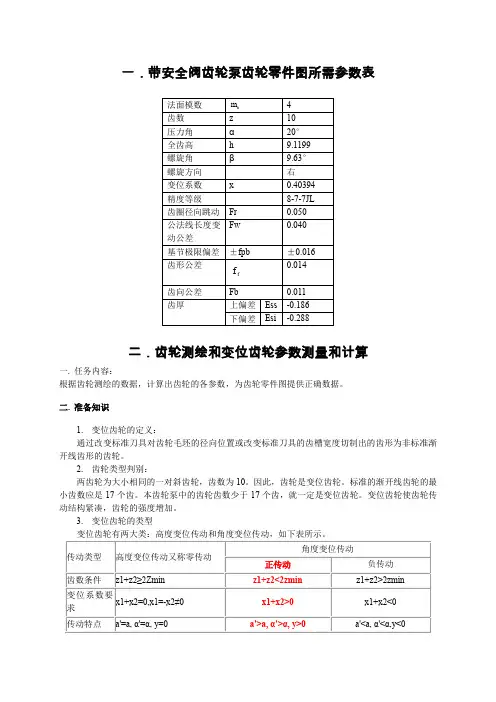
一.带安全阀齿轮泵齿轮零件图所需参数表法面模数nm 4齿数z 10压力角α20°全齿高h 9.1199螺旋角β9.63°螺旋方向右变位系数x 0.40394精度等级8-7-7JL齿圈径向跳动Fr 0.050公法线长度变动公差Fw 0.040基节极限偏差±fpb ±0.016齿形公差ff0.014齿向公差Fb 0.011齿厚上偏差Ess -0.186下偏差Esi -0.288二.齿轮测绘和变位齿轮参数测量和计算一.任务内容:根据齿轮测绘的数据,计算出齿轮的各参数,为齿轮零件图提供正确数据。
二.准备知识1.变位齿轮的定义:通过改变标准刀具对齿轮毛坯的径向位置或改变标准刀具的齿槽宽度切制出的齿形为非标准渐开线齿形的齿轮。
2.齿轮类型判别:两齿轮为大小相同的一对斜齿轮,齿数为10。
因此,齿轮是变位齿轮。
标准的渐开线齿轮的最小齿数应是17个齿。
本齿轮泵中的齿轮齿数少于17个齿,就一定是变位齿轮。
变位齿轮使齿轮传动结构紧凑,齿轮的强度增加。
3.变位齿轮的类型变位齿轮有两大类:高度变位传动和角度变位传动,如下表所示。
传动类型高度变位传动又称零传动角度变位传动正传动负传动齿数条件z1+z2≥2Zmin z1+z2<2zmin z1+z2>2zmin 变位系数要求x1+x2=0,x1=-x2≠0x1+x2>0 x1+x2<0 传动特点a'=a, α'=α, y=0 a'>a, α'>α, y>0 a'<a, α'<α,y<0主要优点小齿轮取正变位,允许z1<zmin ,减小传动尺寸。
提高了小齿轮齿根强度,减小了小齿轮齿面磨损,可成对替换标准齿轮。
传动机构更加紧凑,提高了抗弯强度和接触强度,提高了耐磨性能,可满足a'>a 的中心距要求。
重合度略有提高,满足a'<a 的中心距要求。
齿轮的变位系数的选择齿轮的变位系数什么是变位系数?变位系数x是径向变位系数,加工标准齿轮时,齿条形刀具中线与齿轮分度圆相切。
加工变位齿轮时齿条形刀具中线与齿轮分度圆相切位置偏移距离xm,外移x为正,内移x为负。
除了圆锥齿轮有时采用切向变位xt外,圆柱齿轮一般只采用径向变位。
变位系数x的选择不仅仅是为了凑中心距,而主要是为了提高强度和改善传动质量。
变位齿轮的主要功用如下:(1)减小齿轮传动的结构尺寸,减轻重量在传动比一定的条件下,可使小齿轮齿数zl<zmin,从而使传动的结构尺寸减小,减轻机构重量。
(2)避免根切,提高齿根的弯曲强度当小齿轮齿数z1<zmin时,可以利用正变位避免根切,提高齿根的弯曲强度。
x≥xmin=(Z-Zmin)/Zmin,对α=20o 时,Zmin=17。
(3)提高齿面的接触强度采用啮合角α'>α的正传动时,由于齿廓曲率半径增大,故可以提高齿面的接触强度。
(4)提高齿面的抗胶合耐磨损能力采用啮合角α'>α的正传动,并适当分配变位系数xl、x2,使两齿轮的最大滑动率相等时,既可降低齿面接触应力,又可降低齿面间的滑动率以提高齿轮的抗胶合和耐磨损能力。
(5)配凑中心距当齿数z1、z2不变的情况下,啮合角α'不同,可以得到不同的中心距,以达到配凑中心距的目的。
(6)修复被磨损的旧齿轮齿轮传动中,小齿轮磨损较重,大齿轮磨损较轻,可以利用负变位把大齿轮齿面磨损部分切去再使用,重配一个正变位小齿轮,这就节约了修配时需要的材料与加工费用。
(1)润滑条件良好的闭式齿轮传动当齿轮表面的硬度不高时(HBS<350),即对于齿面未经渗碳、渗氮、表面淬火等硬化处理的齿轮,齿面疲劳点蚀或剥伤为其主要的失效形式,这时应选择尽可能大的总变位系数x,即尽量增大啮合角,以便增大啮合节点处齿廓的综合曲率半径,减少接触应力,提高接触强度与疲劳寿命。
当轮齿表面硬度较高时(HBS>350),常因齿根疲劳裂纹的扩展造成轮齿折断而使传动失效,这时,选择变位系数应使齿轮的齿根弯曲强度尽量增大,并尽量使相啮合的两齿轮具有相近的弯曲强度。
变位齿轮跨齿数计算公式的合理选择 中煤北京煤机公司退休职工 周万峰摘要:目前变位圆柱齿轮的跨齿数,教材、手册上大都给出的是用公式“πααxctg z k 25.01800++=”和“公法线长度 )(**kn k W W 表”进行选择。
其实该公式和该表并不是情况良好的公式和情况良好的选择用表。
本文对此进行了分析和论证,并推荐出情况良好的公式和给出合理的选择用表。
关键词:跨齿数,公法线长度,公法线长度测量点。
目前手册上对变位齿轮的跨齿数大都给出两种确定方法:一种是用公式计算,一种是查图表。
用公式计算绝大多数手册都给出的是下面的公式: απαctg x z k 25.01800++= (直齿) (1) n n n ctg x z k απα25.01800++'= (斜齿) (1) 用查表法手册大都给出的是“020 1====n n m m αα、的标准齿轮的公法线长度表 )(**k k W W ”(见表1)。
笔者认为:公式(1)并不是个情况良好的公式,表1也不是个跨齿数合理的选择用表。
下面进行分析和论证。
表1 公法线长度)(**kn k W W020 1='===αα,m m注:本表选自1991年版由徐灏任主编的《机械设计手册》第三卷“表23·2——13”。
该表跨齿数偏少,公法线的测量点靠近齿根,情况不良。
今天各家手册大都有这个表。
1、表1不是跨齿数合理的选择用表 今天各家手册都给出了表1这样的“公法线长度 )(**k k W W 表”,但该表并不是个公法线长度计算合理的选择用表:⑴ 该表是将“公法线长度”与“基圆弧长”混为一谈的。
该表称“ )(**kn k W W 为 1=m (或)1=n m 的标准齿轮的公法线长度”是不合理的。
对z=86这个齿轮而言,经验证当k=10、k=11时,它们对应的2020.32)(2497.29)(==****kn k kn k W W W W 和是这个标准齿轮的公法线长度;但当k=12、k=13时,它们对应的1060.38)(1540.35)(==****kn k kn k W W W W 和就不是这个标准齿轮的公法线长度了。
因为它们的测量点都在齿顶圆之外,不符合公法线长度的定义,所以它们不是公法线长度。
下面对) 12(k 1540.35==*k W 这条所谓公法线长度的合理性进行验证如下:① 计算1540.35=*k W 的测量点所在圆直径k d 22b k k d W d +=1540.35=*k W ,b d 为基圆直径,8136.8020cos 86d 86861mz d cos 0b ==∴=⨯===,,αd d b 。
1286.888136.801540.3522=+=∴k d 。
② 计算标准齿轮的齿顶圆直径a da a a h h d d , 2+=为齿顶高,∴==, 1m h a 881286=⨯+=a d 。
③ 计算公法线测量点至齿顶的距离a s0643.02)1286.8888( 2)(-=-=∴-=a k a a s d d s ,。
公法线测量点至齿顶的距离为负值,这说明测量点在齿顶圆之外,量具卡脚不能与渐开线齿廓相切,不符合公法线长度的定义,所以) 12(k 1540.35==*k W 这条线段不是公法线长度。
K=12的这条都不是公法线长度,那k=13的这条就更不是公法线长度了。
在这4条线段中有两条是公法线长度,有两条不是公法线长度;而教材、手册一概称它们都是公法线长度,显而易见这种说法是站不住脚的。
那么k=12、k=13这两条线段是什么呢?它们是该齿轮含12个齿和13个齿的基圆弧长而不是公法线长度。
然而把“基圆弧长”说成是“公法线长度”这显然是指鹿为马了。
那么在这种情况下(如表1中既有公法线长度,又有基圆弧长)怎么办呢?笔者认为在这种情况下应将它们一概称做“基圆弧长”是说得通的。
因为凡是公法线长度必然是基圆弧长,而没有公法线长度功能的基圆弧长,它本身就是基圆弧长。
因此在这种情况下一概称它们是“基圆弧长”是合理的,而一概称它们为“公法线长度”是不合理的。
⑵ 表1给出的变位系数范围过大,因而有些跨齿数是不合理的 比如z=86这个齿轮当x>0.6~1.2时k=11,变位系数范围过大了,不合理。
x>0.26~0.903时k=11才是合理的;当x>0.903~1.2时就该按k=12计算了(见表2)。
表1误差如此之大,怎能保证公法线长度的合理性及合理测量呢?须知:跨齿数多跨或少跨1齿有时会给公法线长度的测量造成“测量点在齿顶部或齿根部,使公法线长度测量不准或无法测量”,而且还会给斜齿轮造成不良的后果。
详见拙作《从斜齿轮齿宽能否进行公法线长度的测量的验算结果,看跨齿数选择合理的重要性》一文。
表1的问题是:跨齿数偏少,公法线测量点靠近齿根;公法线长度测量不准,影响齿厚精度。
⑶ 表1只有正变位系数而没有负变位系数是不全面的。
表1中只有正变位系数而没有负变位系数是不全面的。
谁能说只设计正变位齿轮而不设计负变位齿轮呢?当设计负变齿轮时设计者还需另找资料,这不是增加麻烦吗?鉴于表1种种不合理、不完整之情况,笔者不揣冒昧,将表1改造成表2的样子(见表2)。
笔者认为:表2才是变位齿轮跨齿数选择和公法线长度计算的合理用表。
2、公式(1)并不是个情况良好的公式公式(1)是今天众多手册如《机械设计手册》、《机修手册》等手册热选的公式,但它并不是个情况良好的公式。
它的跨齿数往往偏多,公法线的测量点靠近齿顶,情况不良(见表3)。
在众多跨齿数计算公式中下面的公式是情况良好的公式:5.02cos arccos 1800++=x z z z k α (直齿) (2) 5.02cos arccos 1800++'''=n n x z z z k α (斜齿) (2) 经验证,公式(2)确定的跨齿数一般都是合理的,公法线的测量点一般都在齿高的中点部位,情况良好(见表3)。
表2 基 圆 弧 长 *L0201====m m αα注 :① 表2是笔者根据表1改造的。
② 绝对值符号内数字是负变位系数的据对值。
负变位系数按绝对值的大小查取跨齿数是为了习惯上的方便。
如95.0-=x 则取8=k ;如25.1-=x 则取7=k 。
如此而已。
③ 变位系数的范围是由本文公式(2)计算的。
表3 变位齿轮跨齿数选择方法优劣之比较0 注:① 从本表明显看出,表1公法线的测量点靠近齿根,公式(1)的测量点靠近齿顶,情况均不良。
而公式(2)和表2的测量点都在齿高的中点部位,情况甚好。
② 4.1 41==x k ,的跨齿数6=k 也是从“表23·2——13”选取的(见表1的“注”)。
③ 本表的齿数和变位系数肯定不是用于高度变位、而是用于角度变位的。
之所以取mm h 25.11=(实际上)25.11mm h <是为了计算上的方便、省事(偷懒,因为角度变位齿轮的全齿高计算非常麻烦),其说明的道理是一样的。
3、表1、表2、公式(1)、公式(2)优劣之比较下面用表3的数据分析几个齿数,看看表1、公式(1)以及公式(2)和表2是否如笔者所说的那样。
例如当z=86、x=2.7时从表1知k=13,用公式(1)计算k=15 ;而用公式(2)计算或从表2查取都是k=14。
当K=13、k=15、k=14时它们的公法线测量点至齿顶、齿根的距离分别、依次为 4.76 10.051.20 13.12.8,,(见表3)。
显然表1的跨齿数偏少(k=13),公法线的测量点靠近齿根()13.312.8了;而公式(1)的跨齿数又偏多(k=15),公法线的测量点靠近齿顶(05.1020.1)了。
只有公式(2)和表2确定的跨齿数k=14才是合理的,公法线的测量点正在齿高的中点部位(49.676.4),情况甚好。
其他几个齿数亦是如此(见表3)。
这就证明了“公法线长度)(**kn k W W 表”(即表1)和公式(1)确定的跨齿数在这几个算例中都是不合理的。
而公式(2)和表2确定的跨齿数才是合理的。
有鉴于此,笔者建议手册应该选公式(2)或其他情况良好的公式和表2作为变位齿轮跨齿数计算公式和公法线长度的选择用表。
这样才能更好地保障公法线长度的合理性和合理测量,从而更好地保证齿厚精度。
注:该文写于2001年;同年10月投稿给《机械制造》杂志,未发表。
作者赘言齿轮的跨齿数不论用公式计算还是查图表,它们确定的跨齿数本来都应该是一样的。
比如某个齿轮的跨齿数用公式计算是k=5,那么用查图表的方法也应是k=5才对。
然而就在同一本教材或同一部手册上,用它们给出的公式和它们给出的图表查取,它们的结果有时并不一样:有的相差一齿,有的相差2齿,有的甚至相差还多。
比如上世纪90年代以来由徐灏任主编的《机械设计手册》上就是这种情况。
本文的公式(1)和表1就是从该手册上节录下来的。
有的教材也是这样。
让人不解的是各家手册也大都选这样的公式和图表。
然而当有人对教材、手册上的说法、作法等提出异议时,有些学者、专家、权威、教授不是“闻过则喜”,看看人家的说法有无道理;而是“闻过则怒”“闻过则恼”。
千方百计,想方设法否定人家的论点。
实在无法否定时甚至用给作者出难题的办法应付,这就不是实事求是的治学态度和学术态度了。
欲知详情,请看附在该文后面的“附录(9)”《何必在毫无意义的问题上下大功夫呢?——就〈变位齿轮跨齿数计算公式的合理选择〉一文作者对“审稿意见”的评述》一文。
读者肯定要问了:“本文既然将‘公法线长度表’(见表1)改称‘基圆弧长表’(见表2)了,那么公法线长度的计算还怎样表述呢?”笔者考虑到了,这是牵一发而动全身的问题,不能只改此,不改彼。
欲知公法线长度计算如何表述等等问题,请看《变位齿轮公法线长度计算的研究与探索》和《谈谈对〈机械设计手册〉上“公法线长度表”的看法》两篇文章。
何必在毫无意义的问题上下大功夫呢? ——就《变位齿轮跨齿数计算公式的合理选择》一文 作者对“审稿意见”的评述周万峰《变位齿轮跨齿数计算公式的合理选择》这篇文章于上世纪90年代投给江南一家杂志。
之所以写这篇文章是基于以下几个原因:①上世纪90年代以来出版的手册上大都选了ααxctg z k 25.01800++=(直齿)和πααn n ctg x z k 25.01800++'=(斜齿)及)1(1==n m m 或“的公法线长度)(**kn k W W 表”作为变位齿轮的跨齿数计算公式和跨齿数的选择用表。
然而这个公式并不是个情况良好的公式,“公法线长度)(**kn k W W 表”也不是个合理的选择用表。
② 在同一本教材或同一部手册上,跨齿数不论用它们给出的公式计算还是查它们给出的图表,它们的跨齿数都应该是相同的。