层次分析法
- 格式:doc
- 大小:183.00 KB
- 文档页数:8
(一)层次分析法1、层次分析法的概念“层次分析法的基本原理是将复杂系统中的各种因素,依据相互关联及隶属关系划分为一个递阶层次结构;依赖专家经验及直觉评判同一层次内因素的相对重要性,并用一致性准则检验评判的准确性;然后在递阶层次结构内进行合成;以得到决策因素相对于目标的重要性的总排序。
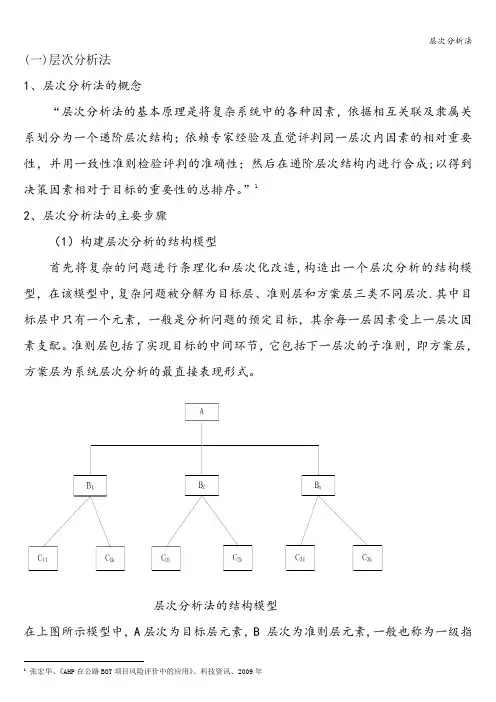
”12、层次分析法的主要步骤(1)构建层次分析的结构模型首先将复杂的问题进行条理化和层次化改造,构造出一个层次分析的结构模型,在该模型中,复杂问题被分解为目标层、准则层和方案层三类不同层次.其中目标层中只有一个元素,一般是分析问题的预定目标,其余每一层因素受上一层次因素支配。
准则层包括了实现目标的中间环节,它包括下一层次的子准则,即方案层,方案层为系统层次分析的最直接表现形式。
层次分析法的结构模型在上图所示模型中,A层次为目标层元素,B 层次为准则层元素,一般也称为一级指1张宏华、《AHP在公路BOT项目风险评价中的应用》、科技资讯、2009年标,C层次为方案层元素,也可称为二级指标。
(2)专家评分建立层次分析法判断矩阵为了建立指标权重评判标准和构造判断矩阵,Saaty提出相对重要性比例标度,即1~9 层次比例标度,相对重要性比例标度的含义如表2—3所示。
假设有n个元素C1、C2,。
,C n给定一个准则,利用上表所给的相对重要性比例标度方,对元素C i和C j做两两比较判断,获得相对重要度的值a ij,构成矩阵。
专家根据评判准则对各个因素的权重两两比较并进行了打分之后,经过整理,可以得到因素权重的判断矩阵A:矩阵 A 中的各元素a ij 表示行指标A i 对列指标A j 相对重要性的比例标度,则判断矩阵A 中指标两两比较的特点有a ij >0,a ij =1,a ij =1/a ji (i ,j=1,2,。
..。
..n )。
如果a ij <1,表示A j 比A i 重要; 如果a ij >1,表示A i 比A j 重要; 如果a ij =1,表示A j 与A i 同样重要.根据判断矩阵A 在选择上的一致性要求,理想情况下,a ik*a jk =a ij (代表相对重要性所具有的传递性原理,满足该性质的矩阵A 称为一致矩阵),虽然在构造判断矩阵A 时并不要求判断具有一致性,但判断偏离一致性过大也是不允许的。

一、层次分析模型和一般步骤1、定义:层次分析法是一种定性与定量分析相结合的多因素决策分析方法。
这种方法将决策者的经验判断给于数量化,在目标因素结构复杂且缺乏必要数据的情况下使用更为方便,因而在实践中得到广泛应用。
2、层次分析的四个基本步骤:(1)在确定决策的目标后,对影响目标决策的因素进行分类,建立一个多层次结构;(2)比较同一层次中各因素关于上一层次的同一个因素的相对重要性,构造成对比较矩阵;(3)通过计算,检验成对比较矩阵的一致性,必要时对成对比较矩阵进行修改,以达到可以接受的一致性;(4)在符合一致性检验的前提下,计算与成对比较矩阵最大特征值相对应的特征向量,确定每个因素对上一层次该因素的权重;计算各因素对于系统目标的总排序权重并决策。
二、建立层次结构模型将问题包含的因素分层:最高层——解决问题的目的;中间层——实现总目标而采取的各种措施、必须考虑的准则等。
也可称策略层、约束层、准则层等;最低层——用于解决问题的各种措施、方案等。
把各种所要考虑的因素放在适当的层次内。
用层次结构图清晰地表达这些因素的关系。
例1购物模型某一个顾客选购电视机时,对市场正在出售的四种电视机考虑了八项准则作为评估依据,建立层次分析模型如下:〔例2〕选拔干部模型练习:画出下列问题的层次模型评选优秀学校某地区有三个学校,现在要全面考察评出一个优秀学校。
主要考虑以下几个因素: (1)教师队伍(包括平均学历和年龄结构)(2)教学设施(3)教学工作(包括课堂教学,课外活动,统考成绩和教学管理) (4)文体活动三、构造成对比较矩阵比较第 i 个元素与第 j 个元素相对上一层某个因素的重要性时,使用数量化的相对权重aij来描述。
设共有 n 个元素参与比较,则称n n ij a A ⨯=)( 为成对比较矩阵。
成对比较矩阵中aij的取值可参考 Satty 的提议,aij按下述标度进行赋值。
在 1— 9及其倒数中间取值。
对例 2, 选拔干部考虑5个条件:品德x1,才能x2,资历 x3 ,年龄x4,群众关系x5。

层次分析法步骤及案例分析层次分析法(AHP)是一种通过对比判断不同因素的重要性来进行决策的方法。
它由匹兹堡大学的数学家托马斯·萨蒙在20世纪70年代初提出,并逐渐应用于各个领域。
本文将介绍层次分析法的步骤,并通过一个实际案例来进行分析。
一、层次分析法的步骤层次分析法主要包括以下几个步骤:1. 确定层次结构:首先,需要明确决策问题的层次结构。
将问题划分为若干个层次,从总目标到具体的子目标,形成一棵树状结构。
例如,在一个购车的决策问题中,总目标可以是“选择一辆适合自己的车”,下面的子目标可以包括“价格”、“外观”、“安全性”等因素。
2. 构造判断矩阵:在每个层次中,需要对不同因素之间的两两比较进行判断。
判断可以基于专家经验、问卷调查或实际数据。
对于两两比较,通常采用一个1到9的比较尺度,其中1表示相等,3表示略微重要,5表示中等重要,7表示强烈重要,9表示绝对重要。
如果因素A相对于因素B的重要性大于1,则B相对于A的重要性是1/A。
3. 计算权重向量:根据判断矩阵中的比较结果,可以计算出每个层次中各个因素的权重向量。
通过对判断矩阵的特征值和特征向量进行计算,可以得到各个因素的权重。
4. 一致性检验:在进行层次分析时,需要检验判断矩阵的一致性。
一致性是指在两两比较中的逻辑关系的一致性。
通常使用一致性指数和一致性比率来判断判断矩阵的一致性程度。
5. 综合评价:通过将各层次中因素的权重向量进行乘积运算,并将结果汇总得到最后的评价结果。
在这一步骤中,可以对不同的决策方案进行排序或进行多目标决策。
二、案例分析为了更好地了解层次分析法的应用,我们来看一个实际案例。
假设某公司需要选择新的供应商,供应商选择的主要考虑因素包括产品质量、交货周期和价格。
我们可以按照以下步骤进行决策:1. 确定层次结构:总目标是选择合适的供应商,下面的子目标是产品质量、交货周期和价格。
2. 构造判断矩阵:对于每个子目标,可以进行两两比较。

层次分析法的概念层次分析法(Analytic Hierarchy Process,简称AHP)是一种多准则决策分析(Multi-Criteria Decision Analysis,简称MCDA)的方法,由美国运筹学家Thomas L. Saaty于20世纪70年代初提出。
AHP方法通过对多个准则进行层级划分和比较,并运用数学计算方法来确定各准则的重要性和不同方案的优先级,从而帮助决策者做出合理的决策。
AHP的基本思想是将复杂的决策问题分解为多个层次,从上到下逐级进行划分,形成一个层次结构模型。
在层次结构模型中,最顶层为目标层,下面的层次依次为准则层和方案层。
目标层描述了整体决策的目标,准则层描述了实现目标所需要的具体准则,方案层描述了可选方案。
每个层次都有若干个元素,分别构成了一个层次结构的树状图。
AHP方法的核心是构建准则间的判断矩阵,并计算出准则的权重。
判断矩阵用来比较和度量层次结构中的元素之间的重要性和优先级,它的维数等于层次中元素的个数,矩阵元素表示了两个元素之间的相对重要性。
决策者通过对每对元素进行两两比较,根据自己的主观判断,利用语义比例尺(由1到9的9个数值构成)对元素的相对重要性进行评价。
评价结果填入判断矩阵中,形成一个与层次结构对应的判断矩阵。
然后,通过计算判断矩阵的特征向量和最大特征值,可以得到准则的权重。
AHP方法还可以计算各个方案的优先级。
在方案层构建判断矩阵的过程中,同样可以通过两两比较不同方案,评价它们的优先级。
根据方案的判断矩阵,结合准则的权重,运用数学计算方法,可以得到每个方案的优先级权重。
这样,决策者可以根据方案的优先级权重,评估和比较各个方案的可行性和优劣程度,作出决策。
AHP方法的主要优势在于能够将复杂的决策问题进行层次化的细分,从而使决策问题更加清晰和可操作。
它考虑了决策者的主观权重评估和相对重要性比较,充分考虑了不同准则和方案之间的相互关系。
此外,AHP方法还能够处理不确定性和模糊性的问题,对决策者的专业知识和经验有较高的要求,同时也可以用来解决多个决策者之间的决策问题。

层次分析法(重定向自AHP法)层次分析法(The analytic hierarchy process,简称AHP),也称层级分析法目录[隐藏]∙ 1 什么是层次分析法∙ 2 层次分析法的基本步骤∙ 3 层次分析法的优点∙ 4 建立层次结构模型∙ 5 构造成对比较矩阵∙ 6 作一致性检验∙7 层次总排序及决策∙8 层次分析法的用途举例∙9 层次分析法应用的程序∙10 应用层次分析法的注意事项∙11 层次分析法应用实例∙12 外部链接∙13 相关条目[编辑]什么是层次分析法层次分析法(The analytic hierarchy process)简称AHP,在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出。
它是一种定性和定量相结合的、系统化、层次化的分析方法。
由于它在处理复杂的决策问题上的实用性和有效性,很快在世界范围得到重视。
它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。
层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。
不妨用假期旅游为例:假如有3个旅游胜地A、B、C供你选择,你会根据诸如景色、费用和居住、饮食、旅途条件等一些准则去反复比较这3个候选地点.首先,你会确定这些准则在你的心目中各占多大比重,如果你经济宽绰、醉心旅游,自然分别看重景色条件,而平素俭朴或手头拮据的人则会优先考虑费用,中老年旅游者还会对居住、饮食等条件寄以较大关注。
其次,你会就每一个准则将3个地点进行对比,譬如A景色最好,B次之;B费用最低,C次之;C居住等条件较好等等。
最后,你要将这两个层次的比较判断进行综合,在A、B、C中确定哪个作为最佳地点。
[编辑]层次分析法的基本步骤1、建立层次结构模型。
在深入分析实际问题的基础上,将有关的各个因素按照不同属性自上而下地分解成若干层次,同一层的诸因素从属于上一层的因素或对上层因素有影响,同时又支配下一层的因素或受到下层因素的作用。




1. 层次分析法(The analytic hierarchy process, 简称AHP)用于解决评价类问题,例如:选择那种方案最好、哪位运动员或者员工表现的更优秀。
评价类问题可以用打分解决。
层次分析法 (The Analytic Hierarchy Process即 AHP)是由美国运筹学家、匹兹堡大学教授T. L. Saaty于20世纪70年代创立的一种系统分析与决策的综合评价方法, 是在充分研究了人类思维过程的基础上提出来的, 它较合理地解决了定性问题定量化的处理过程。
AHP的主要特点是通过建立递阶层次结构, 把人类的判断转化到若干因素两两之间重要度的比较上, 从而把难于量化的定性判断转化为可操作的重要度的比较上面。
在许多情况下, 决策者可以直接使用AHP进行决策, 极大地提高了决策的有效性、可靠性和可行性, 但其本质是一种思维方式, 它把复杂问题分解成多个组成因素, 又将这些因素按支配关系分别形成递阶层次结构, 通过两两比较的方法确定决策方案相对重要度的总排序。
整个过程体现了人类决策思维的基本特征,即分解、判断、综合,克服了其他方法回避决策者主观判断的缺点。
1.1模型介绍1.1.1引例高考结束了,小明该选择华科还是五武大?小明最关心四个方面:学习氛围0.4、就业前景0.3、男女比例0.2、校园景色0.19(权重和为1)(1)学习氛围:经查阅资料查到“学在华工,玩在武大,爱在华师”一句话,因此在学习氛围方面给华科0.7,给武汉大学0.3.(2)就业前景:搜索两所学校就业率差不多,因此在就业前景方面对两所学校均赋予0.5的权重。
(3)男女比例:经查询,华科男女比例2:1,武大1.35:1,因此武大0.7分,华科0.3分(4)校园景色:华科0.25分,武大0.75分整理权重表格:指标权重华科武大学习氛围0.40.70.3就业前景0.30.50.5男女比例0.20.30.7校园景色0.10.250.75华科最终的得分:0.7*0.4+0.5*0.3+0.3*0.2+0.25+*0.1=0.515分武大最终得分:0.3*0.4+0.5*0.3+0.7*0.2+0.75*0.1=0.485分1.1.2 模型1、关键词:打分法、确定评价指标、形成评价体系2、解决评价类问题,首先确定以下三个问题:(1)评价的目标是什么(2)为了达到这个目标有哪几种可选的方案(3)评价的准则或者说指标是什么(我们根据什么东西来评价好坏)。

层次分析法1. 简介层次分析法(Analytic Hierarchy Process,AHP)是一种常用的定性与定量相结合的多标准决策分析方法。
它由美国学者托马斯·L·萨亨于1970年提出,被广泛应用于各种决策问题中。
2. 原理层次分析法的基本思想是将复杂的决策问题分解为一系列具有层次结构的子问题,然后通过对这些子问题的比较与权重评估,最终得出整体问题的决策结果。
2.1 层次结构在层次分析法中,决策问题被组织成一个层次结构。
层次结构通常包括三个层次:目标层、准则层和方案层。
•目标层:表示决策问题的最终目标,通常只有一个。
•准则层:用于评价方案的一组准则,通常包括两个或更多的准则。
•方案层:表示可选择的方案,每个方案都和准则层有关联。
每个层次下面还可以有更多的子层次,形成一个完整的层次结构。
2.2 权重评估层次分析法通过对准则层的权重评估,来确定各个准则的重要性。
权重评估通常采用两两比较的方式,即对准则层中的两个准则进行比较,判断它们的相对重要性。
对两个准则的比较通常使用1至9的九分比较法,其中1表示相同重要性,3表示轻微重要性差异,5表示中等重要性差异,7表示强烈重要性差异,9表示极端重要性差异。
通过两两比较得到的比较矩阵可以利用特征向量法计算权重向量,从而确定准则层的权重。
2.3 方案评估在确定了准则层的权重后,可以利用这些权重对方案进行评估和排序。
通常使用两两比较法将方案与准则进行比较,得到方案层的比较矩阵。
然后,利用准则层的权重和方案层的比较矩阵计算加权矩阵,最终得到方案层的权重。
3. 应用场景层次分析法在各个领域中都有广泛的应用,尤其适用于以下情况:•多准则决策问题:当决策问题涉及到多个准则时,层次分析法可以帮助决策者合理权衡各个准则的重要性,从而做出最佳决策。
•项目评估与选择:当需要评估和选择多个候选项目时,层次分析法可以通过对项目的多个准则进行比较和权重评估,为项目选择提供科学依据。

层次分析法层次分析法是一种应用广泛的决策分析方法,它通过构建层次结构和比较矩阵,来对不同因素进行排序和权重分配,帮助决策者做出合理的决策。
本文将介绍层次分析法的基本原理、应用领域以及一些实际案例。
一、层次分析法的基本原理层次分析法由美国运筹学家托马斯·L·塞蒂提出,它是一种定性和定量相结合的分析方法,能够综合考虑多个因素的重要性和相互关系。
它的基本原理如下:1. 层次结构:将决策问题分解成多个层次,从上至下逐级细化。
顶层是目标层,中间层是准则层,最底层是方案层。
2. 比较矩阵:在每个层次内,通过构建比较矩阵来判断各因素之间的重要性。
比较矩阵是一个n×n的正互反矩阵,其中n是该层次因素的个数。
通过对各因素进行两两比较,得出相对重要性的判断。
3. 加权优先向量:通过对比较矩阵进行特征向量的计算,可以得到各个因素的权重。
特征向量是对比较矩阵的主特征值对应的特征向量,也称为特征向量法。
4. 一致性检验:通过一致性指标和一致性比率的计算,判断构建的比较矩阵是否合理。
一致性指标表示了矩阵的内部一致性程度,一致性比率则是对一致性指标进行归一化,判断是否满足一致性。
5. 综合评价:通过计算得出的权重,进行乘积运算和累加运算,得到方案的综合评价值。
综合评价值越高,方案越优。
二、层次分析法的应用领域层次分析法在许多领域都有广泛的应用,包括经济学、管理学、环境科学、社会科学等。
下面是一些常见的应用领域:1. 投资决策:在投资决策中,可以将不同的投资方案作为方案层,通过比较各个方案的风险性、收益性等因素,来确定投资方向。
2. 供应链管理:在供应链管理中,可以将供应商的价格、质量、交货周期等因素作为准则层,通过比较不同供应商的重要性,来选择合适的供应商。
3. 项目评估:在项目评估中,可以将项目的成本、时限、风险等因素作为准则层,通过比较各个因素的重要性,来评估项目的可行性和优先级。
4. 人才选拔:在人才选拔中,可以将候选人的学历、工作经验、专业技能等因素作为准则层,通过比较各个因素的重要性,来确定最佳人选。
层次分析法(Analytic Hierarchy Process,简称AHP)是将与决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。
该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初,在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法。
1简介2定义3优缺点▪优点▪缺点4基本步骤5注意事项6应用实例简介编辑层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。
尤其适合于对决策结果难于直接准确计量的场合。
在现实世界中,往往会遇到决策的问题,比如如何选择旅游景点的问题,选择升购物层次分析模型学志愿的问题等等。
在决策者作出最后的决定以前,他必须考虑很多方面的因素或者判断准则,最终通过这些准则作出选择。
比如选择一个旅游景点时,你可以从宁波、普陀山、浙西大峡谷、雁荡山和楠溪江中选择一个作为自己的旅游目的地,在进行选择时,你所考虑的因素有旅游的费用、旅游的景色、景点的居住条件和饮食状况以及交通状况等等。
这些因素是相互制约、相互影响的。
我们将这样的复杂系统称为一个决策系统。
这些决策系统中很多因素之间的比较往往无法用定量的方式描述,此时需要将半定性、半定量的问题转化为定量计算问题。
层次分析法是解决这类问题的行之有效的方法。
层次分析法将复杂的决策系统层次化,通过逐层比较各种关联因素的重要性来为分析以及最终的决策提供定量的依据。
定义编辑所谓层次分析法,是指将一个复杂的多目标决策问题作为一个系统,将目标分解为多个目标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法。
层次分析法简介层次分析法(Analytic Hierarchy Process,AHP)这是一种定性和定量相结合的、系统的、层次化的分析方法。
这种方法的特点就是在对复杂决策问题的本质、影响因素及其内在关系等进行深入研究的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。
是对难以完全定量的复杂系统做出决策的模型和方法。
层次分析法的原理:层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同的层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
层次分析法的步骤,运用层次分析法构造系统模型时,大体可以分为以下四个步骤:(1)建立层次结构模型:将决策的目标、考虑的因素(决策准则)和决策对象按他们之间的相互关系分成最高层、中间层和最低层,绘制层次结构图。
最高层(目标层):决策的目的、要解决的问题;中间层(准则层或指标层):考虑的因素、决策的准则;最低层(方案层):决策时的备选方案;(2)构造判断(成对比较)矩阵;表指标之间比较量化值规定因素i比因素j量化值同等重要 1.00稍微重要 3.00较强重要 5.00强烈重要7.00极端重要9.00稍微不重要0.33较强不重要0.20强烈不重要0.14极端不重要0.11两相邻判断的中间值2、4、6、8(3)层次单排序及其一致性检验;(4)层次总排序及其一致性检验;举例:某市中心有一座商场,由于街道狭窄,人员车流量过大,经常造成交通堵塞。
市政府决定解决这个问题,经过有关专家会商研究,制订三个可行方案:a1:在商场附近修建一座环形天桥;a2:在商场附近修建地下人行通道;a3:搬迁商场决策的总目标是改善市中心交通环境,根据当地具体条件和情况,专家组织拟定五个目标作为对可行方案的评价准则:C1:通车能力;C2:方便群众;C3:基建费用不宜过高;C4:交通安全;C5:市容美观。
层次分析法分析方法简介层次分析法(Analytic Hierarchy Process,简称AHP)是一种常用的多标准决策分析方法,由美国运筹学家托马斯·L·赛蒂尔于20世纪70年代提出。
它通过将复杂的决策问题分解为层次结构,对各层次标准进行定量评估和权重分配,最终得到综合的决策结果。
层次分析法是一种基于专家经验和主观判断的定性与定量相结合的决策方法,适用于复杂的多因素多目标决策问题。
它以一种系统化和结构化的方式帮助决策者进行决策分析,提高决策的科学性和准确性。
方法步骤层次分析法主要包括以下几个步骤:1.建立层次结构:首先,需要将决策问题进行逐层分解,形成一个层次结构模型。
层次结构由目标层、准则层和方案层构成,决策问题从目标层开始,经过准则层逐步分解,最终得到方案层。
目标层表示整个决策问题的目标或要达到的结果,准则层表示实现目标所涉及的关键因素,方案层表示可行的解决方案。
2.构造判断矩阵:在层次结构的每一层中,需要对各个元素之间进行两两比较,得到一个判断矩阵。
判断矩阵的每个元素表示两个层次因素之间的相对重要性。
比较的方式可以是定性的,也可以是定量的。
常用的比较方法有9点量表法和1-9标度法。
3.确定权重向量:通过计算判断矩阵的特征向量,可以得到每个层次因素的权重。
特征向量即为判断矩阵的最大特征值对应的特征向量。
通常需要进行一致性检验,判断矩阵的一致性可以通过一致性指标和一致性比率来衡量。
4.计算综合评估值:根据各个层次因素的权重和方案的评价指标,可以计算得到每个方案的综合评估值。
综合评估值可以表示方案的优劣程度。
5.灵敏度分析:层次分析法可以进行灵敏度分析,通过改变判断矩阵中的比较数据,可以检测到不同因素权重发生变化时对决策结果的影响。
优点和应用范围层次分析法具有以下优点:•结构化:通过将决策问题分解成层次结构,使得问题更加清晰和易于理解。
•定量化:通过构造判断矩阵和计算权重向量,将主观因素定量化,提高了决策的科学性。
层次分析法(AHP)AHP(Analytic Hierarchy Process)方法,是由20世纪70年代由美国著名运筹学学家T.L.Satty提出的。
它是指将决策问题的有关元素分解成目标、准则、方案等层次,在此基础上进行定性分析和定量分析的一种决策方法。
这一方法的特点,是在对复杂决策问题的本质、影响因素及其内在关系等进行深入分析之后,构建一个层次结构模型,然后利用较少的定量信息,把决策的思维过程数学化,从而为求解多准则或无结构特性的复杂决策问题提供了一种简便的决策方法。
AHP十分适用于具有定性的,或定性定量兼有的决策分析。
这是一种十分有效的系统分析和科学决策方法,现在已广泛地应用在企业信用评级、经济管理规划、能源开发利用与资源分析、城市产业规划、企业管理、人才预测、科研管理、交通运输、水资源分析利用等方面。
一、递阶层次结构的建立一般来说,可以将层次分为三种类型:(1)最高层:只包含一个元素,表示决策分析的总目标,因此也称为总目标层。
(2)中间层:包含若干层元素,表示实现总目标所涉及的各子目标,包含各种准则、约束、策略等,因此也称为目标层。
(3)最低层:表示实现各决策目标的可行方案、措施等,也称为方案层。
典型的递阶层次结构如下:一个好的递阶层次结构对解决问题极为重要,因此在建立递阶层次结构时,应注意到:(1)从上到下顺序地存在支配关系,用直线段(作用线)表示上一层次因素与下一层次因素之间的关系,同一层次及不相邻元素之间不存在支配关系。
(2)整个结构不受层次限制。
(3)最高层只有一个因素,每个因素所支配元素一般不超过9个,元素过多可进一步分层。
(4)对某些具有子层次结构可引入虚元素,使之成为典型递阶层次结构。
二、构造比较判断矩阵设有m个目标(方案或元素),根据某一准则,将这m个目标两两进行比较,把第i个目标(i=1,2,…,m)对第j个目标的相对重要性记为a ij,(j=1,2,…,m),这样构造的m阶矩阵用于求解各个目标关于某准则的优先权重,成为权重解析判断矩阵,简称判断矩阵,记作A=(a ij )m ×m 。
Satty 于1980年根据一般人的认知习惯和判断能力给出了属性间相对重要性等级表(见表4-4)。
利用该表取a ij 的值,称为1-9标度方法。
表4-4 目标重要性判断矩阵A 中元素的取值若决策者能够准确估计a ij (i,j,k=1,2,…,m ),则有: a ij =1/a ji a ij= a ik ·a kj a ii =1定义4-1 设A=(a ij )m ×m ,A>0,(即a ij >0;i,j=1,2,…,m ),如果满足条件(1)a ii =1(i =1,2,…,m );(2)a ij =1/a ji (i,j=1,2,…,m ),则称矩阵A 为互反正矩阵。
定义4-2 设A=(a ij )m ×m ,A>0,如果满足条件a ij= a ik ·a kj (i,j,k=1,2,…,m )则称矩阵A 为一致性矩阵。
定理4-1 对于任何一个m 阶互反正矩阵A ,均有m ax λ≥m ,其中m ax λ是矩阵A 的最大特征值。
定理4-2 m 阶互反正矩阵A 为一致性矩阵的充分必要条件是A 的最大特征根为m 。
三、单准则下的排序层次分析法的信息基础是比较判断矩阵。
由于每个准则都支配下一层若干因素,这样对于每一个准则及它所支配的因素都可以得到一个比较判断矩阵。
因此根据比较判断矩阵如何求得各因素w 1,w 2, …,w m 对于准则A 的相对排序权重的过程称为单准则下的排序。
这里设A=(a ij )m ×m ,A>0。
(一)本征向量法 利用AW=λW 求出所有λ的值,其中m ax λ为λ的最大值,求出m ax λ对应的特征向量W *,然后把特征向量W *规一化为向量W ,则W=[w 1,w 2, …w m ]T为各个目标的权重。
求λ需要解m 次方程,当m ≥3时,计算比较麻烦,可以利用matlab 来求解。
(二)判断矩阵的近似解法判断矩阵是决策者主观判断的定量描述,求解判断矩阵不要求过高的精度。
这里,介绍三种近似计算方法:根法、和法及幂法。
幂法适于在计算机上运算。
1、根法(1)A 中每行元素连乘并开m 次方,得到向量Tmw w w W),...,,(**2*1*=其中,m mj ijia w ∏==1*(2)对W *作归一化处理,得到权重向量W=(w 1,w 2, …w m )T,其中∑==mi i iiw w w 1**/(3)对A 中每列元素求和,得到向量S=(s 1,s 2, …s m ),其中s j =∑=mi ij a1(4)计算m ax λ的值,SW w s i mi i ==∑=1max λ=∑=m i i iw AW m 1)(12、和法(1)将A 的元素按列作归一化处理,得矩阵Q=(q ij )m ×m 。
其中,∑==mk kj ij ija a q 1/(2)将Q 的元素按行相加,得向量Tm ),...,,(21αααα=。
其中,∑==mj ij i q 1α(3)对向量α作归一化处理,得权重向量W=(w 1,w 2, …w m )T,其中∑==mk ki iw 1/αα(4)求出最大特征值∑==m i ii w AW m 1max )(1λ3、幂法幂法是一种逐步迭代的方法,经过若干次迭代计算,按照规定的精度,求出判断矩阵A 的最大特征值及其对应的特征向量。
定理 3 设矩阵A=(a ij )m ×m,A>0,则CWeA e eA k T k k =∞→lim ,其中,W 是A 的最大特征值对应的的特征向量,C 为常数,向量e=(1,1,…,1)T。
幂法的计算步骤是:①任取初始正向量X (0)=(x 1(0), x 2(0), …, x m (0))T,计算0)0()0()0()0(0/},{max m X Y x X m i i===∞②迭代计算,对于k=0,1,2, …计算1)1()1()1()1(1)()1(/},{,max ++++∞+++====k k k k i ik k k k m X Y x X m AY X③精度检查。
当ε<-+k k m m 1时,转入步骤④;否则,令k=k+1,转入步骤②。
④求最大特征值和对应的特征向量,将Y (k+1)归一化,即1max 1)1()1(,/+=++==∑k mi k i k m y YW λ例 判断矩阵 1 2 5 A = 1/2 1 7 1/5 1/7 1用幂法计算A 的最大特征值m ax λ及其对应额特征向量。
精度ε=0.0001。
解:取初始向量X (0)=(1,1,1)T,迭代过程见下表由上表看出,当k=7时,|m 8-m 7|=|3.1189-3.1189|=0<0.0001,迭代终止,得到m ax λ=3.1189,W=(0.5415,0.3816,0.0769)T四、单准则下的一致性检验由于客观事物的复杂性,会使我们的判断带有主观性和片面性,完全要求每次比较判断的思维标准一致是不太可能的。
因此在我们构造比较判断矩阵时,我们并不要求n(n-1)/2次比较全部一致。
但这可能出现甲与乙相比明显重要,乙与丙相比极端重要,丙与甲相比明显重要,这种比较判断会出现严重不一致的情况。
我们虽然不要求判断具有一致性,但一个混乱的,经不起推敲的比较判断矩阵有可能导致决策的失误,所以我们希望在判断时应大体一致。
而上述计算权重的方法,当判断矩阵过于偏离一致性时,其可靠程度也就值得怀疑了。
因此,对于每一层次作单准则排序时,均需要作一致性的检验。
一致性指标(Consistency Index,CI ):1max --=m mCIλ随机指标(Random Index,RI )一致性比率(Consistency Rate,CR ):CR=CI/RI 当CR 取0.1时,最大特征值'm ax λ=CI ·(m-1)+m=0.1·RI ·(m-1)+m 表4-5 随机指标RI ,'m ax λ取值表表中当n=1,2时,RI=0,这是因为1,2阶判断矩阵总是一致的。
当n ≥3时,若CR<0.1即m ax λ<'m ax λ,认为比较判断矩阵的一致性可以接受,否则应对判断矩阵作适当的修正,直到m ax λ小于'm ax λ通过一致性检验时,求得的W 才有效。
五、层次总排序计算同一层次中所有元素对最高层(总目标)的相对重要性标度(又称权重向量)称为层次总排序。
1、层次总排序的步骤为:(1)计算同一层次所有因素对最高层相对重要性的权重向量,这一过程是自上而下逐层进行; (2)设已计算出第k-1层上有n k-1个元素相对总目标的权重向量为w(k-1)=(w 1(k-1), w 2(k-1),…, w n(k-1)(k-1))T(3)第k 层有个n k 个元素,他们对于上一层次(第k-1层)的某个元素j 的单准则权重向量为p j (k)=(w 1j (k), w 2j (k),…, w nkj)(k))T(对于与k-1层第j 个元素无支配关系的对应w ij 取值为0); (4)第k 层相对总目标的权重向量为w k= (p 1(k), p 2(k),…p k-1(k),)w(k-1)2、层次总排序的一致性检验人们在对各层元素作比较时,尽管每一层中所用的比较尺度基本一致,但各层之间仍可能有所差异,而这种差异将随着层次总排序的逐渐计算而累加起来,因此需要从模型的总体上来检验这种差异尺度的累积是否显著,检验的过程称为层次总排序的一致性检验。
第k 层的一致性检验指标CIk=(CI 1(k-1), CI 2(k-1),…, CIn K(k-1))w(k-1)RI k=(RI 1(k-1), RI 2(k-1),…, RIn K(k-1))w(k-1)CR k=CR k-1+CI k/RI k(3≤k ≤n)当CR k<0.1,可认为评价模型在第k 层水平上整个达到局部满意一致性。
六、递阶层次结构权重解析过程 1、树状结构目标体系目标可分为多个层次,每个下层目标都隶属于一个而且只隶属一个上层目标,下层目标是对上层目标的具体说明。
对于树状结构的目标体系,需由上而下逐步确定权重,即由树干向树梢,求树杈各枝相对于树杈的权重。
2、网状结构目标体系网状结构的目标也分为多个层次,每个下层目标隶属于某几个上层目标(至少有一个下层目标隶属于不止一个上层目标)。
七、AHP 方法的基本步骤层次分析法大体分为以下六个步骤:1、 明确问题;建立层次结构;2、两两比较,建立判断矩阵;2、层次单排序及其一致性检验;3、层次总排序及其一致性检验;4、根据分析计算结果,考虑相应的决策。